Кинематика тел в точечном представлении в гравитационном пространстве в произвольной системе отсчета Метод переменных систем отсчета

Вид материала

Документы

Содержание Пространство, в котором отсутствует феномен гравитации, назовем негравитационным или галилеевым. Весомы тела имеют характеритистику движения в этой системе отсчета подчиняющуюся модернизированному второму закону Ньютона Неинерциальные системы отсчета могут характеризоваться макроописанием (интегральными или глобальными характеристиками) и микрооп W0 и угловая скорость вращения системы отсчета (скорость вращения относительно неподвижных звезд) . Для негалилеевых (гравитирующих) пространств этот постулат в общем случае не имеет места. Но согласно уравнению (1) Универсальные уравнения движения тел в точечном представлении Примеры решения задач на движение тел в гравитационном поле Задача двух тел Задача трех тел Равновесные и гомографические решения многих тел Плоская ограниченная круговая задача трех тел (элементарная теория движения Луны)

Подобный материал:

• Курс I семестр № I № п/п Наименование раздела (модуля) Объем на тематический раздел,, 136.26kb.
• Физика механика кинематика, 60.32kb.
• Тема учебного занятия: «Относительность механического движения», 54.35kb.
• Кратко об ото, 119.01kb.
• ПрограммА для поступающих в Новочеркасское высшее военное командное училище связи (военный, 93.59kb.
• Тема. Часть, 283.33kb.
• 6М072300- «Техническая физика», 175.47kb.
• Примерные программы вступительных испытаний в высшие учебные заведения российской федерации, 47.51kb.
• Отсчета. Модели объектов и процессов, 26.46kb.
• Отсчета, 103.48kb.

Кинематика тел в точечном представлении в гравитационном пространстве в произвольной системе отсчета Метод переменных систем отсчета.


Кинематика многих тел в галилеевом пространствеЮровицкий В.М.,

Российский государственный социальный университет, Москва

E-mail: vlad@yur.ru

Заканчивается разработка теории движения многих тел в точечном представлении, начатая в работах [1] и [2]. Приведены решения принципиально новых задач практической важности.

Универсальные уравнения поля и движения

В качестве системы отсчета используем ньютоно-эвклидовскую систему отсчета на базе абсолютно твердого тела. В качестве характеристики состояния всех элементарных механических объектов используем характеристику весомости W, равную нулю в невесомом состоянии, характеризующем свободное, невзаимодействующее состояние объекта и отличную от нуля при наличии механических воздействий на него со стороны других тел.

Пространство, в котором отсутствует феномен гравитации, назовем негравитационным или галилеевым.

В галилеевом пространстве можно ввести неинерциальную ньютоно-эвклидову систему отсчета. В этой системе она сохраняет жетскость и неизменность без воздействий тел отсчета друг на друга. Другими словами, все элементы инерциальной системы отсчета находятся в невесомом состоянии. Соответственно все невесомые (свободные) тела в этой системе отсчета имеют в качестве кинематической характеристики равномерное и прямолинейное движение или неподвижность.

Весомы тела имеют характеритистику движения в этой системе отсчета подчиняющуюся модернизированному второму закону Ньютона

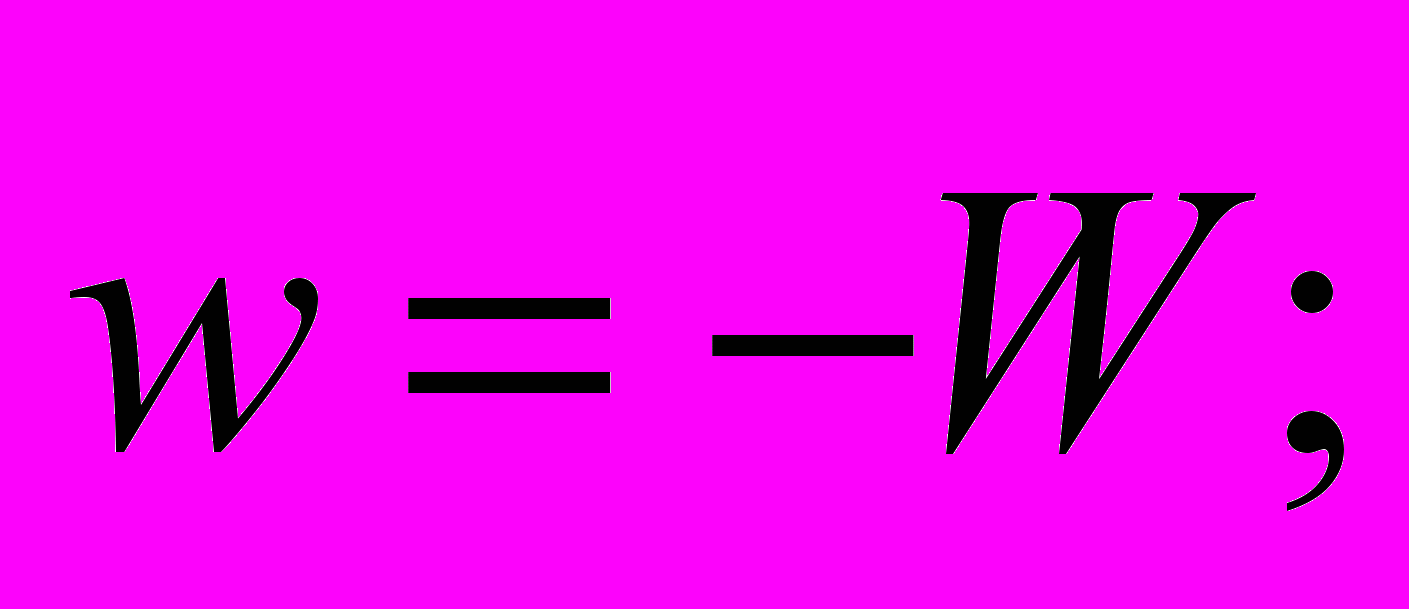(1)

где w ─ ускорение.

В галилеевом (негравитирующем) пространстве можно ввести и неинерциальную ньютоно-эвклидову систему отсчета (на базе твердого тела). Но теперь уже элементы системы отсчета уже будут в общем случае иметь весомое состояние. В том числе весомым может быть и начало системы отсчета W₀.

Неинерциальные системы отсчета могут характеризоваться макроописанием (интегральными или глобальными характеристиками) и микроописаниями.

В качестве макроописания используется две векторные характеристики ─ весомость начала системы отсчета W₀ и угловая скорость вращения системы отсчета (скорость вращения относительно неподвижных звезд) . Микроописание состоит из распределения весомости кординатизированных элементов системы отсчета, т.е. поля весомости H(r). Эти характеристики могут меняться во времени.

Постулат. Неинерциальные системы отсчета в галилеевом пространстве, имеющие одинаковые глобальные характеристики, эквивалентны. В частности, это означает, что любые свободные (невесомые) объекты, имеющие одинаковое начальные характеристики в эквивалентных иеинрциальных системах отсчета, имеют одинаковое кинематическое описание

Для негалилеевых (гравитирующих) пространств этот постулат в общем случае не имеет места.

Связь между глобальными характеристиками и микроописанием дается уравнением состояния системы отсчета ─ уравнениями поля весомости. Для вывода уравнения состояния поля весомости в галилеевом пространстве воспользуемся хорошо известным распределением абсолютных ускорений элементов твердого тела

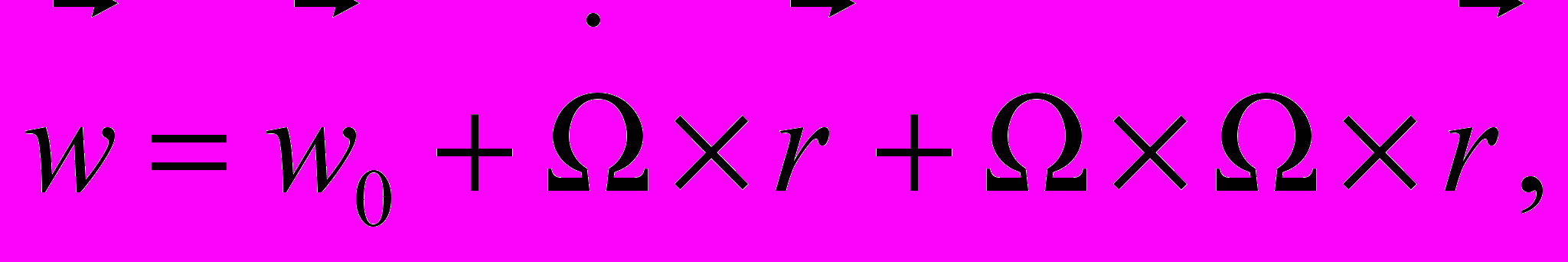(2)

где w ─ абсолютное ускорение (ускорение в инерциальной системе отсчета) элемента твердого тела с радиус-вектором r, w₀ ─ абсолютное ускорение элемента твердого тела в начале системы отсчета,  ─ угловая скорость вращения твердого тела.

Но согласно уравнению (1)

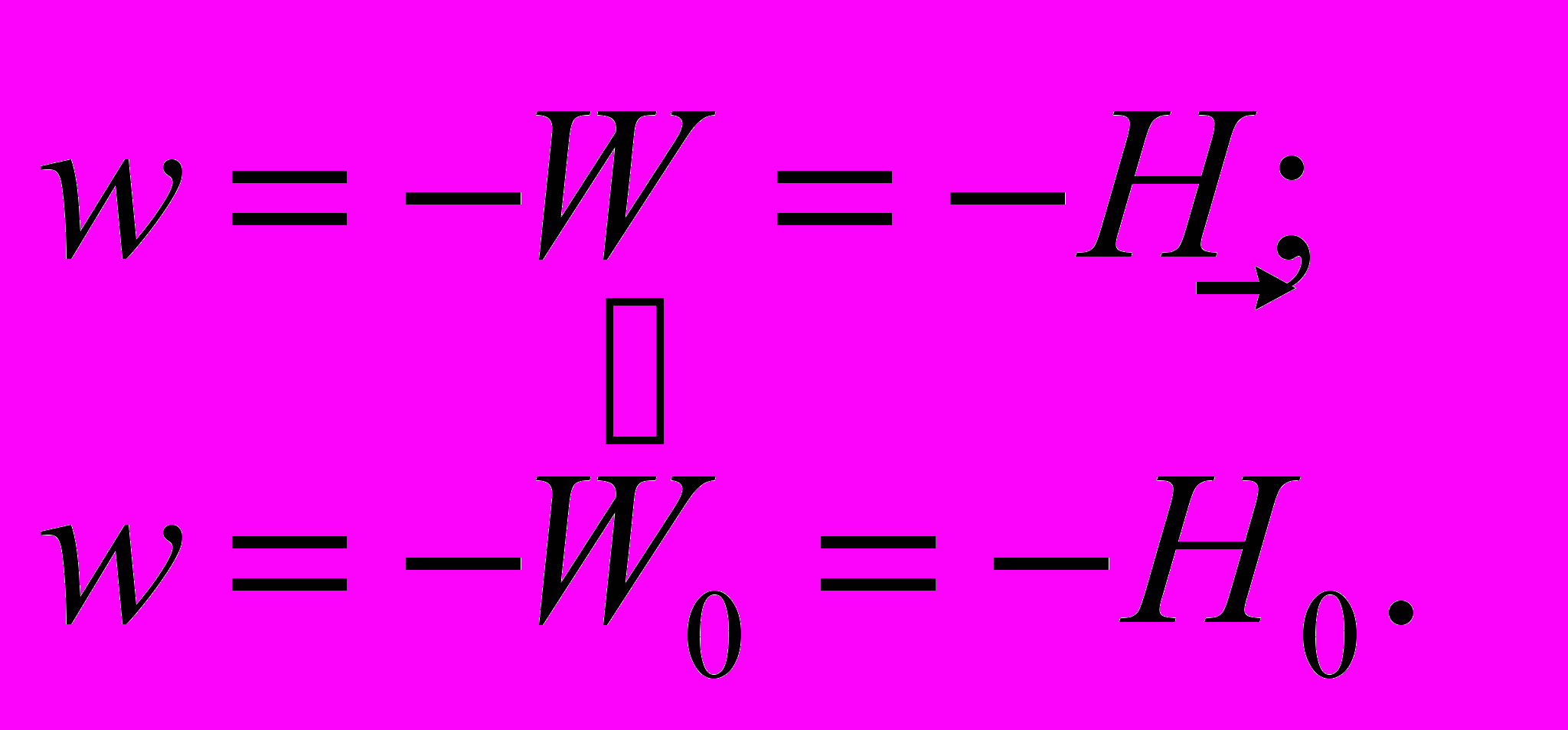(3)

Здесь W ─ весомость элемента системы отсчета, а H ─ напряженность весомостного поля системы отсчета; W₀ ─ весомость начального элемента системы отсчета, а H₀ ─ напряженность начала системы отсчета. Подставляя (3) в (2), получаем уравнение состояния весомостного поля:о

= ()


В работе [1] получены дифференциальные уравнения гравитационного поля в гармонической системе отсчета в концепции полевой гравитации.

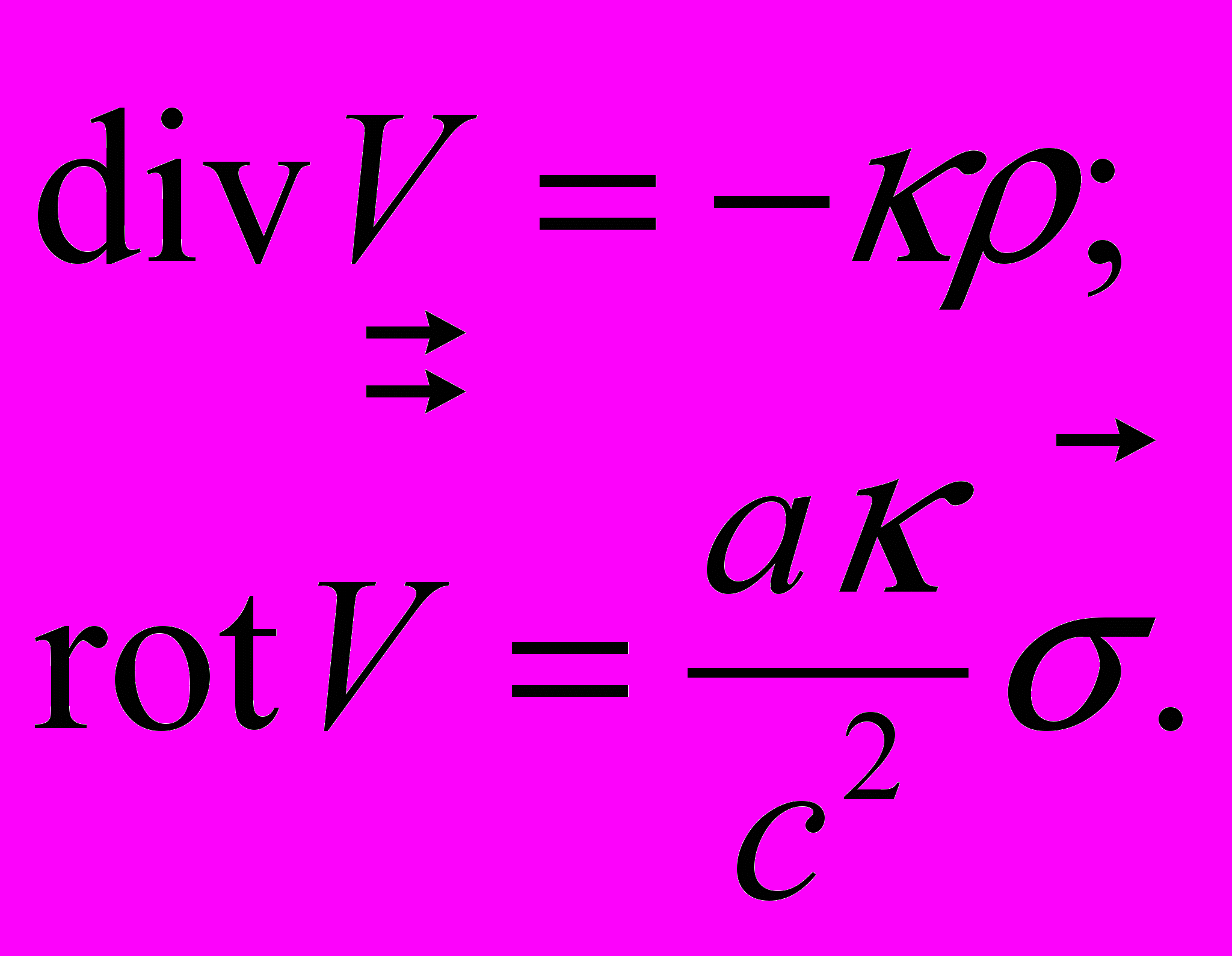(1)

В работе [2] получено уравнение состояния неинерциальной системы отсчета в галилеевом (негравитационном) пространстве:

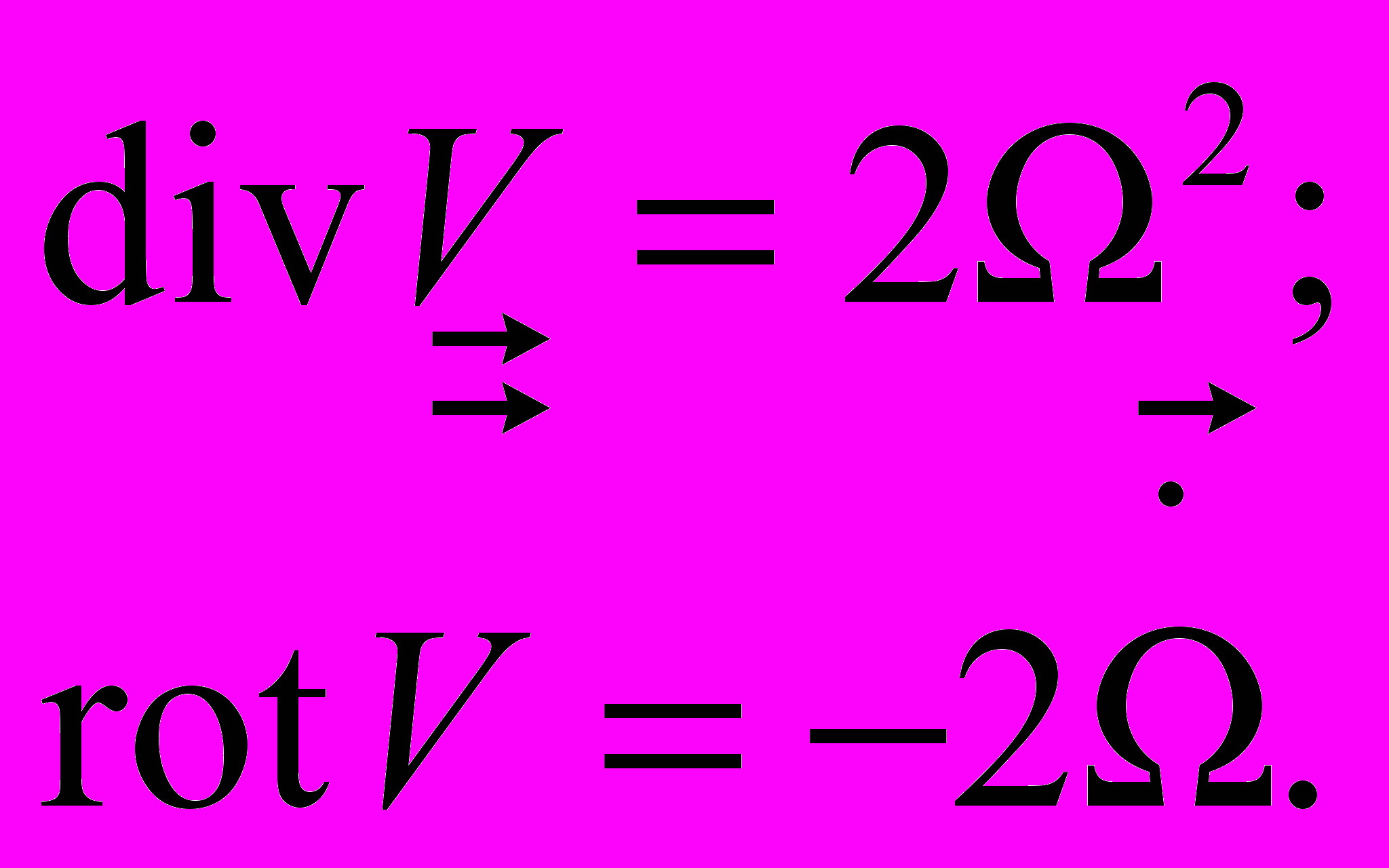(2)

Физический смысл полей V и H одинаков ─ это поля весомости. Поэтому представляется логичной гипотеза, что общее весомостное поле B в произвольной системе отсчета в гравитационном (негалилеевом) пространстве является аддитивным и представляет собой сумму поля весомости неинерциальной системы отсчета при выключенной гравитации H и гравитационного поля в гармонической системе отсчета V, в которой отсутствуют имманентные характеристики системы отсчета? В результате чего получаем уравнение состояния системы отсчета ─ поле весомости произвольного пространства в произвольной системе отсчета:

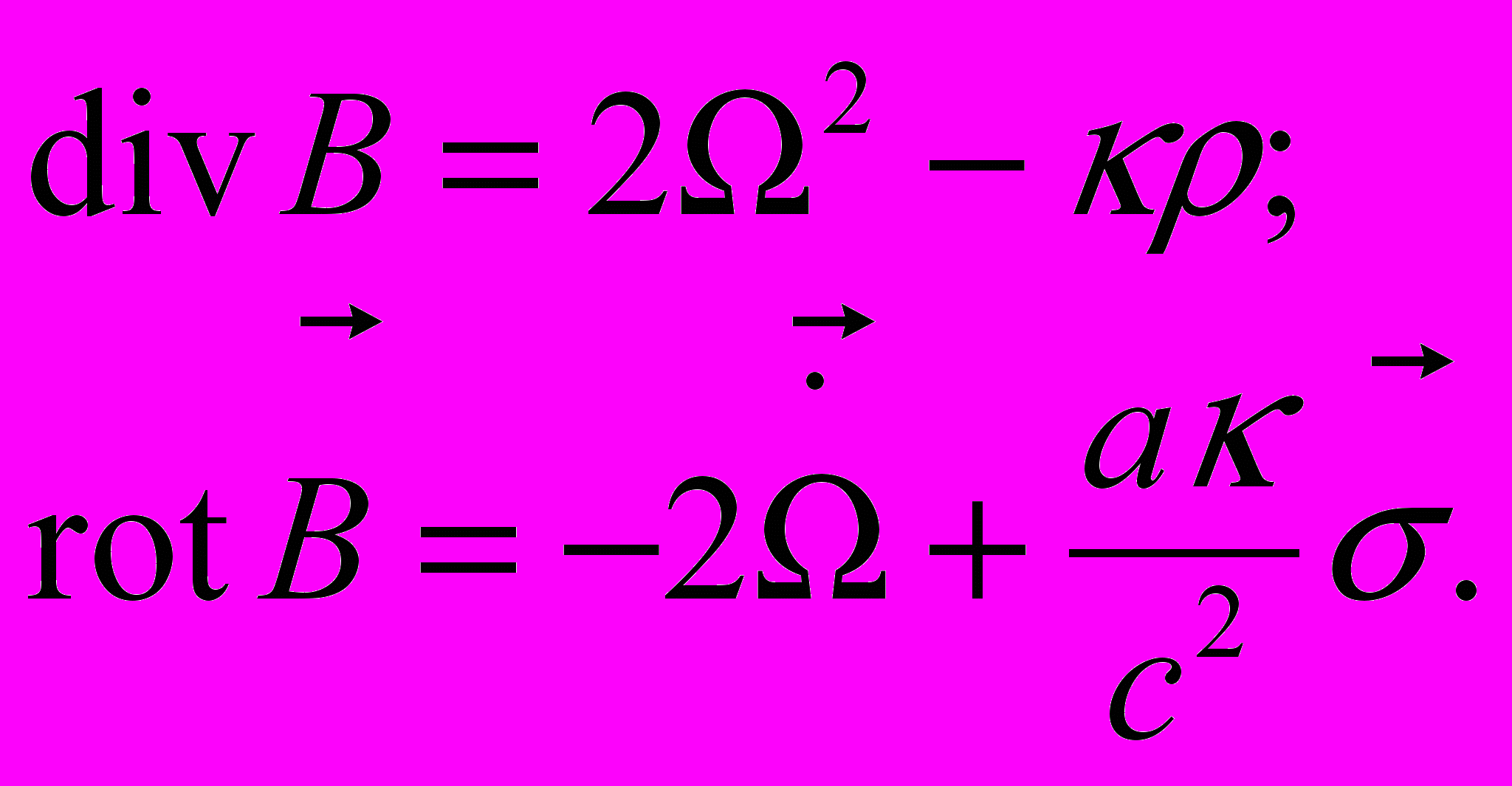(3)

Это максимально полное и универсальное уравнение, описывающее всех системы отсчета на ньютоно-эвклидовом универсуме системы тел отсчета, погруженном в любое пространство, с любой системой отсчета с любой координатизацией ее (имеется ввиду, что оно допускает любые системы координат – декартовые, сферические полярные и иные).

В работе [2] выведены уравнения движения для неинерциальной системы отсчета в галилеевом пространстве.



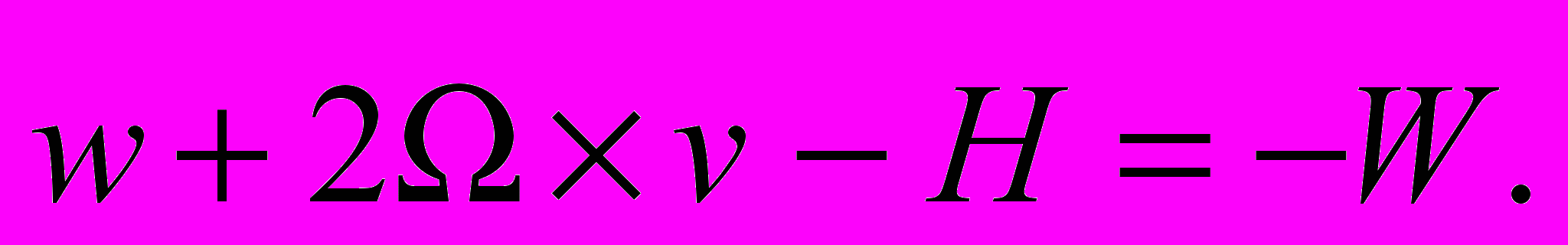
В это уравнение входят глобальный параметр , который сохраняется и в произвольном пространстве, и локальный параметр H, который локально неотличим от параметра V, что и есть, фактически, содержание принципа эквивалентности. А следовательно это уравнение полностью сохраняет силу, если параметр H заменить параметром B. Этим самым мы получаем универсальное уравнение движения произвольного тела в произвольной системе отсчета в произвольном пространстве:

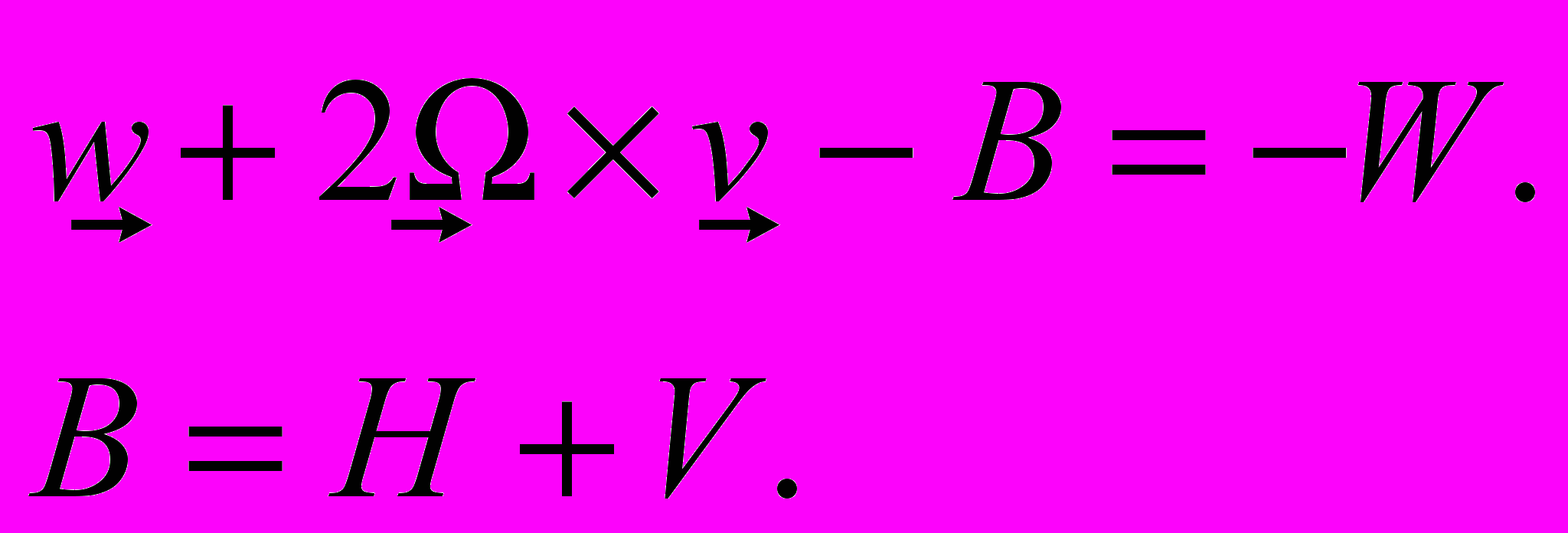(4)

Универсальные уравнения движения тел в точечном представлении

На основании уравнений поля и движения и используя результаты работ [1] и [2] получаем уравнения движения n тел в точечном представлении:

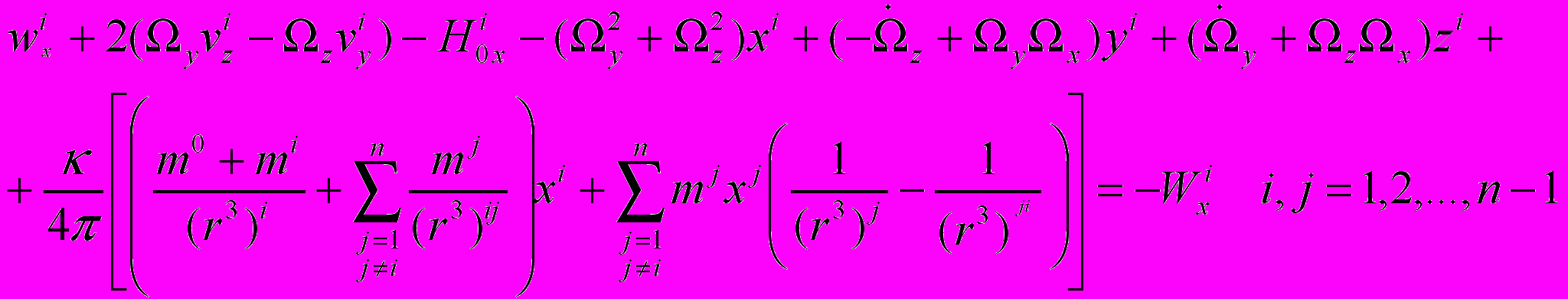(5)

Для y и z компонент уравнения получаются циклической перестановкой (5).

Здесь мы использовали только потенциальные компоненты поля. Гипотетические вихревые составляющие в это уравнение не включены.

В небесной механике рассматриваются как правило свободные движения тел, находящиеся в невесомом состоянии, поэтому все правые части нулевые. Кроме того, наиболее удобно начало отсчета совмещать с одним из тел, т.е. иметь невесомое начало отсчета, что сразу обращает в нуль все компоненты H₀. Однако, в космонавтике, где приходится рассматривать движения на активных участках полета космического объекта в гравитационном поле и еще совершать при этом некоторый маневр, может потребоваться уравнения (5) в полном виде.

Несмотря на устрашающий вид уравнений (5), их использование высокоэффективно. Дело в том, что оно универсально, в них «все включено», и потому использование его состоит в чисто механическом отборе требуемых факторов.

Примеры решения задач на движение тел в гравитационном поле

Мы будем использовать технологию переменных систем отсчета, т.е. использовать системы отсчета наиболее адекватные задаче, но в которых не всех характеристики систем отсчета заранее заданы, а часть их сами являются переменными. И решение задачи состоит как в определении характеристик системы отсчета, так и движений в ней.

Задача двух тел

Решаем наиболее простую и наиболее важную для небесной механики задачу Кеплера, т.е. движение двух тел в гравитационном поле, создаваемым самими телами.

В соответствии с принципами переменных систем отсчета вводим систему отсчета, начало которой на одном из тел, а ось Ox направляем на второе тело. Таким образом, движение тела является одномерным, но сама система отсчета нам неизвестна и ее характеристики (угловая скорость вращения) есть также переменная задачи. Таким образом, переменные задачи есть координата движения второго тела и вектор вращения самой системы. Этот вектор мы не фиксируем ни по величине, ни по направлению. Тогда система (5) сводится к следующей системе трех уравнений:

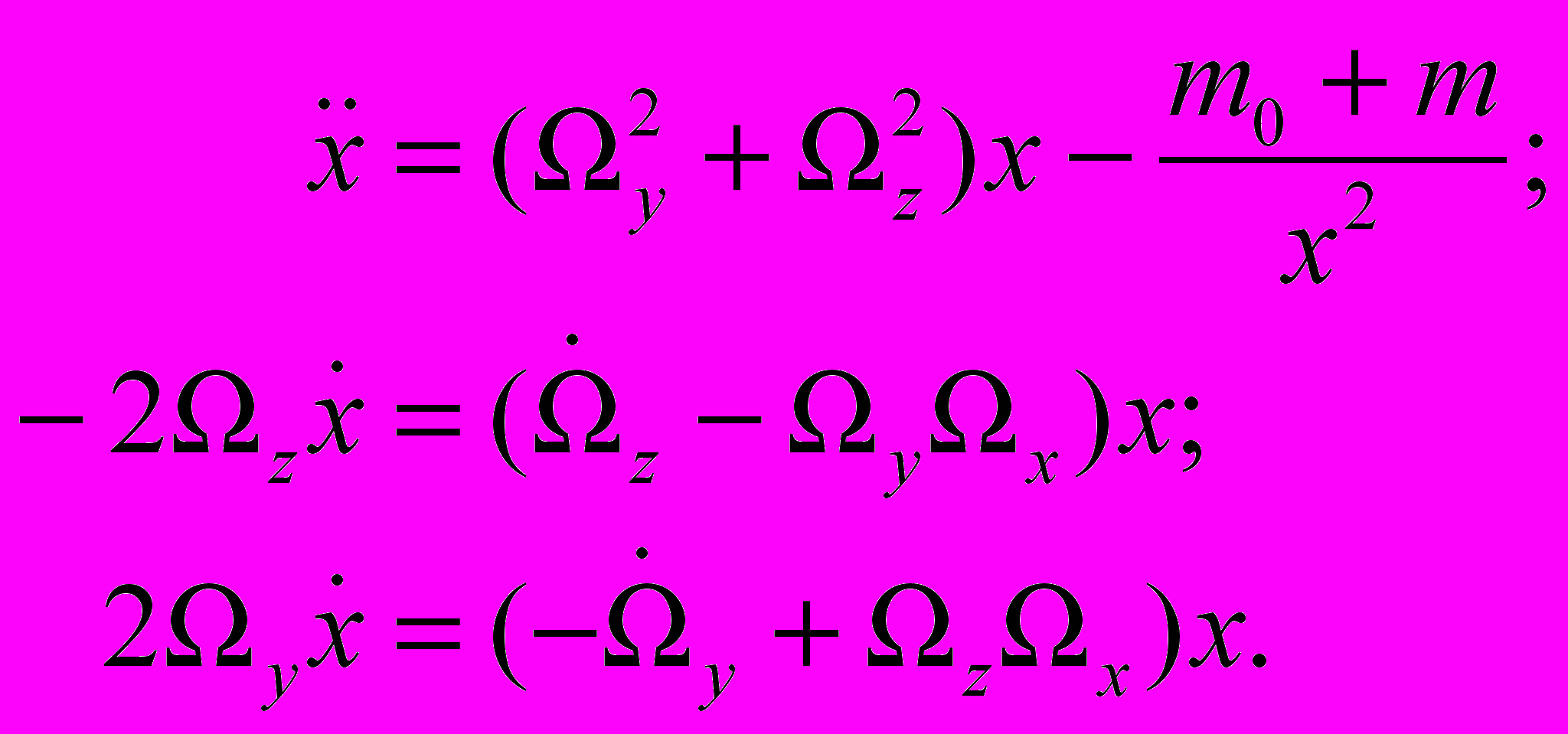(6

Здесь мы использовали как это обычно принято в небесной механике гравитационную постоянную равную 1.

Подставляем 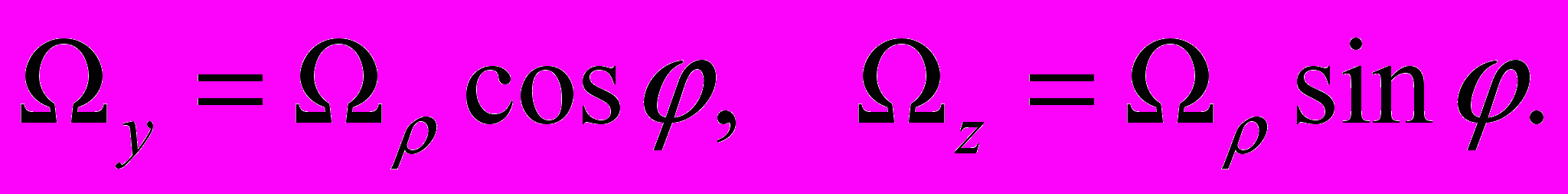Осуществляя стандартные преобразования, мы приходим системе с разделенными переменными:

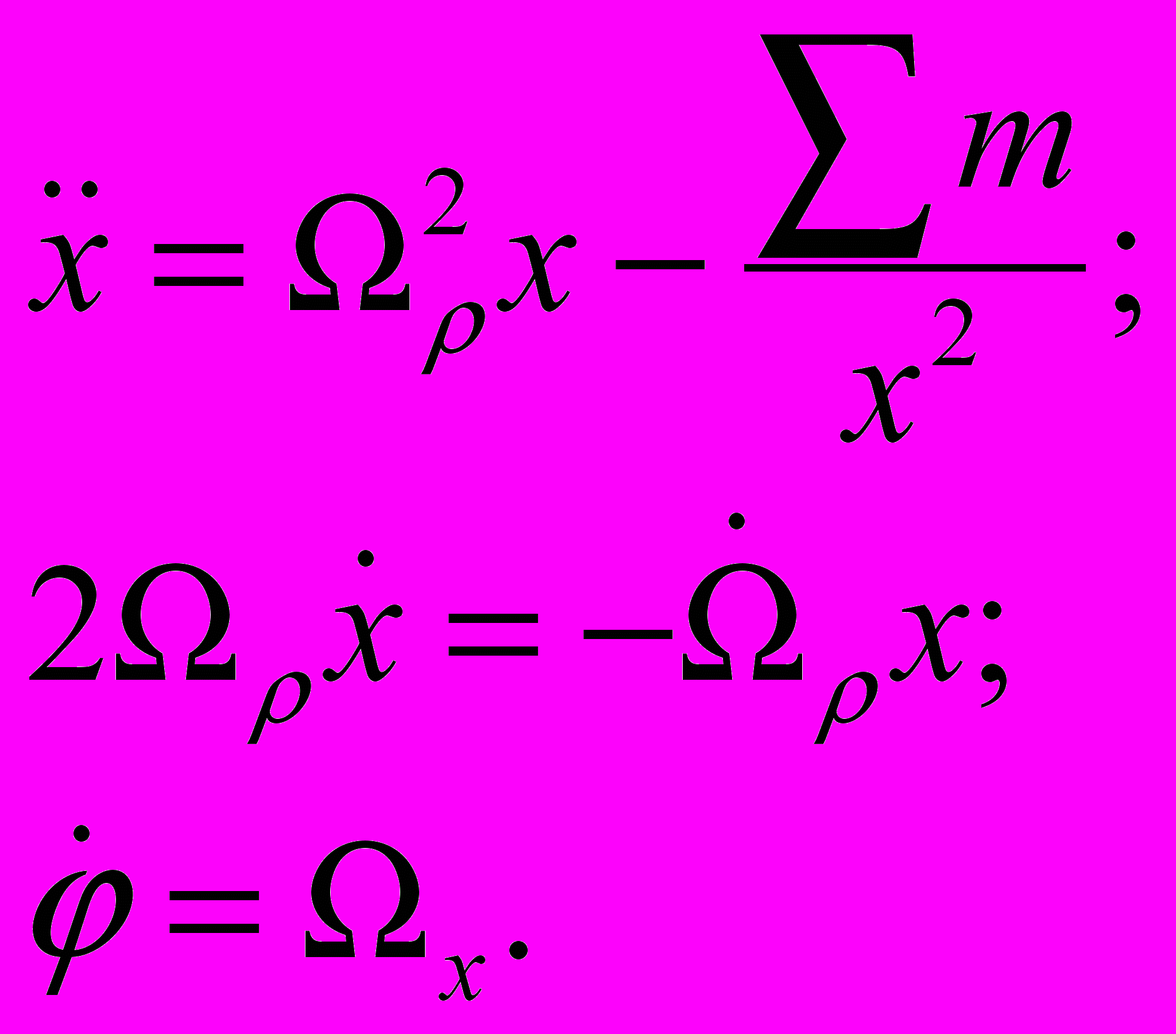(7)

Из последнего уравнения сразу следует:

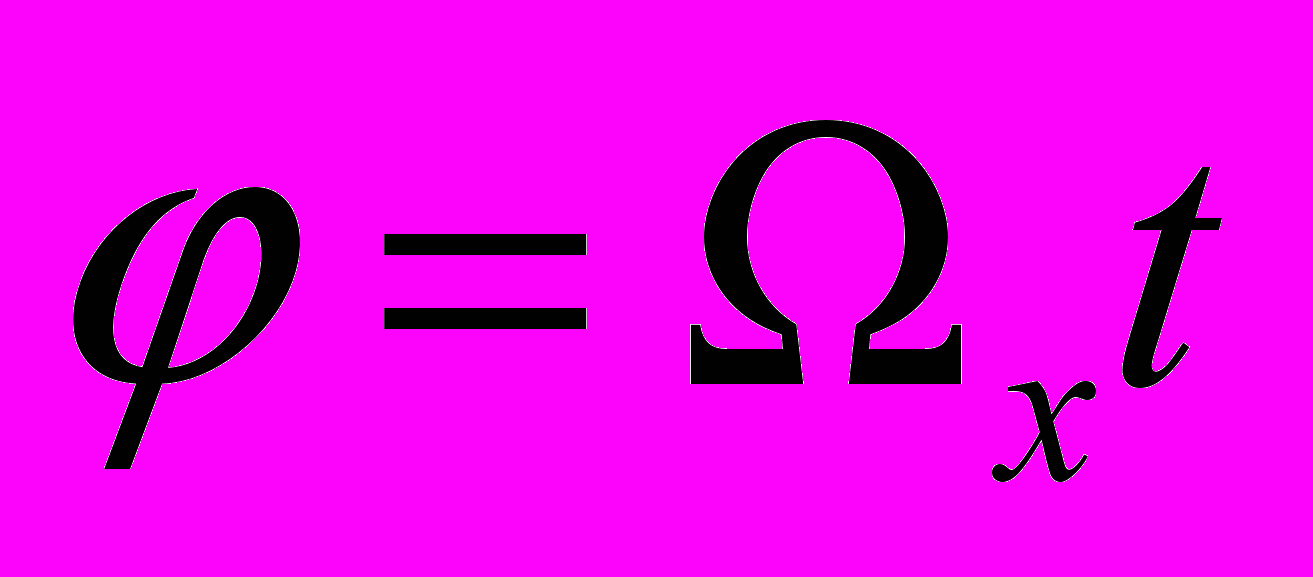(8)

Из второго уравнения

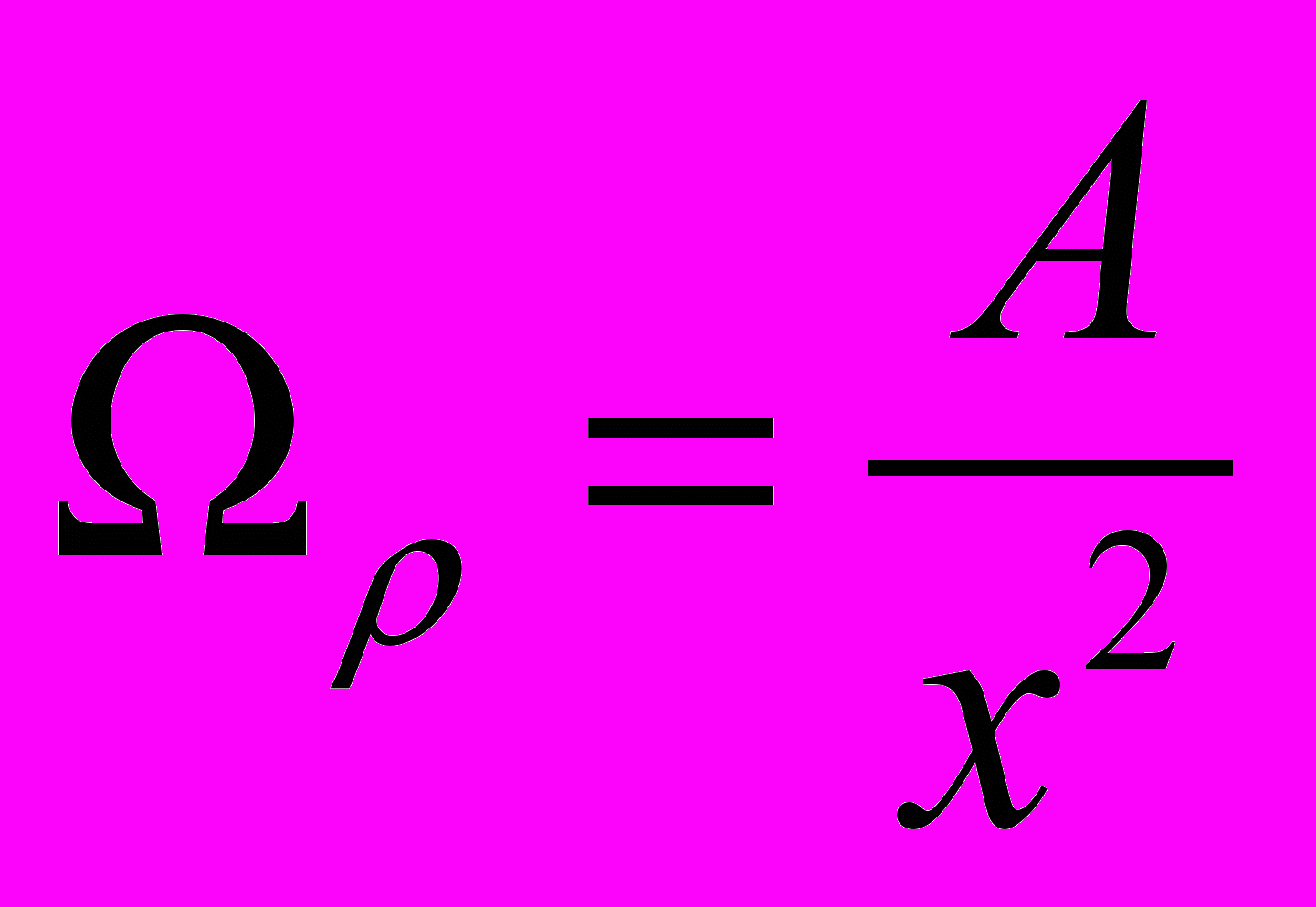(9)

Подставляя в (8), получаем

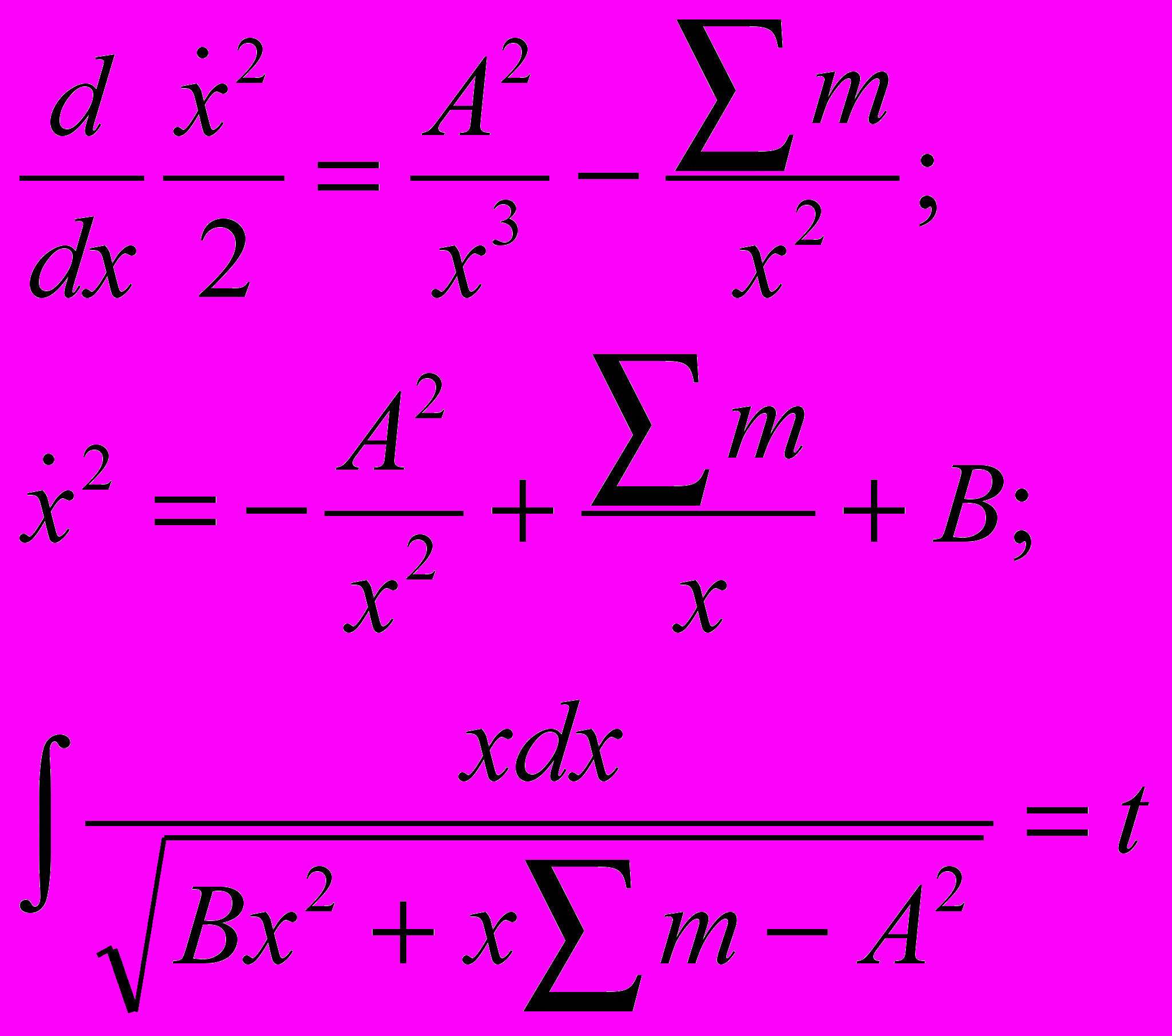(10)

Решение дает обычные движения по линиям конического сечения, отличающиеся от стандартного решения не приведенными массами, а суммой масс ввиду отличных систем отсчета. Главные особенности решения:

1. Показано существование новых решений в насчитывающей уже сотни лет задаче Кеплера. Это движе6ние в прецессирующей плоскости.
   
2. Особенность решения состоит в том, что здесь уже одинаково правомерно рассматривать движение планет вокруг Солнца и движение Солнца относительно мельчайшей пылинки.
   
3. Наконец, нельзя не обратить внимания на большую простоту решения. Классическое решение занимает несколько страниц текста. Наше решение заняло несколько строчек, в то время как в большинстве учебников и монографий решение занимает до 10 страниц (например, в [3] ─ 9).
   
4. Обычно решение этой задачи дается в центре масс с использованием понятия приведенной массы. Единственное найденное автором решение о движении одного тела относительно другого (относительное движение) ─ это решение в [3]. И там эта задача рассматривается цилиндрической, сферической системах отсчета, в форме Клеро-Лапласа, в каноническом виде. Но самого простого и естественного перехода в переменную одномерную неинерциальную систему отсчета так за столетия рассмотрения этой задачи самыми выдающимися механиками не удалось совершить. Из этого видна, сколь нетривиальна концепция переменных систем отсчета.
   
5. В относительном решении задачи Кеплера оба тела равноправны, и этим самым коперникианство, если и не терпит конфуз, то, по крайней мере, его победа над птолемеевизмом приобретает эфемерность. Но и этого вывода до сих пор никто не смог или не решился сделать.
   

Задача трех тел

Берем на нулевом теле начало системы отсчета. На первое тело направляем ось Ox. Второе тело включаем в плоскость xOy. Тогда получаем систему уравнений:

(11)

Гравитационные компоненты:

(12)

Задача трех тел сводится к шести уравнениям ранга 9. Возможно, видимо, понижение ранга системы ввиду отсутствия явной зависимости от времени.


Равновесные и гомографические решения многих тел

Представление задачи многих тел в форме (5) позволяет легко найти все равновесные и гомографические конфигурации многих тел. Такие решения возникают при обращении в нуль нецентральных компонент гравитационных полей.

При произвольных массах это возникает при равенстве всех расстояний между телами либо если нецентральный член вообще отсутствует:

1. В коллинеарной геометрии при произвольном количестве тел на вращающейся и прецессирующей прямой.
   
2. В плоской конфигурации правильного треугольника во вращающейся плоскости.
   
3. В невращающейся конфигурации правильного тетраэдра.
   

Такие решения возможны при любых симметричных многоточечниках

1. В конфигурации любых плоских многоточечников во вращающейся плоскости.
   
2. В конфигурации симметричных пространственных многоточечников в невращающейся системе .
   
3. Все эти решения возможны и с центрированными фигурами, причем масса в центре может быть отличной от массы периферийных тел.
   

Все эти решения легко исследуются в системе уравнений (5).

Плоская ограниченная круговая задача трех тел (элементарная теория движения Луны)

Ограниченной круговой задачей движения трех тел называют задачу о движении тела малой массы в окрестности тел, движущихся друг относительно друга по круговой орбите. Если движение происходит в одной плоскости, то говорят о плоской задаче. В первом приближении к этой задаче сводится задача о движении Луны. Этой задаче посвящено много работ, но до сих пор она не имеет полного решения [3, стр.524].

Рассмотрим задачу о движении Луны вокруг Земли с учетом влияния Солнца в первом приближении.

Обозначим:

М ─ масса Солнца; m ─ масса Земли, μ ─ масса Луны.

R ─ радиус-вектор Земля-Солнце, r ─ радиус-вектор Земля-Луна,  ─ радиус-вектор Солнце-Луна.

Введем систему отсчета с центром на Земле, с осью Ох направленной на Солнце. Принимаем движение системы отсчета с постоянной по направлению и величине угловой скоростью вращения  (плоскость непрецессирующая в системе неподвижных звезд).

Движение Луны происходит в плоскости, координаты ее (x, y). Уравнения движения:

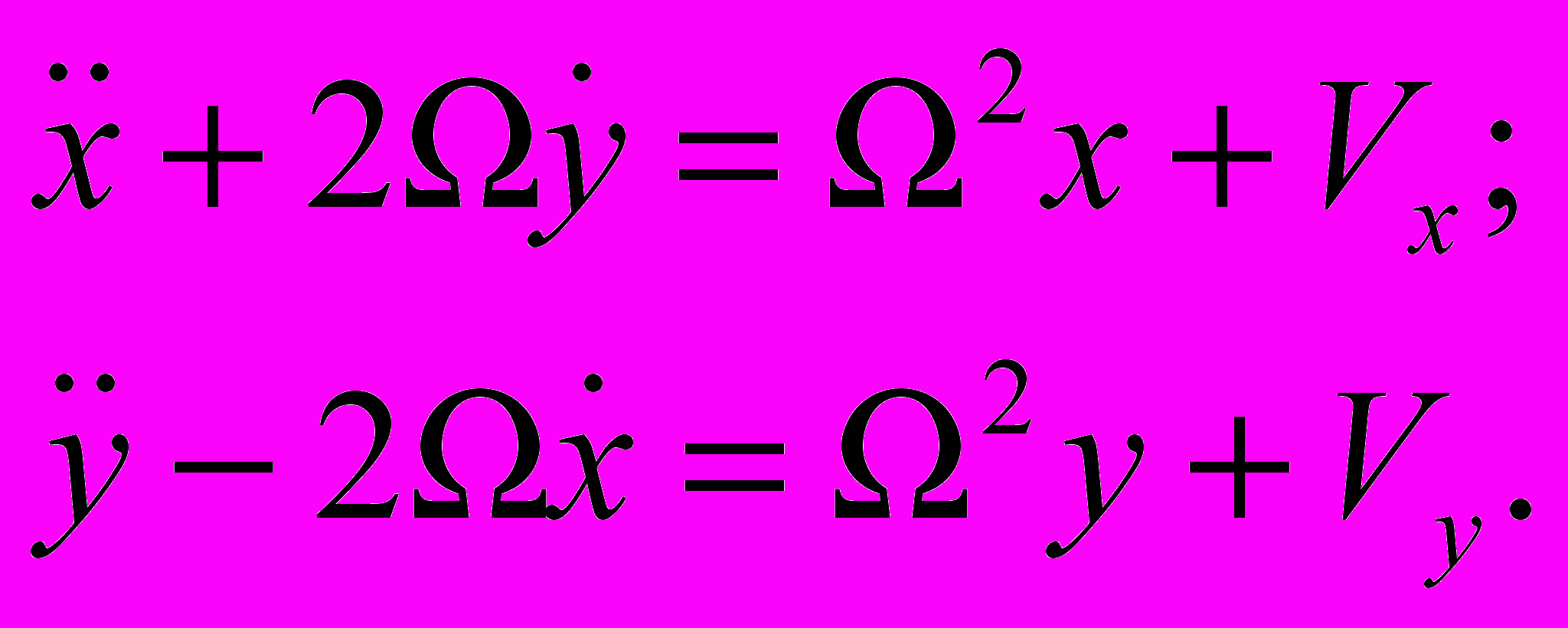(13)

Для гравитационных компонент из (12) имеем:

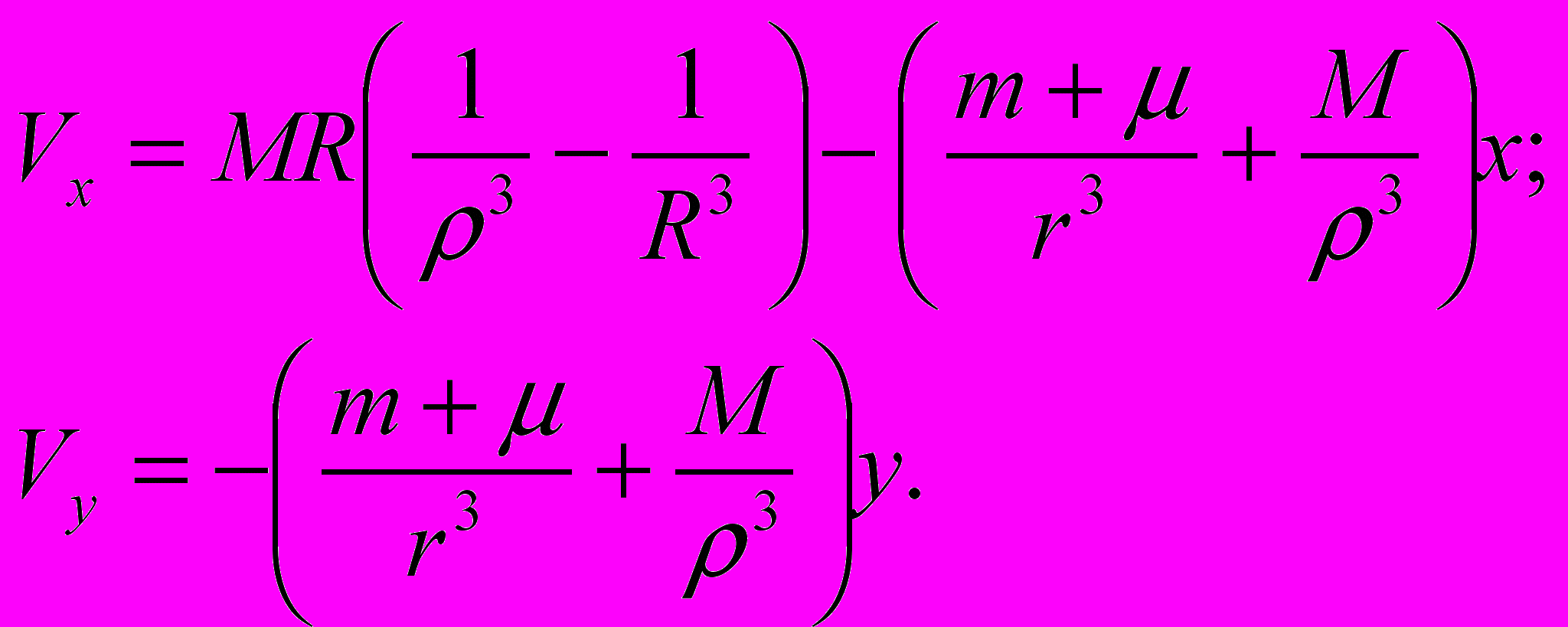(13)

Для первого приближения принимаем, что расстояние Земля-Луна мало по сравнению с расстоянием Земля –Солнце и потому можно принять =R. Поэтому первым членом в уравнении для x-компоненты напряженности гравитационного поля можно пренебречь. Солнечный член есть, фактически, квадрат угловой скорости вращения по круговой орбите Земли вокруг Солнца при пренебрежении влиянием Луны, т.е. ². Член с массой Земли и Луны есть квадрат угловой скорости ₀ вращения в системе Земля-Луна в уединенном положении, т.е. вне влияния Солнца. Итак, получаем систему уравнений:

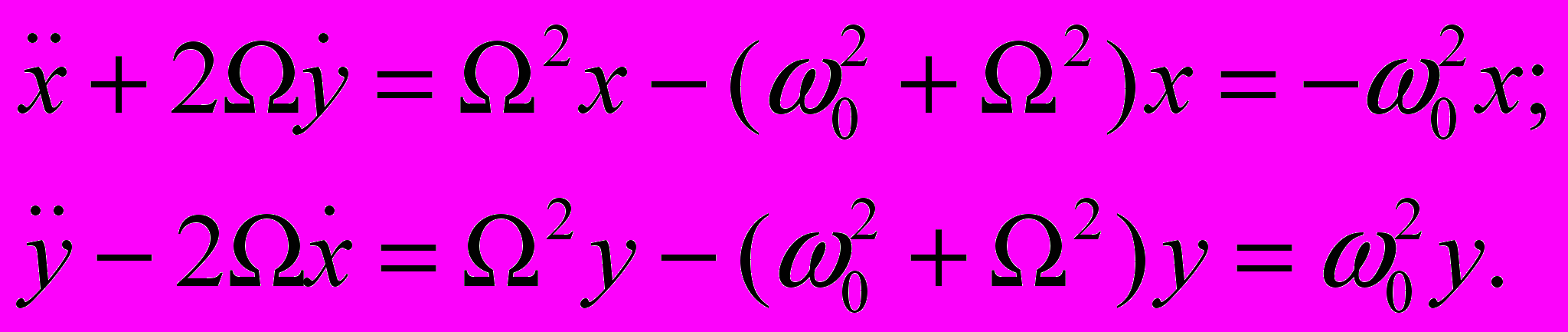(14)

Проверяем, удовлетворяет ли этой системе круговое движение Луны с постоянной скоростью вращения . Для этого принимаем:

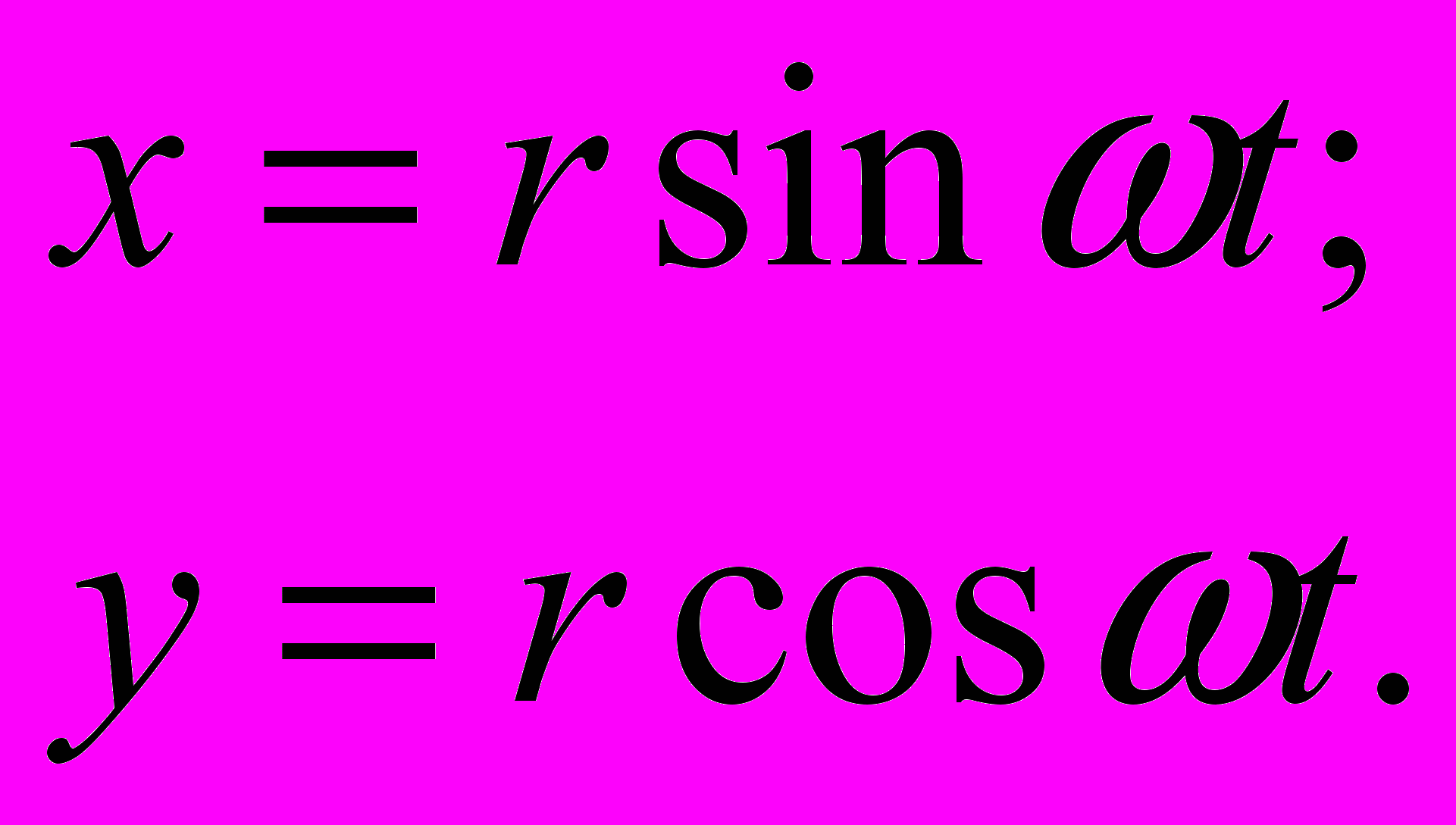(15)

Подставляем в 14

(16)

Отсюда получаем соотношение между частотами:

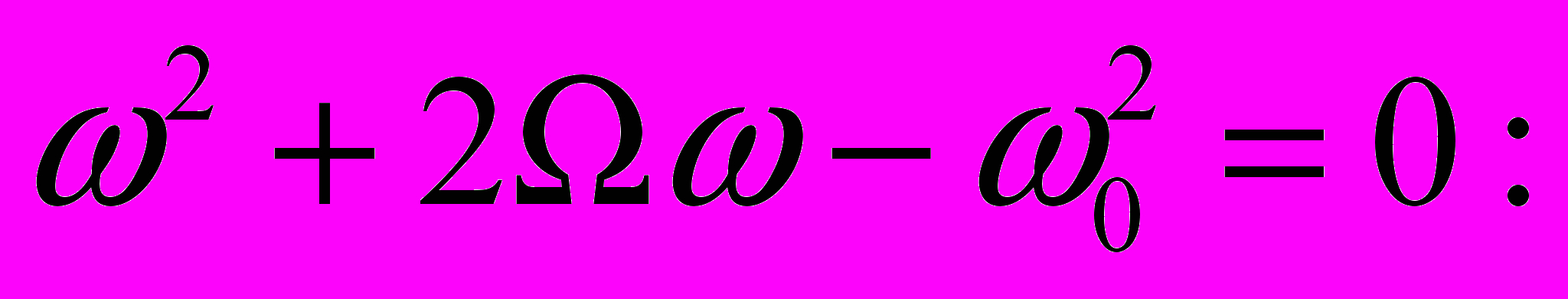(17)

Решение уравнения

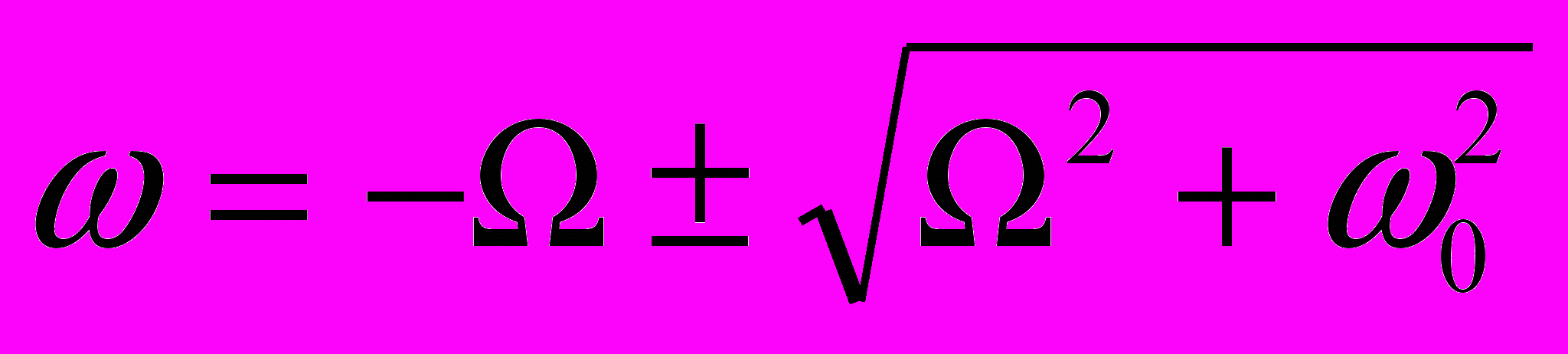(18)

Фактически,  есть угловая скорость _sn синодического периода обращения Луны. Так как движение Солнца и Луны по небесному своду идет в одинаковом направлении, то в формуле (18) надо брать минус. Для получения сидерической угловой скорости _sd надо вычесть угловую скорость обращения Земли вокруг Солнца, т.е.

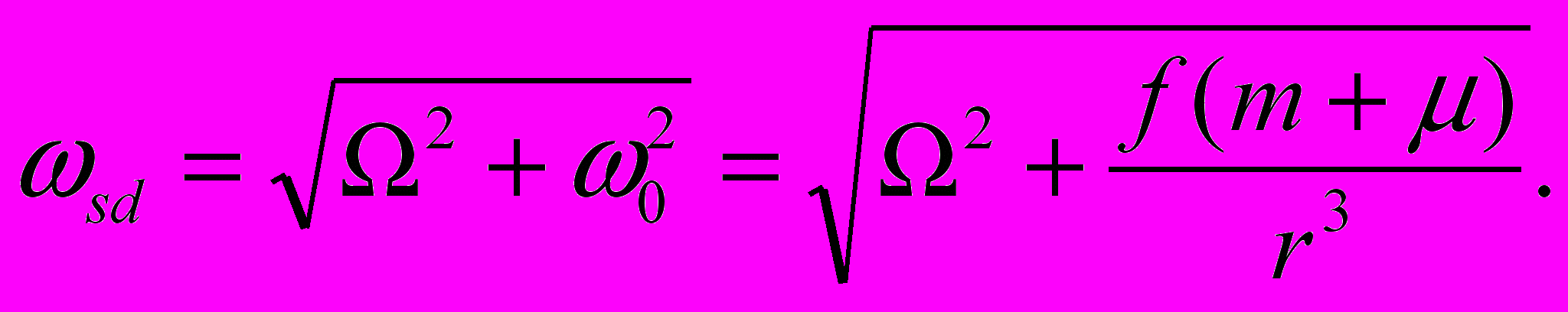(19)

Был произведен расчет сидерического значения Луны по системе астрономических постоянных МАК по формуле (19) и сравнен с средним значением по этим же данным. Расхождение оказалось около 0.7% (2.68*10^-6 с^-1 по расчету и средняя сидерического движение Луны по МАК 2.66*10^-6 с^-1). Для такой простой модели это может быть признано в качестве весьма удовлетворительного результата. Отсюда следует, что эта модель вполне может стать основой, первым приближением к точным расчетам эфемерид Луны, значительно более простым, чем существующие модели, если учесть, что, к примеру, в модели Делоне используется 500 членов, а последние модели насчитывают 1200 членов разложения.

Заключение

Выведены уравнения движения в произвольном пространстве в произвольной системе отсчета произвольного количества тел в произвольном состоянии в точечном представлении. Для решения задач использована техника переменных систем отсчета.

Дано решение задачи двух тел. Показано существование неизвестного до сего времени решения ─ движения в прецессирующей системе отсчета. Одновременно показана совместимость коперникианства и птолемеевизма.

Выписаны развернутые уравнения трех тел в виде шести уравнений ранга 9.

Приведена классификация равновесных и гомографических решений многих тел.

Создана элементарная теория Луны, которая может стать основой новой точной теории Луны


Библиография:

8. Юровицкий В.М. Гравитационное поле точечных тел на самих телах в гармонической системе отсчета в полевой теории гравитации. Представлено в ЖЭТФ.
   

2 Юровицкий В.М., Общая теория неинерциальных систем отсчета в галилеевом пространстве. Представлена в ЖЭТФ.

3 Справочное руководство по небесной механике и астрометрии. Под редакцией Г.Н.Дубошина. М., «Наука», 1976