Проблемы машиностроения и надежности машин ран 2001 №2 стр. 3-11

Вид материала

Документы

Содержание Механика деформируемого и абсолютно твердого тела в пространстве переменных лагранжа

Подобный материал:

• Анализируется современное состояние горного машиностроения в мире и Казахстане. Уделяется, 137.45kb.
• Программа вступительного экзамена в аспирантуру по специальной дисциплине 05. 02., 266.3kb.
• Д. А. Губайдуллин Институт механики и машиностроения Казнц ран, 147.12kb.
• Д. А. Губайдуллин Институт механики и машиностроения Казнц ран, 260.36kb.
• Текст взят с психологического сайта, 2812.86kb.
• Рабочая программа учебной дисциплины по дисциплине «Детали машин и основы конструирования», 251.9kb.
• Закон приморского края, 196.64kb.
• Программа-минимум кандидатского экзамена по специальности 05. 02. 02 «Машиноведение,, 259.98kb.
• Вопросы для подготовки к экзамену по дисциплине «Теория надежности», 8-й семестр, 2011, 20.46kb.
• Статья из сб научных трудов "Современная психология: состояние и перспективы исследований., 275.61kb.

УДК 531.8

МЕХАНИКА ДЕФОРМИРУЕМОГО И АБСОЛЮТНО ТВЕРДОГО ТЕЛА В ПРОСТРАНСТВЕ ПЕРЕМЕННЫХ ЛАГРАНЖА

Алюшин Ю.А., Еленев С.А., Кузнецов С.А.

Россия, г. Москва, МГТУ «СТАНКИН»

В различных разделах современной механики преимущественное распространение получили характеристики и соотношения, ориентированные на описание движения в форме Эйлера. К ним, в частности, следует отнести тензоры деформаций и скоростей деформаций, дифференциальные уравнения равновесия или движения, определяющие соотношения в механике сплошной среды и пр. [1-4].

Недостаточное внимание описанию движения в форме Лагранжа можно объяснить историческим развитием механики от материальной точки к сплошной среде, преимущественным интересом к малым деформациям, когда различия между переменными Эйлера и Лагранжа не являются существенными [1-3].

Однако на современном этапе возрастает актуальность задач, связанных с пространственным движением и большими необратимыми деформациями.

Большинство недостатков современной механики связаны с исходными понятиями, предпосылками и аксиомами, на которых она базируется. К таким недостаткам можно отнести:

• невыполнение законов сохранения в упругой зоне, что побуждает до сих пор вместо энергетических основ, как во всех других разделах физики, использовать принципы статики [2-3];
  
• недостаточную определенность понятий «сила» и «напряжения» [2];
  
• трудности объяснения явлений упрочнения, эффекта Баушингера, определения направления течения в технологических процессах с нежесткими границами, отсутствие достоверной теории технологической пластичности и пр. [3].
  

Эти и другие трудности современной механики создают предпосылки для изменения отношения к выбору аргументов как характеристик движения, так и физических закономерностей.

Очевидные преимущества переменных Лагранжа связаны, прежде всего, с естественной необходимостью формулировки физических закономерностей для их материальных носителей - частиц, а не абстрактных точек пространства наблюдателя [1-3].

Описание движения в форме Лагранжа позволяет находить любые параметры частиц с учетом истории происходящих в них изменений, включая историю деформирования, что необходимо для учета упрочнения, определения интегральных по времени характеристик, таких как пройденный частицей путь, накопленная деформация и пр.

К существенному упрощению математических моделей процессов деформации [4 - 6] приводит переход от напряжений и деформаций Коши к соответствующим характеристикам, зависящим от производных уравнений движения в форме Лагранжа

, (1)

где и - переменные Эйлера и Лагранжа; = при t = 0.

Можно показать [4-6], что известные формы описания закона движения системы материальных частиц, а также аксиомы механики можно рассматривать как следствие более общего принципа постоянства скаляра Пуанкаре [2]: «существует нечто, что остается постоянным».

Действительно, в соответствии с основным постулатом механики [3] поведение системы зависит от положения частиц и их скоростей, т. е. уравнений (1) и их первых производных. Другими словами, в общем случае движения сплошной среды её возможные изменения определяют 5 независимых инвариантных скалярных характеристик: модули векторов перемещения и скорости с компонентами, соответственно,

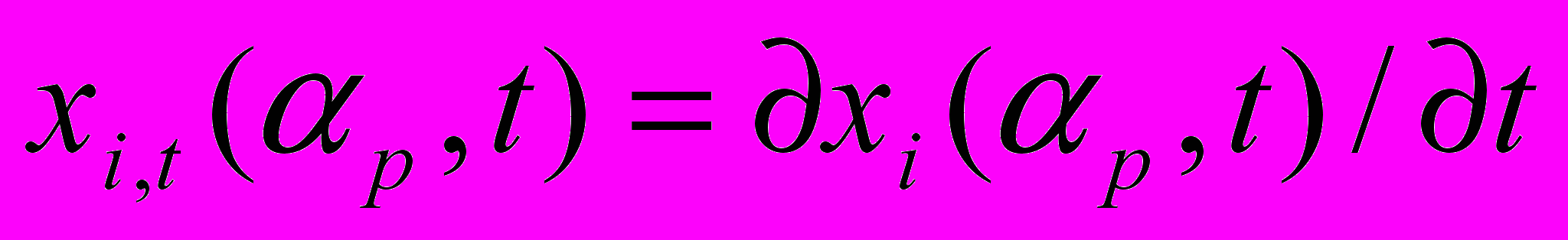; , (2)

а также инвариантные характеристики деформированного состояния частиц [5-6], в том числе отношение объемов частицы в текущем и исходном состояниях

, (3)

сумма квадратов элементов якобиана уравнений движения (1)

(4)

или, в частном случае, при деформации в главных осях - отношение квадратов длин диагоналей куба в исходном и деформированном состояниях, а также экстремальные значения либо среднего значения относительных длин ребер параллелепипеда

; , (5)

либо среднеквадратического отклонения их фактических значений от среднего

, (6)

так как величины Г и е связаны соотношением

. (7)

Изменение каждого из них не накладывает никаких ограничений на величины других. Например, скорость частицы не зависит от её смещения или изменения объема.

Для механической системы достаточно использовать энергетическую интерпретацию скаляра Пуанкаре с дополнительным предположением, что энергию можно представить в виде суммы составляющих, каждая из которых зависит от кинематических инвариантов соответствующего типа. Тогда для приращения энергии бесконечно малой частицы можно записать

, (8)

где слагаемые в левой части уравнения соответствуют приращениям потенциальной энергии положения (E_p), кинетической энергии движения (E_k), энергии деформации (состояния E_d), и диссипируемой части энергии (E_q). Приращение энергии внешних воздействий обеспечивает энергетически эквивалентную замену воздействия отбрасываемых частей при переходе от изолированной системы к замкнутой [4-6].

В уравнениях (8) и ниже, как и в работах [4-6], использованы два различных оператора, которые характеризуют бесконечно малые приращения функций во времени (d) и в пространстве (), соответственно.

Предлагаемый переход к описанию движения в форме Лагранжа и связанным с этим описанием характеристикам (напряжениям и деформациям Лагранжа) позволяет представить уравнение энергетического баланса (8) в новой инвариантной форме. За счет выделения полного дифференциала уравнение для удельной (отнесенной к объему частицы) энергии деформации

(9)

преобразуется к сумме двух составляющих, характеризующих процессы обратимой и необратимой деформации

. (10)

Независимо от свойств среды, среднее напряжение (и первый инвариант тензора напряжений в классической теории), определяют объемную плотность энергии, накапливаемой в частице за счет изменения объема (3)

. (11)

Из условия инвариантности энергии по отношению к выбору систем отсчета координат, скорости и времени [5] компоненты напряжений и деформаций Лагранжа могут отличаться лишь масштабным размерным множителем

. (12)

Это соотношение не противоречит современным представлениям механики деформируемого твердого тела, но приводит к целесообразности перехода к новой шкале средних напряжений. При этом коэффициент следует рассматривать как физическое свойство материала, характеризующее энергию частицы в её исходном состоянии, которое, естественно, может быть изменено за счет предварительной деформации.

Переход к новому началу отсчета шкалы средних напряжений позволяет сократить число упругих констант (до одной), упростить определяющие уравнения и дифференциальные уравнения движения. Особо следует отметить, что при переходе к напряжениям Лагранжа в новой шкале средних напряжений дифференциальные уравнения равновесия для упругой среды преобразуются в уравнения Лапласа

, (13)

методика решения которых хорошо разработана. При этом точность результатов может быть повышена за счет перехода к более определенным кинематическим граничным условиям вместо статических. Такой подход позволяет объяснить энергетический парадокс классической теории при деформации от собственного веса [5].

Из уравнения энергетического баланса следует, что необратимая деформация обязательно сопровождается диссипацией энергии, а соотношения теории пластического течения [3-5] эквивалентны условию положительности диссипируемой мощности, но являются слишком жесткими и существенно сокращают класс возможных решений для немонотонных процессов деформации, в том числе для изгиба, кручения и пр. Предложена новая обобщенная форма условия пластичности в форме

. (14)

Поведение материалов при упругом нагружении следует рассматривать как проявление закона сохранения энергии, при этом второй модуль упругости (коэффициент Пуассона) характеризует фактические условия нагружения и согласует поведение системы с законом сохранения энергии.

Энергетическая модель позволяет достаточно просто объяснить ряд явлений, которые не укладываются в общепринятую теорию, и предложить циклический механизм развития пластической деформации с накоплением энергии за счет изменения объема вплоть до достижения критического среднеквадратического отклонения (6) на первой фазе цикла и выделения её с возвратом объема к исходному значению на второй фазе цикла [4]. Проявлением циклических процессов накопления и диссипации энергии можно также объяснить изменение коэффициента Пуассона по мере накопления деформаций, в том числе при переходе от упругих деформаций к пластическим [4-5]. Ускорения играют определяющую роль в формировании вихревых потоков, возникающих в любых процессах деформации и накладывающих ограничения на возможность реализации однородной деформации.

Энергетическая модель деформации позволяет рассматривать упрочнение и эффект Баушингера как следствие накопления энергии и сдвига начального состояния системы по энергетической шкале. Для начала пластической деформации, в том числе с изменением знака нагружения, требуются меньшие затраты энергии внешних источников, деформация начинается при меньших нагрузках.

Большое прикладное значение могут иметь предлагаемые методы решения с применением переменных Лагранжа различных задач упругой и пластической деформации, в том числе в стержневых системах, при моделировании осадки и растяжения с образованием шейки и бочки, соответственно [4-5]. Весьма перспективным можно считать переход к описанию движения в форме Лагранжа при анализе вопросов устойчивости, турбулентности и пр.

Решение даже таких простых задач, как кручение и изгиб, приводит к неожиданным по современным понятиям результатам.

В частности, энергетически нейтральный слой, в котором объем и массовая плотность энергии частиц не изменяются, при плоском чистом изгибе не совпадает с центральным слоем и находится в области растянутых волокон. Именно вблизи этих волокон целесообразно располагать отверстия, пазы, плоскости спайки и прочие конструктивные особенности, снижающие прочность конструкции.

При кручении круглого вала без изменения его длины более 50% объема металла находится в условиях, близких к всестороннему сжатию. Этот процесс целесообразно использовать вместо гидростатов для повышения плотности материалов и устранения металлургических дефектов.

Переход к описанию движения в форме Лагранжа позволяет сформулировать достаточно простой принцип суперпозиции, в соответствии с которым уравнения совмещенного движения можно получить, заменяя переменные Лагранжа в наложенном (переносном) движении на переменные Эйлера вложенного (относительного) движения. Преимущества этого принципа особенно очевидны для различных разделов механики сплошной среды. В частности, в работах [4-5] он использован для анализа процессов осадки с кручением, пластического изгиба с растяжением, протяжки бойками различной формы, волочения и выдавливания через волоки и матрицы различного профиля.

Не менее важен этот принцип и для механики абсолютно твердых тел. Описание движения в переменных Лагранжа позволяет перейти от графических к аналитическим методам кинематического и динамического анализа шарнирно – рычажных и других типов механизмов, выявлению общих закономерностей движения маятниковых и других изолированных механических систем [6].

В частности, для двойного плоского маятника с сосредоточенными массами m₁ и m₂, подвешенными на нерастяжимых нитях длиной L₁ и L₂, из обобщенного принципа (8) следует, что период колебания массы m₁, соединенной с неподвижной осью подвески, не зависит от значения и положения второй массы и определяется, также как и для простого математического маятника, эллиптическим интегралом первого рода

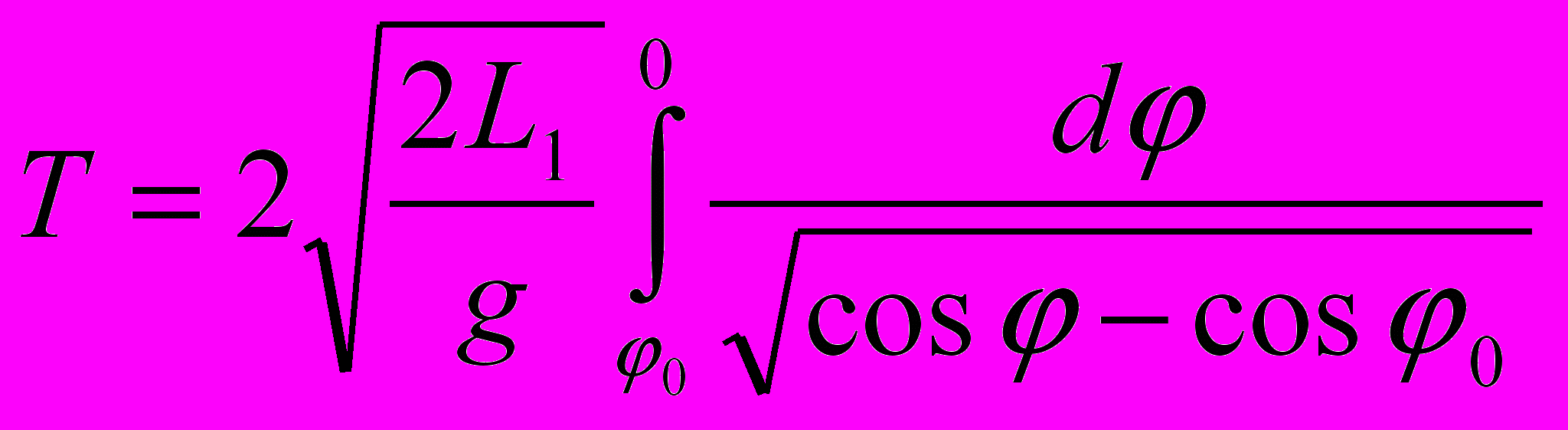, (15)

а колебания массы m₂ описывает дифференциальное уравнение

, (16)

где , – углы наклона нитей с длинами L₁ и L₂ по отношению к оси «х» в текущем или исходном (с индексом «0») состояниях. С учетом изменения угловой скорости для колебания второй массы получаем

, (17)

где

. (18)

Численное решение полученных уравнений не представляет трудностей. Аналогичные уравнения описывают колебания составного маятника с управляемой подвижной массой и двойного пространственного маятника.

Особенно заметны преимущества перехода к переменным Лагранжа и предложенному принципу суперпозиции для пространственных движений.

Положение плоской фигуры в двумерном пространстве однозначно определяет прямая, соединяющая 2 произвольные её точки. Для описания ее движения достаточно знать движение одной точки (две степени свободы), назовем её полюсом Р, и поворот прямой относительно этой точки (1 степень свободы). В общем случае уравнения в форме Лагранжа принимают вид [6]

;

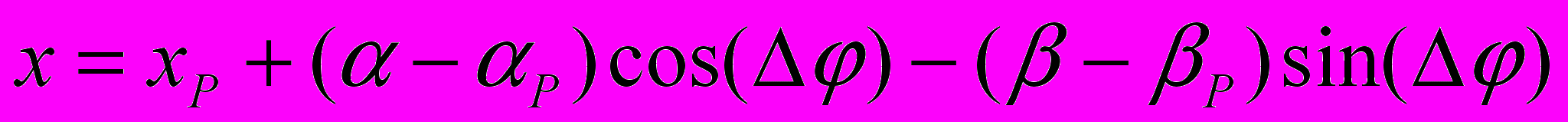. (19)

Всего получаем 3 степени свободы, как и должно быть при плоском движении абсолютно твердого тела.

Для однозначного описания положения пространственной фигуры необходимо, как минимум, 3 точки. Она имеет 6 степеней свободы (3 смещения вдоль осей координат и 3 угла поворота относительной каждой из осей). Для описания пространственного движения абсолютно твердого тела можно воспользоваться различными вариантами:

• описать движение какой – либо его точки, например центра масс (3 координаты), а затем поворот тела относительно каждой из осей (3 угла поворота);
  
• описать движение произвольного отрезка, принадлежащего этому телу (5 координат), а затем поворот тела относительно этого отрезка (1 угол поворота).
  

В математическом отношении при описании движения в форме Лагранжа и при использовании принципа суперпозиции более предпочтительным является второй вариант, при котором наложенным (переносным) следует считать пространственное движение прямой, а вложенным (относительным) – вращение тела вокруг этой прямой. Однако этот вариант применим только для случаев, когда ось вращения абсолютно твердого тела остается фиксированной в пространстве переменных Лагранжа на всем интервале времени, например как при полете снаряда или движении «волчка». Этот вариант удобен, в частности, при анализе пространственных механизмов, имеющих сферические шарниры.

Для определения эйлеровых координат точек, расположенных на прямой, которой принадлежит отрезок РМ с полюсом Р и длиной L, рассмотрим соотношения между координатами точек Р и М в начальный

(20)

и текущий

(21)

моменты времени. Переходя к изменению углов наклона прямой РМ по отношению к осям координат , получаем

, (22)

где - лагранжевы координаты полюса и рассматриваемой точки, соответственно. Частицы совершают движение по поверхности подвижной сферы с центром в полюсе Р. Компоненты скорости зависят от угловых скоростей .



Рис. 1 Рис.2

Этих уравнений достаточно, чтобы описать движение, в частности, шестиподвижного манипулятора по патенту №1661528 [7] (рис. 1). Если известно начальное положение манипулятора, а также конечные координаты точки пространства и ориентация рабочего органа (инструмента) по отношению к осям координат, тогда приведенные уравнения позволяют определить параметры для управления движением манипулятора, в том числе по заданной в параметрическом виде траектории, без использования многомерных матриц и метода конечных элементов.

Для управления лазерной установкой по патентам России №2060135, 2062197 и др. [7] предложена математическая модель управления движением объектива и предметного стола. Схема установки показана на рис. 2. Её можно считать состоящей из двух независимых механизмов для привода объектива и предметного стола. Первый из них состоит из стойки, на которой закреплены неподвижные опоры N и K, и 4-х подвижных звеньев с фиксированными расстояниями L₁– L₄ между осями шарниров N, M, G, L, K . Механизм обеспечивает перемещение и ориентацию зеркал 1 и 2 для направления лазерного луча в заданную точку облучаемого предмета.

Механизм ориентации стола состоит из двух звеньев, вращающихся относительно осей «х» и «у», соответственно, за счет внешних специальных приводов, которые можно рассматривать как кулачковые механизмы, в которых толкателем является ориентируемый в пространстве стол, поворачивающийся при взаимодействии с кулачками относительно осей «х» и «у».

Оба механизма имеют по две степени свободы, что позволяет позиционировать ось лазерного луча в любой точке поверхности стола под любым углом к её нормали.

Третий механизм установки, обеспечивающий фиксированную ориентацию зеркал 1 и 2 под углом 45⁰ к направлению лазерного луча, конструктивно может быть выполнен различными способами.

Ниже приводятся математические соотношения, позволяющие определить управляющие факторы, в качестве которых рассматриваются углы и поворота звеньев механизма, присоединенных к стойке, и углы поворота «кулачков» 1 () и 2 (), обеспечивающие заданную ориентацию стола. Предполагается, что расстояния между осями шарниров и координаты неподвижных (фиксированных на стойке) опор N и F заданы. В основу модели положены общие соотношения для анализа шарнирно – рычажных механизмов с использованием переменных Лагранжа [4].

Задача формулируется так: по заданным координатам точки луча лазера u, v и ориентации стола, т. е. углам между нормалью к поверхности стола и двумя осями, например y и z (третий угол определяется через сумму их квадратов, которая должна быть равна 1), найти углы поворота звеньев NM и KL, а также кулачков 1 и 2.

Из геометрических соотношений для углов и находим

; (23)

, (24)

или

; (25)

. (26)

Последнее уравнение удобно записать в виде

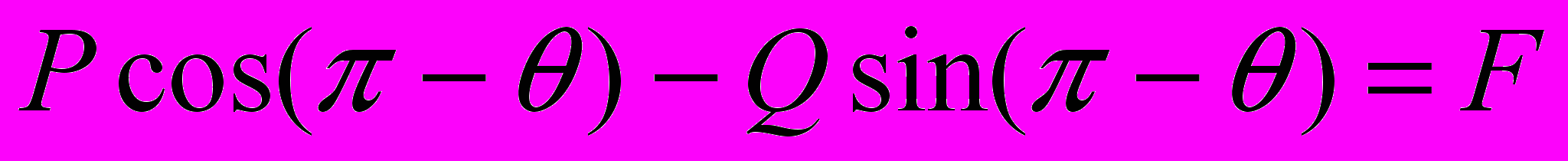, (27)

где

; ; . (28)

Отсюда окончательно для тангенсов половинных углов получаем

; (29)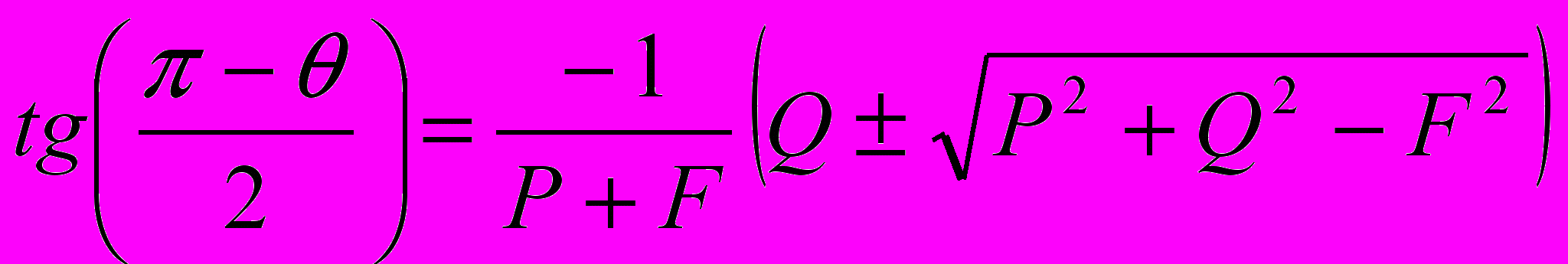

. (30)

Расчет фактических поворотов основного (первого) и регулирующего (четвертого) звеньев должен быть выполнен с учетом их положения в предшествующий момент времени. По этим же соотношениям может быть построена программа для управления движением лазерного луча по заданной траектории или площади обрабатываемой детали.

Для определения управляющих параметров ориентации стола следует учесть, что заданные углы наклона нормали к поверхности стола с осями координат по существу определяют поворот стола относительно соответствующих осей [8]. Действительно, после поворота кулачков на углы и частицы стола B и E должны занять соответственно положения B₁ и E₁ с координатами B₁ (H_x , 0, f _x) и E₁ (0, H_y , f_y). Координаты этих частиц в направлениях осей «х» и «у» определяются не размерами стола, а удаленностью от начала координат плоскостей кулачков, расстояния до которых приняты равными H_x и H_y .

Уравнение плоскости, проходящей через 3 точки (C, B₁ и E₁), имеет вид

. (31)

А так как в уравнении плоскости

(32)

коэффициенты a, b, c определяют направляющие косинусы ее нормали по отношению к соответствующим осям координат

; ;

можно утверждать, что для полученного выше уравнения (31) или

(33)

направляющие косинусы составляют

; ;

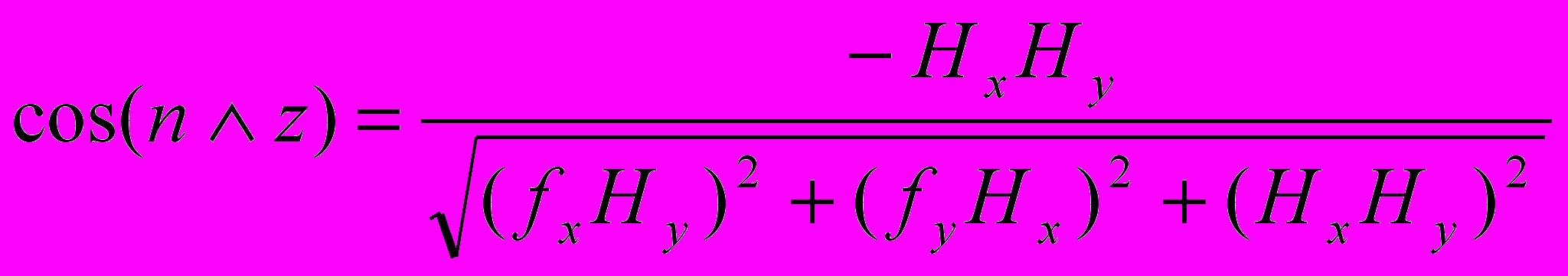. (34)

Если заданы любые два угла или их направляющие косинусы, не представляет труда найти вертикальные смещения f_x, f_y частиц B и E, а затем и углы поворота «кулачков» , так как

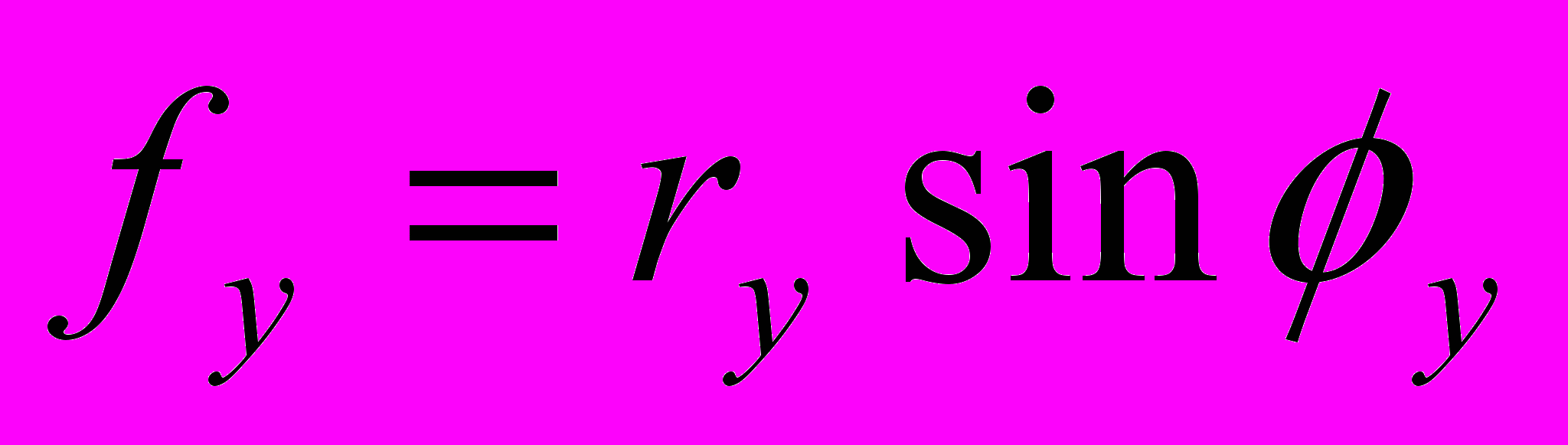; . (35)

Для симметричных кулачков, как показано на рис. 2, поворот может быть выполнен в сторону как положительных, так и отрицательных углов. При выполнении «доворота» следует учитывать текущее положение кулачков.

При моделировании управления установкой на ЭВМ следует учитывать гармонический характер тригонометрических функций, что может привести к несовпадению прогнозируемых и фактических положений объектива, в связи с чем целесообразно ввести коды ориентации различных звеньев по отношению к осям координат системы отсчета наблюдателя.


Рис. 3.

Аналогичная методика использована для построения математической модели управления движением инструмента и заготовки при обработке лопаток турбин авиационных двигателей по патенту № 2063329 (рис. 3). Робот – станок имеет 6 самостоятельных приводов. По существу его можно рассматривать состоящим из двух независимых кривошипно – коромысловых механизмов с регулируемыми положениями осей, закрепленных на стойке. Текущее состояние каждого из них определяет положение центров инструмента и заготовки, относительную ориентацию которых можно изменять с помощью двух других дополнительных приводов.

Анализ математических моделей позволяет предложить ряд изменений, позволяющих обеспечить заданное движение инструмента или заготовки с помощью более простых конструкций манипуляторов.

В частности, можно упростить систему управления для шестиподвижного манипулятора (см. рис. 1) за счет изменения положения шарниров А и В в плоскостях z = const с применением дополнительного неуправляемого поршневого соединения звеньев. Тогда при заданных координатах точки позиционирования инструмента О и углах его наклона положение осей шарниров А и В определяют уравнения (22) без дополнительных математических преобразований.

Таким образом, переход к переменным Лагранжа как при описании движений, так и в общих закономерностях, включая определяющие соотношения для сплошной среды, позволяет существенно снизить математические трудности решения различных задач и повысить точность их решения, в том числе за счет перехода к более достоверным кинематическим граничным условиям, когда «статические» условия недостаточно определены, например на контактных границах инструмента и деформируемой заготовки.

Как показывает опыт, переход к переменным Лагранжа позволяет :

• отказаться от традиционных аксиом механики и рассматривать их как следствие инвариантности приращения энергии по отношению к выбору точки приведения обобщенных сил при движении абсолютно твердых тел;
  
• предложить достаточно простой и удобный принцип суперпозиции движений, применимый как для деформируемых, так и абсолютно твердых тел [4-6];
  
• рассматривать все основные закономерности движения, включая постоянство скаляра Пуанкаре, как следствие инвариантности приращения энергии по отношению к выбору системы отсчета координат, скорости, времени и энергии деформации.
  

Рассматривая элементы якобиана уравнений движения (1) как локальные кинематические и энергетические характеристики движения и переходя к согласованным с ними определяющим соотношениям, возможно существенно сократить математические трудности решения традиционных задач и предложить новые варианты энергетических моделей процессов трения, разрушения, упрочнения, формирования турбулентности и пр.

Однако при дальнейшем развитии предлагаемого направления целесообразен переход к новым характеристикам материалов и методам их определения [4-6]. Ставшие обыденными термины «сила», «момент инерции» и др. приводят к необходимости перехода к новой терминологии при более строгом согласовании понятий с энергетической, геометрической или массовой интерпретацией характеристик движения твердых тел или деформируемых сред.

Учитывая роль механики в различных разделах прикладных наук, трудности перехода к новым понятиям, соотношениям и терминологии очевидны, но их преодоление должно способствовать развитию новых направлений фундаментальных исследований и ускорению научно – технического прогресса.

Литература

1. Лагранж Ж. Аналитическая механика. М. - Л. ГИТТЛ, 1950. - 440 с.
   
2. Пуанкаре Анри О науке. М.: Наука, 1983. – 560 с.
   
3. Ишлинский А. Ю. Механика: идеи, задачи, приложения. М: Наука, 1985.- 624 с.
   
4. Алюшин Ю.А., Еленев С.А., Кузнецов С.А. и др. Энергетическая модель обратимых и необратимых деформаций. М.: Машиностроение, 1995. - 128с.
   
5. Алюшин Ю.А. Механика процессов деформации в пространстве переменных Лагранжа. М.: Машиностроение, 1997. - 136с.
   
6. Алюшин Ю.А. Энергетические основы механики. М.: Машиностроение, 1999. - 192с.
   
7. Компьютерный банк схем и конструктивных решений механизмов, машин и технологического оборудования. Лаборатория теории механизмов и машин института машиноведения Российской академии наук. М.: ИМАШ РАН, 1999
   
8. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М: Наука, 1986, 720 с.
   

Алюшин Юрий Алексеевич – доктор технических наук, профессор кафедры «Теоретическая и прикладная механика» Московского государственного технологического университета «СТАНКИН»


Еленев Сергей Алексеевич – доктор технических наук, профессор, заведующий кафедрой «Теоретическая и прикладная механика» Московского государственного технологического университета «СТАНКИН»


Кузнецов Сергей Алексеевич – доктор технических наук, профессор


МЕХАНИКА ДЕФОРМИРУЕМОГО И АБСОЛЮТНО ТВЕРДОГО ТЕЛА В ПРОСТРАНСТВЕ ПЕРЕМЕННЫХ ЛАГРАНЖА

Алюшин Ю.А., Еленев С.А., Кузнецов С.А.


АННОТАЦИЯ


Показана целесообразность описания движения в форме Лагранжа при решении различных задач механики. Предложены новые меры деформации, дано обоснование принципа суперпозиции при описании движений в форме Лагранжа, общего вида определяющих соотношений, обеспечивающих инвариантность приращения энергии по отношению к выбору системы отсчета координат, скоростей и времени. В качестве обобщенного закона движения произвольной системы материальных частиц принято условие постоянства скаляра Пуанкаре с его энергетической интерпретацией. Приведены некоторые результаты исследования маятниковых систем, пространственных механизмов и процессов деформации с использованием разрабатываемой энергетической модели механики.