Ерения с применением многофункциональных скважинных приборов с обработкой первичных данных в реальном масштабе времени непосредственно в каротажных лабораториях

Вид материала

Документы

Содержание Режим несогласованной нагрузки.

Подобный материал:

• 2 и йодата йода был разработан метод одновременного определения концентраций этих веществ, 18.27kb.
• Реферат по дисциплине: «Информатика и икт» на тему: «Общение в реальном времени», 470.31kb.
• С. Д. Кургалин, Я. А. Туровский,, 63.75kb.
• Комплексный подход к обнаружению сетевых атак, 70.8kb.
• Конспект тема: Виды маркетинговых исследований, 67.12kb.
• Что такое edge? Информация о технологии edge, 52.94kb.
• Исследования на базе лаборатории экологии человека шунгитовая комната, 91.2kb.
• Динамическая система дуального управления качеством на знаниях (инновациях) и гарантирующих, 17.52kb.
• Рекомендации предназначены для врачей-радиологов, занимающихся проблемой лучевой терапии, 84.99kb.
• Рабочая программа По дисциплине «Программирование на языке высокого уровня» По специальности, 280.81kb.

А.В.Давыдов.

Математическая модель каротажного бронированного кабеля

введение

Начиная с 80-90 годов прошлого века в технологиях геофизических исследований скважин (ГИС) наблюдаются существенные качественные изменения, а именно: переход на комплексные многопараметровые измерения с применением многофункциональных скважинных приборов с обработкой первичных данных в реальном масштабе времени непосредственно в каротажных лабораториях. Это требует передачи данных в наземные измерительно-вычислительные устройства, как правило, в цифровой форме и с высокой скоростью. В то же время практически единственной телеметрической линией передачи данных ГИС остается традиционный каротажный кабель.

Каротажный геофизический кабель относится к типу грузонесущих кабельных линий передачи информации от скважинных приборов к каротажной станции и управляющих сигналов на скважинные приборы. Пропускная информационная способность кабеля определяет скорость каротажа, особенно в комплексных методах ГИС. В силу многообразия геофизических датчиков и разнотипности частотных характеристик измеряемых геофизических параметров, кабели должны обеспечивать передачу информации в достаточно широком частотном диапазоне. Но вместе с тем каротажный кабель является тросом с разрывным усилием до нескольких тонн, несущим скважинные приборы в химически- и механически агрессивной среде скважин. По существу, это кабель-трос специального технологического назначения, что накладывает определенные ограничения на его характеристики, как линии связи. Реальный скорость передачи информации (бит/с) современных кабелей в зависимости от их длины ограничиваются диапазоном до 10-100 кГц, что начинает существенно сдерживать развитие и совершенствование технологий ГИС. Отметим также эксплуатацию кабеля в широком диапазоне температур, от минусовых на поверхности до 100-150 и более градусов на больших глубинах и при больших давлениях, что приводит к существенному изменению и вариациям электрических характеристик кабеля в процессе эксплуатации.

С учетом этих факторов, целесообразно обратить внимание на разработку методов обеспечения максимальной скорости передачи данных по каротажному кабелю одновременно с трех позиций: оптимальность формы сигналов при согласовании с частотными характеристиками кабеля; применение фильтров восстановления формы сигналов при приеме сигналов с кабеля, в том числе на высоком уровне статистических шумов; устойчивость передачи сигналов при достаточно больших допусках на вариации электрических параметров кабелей в процессе их эксплуатации.

Задачей настоящей работы является исследование электрических характеристик каротажных кабелей с целью их обобщения по зависимости от конструктивных характеристик и первичных электрических параметров, на основе которого возможно выделение интегральных электрических параметров, позволяющих с высокой степенью надежности прогнозировать и оценивать импульсную пропускную способность кабелей. Практической задачей является создание обобщенной математической модели кабеля, как специфической технологической линии передачи информации, позволяющей моделировать и уточнять передаточные функции кабелей при решении различных производственных задач ГИС применительно к различным типам протоколов передачи данных.

Как правило, кабельные каналы связи рассматриваются в рамках теории однородных длинных линий, предполагающей постоянство электрических параметров кабеля на всех отрезках его длины. Одножильные бронированные каротажные кабели, в принципе, относятся к разновидности коаксиальных кабелей с концентрическим расположением жилы (прямого провода) внутри брони (обратного провода). Взаимодействие электромагнитных полей прямого и обратного проводника в коаксиальном кабеле при равных значениях прямого и обратного тока не создает электромагнитного поля за пределами кабеля, т.е. электромагнитное поле сигналов сосредоточено внутри кабеля, что и обеспечивает эффективную передачу электромагнитной энергии с минимальными потерями. Центральная жила и оплетка коаксиальных кабелей выполняются из немагнитных материалов (медь), что также не создает потерь на перемагничивание магнитных материалов.

Каротажный кабель, в отличие от коаксиального, в качестве оплетки имеют стальную броню без поверхностной изоляции, а, следовательно, локализованного обратного тока в броне не существует как для одножильного, так и для многожильного кабеля. Это действительно как для кабеля на барабане лебедки, где броня представляет в какой-то мере сплошной металлический монолит, так и для кабеля в скважине, где броня – линейный заземленный электрод. Следовательно, в каротажных кабелях появляется весьма существенный источник потерь электромагнитной энергии сигналов – на перемагничивание стальной брони электромагнитными полями токопроводящих жил и межпроводниковыми электромагнитными полями (при двухпроводной передаче сигналов), а также на потери электромагнитной энергии в окружающей среде. Эти потери нарастают с увеличением частоты тока и приводят к существенному затуханию высокочастотных составляющих сигналов и частотному ограничению импульсной пропускной способности кабеля. Параметры потерь и их место в математической модели кабеля подлежать уточнению.

Идеальная кабельная линия.




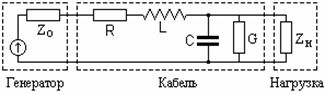
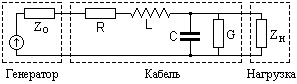
Рис. 1. Кабельная линия передачи сигнала.
Основное уравнение кабельной линии (токопроводящей пары жила-броня в одножильных и пар жила-броня или жила-жила в многожильных кабелях), эквивалентная электрическая схема которой приведена на рис. 1, определяют первичные электрические параметры: активное сопротивление R, индуктивность L, емкость С и проводимость G на единицу длины линии (1 км). На вход линии подключается источник сигналов (генератор) с внутренним сопротивлением Z_o, на выход линии – приемник сигналов с входным сопротивлением Z_н (нагрузка линии). Сигнал на входе линии задается в виде временной функции напряжения 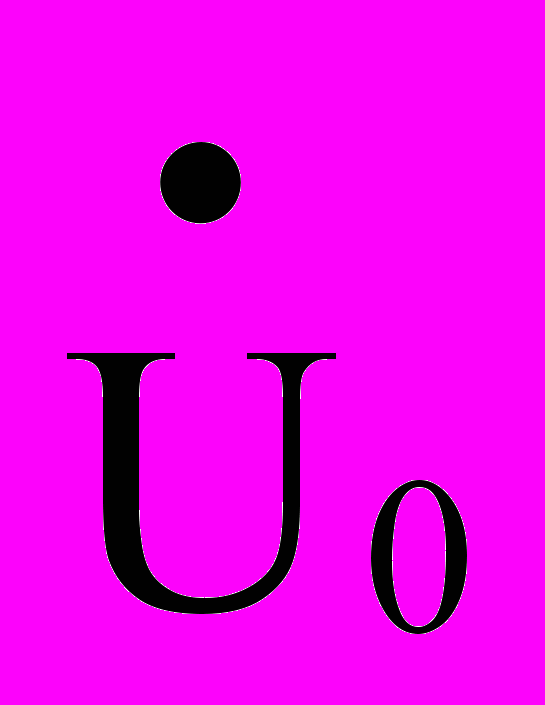и тока 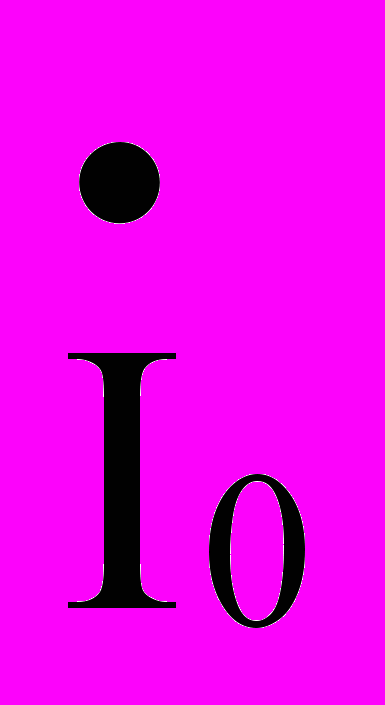. На выходе линии (на нагрузке) соответственно имеем 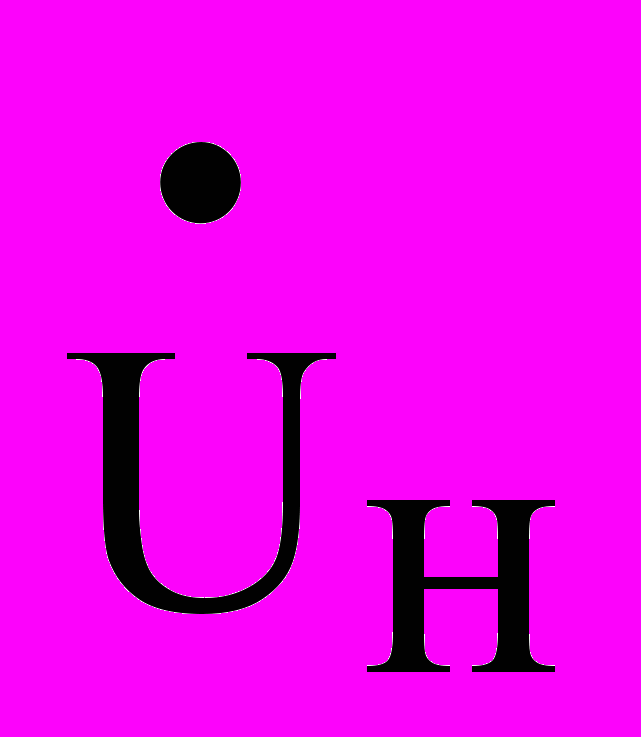и 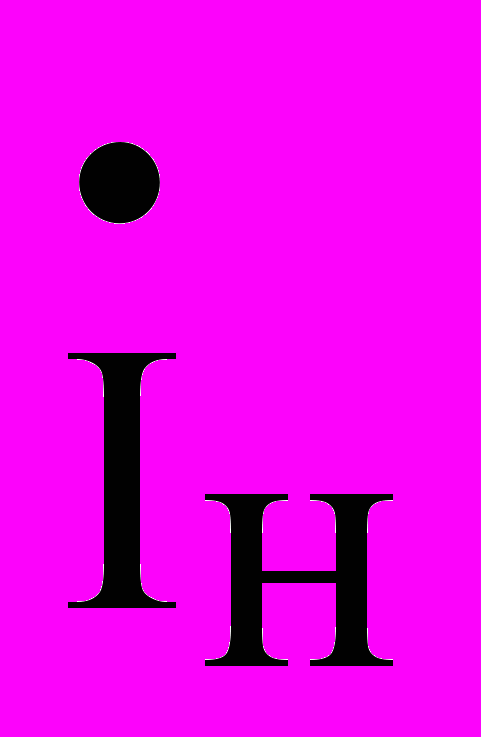. Падение напряжения и утечка тока на произвольном участке dx линии определяются уравнениями:

-d 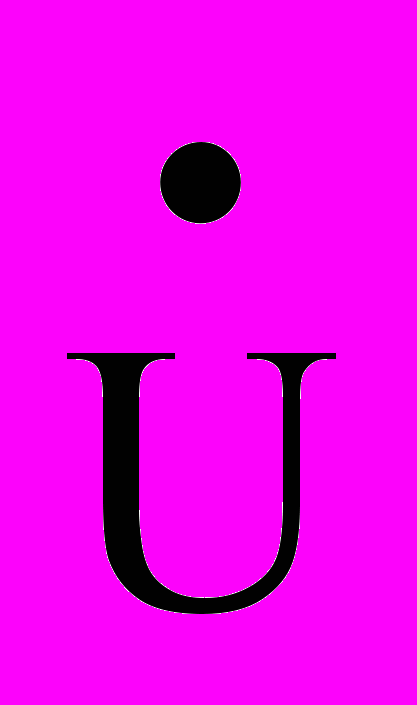/dx = 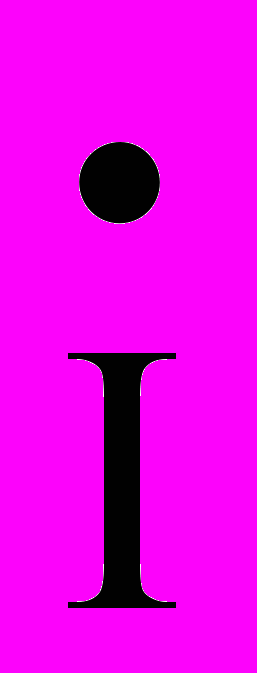(R+jL), -d 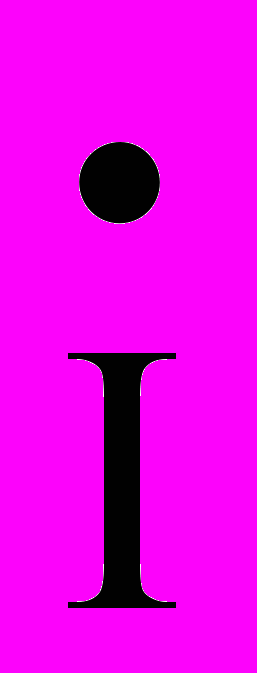/dx = 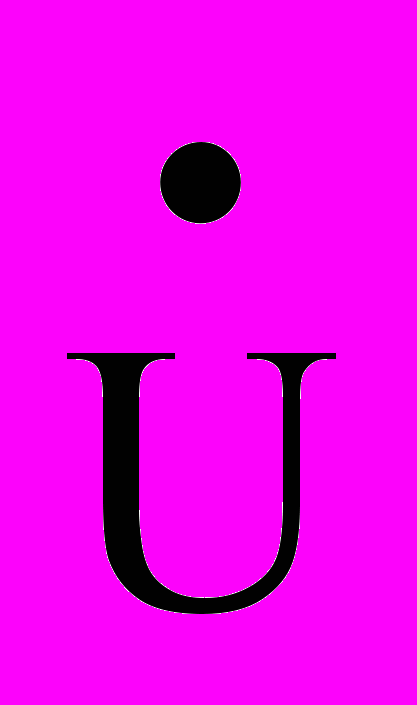(G+jC).

Решение уравнений для напряжения и тока в произвольной точке х линии /1/:

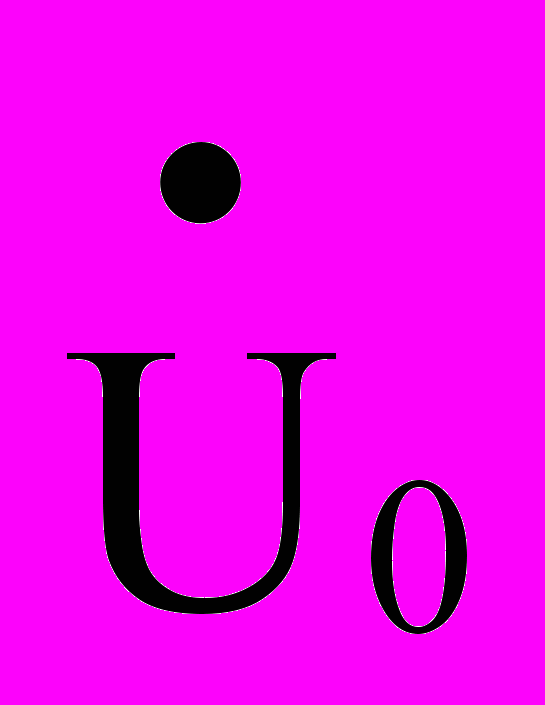=c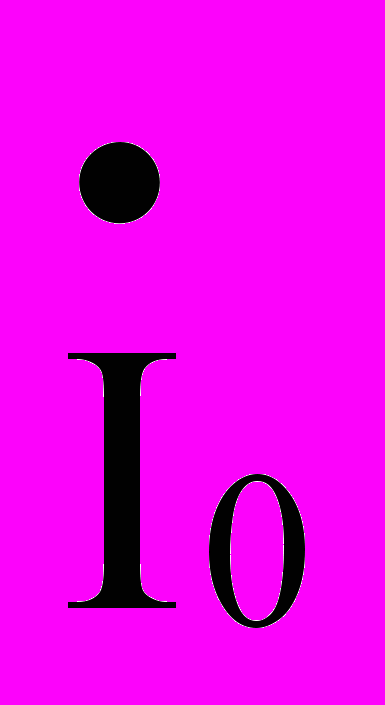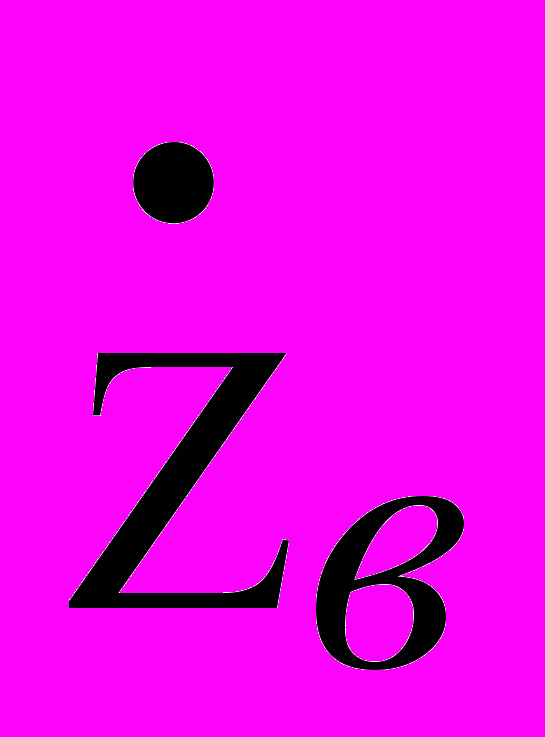h x – sh x, 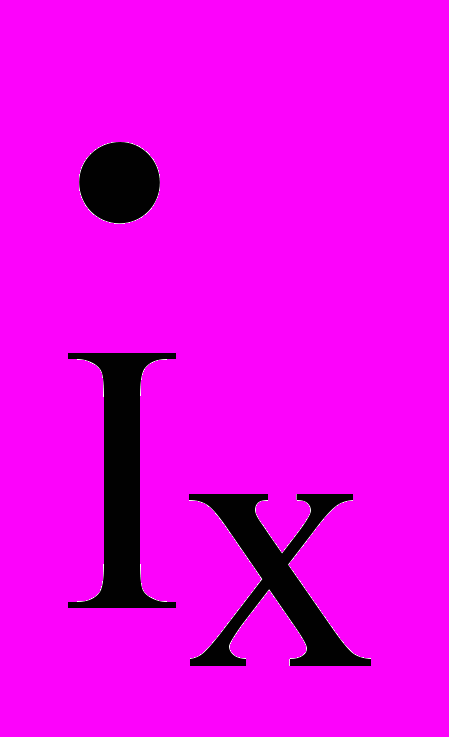=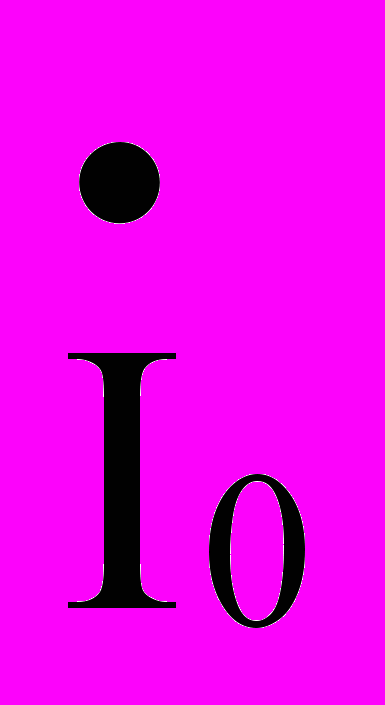ch x – (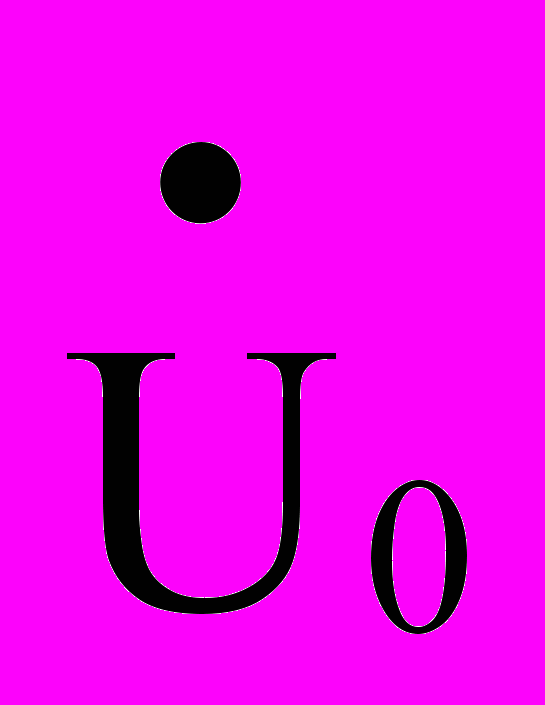/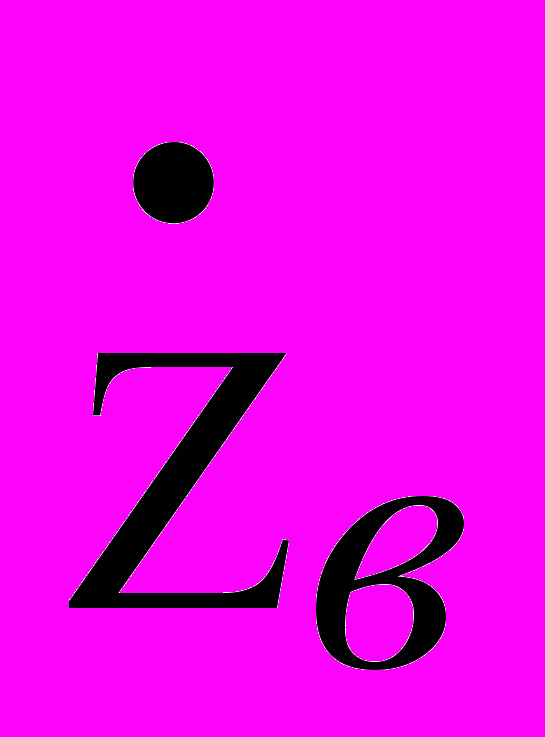) sh x, (1)

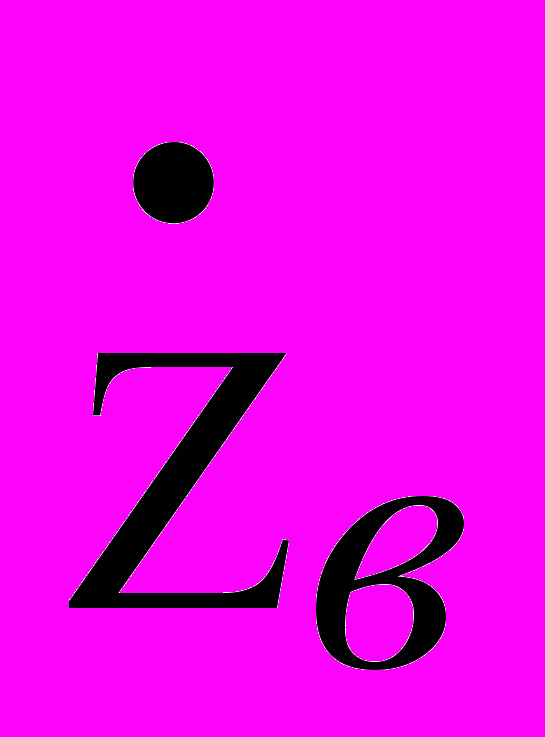= (R+jL)/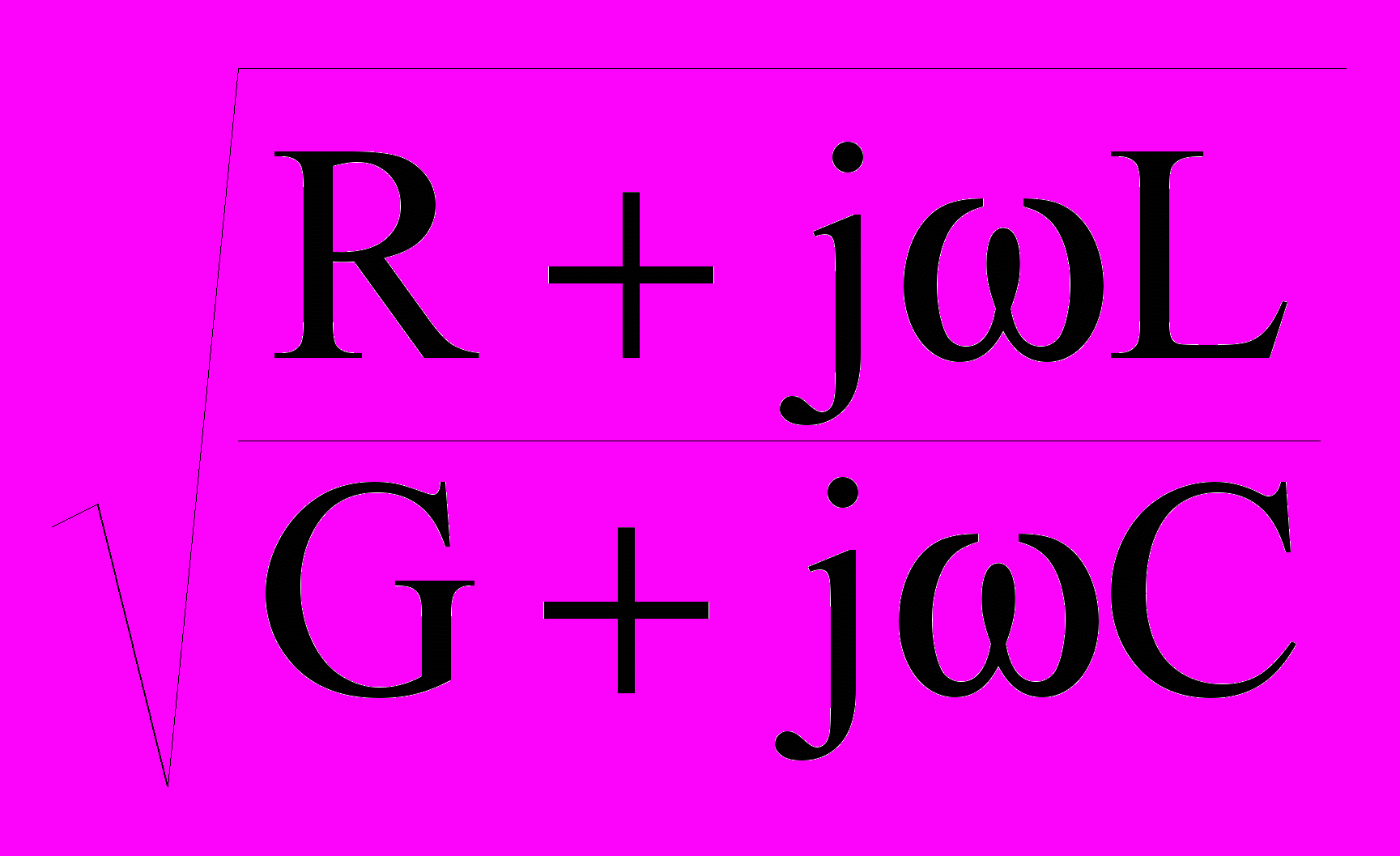 , (2)

где Z_в() - комплексное волновое сопротивление кабеля,  - коэффициент (постоянная) распространения линии:

 =  + j =, (3)

В выражениях (1) первые члены правой части - уравнения падающих волн напряжения и тока (от генератора к нагрузке), вторые члены – уравнения волн, отраженных от конца кабеля, энергия которых не поглотилась в нагрузке. Значения Z_в() и  относят к вторичным параметрам кабеля. Выражения действительны для любой точки кабеля, в том числе на выходе кабеля при x = , где  – длина кабеля. Коэффициенты  и  являются собственными коэффициентами амплитудного затухания и фазового сдвига волны напряжения, проходящей через кабель. Значения коэффициента  обычно приводится в неперах (или в децибелах) на километр. По мере нарастания частоты коэффициент затухания увеличивается с постепенным уменьшением степени увеличения, а начиная с частот порядка 10-20 кГц практически постоянен и стремится к значению  = 0.5(R 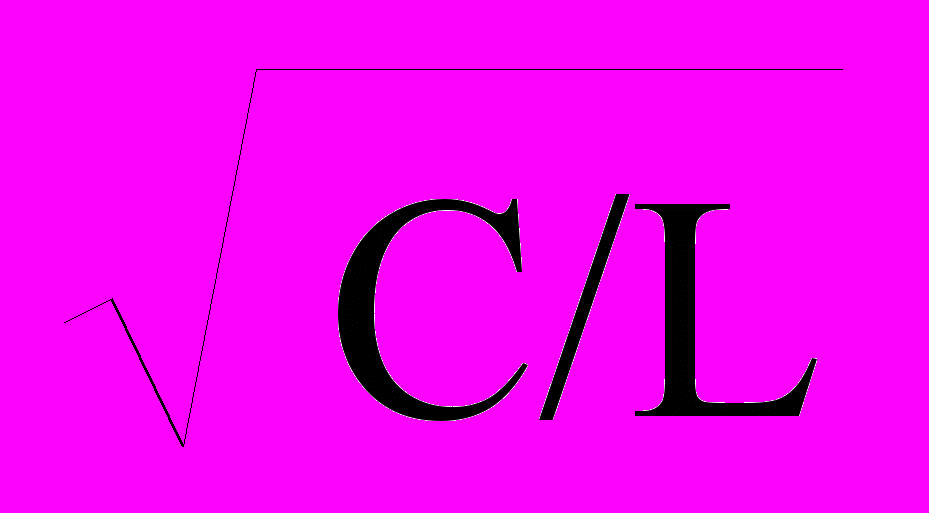+ G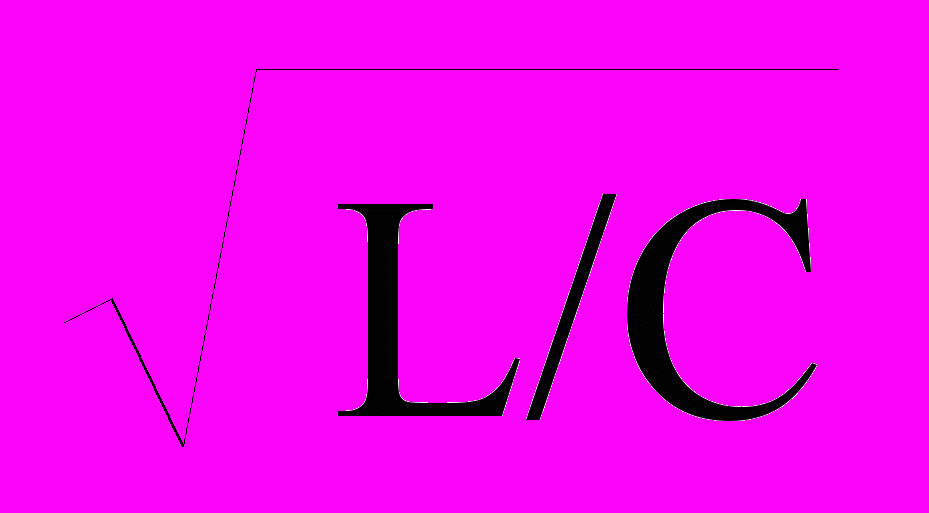). Коэффициент фазового сдвига на низких частотах увеличивается синхронно с коэффициентом затухания (при f < 1 кГц   ), а затем, с частоты порядка 1 кГц, нарастает линейно и пропорционально частоте (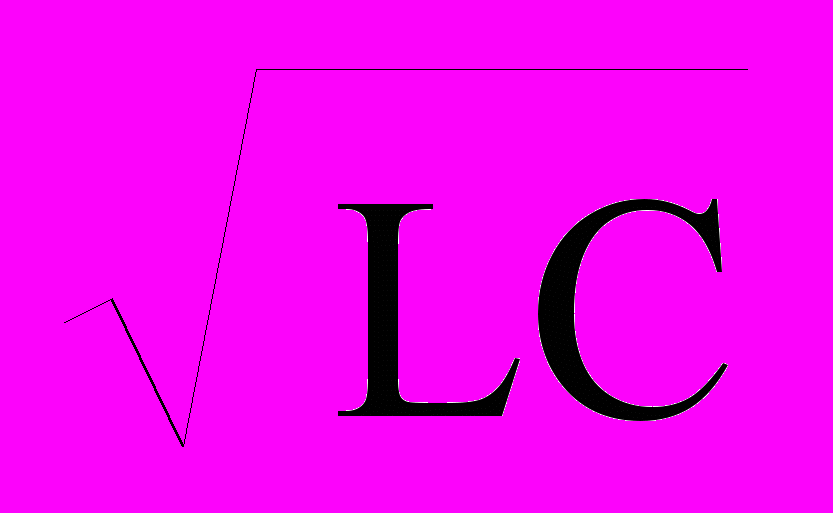 = ). Это обеспечивает формирование фронтальной волны распространения сигнала по кабелю с постоянной скоростью для всех частотных составляющих сигнала, за исключением низких частот.

Волновое сопротивление кабельной линии – это сопротивление электромагнитной волне при ее распространении вдоль линии при отсутствии отражений от концов. Оно зависит от первичных электрических параметров кабеля и частоты сигнала. Если электромагнитную волну представить в виде раздельных волн напряжения и тока, то отношение между ними и представляет собой волновое сопротивление цепи: = /.

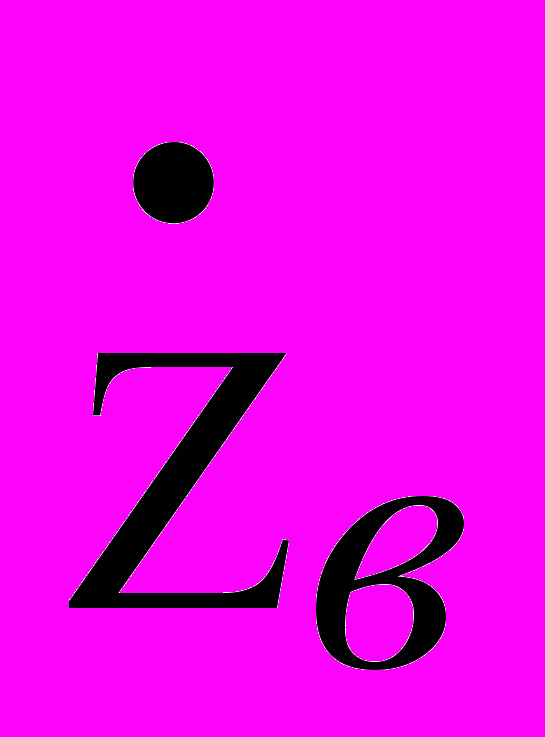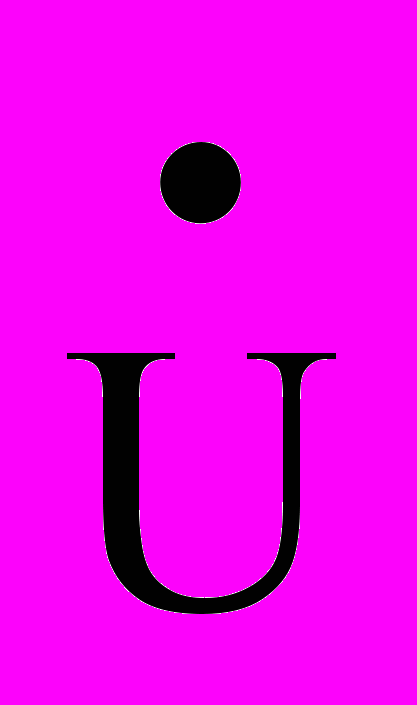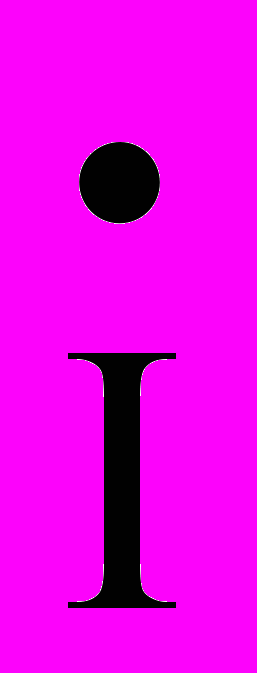Волновое сопротивление - комплексная величина и состоит из активной и реактивной составляющей. Зависимость волнового сопротивления от частоты наиболее существенна в области низких частот и имеет емкостной характер, где волна тока опережает волну напряжения в максимуме на 45^о. В области частот выше 10-20 кГц имеет место L > R, C >> G и значение волнового сопротивления стремится к постоянной величине Z_в(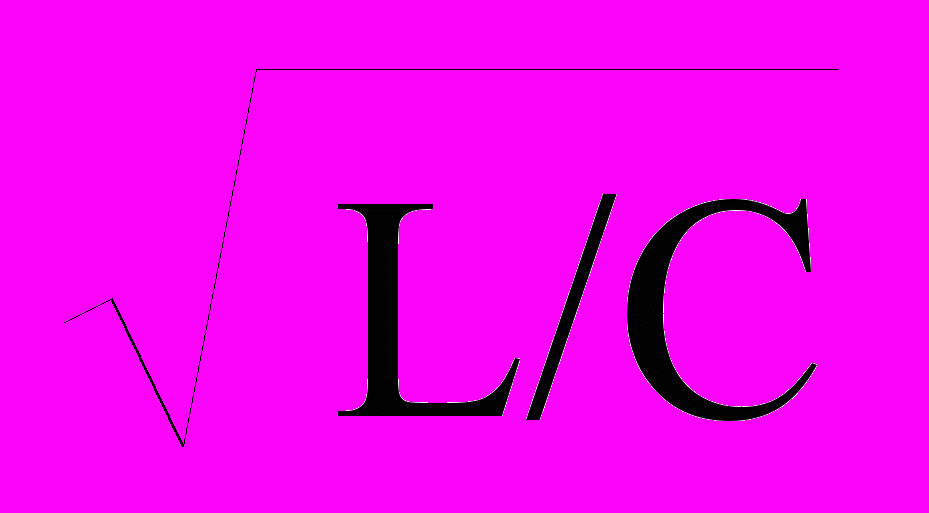)  = R_в, которую называют номинальным (характеристическим) волновым сопротивлением кабеля. В области низких частот модуль волнового сопротивления практически на два порядка выше номинального волнового сопротивления.

Коэффициент передачи сигнала по кабельной линии (передаточная функция кабеля) определяется из выражения (1):

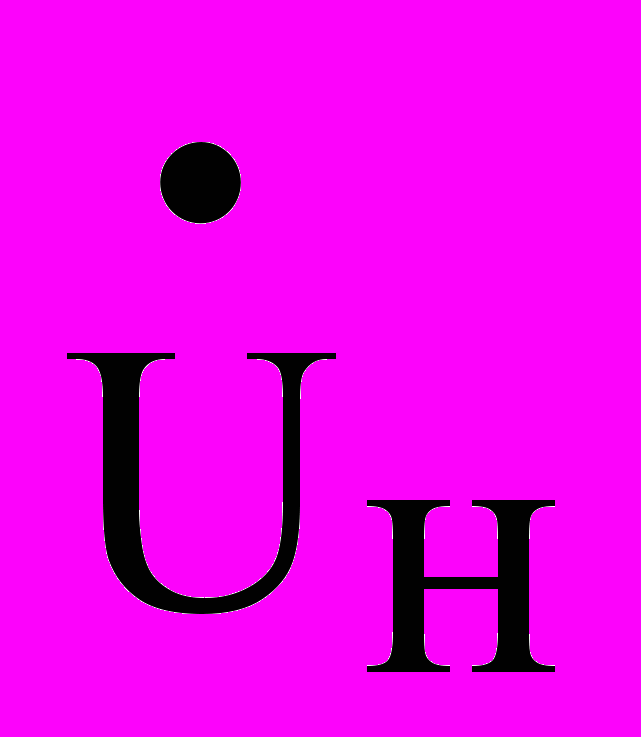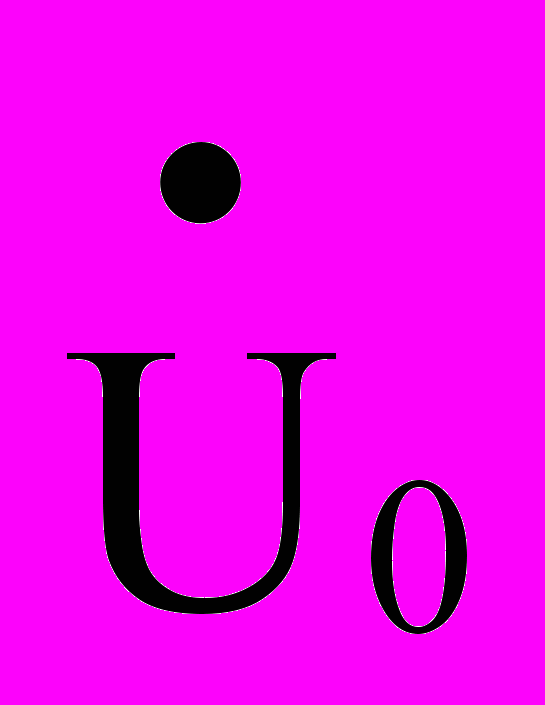=/= ch 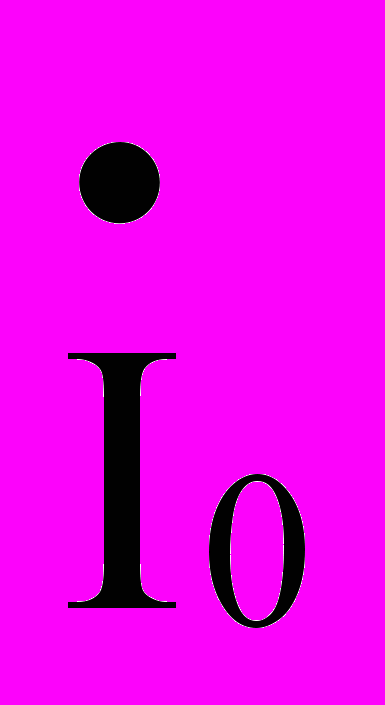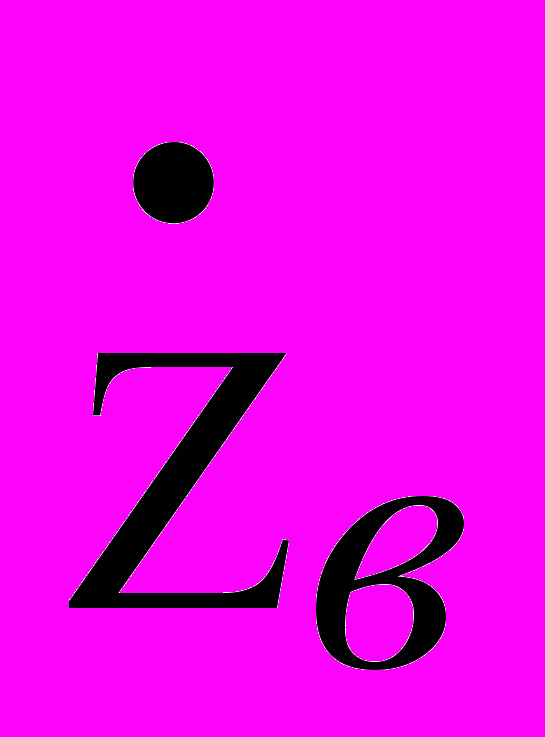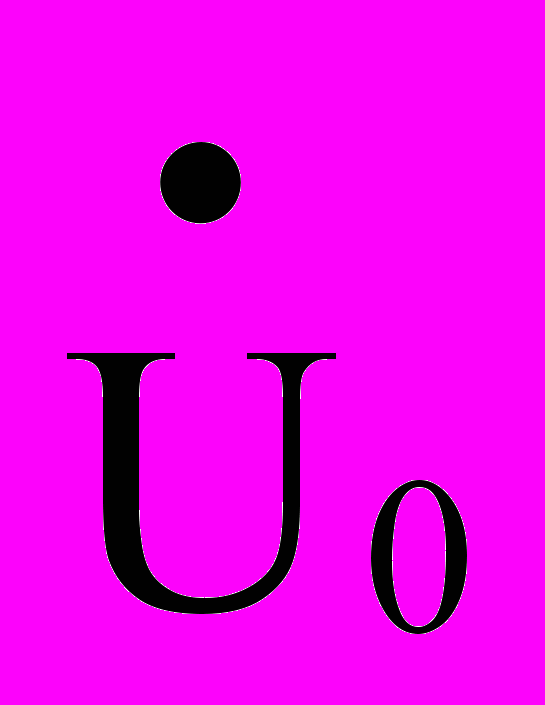 – (/)sh , (4)

= ch 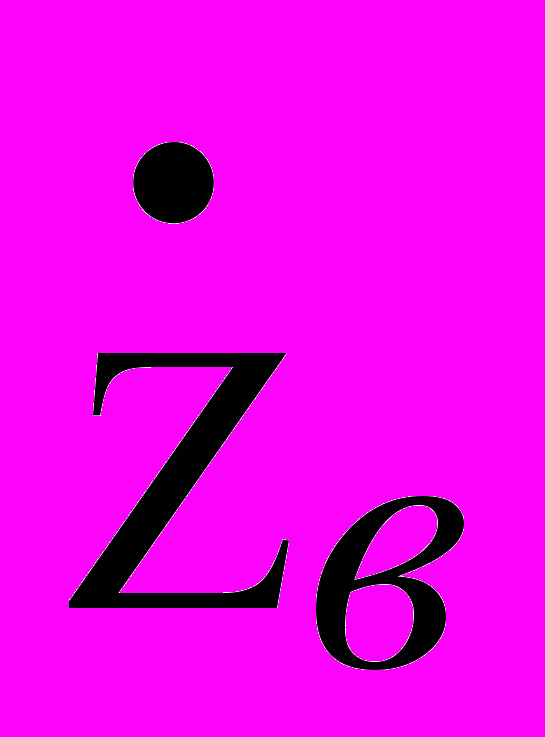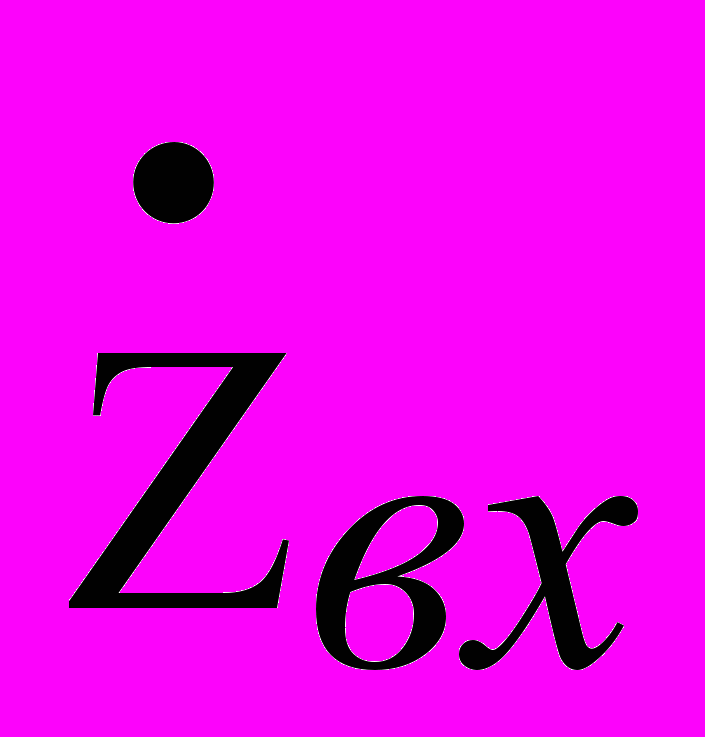 – (/)sh , (4')

где  – длина кабеля, Z_вх – комплексное входное сопротивление кабеля /1/:

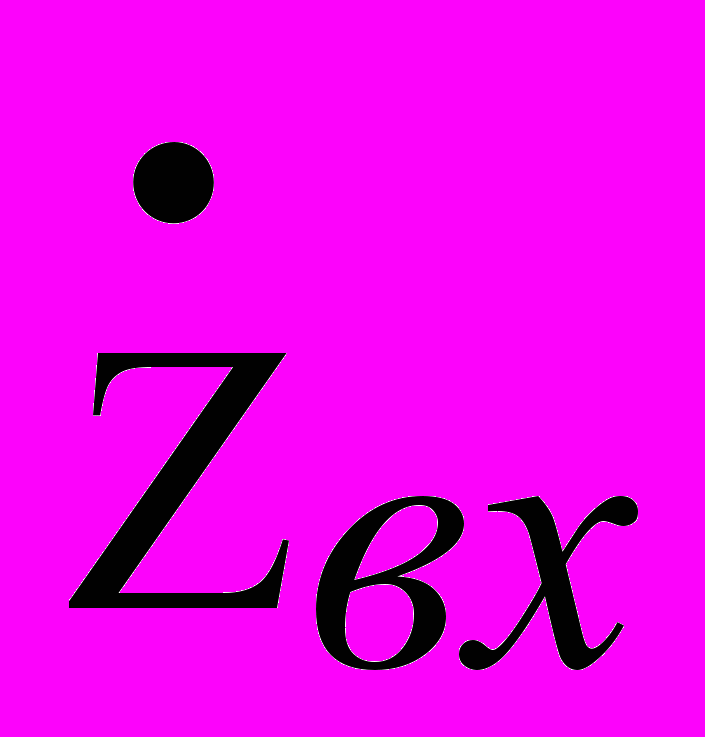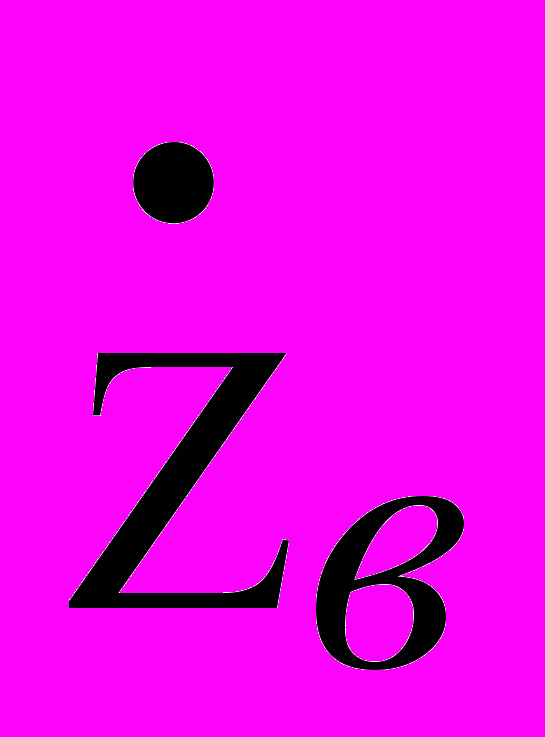= (Z_н ch 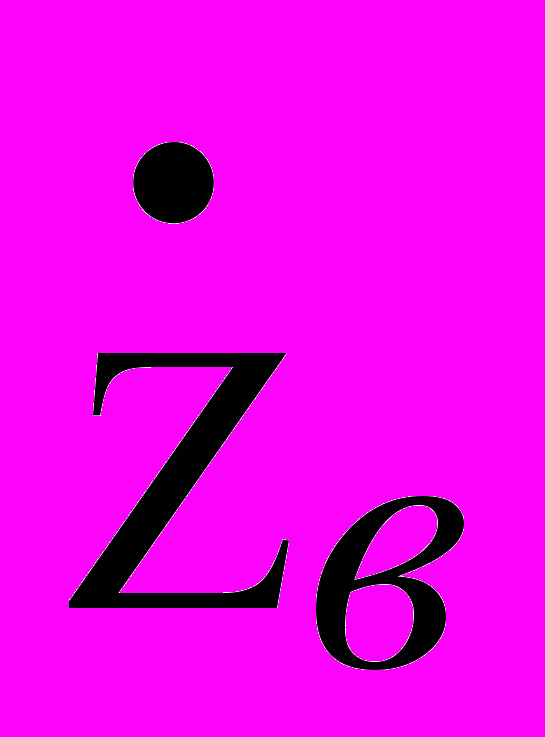 + sh 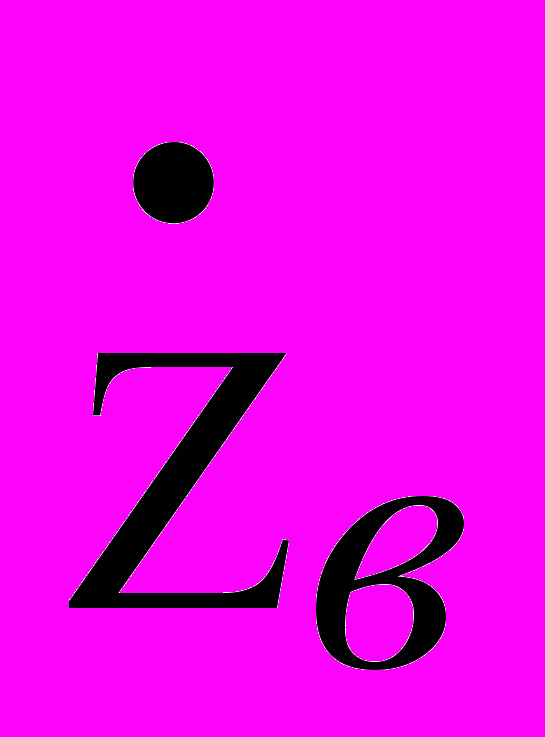) / (ch  + Z_н sh ). (5)

В зависимости от величины нагрузки Z_н различают два режима передачи сигналов:

Режим бегущей волны сигнала при сопротивлении нагрузки Z_н() = Z_в(), равной волновому сопротивлению кабеля по всему частотному диапазону. В этом (полностью согласованном) режиме 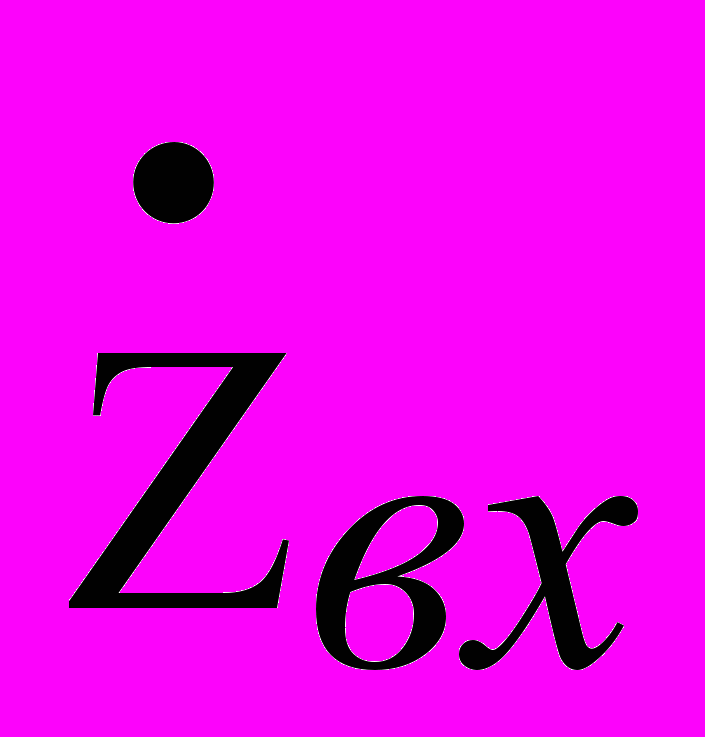= 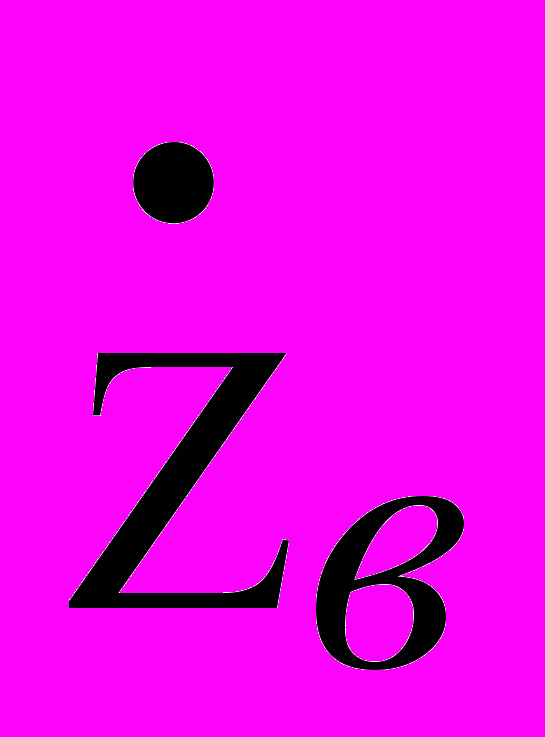, отраженная волна отсутствует и выражения (1) и (4) упрощаются:

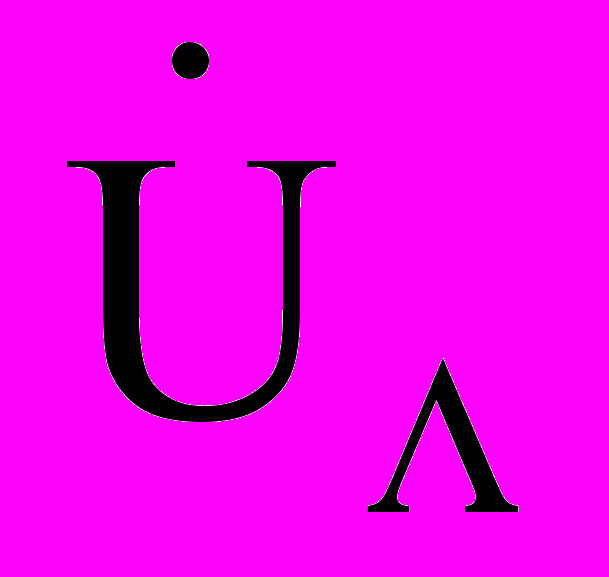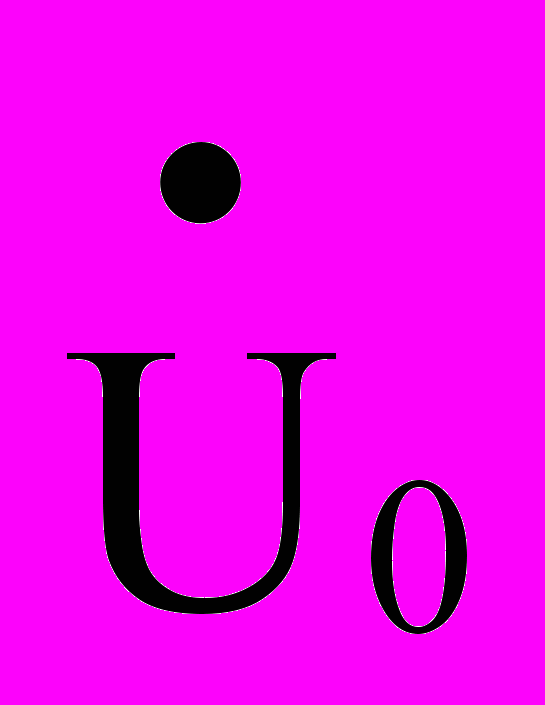=ехр(-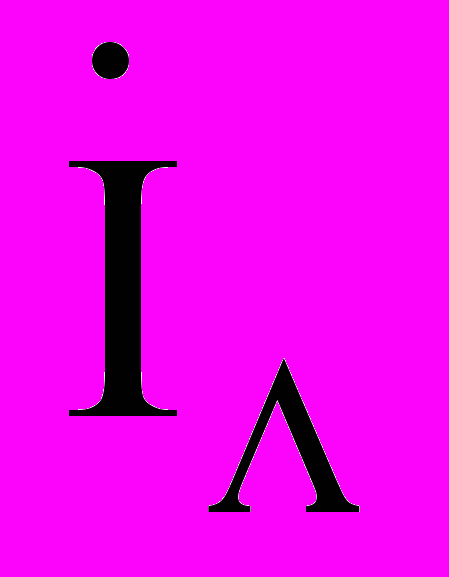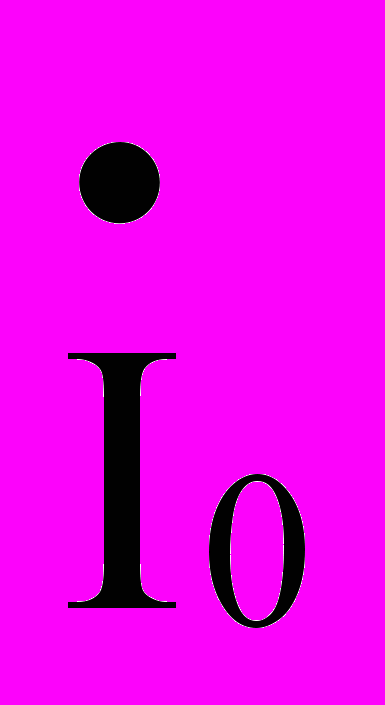), =ехр(-), = ехр(-). (6)

Затухание сигналов в идеальном кабеле определяется потерям энергии, которые подразделяются на два вида: потери в активном сопротивлении кабеля R (нагревание проводников), и потери в изоляции кабеля за счет ее проводимости. Проводимость G зависит от утечки тока через диэлектрик и затрат энергии на его поляризацию:

G = (1/R_и) + Ctg(), (7)

где: R_и – сопротивление изоляции, С – емкость кабеля, tg() – угол диэлектрических потерь. Значение  для изоляции не превышает десятитысячных долей и начинает сказываться на частотах в десятки МГц. Отсюда следует, что частотная зависимость модуля коэффициента передачи кабеля (или АЧХ – амплитудно - частотная характеристика) в области низких частот обусловлена, в основном, изменением соотношения сопротивлений R и Z_н() (постепенное уменьшение коэффициента передачи) и стабилизируется на частотах выше 10 кГц, где Z_н(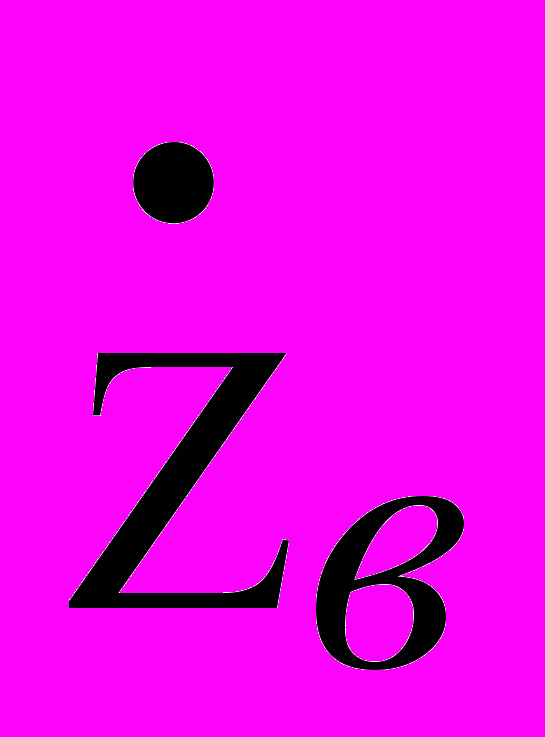) =  R_в = const. Что касается фазочастотных характеристик (ФЧХ) кабелей, то, как это следует из выражения (5), значение фазового угла = - увеличивается с увеличением частоты, а на частотах выше 20 кГц равно -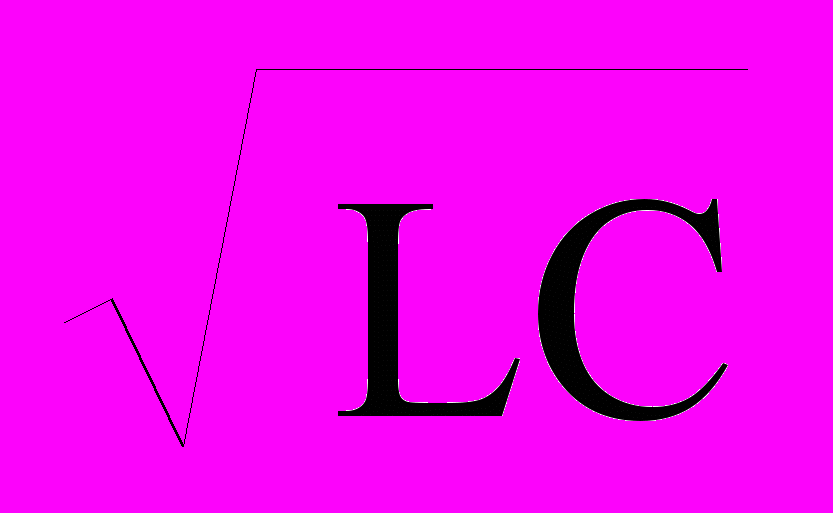, т.е. прямо пропорционально частоте и длине кабеля.

Режим согласованной нагрузки наиболее эффективен при передаче сигналов по кабелю. Однако в пассивных линиях связи обеспечить такой режим при передаче импульсных широкополосных сигналов практически невозможно (Z_н() = Z_в() по всему частотному диапазону). Для решения данной проблемы используются частотно – зависимые корректоры линии связи /8,9/.

Режим несогласованной нагрузки. Как правило, сопротивления генератора и нагрузки представляют собой постоянные величины, независимые или слабо зависимые от частоты. Обычно, их значения устанавливаются равными характеристическому сопротивлению кабеля, но при этом кабель остается существенно рассогласован с генератором и нагрузкой в области низких частот. Неполная согласованность кабеля создает отраженные волны, которые достигают начала кабеля и отражается назад в кабель и т.д., при этом километрический коэффициент затухания на низких частотах зависит от длины кабеля.

Если коэффициент  определяет сдвиг по фазе колебания с частотой f на единице длины, то длина волны  в единицах длины кабеля будет равна длине кабеля, при которой сдвиг по фазе достигает величины 2, т.е.  = 2. С учетом этого скорость распространения частотных волн в кабеле определяется выражением: ff, Максимальная задержка сигнала соответствует низким частотам. На частотах выше 10 кГц при 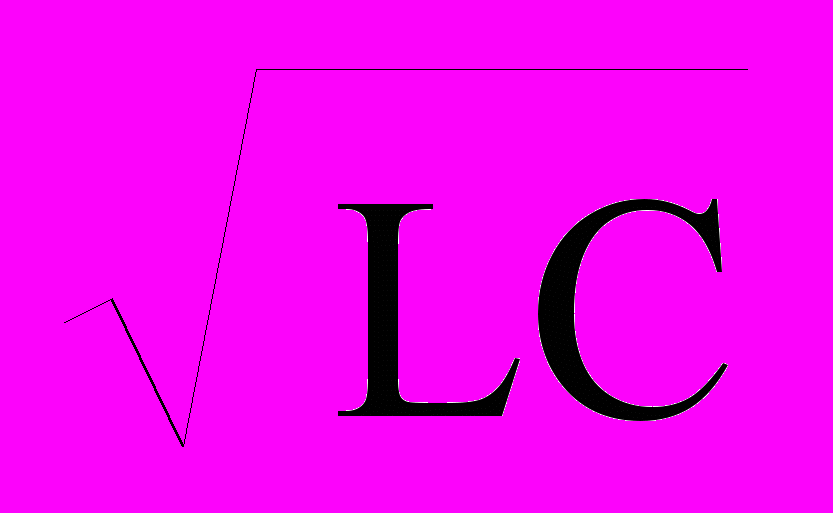 =  значение скорости распространения волны стремится к постоянной величине .

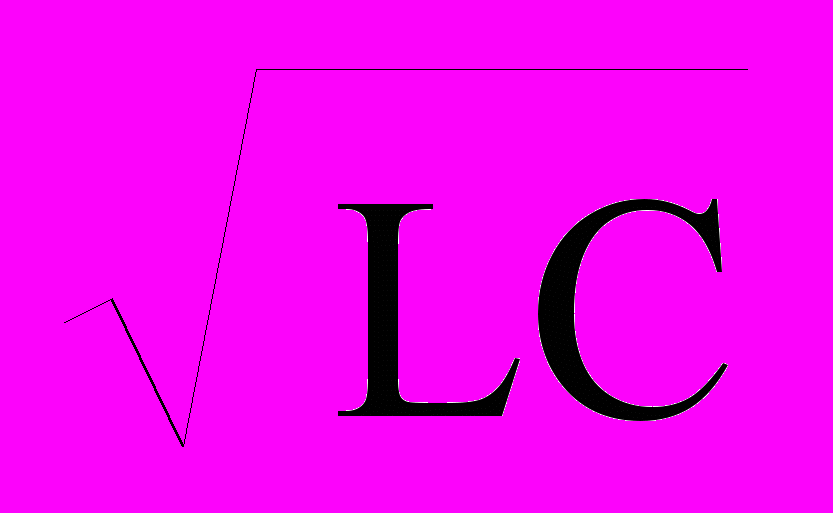Таким образом, начиная с частот порядка 5-10 кГц, кабельные линии связи имеют практически постоянные параметры. В этой частотной области обеспечиваются минимальные искажения спектра сигналов, а соответственно и формы самих сигналов при передаче по кабелю. Отсюда следует, что кабель является оптимальной линией передачи высокочастотных и радиоимпульсных сигналов, энергия частотного спектра которых минимальна в области низких частот.

Реальная кабельная линия.

Реальный каротажный кабель существенно отличается от идеального. При сохранении общей теории однородных длинных линий это требует уточнения электрических параметров кабеля.

Активное сопротивление линии передачи сигналов кабеля состоит из суммы сопротивлений прямого и обратного проводников. Для одножильного (ОБК) и многожильного бронированного кабеля (МБК) с однопроводной линией передачи информации (МБК-1п, броня в качестве обратного проводника) сопротивление постоянному току определяется, в основном, сопротивлением токопроводящей жилы (ТПЖ): длиной и конструкцией жилы, диаметром и материалом проволок жилы и температурой окружающей среды. Сопротивление обратного проводника (брони) много меньше величины сопротивления жил и его значением можно пренебречь. Для двухпроводной линии передачи (МБК-2п) полное сопротивление складывается из сопротивления двух ТПЖ.

Жилы каротажных кабелей – скрутка из нескольких проволок. Со временем переходное сопротивление между проволоками возрастает (окисление поверхности) и сопротивление жилы может увеличиваться на 10-15%. При работе в скважинах с температурой до 150⁰С на забое сопротивление жил кабеля может увеличиваться на 20-30%. Нормальным явлением можно считать изменение сопротивления жил кабелей в процессе каротажа в пределах до 10%. Соответственно, пределом _R  0.1 может ограничиваться и точность математической модели активного сопротивления жил кабеля.

Активное сопротивление кабелей на высоких частотах пропорционально корню квадратному из частоты. Это определяется поверхностным эффектом - вытеснением тока к поверхности проводов, которое возрастает с увеличением частоты, и взаимодействием полей проволок кабеля. Зависимость сопротивления от частоты дополнительно осложняется влиянием скрутки проволок. Методы расчетов электрических параметров многопроволочных проводников каротажных кабелей отсутствуют. По данным работ /3,5/ частотная зависимость полного активного сопротивления жил каротажного кабеля может быть аппроксимирована следующими формулами:

R(f) = R[1+П(f)P(f)], П(f) = 0.0078r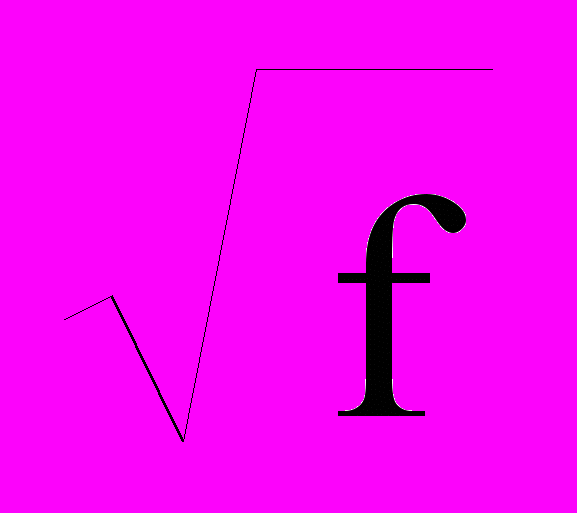, P(f) = 1-exp(-af10^-4). (8)

где: П(f) - коэффициент поверхностного эффекта, P(f) - поправочный коэффициент на конструкцию жилы и кабеля, r - радиус жилы в мм, a - частотная постоянная кабеля порядка (0.1-0.3) для ОБК, ~(0.30.5) для МБК-1п, ~(0.50.8) для МБК-2п, и приближается к 1 для коаксиальных видеолиний.

Проводимость изоляции жил кабеля и электромагнитные потери. Проводимость изоляции жил кабеля G определяется уравнением (7) и на частотах до 1 МГц не имеет значения, т.к. сопротивление изоляции R_и в условиях эксплуатации не менее 10 МОм/км, а параметр  не более 0.0005. Однако, как уже отмечалось, в бронированном каротажном кабеле имеют место существенные электромагнитные потери, точное количественное значение которых предусмотреть практически невозможно. Влияние этих потерь на расчеты коэффициентов затухания сигнала эквивалентно потерям на поляризацию изоляции кабеля (частотно зависимая потеря энергии) и много больше их по значениям. По данным работ /4,6/ затухания сигнала в каротажных кабелях может быть предложена для использования формула аппроксимации эквивалентной проводимости кабеля:

G = 2fCR(f), (9)

где значение  порядка 12-14 для одножильных и 10-13 для многожильных кабелей.

Емкость токопроводящих жил определяется конструкцией кабеля и зависит от материала и толщины изоляции ТПЖ. Для одножильных кабелей емкость ТПЖ (в мкФ/км) может оцениваться по уравнению: С = /(18ln(D/d)), где  - диэлектрическая проницаемость изоляции, D – внешний диаметр жилы по изоляции, d – диаметр токопроводника жилы. Значение емкости, как правило, находится в диапазоне 0.1-0.12 мкФ/км. Емкость между жилой и броней в многожильных кабелях имеет примерно такие же значения для однотипных по конструкции жил, а емкость жила-жила в 1.6-1.8 раз меньше. Зависимость емкостей жил от частоты практического значения не имеет. При повышении температуры емкость жил несколько уменьшается за счет уменьшения диэлектрической проницаемости изоляции, а при повышении давления – увеличивается. В скважинных условиях эти процессы компенсируют друг друга и изменение емкости незначительно.

Индуктивность кабеля. Собственная индуктивность коаксиальных линий с увеличением частоты уменьшается вследствие поверхностного эффекта в проводах. Общая индуктивность пары жила-броня складывается из собственной индуктивности жилы и межпроводниковой индуктивности жила-броня. Для пары жила-броня из разных металлов, она может определяться с помощью уравнения, которое используется для расчетов индуктивности коаксиальных кабелей (в Гн/км):

L(f) = 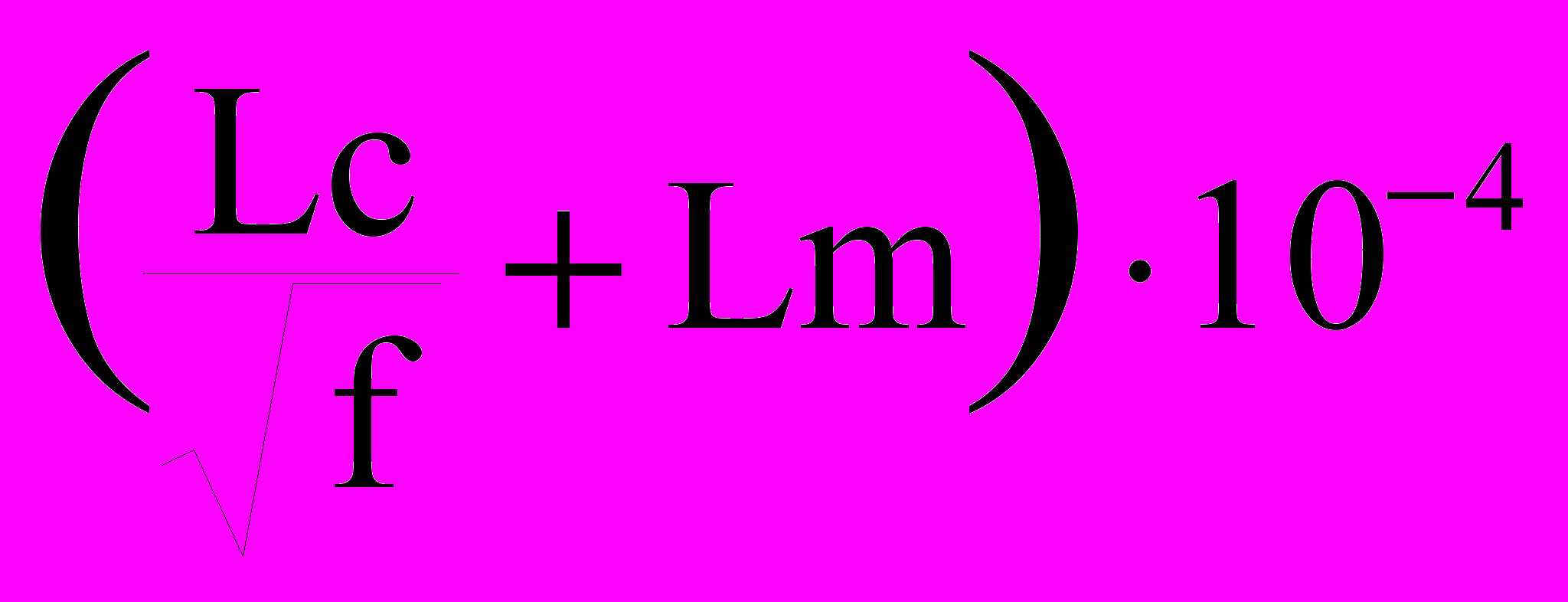, (10)

Lc = 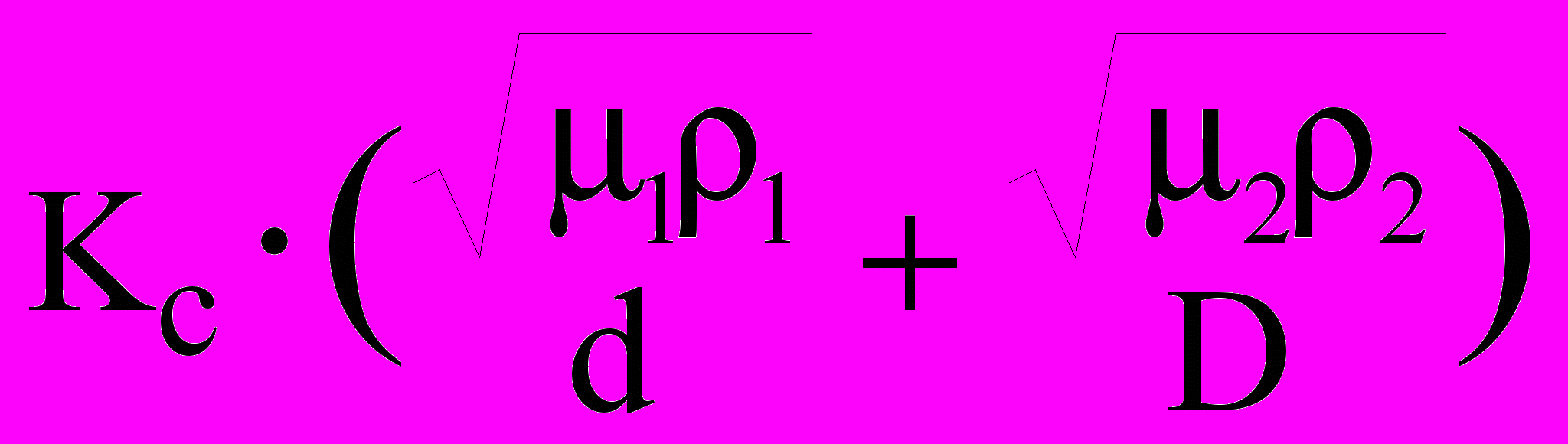, K_c =100/ (11)

Lm = bln(D/d), (12)

где: f - частота тока (Гц),  - магнитные проницаемости жилы и брони (медь ₁=1, сталь ₂=100120),  - удельные сопротивления (₁Оммм²/км, ₂Оммм²/км), d – диаметр жилы (мм), D – внутренний диаметр брони кабеля, (мм), b – коэффициент учета конструкции кабеля (b  2 для ОБК, b  3 для МБК). Значение Lc/ 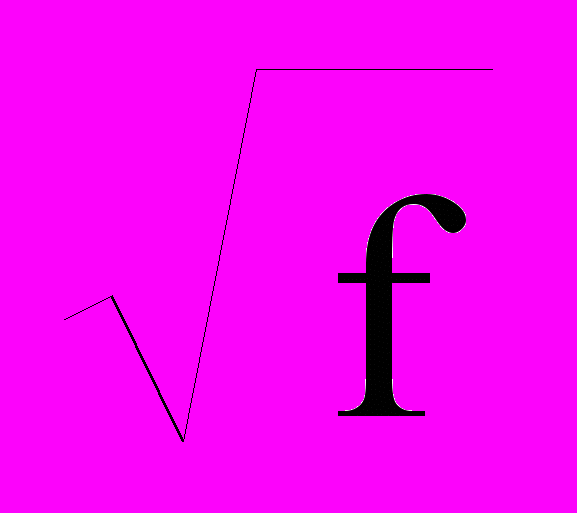- собственная индуктивность жил, Lm – межпроводниковая.

При сопоставлении расчетных значений индуктивности кабелей с результатами измерений индуктивности, приведенными в работах /3,4,6/, отмечено, что формулы (11-13), как правило, завышают значения индуктивностей на частотах выше 100 Гц, играющих основную роль при расчетах вторичных параметров кабеля. По-видимому, здесь играет роль тот же фактор разницы значений прямого и обратного токов в жиле и броне и конструкция брони. Двойной слой из стальных проволок с перекрестным повивом слоев не эквивалентен оплетке коаксиального кабеля. Сходимость расчетных и измеренных значений индуктивностей повышается при использовании в формулах (11-12) значения "эффективного" диаметра D_э = kD кабеля вместо внутреннего диаметра брони D. Величина коэффициента k находится в пределах (1-1.2) для МБК-2п, (1.2-1.4) для МБК-1п и (1.4-1.6) для ОБК. Для ОБК это практически соответствует диаметру по среднему слою брони, что объяснимо по своей физической сущности. Более точная аппроксимация экспериментальных данных может производиться дополнительным изменением коэффициента К_с в пределах 10%.

Как следует из формулы (11), зависимость индуктивности от частоты определяется собственной индуктивностью жил. Она же определяет зависимость индуктивности от температуры (температурное изменение ). В области высоких частот индуктивность определяется, в основном, межпроводниковой индуктивностью. Индуктивности кабелей на лебедке и в скважине практически не отличаются. При намотке кабеля на лебедку его индуктивность может увеличиваться на 1-3% в зависимости от конструкции лебедки и состояния (степени окисления) поверхности брони кабеля.

Межпроводниковая индуктивность многожильных кабелей для пары жила-жила увеличивается за счет взаимной индуктивности пар и влияния соседних жил и может оцениваться по формуле аппроксимации экспериментальных данных:

Lm  bln((D_э/d)+s(2c/d)), (13)

где с – расстояние между центрами жил, s  (0.4-0.5) в зависимости от конструкции кабеля (уточняется по измерениям индуктивности на высоких частотах).

По измеренному значению индуктивности на частоте f₁ частотная функция индуктивности может вычисляться по формуле:

L(f) 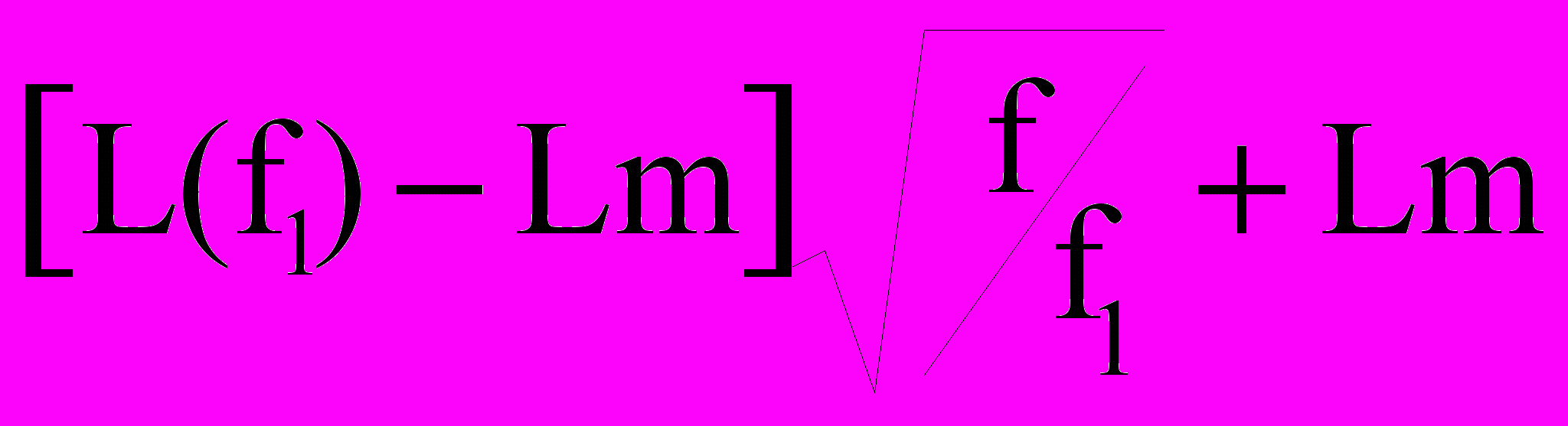 . (14)

Волновое сопротивление. Каротажные кабели не в полной мере удовлетворяют требованиям однородных линий. Однако это не мешает использованию выражения (2) как в теоретическом плане, так и при чисто практических расчетах с погрешностью не более 3-5%, если специфика каротажных кабелей учитывается в функциях частотного распределения первичных параметров. При этом форма зависимости волнового сопротивления от частоты остается без изменения, несколько изменяются только численные значения зависимости. Волновое сопротивление жила-броня многожильных кабелей при однотипных параметрах жил и брони практически не отличается от одножильных, а для пар жила-жила отличается только увеличением числовых значений сопротивления. Что касается фазочастотных характеристик волнового сопротивления реальных кабелей, то за счет существенного возрастания их индуктивности на низких частотах значения и начальный интервал емкостной составляющей волнового сопротивления сокращаются, а на частотах выше 10 кГц в волновом сопротивлении кабеля появляется индуктивная составляющая, которая дает ощутимый фазовый сдвиг высокочастотных составляющих сигнала.

Частотная характеристика реальной кабельной линии.

Передаточная функция (4) со всеми входящими в нее реальными частотно-зависимыми параметрами являются основной системной функцией, обобщающей все электрические параметры ТПЖ кабеля, т.е полной математической моделью кабеля в частотном диапазоне.




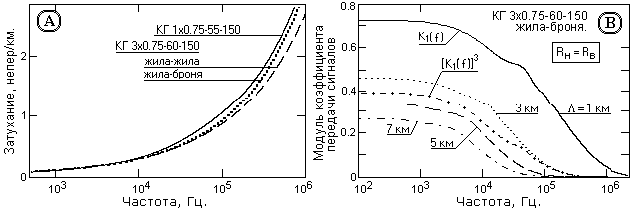
Рис. 2. Частотные характеристики каротажного кабеля.
На рис. 2(А) приведены функции километрического затухания (f) близких по конструкции каротажных кабелей, вычисленные по формуле (3) с учетом реальных частотно-зависимых первичных параметров жил. Затухание реального кабеля существенно отличается от идеального, что определяется, в основном, электромагнитными потерями высокочастотной энергии. Характер частотных зависимостей на низких частотах для одно- и многожильных кабелей практически однотипный. На частотах более 10 кГц затухание одножильных кабелей несколько выше затухания многожильных, причем для последних меньшее затухание имеют пары жила-жила. Однотипность характеристик позволяет при дальнейшем анализе ограничиваться типичной средней частотной характеристикой жил, которая соответствует паре жила-броня многожильного кабеля.

На рис. 2(В) приведены графики модулей рабочих коэффициентов K_p(f) передачи сигналов по кабелю, вычисленные по формуле (4). Электромагнитные потери энергии в реальном кабеле существенно ограничивают его частотный диапазон. Неполная согласованность жил кабеля с нагрузкой по частотному диапазону проявляется в том, что не существует кабельного дискрета, который можно использовать для моделирования кабеля любой длины, как линейной системы. При таком моделировании импульсный отклик кабеля на единичный входной сигнал получается путем свертки импульсных откликов кабельных дискретов, что отображается в частотной области перемножением спектров дискретов. Однако, как это можно видеть на рис. 2(B), даже при дискрете длиной 1 км коэффициент передачи сигнала для кабеля длиной 3 км, полученный перемножением спектров трех дискретов – [K₁(f)]³, существенно отличается от коэффициента передачи, вычисленного по формуле (4). Следовательно, реальный кабель определенной длины даже при оптимальном согласовании с нагрузкой (R_н = R_в) представляет собой самостоятельную систему передачи сигналов с индивидуальными частотными характеристиками.

Формула (4) не учитывает сопротивления источника сигналов, т.е. отражает коэффициент передачи сигналов с входа линии на нагрузку при задании значений сигнала на входе кабеля. Расчет коэффициента передачи с учетом сопротивления источника сигналов (задание сигнала на входе источника сигналов) выполняется по формуле (4) с уточнением значения напряжения U_o:

U_o(f) = U_c(f) Z_вх(f)/(Z_вх(f) + Z_o), (15)

где U_c – сигнал на входе источника сигналов с внутренним сопротивлением Z_o. Согласование кабеля с источником сигналов улучшает монотонность формы частотной характеристики и практически не изменяет относительную зависимость коэффициента передачи сигналов от частоты. Вместе с тем увеличивается относительная зависимость коэффициента передачи от согласования с нагрузкой. Очевидно, что только стабилизация значений сопротивления нагрузки и источника сигналов от влияния дестабилизирующих факторов гарантирует стабильность коэффициента передачи сигналов.

Передаточная функция K_p(f) позволяет дать оценку влияния изменения первичных параметров жил на амплитудно-частотную характеристику кабеля при изменениях первичных электрических параметров жил в процессе эксплуатации. Расчеты показывают, что на низких частотах степень чувствительности АЧХ кабеля порядка 0.5% на 1% изменения активного сопротивления жил, ~0.2% на 1% изменения емкости и индуктивности, и практически отсутствует при изменении электромагнитных потерь. На высоких частотах АЧХ жил практически нечувствительна к изменениям активного сопротивления и индуктивности при повышении степени чувствительности к изменениям емкости и электромагнитным потерям. Учитывая, что в процессе эксплуатации изменения емкости и электромагнитных потерь много меньше изменений активного сопротивления и индуктивности (температурных и пр.) и носят, в основном, долговременный характер (старение кабеля), особое внимание следует обратить на снижение влияния активного сопротивления и индуктивности на передачу сигналов, тем более, что это может достигаться уже рекомендованным методом: энергия сигналов должна быть минимальной в области низких частот.

Что касается устойчивости математической модели передаточных функций жил кабеля к изменению постоянных коэффициентов в расчетных формулах (частотная постоянная «а» в (8), коэффициент учета конструкции кабеля «b» в (12) и пр.), то степень чувствительности передаточных функций к их изменению на порядок ниже, что свидетельствует о достаточной точности модели (не хуже 3-5% по рекомендованным средним значениям). Исключением является коэффициент электромагнитных потерь  прямого действия, значение которого устанавливается непосредственно по передаточной функции (затуханию сигнала на высоких частотах) и приводит модель к фактическим (или паспортным) данным реального кабеля, фиксируя тем самым все возможные факторы отклонения характеристик реального кабеля от идеальной линии передачи сигналов.

Импульсный отклик кабеля.

Полной математической моделью кабеля в реальном масштабе времени, которой также обобщаются все электрические параметры жил, является импульсный отклик жил – форма сигнала на нагрузке жилы при подаче на ее вход единичного дельта-импульса. Импульсный отклик находится обратным преобразованием Фурье частотной передаточной функции кабеля h(t)  K_p(f):

h(t) = 2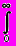K_p(f)cos(2ft) df. (16)

При работе на частотах до 1 МГц масштаб импульсного отклика целесообразно установить в микросекундах и вычислять отклик на единичный входной импульс Ut = 1 (вольтмикросекунда), при этом масштаб значений импульсного отклика на микросекундной временной оси также будет измеряться в вольтах, а площадь импульсного отклика в (вольтмкс), как и положено при прохождении импульса в пассивной линейной системе с потерями энергии, будет меньше 1.



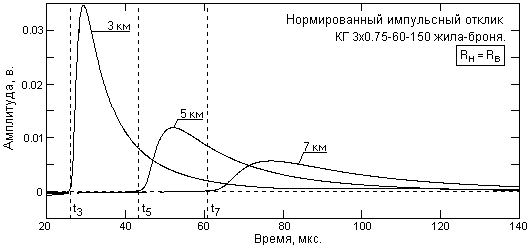
Рис. 3. Импульсные отклики кабелей.

На рис. 3 приведен пример расчета импульсных откликов кабелей различной длины. Задержка фронта откликов показана пунктиром и соответствует расчетному времени задержки на высоких частотах. Форма импульсного отклика жилы кабеля складывается из двух примерно экспоненциальных функций: короткой "зарядной" функции, определяющей фронт отклика, и длинной "разрядной" реакции жилы. При полном согласовании модели с электрическими параметрами жилы, до начала фронта отклика не должно быть никакой реакции, что позволяет производить уточнение основных коэффициентов модели (К_с, D и ) непосредственно в процессе расчетов приведением отклика на данном временном интервале к мало значимым значениям и их обнулением (при условии, что значение обнуляемой площади отклика не превышает 1-2% его полной площади). В связи с зависимостью рабочего коэффициента передачи сигнала от длины кабеля уточнение импульсного отклика для кабелей определенной длины, если имеется необходимость в повышении точности модели, может производиться индивидуально. Появление при расчетах существенного отрицательного выброса перед фронтом импульсного отклика свидетельствует о заниженном значении коэффициентов  или эффективного диаметра D и сопровождается, как правило, занижением расчетных значений R_в относительно фактических (измеренных или среднестатистических). Ликвидацию выброса целесообразно выполнять подбором сначала коэффициента  (грубо), а затем диаметра D (точно).



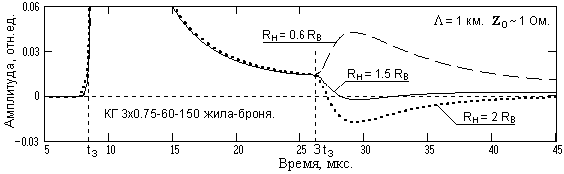
Рис. 4. Форма импульсного отклика при разном согласовании с нагрузкой.

При Z_o  0 форма собственного импульсного отклика кабеля существенно зависит от согласования с нагрузкой. Это определяется тем, что при несогласованной нагрузке отраженная от нагрузки волна полностью отражается от источника сигнала и через утроенное время задержки снова появляется на выходе кабеля, создавая второй пик на спаде отклика, положительный при R_н < R_в или отрицательный при R_н > R_в, что можно видеть на рис. 4 в относительных единицах от максимума отклика. Это позволяет подбором нагрузки R_н > R_в использовать повторный отрицательный пик для компенсации спада импульсного отклика и уменьшать его длительность (пример на рис. 4). Оптимальное согласование достигается при значении R_н порядка (1.2-1.5)R_в в зависимости от длины кабеля (при увеличении длины кабеля этот эффект уменьшается в связи с большим затуханием отраженных волн при двойном прохождении по кабелю). Для кабелей, согласованных с источником сигнала (Z_o ~ R_в), эффект несогласования с нагрузкой уменьшается практически на порядок.

Математическая модель импульсного отклика позволяет проанализировать влияние изменения первичных электрических параметров на форму импульсного отклика. Активное сопротивление жилы практически не изменяет форму отклика и несколько изменяет постоянную времени его «хвоста» за счет изменения низкочастотного состава спектра передаточной функции. Аналогично влияние и изменения индуктивности жил. Более существенно изменение амплитудных значений импульсного отклика при изменении электромагнитных потерь, относительное значение изменения которых приводит к практически такому же относительному изменению амплитуды отклика (обратному по знаку), так как пиковое значение отклика формируется высокочастотными составляющими спектра передаточной функции жил. Влияние изменения емкости жил по характеру и числовым значениям практически аналогично влиянию изменения электромагнитных потерь.

Таким образом, реальный кабель представляет собой линию связи с пониженной добротностью и существенной нелинейной зависимостью передачи сигналов от длины кабеля. Каждый тип каротажного кабеля определенной длины представляет собой самостоятельную и индивидуальную систему передачи сигналов. Фактор пониженной добротности каротажных кабелей в рамках общей теории однородных длинных линий можно учитывать введением в расчетные формулы вторичных электрических параметров жил дополнительного коэффициента электромагнитных потерь.

Полную обобщенную математическую модель каротажного бронированного кабеля образует совокупность формул (2-5, 8-16). Математическая модель отображают реальные электрические параметры кабелей с точностью не хуже 10%.

Принцип неопределенности.

Импульсная пропускная способность кабеля, как и возникающие при передаче данных искажения сигналов, определяются передаточной функцией жил. Однако передаточная функция мало пригодна для сравнения различных типов кабелей по скорости передачи данных. Для этих целей требуются нормированные числовые характеристики.

Эффективная длительность импульсного сигнала (или импульсного отклика линейной системы) и эффективная ширина его спектра (передаточной функции системы) связаны определенным постоянным соотношением. Согласно принципу неопределенности /2,7/, для любого сигнала и системы должно выполняться соотношение: T  1/, где T – эффективная длительность сигнала (импульсного отклика системы),  - эффективная ширина спектра сигнала (полоса пропускания системы), при условии, что мерой T и  служат вторые моменты функций распределения сигнала и его спектра. Для произвольной заданной на интервале (0-) системной функции h(t)  H(f) значения T и определяются по формулам:

(T)² = 4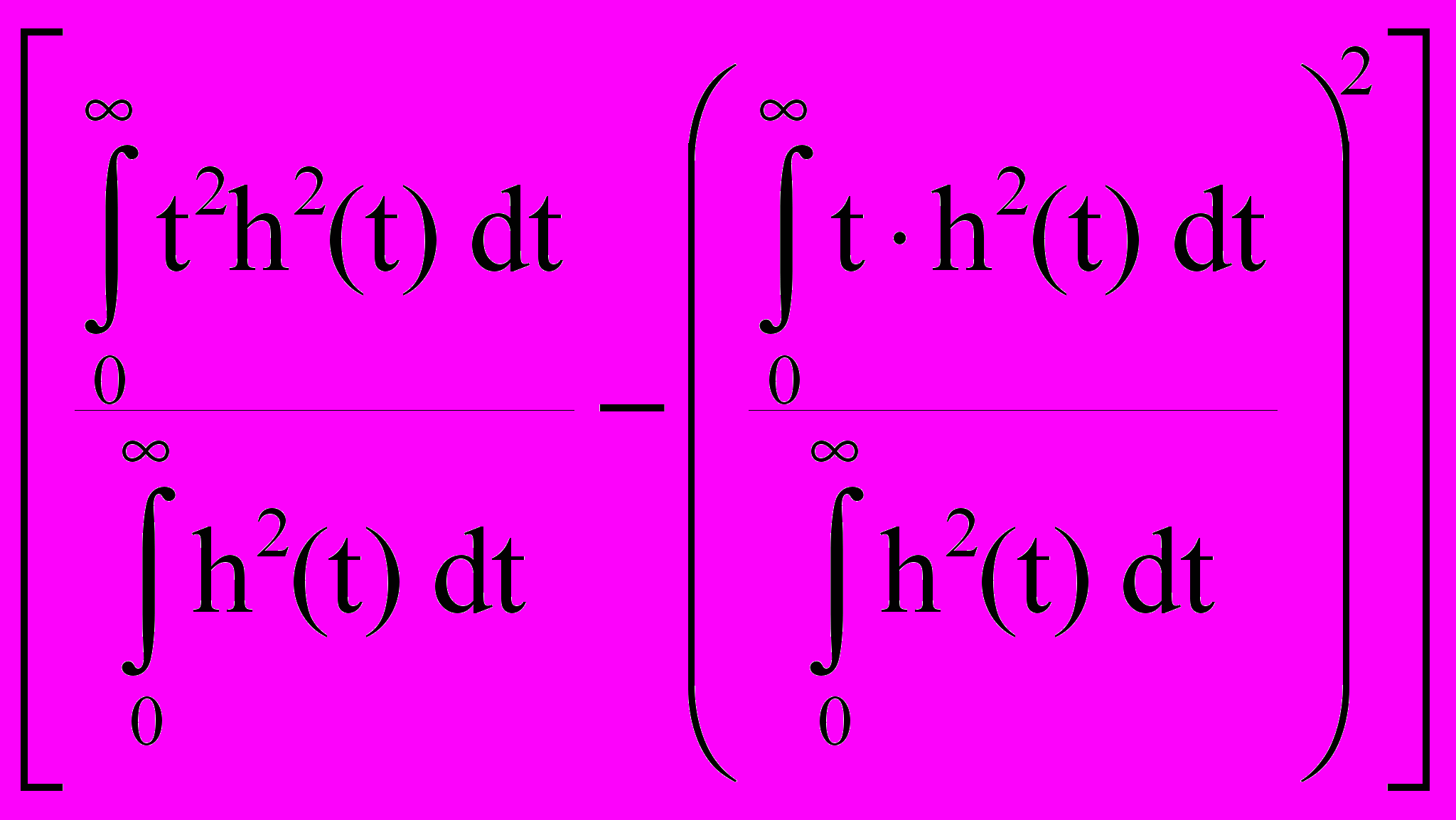, ()² = 4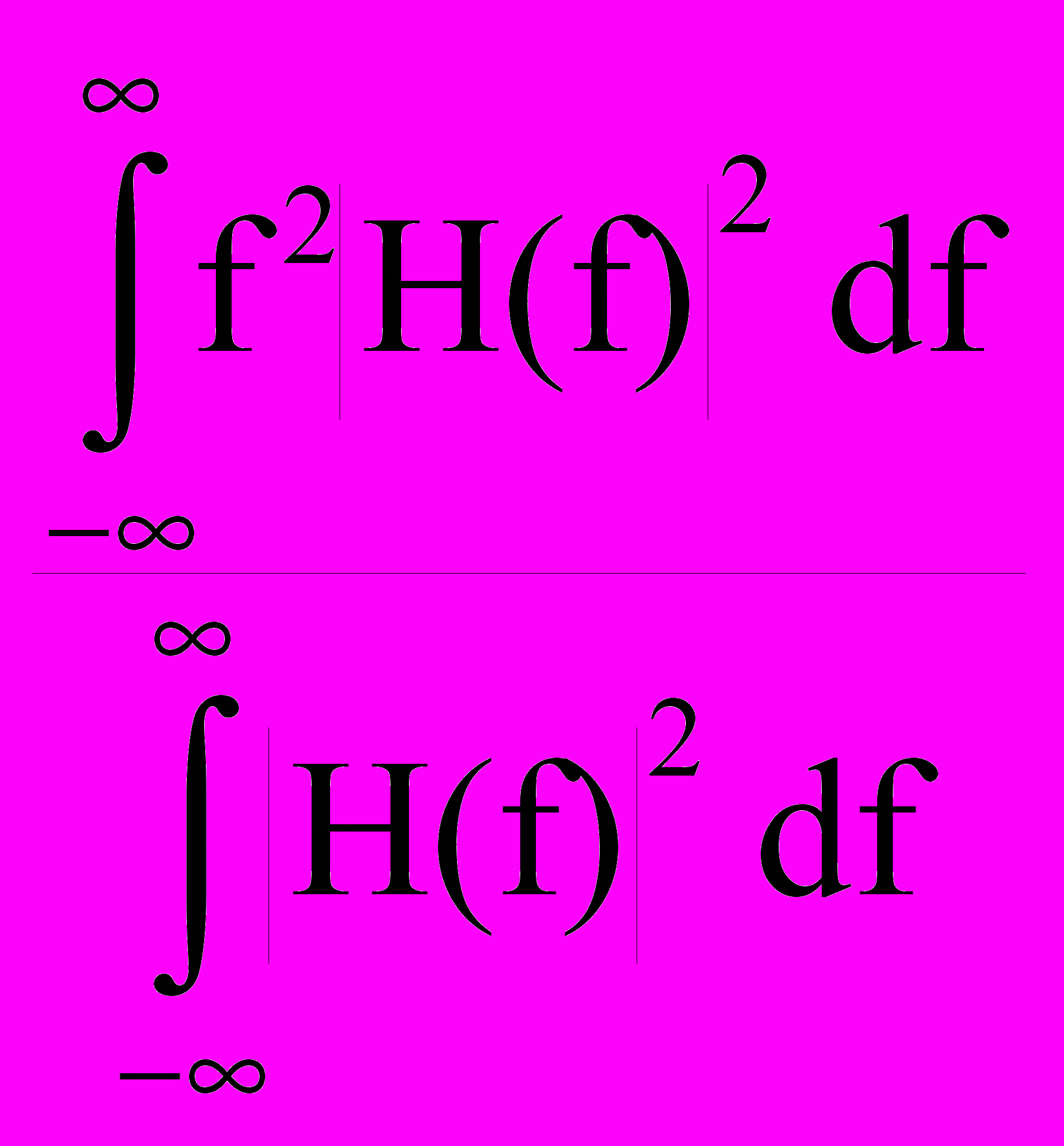. (17)


Таблица 1.

Импульсные параметры кабелей.

Тип кабеля и ТПЖ	ОБК			МБК, жила-броня			МБК, жила-жила
Длина кабеля, км.	3	5	7	3	5	7	3	5	7
Tk отклика, мкс.	19.2	32.9	48.3	14.1	26.1	40.9	8.21	17.4	29.7
k отклика, кГц.	67.6	26.2	15.2	83.6	34.4	19.4	102	40.1	22.1
Индекс Tkk	1.30	0.86	0.73	1.18	0.89	0.79	0.84	0.70	0.66

В таблице 1 приведены расчетные значения параметров ТПЖ, вычисленные по формулам (17). Физическая длительность импульсного отклика в первом приближении должна приниматься равной 2T, а ширина спектра (с учетом отрицательных частот) равной 2. В области реальных частот параметр  - характеристика реальной эффективной полосы пропускания системы.

Индекс неопределенности кабеля T_k_k, равно как и параметры T_к и _к, не устанавливают каких-либо жестких ограничений по импульсной пропускной способности кабеля, так как она существенно зависит как от системы формирования импульсных последовательностей и априорных данных для идентификации сигналов на выходе кабеля, так и от уровня статистических шумов линии передачи. Однако следует учитывать, что при передаче импульсов с  > _к система приводит (в той или иной мере) индекс неопределенности сигналов к собственному индексу неопределенности, а при установленном значении  системы это накладывает ограничения на длительность импульсов. При этом различают полнометрическую, параметрическую и кодовую передачу сигналов.

При полнометрической передаче на выходе кабеля требуется сохранить форму входных сигналов, что возможно с определенной погрешностью для сигналов, эффективная ширина спектра которых много ниже ширины спектра передаточной функции кабеля и достаточно быстро затухает. В общем случае, погрешность восстановления сигналов на выходе кабеля методами частотной коррекции передаточной функции линии определяется безвозвратными потерями высокочастотных информационных составляющих сигналов. С учетом этого импульсный сигнал произвольной формы без скачков и угловых изломов может быть восстановлен на выходе кабеля, если эффективная ширина его спектра не превышает эффективной ширины спектра кабеля, а сам сигнал задается на интервале не менее 2T_k и длительность его фронтов не меньше длительности фронта импульсного отклика кабеля (по уровням 0.1/0.9 амплитудных значений).

При параметрической передаче кабель должен обеспечивать линейную передачу определенных параметров сигналов с заданной точностью. К таким параметрам обычно относятся амплитудные значения, значения площади (энергии) сигналов или временные интервалы между сигналами. По существу, это частный упрощенный вариант полнометрической передачи сигналов. Без восстановления формы минимальный интервал следования сигналов при определениях амплитуд и площадей (энергии) определяется длительностью спада импульсного отклика кабеля (до требуемых значений остаточной реакции на предыдущий импульс). В системах с коррекцией сигналов их форма после коррекции может быть произвольной. При формировании входных сигналов на интервале не менее 2T_k с индексом неопределенности менее T_k_k точность измерений может быть до 1%.

Идентификация кодовых сигналов гарантирована при любой форме приема сигналов (с коррекцией и без коррекции) и при любой форме входных сигналов, задаваемых на интервале 2T_k.

На рис. 5(А, В) приведена форма двух типов импульсов на интервале 2Т_к кабеля (выделен вертикальным пунктиром). Прямоугольный импульс имеет наибольший возможный индекс неопределенности. У треугольного сигнала индекс неопределенности только на 10% больше индекса гауссовских сигналов, имеющих минимально возможный индекс 1/. Длительность сигналов установлена такой, чтобы при свертке с импульсным откликом амплитуды импульсов на выходе кабеля были примерно равными для наглядности сравнения. На рис. 5(C) приведены модули нормированных спектров сигналов в сравнении с модулем передаточной функции жилы.

Как видно на рисунках, оба типа сигналов имеют существенные потери в области высоких частот и форма сигналов на выходе жил становится практически идентичной. Последнее наглядно показывают импульсные характеристики сигналов, приведенные в таблице 2. При сокращении интервала задания импульсов до величины T_к импульсные характеристики сигналов практически приводятся к характеристикам жил кабеля. Отсюда следует, что на предельных частотах передачи сигналов форма входных импульсов значения не имеет. В относительных единицах T_к динамика временных процессов в кабелях различных типов и длины также идентична, что позволяет индекс неопределенности T и параметры T и  считать основными импульсными числовыми характеристиками систем и использовать их в качестве масштабных единиц сравнительного анализа.



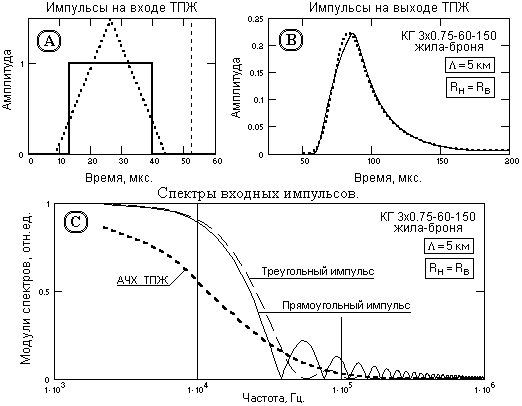
Рис. 5. Форма и спектры однополярных импульсов.



Таблица 2.

Параметры однополярных сигналов на нагрузке кабеля КГ 3х0.75-60-150.

	Тактовый интервал			Т=2Tk							Т=Tk
		Сигналы			Входные			Выходные				Входные			Выходные
Параметры			П				П			П				П		
T импульса, мкс.			15.3			11.2	30.2		29.7	7.8			5.5	27.3		27.1
 импульса, кГц.			326			31.2	16.2		16.6	456			63.6	22.7		23.8
Индекс T			4.98			0.35	0.49		0.49	3.56			0.35	0.62		0.64

Простейший кодовый сигнал, это конечная последовательность однополярных битовых сигналов 0 или 1 с определенной тактовой частотой. В пределе, на одном тактовом периоде сигнал 1 может представлять собой импульс с единичной площадью и с длительностью, много меньшей длительности тактового интервала, т.е. физическое приближение дельта-импульса. Выходным сигналом в этом случае будет импульсный отклик кабеля. Соответственно, кодовое слово будет представлять собой сумму импульсных откликов на последовательность битовых сигналов. Пример такой выходной последовательности с длительностью тактового интервала, равной 2Т_k, кабеля, приведен на рис. 6. Смещение нулевой линии последовательности, определяемое асимметрией импульсного отклика, в этом случае не превышает 1/5 амплитудного значения отклика и является максимально возможным при любой последовательности кодовых импульсов. При увеличении эффективной ширины импульсов в пределах тактового интервала до величины T_к максимальное смещение увеличивается, но не превышает 1/3 от амплитуды импульсов. Выход на практически нулевые значения – 3 тактовых интервала после импульса. Сокращение тактового интервала до величины Т_k приводит к смещению нулевой линии последовательности дельта-импульсов до 2/3 от амплитуды импульсного отклика и практически исключает возможность идентификации импульсов на выходе кабеля, особенно в присутствии шумов.



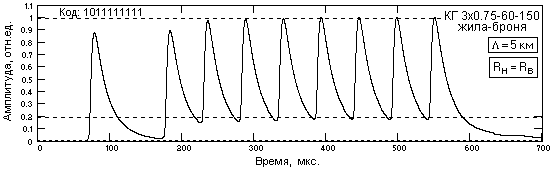
Рис. 6. Последовательность импульсных откликов на выходе кабеля.

(Тактовый интервал 2Т_k)

Таким образом, при передаче по кабелю двоичных кодовых сигналов эффективная длительность однополярных кодовых сигналов не должна превышать эффективной длительности импульсного отклика кабеля. Максимальная частота передачи по кабелю кодовых импульсов соответствует тактовым интервалам, равным удвоенному значению эффективной длительности импульсного отклика кабеля. На предельной частоте передачи сигналы с гладкой формой и минимальной шириной спектра не имеют преимуществ перед прямоугольными сигналами.

Выводы

1. Реальный каротажный кабель представляет собой линию связи с пониженной добротностью и существенной нелинейной зависимостью передаточной функции от длины кабеля. Каждый тип каротажного кабеля определенной длины представляет собой самостоятельную и индивидуальную систему передачи сигналов. Пониженная добротность каротажных кабелей в рамках общей теории однородных длинных линий может быть учтена введением в расчетные формулы вторичных электрических параметров жил дополнительного коэффициента электромагнитных потерь.

2. Разработана и предлагается для практического использования обобщенная математическая модель каротажного бронированного кабеля с учетом его фактических частотно-зависимых первичных электрических параметров и пониженной добротности, которая отображает реальные электрические параметры кабеля точностью не хуже 10%.

3. Основными числовыми характеристиками кабеля, как системы передачи данных, полностью определяющими его импульсную пропускную способность и качество передачи данных, являются эффективная ширина частотного спектра пропускания системы , эффективная длительность импульсного отклика системы T и индекс неопределенности T.

4. Максимальная скорость передачи по кабелю однополярных сигналов соответствует тактовым интервалам, равным удвоенному значению эффективной ширины импульсного отклика кабеля при эффективной длительности импульсов, не превышающей эффективной длительности импульсного отклика кабеля.

5. На предельной частоте передачи данных сигналы с гладкой формой и минимальной шириной спектральной характеристики не имеют преимуществ перед прямоугольными сигналами.


Литература.

1. Белорусов Н.Н., Гроднев И.И. Радиочастотные кабели. – М.: Энергия, 1973. – 328 с.

2. Гоноровский И.С. Радиотехнические цепи и сигналы.– М.: Сов. радио, 1977.–608 с.

3. Горбенко Л.А., Месенжник Я.З. Кабели и провода для геофизических работ. - М.: Энергия, 1977. - 192 с.

4. Горбенко Л.А. и др. Исследование электрических параметров теплостойких каротажных кабелей марок КОБДФ-6(8) и КТБФ-6(10). // Геофизическая аппаратура. – Л.: Недра, 1966, вып.28. – с. 174-180.

5. Гроднев И.И., Фролов Н.А. Коаксиальные кабели связи. - М.: Радио и связь, 1983. - 209 с.

6. Ковальчук И.Н. и др. Исследование электрических параметров бронированных каротажных кабелей. // Геофизическая аппаратура. - Л.: Недра, 1967, вып. 34. - с. 151-163.

7. Сиберт У.М. Цепи, сигналы, системы. Часть 2. – М.: Мир, 1988. – 360 с.

8. Сильвинская К.А., Голышко З.Н. Расчет фазовых и амплитудных корректоров: Справочник. – М.: Связь, 1980. – 104 с.

9. Стрижевский Н.З. Коаксиальные видеолинии. – М.: Радио и связь, 1988. – 200 с.

10. Стандарт ЕАГО-010-01 "Кабели грузонесущие геофизические бронированные. Общие технические условия".


Несколько сокращенный вариант статьи опубликован в трудах УГГГА:

Импульсная пропускная способность каротажных кабелей / Мамлеев Т.С., Давыдов А.В. // Известия Уральской государственной горно-геологической академии. Вып. 15. Серия: Геология и геофизика, 2002, стр. 155-166, рус.


Замечания, предложения, дополнительные материалы по данной теме прошу сообщать по адресу: prodav@narod.ru. Буду благодарен за возможность доработки, улучшения, упрощения математической модели каротажных кабелей (совместно с Вами).


Copyright ©2004 Davydov А.V.