Курс научный Семёнов А. В. Проверили

Вид материала

Содержание

Теоретические основы
Исследование интеграла
Программирования графика

Подобный материал:

8ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУВПО «Самарский государственный архитектурно-строительный университет»

Факультет информационных систем и технологий

Кафедра прикладной математики и вычислительной техники

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К КУРСОВОЙ РАБОТЕ

по дисциплине

ТЕХНОЛОГИЯ

НАУЧНЫХ ИССЛЕДОВАНИЙ

на тему

«Течение жидкости в цилиндрической трубе»

3 СЕМЕСТР 2 КУРС

Научный руководитель: Семёнов А.В.

Проверили:	Выполнил: студент ГИП
1. ФИО оценка подпись дата	подпись дата
2. ФИО оценка подпись дата

Общая оценка _______________

Методический руководитель оценка дата

2008 г

Аннотация к научной работе

Тема работы:

«Течение жидкости в цилиндрической трубе»

Работу выполнил студент II курса Сапов И.С.

Научный руководитель: проф. Д.Т.Н Семёнов А.В.

Методический руководитель: проф. Д.Т.Н Пиявский С.А.

Цель работы

На данном этапе необходимо разработать программу построения графика, в котором отображается скорость течения жидкости на разных расстояниях от оси цилиндрической трубе.

Содержание

Теоретические основы 3

Программирования графика 8

Дальнейшее направление работы 9

Список литературы 10

10

Теоретические основы

Гидроаэромеханика – наука о движении и равновесии жидкостей и газов. При планировании физических экспериментов или при их проведении необходимо создавать теоретические модели, которые либо предсказывают возможные результаты этих экспериментов, либо объясняют уже полученные. Только в тесном взаимодействии теории и эксперимента можно понять то, что происходит в окружающем нас физическом мире. Для создания той или иной количественной или качественной модели физического явления необходим математический фундамент, на основе которого строятся такие модели. Под математическим фундаментом в данном случае подразумеваются те дифференциальные уравнения и те граничные и начальные условия, с помощью которых можно было бы описывать рассматриваемое физическое явление. Гидромеханика и предлагает модели и аппарат для исследования явлений, происходящих в жидкостях и газах.

Развитие Гидроаэромеханики протекало в тесной связи с запросами практики. Первые гидротехнические устройства (каналы, колодцы) и плавающие средства (плоты, лодки) появились ещё в доисторические времена. Изобретение таких сравнительно сложных аэро- и гидромеханических устройств, как парус, весло, руль, насос, также относится к далёкому прошлому. Развитие мореплавания и военного дела послужило стимулом к появлению основ механики и, в частности, гидроаэромеханики

Главной проблемой гидроаэромеханики с самого её возникновения стало взаимодействие между средой (водой, воздухом) и движущимся или покоящимся в ней телом. Первым учёным, внёсшим значительный вклад в гидроаэромеханику, был Архимед (3 в. до н. э.), открывший основной закон гидростатики и создавший теорию равновесия жидкостей. Труды Архимеда явились основой для создания ряда гидравлических аппаратов, в частности поршневых насосов.

Следующий этап развития гидроаэромеханики относится к эпохе Возрождения (16—17 вв.) Леонардо да Винчи сделал первый существенный шаг в изучении движения тел в жидкости или газе. Наблюдая полёт птиц, он открыл существование сопротивления среды. Он считал, что воздух, сжимаясь вблизи передней части тела, как бы «загустевает» и поэтому препятствует движению в нём тел. Сжимаясь под крылом птицы, воздух, по мнению Леонардо, создаёт опору для крыла, благодаря чему возникает сила, поддерживающая птицу в полёте, — подъёмная сила. Б. Паскаль, изучая силу, действующую перпендикулярно к поверхности соприкосновения двух элементарных объёмов жидкости, т. е. давление, установил, что в данной точке жидкости давление действует с одинаковой силой во всех направлениях.

Первое теоретическое определение закона сопротивления принадлежит англ. учёному И. Ньютону, который объяснял сопротивление тела при движении его в газе ударами частиц о лобовую часть тела, а величину сопротивления считал пропорциональной квадрату скорости тела. Ньютон также заметил, что кроме силы, определяемой ударами частиц, существует сопротивление, связанное с трением жидкости о поверхность тела (т. н. сопротивление трения). Рассмотрев силу, действующую вдоль поверхности соприкосновения элементарных объёмов жидкости, Ньютон нашёл, что напряжение трения между двумя слоями жидкости пропорционально относительной скорости скольжения этих слоев друг по другу.

Установив основные законы и уравнения динамики, Ньютон открыл путь для перехода гидроаэромеханики от изучения отдельных задач к исследованию общих законов движения жидкостей и газов. Создателями теоретической гидродинамики являются Л. Эйлер и Д. Бернулли, которые применили известные уже к тому времени законы механики к исследованию течений жидкостей. Л. Эйлер впервые вывел основные уравнения движения т. н. идеальной, т. е. не обладающей вязкостью, жидкости. В трудах французских учёных Ж. Лагранжа и О. Коши, немецких учёных Кирхгофа и Гельмгольца, английского учёного Дж. Стокса, русских учёных Н. Е. Жуковского и С. А. Чаплыгина и др. были разработаны аналитические методы исследования течений идеальной жидкости; эти методы были применены к решению множества важных задач, относящихся к движению жидкости в каналах различной формы, к истечению струй жидкости в пространство, заполненное жидкостью или газом, и к движению твёрдых тел в жидкостях и газах. Большое значение для практических приложений имела разработка теории волн, возникающих на поверхности жидкости, например под действием ветра или при движении судов и т.п.

Основным достижением гидроаэромеханики 19 века был переход к исследованию движения вязкой жидкости, что было вызвано развитием гидравлики, гидротехники и машиностроения (смазка трущихся частей машин). Опыт показал, что при малых скоростях движения тел сопротивление в основном зависит от сил вязкости. Они же определяют сопротивление при движении жидкостей в трубах и каналах. Стокс, рассматривая деформацию элементарного объёма жидкости при его перемещении, установил, что возникающие в жидкости вязкие напряжения линейно зависят от скорости деформации жидкой частицы. Этот закон, обобщивший закон Ньютона для трения, позволил дополнить уравнения движения Эйлера членами, учитывающими силы, возникающие от действия вязкости жидкостей или газов. Вывод уравнений движения вязких жидкостей и газов (Навье — Стокса уравнений) позволил аналитически исследовать течение реальных (вязких) сплошных сред. Однако решение этих уравнений в общем виде представляет большие трудности и по сей день, поэтому при исследовании течений вязкой жидкости часто прибегают к упрощению задачи путём отбрасывания в уравнениях членов, которые для данного случая не являются определяющими. Большую роль в гидроаэромеханике играют экспериментальные методы. Выяснилось ещё одно важное отличие реальных жидкостей и газов от идеальных — способность переносить тепло, характеризуемая величиной теплопроводности. С помощью методов гидроаэромеханики была создана также теория фильтрации жидкости через грунты, которая играет важную роль в гидротехнике, нефтедобыче, газификации и пр.

Решающее значение для всего дальнейшего развития науки о движении реальных жидкостей и газов, обладающих вязкостью и способных переносить тепло, имеет уравнение пограничного слоя, выведенное впервые немецким учёным Л. Прандтлем (1904). Согласно гипотезе Прандтля, всё действие вязкости сказывается лишь в тонком слое жидкости или газа, примыкающем к обтекаемой поверхности, поэтому вне этого слоя течение реальной вязкой жидкости ничем не отличается от движения идеальной (невязкой) жидкости. Т. о., задача о движении вязкой жидкости или газа разделяется на две: исследование течения идеальной жидкости вне пограничного слоя и исследование течения вязкой жидкости внутри пограничного слоя.

Во 2-й половине 19 в. начало развиваться и др. направление гидроаэромеханики — исследование течений сжимаемой сплошной среды. Почти все жидкости практически несжимаемы, поэтому в процессе движения их плотность остаётся неизменной. Газы, наоборот, очень легко изменяют свой объём, а следовательно и плотность под действием сил давления или при изменении температуры. Раздел гидроаэромеханики, в котором изучается движение сжимаемых сплошных сред, называется газовой динамикой. Запросы авиационной (в 1-й четверти 20 в.) и ракетной (во 2-й четверти 20 в.) техники стимулировали развитие аэродинамики и газовой динамики.

Создание ракет и ракетных двигателей на жидком и твёрдом топливе сложного химического состава, наступление эры космических полётов в атмосфере Земли и др. планет, увеличение скоростей атомных подводных лодок — носителей ракетно-ядерного оружия, создание мировой службы погоды с использованием искусственных спутников Земли, синтез различных естественных наук и др. элементы технического и научного прогресса 20 в. существенно повысили роль гидроаэромеханики в жизни человечества. Современная гидроаэромеханика — разветвленная наука, состоящая из многих разделов, тесно связанная с др. науками, прежде всего с математикой, физикой и химией. Движение и равновесие несжимаемых жидкостей изучает гидромеханика, движение газов и их смесей, в том числе воздуха, — газовая динамика и аэродинамика. Разделами гидроаэромеханики являются теория фильтрации и теория волнового движения жидкости. Технические приложения гидроаэромеханики изучаются в гидравлике и прикладной газовой динамике, а приложения законов гидроаэромеханики к изучению климата и погоды исследуются в динамической метеорологии. Методами гидроаэромеханики решаются разнообразные технические задачи авиации, артиллерийской и ракетной техники, теории корабля и энергомашиностроения, при создании химических аппаратов и при изучении биологических процессов (например, кровообращения), в гидротехническом строительстве, в теории горения, в метеорологии и т.п.

Первая основная задача гидроаэромеханики состоит в определении сил, действующих на движущиеся в жидкости или газе тела и их элементы, и определении наивыгоднейшей формы тел. Знание этих сил даёт возможность найти потребную мощность двигателей, приводящих тело в движение, и траектории движения тел. Вторая задача — профилирование (определение наивыгоднейшей формы) каналов различных газовых и жидкостных машин: реактивных двигателей самолётов и ракет, газовых, водяных и паровых турбин электростанций, центробежных и осевых компрессоров и насосов и др. Третья задача — определение параметров газа или жидкости вблизи поверхности твёрдых тел для учёта силового, теплового и физико-химического воздействия на них со стороны потока газа или жидкости. Эта задача относится как к обтеканию тел жидкостью или газом, так и к течению жидкостей и газов внутри каналов разной формы. Четвёртая задача — исследование движения воздуха в атмосфере и воды в морях и океанах, которое производится в геофизике (метеорология, физика моря) с помощью методов и уравнений гидроаэромеханики. К ней примыкают задачи о распространении ударных и взрывных волн и струй реактивных двигателей в воздухе и воде.

Решение практических задач гидроаэромеханики в различных отраслях техники производится как экспериментальными, так и теоретическими методами. Современная техника приходит к таким параметрам течения газа или жидкости, при которых часто невозможно создать условия для полного экспериментального исследования течения на моделях. Тогда в эксперименте производится частичное моделирование, т. е. исследуются отдельные физические явления в движущемся газе или жидкости, имеющие место в действительном течении; определяется физическая модель течения и находятся необходимые экспериментальные зависимости между характерными параметрами. Теоретические методы, основаны на точных или приближённых уравнениях, описывающих течение, позволяют объединить, используя данные эксперимента, все существенные физические явления в движущемся газе или жидкости и найти параметры течения с учётом этих явлений для данной конкретной задачи. Высокое совершенство теоретических методов стало возможным с появлением быстродействующих ЭВМ. Применение ЭВМ для решения задач гидроаэромеханики изменило и методы решения. При пользовании ЭВМ решение производится часто прямым интегрированием исходной системы уравнений, описывающей движение жидкости или газа и все физические процессы, сопровождающие это движение. Прогресс теоретических методов гидроаэромеханики и развитие ЭВМ позволяют решать всё более сложные задачи.

Мой научный руководитель, сделав преобразования формулы Прандтля и сделав некоторые замены, предоставил мне следующий интеграл

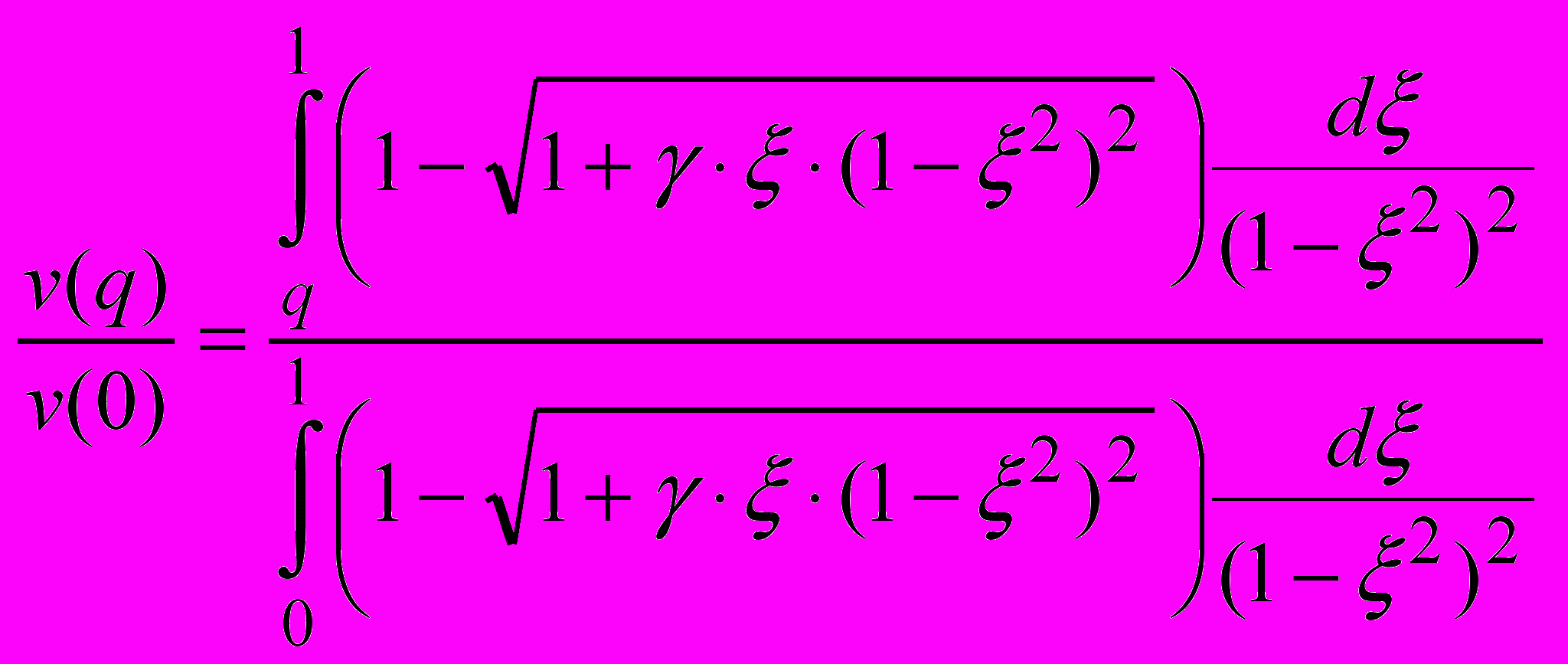
Исследование интеграла

Данный интеграл несобственный и расходящийся. Решение его в аналитическом виде вызывает множество проблем. Но воспользовавшись возможностями компьютера можно посчитать этот интеграл численными методами. Я воспользовался методом трапеций, который заключается в следующем:

В данном методе f(x) заменяется на линейный интерполяционный многочлен, т.е. на элементарном отрезке [ xi-1 , xi ] подынтегральная функция представляет собой отрезок прямой линии. Значение I в пределах [ xi-1 , xi ] , равное площади криволинейной фигуры, заменяется площадью прямоугольной трапеции с высотой hi и основаниями f(xi-1) , f(xi) :

Si = 0.5 (yi-1 + yi) hi , i=1,2,...n .

После сложения этих соотношений получим формулу трапеций

I = 0.5

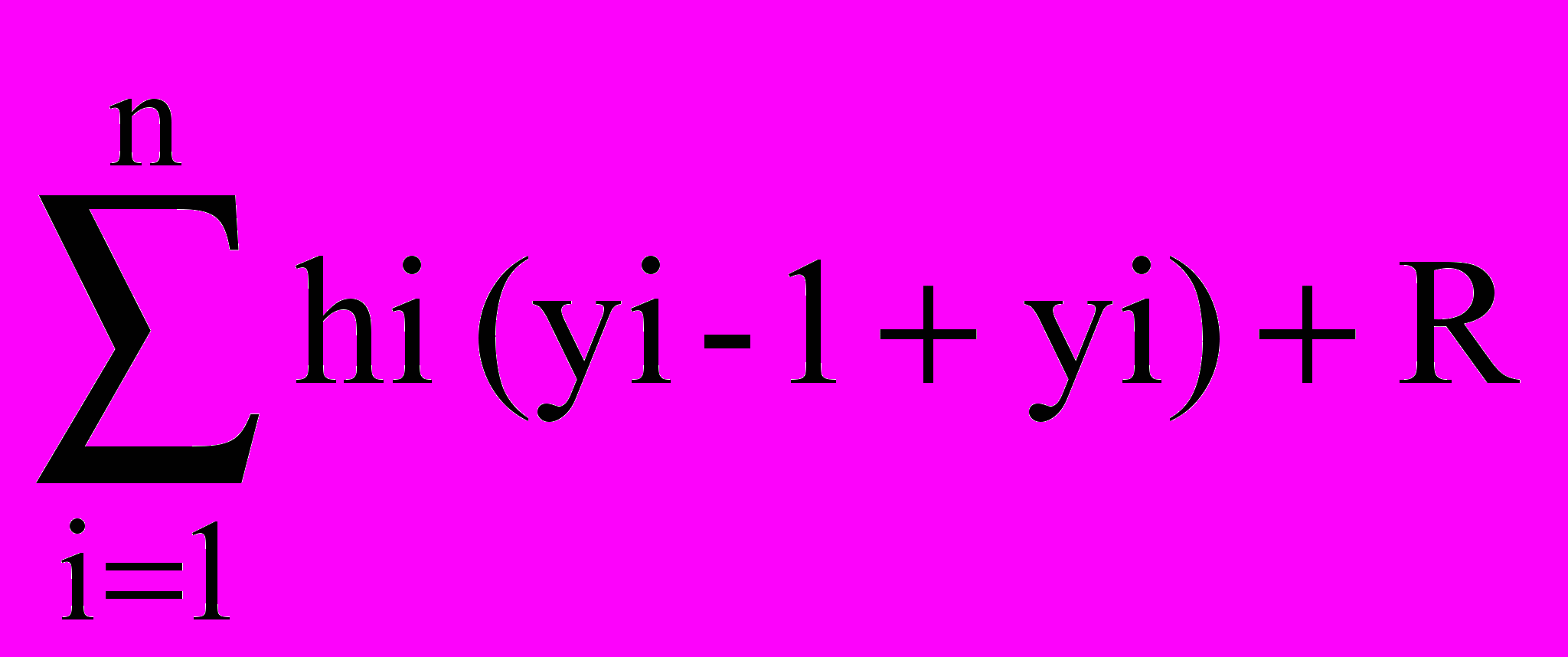
Если шаг интегрирования постоянный ( hi = h = const ) , то

I = h ( (y0 + yn)/2 +

) + R

Программирования графика

Рассчитав интеграл методом трапеций на компьютере, я получил график

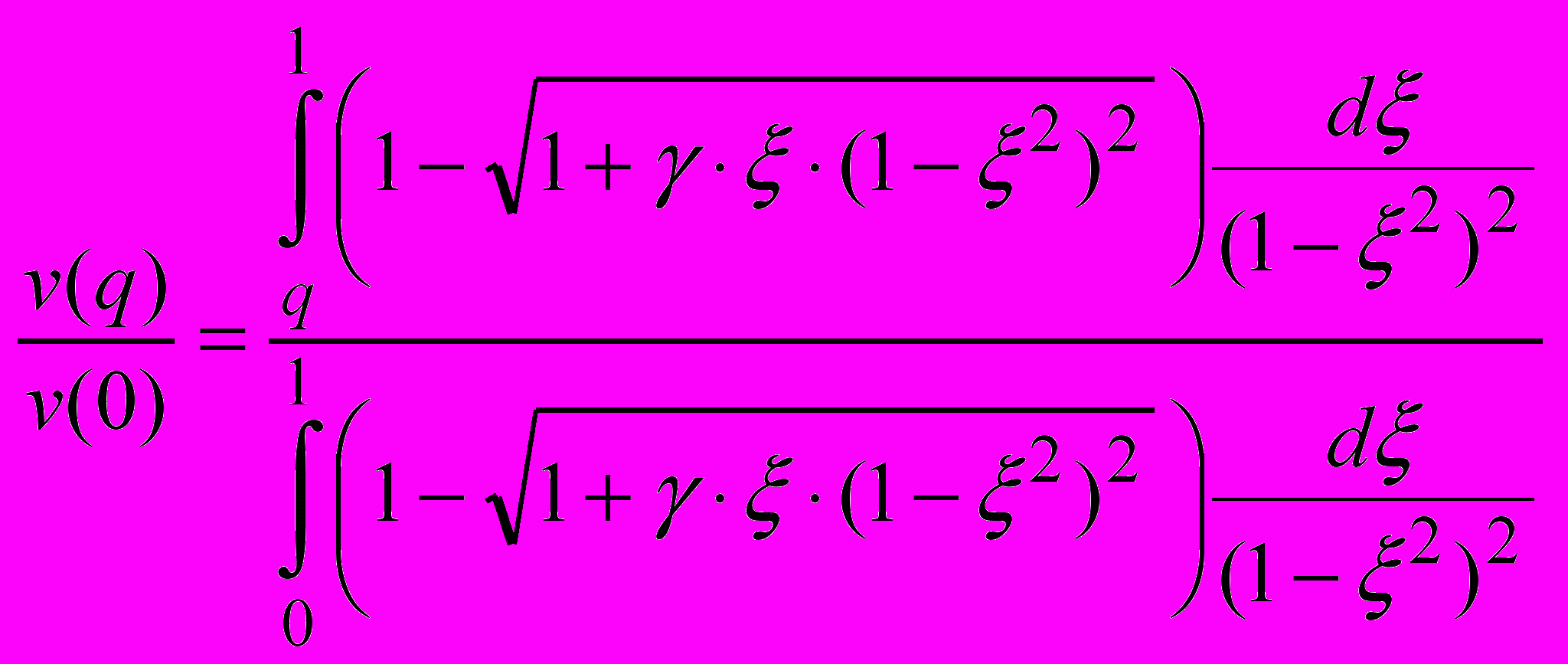
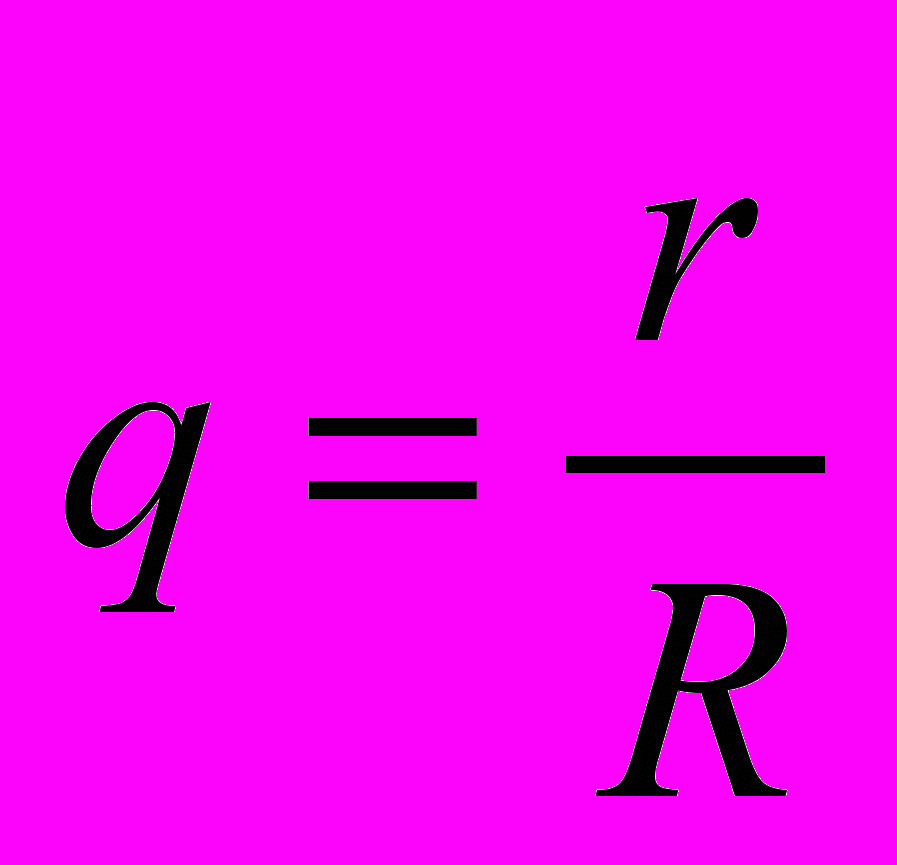, R – радиус трубы (в метрах), r – текущее положение (r = 0 – ось цилиндрической трубы) (в метрах), V(q) – скорость течения жидкости в данном положении r = q*R (в метрах на секунду).

Данный график удовлетворяет всем требованиям на данном этапе.

Дальнейшее направление работы

Попытаться рассчитать интеграл аналитически.

Список литературы