Краткое обзорно-справочное пособие. Книга является первым в своём роде обзорно-справочным пособием по виртуальной физике и рассчитана на широкий круг читателей, интересующихся проблемами Науки вообще и физики в частности

Вид материала

Книга

Содержание 1.3.3.4. Другие распределения Перемещение частиц и деформаций упаковки

Подобный материал:

• Реферат данилюк А. И. Элементы виртуальной физики, 106.58kb.
• Liaise With Europe, Франция создание предприятия от а до я в узбекистане справочное, 2964.95kb.
• Справочное пособие по проблемам здоровья. М.: Корал Клаб, 2000, 627.09kb.
• Тема: Экономика Дагестана, 120.6kb.
• Ю. М. Иванов как стать экстрасенсом москва 1990 Книга, 12883.6kb.
• Иные миры, 3004.29kb.
• Избранные сочинения Александра Григорьевича Столетова издание, рассчитанное на широкий, 3.19kb.
• Книга написана живым, образным языком и рассчитана не только на историков профессионалов,, 2424.55kb.
• И. М. Феигенберг мозг психика здоровье издательство «наука» Москва 1972 Книга, 1509.07kb.
• А. П. Щёголев нужен гразер! Исповедь исследователя с-петербург 2009г. От редакции, 1921.01kb.

1.3.3.4. Другие распределения


Представление о смещении множества равноправных частиц в упаковке приводит к представлению о распределении взаимно обусловленных смещений соседних частиц.

В целом представление о распределении смещений частиц может быть сложным настолько, насколько позволяют представления о кривизне непрерывной упаковки и одинаковости частиц. Но вследствие аддитивности перемещений любые сложные распределения могут быть с достаточной точностью описаны как совокупность более простых распределений.

Одним из простейших случаев является самоустанавливающееся распределение смещений частиц упаковки вокруг одной смещенной частицы. Любое смещение любой частицы в одномерной упаковке вызывало бы смещение других частиц исключительно в том же направлении (других направлений нет, если не учитывать направление оси времени) на такую же величину с запаздыванием во времени, пропорциональным расстоянию между ними. Смещение частицы в многомерной упаковке всегда вызывает смещение окружающих частиц во всех других направлениях. Представление о зависимости ускорений соседних частиц упаковки от расстояния между их центрами приводит к представлению о взаимной зависимости смещения разных частиц в разных направлениях.

Последнее обстоятельство может быть схематически проиллюстрировано двумерным рисунком 1.3.3.4.1. На нем показана схема образования вихреобразной картины относительных смещений _i частиц в плоскости XY при смещении вдоль оси Х единственной частицы в начале координат. Стрелками показаны наиболее существенные смещения частиц. Очевидно, что картина будет похожей в любой другой плоскости, проходящей через ось смещения.

При достаточно малой величине сдвига вследствие определения дифференциалов, отражающего аддитивность перемещений, величина ускорения в каком-либо направлении примерно пропорциональна величине проекции на межцентровое направление относительного перемещения соседних частиц в других направлениях


d_ia_j = C_ar (dR_i - dR_j) cos(dR_i,dR_j) (1.3.3.4-1)


Y

























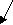
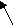
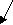
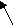
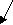
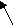
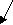
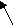
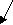
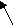
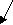
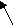
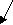
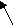
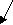
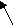
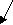
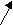
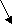
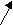
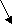
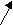
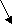
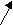
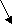
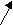
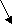
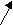
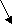
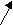
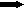
X



















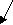
Рис. 1.3.3.4.1. Схема смещений частиц упаковки в системе

координат одной смещаемой частицы


Сумма L^O=ⁱ⁼¹_i=1r_i относительных смещений частиц вдоль любой замкнутой линии всегда равна нулю. Далее в целом картина распределения зависит от мерности деформации и упругости частиц. При одномерной деформации смещение любой частицы вызывает стремление к равному смещению частиц соседних слоев в единственном направлении. В двумерной деформации первичное линейное смещение одной частицы в любом направлении вызывает смещение остальных частиц в двух измерениях, и картина распределения приобретает замкнутые вихреобразные (циркуляционные) составляющие. В трехмерной деформации слои вихря становятся тороидальными и т.д.

Абсолютно жесткие частицы не могут перемещаться относительно других частиц, поэтому такие частицы могут быть перемещены только вместе со своим окружением или вырваны из него. Абсолютно мягкие частицы будут просто сминаться, не смещая окружение. Из-за тривиальности такие крайние случаи неинтересны для нашей задачи. Частицы средней жесткости будут смещаться вместе со своим окружением в абсолютной системе координат, но каждая из частиц будет смещена по-разному, приводя к вихреобразной картине смещений. Смещение многомерного объекта, состоящего из множества частиц, приводит к увеличению смещений частиц вихря-деформации в соответствующем направлении пропорционально количеству частиц объекта. Стационарная картина распределения в абсолютной системе координат зависит от соотношения продольной и тангенциальной упругости и пластичности упаковки, поэтому будет иметь несколько иной вид простого одностороннего прогиба упаковки. При наличии существенного запаздывания распространения деформации и при обрывном скольжении упаковки, например, по боковой поверхности перемещающейся плотной группы-потока частиц, а не отдельной частицы, картина становится вихреобразной и относительно остальной части упаковки. Эта ситуация знакома всем, кто видел брызги воды над местом падения камня.

Вследствие специфики взаимодействия частиц в многомерной упаковке (по сравнению с одномерной) частицы окружения смещаются не только в продольном направлении, но и в направлениях, поперечных к направлению смещения первой частицы, расступаясь перед ней и освобождая ей путь, и смыкаясь за ней. Вместе с конечной скоростью c перемещения деформаций и особенностью центрально-симметричной деформации

M₁r_1j = -M₂r_2j (1.3.3.3-15)

r_2j = -M₁r_1j /M₂  0| _M1<<M2 (1.3.3.3-16)

R_j = R_j+1  C(j) (1.3.3.3-25)

это приводит к существенной зависимости сопротивления упаковки перемещению частицы от скорости v её перемещения из-за

M₂ m (c-v)t  0|_{(c-v)t 0} (1.3.3.4-2)


Вследствие (1.3.3.4-2) упаковка оказывает существенное и увеличивающееся с увеличением скорости v сопротивление любому изменению скорости (ускорению) любых объектов за счет уменьшения времени взаимодействия t, оказывая меньшее, но тоже увеличивающееся при больших скоростях сопротивление их перемещению с постоянной скоростью. Это сопротивление по природе является чисто волновым (динамическим, нестационарным) сопротивлением упаковки, но отражено в неклассической физике для наблюдаемой части мира постулатом об увеличении "массы" перемещающегося объекта с увеличением его скорости. Такая подмена представлений представляется не всегда корректной и не всегда допустимой из-за возможности ошибок в последующих рассуждениях, хотя при достаточно малой скорости волновое сопротивление упаковки может быть для удобства представлено как небольшая часть инерции самого объекта, которой можно пренебрегать. Полученное представление об инерции объектов дополняет полученное ранее общее представление об инерции частиц упаковки и может быть частично отражено постулатом Ньютона об инерции движения материальных объектов. Представление о сопротивлении упаковки переменам движения приводит также к представлению о волнах деформаций и к представлению о пространственно-временном распределении смещений частиц в волнах.

Такое поведение расступающихся и/или сходящихся частиц упаковки может приводить к локальному концентрированию их смещений и, в свою очередь, способно приводить к превышению порогов пластичности и самопроизвольному появлению дефектов упаковки как побочному результату пластичного перемещения её частиц. Этот процесс может существенно облегчаться (ускоряться) и учащаться при наличии в зоне перемещения других деформаций, например, деформаций окружения дефектов и/или волн деформаций соответствующей амплитуды и конфигурации, изменяющих пороги пластичности.

Среди распределений деформаций, вызываемых дефектами упаковки, возможно, следует особо выделить ещё один случай распределения смещений частиц упаковки, точнее, часть такого распределения, устанавливающегося непосредственно на границе дефекта-источника конкретной деформации. Эта граница может быть определена как некоторая условная поверхность, отделяющая совокупность переупакованных пластичной деформацией частиц упаковки (дефектную часть упаковки) от деформированной, но не переупакованной совокупности частиц упаковки (бездефектной части упаковки). На таких границах распределения смещений частиц могут претерпевать более резкое, чем в других частях упаковки, пространственно-временное изменение. Вследствие достаточной условности определения любых границ в квазиоднородной упаковке такие границы при необходимости для удобства можно считать достаточно (бесконечно) тонкими. Тогда конечные изменения распределений смещений частиц на таких границах в большинстве случаев могут быть представлены как достаточно резкие скачки и/или разрывы соответствующих функций распределения и их производных. Такое упрощение представлений вместе с принципом близкодействия позволяет иногда игнорировать внутреннее строение дефектов и рассматривать сами воображаемые границы (поверхности скачков-разрывов) как источники деформаций без особого ущерба для точности последующего описания и прогнозирования событий.

Представление о неодинаковости параметров частиц в пространстве приводит к представлению о пространственном распределении смещений частиц. Представление о неодинаковости-изменении пространственного распределения смещений частиц во времени приводит к представлению о пространственном перемещении деформаций как совокупностей смещений частиц.

Раздел 1.4. Перемещение частиц и деформаций упаковки