Краткое обзорно-справочное пособие. Книга является первым в своём роде обзорно-справочным пособием по виртуальной физике и рассчитана на широкий круг читателей, интересующихся проблемами Науки вообще и физики в частности

Вид материала

Книга

Содержание T как некий параметр, определяющий величину и направление переноса энергии потоками частиц. При таком определении T M, но известна связь между поверхностной n

Подобный материал:

• Реферат данилюк А. И. Элементы виртуальной физики, 106.58kb.
• Liaise With Europe, Франция создание предприятия от а до я в узбекистане справочное, 2964.95kb.
• Справочное пособие по проблемам здоровья. М.: Корал Клаб, 2000, 627.09kb.
• Тема: Экономика Дагестана, 120.6kb.
• Ю. М. Иванов как стать экстрасенсом москва 1990 Книга, 12883.6kb.
• Иные миры, 3004.29kb.
• Избранные сочинения Александра Григорьевича Столетова издание, рассчитанное на широкий, 3.19kb.
• Книга написана живым, образным языком и рассчитана не только на историков профессионалов,, 2424.55kb.
• И. М. Феигенберг мозг психика здоровье издательство «наука» Москва 1972 Книга, 1509.07kb.
• А. П. Щёголев нужен гразер! Исповедь исследователя с-петербург 2009г. От редакции, 1921.01kb.

v₁ = v = - v₂ (1.6.5-148)

m₁ = m₂ = m /2 (1.6.5-149)


поэтому при скорости центра масс v₀ в любой другой системе отсчета импульс агрегата как сумма импульсов частей


m₁ (v₀ + v₁)+ m₂ (v₀ + v₂) = (2 v₀ + v - v) m/2 = v₀ m (1.6.5-150)


Это дает полное право при подсчете ипульсов не учитывать внутреннее строение агрегатов и любые равные взаимные перемещения их частей. Это справедливо и для вращений и для колебаний. Но при подсчете сумм энергий пренебрежение строением агрегата даже в нашем простейшем случае приведет к ошибке, равной самому результату, и мы ошибемся ровно в 2 раза, если скорость одинаковых частей и скорость центра масс одинаковы по величине

(v₀ + v₁)² m₁ /2 + (v₀ + v₂)² m₂ /2 = [(v₀ + v)² + (v₀ - v)²] m/4 =

= [v₀² + 2 v₀ v+ v² + v₀² - 2 v₀ v + v²] m/4 = [2v₀² + 2v²] m/4 = [v₀² + v²] m/2 (1.6.5-151)


При неравенстве масс и/или скоростей ошибка будет меньше, что полностью соответствует приведенному ранее примеру с водяным паром.

В целом даже в нашем простом случае картина получается довольно сложной для описания. Поэтому, чтобы не выходить далеко за пределы поставленной простейшей задачи, воспользуемся принципом достаточности и остановимся на том, что в первом приближении при низких температурах вкладом колебаний частей агрегатов "истинных" газов в их теплоемкость можно пренебрегать, а вклад вращения учитывать в виде некоторой добавки ⁿw_o = ⁿj_o ⁿw_x к кинетической энергии ⁿw_к


ⁿw = ⁿw_к + ⁿw_o = (3 + ⁿj_o) ⁿw_x (1.6.5-152)


Назовем энергией потока W_N сумму энергий w_i = ⁿw_кi+ w_oi всех N_x частиц, составляющих этот поток. По аналогии с предыдущими представлениями следует представление о средней по объему ⁿw и средней по потоку энергии ^Nw и о среднем количестве всех ⁿj , кинетических ⁿj_к и внутренних ⁿj_o степеней свободы частиц. При ⁿj_к = 3


ⁿj = ⁿj_к + ⁿj_o = 3 + ⁿj_o (1.6.5-153)

ⁿw = ⁿj ⁿw_x = (ⁿj_o +3) ⁿw_x (1.6.5-154)

^Nw = ^Nw_к + ^Nw_o = m ^Nv²/2 + m ^Nv_o²/2 (1.6.5-155)

W_N = ^_v=0 w d_vN_x= ^_v=0 w_к d_vN_x + ^_v=0 w_o d_vN_x=

= ^Nw_кN_x+ ^Nw_oN_x = m ^Nv²N_x/2 + m^Nv_o²N_x/2 =

= ^Nw_к ⁿv_xn_x+ ^Nw_oⁿv_xn_x= ^Nw_к ⁿvn /4 + ^Nw_o ⁿvn /4 (1.6.5-156)

С другой стороны,

W_N = ^_v=0 w d_vN_x= ^_v=0 (w_к+ w_o) v_x d_vn_x=

= ^_v=0^{ /2}_=0 mv²vd_vn d_sin² /2^.2^.2 + ^_v=0 ^{ /2}_=0mv_o²vd_vn d_sin² /2^.2^.2 =

= ^_v=0 mv³ d_vn /2^.2^.2 + ^_v=0 mv_o²vd_vn /2^.2^.2 =

= m ⁿ(v³) n/2^.2^.2 + m ⁿ(v_o²v) n /2^.2^.2 = ⁿ(w_кv)n /2^.2 + ⁿ(w_ov) n /2^.2 (1.6.5-157)

W_o = m ⁿ(v_o²v) n/2^.2^.2 = m ^N(v_o²) N_x/2 = m ^N(v_o²) ⁿv n /2^.2^.2 (1.6.5-158)

W_к = m ⁿ(v³) n/2^.2^.2 = m ^Nv²N_x/2 = m ^Nv^{2 n}v n /2^.2^.2 (1.6.5-159)

ⁿv³ m /2 = ^Nv^{2 n}v m /2 = ^Nw_к ⁿv = ⁿ(w_кv) (1.6.5-160)

^Nv^{2 n}v = ⁿ(v³) (1.6.5-161)

^Nw_o ⁿv = ⁿ(w_ov) = ⁿ(v²_ov)m /2 = ^Nv²_oⁿv m /2 (1.6.5-162)

^Nv²_oⁿv = ⁿ(v²_ov) (1.6.5-163)


Суммируя по всем частям и частицам потока N_x


W_N = ^_v=0 (w_к + w_o) v_xd_vn_x = ^_v=0 (w_кx + w_кy + w_o) v_xd_vn_x=

= W_к + W_o = W_кx+ W_кy+ W_o (1.6.5-164)

W_кx= ^_v=0 w_кx v_x d_vn_x= ^_v=0^{ /2}_=0 mv²sin² vd_vn d_sin² /4^.2 =

= ^_v=0^{ /2}_=0 mv²vd_vn d_sin⁴ /4^.2^.2 =

= ^_v=0 mv²vd_vn /4^.2^.2 = ^Nw_кN_x /2 = W_к /2 (1.6.5-165)

W_кy = ^_v=0 w_кx v_xd_vn_x= ^_v=0^{ /2}_=0 mv²cos² vd_vn d_sin² /4^.2 =

= ^_v=0^{ /2}_=0 mv² (1-sin²) vd_vn d_sin² /4^.2 =

= ^_v=0 mv² (1-1/2) vd_vn /4^.2= ^Nw_кN_x /2 = W_к /2 (1.6.5-166)

W_кx= W_кy = W_к /2 (1.6.5-167)

W_o = ^_v=0 w_o v_xd_vn_x= ^_v=0^{ /2}_=0 mv_o²vd_vn d_sin² /4^.2 =

= ^_v=0 mv_o² vd_vn /4^.2= ^Nw_oN_x (1.6.5-168)

W_N = ^NwN_x = 2 ^Nw_кx N_x + ^Nw_o N_x = 2 ^Nw_кy N_x + ^Nw_o N_x =

= 2W_кx+ W_o= 2W_кy+ W_o (1.6.5-169)


Сумма d_uW энергий части d_uN_x потока частиц с w_кxi(0;d_xu)

d_uW = ^duN(w_к+ w_o) d_uN_x= ^duNw_к d_uN_x+ ^duNw_o d_uN_x= d_u^_v=0 (w_к+ w_o)v_xd_vn_x=

= ^_v=0^u_=0 mv² vd_vn d_sin² /4^.2 + ^_v=0 ^u_=0 mv_o² vd_vn d_sin² /4^.2 =

= ^_v=0mv² vd_vn ^u_=0 d_sin² /4^.2 + ^_v=0 mv_o² vd_vn ^u_=0 d_sin² /4^.2 =

= ^_v=0mv² vd_vn sin²_u /4^.2 + ^_v=0 mv_o² vd_vn sin²_u /4^.2 =

= ^_v=0mv² vd_vn v_u² /4^.2v² + ^_v=0 mv_o² vd_vn v_u²/4^.2v² =

= ^_v=0v²d_vn mv_u²/4^.2v + ^_v=0 v_o²d_vn mv_u²/4^.2v =

= (mv_u²/4) ^_v=0v²d_vn /2v + (mv_u²/4) ^_v=0 v_o²d_vn /2v =

= m ^dunv²v_ud_un_x /4 + m^dunv_o²v_ud_un_x /4 =

= m ^dunv²d_uN_x /2 + m^dunv_o²d_uN_x /2 =

= ^dunw_кd_uN_x + ^dunw_od_uN_x=

= ^duNw_кd_uN_x + ^duNw_od_uN_x=

= ^dunw d_uN_x= -^dunw d_xN_x=

= ^duNw d_uN_x= -^duNw d_xN_x=

= ^_v=0v²d_vn mv_u²/4^.2v + ^_v=0 v_o²d_vn mv_u²/4^.2v =

= ^_v=0vd_vn d_xu/4 + ^_v=0 v_o² vd_vn d_xu/4v² =

= d_xu ^_v=0vd_vn /4 + d_xu ^_v=0 v_o² vd_vn /4v² =

= N_x d_xu + ^N(v_o²/v²) N_x d_xu =

= N_x d_xu (1+ ^N(v_o²/v²)) = d_uW (1.6.5-160)

^dunw_o = ^duNw_o (1.6.5-171)

^dunw_к = ^duNw_к (1.6.5-172)

^dunw = ^duNw (1.6.5-173)

N_x d_xu = ^duNw_кd_uN_x = ^duNw_od_uN_x /^N(v_o²/v²) (1.6.5-174)

^N(v_o²/v²) = ^duNw_o /^duNw_к= ^dunw_o /^dunw_к= ^duNv_o² /^duNv_к²= ^dunv_o² /^dunv_к² (1.6.5-175)

d_uW = N_x d_xu (1+ ^N(v_o²/v²)) = N_x d_xu (1+ ^duNw_o /^duNw_к) = N_x d_xu (^duNw_к+ ^duNw_o ) /^duNw_к =

= N_x d_xu ^duNw /^duNw_к = N_x d_xu ^dunw /^dunw_к = ^duNw d_uN_x = ^dunw d_uN_x (1.6.5-176)


При наличии на пути потока частиц N_x потенциального барьера d_xu эта часть d_uW потока энергии всегда теряется потоком вместе с частью d_uN_x отраженного потока частиц.

Остальная часть N_x - d_uN_x потока со скоростью v_x частиц в интервале от v_x= v_u = =(2a_xdx)^½ до v_x= , способна преодолеть такой барьер, но она тоже теряет часть энергии d_vW = d_vW_к вследствие уменьшения скорости частиц полем барьера от v_x до v_x - d_uv_x. При этом количество частиц уже не изменяется, но каждая из них теряет энергию, в точности равную высоте d_xu барьера, поэтому общие потери потока энергии d_NW за счет уменьшения скорости d_uv и количества частиц d_uN можно представить в виде суммы


d_NW = d_vW + d_uW = (N_x - d_uN) d_xu + N_x d_xu (1+ ^N(v_o²/v²)) =

= N_x d_xu (2+ ^N(v_o²/v²)) - d_uN d_xu = N_x d_xu (2+ ^N(v_o²/v²)) – 0² 

N_x d_xu (2 + ^N(v_o²/v²)) =

= 2^dunw_кd_uN_к + ^dunw_od_uN_x =

= 2^duNw_кd_uN_к + ^duNw_od_uN_x =

= d_vW_к + d_uW = d_vW_к + d_uW_к + d_uW_o=

= 2d_vW_к + d_uW_o = 2d_uW_к + d_uW_o (1.6.5-177)

d_vW_к = d_uW_к = N_x d_xu = ^dunw_кd_uN_x = ^duNw_кd_uN_x (1.6.5-178)

d_uW_o = ^dunw_od_uN_x = ^duNw_od_uN_x (1.6.5-179)

d_uN_x /N_x = v_u² / ^dunv_к² = d_xu /^dunw_к = d_xu /^duNw_к (1.6.5-180)

d_uW = N_x d_xu (1+ ^N(v_o²/v²)) = ^dunw_кd_uN_x + ^dunw_od_uN_x (1.6.5-181)

d_vW_x = (N_x – d_uN) d_xu  N_x d_xu  ^dunw_кd_uN_x (1.6.5-182)

Аналогично по объему


W_n = W_nкx+ W_nкy+ W_no= ^_v=0 (w_к + w_o) d_vn_x = ^_v=0 (w_кx + w_кy + w_o) d_vn_x (1.6.5-183)

W_nкx= ^_v=0 w_кx d_vn_x= ^_v=0^{ /2}_=0 mv²sin² d_vn d_sin /2^.2 =

= ^_v=0^{ /2}_=0 mv²d_vn d_sin³ /2^.2^.3 =

= ^_v=0 mv²d_vn /2^.2^.3 = ⁿw_кn_x /3 = W_nк /3 (1.6.5-184)

W_nкy = ^_v=0 w_кx v_xd_vn_x= ^_v=0^{ /2}_=0 mv²cos² vd_vn d_sin /2^.2 =

= ^_v=0^{ /2}_=0 mv² (1-sin²) d_vn d_sin /2^.2 =

= ^_v=0 mv² (1-1/3) d_vn /2^.2= 2ⁿw_кn_x /3 = 2W_nк /3 (1.6.5-185)

W_nкx= W_nкy /2= W_nк /3 (1.6.5-186)

W_no= ^_v=0 w_o d_vn_x = ⁿw_o n_x (1.6.5-187)

d_uW_n = d_uW_nкx+ d_uW_nкy+ d_uW_no= d_u^_v=0 (w_к + w_o) d_vn_x =

= d_u^_v=0 (w_кx + w_кy + w_o) d_vn_x (1.6.5-188)

d_uW_nкx= ^_v=0 w_кx d_vn_x= ^_v=0^u_=0 mv²sin² d_vn d_sin /2^.2 =

= ^_v=0^u_=0 mv³d_vn d_sin³ /2^.2^.3v =

= ^_v=0^u_=0 md_vn d_v_x³/2^.2^.3v =

= ^_v=0 mv_u³d_vn /2^.2^.3v = mv_u^{3 }_v=0 d_vn /2^.2^.3v = mv_u²v_u ^_v=0 d_vn /2v2^.3=

= mv_u²d_un_x /2^.3 = d_xu d_un_x /3 = mv_ud_uN_x /3 (1.6.5-189)

d_uW_nкy = ^_v=0 w_кx d_vn_x= ^_v=0^u_=0 mv²cos² d_vn d_sin /2^.2 =

= ^_v=0^u_=0 mv² (1-sin²) d_vn d_sin /2^.2 =

= ^_v=0^u_=0 mv² d_vn d_sin /2^.2 - ^_v=0^u_=0 mv² sin² d_vn d_sin /2^.2 =

= ^_v=0^u_=0 mv d_vn d_v_x/2^.2 - d_uW_nкx= ^_v=0 mv d_vn v_u /2^.2 - d_uW_nкx=

= ^_v=0 mv d_vn v_u /2^.2 - d_uW_nкx =

= mv_u^_v=0 v d_vn /2^.2 - d_uW_nкx = N_x mv_u - mv_ud_uN_x /3 = mv_u (N_x - d_uN_x /3)  mv_u N_x =

= ^_v=0 mv² v_ud_vn /2v2 - d_uW_nкx = m ^dunv² d_un_x /2 - mv_u²d_un_x /2^.3 =

= (3^dunv² - v_u²) m d_un_x /2^.3  m ^dunv² d_un /2 = ^dunw_к d_un (1.6.5-190)

d_uW_no= d_u ^_v=0 ^u_=0 w_o d_vn_xd_sin /2 = ^dunw_o d_un_x (1.6.5-191)


Сумма d_uW_nк энергий всех d_un_x частиц с v_кxi(0;v_u) и, соответственно, с w_кxi(0;d_xu)


d_uW_nк = d_uW_nкx+ d_uW_nкy = ^_v=0 mv d_vn v_u /2^.2 = mv_u N_x = m ^dunv² d_un_x /2 =

= m ^dunv² v_ud_un_x /2v_u = m ^dunv² d_uN_x /v_u = m ^dunv² d_uN_x /v_u (1.6.5-192)

m ^dunv² d_uN_x /v_u = mv_u N_x (1.6.5-193)

d_uN_x /N_x = v_u² / ^dunv² = d_xu /^dunw_к (1.6.5-194)


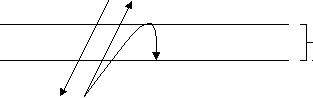
Рассмотрим условия равновесия потоков частиц, а также импульсов и энергий, переносимых потоками частиц через потенциальный барьер высотой d_xu (рис. 1.6.5.4)


d_xu = _xu dx = mv_u²/2 = - a_x dx (1.6.5-195)

N₂ = N₁ - d_uN₁ (1.6.5-196)





N₂N₂

X₂

d_xu

X₁

N₂d_uN₁d_uN₁


N₁


Рис. 1.6.5.4. Схема прохождения потоков частиц через потенциальный барьер.


Суммарный поток частиц N_x1, пересекающих поверхность x₁ в сторону поверхности x₂ со средней по потоку скоростью ^Nv_x1 и энергией ^Nw₁, расщепляется барьером на две части: поток N_x1 - d_uN_x1, пересекающий поверхность x₂, и поток d_uN_x1, поворачивающий обратно из-за w_x < d_xu (^duNw_x < d_xu), где w_x – продольная составляющая кинетической энергии частиц. Суммарный поток частиц N_x2, пересекающих поверхность x₂ в сторону поверхности x₁ со средней по потоку скоростью ^Nv_x2 и энергией ^Nw₂, ускоряется барьером. При этом скорость v_xi2 и энергия w_xi2 каждой частицы возрастают так, что dw_i2 = d_xu, а количество N_x2 частиц не меняется, то есть d_vN_x2. Следовательно, можно считать, что поверхность x₁ пересекают два встречных потока частиц N_x1 и N_x1, а поверхность x₂ пересекают два встречных потока частиц N_x2 и N_x2


N_x2 = N_x1 - d_NN_x1 = N_x1 - d_uN_x1 - d_vN_x1 = N_x1 - d_uN_x1 (1.6.5-197)

N_x1 = N_x2 + d_NN_x2 = N_x2 + d_uN_x1 + d_vN_x2 = N_x2 + d_uN_x1 (1.6.5-198)


Встречные потоки могут быть равны N_x = N_x между собой, и тогда мы можем говорить о механическом макроскопическом равновесии газа, или не равны, и тогда мы можем говорить о механическом макроскопическом неравновесии газа, характеризуемом макроскопическим потоком газа, равном разности (алгебраической сумме) встречных микроскопических потоков N_x через конкретную поверхность x


N_x = N_x - N_x = n_x ⁿv_x - n_x ⁿv_x (1.6.5-199)

P_x = P_x - P_x = N_x^Nv_xm - N_x^Nv_xm= mn_x ⁿv_x^Nv_x - mn_xⁿv_x^Nv_x =

= n_x m ⁿv_x²- n_x m ⁿv_x² (1.6.5-200)

W_x = W_x - W_x = N_x ^Nw - N_x ^Nw = n_x ⁿv_x ^Nw - n_x ⁿv_x ^Nw (1.6.5-201)


В общем случае встречные потоки могут быть разными по величине, но в случае полного (детального) равновесия газа потоки частиц, импульсов и энергий, пересекающие любую поверхность в противоположных направлениях, равны между собой и/или, что то же, их разность равна нулю. Например, при детальном равновесии для каждой частицы, перемещающейся со скоростью v_x,существует парная ей частица, перемещающаяся с равной по величине скоростью v_xв противоположном направлении. Поэтому из такого условия

v_x= v_x (1.6.5-202)

v= v (1.6.5-203)

d_vn_x = d_vn_x (1.6.5-204)

d_vn = d_vn (1.6.5-205)

прямо следует

f₁(v) f₂(v_x) f₃(n_x) = f₁(v) f₂(v_x) f₃(n_x) (1.6.5-206)

и

N_x = N_x - N_x = ^_v=0^{ /2}_=0 (v_xd_vn_x - v_xd_vn_x) = 0 (1.6.5-207)

P_x = P_x - P_x = ^_v=0^{ /2}_=0 m (v_x²d_vn_x - v_x²d_vn_x) = 0 (1.6.5-208)

W_x = W_x - W_x = ^_v=0^{ /2}_=0 (mv²v_xd_vn_x/2 - mv²v_xd_vn_x/2) = 0 (1.6.5-209)


Представление о детальном равновесии эквивалентно представлению об изотропии розеток траекторий в однородном пространстве-времени. Вместе они приводят к представлению о статистической независимости картины распределения траекторий частиц от наличия столкновений. В сферически симметричных розетках всегда есть возможность подмены участков ломаных траекторий одних сталкивающихся частиц подходящими участками траекторий других сталкивающихся частиц, чтобы исправленные траектории принимали вид гладких (неизломанных) траекторий невзаимодействующих (несталкивающихся или пролетающих друг сквозь друга) частиц. Интересующие нас потоки являются интегральными (суммарными) величинами, и вследствие принятых правил счета такая подмена приводит только к изменению последовательности суммирования частей, никак не сказываясь на величине сумм. Поэтому картины распределения траекторий сталкивающихся и несталкивающихся (взаимодействующих и невзаимодействующих) частиц полностью экивалентны для любого (включая наш) анализа интегральных потоков. Исправленную траекторию частицы в силовом поле теперь можно рассматривать как обычную баллистическую траекторию не только на отдельных участках свободного полета между столкновениями, но и в целом, как бы пренебрегая совокупностью симметричных отклонений от нее под действием столкновений.

Определим температуру T как некий параметр, определяющий величину и направление переноса энергии потоками частиц. При таком определении T средняя по потоку N энергия ^Nw частиц должна быть пропорциональна T


^Nw = a_N T (1.6.5-210)

d_x^Nw = a_N d_xT (1.6.5-211)

Пока a_N неизвестно, но условие d_xT = 0 упрощает ситуацию даже в случае a_N = a_N (T), так как при таком определении T при d_xT = 0 разница (алгебраическая сумма) потоков энергии через любую поверхность должна быть равна нулю

W - W= 0 (1.6.5-212)

W = W= W= N ^Nw = N a_NT (1.6.5-213)

d_x^Nw = a_N d_xT = 0 = d_x^Nv_x = d_xⁿv_x (1.6.5-214)

d_xW = d_xN ^Nw + N d_x^Nw = d_xN ^Nw = d_xN a_NT= - N d_xu - ^duNw d_uN (1.6.5-215)

d_xN ^Nw + ^duNw d_uN = d_xN (^Nw - ^duNw) = d_xN ^Nw_x = - N d_xu (1.6.5-216)

d_xN /N = d_xn /n + d_xⁿv_x /ⁿv_x= d_xn /n = - d_xu /^Nw_x (1.6.5-217)

P_x = P_x + P_x = N_x^Nv_xm + N_x^Nv_xm= mn_x ⁿv_x^Nv_x + mn_xⁿv_x^Nv_x =

= n_x m ⁿv_x²+ n_x m ⁿv_x²= nm ⁿv_x²= 2n ⁿw_x (1.6.5-218)

d_xP_x /P_x= d_xn /n + d_xⁿw_x /ⁿw_x= d_xn /n = - d_xu /2ⁿw_x = - d_xu /^Nw_x (1.6.5-219)

2ⁿw_x = ^Nw_x (1.6.5-220)


Представление о равновесии пара над поверхностью конденсата позволяет получить связь давления пара на стенки сосуда с другими параметрами пара.

Давление пара p_x = p_п на жидкость и стенки сосуда состоит из импульсов отдельных i-тых частиц, имеющих размер x₀ и длину свободного пробега _i при импульсе mv_xi, ударяющих в поверхность раздела и улетающих от нее с частотой f_i


p_п =^_v=0 2mv_xi f_i (1.6.5-221)

f_i = v_i /2(_i - x₀) (1.6.5-222)


Количество N_i таких частиц в слое толщиной _xi при концентрации n_i


N_i = n_i_xi (1.6.5-223)


Каждая из них наносит f_i ударов в единицу времени.


p_п =^_v=0 2mv_xi f_i =^_v=0 2mv_xi n_i_xiv_i /2(_i - x₀) =

=^_v=0 mv_xi² n_i_i /(_i - x₀) =ⁿv²_xi nm /(1 - x₀ / ⁿ) (1.6.5-224)

т.к.

v_i_xi = v_i _isin = _i v_isin = _i v_xi (1.6.5-225)


Эффективные кинетическое сечение _к и кинетический объём V_к одной средней частицы при ⁿv²_xi m = kT

 _к = 1 / ⁿn (1.6.5-226)

V_к = x₀ _к (1.6.5-227)

p_п =ⁿv²_xi nm /(1 - x₀ n) = kT /(1/n - V₀) = kT /(V_пу – V_к) (1.6.5-228)


где: V_пу = 1/n - удельный объем, приходящийся на одну частицу пара, и V_к - кинетический объём частицы пара, который в первом приближении можно приравнять к объему V_жу  V_к одной частицы жидкости. Умножая на общее число частиц M


Mp_п (V_пу - V₀) = p_п (V_пар – V_ж) = MkT (1.6.5-229)

На поверхность жидкости давит только приповерхностный слой, для которого неизвестно общее число частиц M, но известна связь между поверхностной n_пов= n_ж и приповерхностной n_припов= n_пар концентрациями частиц


n_пар = n_ж e ^-u/kT (1.6.5-230)


где u – разность потенциалов между поверхностью жидкости и объемом пара за счет взаимного притяжения частиц. С учетом (1.6.5-228) и (1.6.5-230)


p_п = kT /(V_пу - V_к) = kT /(1/n_п - 1/n_ж) = n_п kT /(1 - n_п /n_ж) =

= n_п kT /(1 - e ^-u/kT) = n_ж kT /(e ^u/kT - 1) (1.6.5-231)

u = kT ln (n_жkT /p_п + 1) = kT ln (kT /p_пV_жу + 1) (1.6.5-232)


Выражение (1.6.5-232) позволяет найти зависимость u (V) из экспериментальных данных. В первом приближении для простых сферических частиц при сравнительно низких температурах V_к можно принять равным объему V_жу жидкости и/или твердого тела, а u равным теплоте испарения, которая обычно много больше kT. Тогда


u = kT ln (kT /p_пV_жу + 1) kT ln (kT /p_пV_жу) (1.6.5-233)

p_п = n_ж kT /(e ^u/kT - 1) n_ж kTe ^-u/kT (1.6.5-234)


Если бы поля частиц были строго изотропными, то распределение Больцмана было бы почти одинаковым для всех границ раздела фаз – твердых, жидких и газообразных.


n_п  n_ж e ^{-u(жп)/kT} (1.6.5-235)

n_п  n_т e ^{-u(тп)/kT} (1.6.5-236)

n_ж  n_т e ^{-u(тж)/kT} (1.6.5-237)

n_т  n_т e ^{-u(тт)/kT} (1.6.5-238)


Неизотропность строения агрегатов и, соответственно, конденсатов довольно сильно искажает и усложняет идеальную картину, заставляя использовать разные значения u для разных направлений, что делает полученные выражения менее удобными для практики. Но даже и в этом случае их применение может быть достаточно удобным. Например, график зависимости объема насыщенного пара воды от температуры с приемлемой точностью принимает вид почти прямой линии в координатах lnV_п – 1/T , и начинает заметно отличаться от нее только при температуре выше 300 ^С


ln V_п/V_ж  q_исп /kT (1.6.5-239)


Использование подобных зависимостей при современной вычислительной технике упрощает и уточняет обычные инженерные расчеты и представления, в то время как удобство и точность табличных данных, приводимых даже в очень хороших справочниках, значительно ниже при всей громоздкости и малотиражности этих справочников.

Полученные выражения в принятых представлениях верны для всех изотропных распределений, включая распределение Максвелла в состоянии тепломеханического равновесия газа. Для неизотропных случаев они не верны. Например, в случае ненулевого градиента температур

v_x v_x (1.6.5-240)

vv (1.6.5-241)

d_vn_x  d_vn_x (1.6.5-242)

d_vn  d_vn (1.6.5-243)

прямо следует

f₁(v) f₂(v_x) f₃(n_x)  f₁(v) f₂(v_x) f₃(n_x) (1.6.5-244)


при любом из ограничений


N_x = N_x - N_x = ^_v=0^{ /2}_=0 (v_xd_vn_x - v_xd_vn_x) = 0 (1.6.5-245)

P_x = P_x - P_x = ^_v=0^{ /2}_=0 m (v_x²d_vn_x - v_x²d_vn_x) = 0 (1.6.5-246)

W_x = W_x - W_x = ^_v=0^{ /2}_=0 (mv²v_xd_vn_x/2 - mv²v_xd_vn_x/2) = 0 (1.6.5-247)


Представления о газах как своеобразной упаковке агрегатов могут быть дополнены представлениями о волнах сжатия-разрежения и относительного сдвига частей газа и/или о потоках газа, как волнах с нулевой частотой колебаний, о вихрях и потерях на трение. Все они практически совпадают с существующими представлениями о свойствах газа и, поэтому, пока не интересны для поставленной простейшей задачи.

Принятые представления об агрегатной части газа, в основном, совпадают с неклассическими представлениями об идеальном газе и с выводами термодинамики газов. Не противоречат им и представления о парогазовых тепломеханических циклах, используемых в тепловых машинах. Можно показать, что КПД цикла Карно является предельным для всех возможных газовых и паровых циклов. Одинаковость КПД всех идеальных газовых циклов делает их равноценными и усиливает второй постулат термодинамики, исключая концентрирование тепловой энергии при помощи комбинации тепломеханических устройств-машин, хотя сама по себе не может служить обоснованием постулата, так как справедлива только для частных условий. Но в совокупности со сферическим распределением скоростей агрегатов в потенциальном поле она (одинаковость КПД) исчерпывает все известные варианты процессов переноса энергии в идеальных газоподобных системах, превращая второй постулат термодинамики в закон для таких систем. Следует, однако, отметить, что практикуемое формальное распространение второго постулата термодинамики на все другие системы пока не является обоснованным. Корректность его применения в каждом таком случае требует отдельных доказательств.