Краткое обзорно-справочное пособие. Книга является первым в своём роде обзорно-справочным пособием по виртуальной физике и рассчитана на широкий круг читателей, интересующихся проблемами Науки вообще и физики в частности

Вид материала

Книга

Подобный материал:

• Реферат данилюк А. И. Элементы виртуальной физики, 106.58kb.
• Liaise With Europe, Франция создание предприятия от а до я в узбекистане справочное, 2964.95kb.
• Справочное пособие по проблемам здоровья. М.: Корал Клаб, 2000, 627.09kb.
• Тема: Экономика Дагестана, 120.6kb.
• Ю. М. Иванов как стать экстрасенсом москва 1990 Книга, 12883.6kb.
• Иные миры, 3004.29kb.
• Избранные сочинения Александра Григорьевича Столетова издание, рассчитанное на широкий, 3.19kb.
• Книга написана живым, образным языком и рассчитана не только на историков профессионалов,, 2424.55kb.
• И. М. Феигенберг мозг психика здоровье издательство «наука» Москва 1972 Книга, 1509.07kb.
• А. П. Щёголев нужен гразер! Исповедь исследователя с-петербург 2009г. От редакции, 1921.01kb.

а) вывод распределения, предложенный Максвеллом:


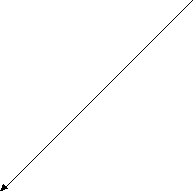
Рассмотрим сферу скоростей частиц (рис.1.6.5.2). Она была использована Максвеллом в качестве модели для вывода названного впоследствии его именем распределения молекул газа по скоростям.



Z


dR



R






0




Y


X

Рис. 1.6.5.2. Сфера скоростей Максвелла. Пространственное распределение разлетевшихся частиц газа.


Для вывода распределения молекул газа по скоростям Максвелл предложил мысленный эксперимент. Если в нуле 3-мерной системы координат разместить порцию любого газа при температуре T и дать всем молекулам возможность одновременно разлетаться, то через достаточно большое время t они окажутся на расстояниях R = vt от центра. Влияние столкновений будет существенным только в начальный момент, а потом, по мере уменьшения объемной концентрации разлетающихся молекул, оно должно быстро падать, и на достаточно больших расстояниях ним можно пренебрегать. При t  конечное распределение молекул в пространстве с точностью до сокращаемой постоянной t будет соответствовать начальному распределению молекул по скоростям,


R_i = v_i t (1.6.5-59)

dR_i = t dv_i (1.6.5-60)


и R_i можно формально заменять на v_i. Тогда вероятность _i нахождения молекул в элементе объема dV = dv_x dv_y dv_z при плотности вероятности (v_i) нахождения частицы в интервале скоростей {v_i; v_i+dv_i} = {[v_xi; v_xi +dv_xi]; [v_yi; v_yi+dv_yi]; [v_zi; v_zi+dv_zi]} равна

d_i =(v_i) dV =(v_i) dv_xi dv_yi dv_zi (1.6.5-61)

Проекции скорости

v_i² = v_xi² + v_yi² + v_zi² (1.6.5-62)

Вероятности независимых событий умножаются. Вследствие предполагаемой однородности пространства все направления равноправны, и скорости не зависят от углов. Если предположить, что компоненты скорости любой частицы независимы, то (1.6.5-61) можно представлять в виде произведения вероятностей


(v_i) = (v_xi) (v_yi) (v_zi) = _xi _yi _zi (1.6.5-63)

ln _i = ln _xi+ ln _yi+ ln _zi (1.6.5-64)


Дифференцируя (1.6.5-64) по каждой из трех независимых компонент


(1/ _i) d_i /dv_xi = (1/ _i)(d_i /dv_i²) d(v_xi² + v_yi² + v_zi²) /dv_xi =

= (1/ _i) (d_i/dv_i²) d(v_xi²) /dv_xi = (1 /_xi) (d_xi/dv_xi²) d(v_xi²) /dv_xi

(1/ _i) d_i /dv_yi = (1/ _i)(d_i /dv_i²) d(v_xi² + v_yi² + v_zi²) /dv_yi =

= (1/ _i) (d_i/dv_i²) d(v_yi²) /dv_yi = (1 /_yi) (d_yi/dv_yi²) d(v_yi²) /dv_yi (1.6.5-65)

(1/ _i) d_i /dv_zi = (1/ _i)(d_i /dv_i²) d(v_xi² + v_yi² + v_zi²) /dv_zi =

= (1/ _i) (d_i/dv_i²) d(v_zi²) /dv_zi = (1 /_zi) (d_zi/dv_zi²) d(v_zi²) /dv_zi

(1/ _i) d_i/dv_i² = (1 /_xi) d_xi/dv_xi² = (1 /_yi) d_yi/dv_yi² = (1 /_zi) d_zi/dv_zi² =

= C(x,y,z) (1.6.5-66)

d_xi /_xi = C₁ dv_xi² (1.6.5-67)

ln _xi = C₁ v_xi² + C₂ (1.6.5-68)

_xi = (v_xi) = C₂ exp (C₁ v_xi²) (1.6.5-69)

При равноправии координат


(v_i²) = (v_xi²) (v_yi²) (v_zi²) = C₃ exp[C₁(v_xi² + v_yi² + v_zi²)] = C₃ exp(C₁v_i²) (1.6.5-70)

d_i =(v_i) dV = (v_i) dv_xi dv_yi dv_zi = C₃ exp(C₁v_i²) 4v_i²dv_i (1.6.5-71)


Условия сходимости (конечности) и положительности вероятности


C₁ = -A < 0 (1.6.5-72)

C₃ = B > 0 (1.6.5-73)

и условия нормирования

^₀ d_i = 1 (1.6.5-74)

^₀ w_id_i = 3 m /2kT (1.6.5-75)

позволяют найти постоянные A и B

A = 1 /2kT (1.6.5-76)

B = 2 ^-1/2 (kT) ^-3/2 (1.6.5-77)

Окончательно

d_w = 4 (m /2kT)^3/2 e ^–w/kT v² dv = 2 ^-1/2 (kT) ^-3/2 e ^-w/kT w^½ dw (1.6.5-78)


Предположение о независимости компонент скорости конкретной молекулы формально приводит к (1.6.5-63) и, соответственно, к (1.6.5-78). Но такое предположение становится, как минимум, неочевидным из-за противоречащего ему использования явной связи (1.6.5-62), что требует доказательства корректности применения (1.6.5-63), которого не было ни в первой, ни в последующих публикациях Максвелла. В одной из публикаций 70-х годов ХХ ст. отмечалось, что сам Максвелл, увлеченный изящным выводом и результатом, не сразу заметил неочевидность и недоказанность этого предположения и опубликовал вывод примерно в таком виде, как приведено выше. Оппоненты, конечно же, заметили недостаток и указали на него. Но скандала не вышло, так как Максвелл почти сразу согласился с ними насчет недостаточности доказательств, оставив за собой право настаивать на правильности общей формы распределения, стремящегося к нулю при нулевой и бесконечной скорости молекул и обладающего явно выраженным максимумом при некоторой наиболее вероятной скорости, однозначно связанной с температурой газа. С тех пор было предпринято много попыток и теоретического и экспериментального опровержения (1.6.5-78), но ни одна из них не увенчалась успехом, как, впрочем, и попытки его корректного вывода. Если все так и было, то выходит, что Максвелл просто угадал это распределение, причем не только его форму, на чем он настаивал, но и количественную зависимость, от которой он сначала тоже отказался, и которая потом с приемлемой (конкуренции не было) точностью совпала со многими экспериментальными данными и результатами, увязанными с другими представлениями. В такой форме выражение для распределения молекул газа по скоростям, получившее впоследствии название распределения Максвелла, используется до сих пор, являясь, по сути, одним из многих постулатов термодинамики и составляя с ними замкнутую группу взаимно эквивалентных постулатов. Его можно выводить из других постулатов, и их можно выводить из него. Но ни один из них не был прямо увязан с другими, более фундаментальными представлениями. Этот случай в целом напоминает случай с КПД Карно, получившим правильное выражение для максимального КПД тепловой машины на основании ошибочного представления о тепловой энергии как жидкости-флогистоне. Распределение Максвелла и КПД Карно являются равноправными членами упомянутой группы постулатов термодинамики наряду с эргодической гипотезой, теоремой Нернста, постулатами о необратимости тепловых процессов, росте энтропии, невозможности вечного двигателя второго рода, вторым началом термодинамики и т.п. Термодинамика, дающая много советов для других наук и служащая им опорой, сама казалась подвешенной в логической пустоте без настоящего фундамента. По этой причине автор тоже предпринял попытку найти подходящее решение, но поскольку результаты не оправдали его ожиданий, то не были опубликованы, если не считать доклад-консультацию в 1986 г. на кафедре теорфизики. Однако сейчас автор все-таки решил включить их в данный раздел, поскольку даже отрицательные результаты могут представлять некоторую ценность для других людей с точки зрения уменьшения неэффективных потерь их времени на уже пройденном кем-то пути.

Для уточнения вывода распределения частиц газа по энергиям было использовано представление о механическом равновесии квазиоднородной газоподобной системы частиц в ускоряющем поле. Возможно, это произошло под влиянием аналогичного способа, приведенного более 30 лет назад в одном из учебников физики, где для подобной цели использовалось представление о гравитационное поле. Автор только несколько изменил его, пытаясь получить более общие результаты, но сущность идеи осталась прежней.


б) вывод распределения для квазиоднородной газоподобной системы частиц в ускоряющем поле:


В классическом представлении пространство имеет три равноправных однородных измерения, и время имеет одно однородное измерение. Вследствие предполагаемой однородности пространство и время изотропны, то есть, все направления равноправны и количества частиц, летящих в любых одинаковых телесных углах равны. Поэтому любые распределения частиц по скоростям, верные для бесконечно малых телесных углов будут верны для любых углов и любых порций газа, что позволяет производить независимый подсчет количества частиц в интервалах скоростей и интервалах углов, уводя от необходимости отвечать на вопрос о зависимости компонент скорости конкретной частицы. Пусть теперь квадрат скорости конкретной частицы будет равен сумме квадратов проекций скорости на все оси координат, пусть они жестко связаны этим геометрическим соотношением, но в таком представлении это уже не имеет никакого отношения к количеству частиц с такой скоростью.

Если пространство и время однородны и, соответственно, изотропны, а частицы неразличимы и неуничтожимы, то при достаточно длительном механическом равновесии газоподобной системы этих частиц в любом ускоряющем, например, гравитационном или электрическом поле всегда для каждого микрообъема системы можно нарисовать сферические розетки скоростей и траекторий находящихся в этом объеме частиц, аналогичные розетке Максвелла. Сферичность-изотропность розеток траекторий и скоростей означает, что для рассеивания частиц газа при соударениях не существует особых направлений в пространстве, несмотря на наличие ускоряющего поля. Поэтому систему сталкивающихся частиц можно заменять системой невзаимодействующих частиц, проникающих сквозь друг друга и/или пролетающих мимо, что позволяет не учитывать форму траекторий и даже сам факт столкновения и, соответственно, длину свободного пробега частиц.

Рассмотрим поток N_i1 частиц, значения энергии w_i которых находятся в интервале (w_i; w_i + dw_i), а скоростей вдоль оси Х – в интервале (v_xi; v_xi + dv_xi). Все частицы с x-составляющей энергии, большей разности потенциалов d_xu

w_xi = mv_xi² /2 > d_xu (1.6.5-79)


преодолеют потенциальный барьер d_xu, уменьшив свою кинетическую энергию на


d_uw_xi = - d_xu = u_x2 - u_x1 (1.6.5-80)


Количество таких частиц, точнее их поток, преодолевающий барьер, должен сохраняться


d_wN_xi1(w_xi1 > d_xu)  d_wN_xi2(w_xi2= w_xi1 - d_xu) (1.6.5-81)

Но поток частиц

d_wN_xi = ½ d_wn_xiv_xi (1.6.5-82)


где d_wn_xi – объемная концентрация частиц с энергией в интервале


(w_i; w_i + dw_i) (1.6.5-83)


Коэффициент ½ учитывает частицы, движущиеся только в одном направлении. Из (1.6.5-81)-(1.6.5-82)

d_wn_xi1 v_xi1  d_wn_xi2 v_xi2 (1.6.5-84)


При сферическом (однородном) распределении скоростей v_i по углу _i = arc sin v_xi /v_i функция их распределения по этому углу f_ (_i)  1, и при концентрации n_i частиц со скоростями v_i

d_ d_wn_xi = d_wn_i f_(_i) cos_i d_i /2= d_wn_i dsin_i /2 (1.6.5-85)

v_xi1 d_ d_wn_xi1 = v_xi2 d_ d_wn_xi2 = v_i1sin d_wn_i dsin_i /2 = v_i1 d_wn_i1 dsin²_i1 /4 =

= v_i1 d_wn_i1 d(v_xi /v_i)²/4 = d_wn_i1 d(v_xi1)²/4v_i1 = d_wn_i2 d(v_xi2)²/4v_i2 (1.6.5-86)

По правилам дифференцирования

d(v_xi1)² = d(v_xi2)² = 2 adx (1.6.5-87)


При сферическом распределении n_i и v_i не зависят от _i, поэтому если в точке x_i1 распределение было сферическим, то оно таким останется и в точке x_i2. Рассеивание частиц при соударениях восстанавливает сферическую симметрию, поэтому распределение частиц по направлениям, в конце концов, должно стать симметричным. Это означает, что в состоянии полного механического равновесия системы распределение частиц по направлениям должно также быть сферически симметричным. Поэтому в потоке частиц находящегося в равновесии газа всегда выполняется равенство


d_wn_i1 /v_i1 = d_wn_i2 /v_i2 (1.6.5-88)


для частиц с любыми скоростями v_i и w_xi1 > d_xu. Запишем n_i через функцию распределения частиц по энергиям f_w(w_i) и концентрацию газа n


d_wn_i = n f_w(w_i) dw_i (1.6.5-89)

Тогда

n₁ f_w1(w_i1) /v_i1 = n₂ f_i2(w_i2) /v_i2 (1.6.5-90)

при

q_i = q_i(w_i) = f_w(w_i) /v_i (1.6.5-91)

n₁ q_i1 = n₂ q_i2 (1.6.5-92)

n₁ / n₂ = q_i2 /q_i1 = q_i2(w_i1 - u) /q_i1(w_i1) = const (w_i) = f(u) (1.6.5-93)

ln (n₂ /n₁) = ln q_i1 - ln q_i2 = const (w_i) = f(u) (1.6.5-94)


w_i1 и u независимы, поэтому (1.6.5-82) справедливо для любых w_i1  u 0, и раздельное дифференцирование по этих w_i1 и u дает

d_w1 ln (n₂ /n₁) = 0 = (1/q_i1) d_w1q_i1 – (1/q_i2) d_w1q_i2 (1.6.5-95)

d_u ln (n₂ /n₁) /du = С₁(w_i) = (1/q_i1) d_uq_i1 /du – (1/q_i2) d_uq_i2 /du =

= (1/q_i1)(d_wq_i1 /dw_i1) d_uw_i1/du – (1/q_i2)(d_wq_i2 /dw_i2) d_uw_i2/du (1.6.5-96)


w_i1 и u независимы, поэтому

d_uw_i1 /du = 0 (1.6.5-97)

d_u(w_i2 = w_i1 + u) /du = 1 (1.6.5-98)

Из (1.6.5-96)

(1/q_i2)(dq_i2 /dw_i2) = (1/q_i)(dq_i /dw_i) = - С₁(w_i) = -A (1.6.5-99)

(1/q_i) dq_i = - Adw_i (1.6.5-100)

q_i = Be^-Aw = f_i(w)/v (1.6.5-101)

f_w(w) = Be^-Aw v = Be^-Aww^½ (1.6.5-102)

d_wn = n f_w(w) dw = Be^-Aww^½ dw (1.6.5-103)

Условия нормирования

^₀ f_w(w) dw = 1 (1.6.5-104)

^₀ f_w(w) w dw = 3/2 kT (1.6.5-105)

- A < 0 (1.6.5-106)

позволяют найти постоянные A и B

A = 1/kT (1.6.5-107)

B = 2 ^-1/2 (kT) ^-3/2 (1.6.5-108)

Окончательно

d_wn = 2n ^-1/2 (kT) ^-3/2 e ^-w/kT w^½ dw = 4n (m /2kT)^3/2 e ^–w/kT v² dv (1.6.5-109)


что полностью совпадает с результатом Максвелла. Распределение (1.6.5-109) получено из представлений о возможности механического (макроскопического) равновесия квазиоднородной (состоящей из одинаковых частиц) газоподобной (частицы основное время находятся в свободном полете и взаимодействуют друг с другом пренебрежимо малое время) системы частиц в силовом поле в однородном и изотропном пространстве и времени, что позволяет строить сферически симметричные розетки скоростей и траекторий в любой точке пространства и, пользуясь законами сохранения частиц и энергии, получать соотношение (1.6.5-88). Выражение (1.6.5-90) превращается в


n₂ /n₁ = (f_w1/v_i1) /(f_w2/v_i2) = e^-A(w2-w1) = e^-u/kT (1.6.5-110)

и

n₂= n₁e^-u/kT (1.6.5-111)


что совпадает с известным распределением Больцмана в потенциальном поле.

При выводе распределений (1.6.5-109)-(1.6.5-111) учет внутреннего строения частиц и формы их траекторий не требовался. Поэтому (1.6.5-109)-(1.6.5-111) должны быть верными для любых газо-подобных систем-скоплений частиц с любым строением и с любыми законами взаимодействия, приводящими к любому изменению формы траекторий в окрестностях точек столкновения при условии сохранения количеств частиц, импульсов и энергии в конкретные моменты времени в конкретных точках пространства. Это условие полностью выполняется в случае так называемых "идеальных" (абсолютно упругих) газов. Поэтому для них (1.6.5-59)-(1.6.5-111) можно считать абсолютно верными. Близкими к ним в первом приближении можно считать некоторые простейшие, например, инертные газы при определенных условиях (не очень низких и не очень высоких температурах и достаточной для изотропности розеток компенсации потерь механической и волновой энергии). В остальных случаях это условие обычно выполняется плохо из-за существенной неупругости столкновений, поэтому реальные распределения могут существенно отличаться от идеального распределения Максвелла-Больцмана (1.6.5-109)-(1.6.5-111). Вопрос только в том, насколько существенны эти отличия для точности описания газа.

Сами по себе (1.6.5-109)-(1.6.5-111) не несут ничего нового. Распределение идеально упругих частиц по скоростям и энергиям в механически равновесном газе в любых стационарных ускоряющих полях должно быть максвелловским или, по крайней мере, близким к нему, со всеми вытекающими последствиями. Некоторую новизну привносит только сам факт вывода распределения из более общих представлений. После такого вывода применение распределения Максвелла-Больцмана в качестве одного из постулатов термодинамики идеальных газов позволяет представлять последнюю уже в виде более фундаментальной науки, базирующейся на основе более фундаментальных представлений об однородности пространства-времени и абсолютной упругости частиц идеальных газов, что делает её выводы бесспорными в рамках этих представлений. К сожалению и/или к счастью (смотря для кого), свойства реальных газов отличаются от свойств идеальных газов, и, соответственно, распределение их частиц по скоростям и энергиям существенно отличается от максвелловского, обесценивая в значительной степени все затраты на его вывод и в п.1.6.5а, и в п.1.6.5б.


в