Шаблоны: определение и использование. Именованные области
| Вид материала | Документы |
- Лекция Шаблоны функций и классов. Исключения, 85.26kb.
- Задание для выполнения лабораторной работы №1 средствами ms word, 50.12kb.
- Практикум по Word. Занятие 12: шаблоны Практическое занятие 12. Работа с текстовым, 58.22kb.
- Ввашей компании, возможно, существуют собственные шаблоны для составления планов, 127.25kb.
- Техническое задание «Определение величины арендной платы за использование причальных, 725.54kb.
- «Использование сети Интернет при проведении урока в рамках образовательного стандарта», 473.36kb.
- Лекция№1 Тема: Определение арт-терапии, 638.33kb.
- Журналистское расследование как средство борьбы с коррупцией, 1289.31kb.
- Тема Содержание финансового менеджмента, 647.78kb.
- «показатели качества воды и их определение» введение, 948.44kb.
ЗАНЯТИЕ 6
1. Шаблоны: определение и использование.
2. Именованные области. Оператор расширения видимости. Директива using.
3. Стандартная библиотека шаблонов (STL). Алгоритмы. Контейнеры. Итераторы.
4. Векторы. Конструкторы. Вставка-удаление элементов. Использование итераторов для доступа к элементам.
5. Задачи.
ссылка скрыта: SRM 193 (SwimmingPool), SRM 194 (Soccer), SRM 212 (YahtzeeScore), SRM 217 (FuelConsumption), SRM 253 (ObjectPacking), SRM 315 (RosePetals), SRM 322 (DerivativeSequence).
1. ШАБЛОНЫ
Шаблоны позволяют определять функции, которые могут работать с разными типами данных. Шаблоны определяются следующим образом:
template
template
Оба определения идентичны. Можно использовать как ключевое слово class, так и typename.
Например, в С можно создать перегруженную функцию вычисления модуля abs:
int abs(int n)
{
return n < 0 ? -n : n;
}
double abs(double n)
{
return n < 0 ? -n : n;
}
Используя шаблон, можно создать единственное определение, которое будет автоматически обрабатывать любой тип данных:
#include
template
{
return n < 0 ? -n : n;
}
void main (void)
{
double d = abs(-4.55);
int i = abs(-7);
printf("%lf %d\n",d,i);
}
Следующий шаблон вычисляет максимум двух чисел:
template
{
return (a > b ? a : b);
}
Переменная Type может принимать любой тип. При вызове функции можно указывать явно тип, с которым она будет работать:
имя функции <тип> (параметры)
Функцию max можно вызвать следующим образом:
int i = max
Разнотиповые аргументы передавать функции max запрещается. Можно определить шаблон функции , которая может принимать разнотиповые приводимые аргументы:
template
{
return (a > b ? a : b);
}
Тогда функцию max можно вызвать одним из следующих способов:
int i = max(7,76);
int i = max
2. ИМЕНОВАННЫЕ ОБЛАСТИ
namespace
Именованные области (namespace) позволяют объединять глобальные классы, объекты, функции под одним именем. Другими словами они позволяют разбивать глобальное пространство на области, в каждой из которых действуют свои объекты.
Определяются именованные области следующим образом:
namespace <идентификатор>
{
<тело именованной области>
}
Тело именованной области может содержать множество классов, объектов и функций. Например:
namespace ivan
{
int a,b;
}
Для доступа к элементам именованной области извне используется оператор расширения видимости :: . Например, для доступа к переменной a следует написать: ivan::a. Следующая программа создает две именованные области, каждая из которых содержит переменную. Переменные и функции из разных именованных областей могут иметь одинаковые имена.
#include
namespace first
{
int var = 5;
}
namespace second
{
double var = 3.1416;
}
void main (void)
{
cout << first::var << endl;
cout << second::var << endl;
}
using namespace
Директива using позволяет ассоциировать текущее глобальное пространство объектов с именованной областью. После выполнения команды
using namespace <идентификатор>
можно напрямую иметь доступ ко всем объектам и функциям именованной области.
#include
namespace first
{
int var = 5;
}
namespace second
{
double var = 3.1416;
}
void main (void)
{
{
using namespace first;
cout << var << endl;
}
{
using namespace second;
cout << var << endl;
}
}
В случае объявления двух именованных областей в одном блоке могут возникнуть проблемы из-за идентичности имен.
3. СТАНДАРТНАЯ БИБЛИОТЕКА ШАБЛОНОВ STL
Стандартная библиотека шаблонов STL (standard template library) – это набор шаблонов функций и классов в языке С++, включающий в себя различные контейнеры данных (список, очередь, множество, отображение, хэш таблица, очередь с приоритетами) и базовые алгоритмы (сортировка, поиск).
Стандартная библиотека шаблонов является именованной областью с именем std. При ее использовании включаемые файлы пишутся без расширения .h, а к некоторым еще добавляется приставка c. Например, аналогом библиотек
Для подключения стандартной библиотеки шаблонов следует воспользоваться директивой:
using namespace std;
-
#include
void main (void)
{
std::cout << "Hello, world!\n";
}
#include
using namespace std;
void main (void)
{
cout << "Hello, world!\n";
}
#include
void main (void)
{
std::printf("Hello, world!\n");
}
#include
using namespace std;
void main (void)
{
printf("Hello, world!\n");
}
Библиотека STL содержит пять основных видов компонентов:
- алгоритм (algorithm): определяет вычислительную процедуру.
- контейнер (container): управляет набором объектов в памяти.
- итератор (iterator): обеспечивает для алгоритма средство доступа к содержимому контейнера.
- функциональный объект (function object): инкапсулирует функцию в объекте для использования другими компонентами.
- адаптер (adaptor): адаптирует компонент для обеспечения различного интерфейса.
Контейнерами называются часто встречающиеся способы организации данных: динамические массивы, списки, очереди, стеки.
Алгоритмы не являются частью контейнеров, а образуют отдельную подсистему. Но при этом почти любой алгоритм может применяться к почти любому контейнеру. Вызывая метод для некоторого алгоритма, мы вызываем этот метод сам по себе, а не для экземпляра некоторого класса. Контейнер же, к которому применяется алгоритм, передается в качестве параметра.
Итератор - это указатель, который может двигаться по элементам контейнера. Итераторы играют такую же роль, как индекс у элемента массива. Через индекс массива мы можем получить некоторый элемент массива, и через итератор мы можем получить некоторый элемент контейнера.
4. ВЕКТОРЫ
Вектором называется последовательность объектов с прямым доступом. Поддерживает константное время вставки-удаления элемента из конца последовательности и линейное время вставки-удаления из середины или начала. Количество элементов вектора изменяется динамически, управление памятью совершается автоматически. Для использования векторов следует включить библиотеку:
#include
Для создания экземпляра вектора можно воспользоваться одним из следующих конструкторов:
-
Конструктор
описание конструктора
vector()
Создание пустого вектора
vector(size_type n)
создание вектора из n элементов
vector(size_type n, const T& t)
создание вектора из n копий t
vector(const vector&)
Копирующий конструктор
Пример 4.1. Рассмотрим работу конструкторов векторов на примерах.
Создание пустого вектора v (массива нулевой длины, не содержащего ни одного элемента):
vector
Создание вектора v длины 10:
vector
Создание вектора v длины 10, все элементы которого равны 5:
vector
Пусть имеется массив чисел m. Для того чтобы создать вектор v, содержащий эти же числа, следует воспользоваться копирующим конструктором:
int m[] = {1,2,3,4,5};
vector
Для создания еще одного вектора u с элементами 3, 4, 5 можно воспользоваться конструктором копированием интервала:
vector
или
vector
Через reference будем обозначать тип “ссылка”. Следующие методы созданы для работы с вектором:
-
Метод
описание метода
void clear()
удаление всех элементов.
Вектор становится пустым
size_type size() const
вычисляет размер вектора
bool empty() const
возвращает истину, если вектор пустой
reference operator[](size_type n)
оператор индексирования, возвращает
n–ый элемент вектора
reference front()
возвращает первый элемент вектора
reference back()
возвращает последний элемент вектора
Пример 4.2. Пусть имеется массив чисел m. Создадим вектор v, скопировав в него данные массива m.
int m[] = {1,2,3,4,5};
vector
Выведем размер вектора:
printf("Size: %d\n",v.size());
Выведем первый и последний элементы вектора:
printf("First: %d, Last: %d\n",v.front(),v.back());
Выведем все элементы вектора, используя оператор индексирования:
for(int i = 0; i < v.size(); i++) printf("%d ",v[i]); printf("\n");
Пример 4.3. Рассмотрим программу, которая создает и выводит содержимое вектора.
#include
#include
using namespace std;
int v[] = {1, 2, 3, 4, 5}, i;
vector
int main(void)
{
for(i = 0; i < u.size(); i++)
printf("%d ",u[i]);
return 0;
}
Следующая таблица описывает методы вставки и удаления элементов вектора:
-
метод
описание метода
void push_back(const T& x)
вставка элемента x в конец вектора
void pop_back()
удаление последнего элемента
Итератором называется указатель на объект. Создается итератор следующим образом:
имя_шаблона<тип>::iterator имя_итератора
Класс vector имеет следующие встроенные итераторы:
-
итератор
описание итератора
const_iterator begin() const
указатель на начало вектора
const_iterator end() const
указатель на конец вектора
Пример 4.4. Занесем в вектор v числа 4, 10, 1. Выведем элементы вектора v при помощи итератора iter.
vector
vector
v.push_back(4); v.push_back(10); v.push_back(1);
for(iter=v.begin();iter!=v.end();iter++) printf("%d ",*iter); printf("\n");
Для вставки и удаления элементов внутри вектора используются методы, аргументами которых выступают итераторы:
-
метод
описание метода
iterator insert(iterator pos,
const T& x)
вставка элемента x в позицию pos
iterator erase(iterator pos)
удаление элемента, на который указывает итератор pos
iterator erase(iterator first,
iterator last)
удаление всех элементов, расположенных в промежутке [first..last]
Пример 4.5. Занесем в вектор v квадраты натуральных чисел от 1 до 10. Удалим из вектора значения 16, 25, 36, 49.
vector
for(i = 1; i <= 10; i++) v.push_back(i*i);
for(i = 0; i < v.size(); i++) printf("%d ",v[i]); printf("\n");
v.erase(v.begin()+3,v.end()-3);
for(i = 0; i < v.size(); i++) printf("%d ",v[i]); printf("\n");
Упражнение 4.1. [Топкодер, SRM 193, SwimmingPool]. Имеется лужа некоторой формы, имеющей определенную глубину. Известно, что поперечный разрез лужи одинаков на всех глубинах. Массив rates содержит скорость наполнения лужи в определенные интервалы времени, durations[i] содержит время, в течении которого лужа наполнялась со скоростью rates[i]. За все интервалы времени, указанные в durations, лужа наполнилась до высоты height. Необходимо определить площадь поперечного разреза лужи.
Класс: SwimmingPool
Метод: int area(vector
int height)
Ограничения: массивы rates и durations содержат одинаковое количество чисел, 1 rates[i],durations[i],height 100.
Вход. Массивы rates и durations, содержащие скорость и время наполнения лужи. Целое число height содержит глубину лужи.
Выход. Площадь поперечного разреза лужи.
Пример входа
-
rates
durations
height
{1,2,3,4,5}
{5,4,3,2,1}
10
{5,4,3,2,1}
{1,2,3,4,5}
100
{100}
{1}
100
Пример выхода
3
0
1
Упражнение 4.2. [Топкодер, SRM 194, Soccer]. В футболе за победу команда получает 3 очка, за ничью 1 очко, за проигрыш – 0. Массивы wins и ties содержат информацию об играх, проведенных футбольными командами в лиге: wins[i] равно числу выигранных матчей i - ой командой, ties[i] равно числу матчей, сведенных i - ой командой вничью. Необходимо найти команду с наибольшим количеством очков.
Класс: Soccer
Метод: int maxPoints(vector
Ограничения: массивы wins и ties содержат одинаковое количество чисел, 0 wins[i],ties[i] 100.
Вход. Массивы wins и ties, содержащие информацию о командах.
Выход. Наибольшее количество очков, заработанное одной командой в лиге.
Пример входа
-
wins
ties
{1,4,3,0,0}
{3,1,5,3,1}
{12,45,20,17,48,0}
{48,10,53,94,0,100}
{35,0}
{0,76}
Пример выхода
14
145
105
Упражнение 4.3. [Топкодер, SRM 315, RosePetals]. Бросаются пять игральных кубиков, стороны которых пронумерованы числами от 1 до 6:
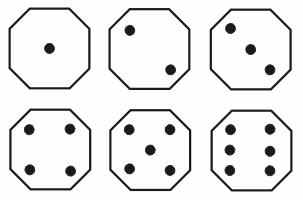
В задаче следует подсчитать суммарное количество точек вокруг центральной точки каждой выпавшей грани. Это напоминает подсчет лепестков роз. Если грань не имеет центральной точки (2, 4, 6), то число лепестков равно нулю. Остальные три грани 1, 3 и 5 имеют центральную точку и количество их лепестков соответственно равно 0, 2 и 4.
Класс: RosePetals
Метод: int getScore(vector
Ограничения: dice содержит 5 чисел от 1 до 6.
Вход. Массив dice, описывающий положение игральных кубиков после броска.
Выход. Количество лепестков в выпавшей конфигурации.
Пример входа
-
dice
{1, 2, 3, 2, 1}
{4, 4, 5, 6, 5}
{2, 2, 2, 2, 2}
Пример выхода
2
8
0
Упражнение 4.4. [Топкодер, SRM 212, YahtzeeScore]. Рассмотрим подсчет очков в игре яте. Бросаются 5 кубиков, на гранях которых расположены числа от 1 до 6. Игрок называет некоторое число. Активными считаются кубики, на которых выпало это число. Игрок получает количество очков, равных сумме чисел, выпавших на активных кубиках. Например, пусть на кубиках выпали значения {2, 2, 3, 5, 4}. Если игрок назовет 2, то активными будут первый и второй кубики, сумма очков на которых равна 4. Если игрок назовет 5, то получит 5 очков (имеется один кубик с 5 очками).
По заданному массиву toss, содержащему выпавшие значения на 5 кубиках, необходимо определить наибольшее количество очков, которое может получить игрок.
Класс: YahtzeeScore
Метод: int maxPoints(vector
Ограничения: toss содержит в точности 5 чисел, 1 toss[i] 6.
Вход. Массив чисел toss.
Выход. Наибольшее количество очков, которое может получить игрок.
Пример входа
-
toss
{2, 2, 3, 5, 4}
{6, 4, 1, 1, 3}
{5, 3, 5, 3, 3}
Пример выхода
5
6
10
Упражнение 4.5. [Топкодер, SRM 217, FuelConsumption]. Необходимо совершить путешествие на машине с ограниченным количеством горючего. Известно количество горючего, потребляемое автомобилем при разных скоростях. Необходимо определить максимальное расстояние, которое можно проехать при оптимальном выборе скорости движения.
Класс: FuelConsumption
Метод: double maximalDistance(vector
vector
Ограничения: 2 velocities[i] 250, 1000 consumptions [i] 20000, 100 fuel 50000, массив velocities не содержит одинаковых элементов.
Вход. Два целочисленных массива velocities, consumptions и исходное количество топлива fuel в миллилитрах. consumptions[i] содержит количество литров, потребляемое автомобилем в течение одного часа при движении со скоростью velocities[i].
Выход. Максимальное расстояние, которое может проехать автомобиль. Скорость автомобиля должна быть постоянной на всем участке движения.
Пример входа
| velocities | consumptions | fuel |
| {100} | {10000} | 10000 |
| {70, 80, 90, 100, 60, 110} | {4000, 4000, 4000, 4000, 4000, 4000} | 40000 |
| {5, 10, 20, 40, 80} | {1000, 2500, 6250, 9000, 18000} | 47832 |
Пример выхода
100.0
1100.0
239.16
Упражнение 4.6. [Топкодер, SRM 253, ObjectPacking]. Имеется несколько коробок прямоугольной формы. Ширина i - ой коробки задается в ячейке boxWidth[i], длина – в boxLength[i]. Задан объект прямоугольной формы, ширина которого равна objWidth, а длина objLength. Необходимо найти коробку с наименьшей площадью, в которую можно поместить объект. Объект можно вращать на 0, 90, 180 или 270 градусов.
Класс: ObjectPacking
Метод: int smallBox(int objWidth, int objLength,
vector
Ограничения: boxWidth и boxLength имеют одинаковую длину и содержат от 1 до 50 чисел, 1 objWidth[i], objLength[i], objWidth, objLength 1000.
Вход. Целые числа objWidth и objLength – размеры объекта, массивы boxWidth и boxLength, содержащие размеры коробок.
Выход. Наименьшая площадь коробки, в которую можно поместить объект. Если объект нельзя поместить ни в одну из имеющихся коробок, вернуть -1.
Пример входа
-
objWidth
objLength
boxWidth
boxLength
7
3
{3}
{7}
5
8
{6,9,3}
{7,4,5}
17
5
{19,10,12,40}
{12,20,15,5}
1
10
{9,1,10}
{10,6,4}
Пример выхода
21
-1
200
40
Упражнение 4.7. [Топкодер, SRM 322, DerivativeSequence]. В массиве a задана последовательность, состоящая из k элементов. По ней можно найти последовательность, состоящую из разностей соседних элементов. Например, из последовательности {5, 6, 3, 9, -1} можно получить {6-5, 3-6, 9-3, -1-9} = {1, -3, 6, -10}. Формально, последовательностью разностей для {a1, a2, …, ak} будет {b1, b2, …, bk-1}, где bi = ai+1 – ai.
Разностью n - го порядка для последовательности a будет такая последовательность, которая будет получена применением выше описанного правила n раз. Например, для вычисления разности второго порядка для {5, 6, 3, 9, -1} следует произвести преобразования:
{5, 6, 3, 9,-1} -> {1, -3, 6,-10} -> {-3-1, 6-(-3), -10-6} = {-4, 9, -16}
По заданной последовательности a требуется найти ее n - ую разность.
Класс: DerivativeSequence
Метод: vector
Ограничения: a содержит от 1 до 20 элементов, -100 a[i] 100, 0 n k -1.
Вход. Массив чисел a и величина искомой разности n.
Выход. n - ая разность последовательности a.
Пример входа
-
a
n
{5,6,3,9,-1}
1
{5,6,3,9,-1}
2
{5,6,3,9,-1}
4
{4,4,4,4,4,4,4,4}
3
Пример выхода
{1,-3, 6, -10}
{-4, 9, -16}
{-38}
{0, 0, 0, 0, 0}
УКАЗАНИЯ К РЕШЕНИЮ УПРАЖНЕНИЙ
Упражнение 4.1. [Топкодер, SRM 193, SwimmingPool]. Вычисляем объем воды, которой наполнилась лужа. Разделив полученный объем на высоту, получим площадь поперечного разреза лужи.
#include
#include
using namespace std;
class SwimmingPool
{
public:
int area(vector
{
int i, vol = 0;
for(i = 0; i < rates.size(); i++)
vol += rates[i] * durations[i];
return vol / height;
}
};
Упражнение 4.2. [Топкодер, SRM 194, Soccer]. Для каждой команды вычисляем полученное количество очков в лиге. Среди набранного количества очков каждой командой находим наибольшее значение.
#include
#include
using namespace std;
class Soccer
{
public:
int maxPoints(vector
{
int i, max = 0;
for(i = 0; i < wins.size(); i++)
if (wins[i] * 3 + ties[i] > max) max = wins[i] * 3 + ties[i];
return max;
}
};
Упражнение 4.3. [Топкодер, SRM 315, RosePetals]. Заведем массив petals, в котором petals[i] содержит количество лепестков грани с числом i. Проходим по массиву dice и суммируем количество лепестков, грань с числом dice[i] содержит petals[dice[i]] лепестков.
#include
#include
using namespace std;
class RosePetals{
public:
int getScore(vector
{
int i, res, petals[] = {0,0,0,2,0,4,0};
for(res = i = 0; i < 5; i++) res += petals[dice[i]];
return res;
}
};
Упражнение 4.4. [Топкодер, SRM 212, YahtzeeScore]. Очевидно, что игрок будет называть число от 1 до 6. Для каждого такого названого числа подсчитаем сумму очков, которое он бы получил. Среди всех найденных сумм очков найдем наибольшую.
#include
#include
using namespace std;
class YahtzeeScore
{
public:
int maxPoints(vector
{
int i, j, s, max;
for(max = 0, i = 1; i <= 6; i++)
{
for(s = j = 0; j < 5; j++)
if (toss[j] == i) s += i;
if (s > max) max = s;
}
return max;
}
};
Упражнение 4.5. [Топкодер, SRM 217, FuelConsumption]. Скорость движения автомобиля должна равняться такому velocities[i], для которого отношение d = velocities[i] / consumptions[i] является наибольшим. Отношение d равно расстоянию, которое можно проехать на одном литре бензина. Максимальное расстояние, которое может проехать автомобиль, равно fuel * d.
#include
#include
using namespace std;
class FuelConsumption{
public:
double maximalDistance(vector
int fuel)
{
double d = 0;
for(int i = 0; i < velocities.size(); i++)
if (1.0 * velocities[i] / consumptions[i] > d)
d = 1.0 * velocities[i] / consumptions[i];
return fuel * d;
}
};
Упражнение 4.6. [Топкодер, SRM 253, ObjectPacking]. Пусть ширина текущей коробки равна W, длина – L. Объект с размерами objWidth и objLength можно поместить в коробку, если выполняется условие
(W >= objWidth) && (L >= objLength)
или
(W >= objLength ) && (L >= objWidth)
Перебираем все коробки, проверяем, можно ли в них поместить имеющийся объект. Если можно – то вычисляем площадь коробки. Находим наименьшую площадь такой коробки.
#include
#include
using namespace std;
class ObjectPacking
{
public:
int smallBox(int objWidth, int objLength,
vector
{
int W, L, i, res = 1000000000;
for(i = 0; i < boxWidth.size(); i++)
{
W = boxWidth[i]; L = boxLength[i];
if (((W >= objWidth) && (L >= objLength)) ||
((W >= objLength ) && (L >= objWidth)))
if (W * L < res) res = W * L;
}
return (res == 1000000000) ? -1:res;
}
};
Упражнение 4.7. [Топкодер, SRM 322, DerivativeSequence]. Задача решается моделированием процесса вычисления разностей.
#include
#include
using namespace std;
class DerivativeSequence
{
public:
vector
{
int i;
while(n--)
{
for(i = 0; i < a.size(); i++) a[i] = a[i+1] - a[i];
a.erase(a.end() - 1);
}
return a;
}
};
