Интерактивная работа с данными на языке idl

Вид материала

Документы

Содержание 2.4Аппроксимация одномерных массивов аналитически заданными функциями N = n_elements(X) Params = [1., 1., 1.] Failed to converge 2.5Полиномиальная аппроксимация N – степень полинома, который мы хотим использовать для аппроксимации. Yfit REGRESS: RESULT = REGRESS(Y, X, Weights, Yfit, a0)

Подобный материал:

• Структура программы в языке программирования С++. Обмен данными между функциями (параметры, 37.24kb.
• Языки манипулирования данными (ямд), 68.4kb.
• Туристическая компания, 188.59kb.
• М. Н. Работа над содержанием задачи, 529.14kb.
• Игровые программы на турбазе Чусовая для групп от10 человек: Детская интерактивная, 18.27kb.
• Лабораторная работа №4 Тема : Структурный тип данных в языке С++, 112.14kb.
• Viii. Управление данными план, 131.4kb.
• Александр Андреевич Иванов. Живопись. Рисунок. Акварель. Интерактивная программа, 300.39kb.
• Лабораторная работа №8 Тема: Интерактивная доска, 103.55kb.
• Учебная программа модульного курса, 29.73kb.

2.4Аппроксимация одномерных массивов аналитически заданными функциями

Нередко, анализируя экспериментальную кривую, мы интерпретируем её как проявление некоторого процесса, который мы можем описать количественно. В таком случае, если мы найдём удовлетворительную аппроксимацию экспериментальных точек ожидаемой функцией, то параметры аппроксимированной кривой дадут нам требуемую информацию об исследуемом процессе. Можно попытаться найти такую удовлетворительную аппроксимацию вручную, варьируя параметры аналитической функции и проводя график полученной кривой на рисунке, на котором изображены экспериментальные точки.⁷ Однако более эффективный и точный способ – использовать методы статистики. Функция IDL CURVEFIT решает эту задачу с помощью метода наименьших квадратов. По умолчанию, если мы не задаём свою функцию для аппроксимации, для аппроксимации используется комбинация полинома второй степени с гауссианой 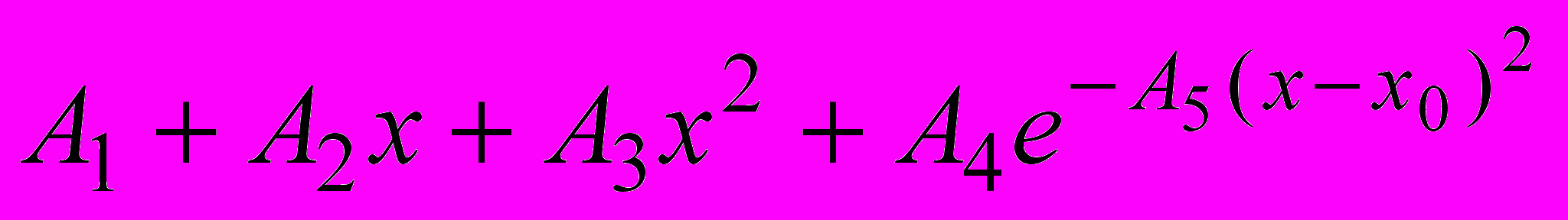. С помощью такой функции можно аппроксимировать многие виды экспериментальных кривых. Однако множество кривых невозможно удовлетворительно аппроксимировать этой зависимостью, и в большинстве случаев мы сами задаём аппроксимирующие функции. Чтобы это сделать, мы должны написать процедуру IDL, которая принимает независимый аргумент и выдает соответствующие массивы функции и её частных производных по искомым параметрам.

Рассмотрим пример аппроксимации экспериментальных данных полиномом второй степени 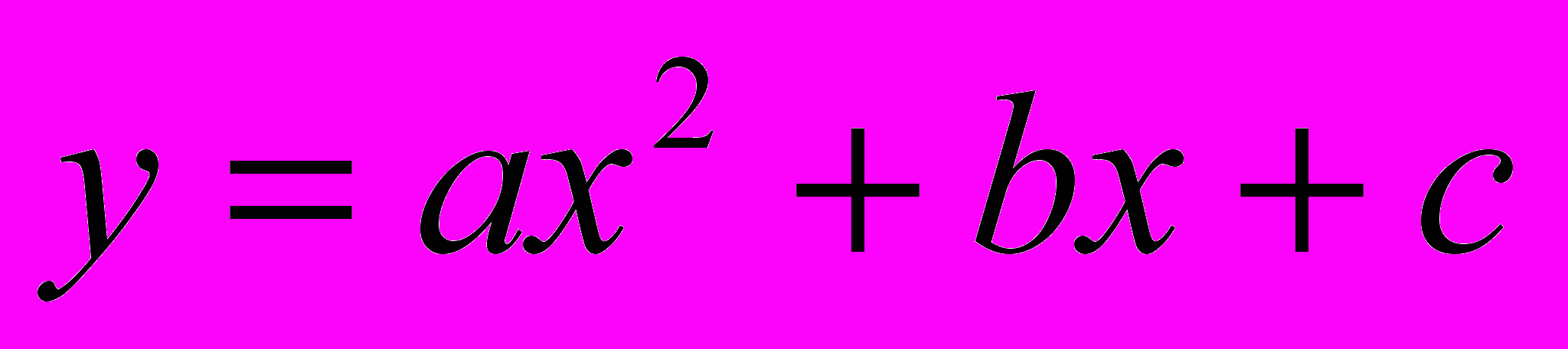. Частные производные по параметрам равны: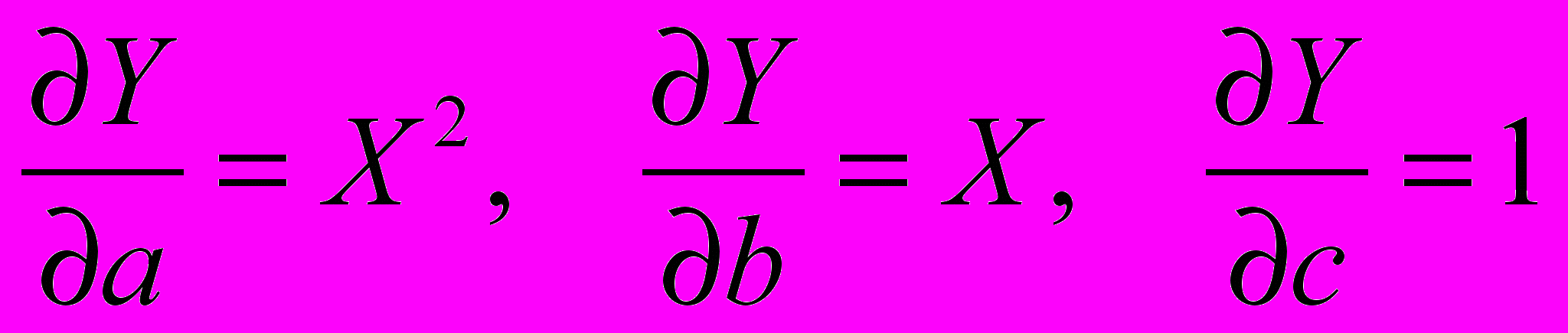



Создаём программный файл, называемый, например, “fit1.pro”:

pro fit1, X, params, F, Pder

N = n_elements(X)

Pder = fltarr (N, 3)


a = params(0)

b = params(1)

c = params(2)


F = a*X2 + b*X + C


Pder(*, 0) = X2

Pder(*, 1) = X

Pder(*, 2) = 1


END


Затем пишем простой программный файл, в котором производится вызов функции CURVEFIT (или же эта часть программы может находиться в том же самом программном файле fit1.pro):


N = 200

x = findgen(N)/(N-1)*!pi

y = sin(x)

weights = replicate(1, N)

PARAMS = [1., 1., 1.]

Result = CURVEFIT(X, Y, Weights, PARAMS, Sigma, funct = 'fit1')

END


Вектор PARAMS должен содержать начальное приближение. Качество этого начального приближения определяет количество итераций. При производительности современных компьютеров мы не встречались с ситуациями, в которых качество начального приближения было бы существенным. При любом начальном приближении мы получим один и тот же результат, но лишь если итерационный процесс сходится, то есть если экспериментальный набор данных и аппроксимирующая кривая на самом деле схожи. Например, если мы попытаемся аппроксимировать точки кривой 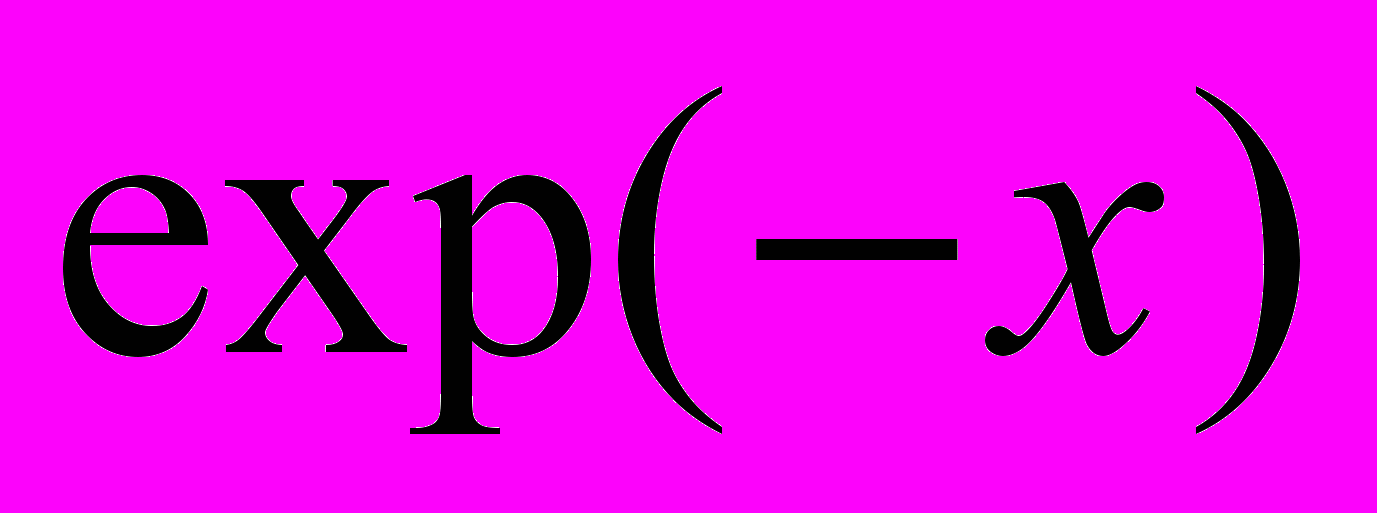функцией 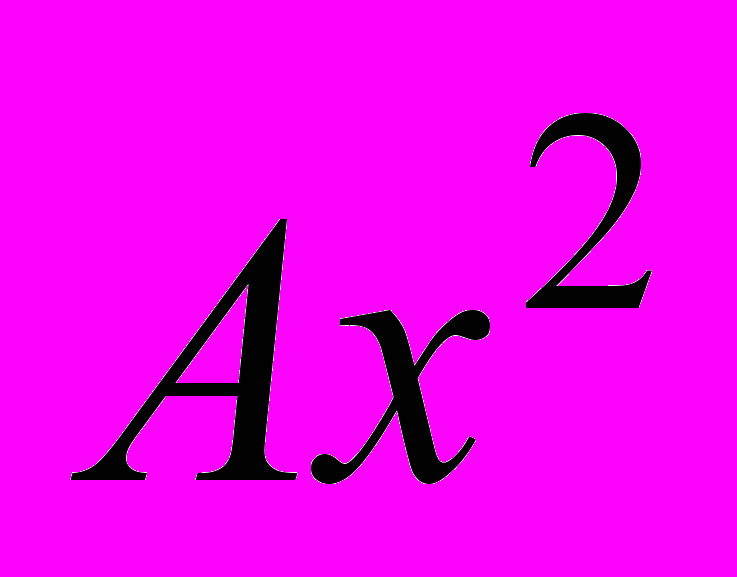, то нам в этом случае вряд ли удастся найти параметр A. Скорее всего, функция CURVEFIT выдаст сообщение:

Failed to converge

Если набор данных, которые мы хотим аппроксимировать, имеет широкий диапазон, может оказаться полезным работать не прямо с экспериментальными точками, а с их логарифмами.

2.5Полиномиальная аппроксимация

Нередко встречается ситуация, когда экспериментальный набор данных может быть аппроксимирован некоторым полиномом. Как раз этот случай рассматривался в предыдущем примере. Наиболее общий случай:



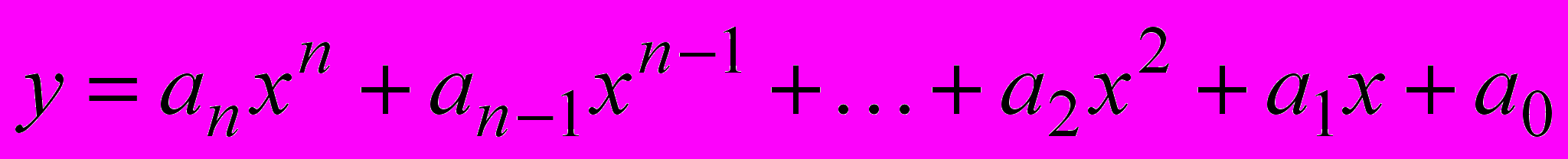
Полиномиальная аппроксимация выполняется функцией IDL POLY_FIT:

Result = POLY_FIT(X, Y, N, Yfit)

Здесь N – степень полинома, который мы хотим использовать для аппроксимации. Yfit – вектор значений аппроксимирующего полинома, соответствующих входному вектору заданных точек X.

2.6Регрессия

Специальная, но достаточно часто встречающаяся ситуация, когда ожидается, что набор экспериментальных точек представляет собой линейную комбинацию значений некоторых других параметров, имеющих то же количество точек:

.

Это – уравнение многопараметрической линейной регрессии.

Параметры 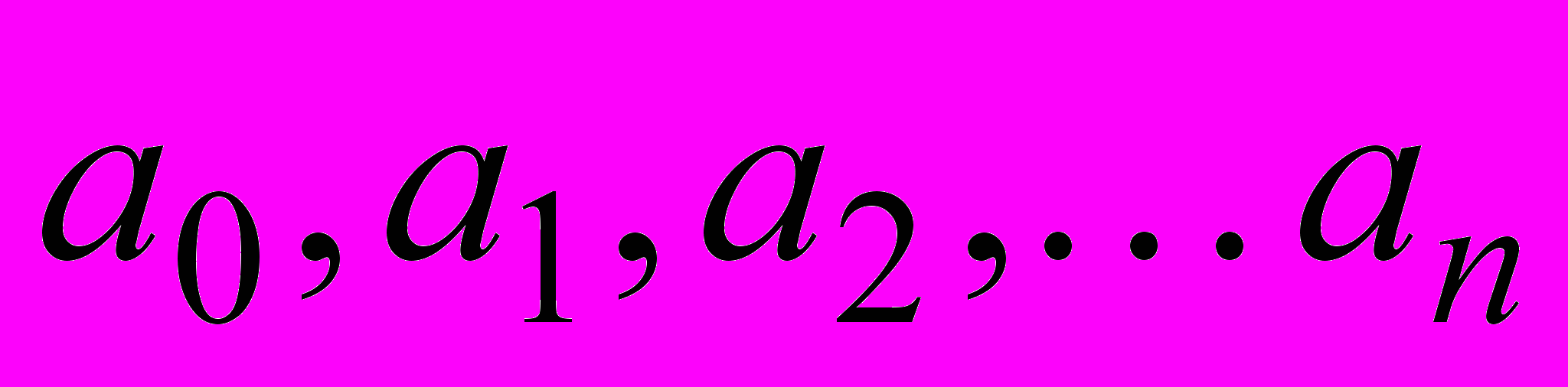можно найти с помощью функции IDL REGRESS:

RESULT = REGRESS(Y, X, Weights, Yfit, a0)

В наиболее часто встречающемся случае однопараметрической регрессии следует задать:

RESULT = REGRESS(Y, transpose(X), replicate(1, n_elements(Y)), Yfit, a0)

Заметим, что RESULT – это вектор, даже в однопараметрическом случае. Поэтому, если мы хотим использовать его значение в каком-либо выражении, его следует преобразовать в скаляр (в однопараметрическом случае!):

Yfit1 = a0 + RESULT[0]*X