Geum.ru

Применение кластерных технологий при разработке минимальных блоков обратной связи для управляемых систем

Вид материалаДокументы
Подобный материал:
ПРИМЕНЕНИЕ КЛАСТЕРНЫХ ТЕХНОЛОГИЙ

ПРИ РАЗРАБОТКЕ МИНИМАЛЬНЫХ БЛОКОВ ОБРАТНОЙ СВЯЗИ

ДЛЯ УПРАВЛЯЕМЫХ СИСТЕМ

Г.Г. Исламов, А.Г. Исламов, О.Л. Лукин

Удмуртский государственный университет, г. Ижевск

Пусть 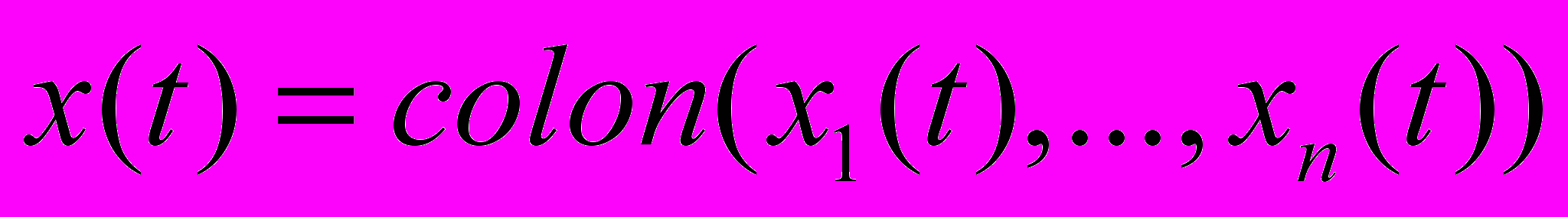есть набор показателей управляемой системы, описываемой дифференциальным уравнением 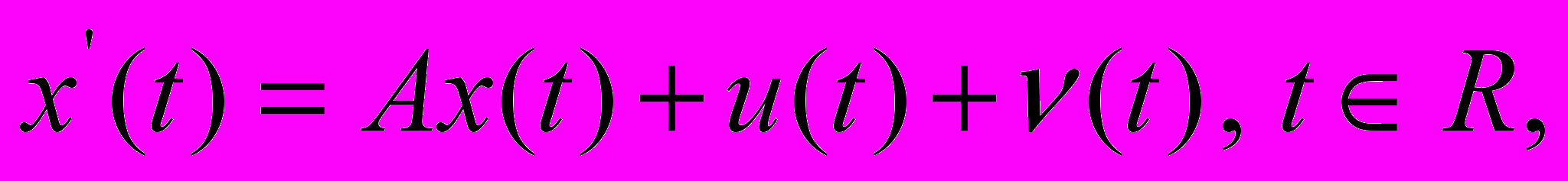где 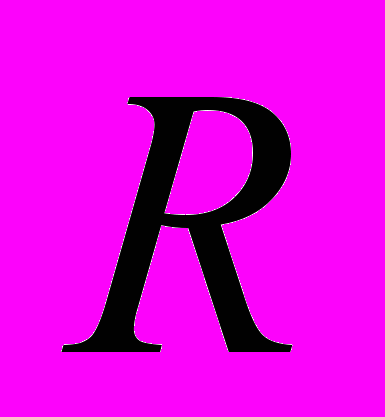- числовая ось, 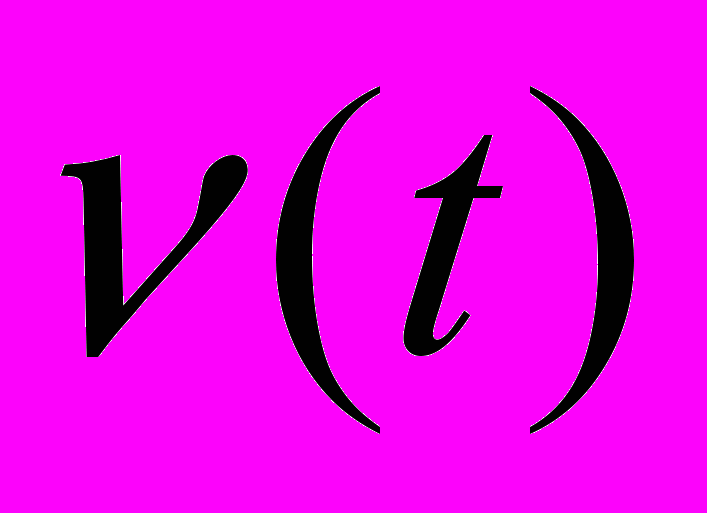- воздействие внешней среды, 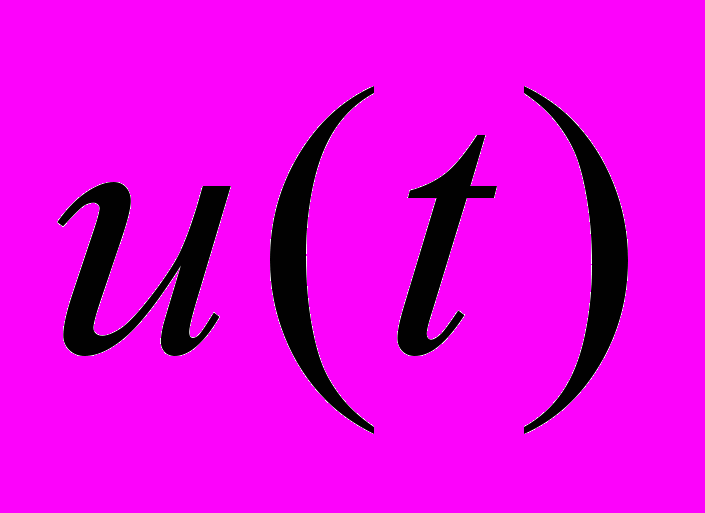- управление, которое формируется по методу обратной связи с запаздыванием: 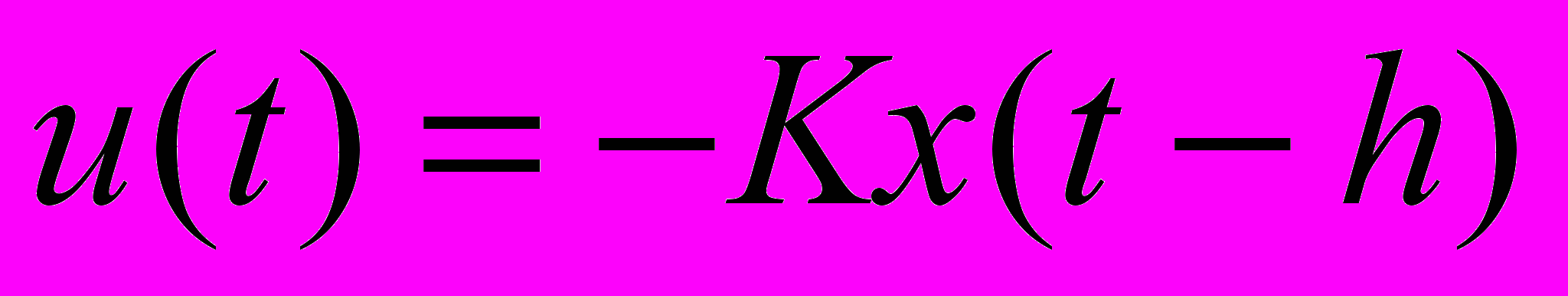. Здесь 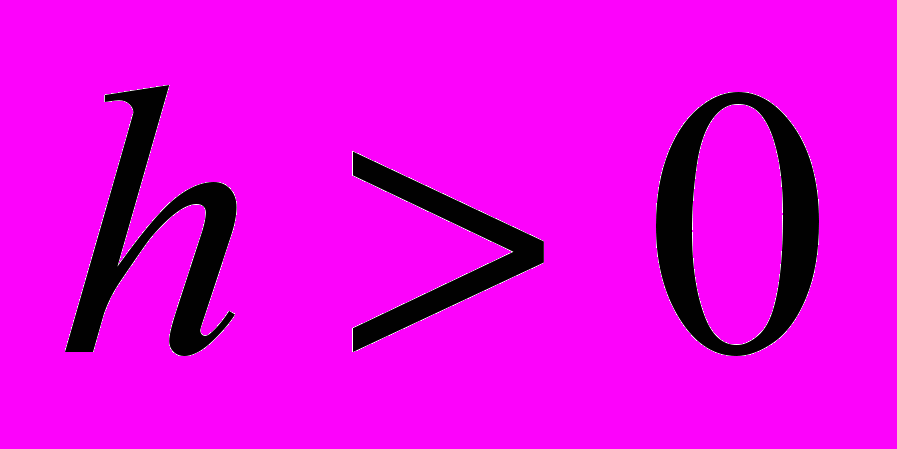- величина запаздывания блока обратной связи, 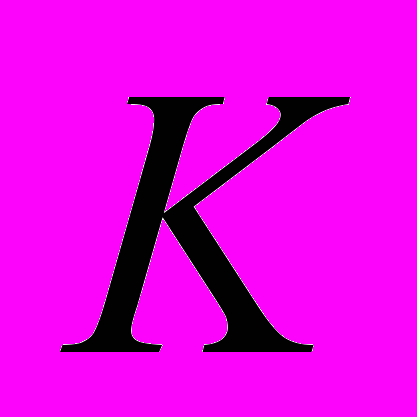- матрица этого блока. Из скелетного разложения матрицы 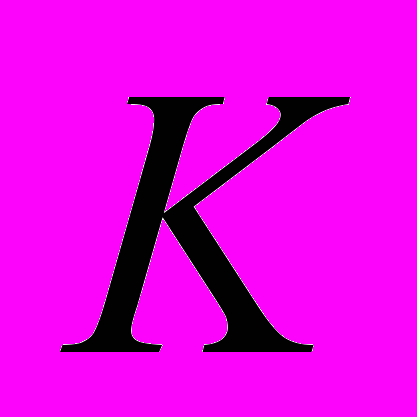следует, что ранг 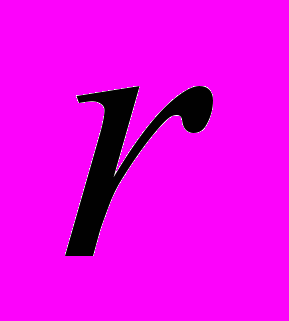этой матрицы определяет число управляющих воздействий на систему со стороны блока обратной связи. Поведение системы с обратной связью может сильно отличаться от поведения системы без обратной связи. Если характер поведения системы задан, то блоки обратной связи с минимальным рангом 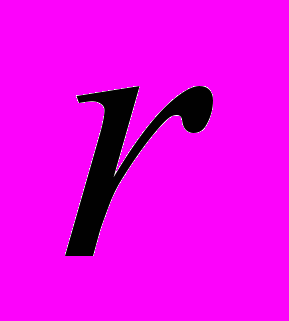, обеспечивающие этот характер поведения, мы называем минимальными блоками обратной связи. В случае небольших размерностей 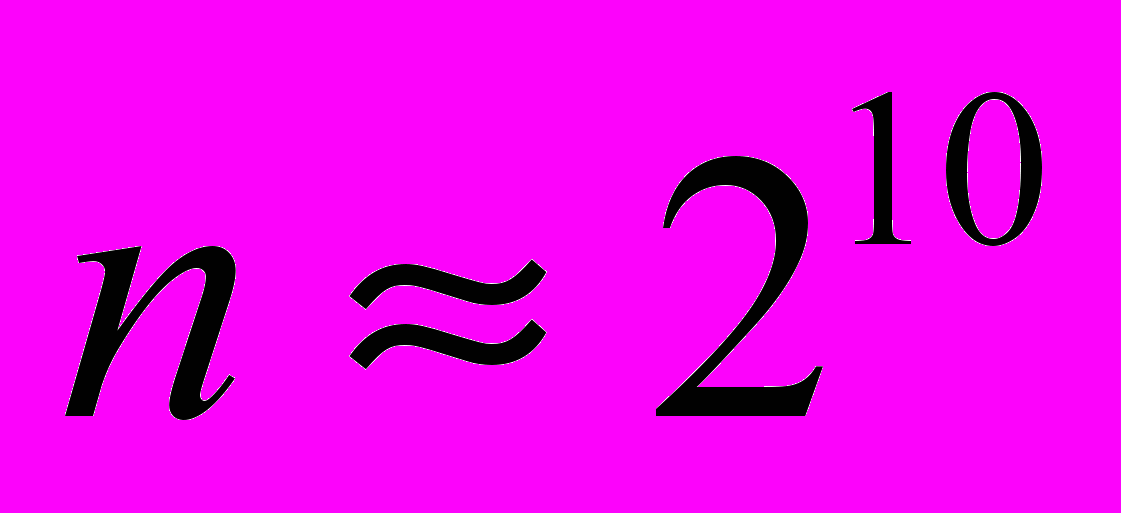управляемых систем конструирование минимальных блоков обратной связи с запаздыванием можно осуществить на персональном компьютере. Однако для систем больших размерностей (возникающих, например, при дискретизации по пространственным переменным управляемых систем с распределёнными параметрами) для построения матрицы 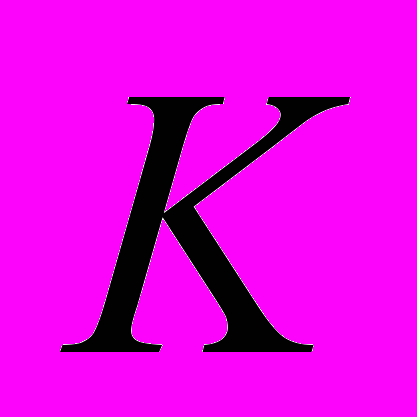минимального блока обратной связи требуется технология распределённых вычислений на специализированных кластерах высокопроизводительных компьютеров. Ниже приводится обоснование этого утверждения.

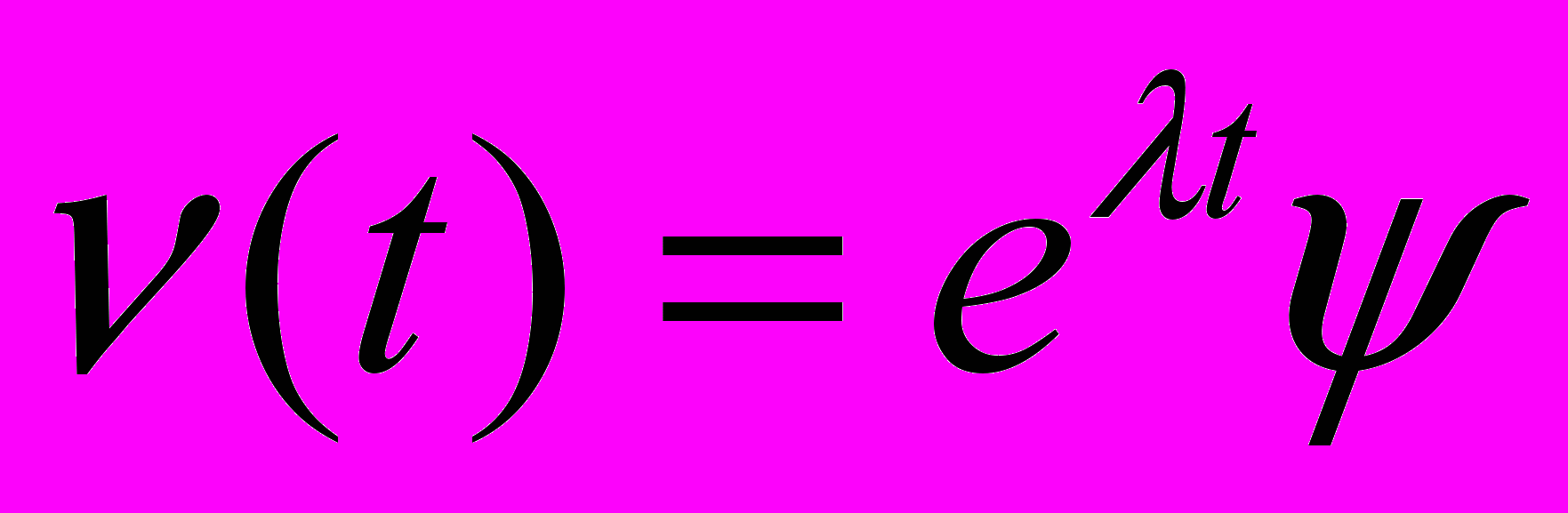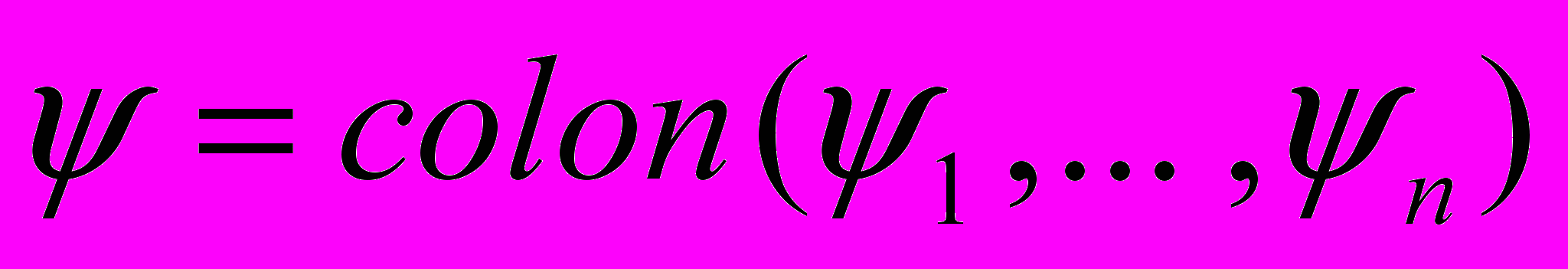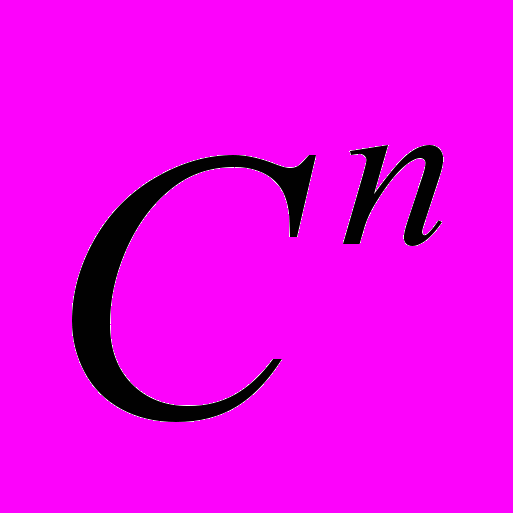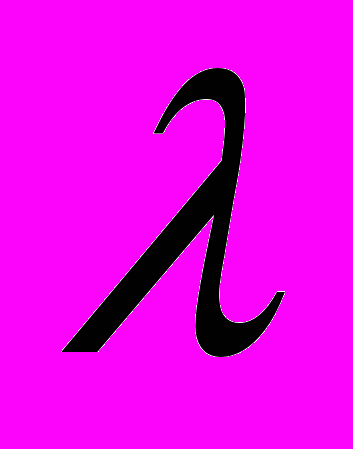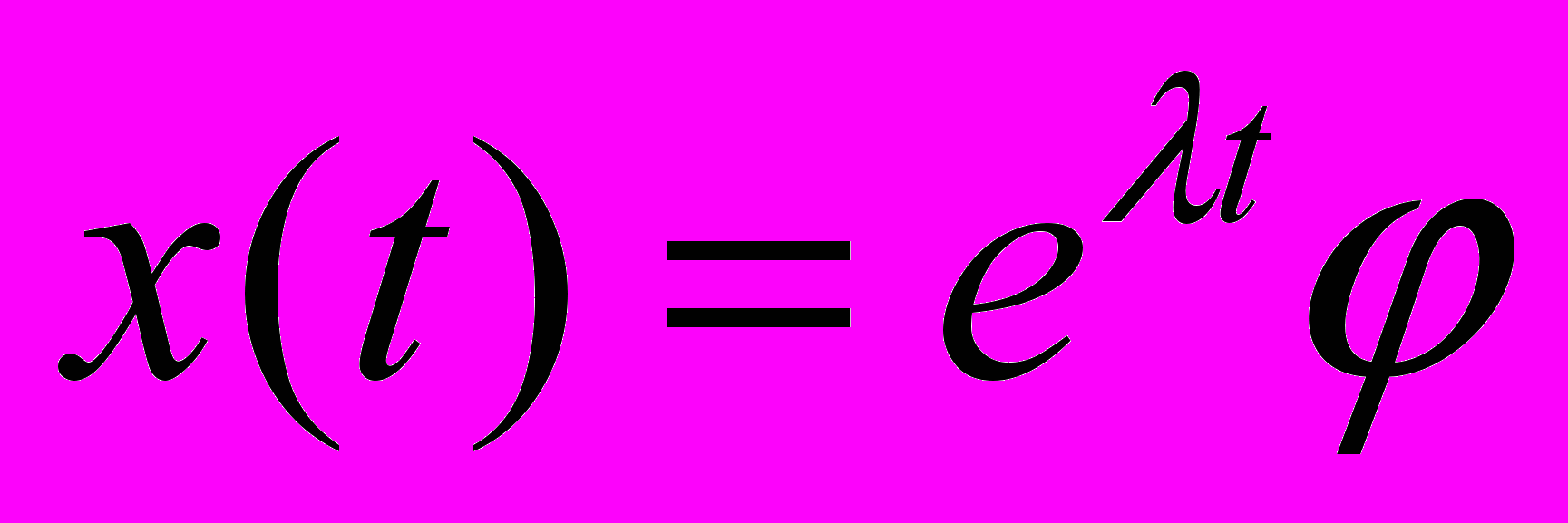Пусть известно, что внешнее воздействие на систему изменяется по простейшему закону , где вектор-столбец может быть любым элементом из пространства , а параметр - любым числом из заданной области комплексной плоскости . Тогда функция , где 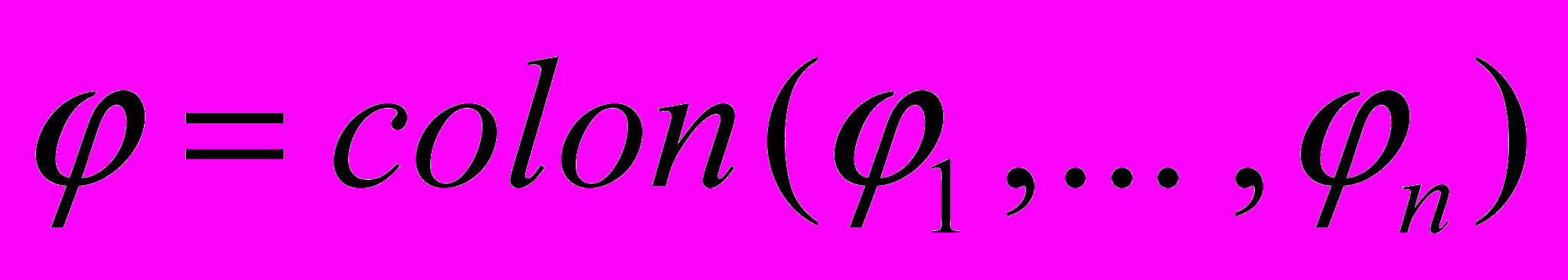, будет решением системы 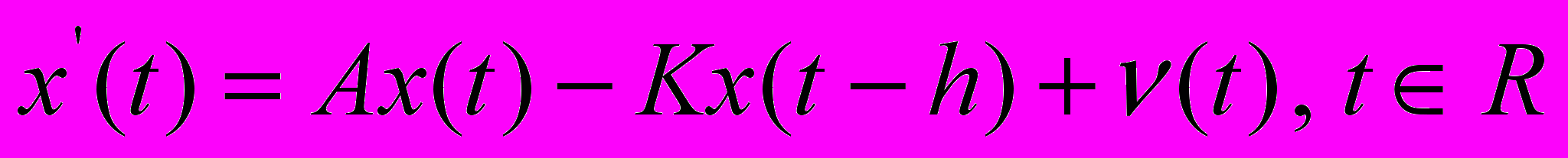тогда и только тогда, когда 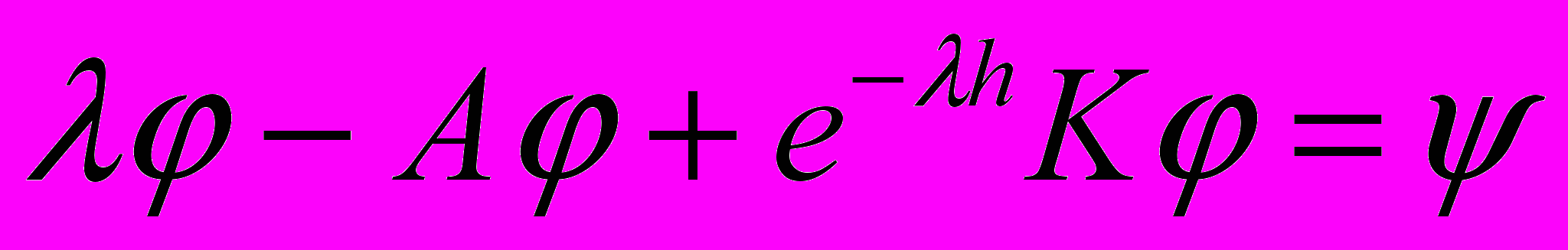. Отсюда видим, что непрерывная зависимость 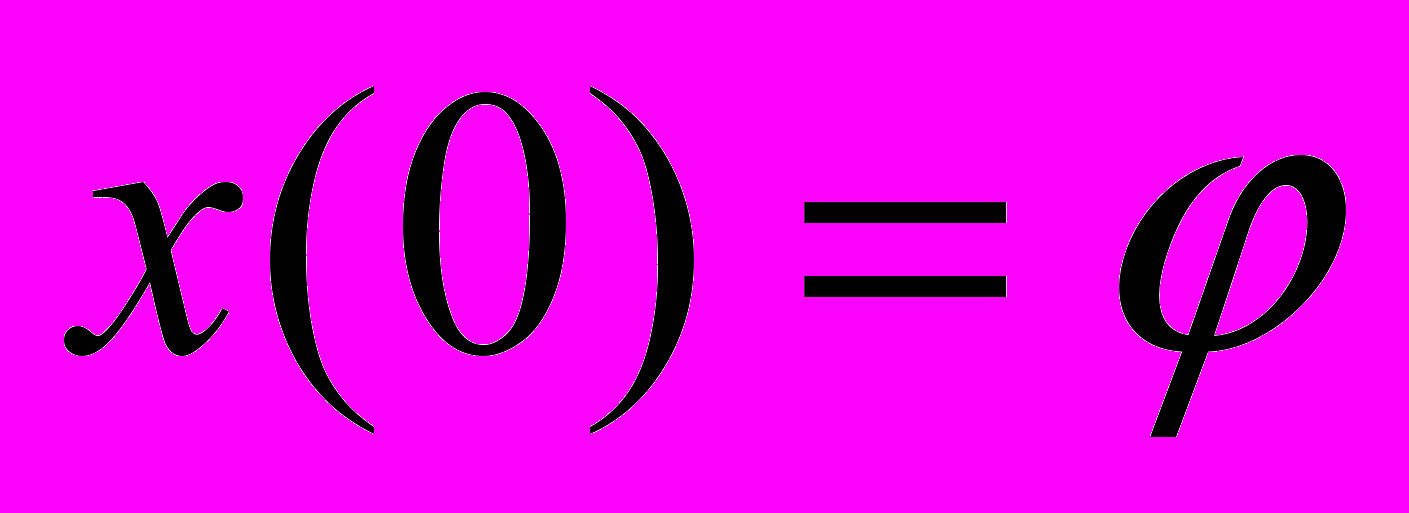от 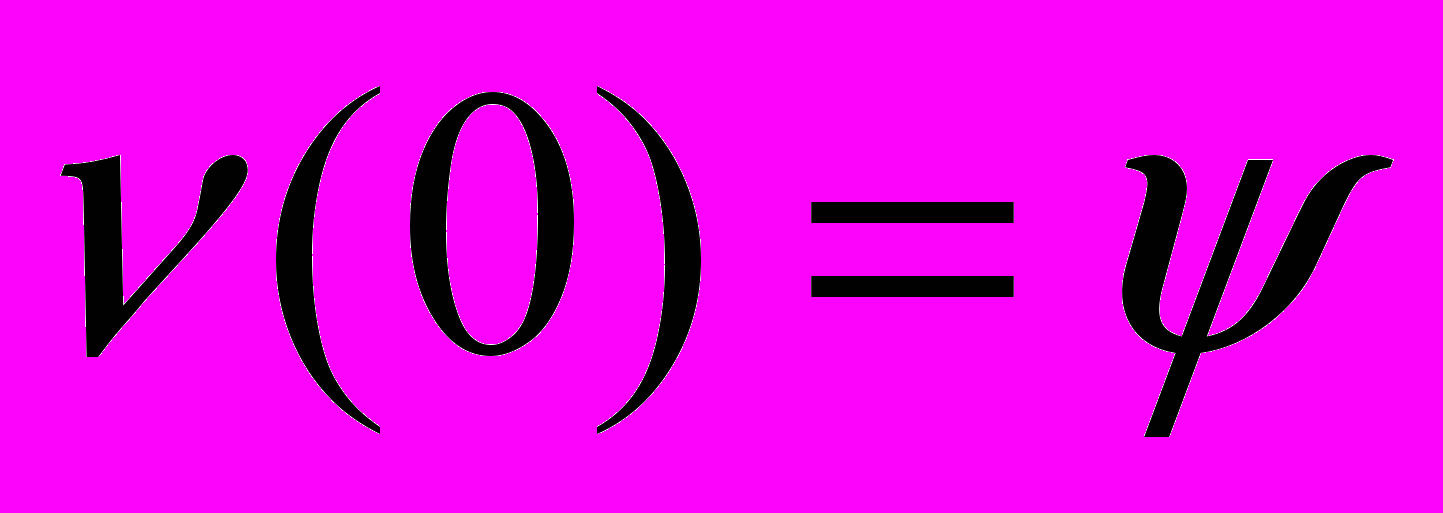имеет место в том и только том случае, когда матрица 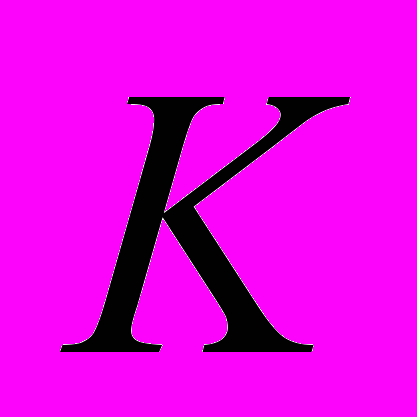блока обратной связи выбрана так, что при всех 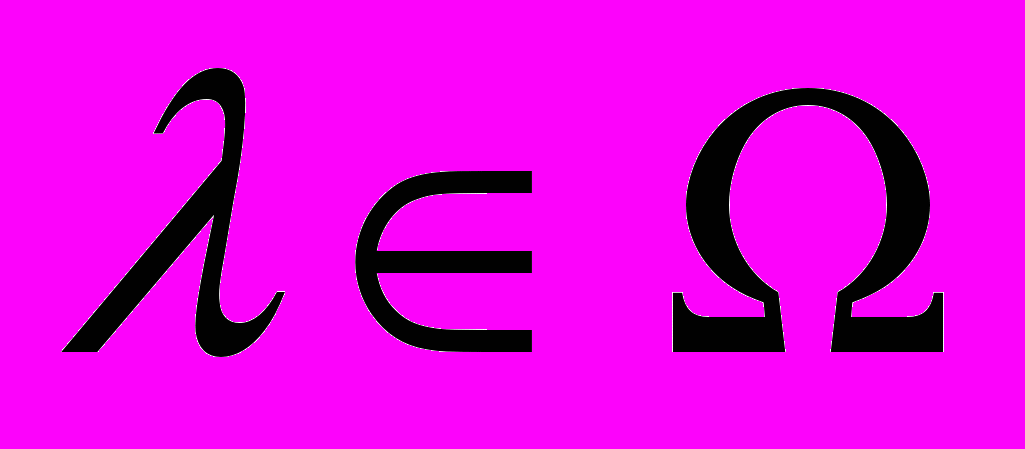обратима матрица 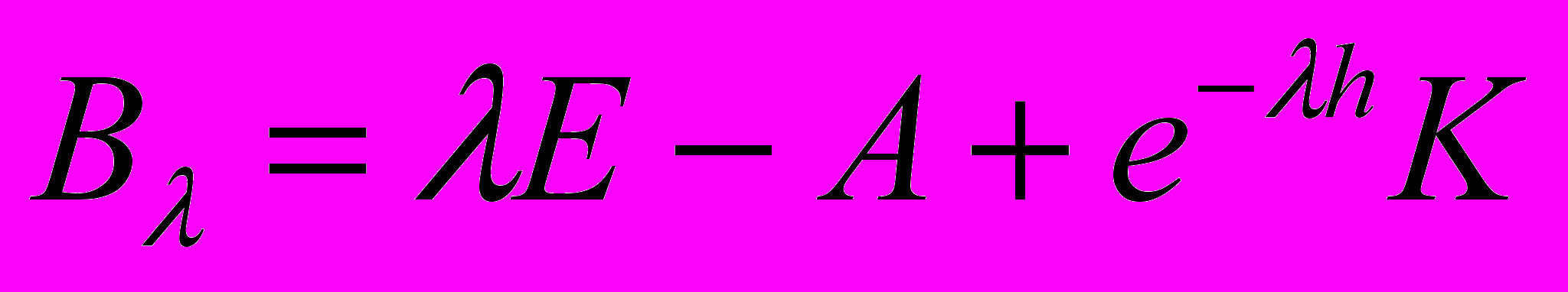порядка 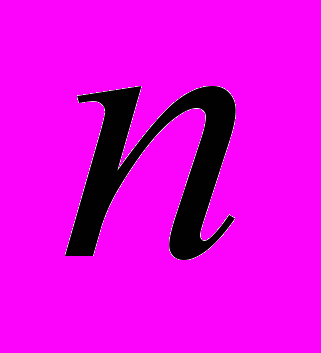. Допустим, что для некоторой матрицы 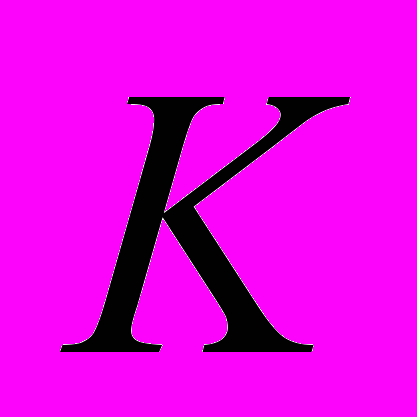выполнено последнее условие. Тогда для 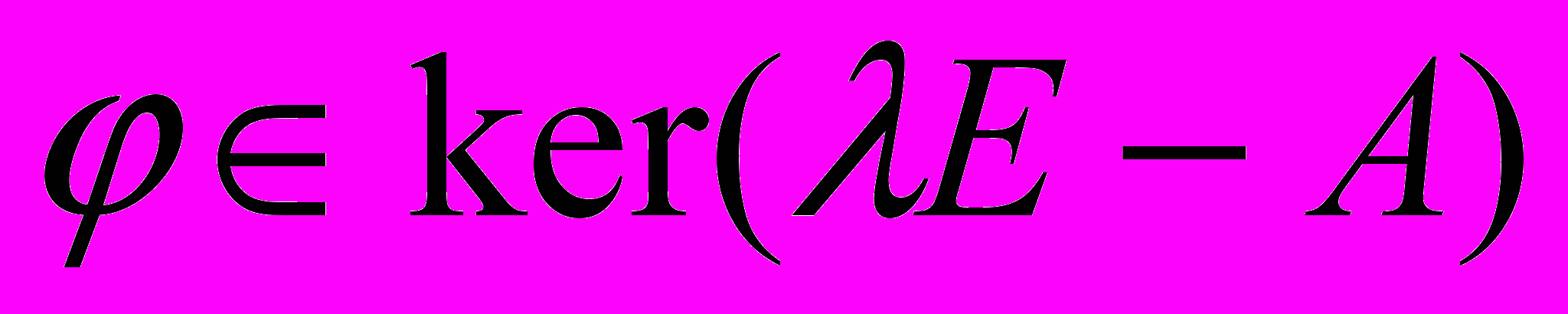имеем 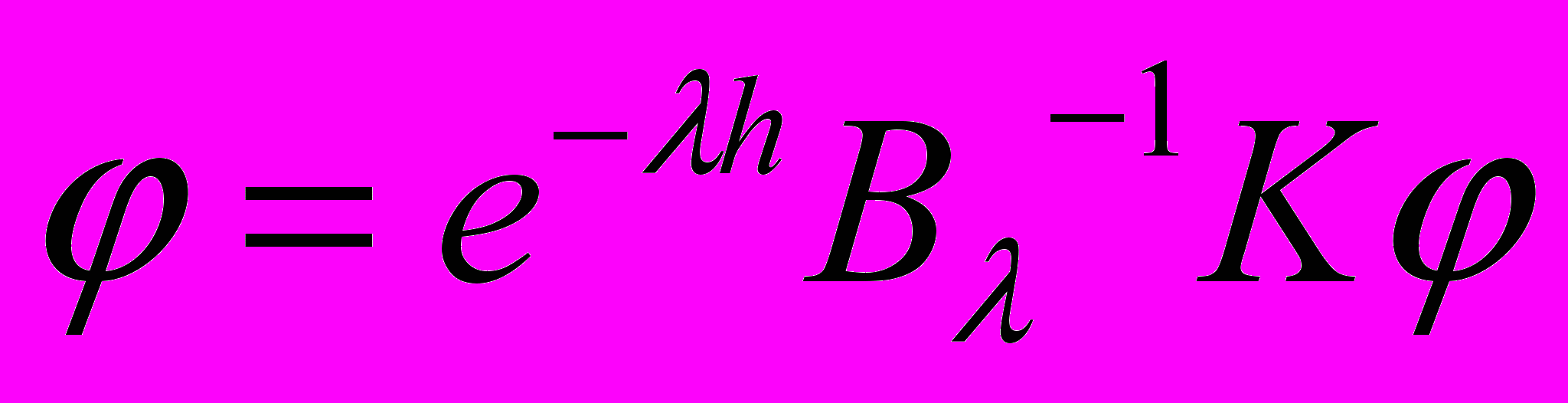, т. е. принадлежит линейному многообразию размерности 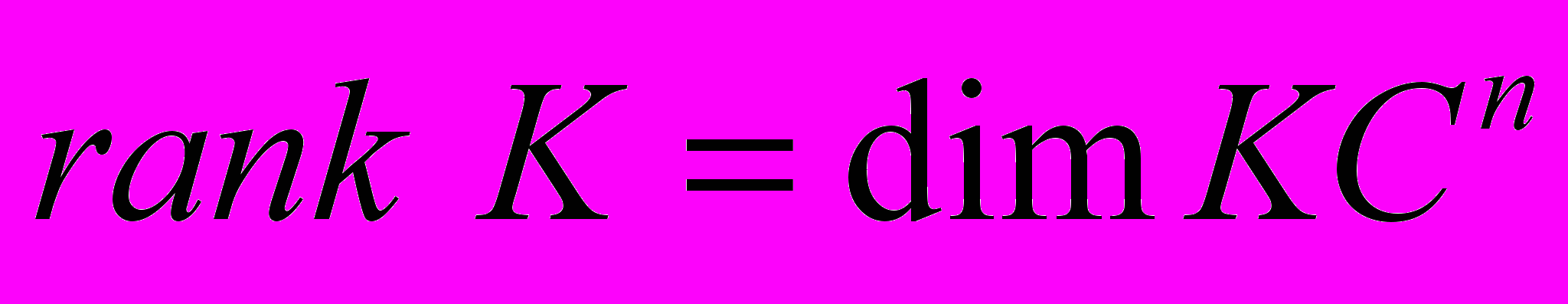. Отсюда получаем оценку снизу для ранга матрицы 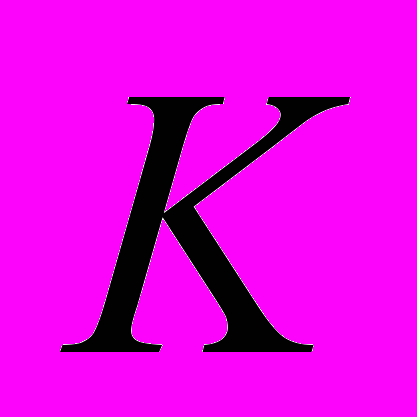блока обратной связи 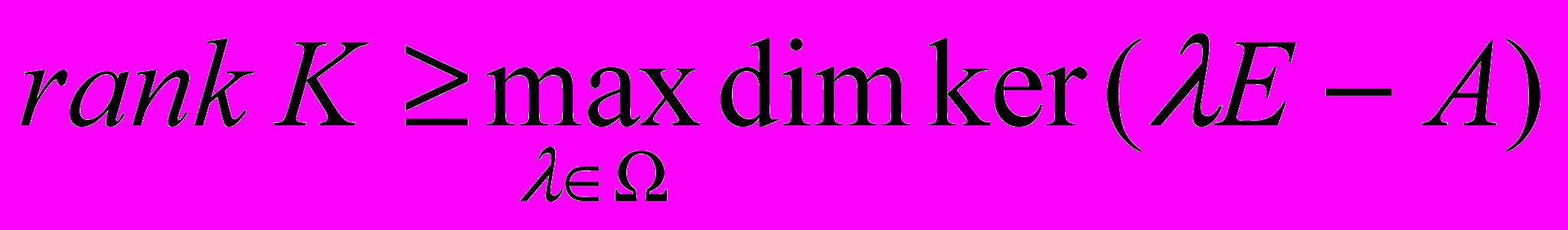, где 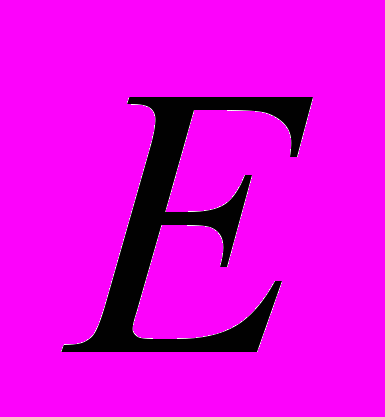- единичная матрица порядка 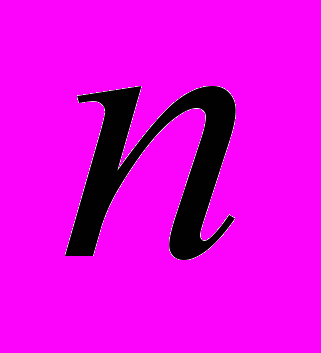. Мы доказываем, что нижняя граница в этом неравенстве достигается, и, тем самым, отвечаем на вопрос о минимальном ранге матрицы 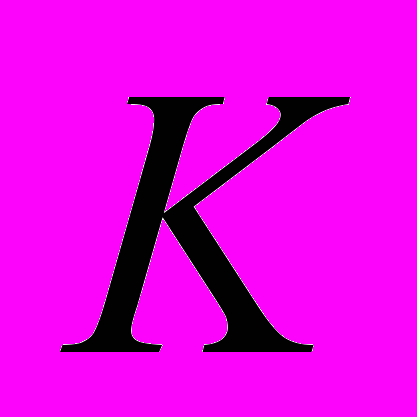блока обратной связи, обеспечивающей важное свойство системы с обратной связью: сохранение «частоты колебаний» внешнего возмущения, а также непрерывную зависимость «амплитуды колебаний» системы от «амплитуды колебаний» этого возмущения для указанного класса возмущений. Доказательство теоремы о минимальном ранге матрицы 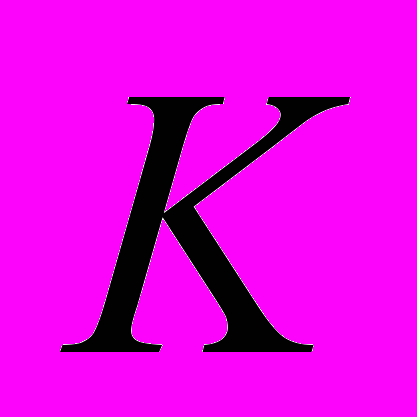блока обратной связи носит конструктивный характер. При построении матрицы 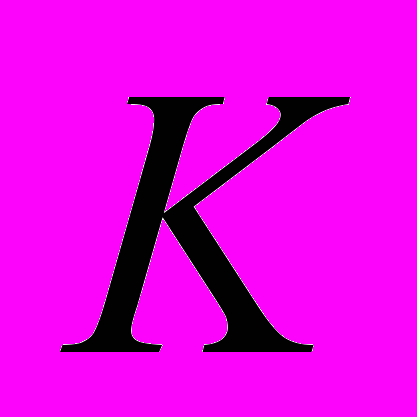используются собственные векторы матрицы системы, отвечающие тем собственным значениям 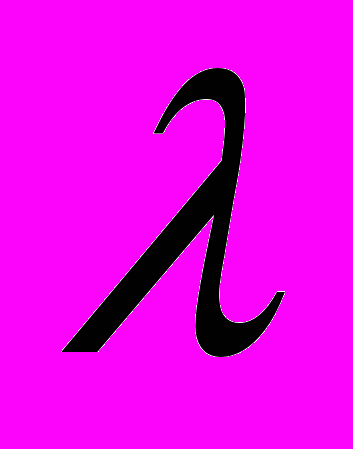, которые лежат в указанной области , фробениусова форма этой матрицы и соответствующая ей преобразующая матрица . Таким образом, мы приходим к классической задаче на собственные значения, задаче вычисления максимальной геометрической кратности собственных значений, лежащих в заданной области комплексной плоскости, и задаче построения фробениусовой формы и преобразующей матрицы для матриц больших размерностей. Все эти задачи требуют больших вычислительных мощностей для обеспечения высокой точности вычислений.

В работе [1] получены точные формулы для вычисления геометрической кратности собственных значений и разработаны численные алгоритмы для вычисления этой кратности. В приводимом ниже фрагменте программы для пакета Mathematica используются четыре формулы для геометрической кратности, которые верны с точки зрения «чистой» математики, однако при численных расчётах могут давать различные и даже неверные результаты. Заметим, что функция Timing измеряет время вычисления указанного выражения, функция PseudoInverse вычисляет обобщённую обратную матрицу Мура-Пенроуза, а семантический смысл остальных функций фрагмента вполне понятен. Фрагмент программы:

r=4000; W=Table[Random[Integer,{-16,16}],{r}]; U=DiagonalMatrix[W]; T=Table[Random[Real,{-16,16}],{i,r},{j,r}]; M=T.U.Inverse[T];

Timing[m=Eigenvalues[M];]; =Re[m[[1]]]; Id=IdentityMatrix[r];

L=M- Id; Timing[PL=PseudoInverse[L];]; Q=Id-L.PL;

Timing[Re[Tr[Q]]]; Timing[Re[Tr[Transpose[Q].Q]]];

Timing[Re[MatrixRank[Q]]]; Timing[r-MatrixRank[L]].

В докладе будут приведены результаты численных экспериментов вычисления максимальной геометрической кратности для матриц порядка 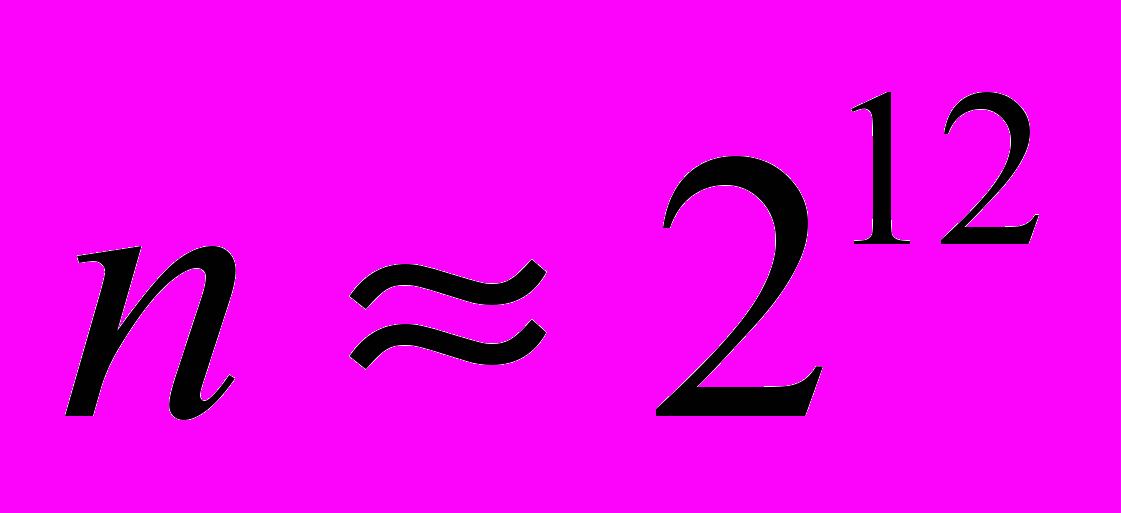на компьютере Aspire 5112WLMi c двумя процессорами AMD Turion 64 x2 Mobile Technology TL50 (1.6 GHz, 512KB L2 cache), оперативной памятью 1 GB DDR2 (support dual-channel) и жёстким диском 120GB 5400rpm SATA HDD.

Автоматизация расчетов для указанных выше задач достигается путем широкого использования пакетов SCALAPACK, PETSC, TAO, SLEPS и др. Вычислительный пакет PETSc (Portable, Extensible Toolkit for Scientific Computation) предназначен для разработки параллельных программ в среде MPI (Message Passing Interface) для решения наиболее трудоемких задач численного анализа: отыскание решений дифференциальных уравнений с частными производными, линейных и нелинейных уравнений большой размерности. В нем имеются средства для разбиения и слияния массивов данных, а также их распределения между процессорами. В полной мере в этом пакете представлена технология объектно-ориентированного программирования. На сайте разработчиков из Аргонской национальной лаборатории (США) (см. ссылка скрыта) можно получить обширную информацию об использовании этого пакета на практике. Вычислительный пакет TAO (Toolkit for Advanced Optimization) предназначен для разработки алгоритмов и создания интерфейса для решения широкого класса оптимизационных задач большой размерности на высокопроизводительных архитектурах. Представляет собой высоко эффективный пакет оптимизации с объектно-ориентированной технологией и может применяться как на отдельных рабочих станциях, так и на высокопроизводительных массивно-параллельных архитектурах. Информацию о последних версиях пакета TAO можно получить на сайте (см. ссылка скрыта). Текущая версия пакета TAO использует инфраструктуру параллельных систем и объекты линейной алгебры, принятые в численном пакете PETSc, основана на модели обмена сообщениями для параллельного программирования и использует MPI для межпроцессорных взаимодействий. Масштабируемая библиотека для алгебраической проблемы собственных значений SLEPc (Scalable Library for Eigenvalue Problem Computations) позволяет решать задачи большой размерности для разреженных матриц на параллельных компьютерах. Подобные матрицы возникают при дискретизации уравнений в частных производных. Пакет обрабатывает как симметричные, так и несимметричные матрицы как с вещественными, так и с комплексными элементами. Пакет SLEPc построен на базе PETSc и использует ряд библиотек (ARPACK и др.). Вся информация, относящаяся к этому пакету, может быть найдена на сайте (см. ссылка скрыта.

Для отладки параллельных программ на информационно-вычислительном кластере PARC Удмуртского госуниверситета установлен ряд средств, из которых упомянем лишь некоторые. GNU отладчик gdb можно использовать в двух режимах: обычном и пакетном. Для его применения требуется отладочная информация, получаемая при компиляции с оцией –g, и даже –O, что делает возможной отладку оптимизированного кода. Возможна отладка запущенного ранее процесса, уничтожение дочернего процесса, отладка программы с несколькими нитями управления. Основная цель применения отладчика – позволить разработчику остановить программу до ее завершения в определенных точках или, в случае нарушений в работе программы, исследовать программу и выяснить причину неполадок. Из всего многообразия имеющихся программных средств визуализации, мониторинга выполнения и отладки параллельных программ на кластере мы выделяем XPVM и TotalView. Удобный графический интерфейс этих средств позволяет проводить тщательный анализ и мониторинг параллельных процессов с целью улучшения их производительности, способствует пониманию их поведения и взаимодействия, а также позволяет оценивать степень загрузки процессоров при выполнении параллельной программы. Несмотря на то, что в первом средстве отсутствует возможность отладки параллельных программ в ходе их исполнения, использование XPVM дает значительный выигрыш при обучении методам разработки параллельных программ.

Литература

1. Islamov G.G. On the exact formula for eigenvalue geometric multiplicity // Современные методы теории функций и смежные проблемы: Материалы конференции, Воронеж: ВГУ, 2005. – С. 7.