Тема XVI экономический рост

Вид материала

Документы

Содержание 16.2. Модели экономического роста Кейнсианские концепции: модели Домара и Харрода Определяющим в экономическом росте является рост инвестиций. Модель Домара. Модель Харрода. Неоклассическая модель Роберта Солоу Рис. 16.2. Функциональная связь роста производитель­ности труда и его капиталовооруженности. Рис. 16.4. Зависимость капиталовооруженности от инвестиций

Подобный материал:

• Лекция Экономический рост, 551.64kb.
• Тема Национальное хозяйство: задачи макроэкономического анализа. Экономический рост, 285.86kb.
• Конкурс научных работ аспирантов, соискателей, научных сотрудников "Экономический рост, 22.12kb.
• Пособие по изучению раздела дисциплины «экономический рост» для студентов всех специальностей, 656.55kb.
• 1. Социально-экономический кризис 1990-1998(99) годов и рост народного хозяйства страны, 71.58kb.
• Социально-экономический и политический кризис XVI – начала XVII, 877.96kb.
• Торговля и экономический рост, 157.32kb.
• Экономический рост в мировой экономике, 6.81kb.
• Всероссийский заочный финансово – экономический институт, 287.3kb.
• Тема : Нидерландская революция XVI века, 59.76kb.

16.2. Модели экономического роста

Формальная теория экономического роста возникла как самостоятельное направление экономического анализа в конце 30-х -40-х годов. Ее основной проблемой стало определение условий устойчивого, равновесного роста, то есть роста при полной занятости (загрузке) факторов производства, когда их совокупная величина растет тем же темпом, что и объем производства. Среди других отраслей экономической теории теория роста, пожалуй, выделяется более тесной зависимостью от реалий хозяйственной жизни.

Существуют два основных типа моделей роста:

1. Кейнсианские модели;
   
2. неоклассические модели, основанные на неоклассической теории производства (теории фирмы).
   

Кейнсианские концепции: модели Домара и Харрода

Практически до 50-х годов превалировал кейнсианский подход при анализе равновесия экономической системы, где рас­сматривалась краткосрочная модель в условиях неполного исполь­зования ресурсов, т. е. в состоянии рецессии, недогрузки мощностей и массовой безработицы. Но уже ближайшие последователи Д.М.Кейнса со­средоточили свои усилия на определении условий поддержания вы­соких и стабильных темпов роста, на исследовании различных ва­риантов динамики процесса воспроизводства. Так, модели английского экономиста сэра Роя Ф. Харрода (1900-1976) и американского экономиста Евсея Домара (род. 1914), положившие начало данной отрасли экономи­ческого знания, были рассчитаны на то, чтобы объяснить периоды длительных диспро­порций, прообразом которых явно была Великая депрессия 1929-1933 гг. Кейнсианские модели роста, как и учение Д.М.Кейнса, в целом основаны на главенствующей роли спроса в обеспечении макроэкономического равновесия. Решающий элемент спроса - инвестиции, которые посредством мультипликатора увеличивают прибыль. Одновременно они сами вызваны к жизни ростом прибыли, так как капитальные вложения представляют собой функцию увеличения прибыли. Отметим, что кейнсианцы не разделяют неоклассическую позицию эффективности производственных факторов и их взаимозаменяемости.

Модели Р. Харрода и Е. Домара⁸ основаны на следуюших предпосылках:

1. рост национального дохода является только функцией накопления капитала. Факторы, влияющие на рост капиталоотдачи, исключаются. Это рост занятости, улучшение организации производства, степень использования НТП;
   
2. это однофакторные мо­дели, в них учитывается только капитал в качестве единственного фактора роста. Но этот фактор как бы «вбирает» в себя потенциал всех остальных факторов;
   
3. принимается постоянной величина капиталоемкос­ти, т. е. отношение объема инвестированного капитала (основной капитал плюс запасы) к валовому национальному продукту (или до­ходу);
   
4. новые капиталовложения не изменяют капита­лоемкости (так называемый «нейтральный технический прогресс» или «нейтральные инвестиции»), т.е. капиталоемкость не зависит от соотношения цен производственных факторов, а определяется техническими условиями производства.
   

Определяющим в экономическом росте является рост инвестиций.

Учитывая, что инвестиции связаны со сбережениями: I ( r ) = S (Y) – экономический рост означает:

• увеличение производственных мощностей фирм;
  
• увеличение дохода и сбережений.
  

Т.е. экономический рост сам создает свои собственные предпосылки, что образует самоподдреживающийся замкнутый процесс: I экономический рост  S I ...

Модель Домара. Простейшей посткейнсианской моделью экономического роста является модель Домара. В ней в явном виде присутствует только рынок благ. Технология производства представлена производственной функцией Леонтьева с постоянными технологическими коэффициентами затрат факторов. Предполагается, что на рынке труда существует избыточное предложение и это обеспечивает постоянство уровня цен. Рынок благ изначально сбалансирован.

Кейнс ограничивал проблему рав­новесия национальной экономики и обеспечения полной занятости коротким периодом. Поскольку в этом периоде потенциальные воз­можности производства (предложения) не меняются, решение зада­чи обеспечения равновесия Кейнс видел в активном воздействии на совокупный спрос. Однако, для развивающейся экономики харак­терен постоянный рост производственных возможностей. Поэтому совокупный спрос, достаточный для обеспечения равновесия в со­стоянии полной занятости в какой-то момент времени, может ока­заться недостаточным в следующий период наблюдения. Неокейнсианцы были вынуждены заняться предложением и исследовать факторы, определяющие уровень и развитие производственного по­тенциала, т. с. прежде всего инвестиций.

При построении своей модели Домар исходил из постулата, что если в начальный момент экономическая система находится в рав­новесии при полной занятости, то для сохранения этого состояния в динамике совокупный спрос должен возрастать тем же темпом, что и производственный потенциал (прирост производственных мощностей), т. е. AD=Qf.

Чтобы выяснить условия выполнения этого равенства, Домар предложил решить систему из трех уравнений.

1. Уравнение предложения. Изменение уровня потенциальных возможностей национального производства зависит от расширения ресурсной базы, изменений в составе и качестве рабочей силы, от величины и структуры капитала, от состояния техники и техноло­гии. Увеличение совокупного предложения составит Qf = К,

где Qf— изменение потенциального объема производства (ВНП, ЧНП,НД);

К— прирост капитала;  — предельная произво­дительность капитала (по условию — посто­янна).

Прирост капитала К обеспечивается соответствующим объемом инвестиций I и производительностью капитала: Qf = I.

2. Уравнение спроса. Из кейнсианской теории была выведена формула мультипликатора: k=Y/I. Преобразуя ее, получим:

Y(AD) = kI,

т. е. темпы прироста производства определяются изменениями в инвестициях, умноженных на мультипликатор. Если учесть, что мультипликатор равен обратной величине предельной склонности к сбережениям (1/MPS), то данная формула будет выглядеть так:

Y=I1/s

где s— обозначена MPS.

3. Уравнение равновесия. Равновесный экономический рост будет достигнут при условии равенства спроса и предложения (совокупного спроса (AD) и производственного потенциала (Qf), т. е. прирост денежного дохода (спрос) равен приросту производственных мощностей (предложение).

AD=Qf или I1/s = I.

Откуда, I/I = s,

т.е. темп прироста инвестиций, которые обеспечивают полную занятость производственных ресурсов и полную загрузку производственных мощностей, должен быть равен произведению предельной производительности ка­питала и предельной склонности к сбережению. Величина  задается технологи­ей производства и, в соответствии с принятыми предпосылками, постоянна, а значит увеличить темпы прироста инвестиций может лишь рост нормы сбере­жений s (но для рассматриваемого периода она берется постоянной).

Поскольку в условиях равновесия инвестиции равны сбережениям, I=S, a S=sY при s=const, уровень дохода является величиной, пропорциональной уровню инвестиций, и тогда Y/Y =I/I = s.

Таким образом, согласно теории Е.Домара, существует равновесный темп прироста реального дохода в экономике, при котором полностью ис­пользуются имеющиеся производственные мощности. Он прямо пропорциона­лен норме сбережений и предельной производительности капитала, или приростной капиталоотдаче (Y/K) . Инвестиции и доход растут с одинаковым постоянным во времени темпом. Такое динамическое равновесие может оказаться неустойчивым, как только темп роста плановых инвестиций частного сектора отклоняется от уров­ня, заданного моделью.

Предположим, что трудоемкость единицы выпуска снижается темпом т (это означает, что производительность труда повышается темпом т). Если численность рабочей силы растет темпом п, возникает своеобразный тупик. Общий выпуск должен расти средним темпом т +п, ибо если выпуск растет медленнее, безработица бесконечно увеличивается, а если быстрее - возникает нехватка рабочей силы. Темп роста экономики, обеспечивающий полную загрузку мощностей (s) и темп роста, обеспечивающий полную заня­тость трудовых ресурсов (т + п) определяются совершенно разными факторами и мо­гут совпасть лишь случайно. Достигаемое в этом случае равновесие оказывается неус­тойчивым (балансированием "на острие ножа"). В случае же расхождения этих темпов возникают кумулятивные процессы (взаимодействие мультипликатора и акселерато­ра), уводящие экономику еще дальше от равновесного состояния. При s > т + п (из­лишке капитала) наступает затяжная стагнация и безработица, при s < т + п (не­хватке капитала) - длительная инфляция.

Модель Е.Домара не претендовала на роль теории роста. Это была по­пытка расширить условия краткосрочного кейнсианского равновесия на более длительный период и выяснить, какими будут эти условия для развивающейся системы.

Модель Харрода. Развитием модели Домара выступает модель Харрода. Как и в предыдущей модели, норма уравновешенного роста является функцией соотношения роста дохлдов и капитальных вложений, что дает повод называть эти модели Харрода-Домара. Однако, если модель Домара базируется на использовании мультипликатора, то в основе модели Харрода лежит теория акселератора и следовательно, она определяет норму сбалансированного роста доходов, с которой связаны капитальные вложения. Модель Харрода позволяет на базе теории акселератора исследовать инвестиционные решения предпринимателей. Харрод исходит из 2-х предпосылок:

1. Накопление представляет постоянную долю национального дохода, оно растет темпами равными темпу роста доходов, предельная и средняя склонность к накоплению равны между собой.

2. Объем осуществляемых капиталовложений есть функция прироста дохода или спроса между двумя периодами, согласно основному уравнению Кейнса для равновесия сумма сбережений должна быть равна сумме инвестиций. Отсюда следует, что норма роста, уменьшенная на капитальный коэффициент, равна удельному весу накоплений в национальном доходе.

Для различных норм роста Харрод выдвигает следующее положение: система свободного предпринимательства будет эффективна функционировать, если доходы будут расти ускоренными темпами. Инвестиции должны предвосхищать динамику потребительского спроса. Равновесие по этой модели весьма неустойчиво. Отсюда следует, что необходимо вмешательство государства через финансовую политику.

G_W C_r = S, где G_W – необходимый/гарантированный темп роста, который обеспечивает равновесие между фактическими сбережениями и предполагаемыми инвестициями, поддерживая его, предприниматели будут полностью удовле­творены своими решениями поскольку спрос будет равен предложению и их ожидания будут сбываться. Такой темп роста обеспечивает полное использова­ние производственных мощностей (капитала), но полная занятость при этом не всегда достигается; C_r – требуемая величина капитального коэффициента, т.е. капиталоемкости; S – cбережения. Сбережения относятся к прошлому периоду – ex post, а темп роста и капиталоемкость – к будущему – ex ante. Уже сделанные сбережения приводят к требуемым для динамического равновесия величинам G_W и C_r, т.е. прошлое формирует будущее. Анализ соотношений между гарантированным и фактическим темпами роста позволил сделать следующий вывод: если фактически запланированный предпринимателями темп роста предложения отличается от гарантированного темпа роста (превышает или не достигает его), то система постепенно отдаляет­ся от состояния равновесия. Помимо гарантированного темпа роста Харрод вводит понятие "есте­ственного" темпа роста. Это максимальный темп, допускаемый ростом активного населения и техническим прогрессом. При таком темпе достигается полная занятость факторов — труда, и капитала.

Если гарантированный темп роста, удовлетворяющий предпринимате­лей, выше естественного, то вследствие недостатка трудовых ресурсов фак­тический темп окажется ниже гарантированного: производители будут ра­зочаровываться в своих ожиданиях, снизят объем выпуска и инвестиции, в ре­зультате чего система будет находиться в состоянии депрессии.

Если гарантированный темп роста меньше естественного, то фактичес­кий темп может превысить гарантированный, поскольку существующий избы­ток трудовых ресурсов дает возможность увеличить инвестиции. Экономическая система будет переживать бум. Фактический темп роста может быть также ра­вен гарантированному, и тогда экономика будет развиваться в условиях дина­мического равновесия, вполне удовлетворяющих предпринимателей, но при на­личии вынужденной безработицы.

Идеальное развитие экономической системы достигается при равенстве гарантированного, естественного и фактического темпов роста в условиях пол­ной занятости ресурсов.

Но поскольку всякое отклонение инвестиций от условий гарантирован­ного темпа роста, как известно, выводит систему из равновесия и сопровожда­ется все более увеличивающимся расхождением между спросом и предложени­ем, динамическое равновесие в модели Харрода также оказывается неус­тойчивым.

Часто обе модели объединяют в одну модель Харрода—Домара. Обе мо­дели приводят к выводу, что при данных технических условиях производства темп экономического роста определяется величиной предельной склонности к сбережению, а динамическое равновесие может существовать в условиях непол­ной занятости.

Ограниченность данных моделей задана уже предпосылками их анализа. Например, используемая в них производственная функция Леонтьева характе­ризуется отсутствием взаимозаменяемости факторов производства — труда и ка­питала, что в современных условиях не всегда соответствует действительности. В модели Харрода, как и в модели Домара, динамическое равновесие в условиях экономического роста неустойчиво. Пессимистический вывод Харрода и Домара о внутренней нестабильности роста рыночной экономики побудил экономистов к более глубокому исследованию проблемы равновесного роста.

Модели Домара и Харрода неплохо описывали реальные процессы эко­номического роста 1920-1950-х гг., но для более поздних наблюдений (50-е — 70-е гг.) наиболее успешно использовалась неоклассическая модель Р.Солоу.

Неоклассическая модель Роберта Солоу

Роберт Солоу, американский экономист, был удостоен Нобелевской премии за разработку теории и методов измерения экономического роста в 1987 году. Неоклассические модели роста преодолевали ряд ограничений кейнсианских моделей и по­зволяли более точно описать особенности макроэкономических процессов. Р.Солоу показал, что нестабильность динамического равновесия в кейн­сианских моделях была следствием невзаимозаменяемости факторов производ­ства.

Модель Солоу основана на производственной функции Кобба-Дугласа Y = F(K;L), в которой труд и капитал являются субститутами и неоклассической теории производства. Другими предпосылками анализа в модели Солоу являются: убывающая пре­дельная производительность капитала, постоянная отдача от масштаба, посто­янная норма выбытия, отсутствие инвестиционных лагов. Взаимозаменяемость факторов (изменение капиталовооруженности) объ­ясняется не только технологическими условиями, но и неоклассической пред­посылкой о совершенной конкуренции на рынках факторов. Необходимым условием равновесия экономической системы является равенство совокупного спроса и предложения. Предложение описывается про­изводственной функцией с постоянной отдачей от масштаба: если оба фактора увеличить в Z раз: zY = F(zK;zL). Это предположение дает основание утверждать, что объем производства на одного рабочего зависит от количества капитала, приходящегося на одного рабочего.

Д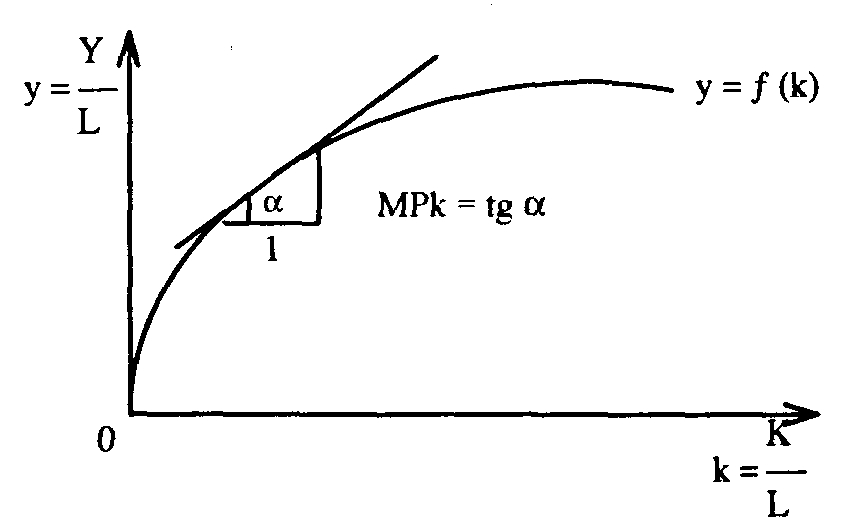опустим, Z =1/L, тогда Y/L = F(K/L; 1) – это уравнение показывает, что объем производства в расчете на 1 работника является функцией капитала в расчете на одного работника. Обозначим Y/L =y, K/L = k, тогда y = F(k;l), где k – капиталовооруженность труда.


Рис. 16.2. Функциональная связь роста производитель­ности труда и его капиталовооруженности.

Графически функциональная связь роста производитель­ности труда и его капиталовооруженности представлена на рис. 16.2. Как видим, по мере роста капиталовооруженности по­вышается производство дохода на одного работника — при каждом увеличении k происходит соответствующий прирост величины дохода у. Эта взаимосвязь приращения дохода на единицу труда от роста его капиталовооруженности выражается предельной продуктив­ностью капитала МРК, т. е. МРК = у/k. В каждой точке кривой она выражается тангенсом угла наклона каса­тельной, проведенной через эту точку, или отношением дифференциалов dy / dk. Тангенс угла наклона tg показывает, сколько дополнительного продукта можно получить на одного рабочего, если увеличить капиталовооруженность на 1 единицу:

tg = MPK = f(k+1;1) – f(k;1)

На графике кривая роста производительности труда имеет выпуклую форму, так как при данной технологии МРК носит убывающий ха­рактер, выражая закон убывающей производительности труда. С ростом капиталовооруженности наклон становится более пологим. Это означает, что каждая дополнительная единица капитала приносит меньшую отдачу, чем предыдущая. Когда запас капитала невелик, то у растет быстрее k, т.е. каждая дополнительная единица капитала дает отдачу большую, чем предыдущая.

Поскольку производительность труда зависит от прира­щения капиталовооруженности, то прирост капитала опре­деляется инвестициями i, а последние при равновесном производстве равны сбережениям s, динамика которых определяется функциональной зависимостью i = s(y).

В модели Солоу спрос на товары предъявляется со стороны потребителей и инвесторов, т.е. y = c + i – продукт, произведенный каждым рабочим, распадается на потребление и инвестиции. Это уравнение похоже на обычное уравнение ВНП для закрытой частной экономики: Y=C+I.

С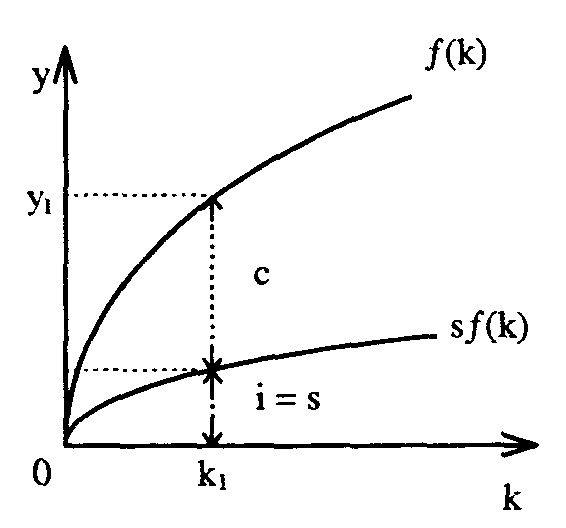олоу принимает, что c = (1– s)y, где s – норма сбережения, 0 s 1. Каждый год часть дохода потребляется, а часть сберегается. Заменим величину с ее выражением через s, тогда y = y(1 – s) + i. Следовательно, i = sy. Данное уравнение показывает, что инвестиции, как и потребление, пропорциональны доходу. Поскольку у = f(k), то равенство инвестиций можно записать: i = sf(k). Разницу между f(k) — sf (k) будет выражать у — s, или объем потребления с. Уточним предыдущий график 16.2 с учетом этих расчетов на рис. 16.3.

Рис. 16.3. Функциональная связь производитель­ности труда и его капиталовооруженности от инвестиций, определяемых величиной сбережений.

График на рис. 16.3 показывает, что капиталовооруженность труда и его производительность зависят от инвестиций в производ­ство, определяемых величиной сбережений. Чем больше их размеры, тем меньше будет потребление с в текущем периоде. Но возрастающие инвестиции, увеличивая капиталовоору­женность труда, обеспечивают повышение его производи­тельности и экономический рост производства в будущем.

В модели экономического роста Р.Солоу учитываются и такие переменные величины, как по­степенный износ, амортизацию и выбытие части капитала , а также прирост населения , для которого необходимо создавать новые рабочие места. Кроме того, накопление капитала идет на повышение квалификации работников g, возрастающее с прогрессом науки и техники. Эти инвестиции не увеличивают капиталовооруженность труда.

Уравнение i = sf(k) показывает, что чем выше уровень капиталовооруженности, тем больше объем производства, тем больше i. Данное уравнение связывает существующие запасы капитала k с накоплением нового капитала, которое происходит через инвестиции. Амортизация учитывается следующим образом: если принять, что еже­годно вследствие износа капитала выбывает его фиксированная часть  (норма выбытия), то величина выбытия будет пропорциональна объему капитала и рав­на k. На графике эта связь отражается прямой, выходящей из точки начала координат, с угловым коэффициентом . Допустим, ежегодно выбывает капитала на величину  – норма выбытия, следовательно, изменение запасов капитала равно разности инвестиций и выбытия: k = ik  k = sf(k) - k. Таким образом, чем выше норма сбережения (накопления), тем более высокий уровень выпуска и запаса капитала может быть достигнут в состоянии устойчивого равновесия. Однако повышение нормы накопления ведет к ускоре­нию экономического роста в краткосрочном периоде до тех пор, пока экономи­ка не достигнет точки нового устойчивого равновесия.

Очевидно, что ни сам процесс накопления, ни увеличение нормы сбере­жения не могут объяснить механизм непрерывного экономического роста. Они показывают лишь переход от одного состояния равновесия к другому.

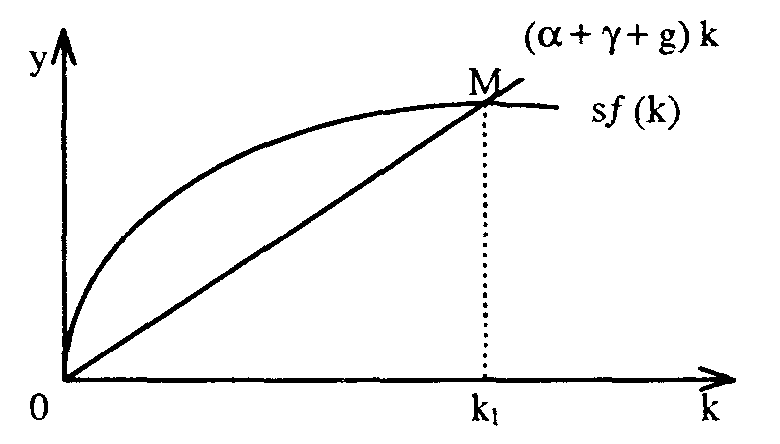Принимая во внимание все факторы, сдерживающие рост капиталовооруженности, уравнение, показывающее изменение k с течением времени, можно записать так: k = sf (k) — ( + у + g) k. С учетом их линейного изменения график зависимости капиталовооруженности от инвестиций представ­лен на рис. 16.4. На графике видно, что при замедлении роста сбережений и инвестиций их размеры могут сравняться с общей вели­чиной факторов, сокращающих капиталовооруженность труда, что представлено поворотной точкой М, в которой сбережения и инвестиции становятся равными выбытию капитала, приросту населения и росту человеческого капи­тала.


Рис. 16.4. Зависимость капиталовооруженности от инвестиций

"Золотое правило" накопления капитала Э. Феллса гласит, что рост инвестиций и увеличение капиталовоо­руженности должны достигать такого устойчивого состоя­ния, при котором обеспечивается наибольшая величина удовл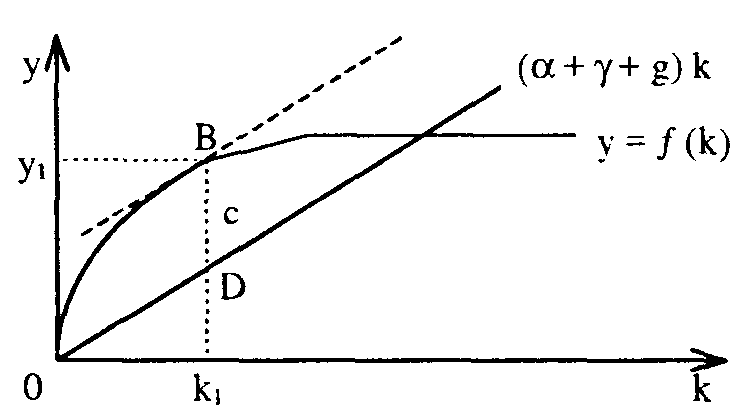етворения потребностей общества с, что представле­но на рис. 16.5.

Отрезок BD на графике выражает наибольшую разницу между величиной переменных, ограничивающих рост капи­таловооруженности труда, и производством дохода на еди­ницу вложенного труда.

Рис. 16.5. Золотое правило накопления капитала

Таким образом, при уровне капи­таловооруженности, соответствующем "золотому правилу", должно выполняться условие: MPK=  (предельный продукт капитала равен норме выбытия), а с учетом роста населения и повышения квалификации работников, возрастающей с технологическим прогрессом MPK=  + у + g.

В рассмотренной модели экономического роста нара­щивание капиталовооруженности труда на основе инвести­ций и сбережений доходов общества является условием по­вышения производительности труда. Но убывающий характер проявления этой закономерности свидетельствует о том, что количественное наращивание капиталовооруженности долж­но сопровождаться таким качественным изменением струк­туры инвестиций и капитала, которое выводило бы произ­водство на более совершенный технологический уровень, когда преодолевалась бы закономерность понижения про­изводительности труда при данной его технологии.

Любой прирост ВНП, не связанный с краткосрочными изменениями затрат труда или капитала, принято относить к так называемому остатку Солоу. На этот "остаток" приходится 50% от прироста ВНП в развитых странах в исторической ретроспективе Неоклассическая теория рассматривает его как результат действия экзогенного, т.е. совершенно независимого от экономической системы фактора - технического прогресса.

Учет в модели Солоу технологического прогресса видоизменяет исход­ную производственную функцию. Предполагается трудосберегающая форма тех­нологического прогресса. Технологический прогресс в модели Солоу является единственным условием не­прерывного роста уровня жизни, поскольку лишь при его наличии наблюдается устойчивый рост выпуска на душу населения (у).

Выводы:

1. Модель Солоу показывает, что норма сбережений является ключевым параметром экономического роста;
   
2. Модель Солоу показывает, что само по себе накопление капитала не может объяснить экономический рост. А именно, высокий уровень сбережений сначала увеличивает темпы роста, но экономика приближается к устойчивому состоянию, при котором запасы капитала и объем производства постоянны.
   
3. В модели Солоу найдено объяснение механизма непре­рывного экономического роста в режиме равновесия при полной занятости ре­сурсов.
   

Разработанная Солоу и его единомышленниками неоклассическая теория экономи­ческого роста господствовала в теоретической литературе до середины 70-х годов (оппозицию ей составляли, главным образом, обычно называемые посткейнсианскими модели роста Н. Калдора, Дж. Робинсон и др., часто более дезагрегированные, включавшие в рассмотрение большее количество информации о реальном устройстве экономики, но сильно уступавшие неоклассическим моделям по части обозримости и ясности выводов, не говоря уже об аналитической элегантности и педагогических достоинствах). Далее, однако, интерес к ней, как и к проблематике долговременного роста вообще, резко снизился под влиянием потрясений, связанных с нефтяным кризисом, стагфляцией и т.д. (не случайно в это же время новый расцвет пережили вышедшие ранее из моды теории экономического цикла). Казалось, что все инте­ресное в области теории экономического роста уже сказано. Однако сегодня проблемы долгосрочного роста стали занимать все большее место в макроэкономических исследованиях, отмечаются важные новые аспекты проблемы - учет влияния несовершенной конкуренции, роль возможных изменений нормы прибыли и др. С середины 80-х годов возник ряд теоре­тических моделей, в которых научно-технический прогресс выступает в качестве одного из эндогенных факторов экономического роста (П. Ромер, Р. Лукас, Г. Грос­сман - Э. Хелпман, Н. Стоуки). Особый интерес вызывают оценки ключевой теоретической гипотезы "новой теории роста" - гипотезы об эндогенном характере важнейших производственно-технических нововведений. Фигурирующие в этих высокоформализованных моделях механизмы экономического роста П. Ромер и Р. Лукас предполагают интерпретировать как возрастающую общественную отдачу, получаемую, соответственно, от вложений в научно-технический прогресс и вложений в человеческий капитал. Плоды от этих инвестиций достаются не только тем, кто их осуществлял, но и всему обществу. Эти внешние эффекты "обосновывают", в частности, возрастание разрыва в темпах роста между развитыми странами (где велики вложения в НИОКР и в человеческий капитал) и развивающимися государствами.