Geum.ru

Ні підходи до прогнозування соціально-економічних показників, побудовано моделі прогнозу курсу валют на основі нейронних мереж та експоненціального згладжування

Вид материалаДокументы

Содержание


Результати дослідження.
Подобный материал:
MI28

ЕКОНОМІКО-МАТЕМАТИЧНІ МОДЕЛІ ТА ІНФОРМАЦІЙНІ ТЕХНОЛОГІЇ У ПРОГНОЗУВАННІ СОЦІАЛЬНО-ЕКОНОМІЧНИХ ПРОЦЕСІВ


В роботі досліджено сучасні підходи до прогнозування соціально-економічних показників, побудовано моделі прогнозу курсу валют на основі нейронних мереж та експоненціального згладжування. Проведено їх аналіз та окреслені особливості.

Ключові слова: економіко-математичні моделі, прогнозування, соціально-економічні показники, нейронні мережі, експоненціальне згладжування, інформаційні технології, MATLAB, Statistica.

The article deals with modern approaches of forecasting the socio-economic indicators. The forecasting models of exchange rate on the basis of neural networks and exponential smoothings have been constructed, analyzed and delineated by particular qualities.

Keywords: economic and mathematical models, forecasting, social and economic indicators, neural network, exponential smoothing, information technology, MATLAB, Statistica.

Вступ.

Формування стабільного та якісного розвитку соціально-економічної сфери діяльності України ставить перед науковцями широкий спектр задач, що пов’язані не лише з удосконаленням сучасної економіки, а й створенням новітніх методів та способів вирішення соціально-економічних питань. Важливе місце серед них займає прогнозування соціально-економічних процесів. Якщо ми знаємо своє майбутнє – ми маємо можливість адекватно його сприймати, використовувати й покращувати вже сьогодні. В наш час існує досить багато програмних продуктів, що дозволяють нам «зазирнути» в майбутнє. Проте постають питання: яким же методом користуватися, що слід передбачити, які переваги та недоліки цих систем тощо.

Метою даної статті є аналіз сучасних економіко-математичних моделей та інформаційних технологій для прогнозування показників соціально-економічного розвитку. В ході проведеного дослідження було використано методи економіко-математичного моделювання, аналізу, синтезу, статистики.

Питанню прогнозування соціально-економічних процесів присвячено досить багато робіт, як вітчизняних, так і зарубіжних науковців. Зазначимо серед них наступних: Балацький О.Ф., Телиженко А.М [1], Баранов С.В., Скуфьина Т.П. [2], Гнип Н.О. [3], Завгородня Т.П., Григорук П.М., Олійник Д.І. [4], Присенко Г.В. [6], Швець Л.П., Захаркевич Н.П. [7], та інші.

Проте, незважаючи на велику кількість наукових праць щодо прогнозування соціально-економічних процесів, на даний час залишається відкрите питання адекватного застосування інформаційних технологій та економіко-математичних моделей у даних дослідженнях.

Результати дослідження.

Весь навколишній світ – джерело інформації. Вона пронизує всі можливі сфери діяльності людини. Проте без адекватних методів та технологій аналізу даних людині складно використовувати їх на своє благо. Без правильних підходів ми не можемо аналізувати, прогнозувати, досліджувати.

Сучасні інформаційні системи допомагають вирішити ці задачі. Які ж дані слід використовувати для прогнозування соціально-економічних процесів? Так, наприклад, використовуючи у своїх економічних дослідженнях теорію часових рядів, С. Кузнець встановив ряд загальноекономічних закономірностей. Він виявив так звані «цикли Кузнеця» - довгострокові чергування швидкого та повільного темпу росту науково-технічного процесу, чисельності населення, національного доходу.

Одним з новітніх методів прогнозування соціально-економічних процесів є нейромережеве моделювання. Сама ідея нейронних мереж виникла в результаті спроб змоделювати поведінку живих створінь, які сприймають дію зовнішніх чинників та навчаються на власному досвіді.

Розглянемо моделі на підґрунті різного математичного інструментарію та інформаційних систем на прикладі прогнозування курсу гривні до долара США за даними Національного банку України.

У дослідженні використано декілька підходів. Перший з них - використання нейронних мереж в програмному засобі Statistica. Зазначимо, що система Neural Networks даного програмного продукту, може вирішувати клас задач регресійного аналізу, класифікації, прогнозування, кластеризації. При цьому можуть бути використані різноманітні типи мереж: лінійні, загальна регресійна нейронна мережа, радіальна базисна функція, тришаровий персептрон, чотирьохшаровий персептрон і тощо. Більш детально про ці мережі можна почитати у роботах Д. Паттерсона [10], Д. Спічта [11], К. Бішопа [8], С. Хайкіна [9] та інших.

Сформувавши часовий ряд курсу долара до гривні в період з 1996 року по 3 лютого 2011 року, ми отримали часовий ряд з 3576 значень.

На його основі ми сформували додаткові чотири часові ряди, а саме: перший – курс долара на минулий банківський день (2 лютого 2011 року), другий – курс долара на позаминулий банківський день (1 лютого 2011 року) третій та четвертий, відповідно, курс на 31 січня 2011 року і 28 січня 2011 року. (рис.1).



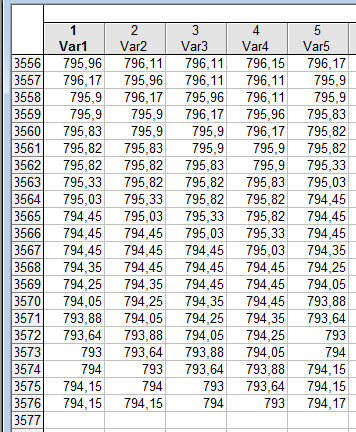
Рис.1 Вхідні дані моделі

У системі нейронних мереж Statistica Neural Networks ми обрали, як вхідні дані, ряди за 1-2 лютого та 28-31 січня 2011 року. В свою чергу часовий ряд за 3 лютого 2011 року ми позначили, як вихідний. Це дає можливість інформаційній системі розрахувати прогнозне значення ряду на основі сформованої статистики минулих значень.

Серед параметрів самої моделі ми позначили, що кількість сформованих мереж буде дорівнювати 500. Даний параметр визначає яку кількість мереж слід сформувати системі, серед яких буде обрано найкращі.

Після навчання моделі ми отримали п’ять найкращих моделей (рис. 2 та 3). Відбір моделей ґрунтувався на отриманих значеннях відношень стандартних відхилень – відношення стандартного відхилення похибки прогнозу до стандартного відхилення вхідних даних. Чим менший цей показник, тим більш точний прогноз ми отримали.



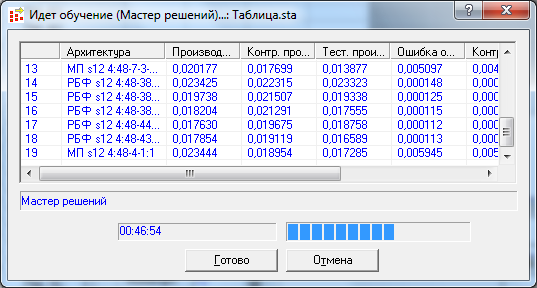
Рис. 2 Процес навчання моделі



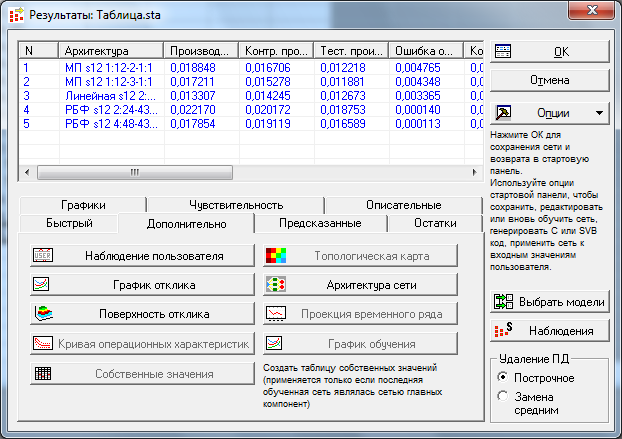
Рис. 3 Результат навчання моделі

Як бачимо, найкращою моделлю серед представлених виявилася лінійна модель, показник відношення стандартних відхилень якої дорівнює 0,0134 (рис. 4).



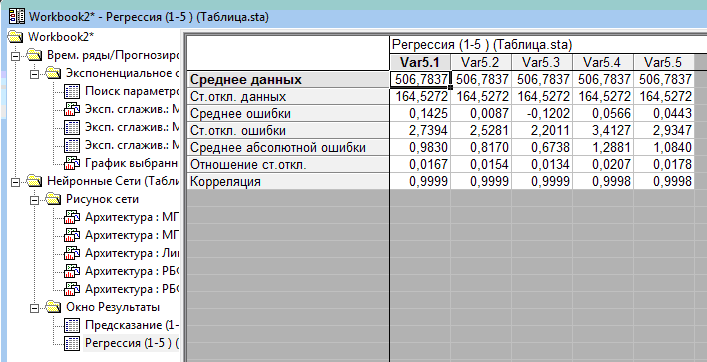
Рис. 4 Таблиця описових статистик

Для отримання значення прогнозу на наступний банківський день інформаційна система пропонує зазначити на який крок нам слід отримати прогнозне значення по кожній з п’яти моделей. Так як всього ми маємо 3576 вхідних значень, то прогнозне значення на 4 лютого 2011 року буде дорівнювати кроку 3577. В результаті ми отримали наступні прогнозні значення моделі:
  1. Багатошаровий персептрон №1 – 793,7128;
  2. Багатошаровий персептрон №2 – 794,5985;
  3. Лінійна – 794,2378;
  4. Радіальна базисна функція №1 – 794,3351;
  5. Радіальна базисна функція №2 – 794,4286.

У той же час курс долара на 4 лютого 2011 року за даними Національного банку України склав 794,37. Як бачимо, найбільш точним прогнозним значенням серед розрахованих вийшло значення радіальної базисної функції №1 з фактичним відхиленням 0,0349. Це можна пояснити тим фактом, що курс валют є нелінійною функцією і, як результат, лінійна модель для даного часового ряду не показує найкращого прогнозу. Проте, в свою чергу, вищезазначена модель показала кращі результати у порівнянні з розрахованим значенням багатошарового персептрона.

Головною перевагою даної моделі є одночасне використання декількох нейронних мереж для отримання прогнозу з подальшим відбором найкращих серед них, та можливість отримання значень прогнозу на декілька періодів вперед. Недоліком моделі є досить високі вимоги до апаратного забезпечення, довготривалість формування моделей.

Ще один підхід запропоновано Леоненковим [5], де розглянуто модель адаптивних систем нейрон-нечіткого виходу (ANFIS, Adaptive neuro-fuzzy inference system) у середовищі програмного забезпечення MATLAB.

Зазначимо, що дана модель використовує гібриду мережу, яка представляє собою багатошарову нейронну мережу спеціальної структури без зворотних зв’язків. З одного боку, гібридна мережа ANFIS представляє собою нейронну мережу з єдиним виходом та декількома входами. З іншого боку гібридна мережа ANFIS представляє собою систему нечіткого виводу FIS (Fuzzy Inference System) типу Сугено.

В процесі реалізації цієї моделі, нами було запропоновано наступні умови: для кожної з чотирьох вхідних змінних задано три лінгвістичних терма; тип функції належності – трикутний.

Після навчання мережі було отримано структуру побудованої нечіткої моделі (рис. 5).



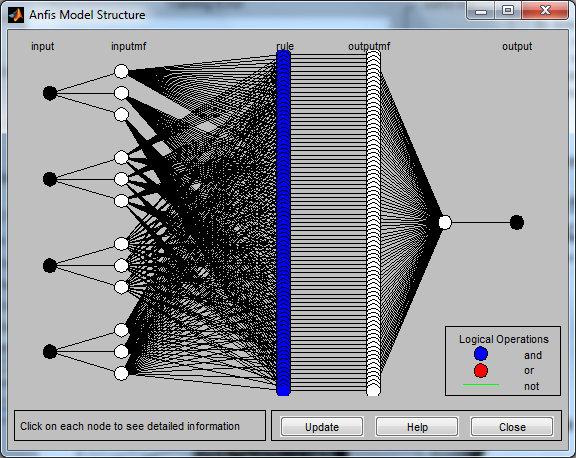
Рис. 5 Структура нечіткої моделі

Проте, виключно графічних можливостей для вирішення поставленої задачі, а саме, отримання значення прогнозу курсу долара на 4 лютого 2011 року, не достатньо. Тому було запропоновано використати функцію evalfis (функція нечіткого логічного виводу):

out=evalfis([794.17 794.15 794.15 794], USD);

де, out – умовне ім’я вихідної змінної;

[794.17 794.15 794.15 794] – вектор значень курсу долара за три попередні дні;

USD – ім’я створеної структури нечіткої моделі.

В результаті розрахунків даної моделі нами було отримано прогнозоване значення курсу долара на 4 лютого 2011 року:

out = 794.1323

Порівнюючи результати розрахунків з реальними даними курсу валют Національного банку України, отримали, що похибка прогнозу склала 0,2377. Таким чином, побудована нечітка модель гібридної мережі показала досить непогані результати прогнозу. Серед переваг моделі зазначимо менший час на навчання моделі, у порівнянні з вищезазначеною моделлю в системі Statistica. Проте, модель має досить важливий недолік - неможливість отримання прогнозних значень на декілька періодів вперед.

Для порівняння, ми вирішили застосувати один з найбільш розповсюджених методів прогнозування часових рядів – метод експоненціального згладжування. Задача реалізації даної моделі була знову покладена на програмний продукт Statistica, який дає змогу врахувати якісні характеристики часового ряду (тренд, сезонність) та параметри моделі (альфа -α, дельта – δ та гамма - γ). Більш детальну інформацію можна отримати на офіційному сайті розробників програмного засобу Statistica [12]. Зазначимо, що в процесі розрахунку було отримано наступні показники параметрів моделі: α = 0,9, δ = 0,1 та γ = 0,5.

Згідно розрахунків прогнозне значення курсу долара на 4 лютого 2011 року за допомогою експоненціального згладжування склало 794,2332. Як бачимо, відхилення від реальних значень склало 0,1368. Перевагами даного методу можна назвати простоту використання, можливість отримання прогнозних значень на декілька кроків вперед. Серед недоліків ми б виділили наступні: модель будує прогноз виключно на попередніх значеннях цього ж часового ряду, існує необхідність попереднього аналізу часового ряду (визначення тренду, сезонності, автокореляції і т.д.).

Підсумовуючи викладене, зазначимо, що всі три моделі показали досить непогані результати. Проте, використання кожної з них у конкретному випадку, перш за все залежить від поставлених цілей, сформованих завдань та наявної інформаційної бази.

Висновки. Як бачимо, сучасний світ вимагає ретельного дослідження та розробки новітніх технологій та методів для прогнозування соціально-економічних процесів. З огляду на це, було запропоновано три моделі прогнозу курсу долара США. Перша – нейромережеве прогнозування у програмному засобі Statistica, друга – гібридна мережа адаптивних систем нейрон-нечіткого виходу у середовищі програмного забезпечення MATLAB та третя – метод експоненціального згладжування. Всі моделі отримали, на нашу думку, прийнятні прогнозні значення і демонструють високу міру адекватності реальним даним, що дає можливість зробити висновок щодо можливості практичного застосування даних моделей. Але ми б хотіли наголосити, що найкращий прогноз з представлених отримала нейромережева модель радіальної базисної функції №1 – похибка прогнозу склала 0,0349.

Представлені підходи формують собою перспективний шлях розвитку для побудови моделей прогнозу соціально-економічних процесів.


Література
  1. Балацький О.Ф., Телиженко А.М Прогнозирование социально-экономического потенциала территории: методические подходы // Вісник СумДУ. Серія Економіка, №2, 2008р. Том 2.
  2. Баранов С.В., Скуфьина Т.П. Социально-экономическое прогнозирование: история, своременность, проблемы преподавания // Вестник МГТУ. – 2005г. - №2. – том 8. с. 201-207.
  3. Гнип Н.О. Організаційно-економічні засади прогнозування фінансового потенціалу підприємств // Журнал «Держава та регіони. Серія: Економіка та підприємництво» - 2010р. №1, с. 64-67.
  4. Завгородня Т.П., Григорук П.М., Олійник Д.І. Особливості прогнозування соціально-економічного розвитку регіону на сучасному етапі // Вісник Хмельницького національного університету. – 2009р. – №6, Т. 2.
  5. Леоненков А.В. Нечеткое моделирование в среде MTATLAB и fuzzyTECH. – СПб.: БХВ-Петербург, 2005. – с. 479-487.
  6. Присенко Г. В., Равікович Є. І. Прогнозування соціально-економічних процесів: Навч.посіб. — К.: КНЕУ, 2005.
  7. Швець Л.П., Захаркевич Н.П Прогнозування показників інноваційного розвитку виробничого потенціалу регіону // Вісник Хмельницького національного університету. – 2009р. – №3, Т. 2.
  8. Bishop, C. Neural Networks for Pattern Recognition. Oxford: University Press, 1995.
  9. Haykin, S. Neural Networks: A Comprehensive Foundation. New York: Macmillan Publishing, 1994
  10. Patterson, D. Artificial Neural Networks. Singapore: Prentice Hall, 1996.
  11. Specht, D. A general regression neural network\ IEEE Trans. Neural Networks, 1991.
  12. Офіційний сайт російського представника компанії StatSoft Inc. – узел oft.ru.