Хамидов Лутфулла Абдуллаевич количественные модели концентрации напряжений в зонах сейсмоактивных разломов земной коры 04. 00. 22 Геофизика автореферат

Вид материала

Автореферат

Содержание Во второй главе В третьей главе Рис.1 Картина распределения S Сейсмотектонический подход. Сейсмофизический подход

Подобный материал:

• А. А. Трофимука Приоритетное направление со ран геофизика, геодинамика Физические поля, 208.47kb.
• Самостоятельная работа 46 Вид итогового контроля Экзамен, 118.98kb.
• Учебно-методический комплекс по дисциплине типы загрязнений окружающей среды, 339.18kb.
• Структура разломных зон земной коры по данным радоновой съемки (на примере Западного, 290.04kb.
• Н. Г. Чернышевского рабочая программа, 145.62kb.
• Н. И. Николаев глава XX комплексное изучение молодых движений земной коры, 442.36kb.
• Физико-геологические модели сейсмогенерирующих неоднородностей земной коры среднего, 249.76kb.
• Краткое содержание курса, 84.97kb.
• Урок на тему : «Строение земной коры. Горные породы и минералы», 153.61kb.
• Практическая работа №3. Тема: Объяснение зависимости расположения крупных форм рельефа, 31.81kb.

Первая глава посвящена оценке состояния вопроса формализации подходов к построению количественных моделей, а также методов решения соответствующих краевых задач с обоснованием способов обеспечения устойчивости результатов. Выбирается подход к созданию количественной модели геофизического процесса концентрации напряжений в линейно-упругом массиве при наличии разрывных нарушений.

Методические основы к изучению напряженного состояния коры были определены М.В.Гзовским (1975). Достаточно глубокие инструментально-экспериментальные исследования по реконструкции полей напряжений приведены в работах А.С.Григорьева, О.И.Гущенко, Д.И.Осокиной, А.В.Михайловой, Ш.Д.Фатхуллаева, М.К.Турапова и др., разработан метод кинематического анализа структур разрушения. Проведена реконструкция полей тектонических напряжений, для этого предложена схема строения полей напряжений для геологических структур методами физического моделирования. Методологически близкий к этим работам являются исследовании П.Н.Николаева (1992), который предложил системный анализ полей напряжений. Он впервые выявил взаимосвязь и неразрывность тектонических движений-деформаций и напряженного состояния, что явилось практически первым шагом тектонофизического осмысления ранговой локализации полей тектонических напряжений.

Периоды деформирования горных пород в процессе подготовки и развития разрывных сейсмотектонических процессов в локальных участках сейсмоактивных разломов разделены на несколько этапов. Зоны разломов при количественном моделировании и составлении соответствующих краевых задач математической физики назовем внутренними кусочными неоднородностями земной коры. Типы концентраторов напряжений разделим на две части. Первая - это геоморфологически выраженные на открытой поверхности Земли концентраторы, вызывающие концентрацию напряжений на поверхности геологического тела типа антропогенных отложений, неровностей топографии и рельефа, каньонов и др. Вторая - это геотектонически погребенные, т.е. внутренние концентраторы. К ним можно отнести отверстия (геологические разрывы в зонах тектонических растяжений), щели (геологические разрывы с зонами контакта и без него), разрезы и включения разного вида внутри геологического тела. Согласно цели исследований, нас, в основном, интересуют внутренние концентраторы.

Все количественные модели, реализованные в данной работе, действуют в пределах малых деформаций: ():{10^-11<₀<10^-4}.

Cформулированные Х.К.Фенгом (Feng, 2004) и обоснованные на мировом материале тезисы о возрастании тектонических напряжений по линейному закону с глубиной позволяют предположить, что геодинамические поля напряжений на более значительной глубине охватывают всю земную кору. Согласно Д.Теркоту (1985) и Ж.Хадсону (2001), эти “избыточные” горизонтальные напряжения значительно превышают геостатические. Поэтому при формализации состояния сил в слоях земной коры в зависимости от решаемых геофизических задач введены следующие дополнительные ограничения: будем считать геофизическую среду упругим и соответствующим моделируемому геологическим телом в рамках действия линейных законов механики; макроскопические геологические объемы будем считать однородными или кусочно-однородными в пределах усредненных изменений модулей упругости и сдвига; масштабный уровень будем считать ограниченным в пределах соотношения {L_min / D_max >_min}, где L_min - минимальная длина концентратора в моделируемом объеме; D_max - максимальная длина (ширина или глубина) моделируемого объема и _min – нижняя граница деформаций, принятая нами пределом, при котором действие моделей, построенных для исследуемого состояния геофизической среды, оправданы; физическое состояние среды при любых условиях нагружения будем считать гомогенным, каждый шаг последующего нагружения - новым квазиравновесным состоянием среды, сформированной при предыдущем нагружении.

Во второй главе построены количественные модели квазистатического деформирования с различными внутренними концентраторами. Получены и построены аналитические решения краевых задач для упругого полупространства со щелью, включением и трещиной сдвига при заданной деформации сжатия. Анализируются численные результаты концентрации напряжений вблизи одиночных концентраторов.

Подробно изложен метод, который назван Х.А.Рахматулиным (1971) методом «источников» и «стоков». Решение задачи этим методом находится в виде линейной комбинации первых N функций фундаментальной системы теории упругости. Рассмотрено геологическое тело, имеющее цилиндрический концентратор с менее плотным заполнителем. Контуры неоднородности выбраны: в первом случае свободный от внешних напряжений; во втором - с жестким контактом; в третьем – связанный с законом трения Кулона. Напряженное состояние на бесконечности представляет одноосное сжатие с деформацией ₀ в направлении, составляющем угол  с продольной осью концентратора. Во всех случаях на свободной поверхности 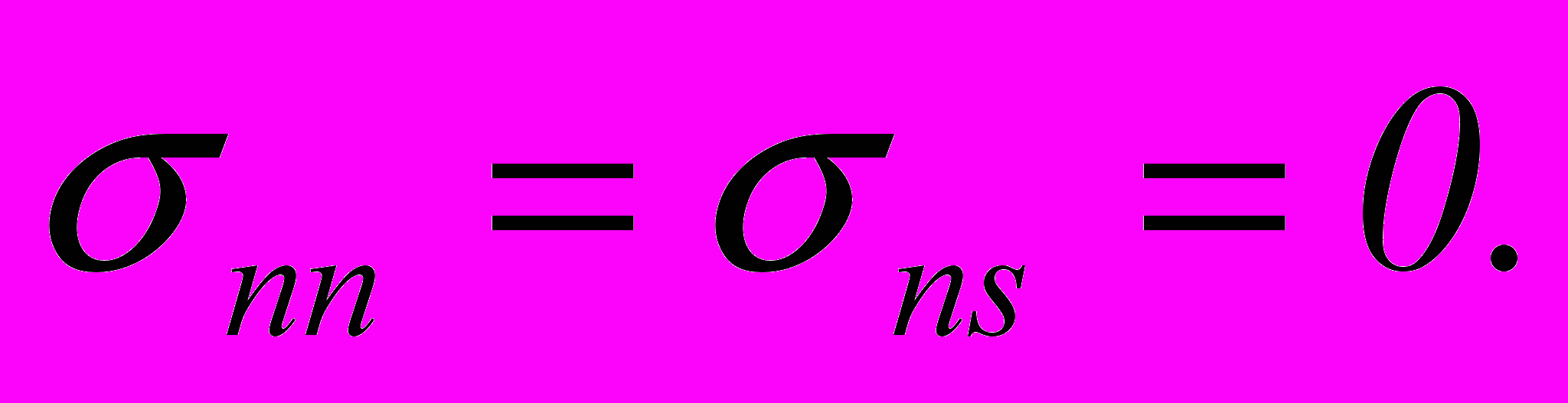Распределяя непрерывно источники внутри концентратора вдоль дополнительной кривой Г₁, получим решение в перемещениях W(u,v):

;,

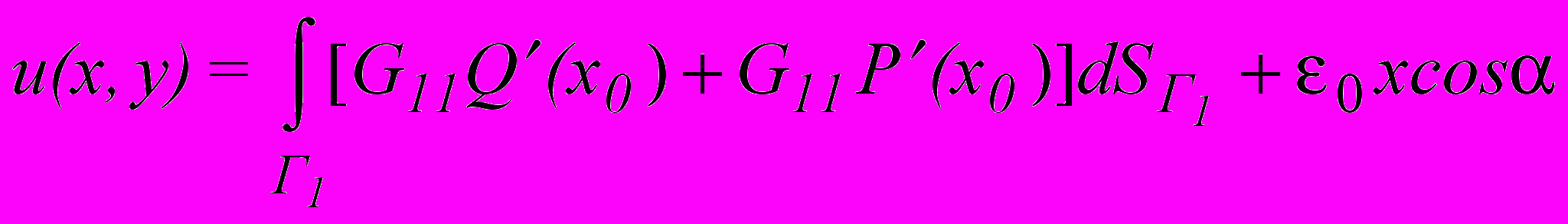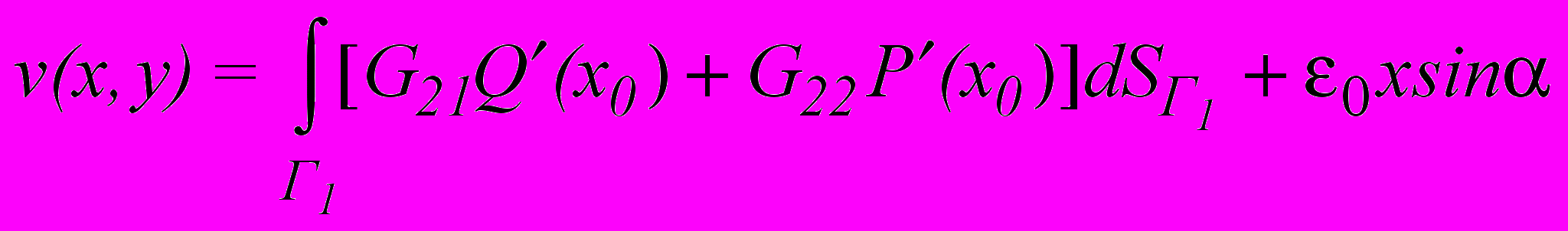которые тождественно удовлетворяют уравнение равновесия. Граничные условия вдоль контура Г приняты в виде :

,

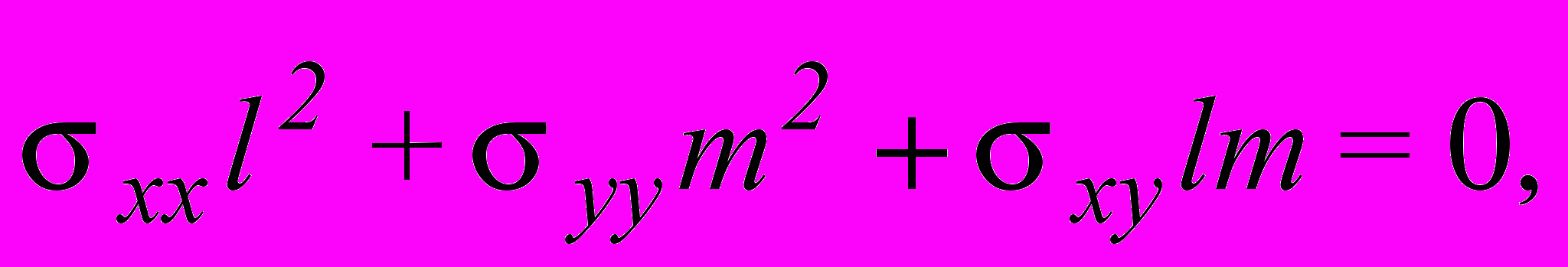
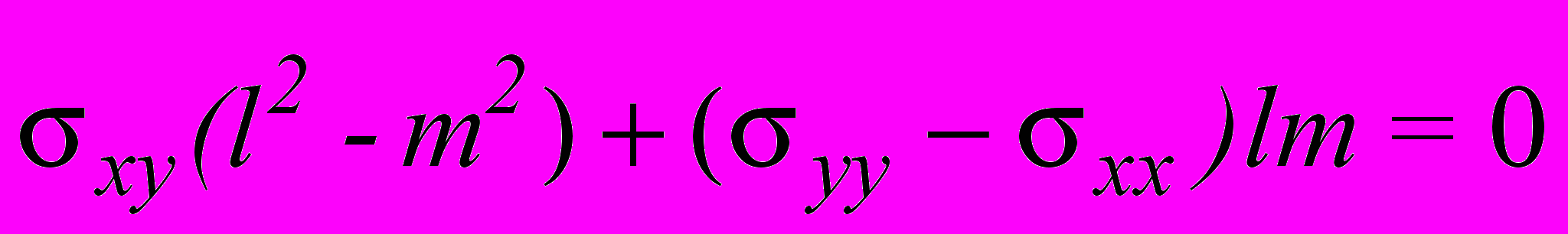где - направляющие нормали,

а,б – длина и ширина концентратора; x,y – Декартовы координаты точки.

Интегралы заменяем соответствующими суммами, взяв достаточное количество слагаемых:





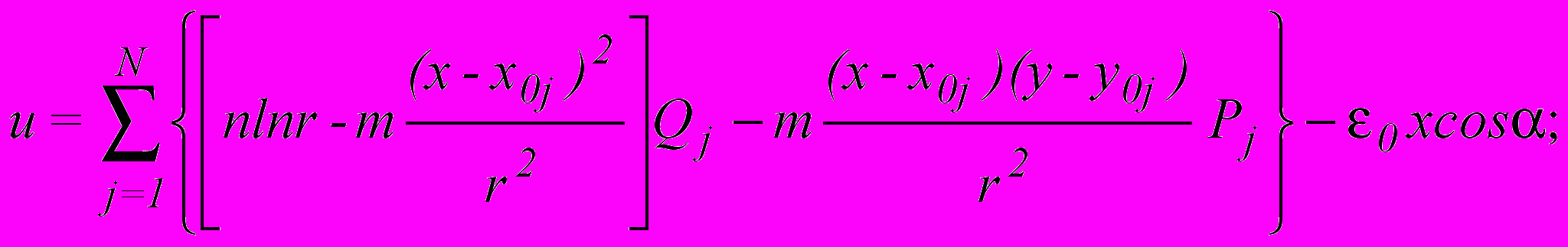
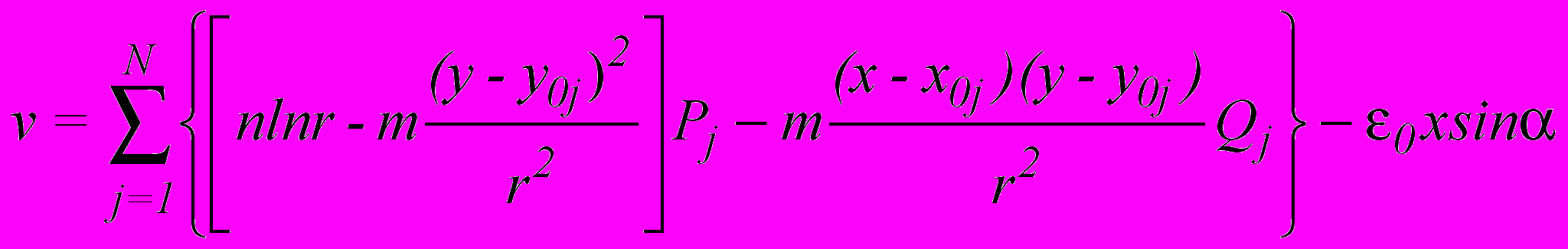
Во все задачи введем следующие безразмерные параметры:



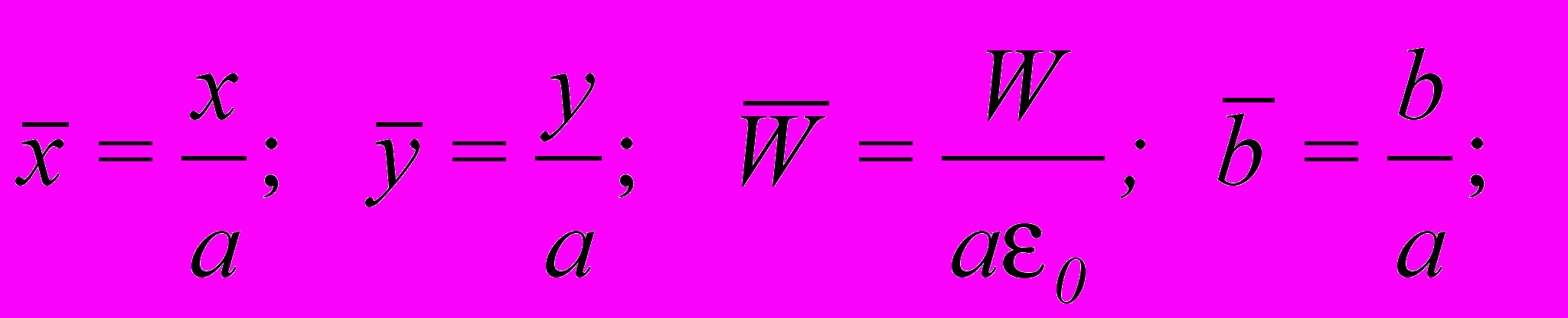
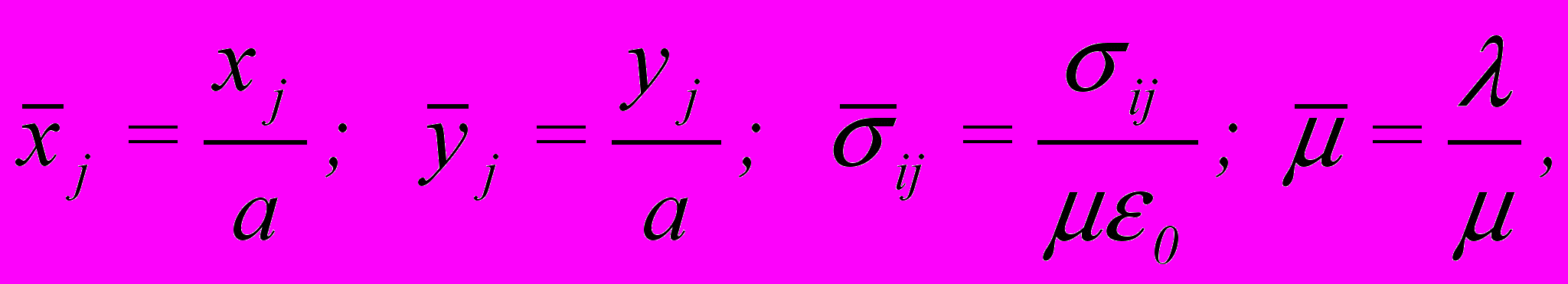
где  ,  - коэффициенты Ламе.

Расчеты проведены при следующих параметрах: число источников (или элементов на границе) 2N=40; ширина границы Г- 2b=200м; длина границы Г- 2a=5000м; модуль Юнга, коэффициент Пуассона и деформации сжатия введены для гранодиорита, определенного экспериментально для Ташкентского сейсмоактивного района в процессе деформирования при высоких давлениях: E=1,29x10⁴МПа;=0,32; ₀=1,16x10^-5; =4,77x10⁴МПа. Коэффициент сухого трения k_s=0,3; угол наклона к горизонтали =70^; центр области D по отношению к исходной системе: 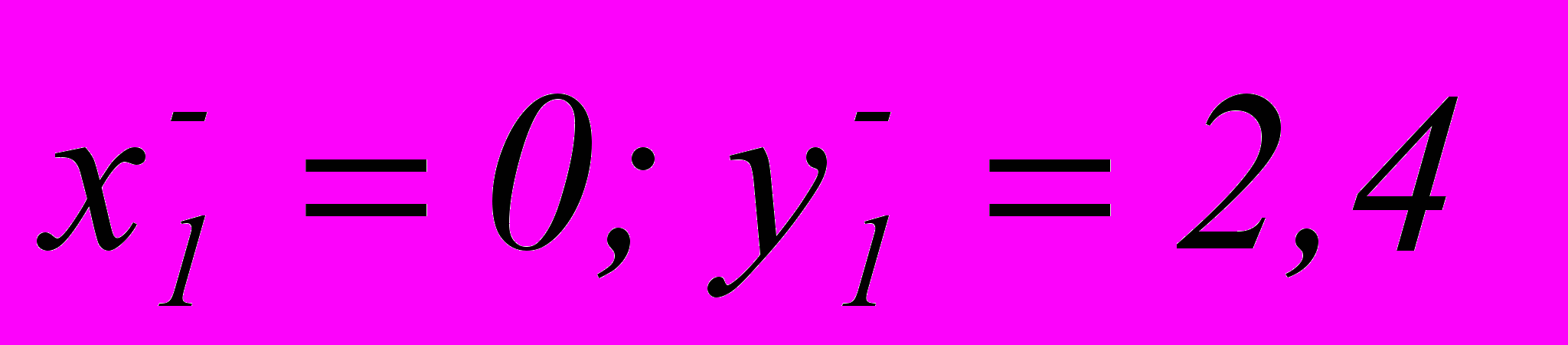. Как показали вычисления, достаточно высокая устойчивость алгоритма получена в пределах 0,068. При более низких значениях b/a устойчивость алгоритма по отношению к исходным данным снижается, а при более высоких счет останавливается из-за уменьшения правой части полученных нами из краевых условий системы уравнений. Пользуясь методом регуляризации, границу устойчивости алгоритмов для разных значений b/a удалось увеличить до 0,021Качественное сравнение картины распределения касательных напряжений с результатами, полученными А.Р.Ярмухамедовым (1988,2003), и другими инструментальными наблюдениями, показало хорошее совпадение. Основные и дополнительные напряжения в решенных нами задачах рассматривались суммарно. Поэтому из общего необходимо вычесть решения для основных напряжений, и тогда определяется решение для дополнительных напряжений. Если длина концентратора, а большая, то смещения поверхности малы, так как сила, необходимая для соприкосновения берегов, например, щели, невелика. Если глубина расположения h=5км, длина, а=1км то в точке x=3км вертикальное перемещение будет v=-0,32мм, а напряжение _xx=-58,8МПа. Исследовано сследовано иенаповедение геоморфологически выраженных на поверхности за современное время перемещений, напряжений и энергии деформаций в области, обусловленной разломом при сценарных нагрузках, и оценено изменение вертикального смещения при различной ориентации разломов к оси сжатия. Получено, что при разных углах падения внутреннего концентратора напряжений к горизонтали угол внутреннего трения будет разным. В пределах упругих констант, свойственных для диоритов, гранодиоритов и ряда кварцевых пород: 0,2<<0,35; 0,2x10⁴МПа⁴МПа; 2,25x10⁴МПа<<1,7x10⁵МПа получены смещения и для тонких включений. Выявлено, что при прочих равных условиях картина смещений свободной поверхности, когда разрывная структура находится строго вертикально или строго горизонтально, не зависит от типа концентратора.

В третьей главе рассматривается модель напряженно-деформированного состояния земной коры при наличии в области нескольких концентраторов напряжений, анализируются параметры палеодислокаций расчетным и эмпирическим способами на примере палеоструктур Узбекистана. Решена квазистатическая задача концентрации напряжений в слоистой структурированной геологической среде с внутренними произвольно расположенными концентраторами, т.е. низкоскоростные зоны с менее плотным заполнителем (элемент наличия разрывных зон), находящиеся в поле действующих упругих (сжимающие или сдвиговые) сил (элемент воздействия тектонических сил) в полупространстве. Выбрав центр координат так, что бы одна ось была направлена по оси концентратора, а остальные - по условию выбора правой системы, задачи сведены к статическим, и решается уравнение Ламе:

()grad(divW)+()²W=0,

где Wu,v,w: u=u(x,y,z); v=v(x,y,z); w=w(x,y,z) - компоненты перемещений;

, - упругие постоянные Ламе. На границах раздела приняты:

⁽ⁱ⁾_nn=⁽ⁱ⁺¹⁾_nn ; Wⁱ₁ = Wⁱ₂ ; ⁽ⁱ⁾_ns=⁽ⁱ⁺¹⁾_ns ; для сочетания групп концентраторов

⁽ⁱ⁾_nn=⁽ⁱ⁺¹⁾_nn ; Wⁱ₁ = Wⁱ₂ ; ⁽ⁱ⁾_nn=k⁽ⁱ⁾_{ns ,} где ⁽ⁱ⁾_jj - jj-тые компоненты напряжений в i-том концентраторе; k-коэффициент Кулона (трение покоя).

_nn= 0 ; _ns =0 - на свободной поверхности и _xx/x=_o._.

Основным напряженным состоянием выбрана область без концентраторов, тогда дополнительные напряжения появляются за счет наличия нескольких разрывов: _pq=⁰_pq+^*_pq+^**_pq ; p~q~ (1,2,3,..). Пользуясь законом Гука и формулами Коши, а также используя аффинное преобразование условий на границе, например, для первого условия, получим:

_i+_icos²²_i+_i+_isin²m²_i -_i^_i m^_i sin2⁽ⁱ⁾_xx - -_i+1+_i+1cos²²_i +

+_i+1+_i+1sin²m²_i-_i+1^_im^_i sin2⁽ⁱ⁺¹⁾_xx +_i+_icos²² _i+_i+_isin²m²_i-

-_i^_im^_isin2⁽ⁱ⁾_yy-_i+1+_i+1cos²²_i+_i+1+_i+1sin²m²_i-_i+1^_im^_I sin2⁽ⁱ⁺¹⁾_yy+2_i (²_i+ m²_i) sin²+^_i m^_i cos2⁽ⁱ⁾_xy -2_i+1(²_i+ m²_i) sin²+

^_i m^_i cos2⁽ⁱ⁺¹⁾_xy = _o 2_i^_i m^_i sin2-_i+_icos²²_i++_i+_isin²m²_i,

где .

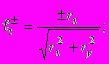
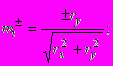
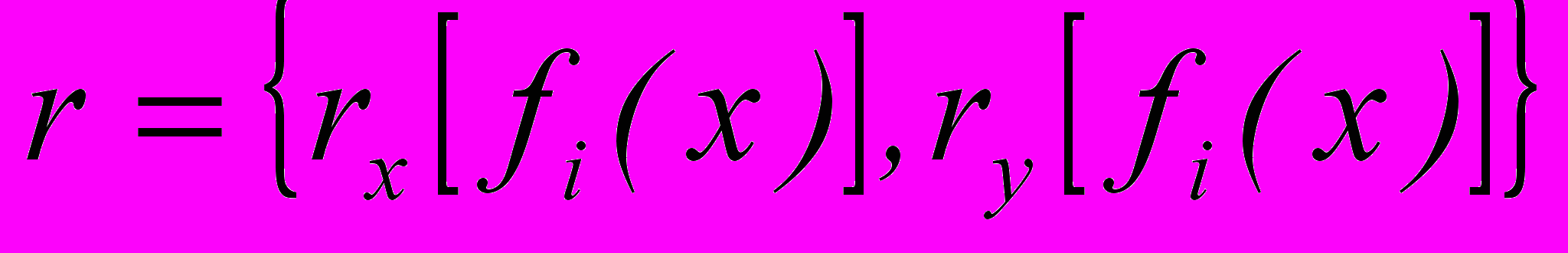Все условия и уравнения сведены к безразмерному виду, в качестве тензора фундаментальных решений использованы: для плоского деформированного состояния тензор Кельвина, полупространства - тензор Миндлина. Условия на границе в частном случае дают решение следующих задач с внутренними концентраторами:

1. При k_s=0, ₂=0, ₂=0, ₀<0 получим задачу о растяжении полуплоскости с произвольно расположенным отверстием.

2. Если k_s=0, ₀>0, то получим задачу о сжатии полуплоскости с произвольно расположенным включением.

3. Если ₁=₂, ₁=_2,, ₀>0,то получим задачу для трещины сдвига, добавляя 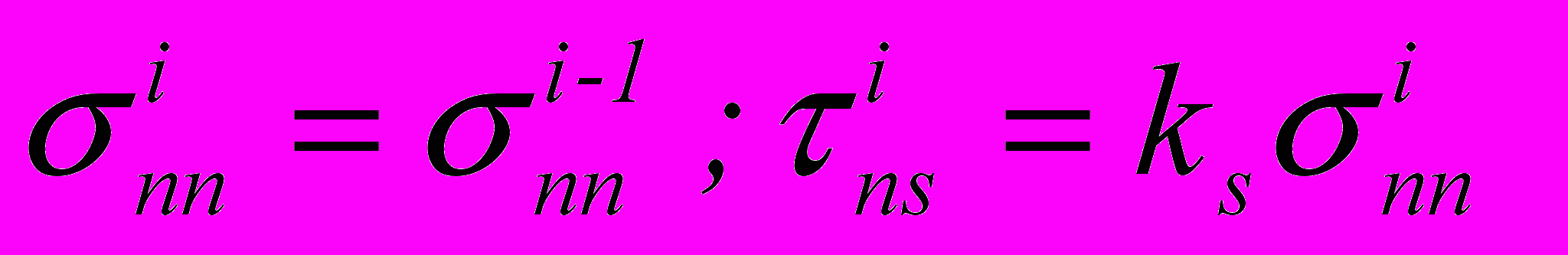на границе двух трещин, ограничивающих полость шириной b.

Исходными данными являются: геометрические параметры (длина - a, глубина - h, малая ширина - b, угол наклона разломов- ,, количество кусков – m, узлов - n и географическое их расположение- ₀₀ (можно в палетке), масштабы представления- 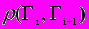; уровень максимальных деформаций в год- ₀; геодезические данные о современном вертикальном движении области-v_0j; максимальное количество землетрясений в этой области - N_max; количественное падение напряжений-_j ; осредненные значения плотности _ср; коэффициента Пуассона-_ср и модуля сдвига или упругости E.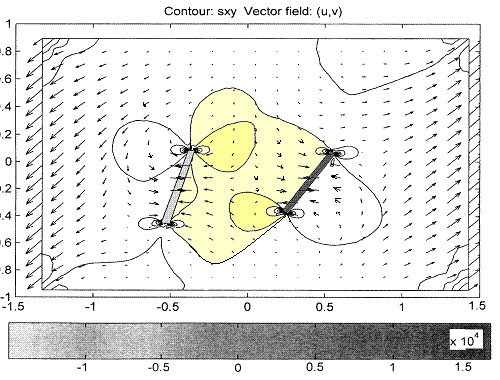




Рис.1 Картина распределения S_xy при малом сжатии-сдвиге


При углах =60^,80^, что близко к реальной структуре, а =30^,45^ и при: =2,72 г/см²; Е=2,28х10⁵МПа; =2,61х10⁵МПа; =8,25х10⁴МПа; ₀=2,55х10^-5; =0,38; k_s1=0,3; k_s2=0,4 рассчитаны поля напряжений вблизи двух структур. Изолиниями выделены области равных напряжений (рис.1). При разных  внутренняя зона закрыта однозначной линией (для ₀=10МПа она равна 0,4МПа, для ₀=20МПа -0,6МПа). Подобная зона появлялась в каждом случае изменения условий залегания концентраторов, когда 50^85^ и 50^85^. Подобный образ изолиний может выделить определенную область, где _внш. >_внут.. Его можно назвать следом, появляющимся за счет наличия разлома.

Выявлено, что модель должна основываться на двух путях приближения к схематизации. Первый условно назван формализованным сейсмотектоническим подходом, при котором деформации сейсмоактивных разломов обусловлены действием основной тектонической силы геоструктур, и описываются известным уравнением квазиравновесия. Второй так же условно можно назвать сейсмофизическим, при котором деформации структур обусловлены, в основном, избыточными напряжениями от точечных источников. Эти понятия условные, но соответствуют тому, что в первом случае, выделяя высоконапряженные активные тектонические разломы за неогенный период, можно определить возможные изменения компонент силовых полей, а во втором, пользуясь суммой действия сил, т.е. избыточных напряжений в локальных участках геоструктур, количественно определить поля вариации напряжений.

Сейсмотектонический подход. В количественной схеме сейсмотектонический процесс является концентрацией избыточных напряжений в зонах активных разломов вследствие современных движений земной коры. Она соответствует задаче определения концентрации напряжений в структурах геологической среды таким образом, чтобы смещения на основании одного пласта могли повлечь за собой деформацию находящихся над ними более мягких напластований, под которыми сосредоточены локальные концентраторы. В первом приближении, эти напластования из-за сложности математических выкладок и решений можем считать однородными в пределах усредненности физических параметров для каждой однородности пластов и структур. Тогда переходим к следующей задаче. Пусть полупространство со структурированными разрывами вертикального или субвертикального расположения находится в предварительно напряженном состоянии, которое вызывает деформации в ближней зоне имеющихся структур. Для определения картины распределения полей напряжений и области максимальных касательных напряжений система координат выбрана так, чтобы область, входящая в схему, например, участок Западного Тянь-Шаня, находилась на первой четверти координатной системы, начало которой установлено в нижнем левом углу схемы.

Сейсмофизический подход полностью основан на данных сейсмометрии, по которым уже определены механизмы очагов землетрясений. Если в предыдущем подходе перемещения выбирались по данным геодезических и тектонических съемок, то здесь на базе эмпирических формул, согласно заданным значениям, по механизму разрыва в очаге и тензору Грина для перемещений u,v,w вычисляются те же напряжения _xy. Решение задачи о сосредоточенной силе в пространстве следующее:







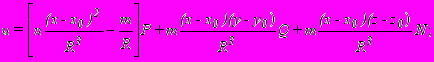
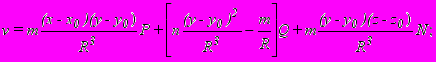
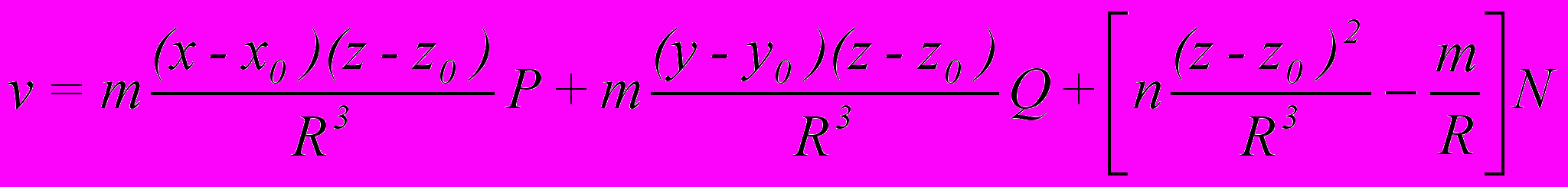
где u,v,w - компоненты вектора перемещений; x ₀ ,y₀ - точки приложения сил (точки сингулярности); P,Q,N - соответствующие компоненты силы по направлениям осей x,y,z ,

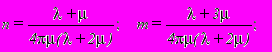размерность P,Q,N- кГ.

Пусть x_i,y_i,z_i соответствуют точке подвижки от исходной по i-той площадке разрыва с падением  . Тогда функция _ij(u,v,w), удовлетворяющая уравнение Ламе для пространства при определенных P,Q,N и соответствующем _i, отображает картину этого распределения. При этом можем предположить, что точки x₀,y₀,z₀ и x_0j,y_0j,z_0j приложения сосредоточенной силы находятся в середине разрыва. Например, для точки приложения силы в разрыве (x₀₁,y₀₁,z₀₁) его -тый конец является точкой вычисления перемещений по нему. Ориентацию v_i0 по отношению к u,v,w в пространстве определяем, пользуясь формулами перехода 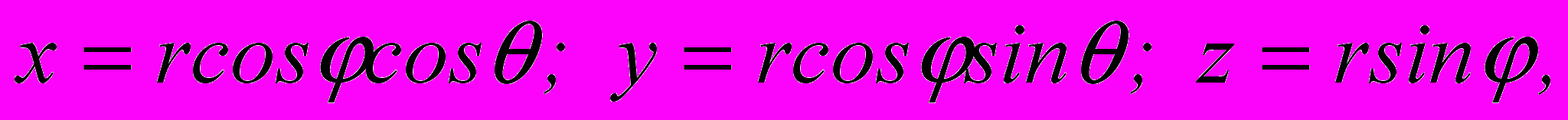а также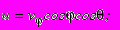

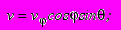
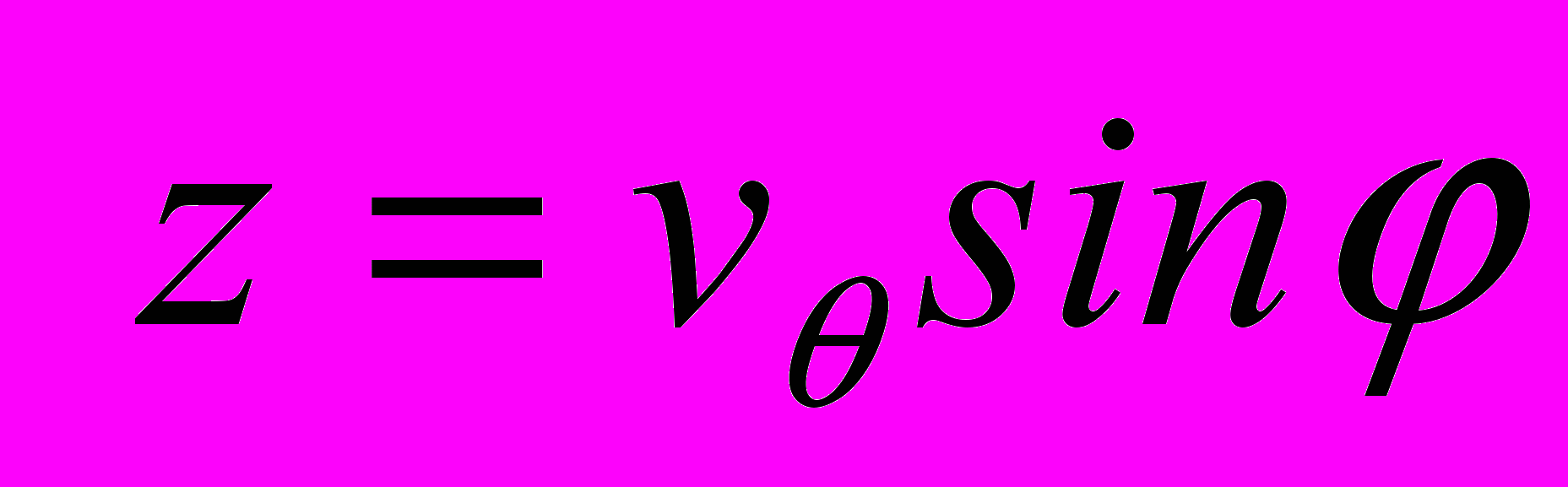. Отметим, что, если значения ₀, можно найти из построенных механизмов очагов или по данным полевых тектонофизических съемок, то вертикальное перемещение - по вычисленным интегралам. Пользуясь _xy =E_xy и подставив соответствующие выражения из решения математической модели для произвольного внутреннего концентратора, вычитая из него решение для области без концентратора, получим разницу двух состояний. Разница (или вариация) двух напряженных состояний в приразломных зонах будет:



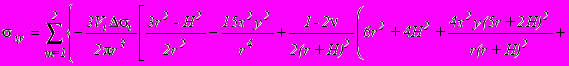
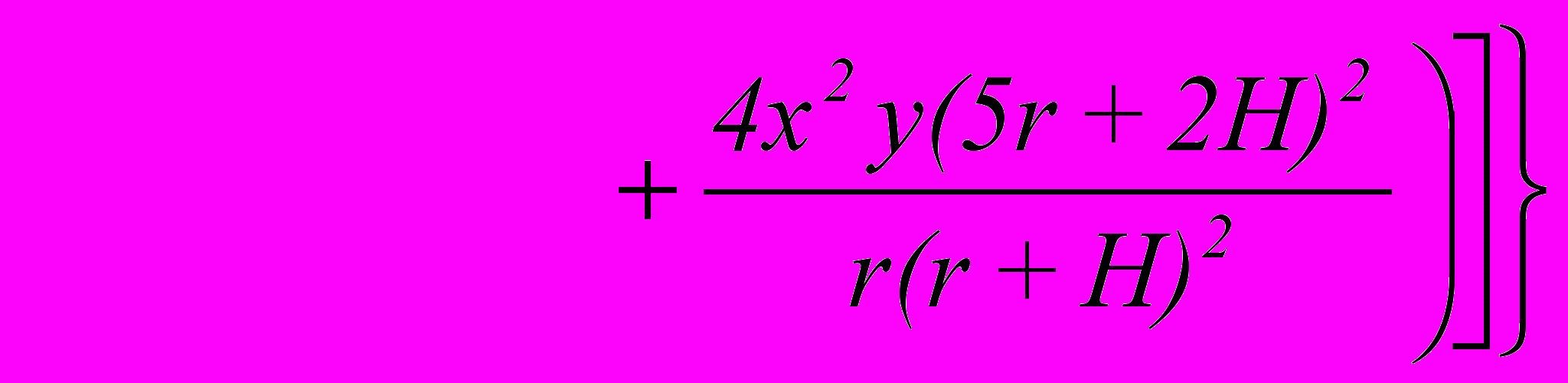где V- объем очаговой зоны равен 10^1,24-4,47M км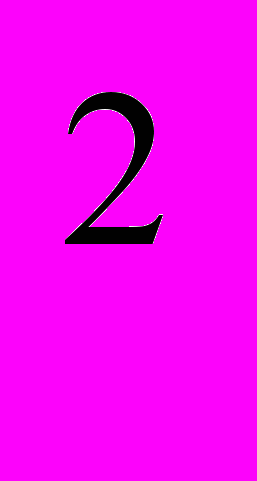 (по Ю.В.Ризниченко), ₁=k₀₁₀ - падение напряжения (разница двух упругих состояний при наличии первого разрыва), где k_s1~tg; ₂=k₀₂₀- падение напряжения при наличии второго разрыва, где k_s2~tg. Пользуясь выражениями ₀= 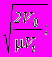V₀=10^8+1,1M; lg=0,19М+0,36 и подставив их вместо _xy,  и ₀ с учетом 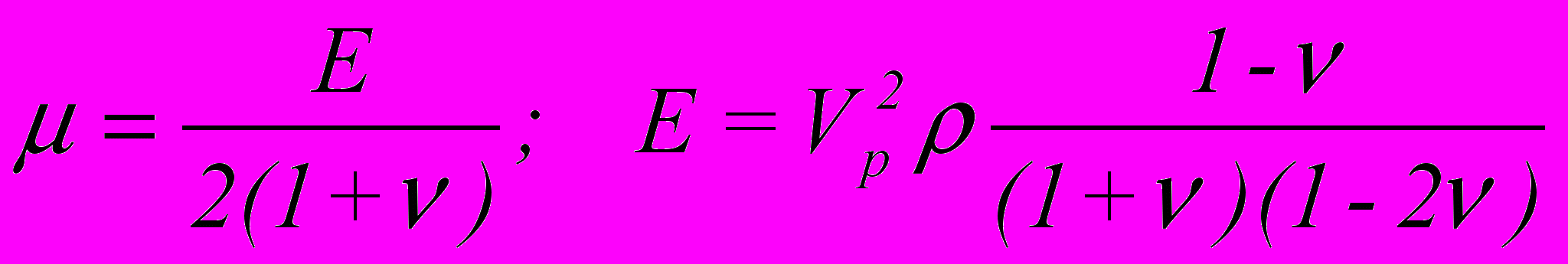, а также при осредненных значениях =0,25; =2,6 г/cm; а/b=35; c/d=25, получим для магнитуды выражение, связывающее М с деформацией в очаге ₀ и падающим напряжением ₀:

М=11,4+2,37 lg₀+1,54 lg₀.

Разделив известное среднее значение смещения поверхности Тянь-шаньского орогена за современный период на толщину земной коры, можно приблизительно оценить верхнюю границу средней деформации. Средний уровень сейсмической активизации Восточного Узбекистана, по данным Р.Н.Ибрагимова, И.Б.Яковлевой (1983, 1994), составляет от 20 до 50 лет (среднее 30). Поэтому ₀=_тект.х30 будет тем вероятным значением вариации деформации, при котором реализуется соответствующий процесс с падением напряжений в пределах той длины разрыва, критические размеры которой соответствовали бы длине внутреннего концентратора при этом же значении деформации (при прочих равных условиях).

Рассмотрим район горных сооружений Тамдытау и Джетымтау (Центральный Кызылкум), в которых интенсивно развиваются гигантские трещины. Общая длина этих трещин L=77км, средняя ширина открытой части D₀=3м. Глубина известна по инструментальным наблюдениям - H=110м. Согласно мировым эмпирическим формулам, вычисленные значения магнитуды по разным выражениям соответствуют значению глубины раскрывшейся трещины H : М=8,3; по значению ширины раскрывшейся трещины D₀: М=7,8; по значению длины раскрывшейся трещины L: М=7,97. Принимая за среднее из них М=8 и используя эмпирические зависимости, получим радиус зоны существенных деформаций r=53,6км. Являются ли эти гигантские трещины следом палеоземлетрясений с вычисленной магнитудой, вопрос спорный. Следует отметить, что при исследовании динамики земной коры В.И.Уломовым (1976) допущено предположение о существовании сильных палеоземлетрясений в Западном Узбекистане. С другой стороны, в 170 км от этого участка произошли три сильнейших Газлийских землетрясения 1976,1984гг. с М7 (Газлийские землетрясения…,1986). Это подтверждает возможность существования в этом районе палеоземлетрясений с указанной магнитудой. В таком предположении, смещение на поверхности Земли d₀=149,95см при средней ширине раскрывшейся части трещины на поверхности будет D₀=250см. Такие перемещения земной поверхности данного района не очень спорны. По данным геодезических съемок, за последние 40 лет район поднялся на 40-50см. Скорость движения, по геодинамическим данным, превышает 10-20мм/год (Д.Х.Якубов,1990) .

А.К.Ходжаев (1985), изучая палеосейсмодислокации некоторых участков Восточного Узбекистана, допускает возможность существования исторических палеоземлетрясений М >7 и более в районе Чаткало-Кураминской горной зоны (табл.1). По палеотектоническим данным можно рассчитать вероятную магнитуду на основе выявленных нами зависимостей. Например, для сейсмогенной структуры Сандалаш градиент скоростей новейших тектонических движений составляют v=0,7-1,010^-8год^-1, максимальные относительные вертикальные смещения превышают 4,5м. Ширина достигает 5-8м, видимая протяженность - 0,7-0,9км.

Область разброса палеосейсмодислокаций - приблизительно в пределах 5км. Тип палеосейсмоструктуры - сейсмотектонический. По тем же данным, предполагаемая максимальная величина магнитуды, образовавшей эти палеосейсмодислокации, М=7. Нами проведены расчеты и сопоставление результатов на основе этих данных, пользуясь вышеизложенными математическими моделями и эмпирическими формулами для каждой структуры отдельно. В табл.1 показаны параметры палеосейсмоструктур и результаты расчетов возможных магнитуд палеоземлетрясений по этим параметрам.

Таблица 1

Данные о палеосейсмодислокациях, сопоставление значений

параметров и магнитуд по ним

Палеоструктура	Сандалаш	Терс	Кальтагол	Карабугуз	Кугала
Деформация о х10-5	1,50	0,83	2,7	1,30	1,3 0
Сброс напряжений в бар.	90,0	90,0	90,0	95,0	95,0
Глуб. разрыва h, м	50,0	50,0	25,0	80,0	50,0
Магнитуда по глубине	7,56	7,56	7,10	7,78	7,56
Ширина разрыва Do , см	80,0	35,0	80,0		50,0
Магнитуда по ширине Do	7,39	7,57	7,35		7,45
Амплитуда смещения do	45,0	25,0	80,0	40,0	40,0
Магнитуда по смещению	6,72	6,39	7,05	6,62	7,96
Длины глав.разрыв. L, км	5,00	5,00	25,0	9,00	15,0
Магнитуда по L	5,99	5,99	7,16	6,42	6,79
Зона деформации r , км	25,0	15,0	35,0	35,0	50,0
Магнитуда по r	6,73	6,29	7,02	7,02	7,33
Ср.магнитуда по модели	6,86	6,80	6,92	7,11	7,11
Ср.магнитуда по палеоданным (А.К.Ходжаев)	7,00	7,00	6,50	7,20	7,20
Общее среднее	6,91	6,85	6,85	7,10	7,24

Примечание: деформация lg_о=0,157M-4,512;

сброс напряжений: lg=0,649M-1,539;

М- по глубине M_h=6+0,22xh^1/2; М- по ширине M_D=8,5-0,6xlgD_o;

М- по смещению M_d=4,58+1,3xlgd_o; М- по длине M_L=4,83+1,67xlgL

М- по зоне max.деформаций M_r=3,94+2,0xlg2r.

Сравнивая полученные результаты с теоретическими, можно убедиться, что устойчивость результатов расчета даже с привлечением эмпирических формул, достаточно высока. Магнитуды предполагаемых палеоземлетрясений, рассчитанные на основе определенных теоретических моделей, сейсмотектонических исследований и эмпирических формул, достаточно хорошо согласуются.