Электромагнетизм. Переменный ток. Колебательный контур
| Вид материала | Закон |
- 46. Переменный ток, 62.84kb.
- Научно-производственное предприятие зао «нпп импалс» контур®, 156.93kb.
- Самостоятельная работа «Переменный электрический ток» Вариант 1 Когда магнитное поле, 29.04kb.
- Вопросы по дисциплине отц. Третий семестр, 30.78kb.
- Лабораторная работа 7 Изучение регенеративного радиоприемника, 92.31kb.
- Переходные процессы в линейных электрических цепях, 378.64kb.
- Программа вступительного экзамена в магистратуру по направлению подготовки 010800., 64.76kb.
- Вынужденные электромагнитные колебания, 39.6kb.
- Курсовая работа по электронике «lc -генератор с обратной связью», 106.97kb.
- Переменный электрический ток начальный уровень, 51.49kb.
Электромагнетизм. Переменный ток. Колебательный контур
1. Электромагнитная индукция.
- В 1831 году Майкл Фарадей установил, что электрический ток может возникать в контуре при любом изменении магнитного потока, пронизывающего контур – открыто явление электромагнитной индукции – явление возникновения электрического тока в замкнутом контуре при изменении потока магнитной индукции через поверхность, ограниченную эти контуром. Этот ток называется индукционным.
- З
 акон Фарадея-Максвелла. ЭДС электромагнитной индукции в замкнутом контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром. ξ = –∆Ф/ ∆t = – Фۥ = – L I ۥ. , ξ = –Ф’ = ξmax sinωt = BSωsinωt
акон Фарадея-Максвелла. ЭДС электромагнитной индукции в замкнутом контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром. ξ = –∆Ф/ ∆t = – Фۥ = – L I ۥ. , ξ = –Ф’ = ξmax sinωt = BSωsinωt
- Правило Ленца определяет направление индукционного тока. Индукционный ток в контуре имеет такое направление, что созданный им магнитный поток через поверхность, ограниченную контуром, препятствует изменению магнитного потока, вызвавшего этот ток.
- Способы индуцирования тока. Самоиндукция.
- Опыты Фарадея. При относительном движении магнита (электромагнита) и катушки возникает индукционный ток, а также при изменении магнитного потока через площадь ограниченную контуром.
- В проводнике, движущемся в магнитном поле под действием силы Лоренца, происходит разделение разноимённых зарядов и на концах проводника возникает разность потенциалов или ЭДС индукции ξ = U = υB┴ l
- Т
 оки Фуко. В массивных проводниках, движущихся в магнитных полях, или находящихся в переменном магнитном поле возникают вихревые токи – токи Фуко. При вращении диска вокруг оси параллельной линиям магнитной индукции возникает ЭДС индукции ξ = BSν, где ν частота вращения радиус-вектора диска, замкнутого на резистор или гальванометр.
оки Фуко. В массивных проводниках, движущихся в магнитных полях, или находящихся в переменном магнитном поле возникают вихревые токи – токи Фуко. При вращении диска вокруг оси параллельной линиям магнитной индукции возникает ЭДС индукции ξ = BSν, где ν частота вращения радиус-вектора диска, замкнутого на резистор или гальванометр.
- Опыты Генри. ЭДС индукции возникает в катушке при изменении тока, протекающего по катушке – самоиндукция. Быстрое изменение тока происходит при замыкании (направление индукционного тока совпадает с направлением тока в контуре) и размыкании (направление индукционного тока противоположно направлению тока в контуре) цепи. ε = –L∆I / ∆t, где ∆t – время релаксации (время возрастания тока в контуре при замыкании, или время убывания тока при размыкании).
- Индукционный ток возникает при движении в магнитном поле проводника, концы которого замкнуты.
- Учёт самоиндукции. В зависимости от индуктивности контура ЭДС самоиндукции может быть очень большой, даже превышать ЭДС источника тока (горит обмотка двигателей, перегорают лампы). Самоиндукция задерживает увеличение и уменьшение тока в электрических схемах и линиях передачи сигналов, приводя к искажению передаваемых сигналов. Явление самоиндукция подобно явлению инерции в механике.
3. Использование электромагнитной индукции.
- Генерирование переменного тока. При изменении магнитного потока, пронизывающего замкнутый контур, в последнем возникает ЭДС индукции. При вращении контура в магнитном поле изменение магнитного потока через контур будет гармоническим Ф = ВΔScosωt, ξ = –Ф’ = ξimax sinωt. Зависимость ЭДС от времени является гармонической. В мощных генераторах переменного тока контуры, в которых возникает ЭДС индукции, расположены на корпусе, а многополюсной электромагнит является ротором, который, вращаясь, создаёт переменное магнитное поле. Наличие N пар полюсов у ротора позволяет в N раз уменьшить частоту вращения ротора – ω. Частота переменного тока, используемого в промышленности и в быту 50 Гц, напряжение для бытовых целей 220 В.
- Трансформатор – устройство, состоящее из двух и более катушек на общем сердечнике. Применяется для повышения или понижения переменного напряжения. При изменении тока в одной из катушек, магнитный поток, возникающий в сердечнике возбуждает ЭДС индукции в каждом витке. Результирующая ЭДС в катушках определяется числом витков в них ε = –NФ,ۥ. При малом сопротивлении обмоток ε = U. Коэффициент трансформации – величина, равная отношению напряжений в первичной и вторичной катушках. k = U1/U2 =N1/N2.
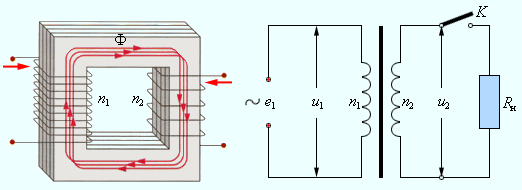 Повышающий трансформатор k < 1, и понижающий трансформатор k > 1. При повышение напряжения во столько же раз уменьшается сила тока, что приводит к уменьшению потерь мощности.
Повышающий трансформатор k < 1, и понижающий трансформатор k > 1. При повышение напряжения во столько же раз уменьшается сила тока, что приводит к уменьшению потерь мощности.- Индукционные детекторы позволяют находить металлические предметы. Например, в аэропортах детектор металла фиксирует поля индукционных токов в металлах.
- Отталкивание сверхпроводящих катушек с током, размещённых на дне вагона и катушек на полотне дороге приподнимает вагон над землёй в поездах на магнитной подушке.
- Электроплавильные печи и микроволновые печи работают благодаря индукционным токам (токам Фуко).
- Запись и воспроизведение записей с магнитных лент также осуществляется при помощи индукционных токов: переменное магнитное поле в записывающей головке ориентирует домены на магнитной ленте, а переменное поле магнитной ленты возбуждает переменные индукционные токи в головке воспроизведения.
4. Переменный ток
- Переменное напряжение, получаемое потребителем от электростанции изменяется с течением времени по гармоническому закону u = Umax cos( ωt + φо ), где u – мгновенное значение напряжения, Umax – амплитуда напряжения, (ωt + φо) – фаза колебания напряжения, φо – начальная фаза колебания. В цепь переменного тока могут быть подключены резисторы, катушки индуктивности, конденсаторы и т. д.
- А
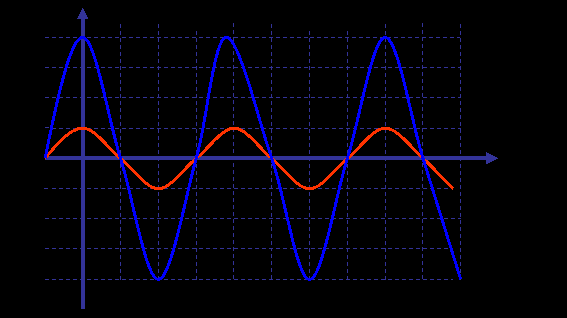
 ктивное сопротивление – элемент электрической цепи (резистор), в которой электрическая энергия преобразуется во внутреннюю. Колебания тока и напряжения на резисторе u = Umax cos( ωt ), i = Imax cos ( ωt ) совпадают по фазе. . Активное сопротивление вычисляется по формуле R =ρl/S.
ктивное сопротивление – элемент электрической цепи (резистор), в которой электрическая энергия преобразуется во внутреннюю. Колебания тока и напряжения на резисторе u = Umax cos( ωt ), i = Imax cos ( ωt ) совпадают по фазе. . Активное сопротивление вычисляется по формуле R =ρl/S.
- Д
 ля измерения переменного напряжения и переменного тока используются специальные приборы, измеряющие действующие значания силы тоа и напряжения. Сила переменного тока 1 А – сила тока, веделяющего в проводнике такое же количество теплоты, что и постоянный ток 1А за тот же промежуток времени. Действующее значение силы переменного тока равно силе постоянного тока, при котором в проводнике выделяется такое же количество теплоты, что и при переменном токе за тот же промежуток времени. Iд = Im/√2, Uд = Um/√2
ля измерения переменного напряжения и переменного тока используются специальные приборы, измеряющие действующие значания силы тоа и напряжения. Сила переменного тока 1 А – сила тока, веделяющего в проводнике такое же количество теплоты, что и постоянный ток 1А за тот же промежуток времени. Действующее значение силы переменного тока равно силе постоянного тока, при котором в проводнике выделяется такое же количество теплоты, что и при переменном токе за тот же промежуток времени. Iд = Im/√2, Uд = Um/√2
-
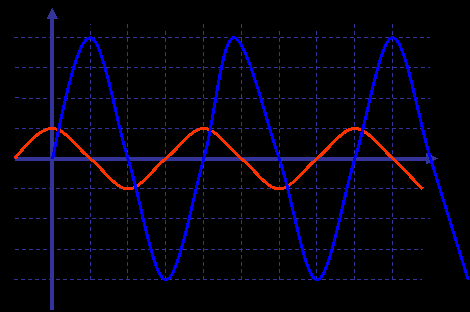
 Конденсатор в цепи переменного тока. Колебания силы тока опережают колебания напряжения на π/2, т.к. напряжение на обкладках конденсатора создаётся зарядами, перенесёнными током , i = Imax cos (ωt + π/2), u = Umax cos( ωt). Сопротивление конденсатора называется емкостным сопротивлением ХС = 1/ωC.
Конденсатор в цепи переменного тока. Колебания силы тока опережают колебания напряжения на π/2, т.к. напряжение на обкладках конденсатора создаётся зарядами, перенесёнными током , i = Imax cos (ωt + π/2), u = Umax cos( ωt). Сопротивление конденсатора называется емкостным сопротивлением ХС = 1/ωC.
-

 Катушка индуктивности в цепи переменного тока.
Катушка индуктивности в цепи переменного тока.
Колебания тока отстают от колебаний напряжения на π/2, из-за ЭДС самоиндукции i = Imax cos (ωt – π/2), u = Umax cos( ωt). Сопротивление катушки – индуктивное сопротивление XL= ωL.
Сопротивление катушки и конденсатора называют реактивным сопротивлением.
- Мощность переменного тока определяется произведением действующих значений силы тока и напряжения. P = Iд Uд, P = Im Um /2.
5
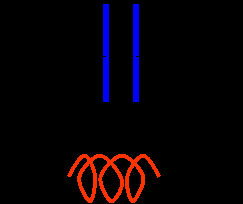 . Колебательный контур
. Колебательный контур- Колебательный контур – цепь, состоящая из последовательно соединённых катушки и конденсатора. Если конденсатор сначала зарядить, а потом соединить с катушкой, то в контуре возникнут свободные электромагнитные колебания – колебания тока, напряжения в контуре.
- 1
 -ю четверть периода конденсатор разряжается до 0, 2-ю четверть периода конденсатор перезаряжается благодаря индуктивности катушки, 3-ю четверть периода перезаряженный конденсатор разряжается до 0, 4-ю четверть периода он снова перезаряжается. Колебания тока и напряжения являются гармоническим и описываются уравнениями i = Imax cos (ωt ), u = Umax cos( ωt + φ),
-ю четверть периода конденсатор разряжается до 0, 2-ю четверть периода конденсатор перезаряжается благодаря индуктивности катушки, 3-ю четверть периода перезаряженный конденсатор разряжается до 0, 4-ю четверть периода он снова перезаряжается. Колебания тока и напряжения являются гармоническим и описываются уравнениями i = Imax cos (ωt ), u = Umax cos( ωt + φ),
г
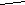 де φ – разность фаз между колебаниями тока и напряжения.
де φ – разность фаз между колебаниями тока и напряжения.- Период колебаний в контуре определяется по формуле Томсона T=2π√LC.
 Следовательно, частота собственных колебаний контура ω=1/√LC.
Следовательно, частота собственных колебаний контура ω=1/√LC.- Э
 нергия контура состоит из энергии электрического поля конденсатора и WC=q2/2C и энергии магнитного поля катушки WL = Li2/2. Полная энергия контура равна сумме энергий на конденсаторе и на катушке, а также равна макс энергии конденсатора или макс. энергии поля катушки W = Q2/2C = LIm2/2.. W = q2/2C + Li2/2 – энергия контура в данный момент времени. Если активное сопротивление контура равно 0, то колебания будут незатухающими, и энергия контура не изменяется q2/2C.+ Li2/2=const Производная от постоянной величины =0. (Li2/2.+q2/2C)I=0 и получаем уравнение электромагнитных колебаний Lq//+q/C =0 q// =-q/LC. ω=1/√LC. Следовательно. q// =- ω2 q.
нергия контура состоит из энергии электрического поля конденсатора и WC=q2/2C и энергии магнитного поля катушки WL = Li2/2. Полная энергия контура равна сумме энергий на конденсаторе и на катушке, а также равна макс энергии конденсатора или макс. энергии поля катушки W = Q2/2C = LIm2/2.. W = q2/2C + Li2/2 – энергия контура в данный момент времени. Если активное сопротивление контура равно 0, то колебания будут незатухающими, и энергия контура не изменяется q2/2C.+ Li2/2=const Производная от постоянной величины =0. (Li2/2.+q2/2C)I=0 и получаем уравнение электромагнитных колебаний Lq//+q/C =0 q// =-q/LC. ω=1/√LC. Следовательно. q// =- ω2 q.
- Чтобы найти полное сопротивление цепи нужно, согласно закона Ома для участка цепи, макс. значение напряжения разделить на макс. значение силы тока Z = Um/Im Мгновенное значение приложенного напряжения равно сумме мгновенных значений напряжений на последовательно включённых элементах цепи. В реальной цепи активное сопротивление не равно 0, а это аналогично последовательно включённому резистору.
- С
 ледовательно u = uR + uC + uL. uR = URm cos( ωt ), URm = Im R, uC = UСm cos( ωt – π/2 ), UCm = Im XC,, uL = ULm cos( ωt + π/2), ULm= Im XL где ω циклическая частота вынужденных колебаний силы тока. Из векторной диаграммы напряжений Um2 = UmR2 + (UmL - UmC) 2, следовательно Z = Um/Im= √ R2+ ( XL – XC )2. Im = Um/ Z – закон Ома для цепи переменного тока
ледовательно u = uR + uC + uL. uR = URm cos( ωt ), URm = Im R, uC = UСm cos( ωt – π/2 ), UCm = Im XC,, uL = ULm cos( ωt + π/2), ULm= Im XL где ω циклическая частота вынужденных колебаний силы тока. Из векторной диаграммы напряжений Um2 = UmR2 + (UmL - UmC) 2, следовательно Z = Um/Im= √ R2+ ( XL – XC )2. Im = Um/ Z – закон Ома для цепи переменного тока
- Из формулы сопротивления видно, что максимальная сила тока в контуре будет при XL = XC , ωL = 1/ωC.
ω
 2= 1/CL, то есть при совпадении частоты вынужденных колебаний тока с частотой свободных колебаний контура.
2= 1/CL, то есть при совпадении частоты вынужденных колебаний тока с частотой свободных колебаний контура.Резкое возрастание амплитуды колебаний тока в контуре при совпадении частоты вынужденных колебаний с частотой собственных колебаний в контуре называется резонансом. Чем меньше активное сопротивление контура, тем круче резонансная кривая. Явление резонанса широко используется в радиотехнике в схемах настройки радиоприёмников, усилителей, генераторов высокочастотных колебаний.
6. Выпрямление переменного тока.
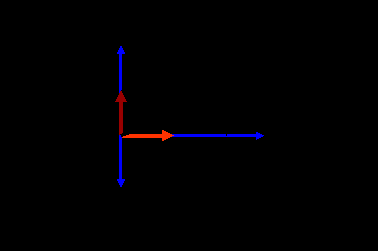
- Д
 ля выпрямления переменного тока используют полупроводниковый диод – элемент электрической системы, содержащий р – п-переход и два вывода для включения в электрическую цепь. р – п-переход обладает односторонней проводимостью. Выпрямитель с одним диодом даёт однополупериодное выпрямление тока. Схема, включающая четыре диода, даёт двухполупериодное выпрямление тока.
ля выпрямления переменного тока используют полупроводниковый диод – элемент электрической системы, содержащий р – п-переход и два вывода для включения в электрическую цепь. р – п-переход обладает односторонней проводимостью. Выпрямитель с одним диодом даёт однополупериодное выпрямление тока. Схема, включающая четыре диода, даёт двухполупериодное выпрямление тока.
Формулы по теме «Электромагнетизм. Переменный ток»
- ξ= U = υB┴ l - ЭДС индукции в движущихся проводниках.
- ξ = BSν - ЭДС индукции возникающая в диске, вращающемся в магнитном поле (ось вращения диска параллельна индукции магнитного поля).
- ξ = –∆Ф/ ∆t = – L∆ I/∆t - закон электромагнитной индукции.
- ξ = –Ф’ = ξmax sinωt = BSωsinωt – ЭДС в рамке, вращающейся в магнитном поле
- ξmax = BSω – максимальная ЭДС в рамке, вращающейся в магнитном поле
- ξmax = nBSω – максимальная ЭДС в контуре из n витков.
- k = U1/U2 =N1/N2 – коэффициент трансформации.
- u = Umax cos( ωt + φо ), i = Imax cos (ωt ) – колебания напряжения и тока в цепи переменного тока
-

 T=2π√LС - формула Томсона
T=2π√LС - формула Томсона
- ω=1/√LC – циклическая частота собственных колебаний контура
- W = Cu2/2 + Li2/2, W = CUm2/2 = LIm2/2.– энергия контура
- R =ρl/S –сопротивление резистора
- ХС = 1/ωC – сопротивление конденсатора
-
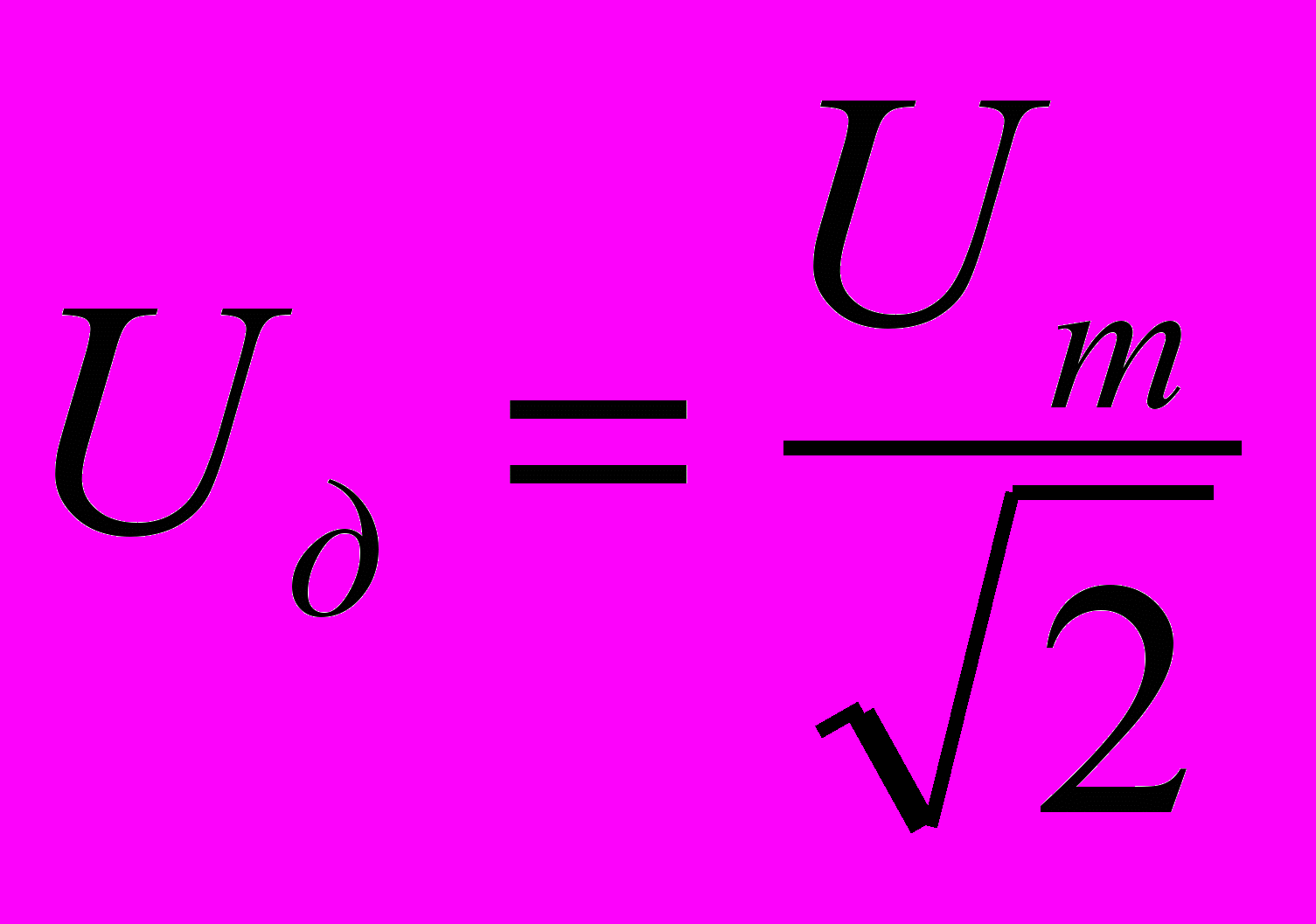
 XL= ωL – сопротивление катушки
XL= ωL – сопротивление катушки
- Действующие значения силы тока и напряжения
- P = Iд Uд, P = Im Um /2 – мощность переменного тока.

- Z = Um /Im= √ R2+ ( XL – XC )2 – полное сопротивление контура
- Im = Um / Z – закон Ома для цепи переменного тока
- XL = XC , ωL = 1/ωC – условие резонанса в цепях переменного тока.

Решение задач:
З
 адача 1. Колебательный контур настроен на частоту 10 кгц. Максимальное напряжение на обкладках конденсатора 3 В, а максимальная энергия поля конденсатора 90 мкДж. Найти электроёмкость конденсатора, индуктивность катушки. Какой максимальный ток проходит через катушку?
адача 1. Колебательный контур настроен на частоту 10 кгц. Максимальное напряжение на обкладках конденсатора 3 В, а максимальная энергия поля конденсатора 90 мкДж. Найти электроёмкость конденсатора, индуктивность катушки. Какой максимальный ток проходит через катушку?Решение. WC=Cu2/2, C = 2W/U2 =2·10-5Ф. ν = 1/Т , T=2π√LC , L = 1/ ν2 π2 C = 0,125мГн.
WCm = WLm, , Im2 = CUm2/ L = 1,44 A2, Im = 1,2 A.
Задача 2. Коэффициент трансформации равен 10. На первичной катушке колебания напряжения тока описываются уравнением u = 180 cos100πt. Написать уравнение колебания напряжения на вторичной катушке. Какой характер имеют потери мощности в трансформаторе? Какая обмотка должна иметь большее сечение и почему?
Р
 ешение. Um1 =180 В , Um2 = 180/10 =18 В, u2 = 18 cos100πt. Потери мощности на обмотке тепловые. Вторая катушка должна иметь большее сечение, потому что по ней протекает большой ток.
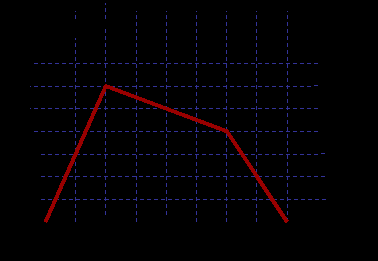
ешение. Um1 =180 В , Um2 = 180/10 =18 В, u2 = 18 cos100πt. Потери мощности на обмотке тепловые. Вторая катушка должна иметь большее сечение, потому что по ней протекает большой ток.Задача 3. Сила тока, протекающая через катушку индуктивностью L = 6 Гн. изменяется со временем как показано на рисунке. Найти ЭДС индукции, возникающей в катушке в момент времени 1 сек, 3 сек, 7сек.
Решение. ε1 = –L∆I / ∆t = - 6Гн·6А/2с = 18В, ε2 = 3В, ε2 = 12В.
З
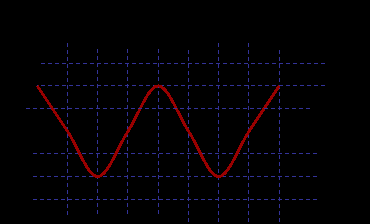 адача 4. По графику зависимости напряжения от времени на резисторе сопротивлением 100 Ом найти максимальное значение напряжения и силы тока на резисторе, среднюю мощность, выделяемую током на резисторе. Написать уравнения зависимости напряжения и силы тока от времени на резисторе.
адача 4. По графику зависимости напряжения от времени на резисторе сопротивлением 100 Ом найти максимальное значение напряжения и силы тока на резисторе, среднюю мощность, выделяемую током на резисторе. Написать уравнения зависимости напряжения и силы тока от времени на резисторе. Решение. Um = 50 В, T = 0,8 c, Im = Um/R = 0,5 A, Im = Um/R=0,5 A, P = Iд Uд , P = Im Um /2 = Um2/2R = 12,5 Вт. ω =2π/T =2π/0,8 =2,5π с -1
u = Umax cos( ωt ) = 50 cos( 2,5 π t ), i = Imax cos ( ωt ) =0,5 cos( 2,5 π t ).

Задача.5. Магнитный поток, пронизывающий рамку меняется по закону Ф = 0,01 sin 10πt. Найти максимальное значение магнитного потока и частоту вращения рамки. Написать формулу зависимости ЭДС от времени. Вычислить значение ЭДС через 0,02 сек от начала отсчёта времени.
Решение. Фм = 0,01 Вб. ω = 10 π с -1. ν = ω/2π = 5 с -1.
ε = –∆Ф/ ∆t = – Фۥ= – 10·0,01cos10πt = – 0,314 cos10π0,02. ε = –0,314cos18= –0,314·0,95=0,3 В.
Задача 6. В однородном магнитном поле с индукцией 0, 1 Тл вращается проводящая рамка площадью 500см2. Частота вращения 20 Гц. Амплитуда ЭДС, возникающей в рамке 63 В. Найти максимальный поток, пронизывающий рамку. Сколько витков имеет рамка? Написать формулы зависимости магнитного потока и ЭДС от времени.
Решение. Фm = BS = 0,1Тл · 0,05 м2 = 0,005 Вб. ξ = BSω= BS2π ν = 0,005·6,28·20 = 0,628 В.
εм= ε1·N, N = εм/ ε1, N = 100 . ξ = ξmax sinωt = 63sin40πt.
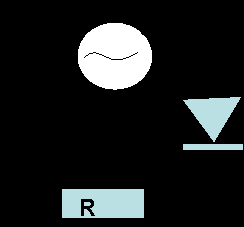
Задача 7. Колебательный контур, подключённый к генератору, содержит резистор, сопротивление которого 5 Ом, катушку индуктивностью 5 Гн и конденсатор. Определите электроёмкость конденсатора, при которой в контуре при частоте в 1 кГц возникает резонанс. Найдите показания амперметра, (включённого в сеть) при резонансе, если действующее напряжение на генераторе 220 В.
Решение. XL = XC , ωL = 1/ωC, С=1/ω2L = 5·10-9Ф. Iд = Uд/R =220 В / 5 Ом = 44 А.
Задача 8. К генератору переменного тока с частотой ν = 100 Гц подключены катушка индуктивностью 0,5 Гн, конденсатор ёмкостью 4 мкФ и резистор сопротивлением 54 Ом. Сила тока в цепи 0,5 А Найдите полное сопротивление цепи и максимальное напряжение на генераторе.
Р
 ешение. Z = Um/Im= √ R2+ ( XL – XC )2 = 101,5 Ом. Um = Z Im = Z Iд1,4=70,7 В
ешение. Z = Um/Im= √ R2+ ( XL – XC )2 = 101,5 Ом. Um = Z Im = Z Iд1,4=70,7 ВЗадача 9. Колебательный контур состоит из катушки индуктивностью 0,05мГн и конденсатора ёмкостью 20 пФ. Максимальное напряжение на конденсаторе 100 В при частоте 5 МГц.
- Найти сопротивления катушки и конденсатора и полное сопротивление контура.
- Написать уравнение колебаний напряжения на конденсаторе.
- Как увеличить частоту свободных колебаний контура.
Р
 ешение. ХС = 1/ωC = 1/ 2·3,14·5·106 с -1 ·20·10 -12Ф = 1600 Ом.
ешение. ХС = 1/ωC = 1/ 2·3,14·5·106 с -1 ·20·10 -12Ф = 1600 Ом. XL= ωL = 2·3,14·5·106 с -1 ·5·10 -5Гн=1570 Ом. Z = Um/Im= √ R2+ ( XL – XC )2 = 30 Ом.
u = Umax cos( ωt ) = 100 cos(107 π t).
Увеличить частоту свободных колебаний контура можно уменьшая электроёмкость и индуктивность.
Для самостоятельного решения
Задача 10. В магнитном поле с индукцией 0,4 Тл вращается рамка, площадью 200 см2 с частотой 5Гц. В начальный момент рамка перпендикулярна линиям магнитной индукции.
- Найти максимальный магнитный поток и максимальное значение Э.Д.С. индукции в рамке.
- Найти начальную фазу колебаний. Написать уравнения зависимости магнитного потока и ЭДС от времени.
- Н
 айти значение Э.Д.С. через 0,2 с., если начальная фаза будет равна π/6.
айти значение Э.Д.С. через 0,2 с., если начальная фаза будет равна π/6.
Ответ: 0,008Вб; 0,2512 В; 0; ξ = 12,3·10 - 4 В.
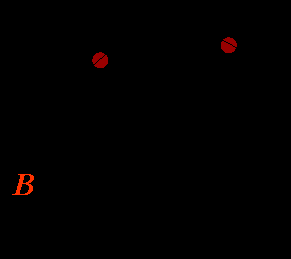
Задача 11. Индукция направлена перпендикулярно плоскости листа к нам.
- Какой способ индуцирования тока изображен на рисунке?
- Какой знак имеет разность потенциалов в точках К и М?
- Что произойдёт, если проводник КМ будет двигаться в обратную сторону?
Задача 12. Цепь, состоящую из катушки индуктивностью 0,2 Гн, конденсатора, ёмкостью 10мкФ и резистора, сопротивлением 50 Ом подключили, соединённых последовательно, подсоединили к промышленному генератору переменного тока. Сила тока в цепи 2 А.
- Найти сопротивление катушки, конденсатора и полное сопротивление цепи.
- Написать уравнение колебаний тока на катушке.
- При какой частоте в цепи будет наблюдаться резонанс?
Ответ: 63 Ом; 320 Ом; 262 Ом; 71 Гц.
Задача 13. На первичной катушке трансформатора колебания напряжения описываются уравнением u =308 Cos 100πt. На вторичной катушке вольтметр показал напряжение 6,3 В.
- Найти коэффициент трансформации, максимальное и действующее значение напряжения на первичной катушке.
- Определить частоту переменного тока. Написать уравнение колебания напряжения на вторичной катушке.
- И
 з какого ферромагнетика изготавливают сердечник трансформатора.
з какого ферромагнетика изготавливают сердечник трансформатора.
Ответ: 35; 305 В; 220 В; 50 Гц;
Задача 14. Индукция поля линейно возрастает с течением времени.
1.Какой способ индуцирования тока изображён на рисунке?
2.Какой знак имеет разность потенциалов в точках M и N?
3.Что произойдёт, если индукция поля начнёт линейно уменьшаться с течением времени?
Электромагнетизм. Переменный ток. Z. Rodchenko
