Явление электромагнитной индукции

Вид материала

Лекция

Подобный материал:

• «Явление электромагнитной индукции», 114.8kb.
• Магнитное поле. Сила Ампера. Сила Лоренца. Явление электромагнитной индукции, 98.2kb.
• Штейн Б. М. Взаимосвязь изучения электромагнитной индукции и электромагнитного поля, 136.4kb.
• Тема Что должен знать/понимать, 61.85kb.
• Программа собеседования по направлению «Электроэнергетика и электротехника», 200.29kb.
• Б. М. Явление электромагнитной индукции при изучении электромагнитных волн, 48.02kb.
• С помощью программы 1С: Образование Школа. На уроке применяются цоры из главы X «Явление, 51.23kb.
• Предисловие к третьему изданию, 722.32kb.
• Задачи: Образовательная. Актуализация знаний о магнитных явлениях и продолжение, 116.66kb.
• Vii международный симпозиум по электромагнитной совместимости и электромагнитной экологии, 50.03kb.

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ


Опыты Фарадея. Основной закон ЭМИ. Правило Ленца. Объяснение ЭМИ Гельмгольцем и Максвеллом. Э.д.с. индукции. Токи Фуко. Индуктивность. Самоиндукция и взаимная индукция. Трансформатор. Энергия МП соленоида. Экстратоки замыкания и размыкания.

1. Явление электромагнитной индукции открыто Фарадеем.
   
2. Электромагнитной индукцией называется возникновение электродвижущей силы в проводнике при его перемещении в магнитном поле либо в замкнутом проводящем контуре вследствие его движения в магнитном поле или изменении самого поля.
   
   1. Эта электродвижущая сила ξ_инд называется электродвижущей силой электромагнитной индукции.
      
   2. Под ее влиянием в замкнутом проводнике возникает индукционный ток.
      
3. Электродвижущая сила электромагнитной индукции в контуре пропорциональна и противоположна по знаку скорости изменения магнитного потока Ф_m сквозь поверхность, охватываемую контуром (закон Фарадея-Максвелла), то есть
   

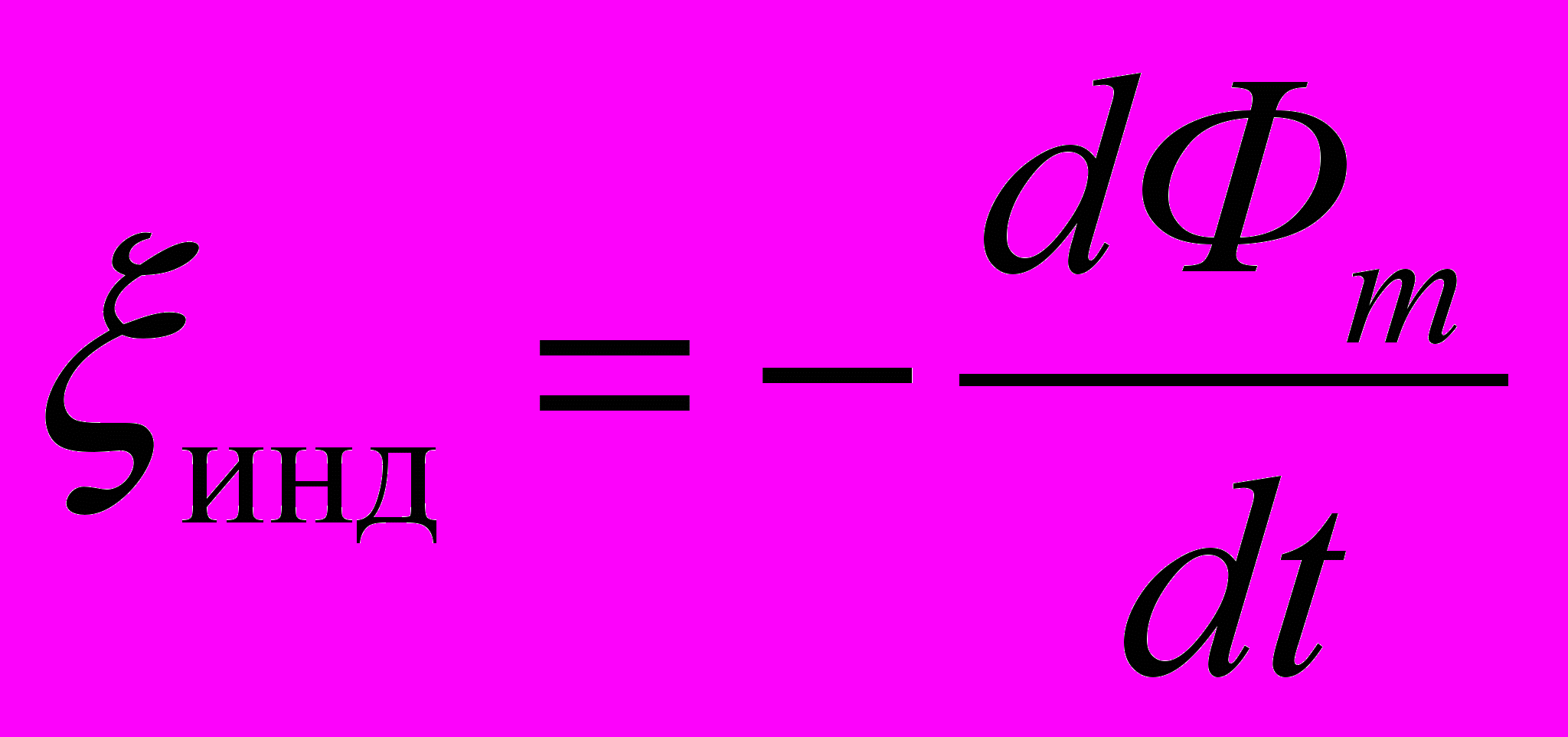
Направление обхода контура задается правилом Максвелла.

Правило Ленца: при всяком изменении магнитного потока сквозь поверхность, охватываемую замкнутым проводящим контуром, в контуре возникает индукционный ток такого направления, что создаваемое им поле стремится компенсировать изменение магнитного потока, вызвавшее индукционный ток.

4. ЭДС электромагнитной индукции возникает в каждом отрезке проводника, пересекающем при своем движении линии магнитной индукции поля (действие силы Лоренца).
   
   1. При движении проводника в магнитном поле на электроны проводимости действует сила Лоренца
      

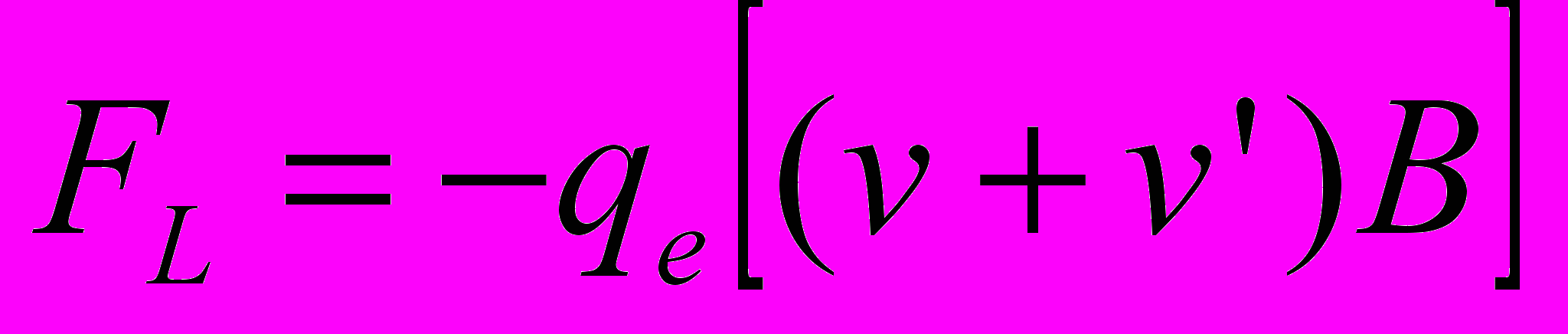
где v – скорость перемещения проводника в направлении перпендикулярном вектору магнитной индукции; v' – скорость движения электронов вдоль проводника под действием силы Лоренца.

2. Движение электронов в разомкнутом проводнике прекратится, когда в нем возникнет электрическое поле, компенсирующее действие силы Лоренца, которая играет роль сторонней силы
   

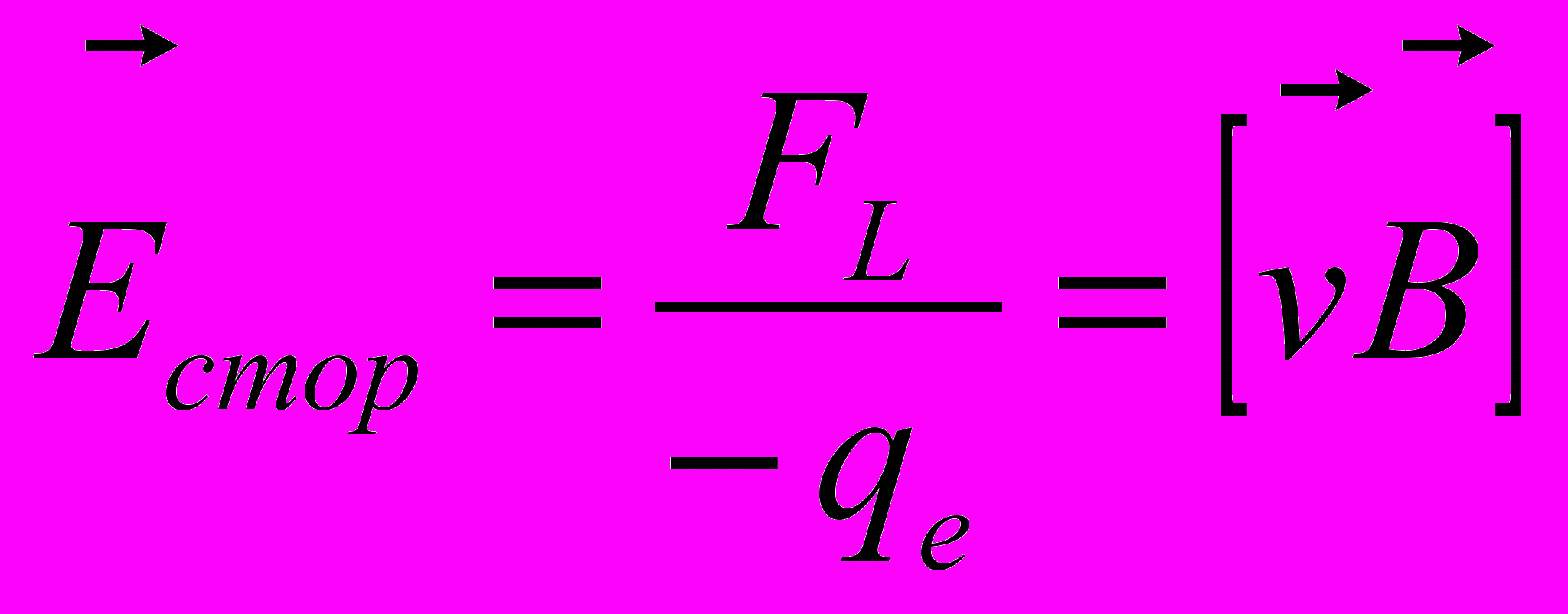
3. Величина ЭДС электромагнитной индукции в проводнике может быть определена
   

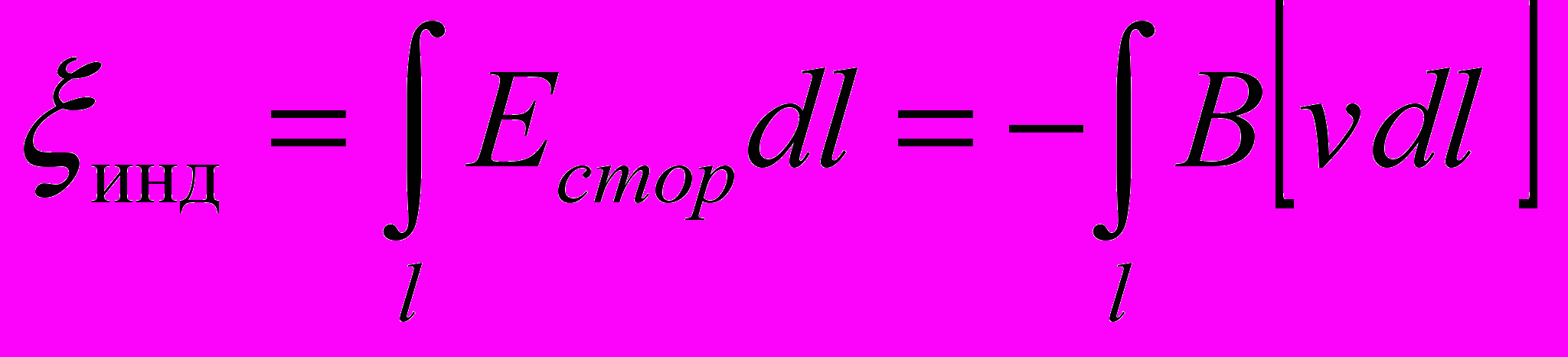
где интегрирование производится по всей длине проводника.

Так как , то

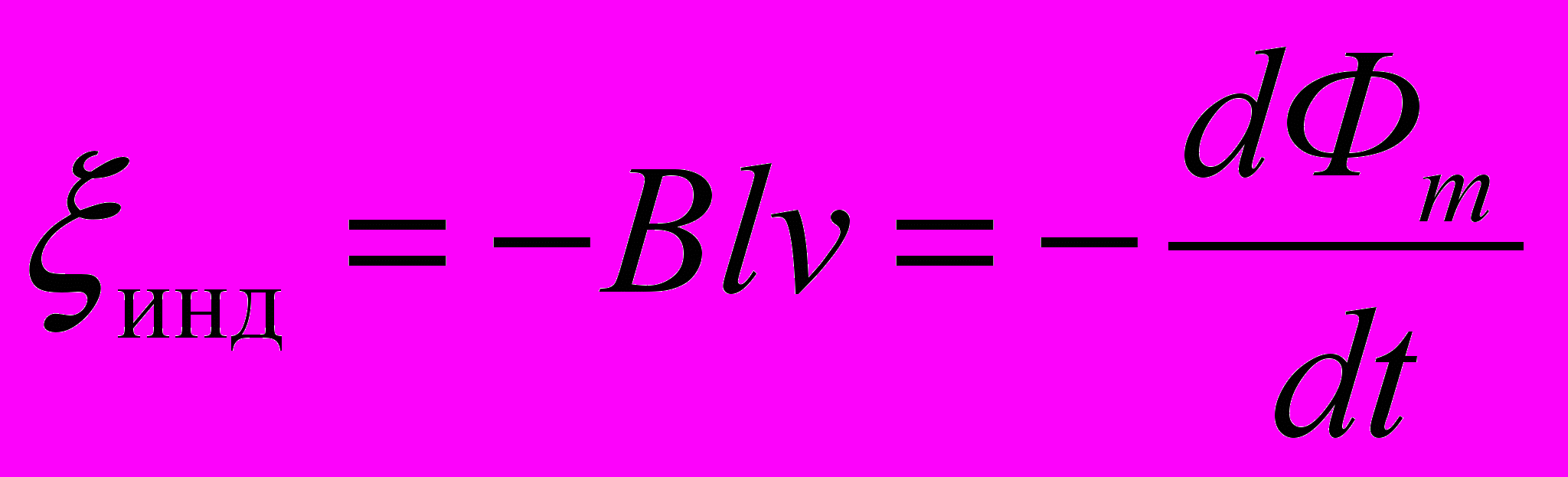
5. Согласно закону сохранения энергии, работа источника тока ξIdt за время dt будет равна сумме работы по перемещению проводника в магнитном поле и выделившейся джоулевой теплоты (объяснение Гельмгольца)
   

→

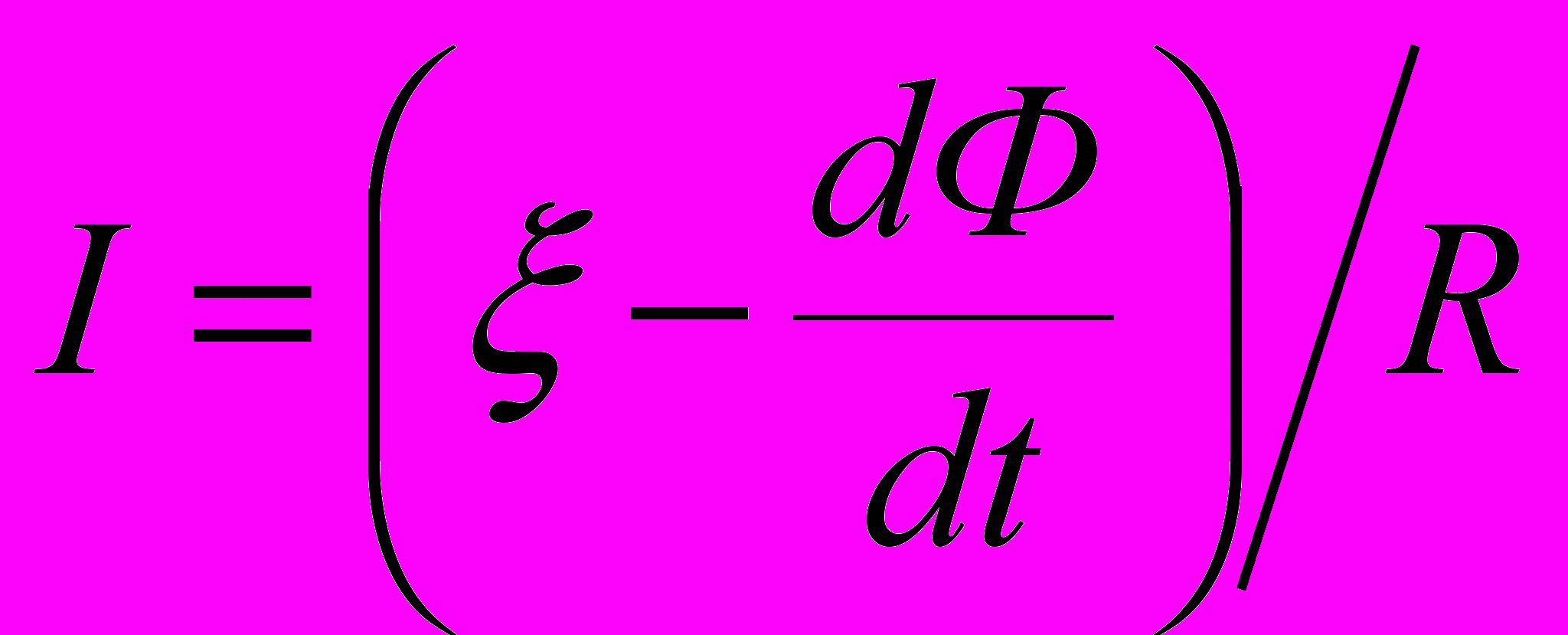
где R – полное сопротивление контура, а равно ЭДС электромагнитной индукции.

6. При вращении рамки в однородном магнитном поле в ней будет возникать переменная ЭДС электромагнитной индукции
   
   1. Магнитный поток, сцепленный с рамкой в любой момент времени равен
      

где ω – угловая скорость вращения рамки.

2. Изменение магнитного потока приводит к возникновению ЭДС
   

которая изменяется по гармоническому закону.

7. В неподвижном проводнике, находящемся в переменном магнитном поле возникает вихревое индуцированное электрическое поле, циркуляция вектора напряженности Е которого вдоль замкнутого проводящего контура равна ЭДС электромагнитной индукции
   

(объяснение Максвелла)

8. В массивных проводниках вихревое индуцированное электрическое поле приводит к возникновению замкнутых токов (токи Фуко). Эти токи используются:
   
   1. для демпфирования – успокоение подвижных частей приборов;
      
   2. для объемного нагрева металлов – индукционный нагрев;
      
   3. для поверхностного нагрева металлов – вследствие скин-эффекта быстропеременный ток распределен по сечению проводника неравномерно (вытесняется на поверхность).
      
9. Так как сцепленный с контуром магнитный поток Ф пропорционален току в контуре
   

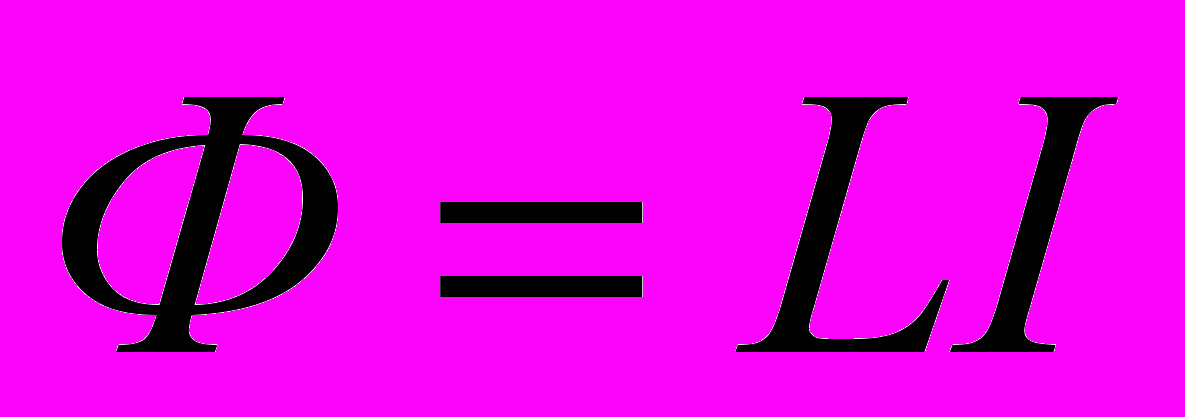
то при изменении силы тока в контуре будет изменяться и связанный с ним магнитный поток.

1. При изменении магнитного потока в контуре будет индуцироваться ЭДС
   

2. Если контур не деформируется, то L=const и
   

где знак минус показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем.

3. При всяком изменении силы тока в проводящем контуре возникает ЭДС самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции.
   
4. При возрастании внешнего тока ток самоиндукции направлен навстречу внешнему току. Если ток со временем убывает, то ток самоиндукции имеет то же направление, что и внешний ток, и замедляет его убывание.
   
5. При выключении источника тока экстратоки имеют то же направление, что и ослабевающий ток.
   
   1. В каждый момент времени ток в цепи подчиняется закону Ома
      

→ →

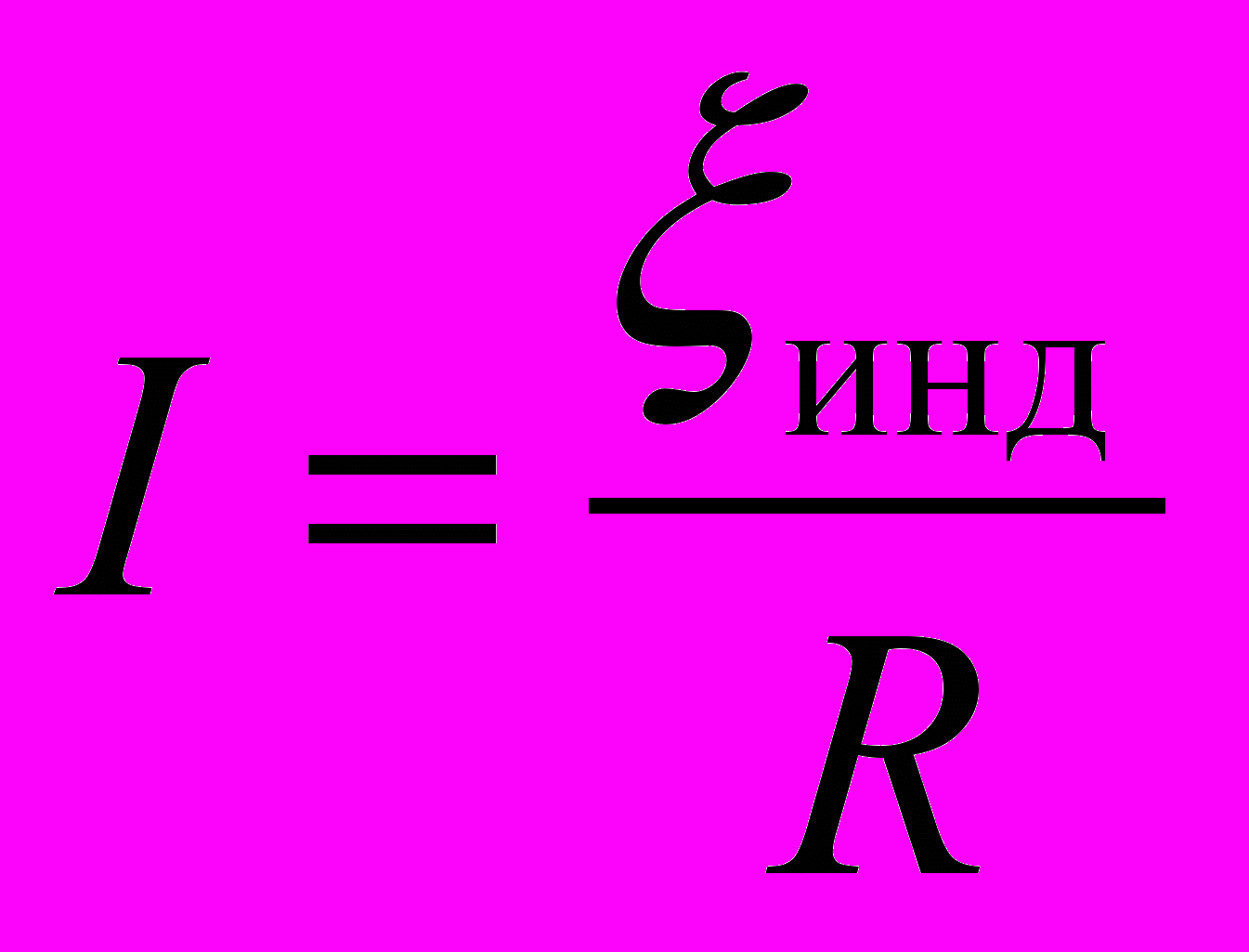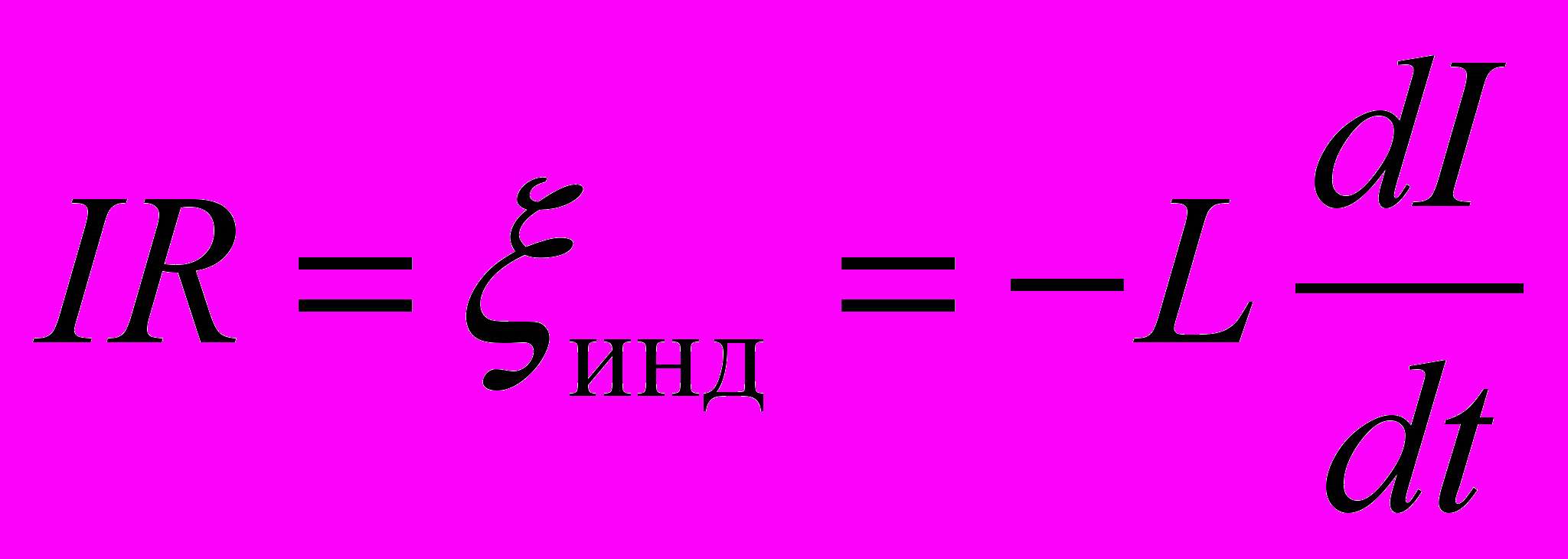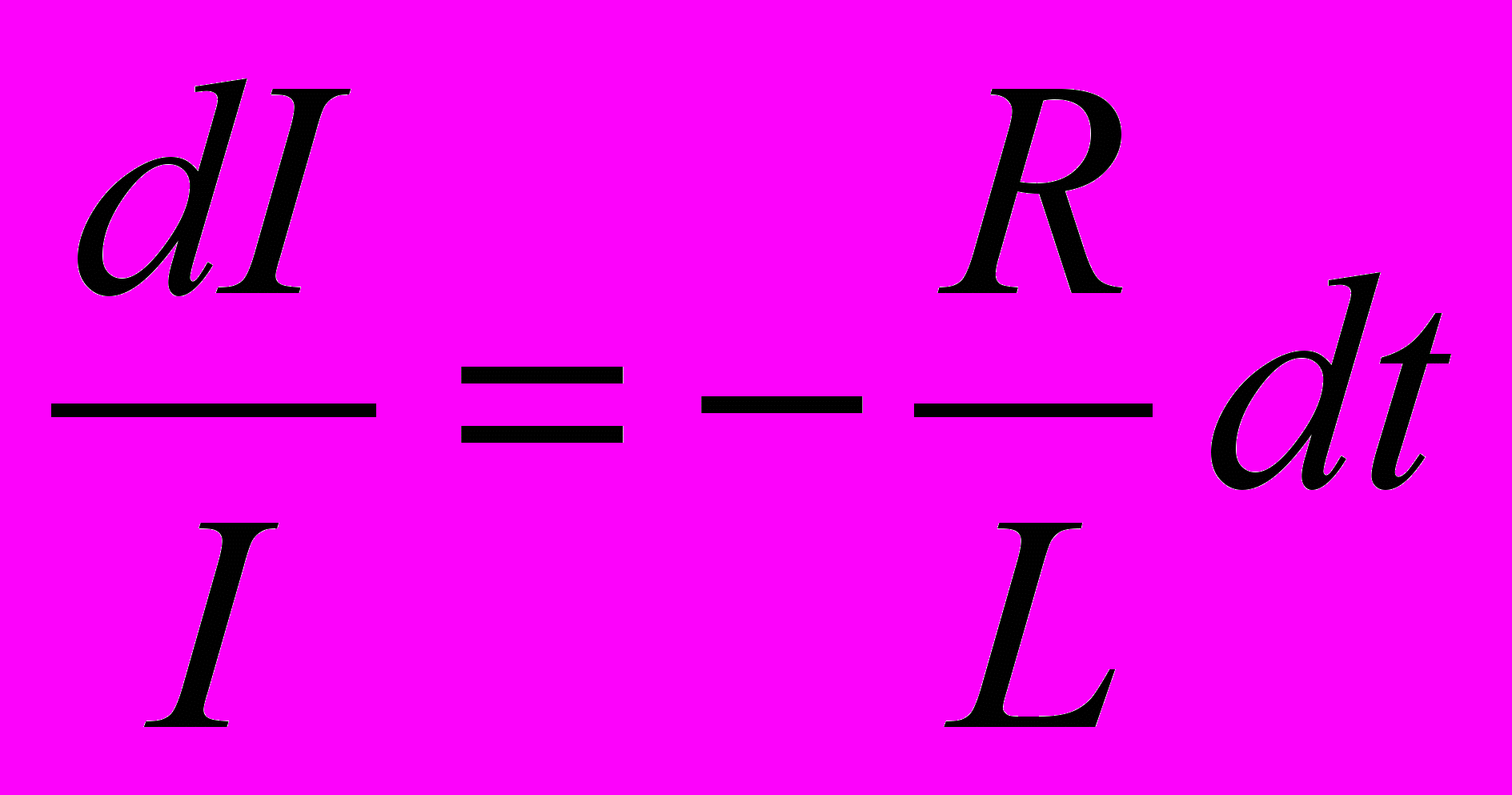
2. Интегрирование приводит к уравнению
   

→

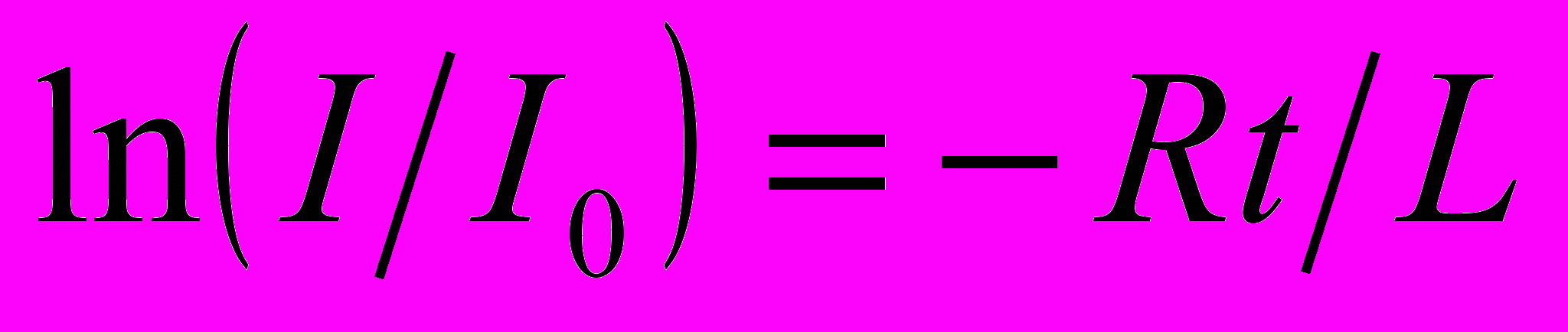где 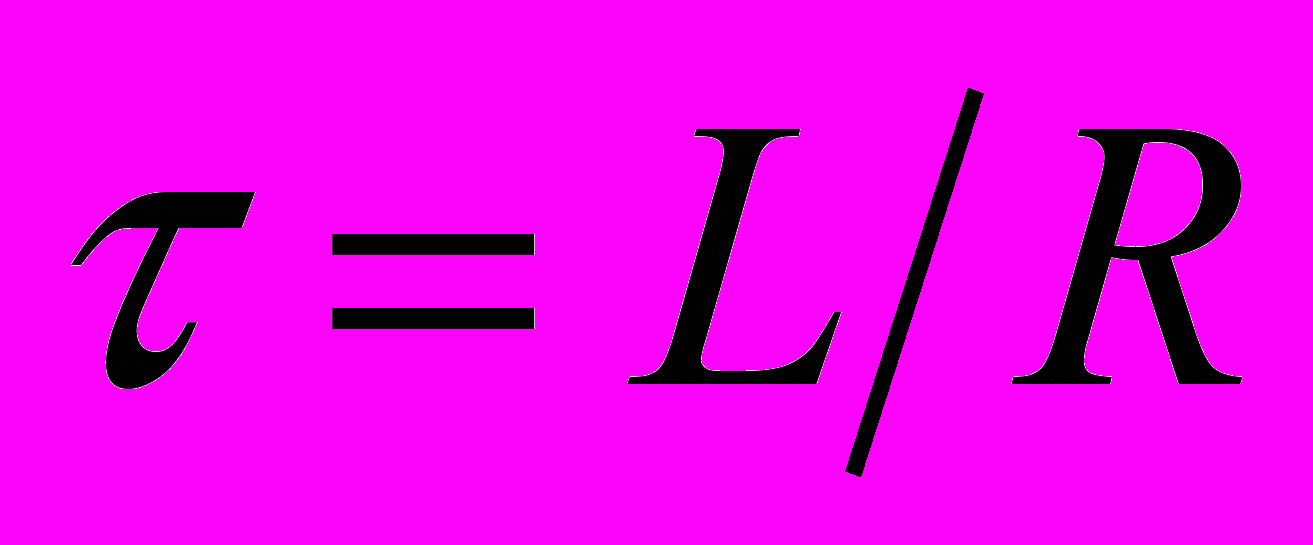- называется временем релаксации (время, в течение которого сила тока уменьшается в е раз).

3. При отключении тока величина тока в цепи уменьшается тем медленнее, чем больше индуктивность цепи.
   
4. Если в цепи течет ток , то ЭДС самоиндукции
   

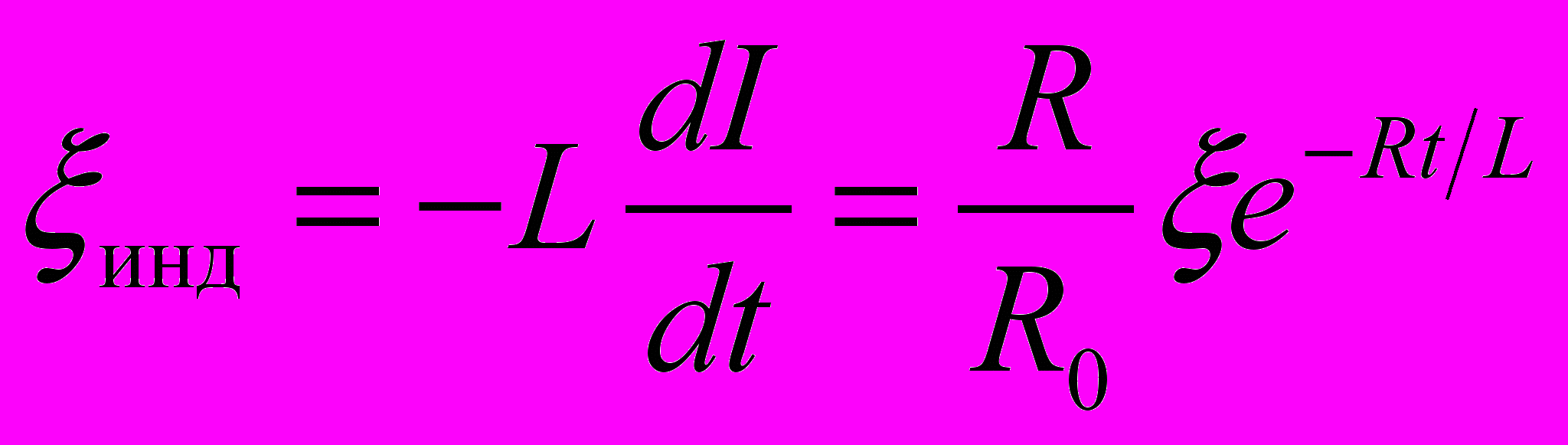
то есть при большой индуктивности цепи ЭДС самоиндукции может во много раз превышать ЭДС источника тока.

6. При замыкании цепи помимо внешней ЭДС начинает действовать ЭДС самоиндукции, препятствующая возрастанию тока.
   
   1. По закону Ома
      

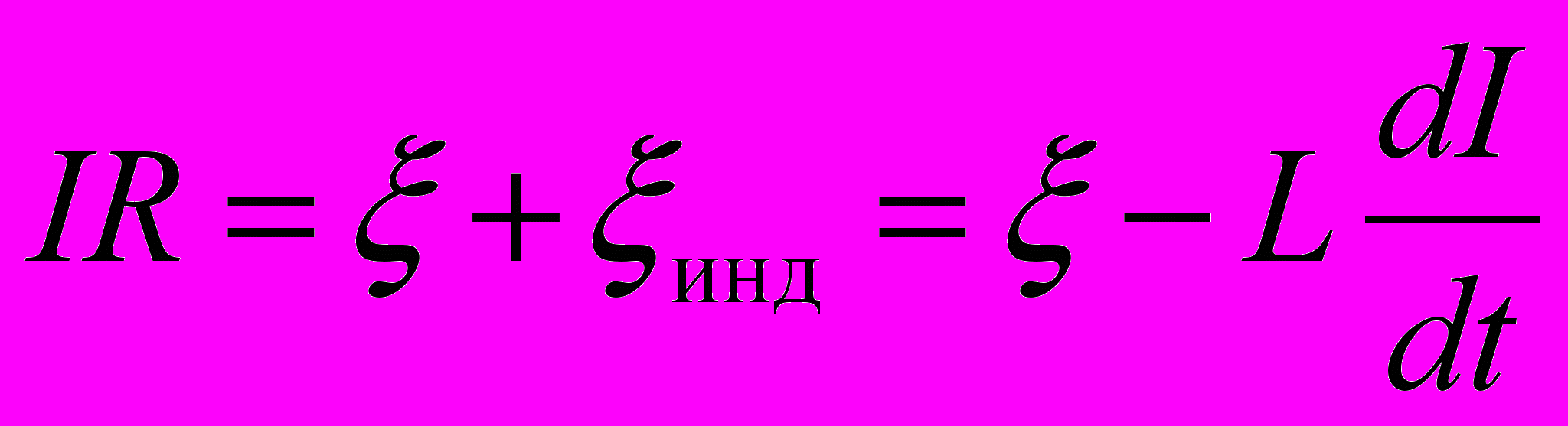
2. Введем переменную , тогда уравнение можно преобразовать к виду
   

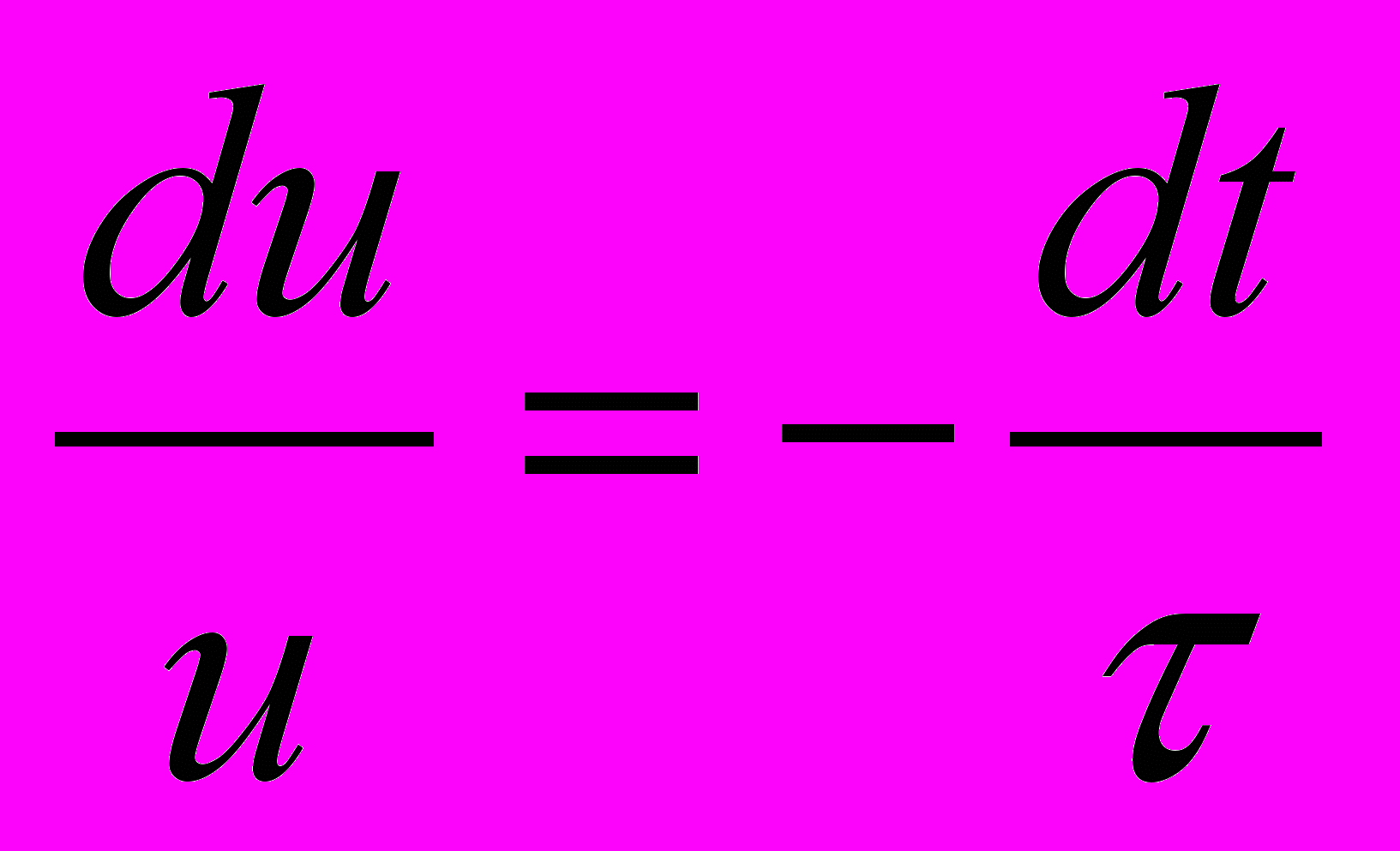
3. При t=0 сила тока I=0 и u=-ξ. При интегрировании получится
   

→

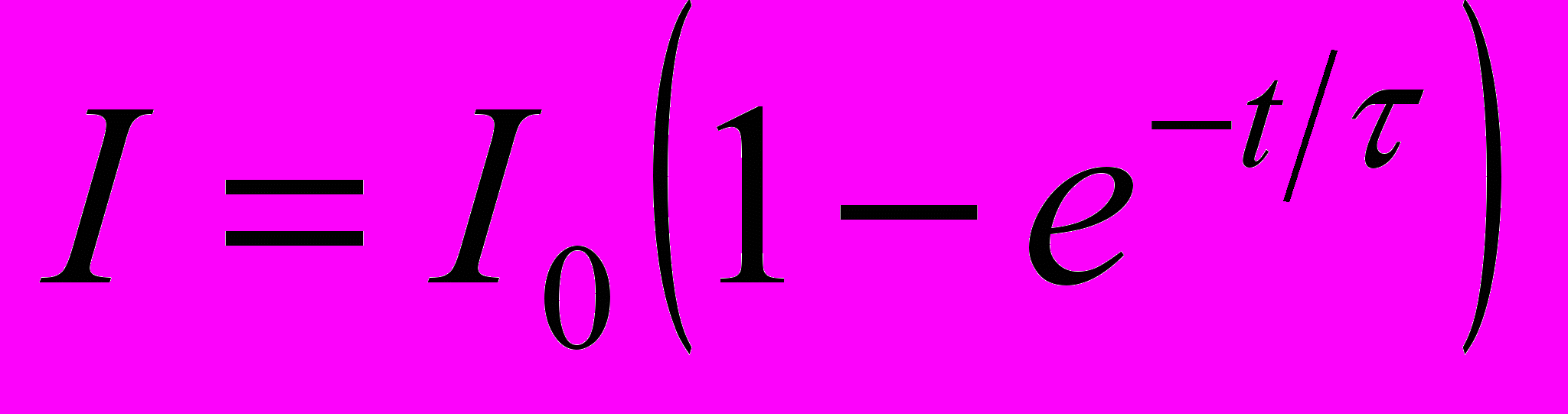
10. Два контура имеющие общий магнитный поток взаимодействуют через поле, создаваемое одним из контуров
    
    1. Если в первом контуре течет ток I₁, то магнитный поток, создаваемый этим контуром пропорционален величине тока
       

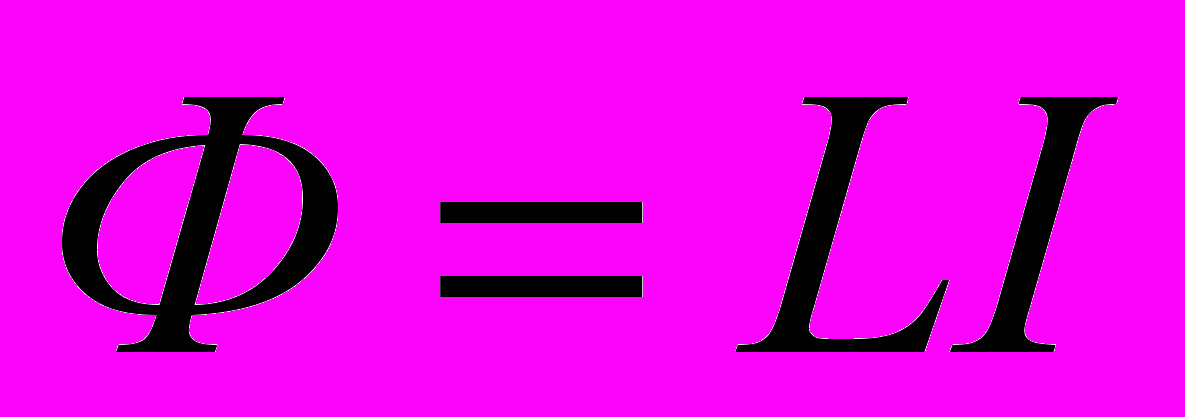
2. Та часть потока, которая пронизывает второй контур, также будет зависеть от величины тока в первом контуре
   

где L₂₁ – коэффициент пропорциональности.

3. Если ток в первом контуре изменяется, то во втором контуре возникает ЭДС, которая по закону Фарадея равна и противоположна по знаку скорости изменения магнитного потока Ф₂₁
   

4. Если аналогичным образом рассмотреть изменение тока во втором контуре, то
   

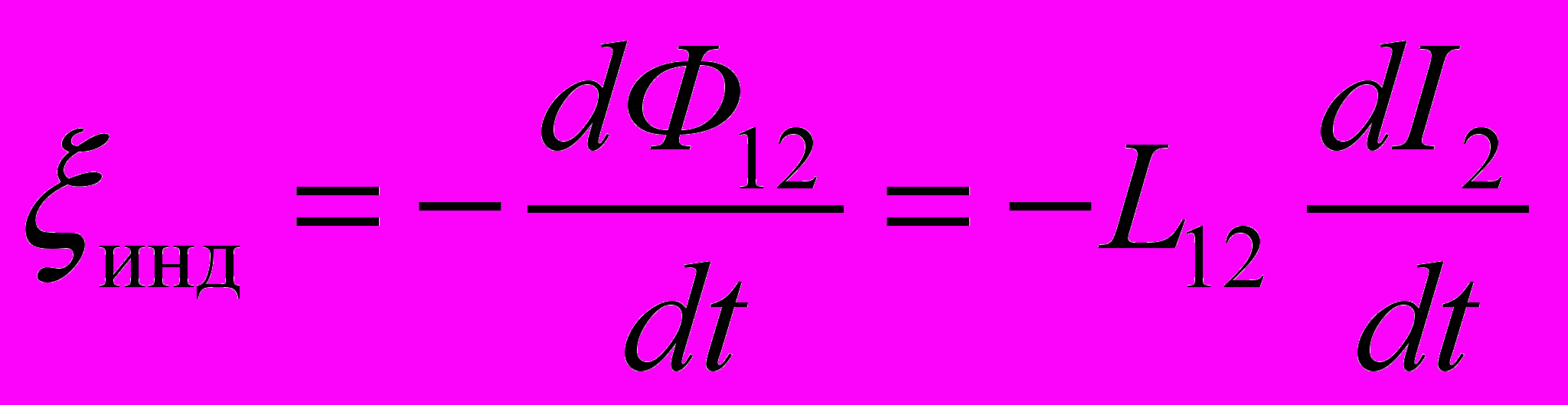
5. Коэффициенты L12 и L21 равны друг другу и называются взаимной индуктивностью контуров.
   
   1. Магнитная индукция поля катушки длиной l с количеством витков N₁
      

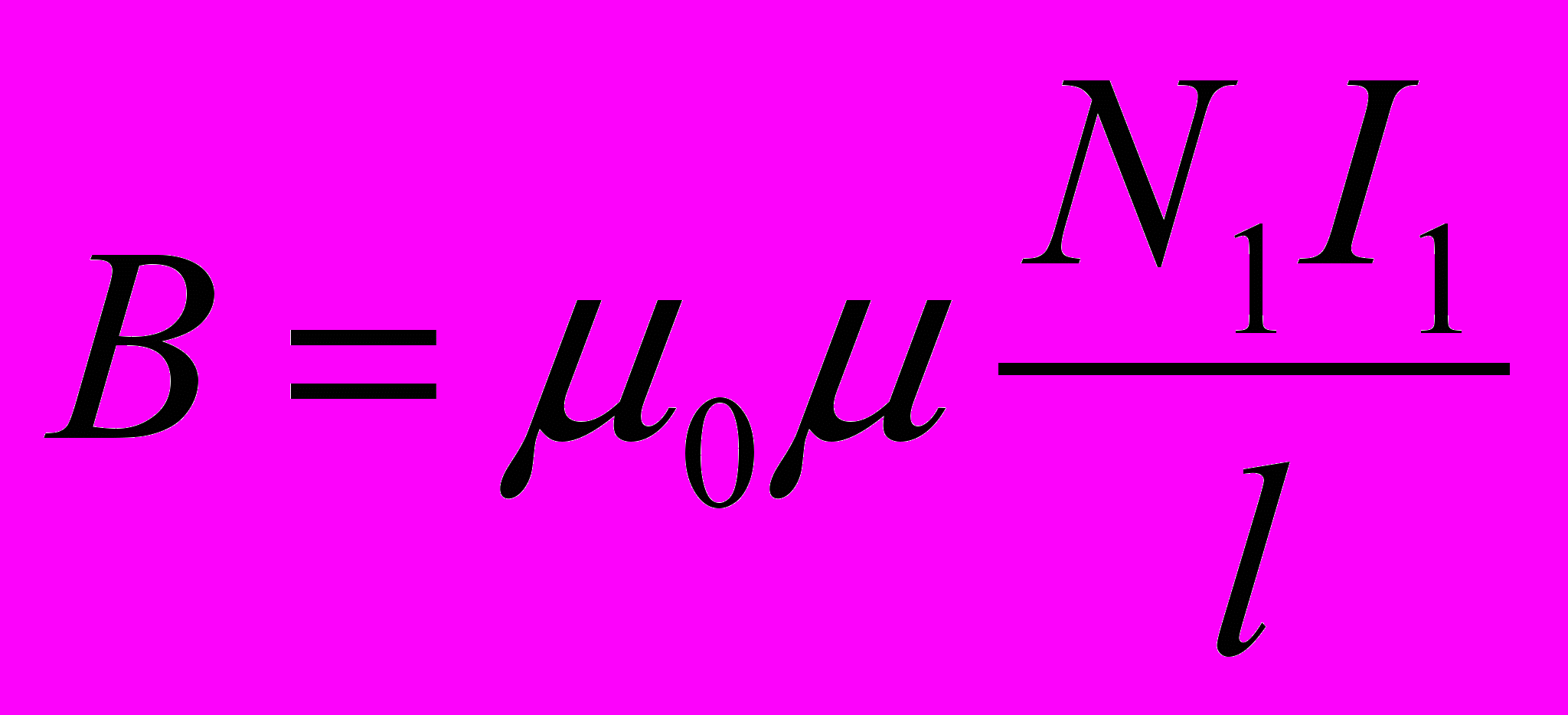
2. Магнитный поток сквозь вторую катушку, намотанную параллельно первой и содержащей N₂ витков, будет равен
   

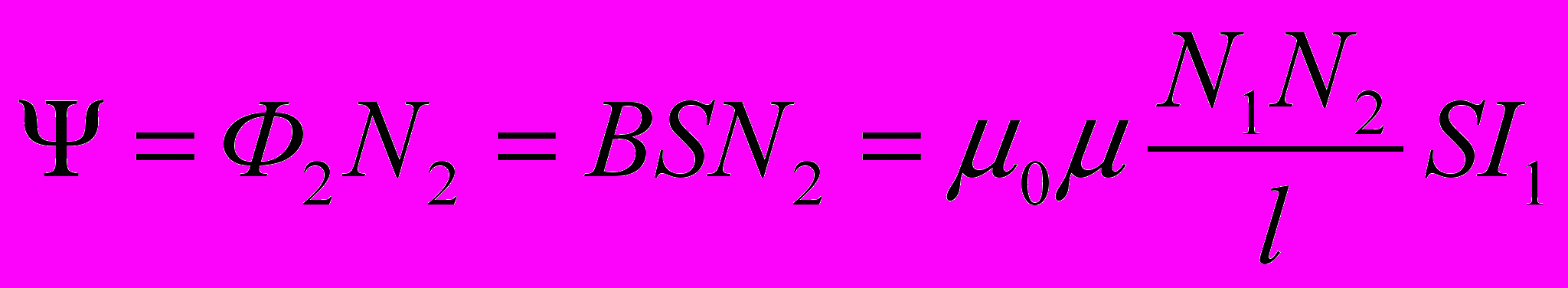
3. Отсюда можно получить выражение для взаимной индуктивности катушек с общим магнитным потоком
   

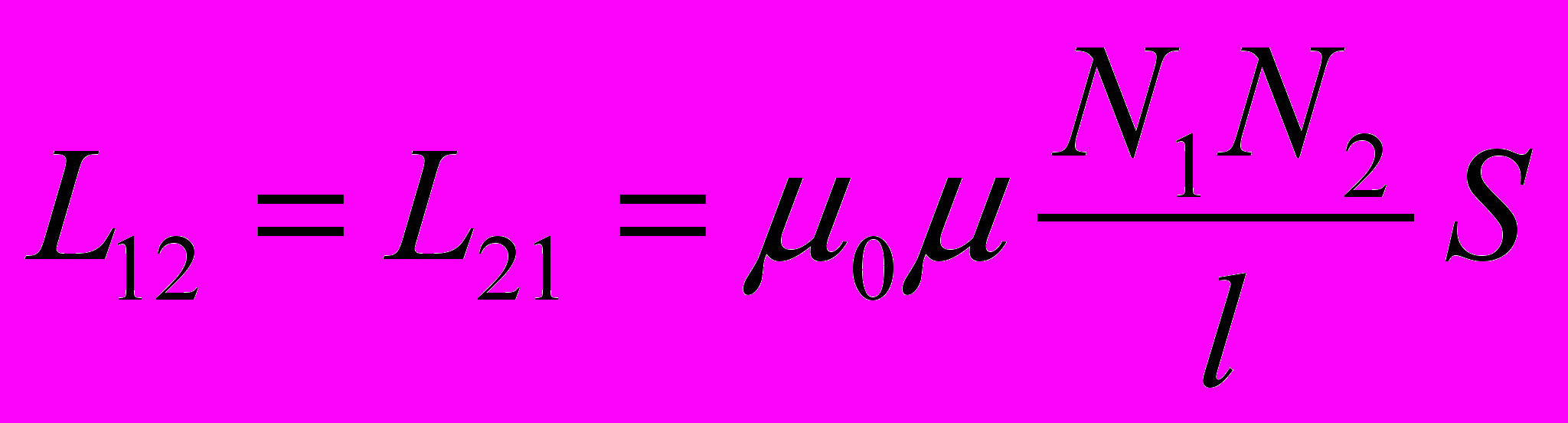
6. На явлении взаимной индукции основано действие трансформаторов
   
   1. Ток в первичной обмотке трансформатора подчиняется закону Ома
      

где R₁ – сопротивление первичной обмотки, а второе слагаемое в левой части – ЭДС самоиндукции.

2. Малое сопротивление катушек трансформатора приводит к малому падению напряжения на них. Тогда
   

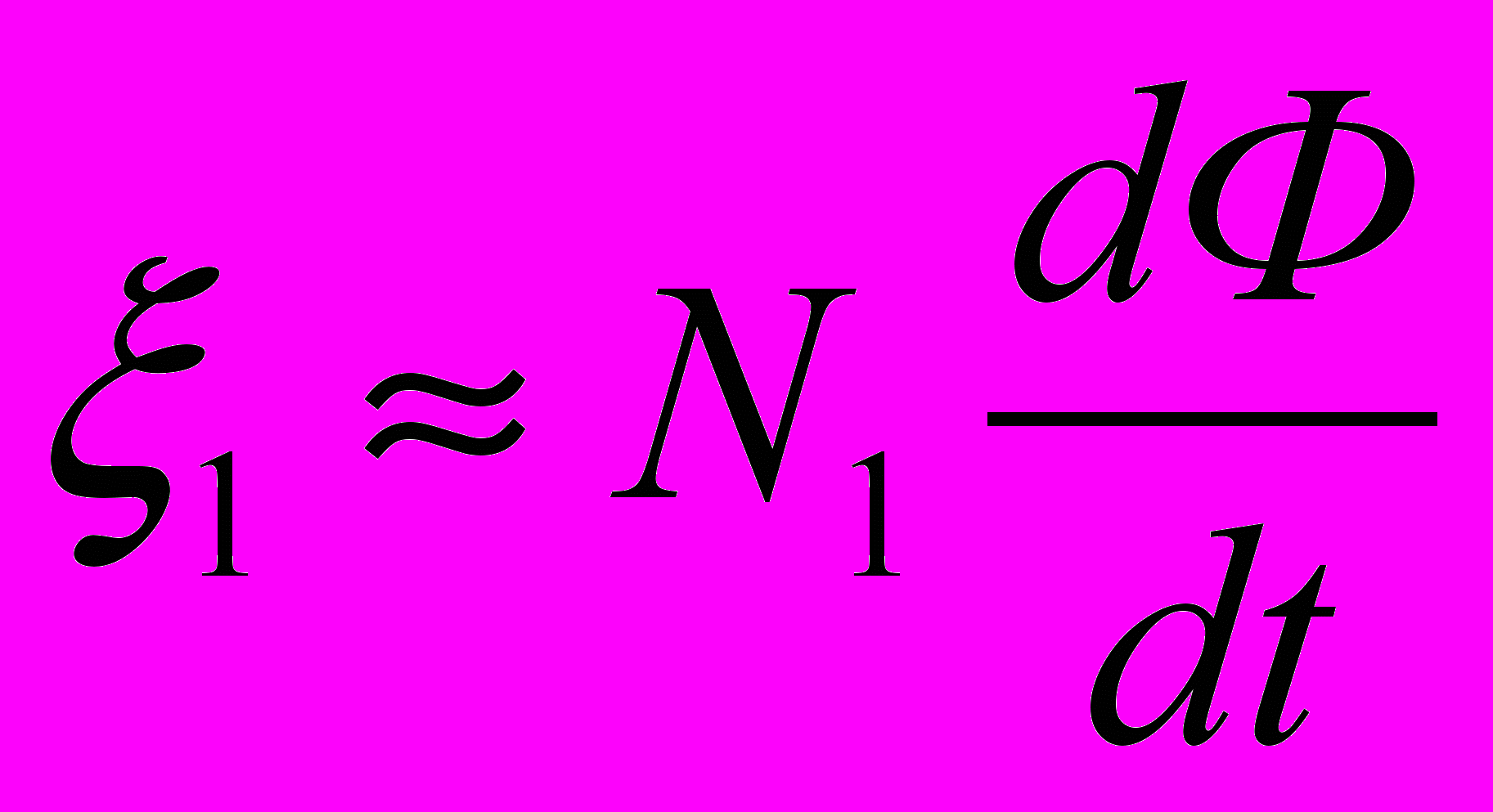
3. ЭДС взаимной индукции, возникающая во вторичной обмотке,
   

4. Так как обе катушки имеют общий магнитный поток, то
   

→

где отношение числа витков вторичной обмотки к числу витков первичной обмотки называется коэффициентом трансформации.