2 статья. Удк 539 083: 550. 83: 621. 315. 2

Вид материала

Содержание

Оптимальная форма сигналов.
Кодовые сигналы.
Частотная коррекция сигналов на выходе кабеля.
Принципы реализация фильтров частичной деконволюции.

Подобный материал:

А.В.Давыдов. 2000 г.

2 статья.

УДК 539.1.083: 550.83: 621.315.2

Повышение скорости передачи данных по каротажным кабелям

Как было рассмотрено в предыдущей статье и работе /5/, каротажный кабель представляет собой линию связи с пониженной добротностью и нелинейной зависимостью передаточной функции от длины кабеля. Импульсную пропускную способность кабеля и качество передачи данных определяют эффективная ширина частотного спектра _к, эффективная длительность импульсного отклика T_к и индекс неопределенности T_к_ктокопроводящих жил кабеля. Максимальная частота передачи по кабелю кодовых импульсов соответствует тактовым интервалам, равным 2T_к, при эффективной длительности импульсов, не превышающей эффективной длительности отклика кабеля.. На предельной частоте передачи однополярные сигналы с гладкой формой и минимальной шириной спектра не имеют преимуществ перед прямоугольными импульсами.

Оптимальная форма сигналов.

Однополярные импульсы по отношению к электрическим параметрам кабеля и его частотным характеристикам не являются оптимальными. Практически все первичные и вторичные электрические характеристики кабеля, за исключением емкости, существенно нелинейны в области низких частот, где сосредоточена значительная часть энергии однополярных сигналов. Соответственно, кабель оказывается рассогласованным на этих частотах с нагрузкой, а стабильность передачи сигналов зависит от изменения степени рассогласования при влиянии на кабель дестабилизирующих факторов (температуры, условий заземления оплетки в скважине и пр.). При однополярных сигналах на ограничение импульсной пропускной способности кабеля оказывает влияние и существенное смещение нулевой линии, определяемое резкой асимметрией импульсного отклика кабеля и зависимое от конкретной импульсной нагрузки кодовых последовательностей. По этой же причине для однополярных кодов не может быть выполнена система надежной автоматической синхронизации тактовых частот передатчика и приемника.

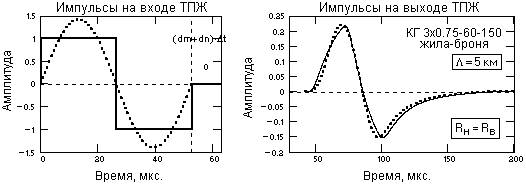
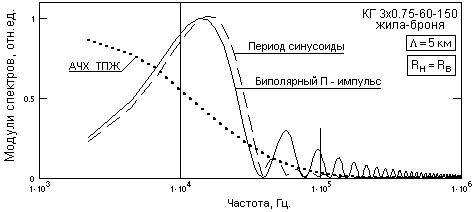
Рис. 1. Форма и спектры биполярных импульсов.

Решение данной проблемы в радиотехнике известно: частотное перераспределение энергии сигналов со смещением в средне- и высокочастотную область спектра кабеля, т.е. применение биполярных сигналов с нулевым средним значением по тактовым интервалам.

Таблица 1.

Параметры биполярных сигналов на кабеле КГ 3х0.75-60-150

(T_к 26 мкс, _к 34.4 кГц, T_к_к  0.9).

Тактовый интервал	Т=2T_k				Т=T_k
Сигналы	Входные		Выходные		Входные		Выходные
Параметры	Би-П	Син.	Би-П	Син.	Би-П	Син.	Би-П	Син.
T импульса, мкс.	30.3	27.9	39.3	36.2	15.2	13.9	24.9	23.5
 импульса, кГц.	400	38.2	26.3	28.2	566	76.4	44.1	48.0
Индекс T	12.1	1.06	1.03	1.02	8.06	1.07	1.10	1.13

На рис. 1 приведена форма двух типов биполярных сигналов равной энергии (П-импульсов и синусоиды) пределах тактового периода Т = 2Т_к. Модули спектров сигналов приведены в нормированном виде в сопоставлении с передаточной функцией кабеля (пунктирная кривая). Импульсные параметры сигналов приведены в таблице 1.

Из рисунка и таблицы можно видеть, что потеря сигналами высокочастотных составляющих приводит их к практически идентичной форме и гладкая форма входных сигналов на предельных тактовых частотах, как и для однополярных импульсов, не имеет преимуществ перед прямоугольными импульсами.

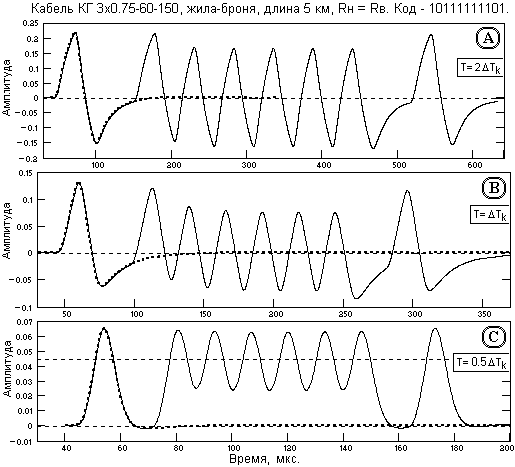
Рис. 2. Форма выходных биполярных кодовых сигналов на разных тактовых интервалах.

Пример двоичного кодового сигнала, переданного биполярными П-импульсами с тактовым интервалом Т = 2Т_к, приведен на рис. 2(А). Пунктиром на рисунке приведена форма единичного (первого) импульса. Биполярные импульсы не дают смещения нулевой линии в пределах кодового слова, при этом по внутритактовому пересечению нуля может выполняться автоматическая синхронизация тактовых частот передатчика и приемника. Кроме того, импульсы отрицательной полярности представляют собой дублирующую кодовую информацию, сдвинутую на половину такта. Она также может быть использована для повышения достоверности идентификации импульсов и допустимого уровня шумов (детектирование сигналов по полярности на два канала, задержка канала положительных импульсов на полтакта, инверсия полярности канала отрицательных импульсов и суммирование каналов, при этом амплитуды импульсов увеличиваются в 2 раза, а среднеквадратический уровень статистических шумов уменьшается в

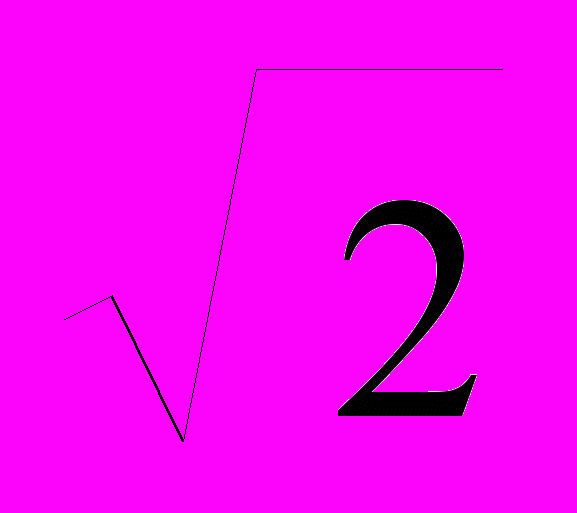раз).

На тактовых интервалах T_k (рис. 2(В)) взаимное влияние битовых сигналов становится достаточно существенным, но идентификация сигналов по синхроимпульсам сомнений не вызывает. Без специальных устройств декодирования сигналов этот интервал может считаться предельным для передачи данных с использованием биполярных кодов.

Заметим, что на предельных частотах передачи первые выходные импульсы в кодовых комбинациях и импульсы после нулевых битов несколько больше по значениям последующих импульсов в непрерывной последовательности. При необходимости этот эффект может быть устранен уменьшением амплитуды входных импульсов, следующих за нулевыми интервалами.

В принципе, для биполярных сигналов интервал T_k не является предельным. Биполярная форма импульсов позволяет подобрать соотношение длительности положительных и отрицательных частей импульсов (или их амплитудных значений) таким образом, чтобы в определенной мере компенсировать асимметрию импульсного отклика кабеля. На рис. 2(С) приведен пример формы сигналов на выходе кабеля для биполярных импульсов на входе кабеля с тактовым интервалом 0.5Т_k при равных значениях длительности импульсов и амплитуде отрицательного импульса порядка ¾ амплитуды положительного. Амплитудная асимметрия биполярного импульса создает "разрядный" импульс на входе кабеля, обратный ток которого, сдвинутый на полтакта, вычитается из тока среза "зарядного" импульса и компенсирует тем самым обратную по знаку асимметрию импульсного отклика кабеля. Результатом является практически симметричная однополярная форма единичного выходного сигнала (на рисунке показана пунктиром) и одноуровневая форма кодового слова, которая хорошо декодируется.

Таким образом, при кодовой передаче информации по каротажному кабелю максимальная скорость передачи данных обеспечивается при использовании биполярных импульсов.

Кодовые сигналы.

Скорость передачи информации (бит/с) зависит не только от тактовой частоты передачи данных, но и от протокола кодирования информации. Хотя каротажную линию с трудом можно отнести к информационной магистрали, скорее это специальная технологическая линия управляемого сбора данных, тем не менее, протокол передачи каротажных данных целесообразно заимствовать из стандартов открытых систем обмена информацией OSI (Open System Interconnect).

С учетом специфики и условий эксплуатации (один приемник, большое разнообразие и частая смена передатчиков – скважинных приборов) для каротажных систем используются, как правило, только двух и трехуровневые коды RZ (Return to Zero), NRZ (Non Return to Zero) и Манчестер-II.

Двухуровневый код NRZ (ноль – нижний уровень, 1 – верхний) имеет информационные переходы на границе битов. Максимальная частота кода – при чередовании единиц и нулей, минимальная (нулевая) – при передаче последовательности одинаковых битов. Достоинство кода – максимальная простота. Основной недостаток – отсутствие надежной синхронизации и необходимость для синхронизации специальных (пакетных старт-стоповых) служебных битов.

Трехуровневый код RZ обеспечивает возврат к нулевому уровню после каждого бита информации. Логическому нулю соответствует положительный импульс, единице – отрицательный. Информационный переход осуществляется в начале бита, возврат к нулю – в середине бита. Код синхронизируется по битам переходом по его центру.

Код Мачестер-П является двухуровневым кодом с автосинхронизацией. Нулевому сигналу соответствует переход на верхний уровень в центре битового интервала с возвратом на нижний по концу битового интервала, если следующий бит также нулевой. Соответственно, логической единице – переход на нижний уровень с возвратом на верхний по концу интервала, если следующий бит также 1. Бит обозначен переходом в центре бита, по которому выделяется синхросигнал.

Максимальная частота кода – при передаче нулей или единиц, при чередовании нулей и единиц частота кода уменьшается в два раза, что можно видеть на рис. 3. Достоинство кода – отсутствие постоянной составляющей при передачах последовательностей нулей или единиц.

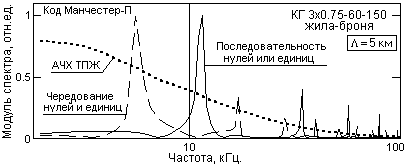
Рис. 3. Частотные характеристики кода Манчестер-П.

На рис. 4 приведен пример кодировки одной битовой последовательности тремя данными кодами по тактовым интервалам 2Т_к жилы кабеля и сигналы кодов на выходе кабеля. Масштаб выходных сигналов (утолщенные линии) – в единицах амплитуды входных сигналов. Тонкими линиями показаны входные сигналы, приведенные к выходу кабеля с учетом безвозвратных потерь энергии в кабеле умножением на площадь импульсного отклика и смещенные на время задержки.

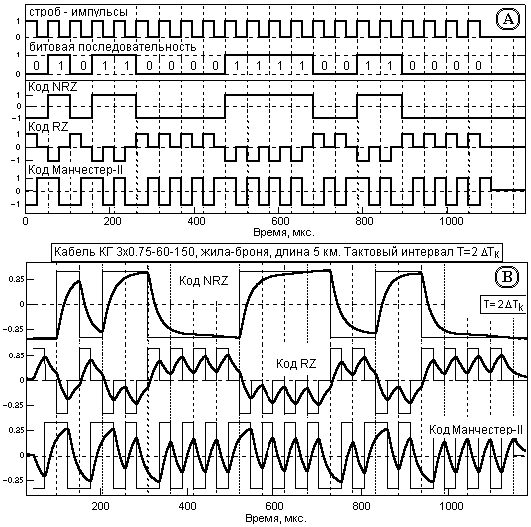
Рис. 4. Примеры кодировки сигналов и форма сигналов на выходе кабеля.

Сравнение кодов достаточно наглядно. Скорость передачи данных f_T = 1/(2Т_к) бит/с можно считать предельной для всех трех типов кодов. Код NRZ имеет преимущество и определенный запас "прочности" по амплитудным параметрам выходных сигналов, но без "жесткой" синхронизации приемника и передатчика надежное декодирование сигналов в присутствии шумов не гарантируется. Амплитудные характеристики кода Манчестер-П практически в 2 раза лучше кода RZ и, соответственно, выше помехозащищенность кода и надежность автосинхронизации. Кроме того, две основных несущих частоты кода позволяют при приеме сигналов применять полосовые фильтры и тем самым повышать помехозащищенность линии передачи данных.

Таким образом, оптимальной формой сигналов для каротажного кабеля при кодовой передаче сигналов, обеспечивающей максимальную скорость передачи данных, являются биполярные импульсы. Основным кодом передачи каротажных данных, максимально использующим возможности каротажного кабеля, можно считать код Манчестер-П.

Частотная коррекция сигналов на выходе кабеля.

Принципы частотной коррекции сигналов при их искажениях в линиях связи известны /3,4/. Заметим, что говорить о восстановлении формы сигналов с определенной погрешностью имеет смысл только в том случае, если эффективная ширина спектра сигналов много меньше эффективной ширины спектра импульсного отклика кабеля и затухает достаточно быстро. Для импульсных широкополосных сигналов, передаваемых по кабелю, возможна только частичная деконволюция импульсного отклика жил, т.е. применение фильтров сжатия импульсных откликов до определенной формы. Форма выходных импульсов кодовых сигналов значения не имеет, если не нарушается пространственное распределение импульсов. Оптимальной с позиции минимального значения коэффициента усиления дисперсии шумов в этом случае считается симметричная гауссовская форма выходных импульсов фильтров частичной деконволюции (ЧД) импульсных откликов.

Общая методика синтеза фильтров ЧД включает следующие операции:

1. Задание длины кабеля, определение его импульсного отклика и сдвиг отклика (по началу фронта) в начало координат. Полученную функцию будем считать амплитудным откликом h(t) кабеля (без учета задержки сигнала), над которым выполняется преобразование Фурье h(t)  H().

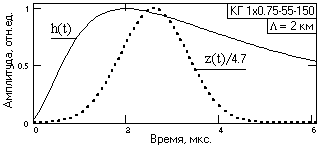
Рис. 5. Форма импульсов.
2. Задание формы выходного импульса z(t) фильтра ЧД в виде гауссовской функции и определение ее спектра z(t)  Z(). Временное расположение импульса z(t) должно быть таким, чтобы площадь импульса практически полностью располагалась за пределами фронта импульсного отклика кабеля. Максимум z(t) должен располагаться за максимумом отклика кабеля (пример на рис. 5). Ширина импульса z(t) подбирается по допуску на коэффициент усиления дисперсии шумов (после расчета оператора ЧД), значение которого, с учетом усиления фильтром амплитуды импульсов, не должно, как правило, увеличивать отношение сигнал/шум. Чем меньше значение  импульса z(t) (больше эффективная ширина T), тем меньше коэффициент усиления дисперсии шумов.

3. Вычисление спектральной плотности передаточной функции фильтра ЧД, которое выполняется по формуле: Hd() = Z()/H(). Функция Hd() имеет смысл только в области значимых значений H() и за пределами этой области должна быть обнулена, что исключит усиление фильтром высокочастотных шумов кабеля.

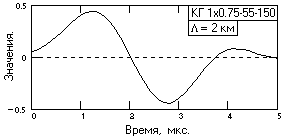
Рис. 6. Оператор ЧД.
4. Обратным преобразованием Фурье функции Hd() вычисляется оператор фильтра ЧД: Hd()  hd(t) (пример оператора на рис. 6).

При подаче на вход кабеля импульса Кронекера _o на выходе фильтра ЧД будем иметь:

s(t)=_o_*h(t)_*hd(t)  1H()Hd()=Z()  z(t),

т.е. выходной единичный импульс вместо асимметричной формы импульсного отклика кабеля будет иметь симметричную форму гауссовского импульса.

Точность воспроизводства фильтром ЧД формы заданной функции выходного импульса определяется размером оператора ЧД, который имеет существенное значение при его технической реализации. Основная часть энергии оператора (более 99%) сосредоточена в пределах интервала, примерно равного (2-3) значениям фронта импульсного отклика, т.е. начальная часть импульсного отклика содержит практически всю информацию о форме сигналов на входе кабеля. Однако, вследствие достаточно длинного спада отклика с постепенным уменьшением скорости спада, чрезмерное ограничение размера оператора ЧД может приводить к появлению на его выходе послеимпульсных «выбросов» и затянуть восстановление нулевой линии.

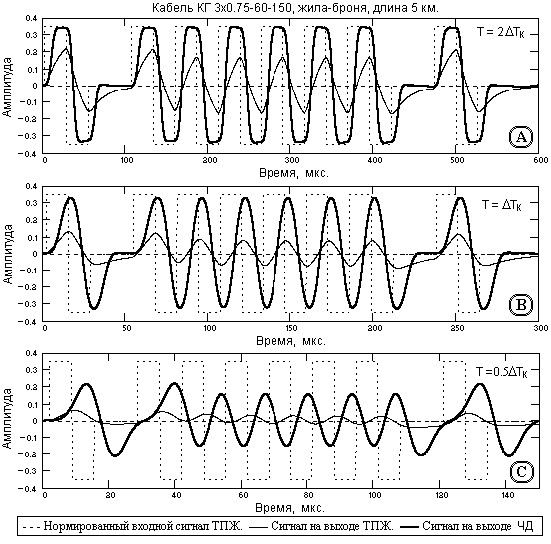
Рис. 7. Биполярные импульсы на входе и на выходе фильтра ЧД.

Пример применения фильтра ЧД для кодовой последовательности биполярных П-импульсов с единичной амплитудой на тактовых интервалах Т = 2T_k, Т = T_k и Т = 0.5T_k мкс (тактовые частоты 19, 38 и 76 кГц) приведен на рис.9. Пунктиром на рисунке показаны входные импульсы, приведенные к выходу кабеля с учетом безвозвратных потерь и задержки в кабеле. Длительность оператора ЧД 20 мкс, коэффициент усиления дисперсии шумов ~0.65, коэффициент усиления амплитуды импульсного отклика жилы ~3.8. Как следует из этого рисунка при его сопоставлении с рисунком 2, применение фильтра ЧД позволяет уменьшить предельный тактовый интервал следования битовых импульсов при идентификации кода минимум в 2 раза, т.е. в 2 раза увеличить скорость передачи информации по кабелю. При коэффициенте усиления дисперсии шумов данного оператора ЧД не более 1 отношение сигнал/шум на выходе фильтра ЧД улучшается практически в 2 раза, т.к. оператор ЧД в этом случае выполняет и роль низкочастотного сглаживающего фильтра.

На рис. 8(A) показана деконволюция кодовых сигналов с тактовой частотой 38 кГц, приведенных ранее без деконволюции на рис. 4 на предельной тактовой частоте 19 кГц. Как следует из рисунка, деконволюция позволяет практически полностью восстановить амплитудные значения сигналов (за вычетом безвозвратных потерь) на удвоенной тактовой частоте, т.е. импульсная пропускная способность кабеля повышается минимум в 2 раза. Что касается предельной импульсной пропускной способности кабеля, то она повышается практически в 4 раза по сравнению с приемом сигналов без деконволюции, о чем достаточно наглядно свидетельствует пример формы тех же кодовых сигналов на тактовой частоте 76 кГц, приведенный на рис. 8(B). Преимущество кода Манчестер-II перед кодом RZ также очевидно. С определенным запасом "прочности" можно считать, что при передаче информации биполярными кодами предельная скорость передачи данных с использованием частичной деконволюции импульсного отклика кабеля может быть увеличена минимумом в 3 раза.

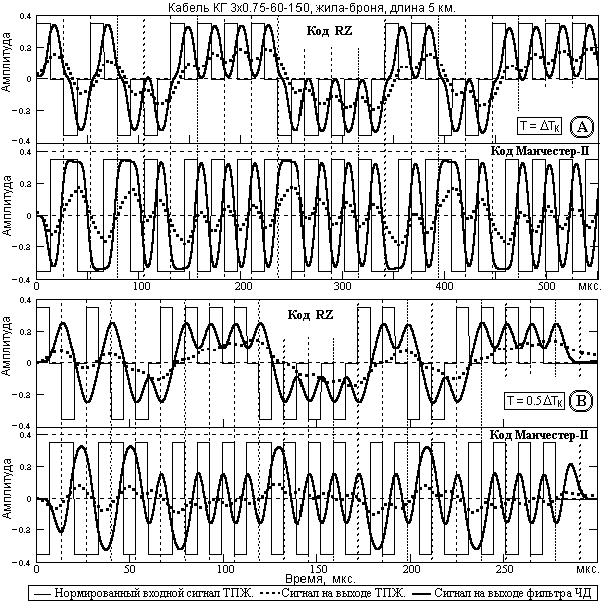
Рис. 8. Деконволюция кодовых выходных сигналов, тактовые частоты 38 и 76 кГц.

Принципы реализация фильтров частичной деконволюции.

Основное условие технической реализации фильтров ЧД – работа в реальном масштабе времени. Дополнительное и желательное условие – автономность, которая позволит включать фильтры ЧД на выход кабеля в состав любой станции, если в том появится необходимость.

Достаточно простая форма передаточной функции фильтра ЧД позволяет выполнить его реализацию непосредственно в виде аналогового нерекурсивного или рекурсивного фильтра. Следует отметить, что такие фильтры будут являться индивидуальными для кабелей различных типов и различной длины (в определенных пределах возможной подстройки) и могут отличаться по исполнению: нерекурсивные - для фильтров с короткой функцией отклика, и рекурсивные для кабелей с длиной 3 и более км.

С учетом темпов развития электроники перспективным и универсальным направлением следует считать цифровые фильтры, микропроцессорные или программные в составе каротажных измерительно-вычислительных комплексов. Детерминированность кодовых сигналов позволяет выполнять цифровые ЧД с автоматической адаптацией под кабель, стоящий на каротажной станции.

Комбинацией дискретного синтеза с аналоговой фильтрацией являются трансверсальные фильтры на линиях задержки. Условия для их реализации аналогичны цифровым фильтрам.

Таблица 2.

Параметры передачи данных (кабель КГ 3х0.75-60-150, жила-броня).

Длина кабеля	км	1	2	3	4	5	6	7
Предельная частота f_пр [по уровню 0.01К_max]	кГц	2460	718	358	220	151	111	85
Шаг дискретизации на предельной частоте (1/2f_пр)	мкс	0.2	0.7	1.4	2.3	3.3	4.5	5.9
Эффективная ширина импульсного отклика T_к	мкс	3.3	8.6	14.1	19.9	26.1	33.1	40.9
Тактовая частота передачи данных f_Т=1/T_к	кГц	306	117	71	50.3	38.3	30.3	24.4
Шаг дискретизации по тактовой частоте (1/4f_Т)	мкс	0.4	1.0	2.2	2.5	3.3	4.1	5.1
Размер оператора ЧД (>98% энергии оператора)	мкс	2.6	5.1	9	13.5	19	25	32
Оптимальный шаг дискретизации данных t	мкс	0.12	0.24	0.4	0.65	1	1.2	1.5

Возможность цифрового исполнения фильтров ЧД можно оценить по таблице 2.

При определении частоты Найквиста цифрового фильтра по частоте f_пр передаточной функции кабеля значение шага дискретизации данных на выходе кабеля находится в диапазоне 0.2-6 мкс в зависимости от длины кабеля. Этот диапазон хорошо согласуется с шагом дискретизации данных по предельной тактовой частоте передачи информации биполярными импульсами (частота Найквиста за третьей гармоникой тактовой частоты). Для исключения трансформации высокочастотных шумов в частотный диапазон, фильтру ЧД должен предшествовать низкочастотный аналоговый фильтр с полосой пропускания до частоты Найквиста или полосовой фильтр основных кодовых частот.

Усиление дисперсии шумов оператором цифрового фильтра зависит от интервала дискретизации его коэффициентов. При увеличении шага дискретизации количество коэффициентов оператора ЧД уменьшается, а их значения возрастают, что вызывает увеличение коэффициента усиления дисперсии шумов. При значении коэффициента усиления дисперсии помех на уровне, не большем 1, шаг дискретизации коэффициентов фильтра ЧД соответствует 20-30 значениям в пределах длительности значимой части оператора ЧД. Соответственно, диапазон оптимальных значений шага дискретизации данных на входе фильтра ЧД, показанных в последней строке таблицы 2, установлен по длине операторов ЧД и составляет от 0.12 до 1.5 мкс. В принципе, такой тактовый диапазон при 20-30 операциях умножения и сложения вполне доступен для современных микропроцессорных систем, особенно для кабелей большой длины, для которых фильтр ЧД и необходим в максимальной степени.

В трансверсальных фильтрах сигнал с кабеля подается на последовательную цепочку линий задержки (ЛЗ), в каждой из которых осуществляется задержка сигнала на интервал дискретизации данных. К выходам ЛЗ подключается матрица резисторов, значения которых обратно пропорциональны значениям коэффициентов оператора ЧД. Токи через резисторы, пропорциональные положительным и отрицательным значениям коэффициентов оператора, суммируются раздельно (на входах операционных усилителей), после чего из "положительного" тока вычитается "отрицательный" и результат подается на вход аппаратуры станции, как выходной сигнал фильтра ЧД. Трансверсальный фильтр хорошо приспособлен для исполнения в качестве автономного промежуточного блока между кабелем и станцией. При переменных сопротивлениях резисторной матрицы фильтр легко подстраивается под любой тип и любую жилу кабеля, а при изменении длины кабеля изменение интервала дискретизации данных выполняется заменой ЛЗ. Некоторые технические трудности могут возникать только в наборе линий задержки для длинных кабелей (большое время задержки) с дополнительным затуханием сигнала в самой ЛЗ, но последнее компенсируется соответствующим изменением коэффициентов резисторной матрицы.

Возможно и комбинированное цифро-аналоговое исполнение фильтра ЧД, в котором роль ЛЗ исполняет сдвиговый цифровой регистр с АЦП на входе (тактовая частота сдвига определяет шаг дискретизации данных), каждая цифровая ячейка которого имеет обратный резисторный ЦАП. Дальнейшая обработка токов ЦАП и формирование выходного сигнала аналогично трансверсальному фильтру. Для кодовых сигналов объем цифровых ячеек регистра может быть в пределах 6-8 двоичных разрядов. В таком исполнении фильтр ЧД становится автономным универсальным блоком с простой и гибкой настройкой под любой тип кабеля любой длины с изменением интервала дискретизации данных частотой тактового сдвига цифрового регистра.

Краткие выводы по возможностям повышения импульсной пропускной способности каротажных кабелей:

1. Качество приема и надежность идентификации кодовой информации на выходе кабеля могут быть существенно повышены при частичной деконволюции импульсного отклика кабеля до симметричной (гауссовской) формы.

2. Скорость передачи кодовых данных при использовании частичной деконволюции импульсного отклика может быть увеличена минимум в 2 раза при любых методах кодирования и равна 1/T_к. При передаче информации биполярными импульсами предельная скорость передачи данных может быть увеличена минимум в 3 раза.

Литература.

1. Гоноровский И.С. Радиотехнические цепи и сигналы.– М.: Сов. радио, 1977.–608 с.

2. Сиберт У.М. Цепи, сигналы, системы. Часть 2. – М.: Мир, 1988. – 360 с.

3. Сильвинская К.А., Голышко З.Н. Расчет фазовых и амплитудных корректоров: Справочник. – М.: Связь, 1980. – 104 с.

4. Стрижевский Н.З. Коаксиальные видеолинии. – М.: Радио и связь, 1988. – 200 с.

5. Мамлеев Т.С., Давыдов А.В. Импульсная пропускная способность каротажных кабелей. // Известия УГГГА. Вып. 15. Серия: Геология и геофизика, 2002, стр. 155-166.

Несколько сокращенный вариант статьи опубликован в трудах УГГГА:

Частичная деконволюция импульсного отклика каротажного кабеля. / Давыдов А.В., Мамлеев Т.С. // Известия Уральской государственной горно-геологической академии. Вып. 15. Серия: Геология и геофизика, 2002, стр. 149-155, рус.

Математическое моделирование передачи данных по кабелю показало, что качество приема и надежность идентификации кодовой информации на выходе кабеля могут быть существенно повышены при частичной деконволюции импульсного отклика кабеля до симметричной (гауссовской) формы. Предельная скорость передачи кодовых данных при использовании частичной деконволюции импульсного отклика может быть увеличена минимум в 2 раза при любых методах кодирования и минимум в 3 раза при передаче информации биполярными импульсами. Разработаны принципы реализации фильтров частичной деконволюции импульсных откликов кабелей.

Замечания, предложения, дополнительные материалы по данной теме прошу сообщать по адресу: prodav@narod.ru. Буду благодарен за возможность доработки, улучшения, упрощения математической модели каротажных кабелей (совместно с Вами).

Blog

2 статья. Удк 539 083: 550. 83: 621. 315. 2

Содержание