Geum.ru

Визначення розмірів земної тіні під час місячного затемнення

Вид материалаДокументы

Содержание


Подставим значение в формулу (5)
Подобный материал:

Катане Юлія

ВИЗНАЧЕННЯ РОЗМІРІВ ЗЕМНОЇ ТІНІ
ПІД ЧАС МІСЯЧНОГО ЗАТЕМНЕННЯ.


Робота виконана Катане Юлією Олександрівною

Ученицею 10 класу ЗОШ №31 м.Одеси

Науковий керівник – канд. фіз. – мат. наук,


науковий співробітник Астрономічної

обсерваторії ОНУ Марсакова В.І.

2003 р.


Во все времена людей привлекало все неизвестное и таинственное. Например, лунные и солнечные затмения. Наблюдая их люди в стародавние времена нередко испытывали страх. Во время лунного затмения Луна покрывалась непонятной им тенью, часто при этом становилась красной, будто обливалась кровью. Суеверные люди видели в этом явлении нападение чудовищ или злых духов на Луну, тоже считавшуюся у язычников божеством, ее ранение или даже убийство. А во времена господства христианской религии усиленно распространялись слухи о том, что это Бог напоминает грешникам о первом злодеянии Каина, старшего сына первых людей Адама и Евы, убившего своего брата Авеля.

В своем вечном движении вокруг Солнца Земля не одинока ее сопровождает единственный естественный спутник Луна- самое близкое к Земле небесное тело. Вместе со звездами Луна восходит над горизонтом в восточной стороне неба постепенно поднимается и смещается в сторону южной его области, а достигнув в ней наибольшей высоты, медленно опускается к западной стороне горизонта и наконец исчезает за ним. Это движение Луны вместе с небом с востока к западу, аналогичное суточному движению звезд и Солнца, объясняется вращением Земли вокруг своей оси.

Наблюдения показывают, что Луна перемещается на фоне звезд по большому кругу лунному пути, который, подобно эклиптике, тоже пролегает по зодиакальным созвездия, поднимается, но не совпадает, а пересекается с нею под углом 5°09' (измеряющемся от 4°59' до 5°19') в двух диаметрально противоположных точках называемых лунными узлами и отстоящих друг от друга на расстоянии в 180°. Водном из них, получившем название восходящего узла, Луна в своем движении пересекает эклиптику, поднимается над ней в северном направлении и постепенно удаляется от нее на 5°9', а затем приближается к ней, в противоположном, снисходящем узле снова ее пересекает и отходит к югу на то же расстояние.

Луна обращается вокруг Земли по большому кругу – Лунному пути, с периодом 27,32 суток, причем ее движение неравномерно. При каждом своем обороте Луна то приближается к Земле, то несколько удаляется от нее, и с такой же правильностью возрастает и уменьшается скорость движения Луны в пространстве. Следовательно, можно утверждать, что Луна обращается вокруг Земли с Запада к Востоку по эллиптической орбите, в одном из фокусов которой расположена наша планета. Плоскость Лунной орбиты в пересечении с небесной сферой образует большой круг – Лунный путь, а плоскость Земной орбиты, как нам уже известно, пересекается с небесной сферой по эклиптике, и так как в пространстве первая плоскость образует со второй угол 5°09', то поэтому и Лунный путь наклонен к эклиптике под таким же углом. Обе эти плоскости пересекаются друг с другом по прямой линии, проходящей через центр Земли и называемой линией узлов Лунной орбиты, и как раз на этой линии лежат лунные узлы в диаметрально противоположных направлениях от Земли, то есть на 180° друг от друга.

В греческом языке Земля именуется словом «Гея», и от этого слова произошли следующие названия: геоцентрическое расстояние – расстояние от Земли; перигей (П) – ближайшая к Земле точка лунной орбиты; перигейное расстояние (q) – расстояние перигея от Земли; апогей (А) – наиболее удаленная от Земли точка Лунной орбиты; апогейное расстояние (Q) – геоцентическое расстояние апогея.

Перигей и апогей лежат на большой оси Лунной лорбиті, а средним геоцентрическим расстоянием Луны является большая полуось ее орбиты.

И вот выяснилось, что при каждом обороте вокруг Земли Луна приближается к ней и удаляется от нее на неодинаковые расстояния: перигейное расстояние Луны систематически изменяется в пределах от 256410 км до 369960 км, а апогейное расстояние – от 404180км до 406740км. Поэтому Лунный диск, диаметр которого близок к 0°5', несколько меняет свои размеры: когда Луна проходит перигей, ее угловой диаметр может быть от 33',5 до 32',5, а при прохождении апогея – от 29',6 до 29',3. Наиболее часто перигейные расстояния Луны q=363300км, а апогейное расстояние Q=405500км, и, следовательно, среднее геоцентрическое расстояние а=384400км, при котором диаметр лунного диска d=31',1.

Лунный путь не занимает постоянного положения на небе, а сравнительно быстро сдвигается от востока к западу, и поэтому за сидерический месяц Лунные узлы перемещаются по эклиптике в том же направлении, то есть навстречу движению Луны, на 1°,5, а за год - 19°,3. Это движение Лунных узлов по эклиптике с востока к западу называется отступлением узлом, потому что в астрономии прямым движением считается движение в восточном направлении. Отступление Лунных узлов объясняется поворотом в пространстве самой плоскости Лунной орбиты, в следствии чего поворачивается ее линия узлов, и полный поворот на 360° по эклиптике Лунные узлы проходят за период времени Ту=360/19°,3=18,6года или 18 лет 7 месяцев.

Всем хорошо известно изменение виды Луны от тонкого серпа ло полного диска, и снова к тонкому серпу. Вид Луны называется Лунной фазой. Обращаясь вокруг Земли, Луна последовательно занимает различные положения относительно Солнца, и так как с Земли видна только освещенная часть Лунного шара, то происходи смена Лунных фаз. Поэтому, более точно, Лунная фаза представляет собой видимую в солнечном освещении часть Лунного диска и определяется отношением наибольшей ширины (b) этой части к его диаметру (d), то есть фаза ф=b/d и математически всегда выражается десятичной дробью с точностью, как правило, до 0,001.

Когда Луна проходит между Землей и Солнцем, к Земле обращено неосвещенное Лунное полушарие, Луна не видна, ее фаза ф=0,00 называется новолунием. Лунную фазу иногда характеризуют условным возрастом Луны, то есть числом суток, протекающих после новолуния, при котором принимается возраст д=0д,0.

После новолуния Луна постепенно отходит к востоку от Солнцу и приблизительно через двое суток при удалении от него на 26 градусов, становится видимой по вечерам в западной половине еще светлого неба в форме узкого серпа (фаза близка к 0,1).

По мере смещения луны к востоку от Солнца видимая с Земли освещенная часть Лунной поверхности увеличивается, Лунная фаза растет, и через неделю после новолуния, когда Луна отойдет на 90 градусов от солнца, уже видна вся правая половина диска – наступает фаза первой четверти (ф=0,50, возраст д=7д,7).

Через 14-15 суток после новолуния Луна приходит в противостояние с Солнцем ( на 180 градусов от него) и ее фаза становится полной (ф=1,00, возраст д=14д,8), так как солнечные лучи освещают все Лунное полушарие, обращенное к Земле.

После полнолуния Луна постепенно приближается к Солнцу с запада, освещается ним слева и поэтому ущерб Луны, то есть уменьшение ее фазы, начинается с правого края, а выпуклость освещенной части обращена к востоку.

Примерно через неделю, когда угловое расстояние между Луной и Солнцем сократилось на 90 градусов, наступает фаза третьей, или последней четверти (ф=0,50, д=22д,2).

При дальнейшем сближении Луны с Солнцем ее убывающие фазы становятся серповидными с выпуклостью влево, напоминая букву «С».

Лунные затмения представляют собой физические явления прохождения Луны сквозь Земную тень, имеющую, как и у Луны, форму сходящего круглого конуса, окруженного расходящейся полутенью. В зависимости от гелиоцентрического расстояния Земли, длина ее тени может быть различной – от 1 359 тыс.км до 1 405 тыс.км., а при среднем расстоянии близка к 1 382 тыс.км., то есть всегда больше геоцентрического расстояния Луны. Чтобы произошло Лунное затмение, Луна должна противостоять Солнцу, то есть быть в фазе полнолуния. Перед погружением в Земную тень Луна проходит сквозь полутень Земли, но ослабление Лунного света при этом настолько ничтожно, что невооруженным глазом не обнаруживается.

Участок эклиптики, на котором происходят Лунные затмения, называется зоной Лунных затмений, и ее границы определяются внешним касанием Луны с Земной тенью.

Положение этих границ относительно Лунного узла вычисляется по формуле: sin l =tg *ctg i, в которой наклонение Лунного пути к эклиптике i = 5°,2 =5°09', а угловое расстояние между центрами Лунного диска и Земной тени  =  =r+r( , где r – радиус Земной тени и r( - радиус Лунного диска. Видимый радиус Луны меняется в пределах от 14'40'' до 16'46'', а ее горизонтальный параллакс П, даже при одно геоцентрическом расстоянии, несколько различен в разных местах Земли из-за ее сплюсности у полюсов. Чем ближе к Лунному узлу происходит Лунное затмение, тем больше его фаза.

Фазой Лунного затмения называется степень покрытия Земли Луной и измеряется отношением закрытой части (d) диаметра Лунного диска ко всему диаметру (d().

Ф = d/ d(

Фаза Лунного затмения всегда выражается десятичной дробью. Для любого момента затмения его фаза может вычисляться по радиусам земной тени, Солнечного диска и угловому расстоянию. Поскольку d( = 2 r( ; d= r(- ( - r).

Ф=( r( + r-)/(2 r()

Последовательность солнечных и Лунных затмений зависит от условий наступлений новолуний и полнолуний вблизи Лунных узлов. Так как на протяжении одного календарного года происходит от одного до пяти солнечных и от 0 до 3-х Лунных затмений, и , казалось бы наибольшее число затмений в году равно 8. Однако здесь, образно говоря, арифметика «нарушается». Ведь пятое солнечное и третье Лунное затмения происходя из=за смещения Лунных узлов навстречу Солнцу и Луне, и поэтому лишь одно из них может произойти в конце текущего календарного года, а второе придется уже в начало года. Таким образом, наибольшее число затмений в одном календарном году не превышает 7.Обычно на протяжении года происходят от2 –3 Солнечных и 1 –2 Лунных затмения. Тем не менее Лунные затмения наблюдаются значительно чаще только потому, что они видны со всего ночного полушария Земли, в то время, как Солнечные – только из области Лунной тени и полутени, да и к тому же частные Солнечные затмения не привлекают к себе внимания и потому проходят незаметно.

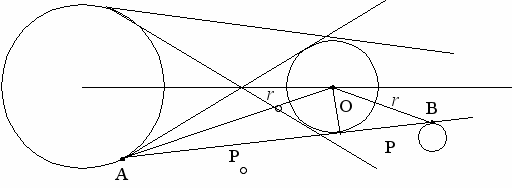
Чтобы охарактеризовать размеры Земной тени во время лунных затмений найдем угловой радиус лунной тени и полутени. Угловой радиус тени обозначим буквой r , а полутени - R. Рассмотрим рисунок 1:


Р
исунок 1.



(1)

Рассмотрим треугольник AОB:



(2)

Мы выразили угол O через параллаксы луны и солнца теперь подставим выражение угла O в формулу (1):





Задача предвычислений лунных затмений состоит в определении моментов касания Луны с тенью и полутенью Земли. Вследствие наличия у Земли атмосферы, контуры земной тени и полутени всегда несколько размыты. Эта размытость учитывается введением в размеры контуров тени и полутени поправочного коэффициента k = 1,02. Горизонтальный параллакс Луны P´ относят не к экваториальному радиусу Земли а к ее серединному радиусу, соответствующему географической широты 45º, поэтому P´ = 0,99833 P.

Учитывая эти коофициэнты, имеем:

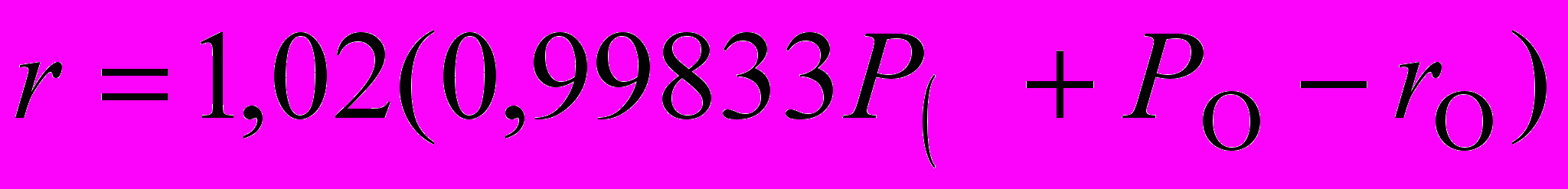(3)

Ч
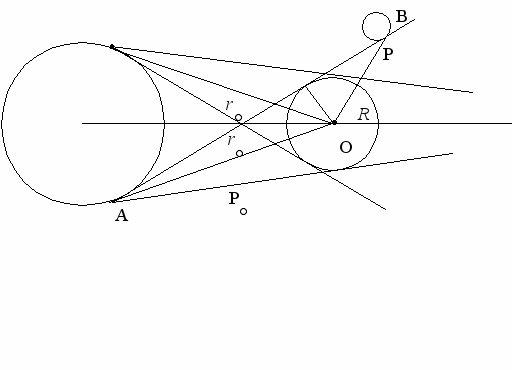
тобы найти угловой радиус лунной полутени рассмотрим другой рисунок(рис. 2):


Рисунок 2.


Рассмотрим треугольник АОВ:









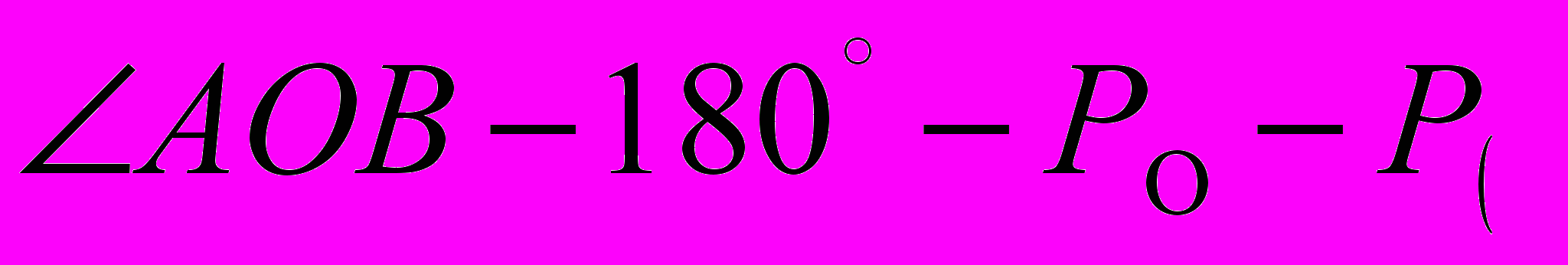
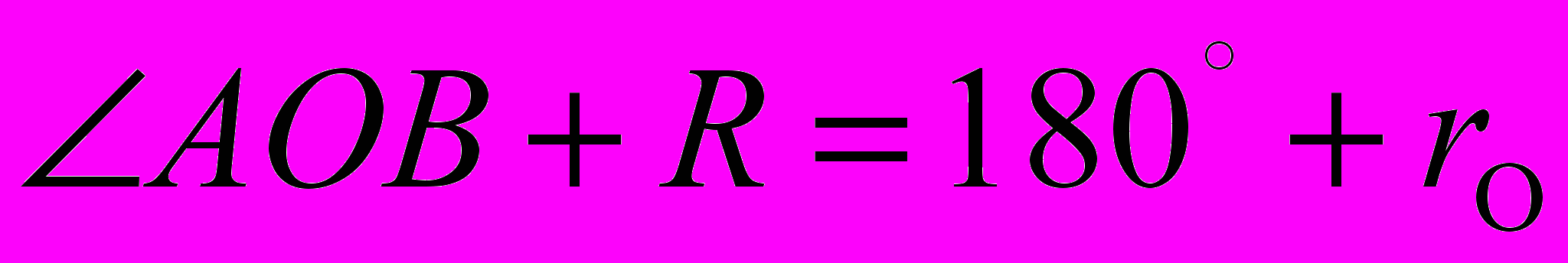
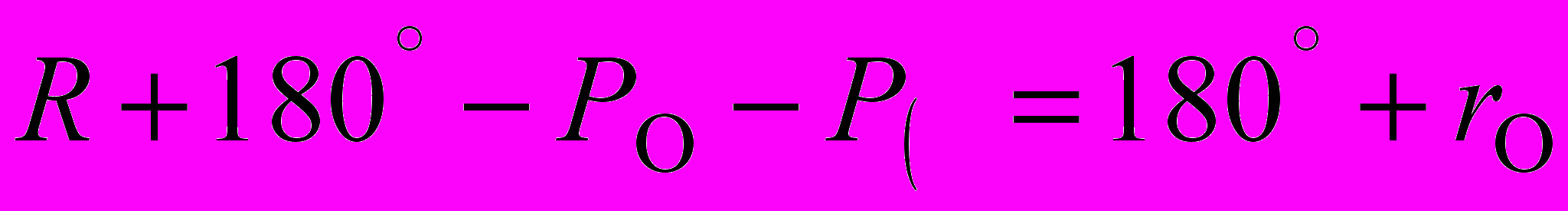
Учитывая коэффициенты, поданные выше, получаем формулу:

(4)

Теперь выражаем параллаксы Луны и Солнца через радиусы Земли, Солнца и Луны и видимого углового радиуса Солнца и Луны.

Рассмотрим рисунок 3:

Р
исунок 3.

Пускай расстояние от центров Земли и Луны равняется x. Тогда

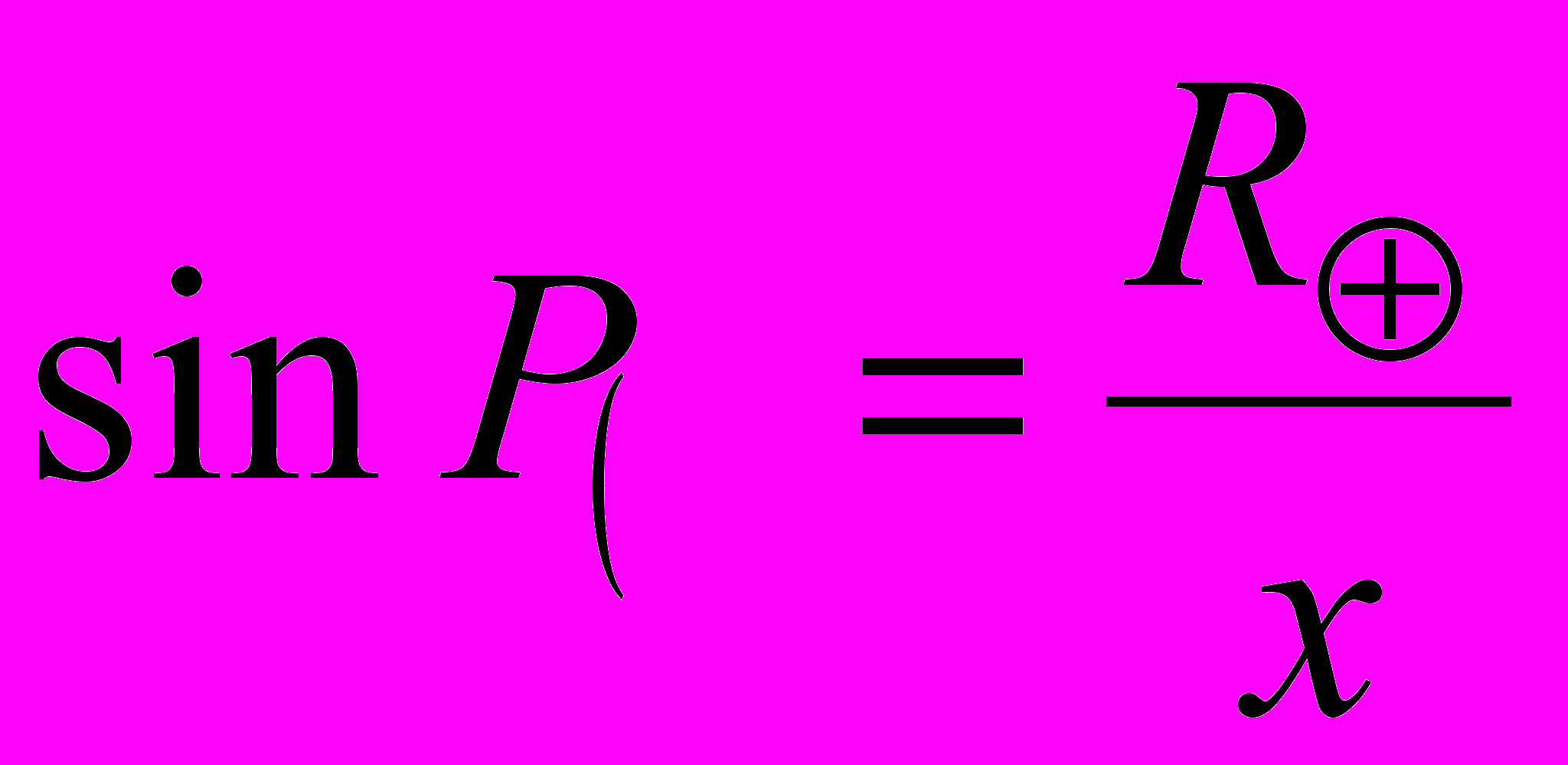(5)

рассмотрим рис.4

Р
исунок 4



С помощью рисунка 4 выражаем расстояние от центров Земли и Луны:

(6)

где 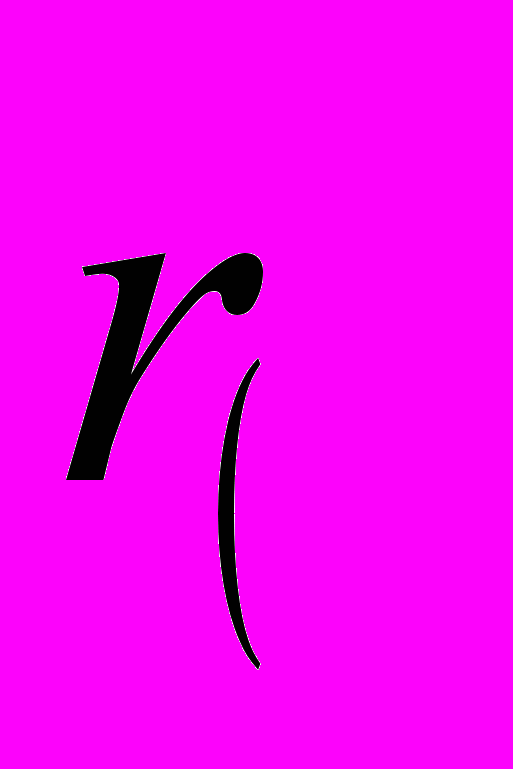- видимый радиус Луны.

Подставим значение в формулу (5):


.

Аналогично вычисляем параллакс Солнца:

,

где 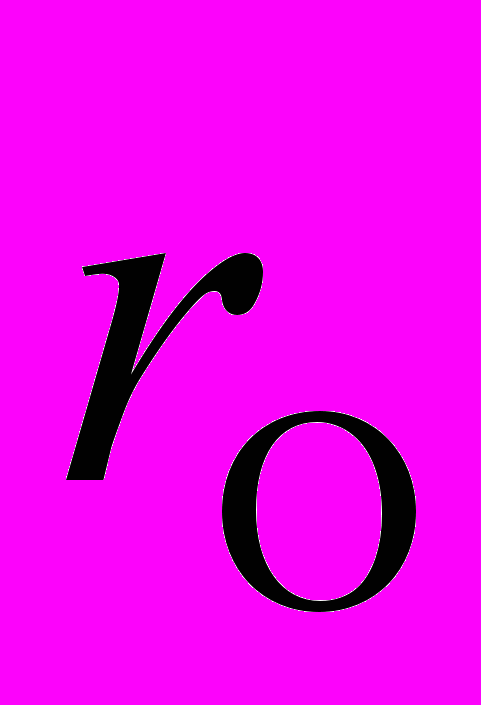- видимый радиус Солнца.

Но значения параллаксов Луны и Солнца настолько малы, что синус угла равен самому углу, поэтому:





Подставим выражения параллаксов Луны и Солнца в формулы (3) и (4):





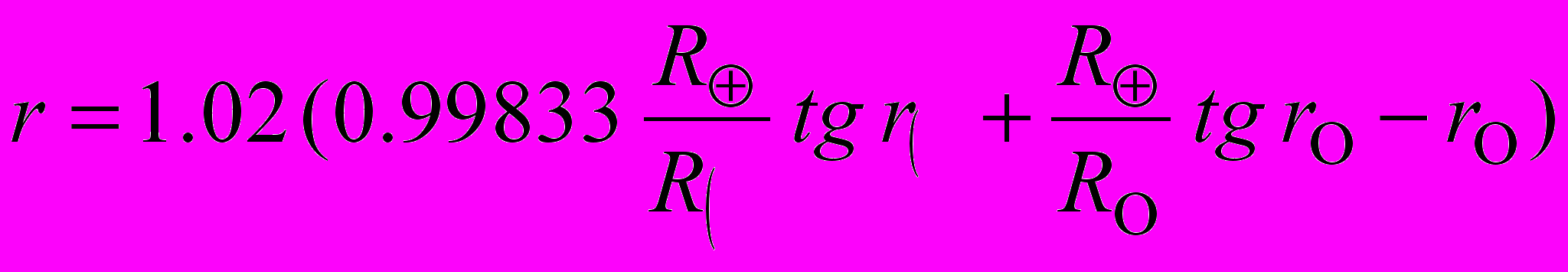
Из астрономического словаря за 2001 год найдем значения видимого диаметра Луны во время лунного затмения 09.01.01 и видимый диаметр Солнца :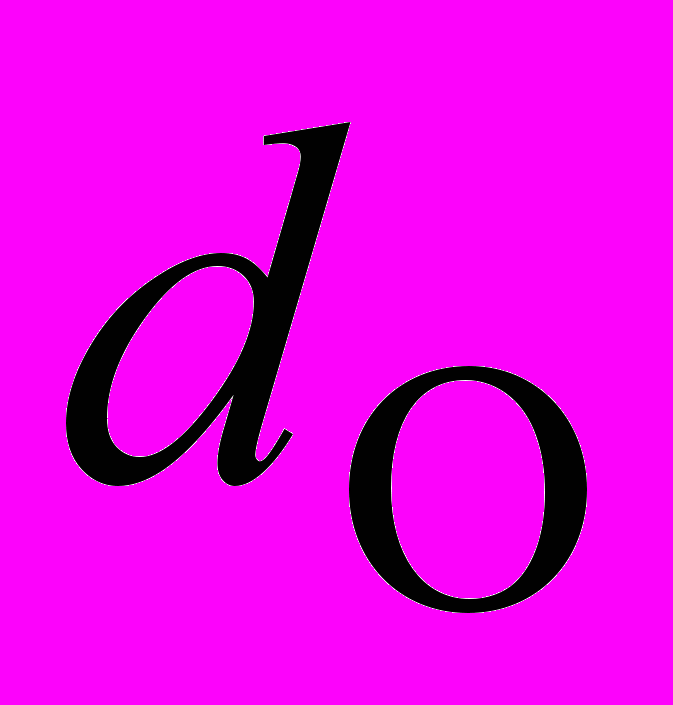

,

,





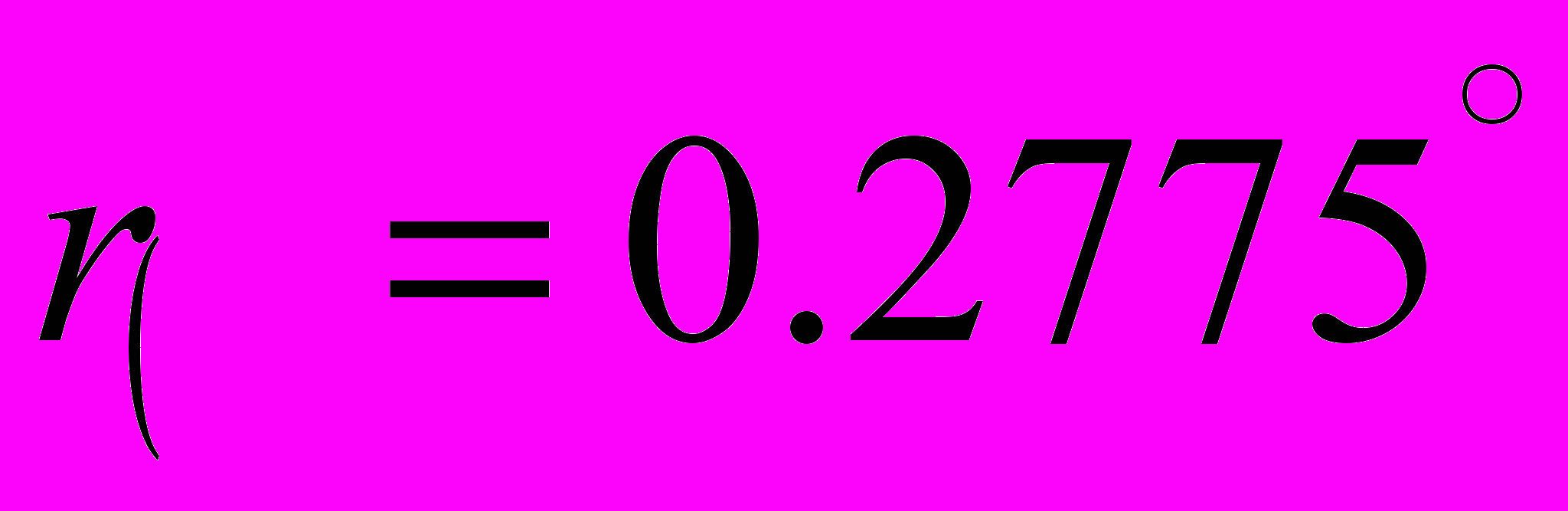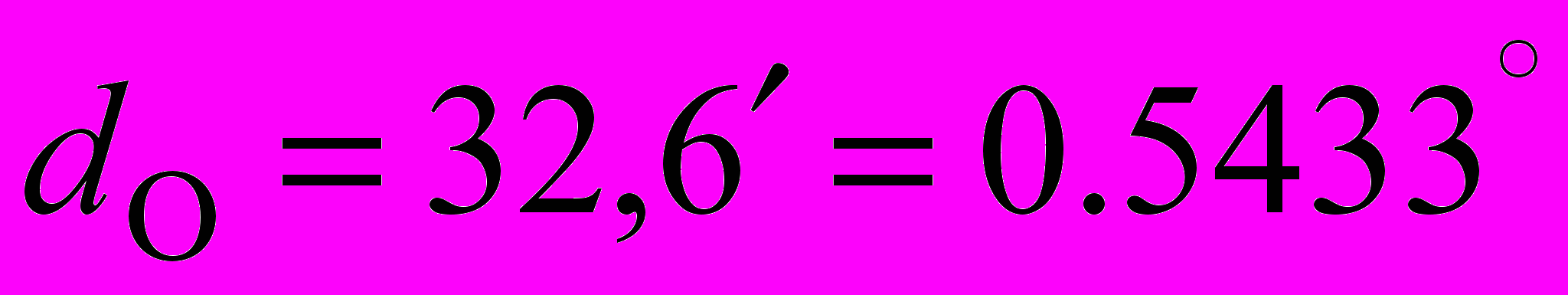
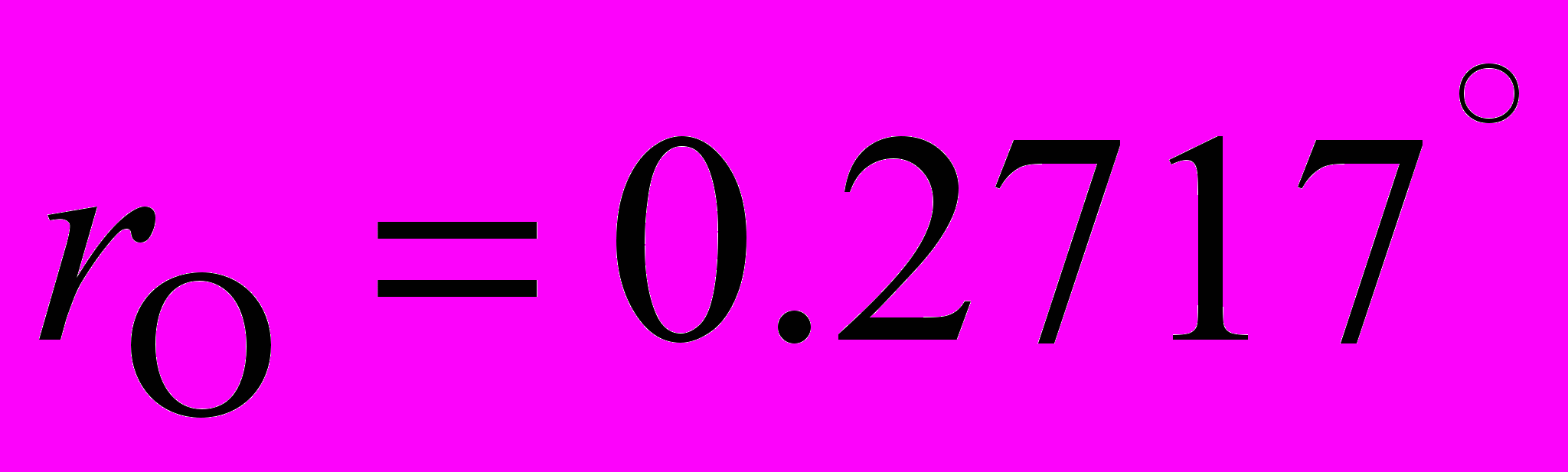
Итак, зная видимые радиусы Луны и Солнца, радиусы Луны и Солнца, мы можем вычислить угловой радиус тени и полутени Луны во время Лунного затмения 9 января 2001 года:






Мы нашли числовые значения видимых угловых радиусов тени и полутени Луны. Теперь найдем числовые значения видимых радиусов тени и полутени Луны, выраженных в километрах. Чтобы найти значение видимого радиуса тени Луны в километрах (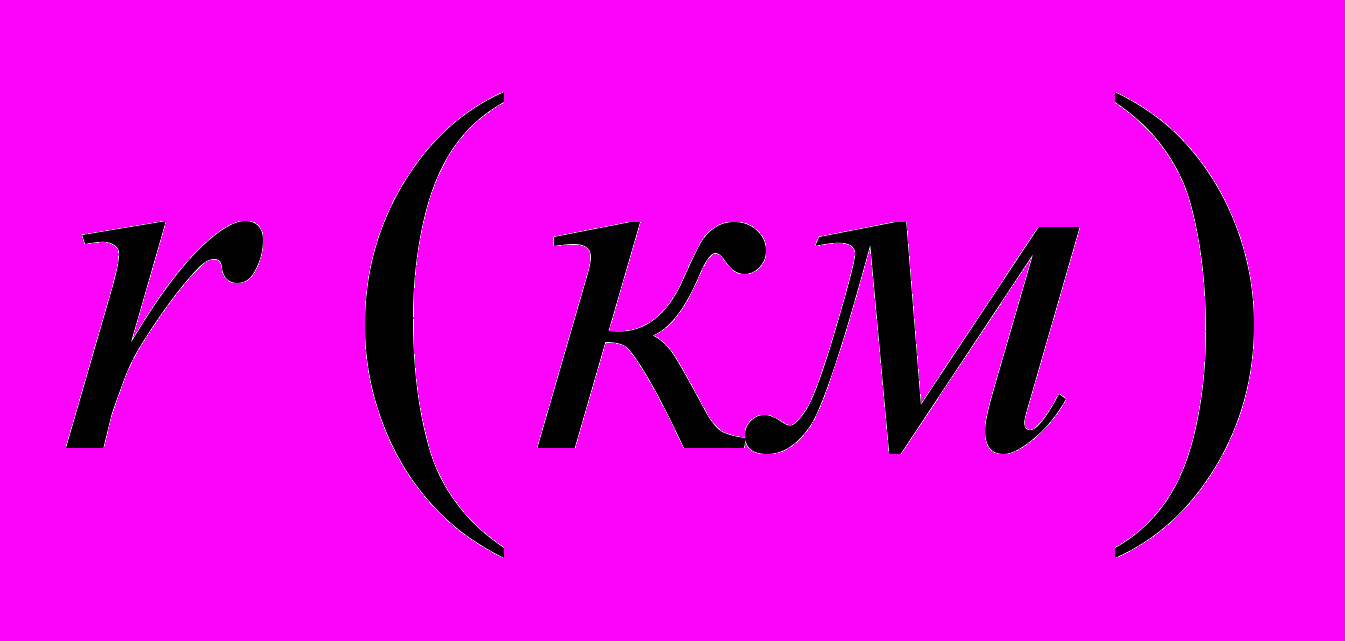), поделим видимый угловой радиус Луны на видимый радиус Луны, который мы взяли в Астрономическом словаре за 2001 год, и умножим на радиус Луны ( ):



Аналогично, для вычисления видимого радиуса полутени (R(км)):



Теперь сравним полученный R(км) с тем, который мы може посчитать с помощью фотографий (r'(км)). Чтобы точнее посчитать видимый радиус тени во время Лунного затмения (r'(км)) возьмем среднее арифметическое из видимых радиусов тени, которые мы посчитаем для 4 фотографий:

r'(км) = (r1'(км)+ r2'(км)+ r3'(км)+ r4'(км))/4

Видимый радиус тени во время Лунного затмения можно вычислить по формуле:

ri'(км) = a/(2sin (/2)),

где а – хорда к окружности тени, которую мы видим на фотографии,  - угол между радиусами, проведенными к концам хорды.

1 фотография

=49°

а=6см

r1'(км) = 6/(2* sin(49°/2))=7,23


2 фотография

=37°

а=5,9см

r1'(км) = 5,9/(2* sin(37°/2))=9,30


3 фотография

=35°

а=5,3см

r1'(км) = 5,3/(2* sin(35°/2))=8,81


4 фотография

=23°

а=4,4см

r1'(км) = 5,3/(2* sin(35°/2))=11,03

Таким образом,

r'(км) = 9,9см.

Получено расчетное значение радиуса (по фотографии) 4576,6км, что близко к данным, полученным в результате проведенных вычислений.

Таким образом, значение вычисленного радиуса Земной тени соответствует определенному по фотографии радиусу.