Geum.ru

Ввода-вывода (bios). Понятие cmos ram 7 базы данных. Системы управления базами данных 8

Вид материалаДокументы

Содержание


Логическая схема полусумматора. сумматор двоичных чисел
А, В — слагаемые и Ро — перенос из младшего разряда и два выхода: сумма S и перенос Р.
Логическая схема триггера
R (Reset — сброс) и два выхода Q
R = 0 и S = 0,_то триг­гер находится в режиме хранения, на выходах Q
Логическое сложение. таблица истинности
Подобный материал:
1   ...   16   17   18   19   20   21   22   23   ...   49

ЛОГИЧЕСКАЯ СХЕМА ПОЛУСУММАТОРА. СУММАТОР ДВОИЧНЫХ ЧИСЕЛ


Вспомним, что при сложении двоичных чисел образуется сумма в данном разряде, при этом возможен перенос в стар­ший разряд. Обозначим слагаемые как А, В, перенос — как Р и сумму — как S. Таблица сложения одноразрядных дво­ичных чисел с учетом переноса в старший разряд выглядит следующим образом:



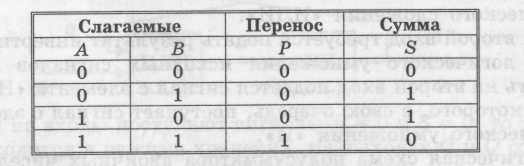
Из этой таблицы видно, что перенос можно реализовать с помощью операции логического умножения:

Р =А&В.

Получим теперь формулу для вычисления суммы. Значе­ния суммы близки к результату операции логического сложения (кроме случая, когда на входы подаются две едини­цы, а на выходе должен получиться нуль).

Нужный результат достигается, если результат логиче­ского сложения умножить на инвертированный перенос. Та­ким образом, для определения суммы можно применить сле­дующее логическое выражение:



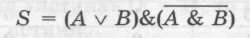
Построим таблицу истинности для данного логического выражения и убедимся в правильности нашего предположе­ния.

Т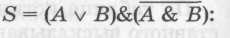аблица истинности логической функции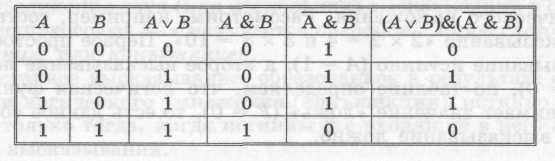



Теперь, на основе полученных логических выражений, можно построить из базовых логических элементов схему полусумматора.

По логической формуле переноса легко определить, что для получения переноса необходимо использовать логиче­ский элемент «И».

Анализ логической формулы для суммы показывает, что на выходе должен находиться элемент логического умноже­ния «И», который имеет два входа. На один из входов пода­ется результат логического сложения исходных величин A \/ В, то есть на него должен подаваться сигнал с элемента логического сложения «ИЛИ».

На второй вход требуется подать результат инвертирован­ного логического умножения исходных сигналов 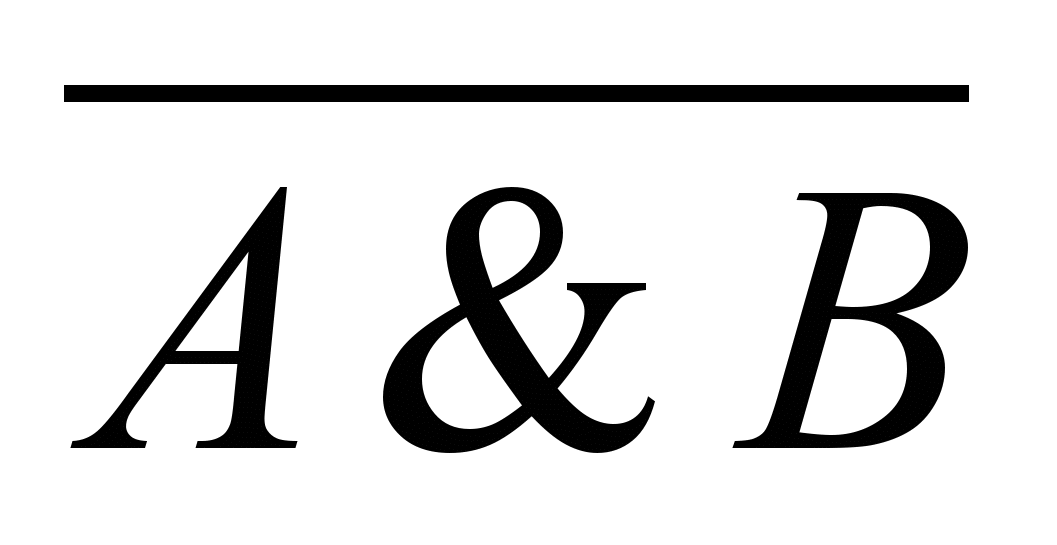, то есть на второй вход подается сигнал с элемента «НЕ», на вход которого, в свою очередь, поступает сигнал с элемента логического умножения «И».

Логическая схема полусумматора двоичных чисел:



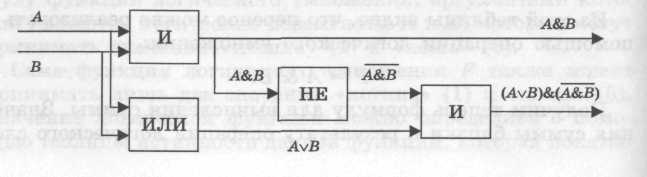
Данная схема называется полусумматором, так как реа­лизует суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.

Полный одноразрядный сумматор должен иметь три вхо­да: А, В — слагаемые и Ро — перенос из младшего разряда и два выхода: сумма S и перенос Р.

Многоразрядный сумматор процессора состоит из полных одноразрядных сумматоров. Сложение каждой пары раз­рядов реализует одноразрядный сумматор, причем выход (перенос) сумматора младшего разряда подключен ко входу сумматора старшего разряда.

ЛОГИЧЕСКАЯ СХЕМА ТРИГГЕРА


Важнейшей структурной единицей оперативной памяти компьютера, а также внутренних регистров процессора яв­ляется триггер. Это устройство позволяет запоминать, хра­нить и считывать информацию (каждый триггер может хра­нить 1 бит информации).

Триггер можно построить из двух логических элементов «ИЛИ» и двух элементов «НЕ». Триггер имеет два входа S (Set — установка) и R (Reset — сброс) и два выхода Q и .

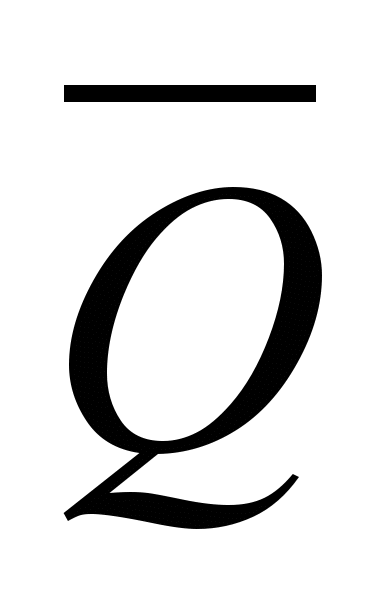Логическая схема триггера:



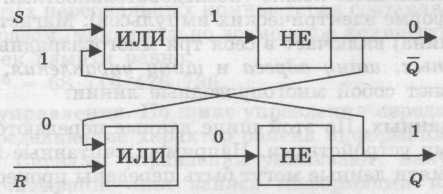
Если на входы поступают сигналы R = 0 и S = 0,_то триг­гер находится в режиме хранения, на выходах Q и сохра­няются установленные ранее значения.

Если на установочный вход S поступает на короткое время сигнал 1, то триггер переходит в состояние 1 и после того, как сигнал на входе S станет равен 0, триггер будет со­хранять это состояние, то есть будет хранить 1.

При подаче 1 на вход R триггер перейдет в состояние 0.

Подача на оба входа S и R логической единицы может привести к неоднозначному результату, поэтому такая ком­бинация входных сигналов запрещена.




ЛОГИЧЕСКОЕ СЛОЖЕНИЕ. ТАБЛИЦА ИСТИННОСТИ


Объединение двух (или нескольких) высказываний с по­мощью союза «или» называется операцией логического сло­жения или дизъюнкцией.

Составное высказывание, образованное в результате ло­гического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых выска­зываний.

Так, из приведенных ниже четырех составных высказыва­ний, образованных с помощью операции логического сложе­ния, ложно только первое, так как в последних трех состав­ных высказываниях хотя бы одно из простых высказываний истинно:
  1. «2x2=5 или 3 х 3 = 10»
  2. «2x2=5 или 3x3=9»
  3. «2x2 = 4 или 3x3 = 10»
  4. «2x2 = 4 или 3x3 = 9»

Запишем теперь операцию логического сложения на фор­мальном языке алгебры логики. Операцию логического сло­жения (дизъюнкцию) принято обозначать либо знаком «v», либо знаком сложения «+». Образуем составное высказыва­ние F, которое получается в результате дизъюнкции двух простых высказываний:

F = A v В.

С точки зрения алгебры высказываний, мы записали фор­мулу функции логического сложения, аргументами которой являются логические переменные А и В, которые могут при­нимать значения «истина» (1) и «ложь» (0).

Сама функция логического сложения F также может при­нимать лишь два значения «истина» (1) и «ложь» (0). Значе­ние логической функции можно определить с помощью таб­лицы истинности данной функции, которая показывает, какие значения принимает логическая функция при всех возможных наборах ее аргументов.

Таблица истинности операции логического сложения:




По таблице истинности легко определить истинность со­ставного высказывания, образованного с помощью операции логического сложения. Рассмотрим, например, составное высказывание «2x2 = 4 или 3 х 3 = 10». Первое простое вы­сказывание истинно (А = 1), а второе высказывание ложно (В = 0), по таблице определяем, что логическая функция принимает значение «истина» (F = 1), то есть данное состав­ное высказывание истинно.