Вертгеймер М. В 35 Продуктивное мышление: Пер с англ./Общ ред. С. Ф. Горбова и В. П. Зинченко. Вступ ст. В. П. Зин­ченко

Вид материала

Книга

Содержание См. также См. также См. также См. также См. также См. также См. также См. также См. также См. также См. также См. также См. также

Подобный материал:

• Productive thinking, 4226.18kb.
• Сорокин П. А. С 65 Человек. Цивилизация. Общество / Общ ред., сост и предисл., 11452.51kb.
• Вступительная статья, 4331.44kb.
• Жизнь счастливого человека (А. Маслоу), 76.37kb.
• Ганс Селье. От мечты к открытию, 5951.77kb.
• Вебер М. Избранные произведения: Пер с нем./Сост., общ ред и послесл. Ю. Н. Давыдова;, 402.04kb.
• Новые поступления литературы (июль сентябрь 2002) математика инв. 62350 в 161., 125.41kb.
• Книга может быть использована как учебное пособие теми, кто интересуется теорией личности, 4021.86kb.
• Декарт Р. Д 28 Сочинения в 2 т.: Пер с лат и франц. Т. I/Сост., ред., вступ ст., 8822.95kb.
• Р. Глен. Гроші, фінансова система та економіка, 247.83kb.

Уравновешивание палки

Когда вы предлагаете детям построить из кубиков Т-об­разную конструкцию, положив один из кубиков вертикаль­но и уравновешивая второй на вершине первого в горизон­тальном положении, интересно наблюдать за развитием действий испытуемых, следить за тем, как они приходят к пониманию того, что устойчивость структурно требует симметрии.

Эту же проблему предполагает задание по переносу длинных палок (выполнение которого интересно изучать и на собаках). Сначала дети экспериментируют с палкой, часто они сдаются после нескольких отрицательных проб. Но некоторые дети упорствуют, и большинство из них через некоторое время возвращается к задаче. Интересно наблюдать, как они учатся на своих ошибках. Пробы, при­водящие к отрицательным результатам, являются не про­сто негативными случаями. Конечно, иногда ребенок про­изводит слепые изменения, но очень часто мы наблюдаем, что он действует вполне осмысленно. Например, берет пал­ку левее центра, и она падает направо, в следующей по­пытке ребенок может слепо повторить действие, схватив палку в том же самом месте — или даже еще левее, — но часто дети осмысленно корректируют свои действия, они хватают ее немного правее. Они могут схватить палку не­достаточно или слишком далеко, но в следующей попытке они стараются произвести осмысленную коррекцию. Часто поведение в целом является вполне последовательным. В этом заключается основное различие между последова­тельностью случайных проб и последовательностью проб, которая обладает осмысленной структурой.

Например, если кто-нибудь стреляет, не видя цели и не имея возможности посмотреть, куда попала пуля, и только получая информацию (или как-то иначе узнавая) о том, что он не попал в цель, то он не сможет осмысленно изме­нить направление следующего выстрела. Но если он смо-

324

жет увидеть, к какому отрицательному результату приве­ла его попытка, то тогда выбранное им направление пока­жет различие между бессмысленным и осмысленным пове­дением. Предположим, что, выстрелив первый раз, он попал в точку 1, расположенную правее цели. Было бы глупо в следующий раз стрелять еще правее.

2 t 3 1

Разумнее в следующий раз прицелиться так, чтобы по­пасть в точку 2 или 3, корректируя прицел на основании отклонения и таким образом продолжая приближаться к цели.

Мы вскоре замечаем, что дети, решая задачу с кубика­ми или с длинной палкой, склонны фокусировать свое вни­мание примерно на середине.

Естественно, что при произвольном введении какого-ни­будь скрытого фактора возникают трудности. Но даже в экспериментах с такой измененной палкой часто встреча­ются разумные действия (например, в случае, когда в ка­ком-то месте палки находится свинец). Но то, что ребенок научился успешно действовать в такой ситуации, может не привести к осмысленным попыткам в других случаях, когда свинец может находиться в каком-нибудь другом месте, поскольку оно является совершенно произвольным.

Если, однако, внешний вид объекта свидетельствует о явной асимметрии, как, например, на следующих рисун­ках, то ситуация оказывается совершенно иной.



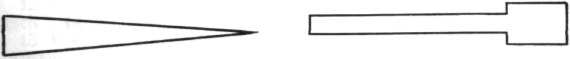
Рис. 183

В этом случае с самого начала отсутствует тенденция схватить палку точно посередине, дети склонны скорее ка­ким-то образом компенсировать асимметрию.

Следует различать случаи, когда ребенок руководству­ется какой-нибудь внешней произвольной связью, и слу­чаи, когда его действия соответствуют разумной корреля­ции факторов. Если, к примеру, ребенок обучен держать палку за середину, где расположено красное пятно, или — в том случае, когда одна половина палки окрашена в крас­ный цвет, а другая — в зеленый, — в месте, где меняются

325

цвета, то ситуация становится с теоретической точки зре­ния двусмысленной. Но здесь мы можем ввести вариации и посмотреть, что произойдет.



Рис. 184

В данном случае выполняются одни и те же условия в отношении цвета, увеличивается только длина одного из концов. Ухватятся ли дети за цветную отметку? Если мы введем два способа обучения — с упором на цвет и с упо­ром на симметрию размеров, — то переход от слепого обу­чения к структурно осмысленному окажется для открытых умов более легким, чем переход от структурной осмыслен­ности к произвольности. Мы снова видим, что дело не про­сто в обобщении, а в том, как это обобщение производится: структурно осмысленным образом или в соответствии со слепыми ассоциациями, слепыми связями. Представляется, что здесь решающим является ρ-отношение между сим­метрией и устойчивостью.

Список основных работ Макса Вертгеймера

1. Psychologische Tatbestandsdiagnostik (с J. Klein). — "Arch. f. Kriminalanthrop. u. Kriminalistik, 1904, 15, 72—113.
   
2. Experimentelle Untersuchungen zur Tatbestandsdiagnostik.— "Ach. f. d. ges. Psychol.", 1905, 6, 59—131.
   

3. Über die Assoziationsmethoden.—"Arch. f. Kriminalanthrop. p. Kriminalistik", 1906, 22, 293—319.

4. Tatbestandsdiagnostische Kombinationsversuche, (c 0. Lipp­mann).—"Zschr. f. angew. Psychol.", 1907, l, 119—128.
   
5. Musik der Wedda. — "Sammelbände d. internal. Musikgesellschaft", 1910, Н, 300—309.
   
6. Über das Denken der Naturvölker: 1. Zahlen und Zahlgebilde.-"Zschr. f. Psychol.", 1912, 60, 321—378.
   
7. Experimentelle Studien über das Sehen von Bewegung. — "Zschr. f. Psychol.", 1912, 61, 161—265.
   
8. Über Schlussprozesse im produktiven Denken. Berlin, De Gruy­ter, 1920, 22.
   
9. Über die Wahrnehmung der Schallrichtung (c E. M. von Horn­bostel). — "Sitzungsber. d. preuss. Akad. d. Wiss.", Berlin, 1920, 20, 388—396.
   

10. Untersuchungen zur Lehre von der Gestalt: I. Prinzipielle Be­merkungen. — "Psychol. Forsch.", 1922, l, 47—58.

Н. Bemerkungen zu Hillebrands Theorie der stroboskopischen Bewegungen. — "Psychol. Forsch.", 192S, 3, 106—123.

12. Untersuchungen zur Lehre von der Gestalt: Н. — "Psychol. Forsch.", 1923, 4, 301—350.
    
13. Über Gestalttheorie.—"Symposion: Philos. Zschr. f. Forschung u. Aussprache", 1925, l, 39—60.
    
14. Zu dem Problem der Unterscheidung von Einzelinhalt und Teil. — "Zschr. f. Psychol.", 1933, 129, 353—357.
    
15. On truth. — "Soc. Res.", 1934, l, 135—146.
    
16. Some problems in the theory of ethics.—"Soc. Res.", 1935, 2, 353—367.
    
17. On the concept of democracy. — In: A s с о 1 i M. and L e h m a n n F. (Eds.). Political and economic democracy. New York, Nor­ton, 1937, p. 271—283.
    
18. A story of three days. — In: A n s he n Ruth N. (Ed.). Free­dom: its meaning. New York, Harcourt, Brace, 1940, p. 555—569.
    
19. Productive thinking. New York. Harper, 1945, 1959.
    

УКАЗАТЕЛЬ

Абсолютное движение 249—250, 260

Абсолютный покой 248—250, 264

Абстрагирование 72, 187, 284, 310 - 312

А— B-метод 45—51,92—93, ,86—101, 132—133, 152—153, 158, 273

См. также A-реакции и В-реакции

Ad hoc гипотеза 252, 264

Аккерман В. 292

Аксиомы 64, 185, 258, 262-263

См. Традиционная логика Алтарное окно, задача 303—305

Аналогии процессов мышле­ния

• механические 93
  
• перцептивные 85—86, 105-106, 159—162
  

См. также Волшебные миры; Машины; Музыкальные ил­люстрации

Антропологические иллюстра­ции (неспособности к абст­рагированию) 310—312

Анхен Рут 210

Априорный анализ 194, 238— 239

A-реакции и B-реакции 45— 51, 96—99, 132—133, 135—138, 150—153

См. также А—В-метод

Аристотель 33

Арифметика

— обучение 160—161, 166—168, 188—197

См. также Последствия для обучения

Ассоциативная теория 28—29, 34-36, 37-38, 71-72, 80-81, 88—96, 99—101, 117,. 121—128, 130, 167—169, 188—197, 270, 272—

273, 282—283, 286—287

Aufgabe 38

Ах. Н. 38

Аш С. 167, 280

Бадминтон, игра, задача 198—211

Бихевиоризм 32—33, 198, 271

См. также Ассоциативная теория

Бор Н. 54

Брауэр Л. Э. Я. 67

Буридан Ж. 37

Бэрдсли Д. 84, 95, 125, 160

Бюлер К. 38

Вертгеймер Майкл 84, 95, 108, 110, 111, 125, 160, 162,180,188, 193, 280

Вертгеймер Макс 32, 84, 85, 86, 87, 95, 96, 111, 125, 160, 162, 180, 199, 200, 207, 210, 213, 270, 274, 282, 285, 295, 311

Вертикальные углы, задача 129-140

Вечное движение 257—258

Внешние телесные углы

— сумма, задача 232—237
Внешние углы многоугольника

— сумма, задача 198, 224—237

Внутренние отношения см. Гештальтподход, Гештальттеория

Внутренние углы многоуголь­ника

— сумма, задача 230—236
Вознаграждение 38, 117, 124,

202—203

Волвилл Э. фон 238


Волшебные миры 117, 123—124, 195

Вудвортс Р. С. 176

Вюрцбургская школа 38

Галилей Г. 183, 199, 238—247, 258

Гальванометр, задача 180—187

Гаусса задача 141—179, 198

— структурный анализ 154—155

Гегель Г. В. Ф. 38

Геометрия

— евклидова 64, 162

— неевклидова 64, 233
Гештальтподход 96, 166, 177—179, 198—200, 245-246, 269— 271, 283-284, 295

— к Гаусса задаче 155

• к задаче с бадминтоном 205—211
  
• к задаче с вертикальными углами 135—140
  
• к задаче с мостом 122—128
  
• к задаче на определение суммы углов 235—237
  
• к задаче: плюс 3, минус 3 182—187
  
• к коммутативности 101—105
  
• к описанию конторы 213—223
  
• к площади параллело­грамма 79, 81—87
  
• к площади прямоуголь­ника 68—71
  
• к развитию теории отно­сительности 261—268
  

- к юмору 306—308

См. также А—B-метод; По­следствия для обучения; Средства и цели; Структур­ная логика; Целостные свойства

Гештальттеория 246, 271—296, 297—302

- задачи с бадминтоном 205-210

— задачи с вертикальными углами 135—137

- задачи с мостом 125—127

• задачи на определение суммы углов 235—237
  
• задачи: плюс 3, минус 3 182—187
  

См. также Гомолог; «Если..., то» в логике; «И» в логике; Истина; Класса понятие: «Не» в логике; Помощь; Про­белы; Отношение; ρ-отноше-ние; Тождество; Центрирова­ние.

Гильберт Д. 292

Гомолог 126, 138, 182—183, 217, 297—300

Группировка 69, 135—136, 143, 145, 148, 158—160, 269, 271 См. также Гештальтподход

Гуссерль Э. 38

Движение см. Абсолютное дви­жение; Эйнштейн

Движение сверху вниз см. Гештальтподход, Гештальттеория

Дедукция см. Традиционная логика

Деление

— структурный смысл 168—169

— суммы, задача 164—165
«Denkpsychologie» 38
Джевонс У. С. 37

«Дикие» процедуры 51—54, 57—61, 65—66, 70—72, 79—80

Доказательство 33—34, 43, 59—61, 101, 106—107, 129, 138, 309, 321—323

— «слепое» 53, 61—63

• с помощью принципа исключенного третьего 67
  
• теоремы о вертикальных
  углах 129—139
  
• теоремы о параллелограмме 41
  

Дункер К. 167

Дьюи Дж. 38, 39


Einstellung 50, 166—168 «Если..., то» в логике 291, 294

Заучивание наизусть см. Ас­социативная теория; Повто­рение; Пробы и ошибки; Прошлый опыт; Упражне­ния

Зельц О. 38

Зенер К. 167

Зиммель Г. 185

Знакомость 47, 87, 105

См. также Прошлый опыт

«И» в логике 225, 291—293

Индуктивная логика 34, 54-ое, 238, 244, 285—286

Инерции закон 238—246

Инсайт 92, 98, 169—171, 178, 198—200, 232—233, 236, 282, 316 319

Интеллект 33, 111, 121, 310— 312

Интуиция 227—228, 235—236

Инфельд Л. 243, 263

Исключенного третьего прин­цип 67

Исследование мышления

— стратегии 29—31, 91—92, 116—117, 269—272

См. также А—B-метод; «Ди­кие процедуры»; «Помощь»

Истина 31, 33, 94, 270—271, 273, 278, 279, 291—293, 295

История психологии мышле­ния см. Ассоциативная тео­рия; Традиционная логика; Традиционные взгляды па мышление


Кант И. 140

Катона Дж. 107, 128, 167, 193, 282

Катящиеся тела 239—241

Квадрат

— площадь 59, 63
«Квадратные наборы» 159—160
Кёлер В. 117

Класса понятие 31, 160, 174, 284, 287—291

Классическая логика см. Тра­диционная логика

Койре А. 238

Коммутативности закон 101— 107

Констеляции теория 38

Копферман Г. 84

Кристаллизация, проблема в физике 88

Кролик В. 87

Кюльпе О. 38


Лабиринт

— движение по 157, 281
Лачинс А. 167

Леви Э. 96, 210, 213, 277

Левин К. 96

Lex parsimoniae 66

Линней К. 288

Липман Г. 37

Личность и мышление 39, 95—96, 205—206, 209—211, 212—223, 308

Логика

• машин 37
  
• и мышление 28—29, 36, 64—65
  
• музыкальная см. Музы­
  кальные иллюстрации
  

См. также Гештальттеория; «Если..., то» в логике; «И» в логике; «Индуктивная логи­ка»; «Не» в логике; Тради­ционная логика

Логистика 38, 213—223, 271, 293

Лоренца преобразование 252, 258, 259, 264, 266, 268

Луллий Р. 37

Любопытство 124, 202


Майер Н. Р. Ф. 89, 90, 92, 122, 166, 167

Майкельсона эксперимент 250—253, 264, 266, 267

Максвелла уравнения 249— 250, 264

Маркс К. 38

Математика см. Алтарное ок­но; Арифметика; Вертикаль­ные углы; Внешние углы; Внутренние углы; Гаусса задача; Деление; Квадрат; Параллелограмм; Плюс три, минус три; Последствия для обучения; Произведение ря­дов; Прямоугольник; Сторо­ны, число; Сумма векторов; Сумма рядов; Сумма углов; Трапеция; Треугольник; Уг­лы; Углы куба; Эйнштейн

Математическая -логика см. Ло­гистика

Мах Э. 228, 238

Машины

• для вычисления площади
  параллелограмма 99
  
• для вычисления площади
  прямоугольника 56
  
• для имитации траектории
  движения мяча 93
  

 логические 37

• «обучающие» 127—128, 193—195
  

Менделеев Д. И. 54

Методы изучения мышления 30—31

См. также Исследование мышления, стратегии; Опе­рации

Милль Дж. С. 34

Мозли Г. Г. 54

Мост, задача 111—128

• анализ решения 121—128
  
• гештальттеория 125—127
  
• «слепая» машина для ре­шения 127—128
  

См. также Уравновешивание палки

Мотивация 27—28, 108—110, 121, 124, 169—171, 178—179, 208-210, 233, 252—253; 269— 276, 279—280, 299, 301, 321

Музыкальная логика см. Му­зыкальные иллюстрации

Музыкальные иллюстрации 150, 185, 277—278, 288—291, 301—302

Навык 196, 281

См. также Ассоциативная теория; Повторение; При­вычка; Упражнение

Навыков системная иерархия 38

«Натуралистический подход 39

Небесная механика 245

«Не» в логике 291, 294

Негативный опыт и мышление 114—115, 122

Нептун, открытие 32

Ньютон И. 246, 260

Обобщение 32, 33, 49—55, 63, 71, 72, 144, 187, 284, 326 См. также Ассоциативная теория; Традиционная логи­ка

Обусловливание 34, 35, 38, 169, 282

См. также Ассоциативная теория

«Обучающие» машины см. Ма­шины —

«обучающие»


Операции

— ассоцианизма, таблица 35

— гештальттеории, таблица —269, 270—271

—индуктивной логики, таб­лица 34

• традиционной логики, таблица 32
  

См. также Ассоциативная теория; Гештальттеория; Традиционная логика

«Органон» Аристотеля 33

Осмысленные процедуры см. Гештальтподход; Гештальт­теория

Отвлечение

• влияние на продуктивное мышление 48. 49
  

Относительности теория 247— 268

«Отношения» (как не критиче­ский элемент продуктивного мышления) 71—72, 136—138, 292, 293, 298

Отрицание см. «Не» в логике

Параллелограмм, задача па определение площади 40—56, 74—110, 198, 306, 317—321

• А— B-метод 45—51, 96—101
  
• «дикие» процедуры 51—56, 57—61
  
• доказательство 41, 51, 59—61, 106-107, 321—323
  
• индукция 54—56
  
• операции традиционной логики 101—107
  
• осмысленный подход 76—87, 97—101
  
• проверка понимания 42—50
  
• прошлый опыт 88—101
  
• решение с кольцом 78, 82, 83, 85
  
• решение с помощью нож­ниц 76—77, 88—89
  
• решение с помощью складного метра 75
  
• решение с помощью бес­конечно малых рядов 78
  

— «слепые» реакции 44—56, 60, 80—81

• традиционное обучение 40-42, 47—48, 52, 92, 96
  
• экспериментальный анализ 44—56
  

331

Перенос 42, 63, 71, 97, 98-100, 128, 158, 184. См. также Транспозиция

Перцептивные аналогии см. Аналогии процесса мышле­ния

Пиллсбери У. Б. 36, 39

Площадь, задача па опреде­ление см. Алтарное окно; Квадрат; Параллелограмм; Последствия для обучения; Прямоугольник; Рама; Тра­пеция; Треугольник

Плюс три, минус три, задача 180—187

— анализ решения 183—187
Поведение и логика 33
Повторение 35, 38, 49, 149, 166—168, 281, 286—287, 313, 320—321

См. также Ассоциативная теория; Навык; Привычка; Упражнения

Подкрепление см. Ассоциатив­ная теория; Вознаграждение

Политическое мышление 109— НО, 279—280

«Помощь» 89—92, 98, 122, 123

Понимание

— операциональное определение с помощью А—B-метода 50

Последствия для обучения 28—29, 52-53, 69, 109-110, 161—162, 166—169, 188—197, 309—312, 313—321

Постановка проблемы 178, 277

Прагматизм 33, 38

Праут У. 54

Прегнантности закон 274, 279

Привычка 35, 36, 49, 132, 140, 155, 166—168, 188—190, 195, 197, 201, 269, 279 См. также Ассоциативная теория; Повторение; Упраж­нения

Приложенная сила 238, 239, 245

Примитивное мышление см. Антропологические иллюст­рации

Пробелы в структурах в про­цессе мышления 79, 161, 200, 270, 275, 278

Проблемные ситуации

— типы 273-278, 280—282
См. также Бадминтон; Ма­тематика; Социальные ситу­ации; Сумма векторов; Фи­зика

Пробы и ошибки 35, 36, 38, 79—80, 99—100, 114, 121, 233, 237, 262, 268, 279, 280—281, 282, 286, 324—325

См. также Ассоциативная теория; Вознаграждение

Продуктивное мышление

— общая природа 27—29, 269—296

Произведение рядов 150—151

Прошлый опыт 35, 72, 87, 88 — 102, 121—122, 124, 286—287

См. также Ассоциативная теория; Навык; Привычка; Повторение; Упражнение Прямоугольник, задача на оп­ределение площади 57—64, 309, 314—321

• ассоциативная теория 71—73
  
• осмысленные процедуры 61—62, 68—69
  
• «слепые» процедуры 56—65
  

— традиционная логика 71—73

Рама

— площадь 109
Рассел Б. 38

Реакций типы см. Типы реак­ций на проблемные ситуа­ции

Резерфорд Э. 54

Ренессанс 33

Реорганизация см. Гештальт-подход

-отношения 70, 91, 97, 115, 123, 124—126, 135, 182, 183, 189, 195—196, 271, 307, 326

Самоцентрирование см. Эго­центрическая ориентация

Сети отношений 38, 106, 213— 223, 291, 297

Симметрия см. Гештальтпод­ход; Гештальттеория

Симссен Мисс 157

«Сколько волос у лошади?» 306-308

332

Скорость света 248—260, 264—268

Слова и мышление 263 Смежность 35

См. также Ассоциативная теория Социальные ситуации

— гештальтанализ 39, 198—223

Спиноза Б. 36

Среда и мышление 95—96, 116 См. также Отвлечение

Средства и цели 72, 97—101, 110