II. Логика и язык
| Вид материала | Тесты |
- Программа курса и темы практических занятий; Логика в таблицах и схемах. Логика как, 1722.34kb.
- Логика в образовании, 153.37kb.
- Математическая логика, 1012.22kb.
- Математическая логика Лектор 2010/11 уч года: к ф-м наук Носов В. А. Аннотация, 34.32kb.
- Логика богочеловечества, 213.06kb.
- Начальное общее образование, 391.69kb.
- Н. В. Папуловская Математическая логика Методическое пособие, 786.38kb.
- Основы логики. Логика, 20.66kb.
- А. А. Ивин логика учебное пособие, 3160.22kb.
- Вопросы к экзамену по дисциплине «Логика», 15.87kb.

Теория бинарных отношений.
Содержание темы:
Понятие отношения. Объем (экстенсионал) и содержание (интенсионал) отношения. Виды отношений (бинарные, тернарные и пр.) Область и противообласть бинарного отношения. Однозначные и неоднозначные отношения.
Теория бинарных отношений (ТБО), её связь с логикой предикатов. Язык и семантика ТБО. Логические операции над отношениями (дополнение, пересечение, объединение, вычитание, конверсия, композиция). Реляционные константы. Основные законы алгебры отношений.
Основные логические свойства бинарных отношений (рефлексивность, симметричность, транзитивность) и классификация отношений по этим свойствам. Теория родства как прикладная часть ТБО.
Цели и задачи изучения темы:
- Сформулировать понятие об отношениях, их содержании и объеме.
- Рассмотреть язык теории бинарных отношений и задать его семантику с помощью графов.
- Раскрыть связь теории бинарных отношений с КЛП.
- Выделить основные законы теори бинарных отношений.
- Сформулировать главные логические свойства отношений и дать их классификацию на основании этих свойств.
- Перечислить наиболее важные типы отношений (тождество, подобие, частичный и линейный порядок).
Изучив тему, студент должен:
Знать:
- Что такое реляционные суждения.
- Какие существуют виды отношений.
- Какие логические операции можно выполнять над отношениями.
- Как они выражаются в языке ТБО.
- Каковы основные законы ТБО.
- Каковы основные свойства бинарных отношений.
- Какую классификацию бинарных отношений зажают эти свойства.
- Какие типы бинарных отношений чаще всего фигурируют в научных теориях, в чем их логические особенности.
Уметь:
- Анализировать структуру реляционных суждений.
- Определять, к каким видам относятся фигурирующие в них отношения.
- Записывать эти отношения на языке ТБО.
- Осуществлять логические операции над бинарными отношениями.
- Применять законы ТБО для преобразованияи и сокращения реляционных формул (в частности, выражающих отношения родства).
При изучении темы необходимо акцентировать внимание на следующих понятиях:
- Бинарное отношение
- Тернарное отношение
- Граф
- Дополнение отношения
- Конверсия отношений
- Пересечение отношений
- Объединение отношений
- Вычитание отношений
- Композиция отношений
- Оператор исключительности
- Пустое отношение
- Универсальное отношение
- Рефлексивность
- Симметричность
- Транзитивность
- Тождество
- Подобие
- Частичный порядок
- Линейный порядок
Порядок изучения темы:
Для изучения темы выделяется 1,5 лекционных часа, 1,5 часа семинарских занятий, 1,5 часа самостоятельной работы.
Формы самостоятельной работы:
- Подготовка к лекции.
- Подготовка к семинарскому занятию.
- Подготовка докладов и рефератов по рекомендации преподавателя.
- Участие в чатах.
- Участие в тьюториалах.
Методические указания:
Вопросы лекции и семинарского занятия:
- Язык и семантика теории бинарных отношений.
- Основные законы теории бинарных отношений.
- Логические свойства бинарных отношений и их классификация на основании этих свойств.
Начните подготовку с ознакомления с темой.
При изучении 1-го вопроса
Готовясь к лекции, студент должен
- Прочитать:
- Горбатов В.В. Логика. – М.:МЭСИ, 2006. Тема VI, § 1-2.
- Тарский А. Введение в логику и методологию дедуктивных наук. – Биробиджан: Тривиум, 2000. Глава V.
- Сформировать общее представление
- О сущности и области применения реляционных суждений.
- О целях и задачах ТБО.
- О том, как строится ее язык и каковы его выразительные возможности.
Самое главное – разобраться с формальным языком ТБО и его семантикой. Теория графов является весьма удобным и наглядным средством для изучения бинарных отношений.
Внимательно изучите схемы перевода формул ТБО на язык логики предикатов. Это будет полезно для усвоения следующих параграфов учебника, где говорится о логических свойствах бинарных отношений и их классифиации на основани этих свойств.
При подготовке к семинарскому занятию, студент должен
- Прочитать:
- Горбатов В.В. Логика. – М.:МЭСИ, 2006. Тема VI, § 1-2.
- Тарский А. Введение в логику и методологию дедуктивных наук. – Биробиджан: Тривиум, 2000. Глава V.
- Изучить дополнительные материалы:
- Шрейдер Ю.А. Равенство, сходство, порядок. – М., 1971.
- Шрейдер Ю.А., Бирюков Б.В. Категория отношения и ее когнитивные аспекты. // Вестник Московского университета. Серия 7. Философия. №3, 2002.
- Выполнить упражнения и практические задания:
- в учебнике Горбатов В.В. Логика. – М.:МЭСИ, 2006. Тема VI, упражнения 1-3.
- в учебнике Тарский А. Введение в логику и методологию дедуктивных наук. – Биробиджан: Тривиум, 2000. Глава V, упражнения 1-5, 26.
Начните с разбора самого понятия отношения. Какие двух- трех- и четырех-местные отношения, кроме упомянутых в учебнике, вы можете назвать?
Попрактикуйтесь в формализации бинарных отношений с помощью языка ТБО. В частности, попробуйте формализовать известные вам отноешния родства – это пригодится при изучении следующего параграфа.
Чат. Совместно с товарищами обсудите вопрос о том, в каких науках фактически используется теория бинарных отношений. Каково методологическое значение этой теории?
Тьюториал. В группах по 3-4 человека попробуйте вспомнить физические законы, в которых идет речь о трех- и четырех-местных отношениях. Обсудите их логическую форму.
При изучении 2-го вопроса
Готовясь к лекции, студент должен
- Прочитать:
- Горбатов В.В. Логика. – М.:МЭСИ, 2006. Тема VI, § 3;
- Сформировать общее представление
- Об основных законах ТБО.
- О способах преобразования и сокращения реляционных формул на основании этих законов.
Вы видите, что многие реляционные связки по смыслу совпадают с логическими союзами пропозициональной логики. Многие законы логики теории отношений также имеют простое алгебраическое содержание и фактически известны вам из предыдущих глав.
Но в то же время, теория бинарных отношений содержит операции и законы, характерные только для нее. Это конверсия, композиция и оператор исключительности. На них надо обратить особое внимание. В частности, закон конверсии и хаконы сокращения помогут вам справиться с практическими заданиями, приведенными в учебнике.
При подготовке к семинарскому занятию, студент должен
- Прочитать:
- Горбатов В.В. Логика. – М.:МЭСИ, 2006. Тема VI, § 3.
- Тарский А. Введение в логику и методологию дедуктивных наук. – Биробиджан: Тривиум, 2000. Глава V.
- Изучить дополнительные материалы:
- Шрейдер Ю.А. Равенство, сходство, порядок. – М., 1971.
- Шрейдер Ю.А., Бирюков Б.В. Категория отношения и ее когнитивные аспекты. // Вестник Московского университета. Серия 7. Философия. №3, 2002.
- Выполнить упражнения и практические задания:
- в учебнике Горбатов В.В. Логика. – М.:МЭСИ, 2006. Тема VI, упражнения 4-5.
- в учебнике Тарский А. Введение в логику и методологию дедуктивных наук. – Биробиджан: Тривиум, 2000. Глава V, упражнения 6-10.
Советую обратить особое внимание на практические задания. Постарайтесь разобраться в технике сокращения реляционных формул.
Тьюториал. В группах по 3-4 человека попробуйте самостоятельно составить и упростить цепочки родства. Желательно использовать отношения родства, известные вам из вашего ближайшего социального окружения.
При изучении 3-го вопроса
Готовясь к лекции, студент должен
- Прочитать:
- Горбатов В.В. Логика. – М.:МЭСИ, 2006. Тема VI, § 4;
- Сформировать общее представление
- О логических свойствах бинарных отношений
- О классификации бинарных отношений на основании этих свойств
- О наиболее важных типах бинарных отношений и их логических особенностях.
Обратите внимание на три основные своства бинарных отношений – рефлексивность, симметричность и транзитивность. Проанализируйте их определения в языке ТБО и сравните их с определениями в язык КЛП. Убедитесь, что их смысл совпадает.
Полна ли приведенная в таблице классификация отношений? Если вы считаете, что нет, сформулируйте другие разновидности бинарных отношений по приведененным в ней признакам. Придумайте для них названия.
При подготовке к семинарскому занятию, студент должен
- Прочитать:
- Горбатов В.В. Логика. – М.:МЭСИ, 2006. Тема VI, § 4.
- Тарский А. Введение в логику и методологию дедуктивных наук. – Биробиджан: Тривиум, 2000. Глава V.
- Изучить дополнительные материалы:
- Тарский А. Введение в логику и методологию дедуктивных наук. – Биробиджан: Тривиум, 2000. Глава III.
- Шрейдер Ю.А. Равенство, сходство, порядок. – М., 1971.
- Выполнить упражнения и практические задания:
- в учебнике Горбатов В.В. Логика. – М.:МЭСИ, 2006. Тема VI, упражнения 6-7.
- в учебнике Тарский А. Введение в логику и методологию дедуктивных наук. – Биробиджан: Тривиум, 2000. Глава V, упражнения 14-16.
Начните с анализа определений логических свойств бинарных отношений. Попрактикуйтесь, применяя их на примерах. Пострайтесь выделить группы отношений с похожими наборами логических свойств. Объясните, чем, на ваш взгляд, обусловлено это сходство.
Чат. Обсудите с товарищами перспективы применения теории бинарных отношений в вашей профессиональной области. Результаты обсуждения изложите на семинаре.
Контрольные вопросы:
- Чем отличаются реляционные суждения от атрибутивных?
- Какие отношения называются бинарными? Тернарными?
- Какие логические операции можно осуществлять над бинарными отношениями?
- Каковы основные законы ТБО?
- Какие из них знакомы вам из пропозициональной логики, а какие специфичны для теории отношений?
- Что такое рефлексивность отношения?
- Что такое симметричность отношения?
- Чем несимметричные отношения отличаются от антисимметричных?
- Что такое транзитивность отношения?
- Какое отношение задается набром свойств «рефлексивность + симметричность + транзитивность»?
- Каким логческим свойством отличается отношение тождества от отношения подобия?
- Чем отличается частичный порядок от линейного?
При изучении темы необходимо:
Прочитать литературу:
Основная:
- Горбатов В.В. Логика. – М.: МЭСИ, 2006. Тема VI.
- Тарский А. Введение в логику и методологию дедуктивных наук. – Биробиджан: Тривиум, 2000. Глава V «О теории отношений».
Дополнительная:
- Шрейдер Ю.А. Равенство, сходство, порядок. – М., 1971
- Шрейдер Ю.А., Бирюков Б.В. Категория отношения и ее когнитивные аспекты. // Вестник Московского университета. Серия 7. Философия. №3, 2002.
Посетить сайты:
- ссылка скрыта: Учебные материалы по курсу логики (определения, задачи, примеры и т.д.).
- ссылка скрыта: Электронный журнал «Логические исследования».
- ссылка скрыта – статья «Категория отношения и ее когнитивные аспекты», авторы Шрейдер Ю.А. и Бирюков Б.В.
- ссылка скрыта Психологика (сайт Мирослава Войнаровского).
§1. Отношения и их виды.
К

ак вы помните, в силлогистике изучаются только атрибутивные суждения (суждения о свойствах). Реляционные суждения (суждения об отношениях) изучает специальный раздел логики – теория отношений. Очевидно, что суждения об отношениях могут нести в себе информацию об объектах, которую нельзя передать атрибутивными высказываниями.
О
А. Де Морган (1806-1871)
сновы логической теории отношений были заложены Августом Де Морганом, идеи которого были развиты Ч. Пирсом и Э. Шрёдером.
В настоящее время теория отношений (и ее геометрический вариант – теория графов) широко используется в социальных науках. С помощью графов в науках о человеке и обществе передаются отношения и системы отношений в социальных группах, процессы коммуникации, цепочки связей между индивидами, разного рода социопсихологические шкалы и метрики. Алгебра отношений позволяет создавать и обрабатывать всевозможные базы данных.
О
 тношение – это такая связь между объектами, которая не сводится к собственным свойствам этих объектов, но объединяет их в единый комплекс. Например, Ромео и Джульетта были связаны в единый коплекс (пару) неким отношением (любовь), которое невозможно дедуцировать из собственных свойств Ромео или Джульетты.
тношение – это такая связь между объектами, которая не сводится к собственным свойствам этих объектов, но объединяет их в единый комплекс. Например, Ромео и Джульетта были связаны в единый коплекс (пару) неким отношением (любовь), которое невозможно дедуцировать из собственных свойств Ромео или Джульетты.В естественном языке отношения обозначаются при помощи абстрактных имен («дружба», «вражда», «родство» и т.п.) или функциональных выражений («больше», «меньше», «равно» и т.п.). Иначе говоря, отношения обозначаются двух- и более местными предикаторными выражениями.
С
 одержание (интенсионал) отношения составляет система признаков, характеризующих данную связь между объектами. Например, в содержание отношения руководство входят такие признаки как контроль, координация и пр.
одержание (интенсионал) отношения составляет система признаков, характеризующих данную связь между объектами. Например, в содержание отношения руководство входят такие признаки как контроль, координация и пр. Объем (экстенсионал) отношения представляет собой множество упорядоченных n-ок объектов, находящихся в этой связи друг с другом. Так, объем отношения руководство можно представить в виде множества пар «руководитель + подчиненный».
В зависимости от того, какое количество объектов необходимо для данного отношения, выделяются различные виды отношений:
1) бинарные (двухместные)
2) тернарные (трехместные)
...
n) n-арные (n-местные)
Так, например, отношение «столица» – двухместное, ибо требует как минимум двух объектов – город, являющейся столицей, и страна, столицей которой он является. А отношение «сводничество» следует назвать трехместным, ибо для него необходимы как минимум три объекта – сводник и те двое, кого он сводит друг с другом.
Упражнение 1. Определите, к каким видам принадлежат следующие отношения:
а) знакомство
б) продажа
в) подчинение
г) наследование
д) обмен
В дальнейшем для простоты мы будем исходить из предположения, что любое n-местное отношение можно представить как конъюнкцию определенного количества двухместных отношений. Скажем, трехместное отношение «ревность», имеющее место между а, b и с, можно представить как систему бинарных отношений: а любит b, b любит с, а ненавидит c.
У бинарных отношений принято выделять их область и противообласть.
О
 бластью называется множество предметов, которые состоят в этом отношении к каким-либо другим предметам (т.е. множество исходящих вершин графов).
бластью называется множество предметов, которые состоят в этом отношении к каким-либо другим предметам (т.е. множество исходящих вершин графов). Противообластью называется множество предметов, к которым некие другие предметы находятся в данном отношении (т.е. множество входящих вершин графов).
По характеру взаимозосвязи между областью и противообластью отношения можно делить на исключительные и неисключительные.
О
 тношение между а и b называется исключительным, если известно, что только a находится в этом отношении к b; оно называется неисключительным, если возможно, что не только a находится в этом отношении к b.
тношение между а и b называется исключительным, если известно, что только a находится в этом отношении к b; оно называется неисключительным, если возможно, что не только a находится в этом отношении к b. Если и само отношение, и его конверсия являются исключительными, такое отношение называется взаимно-однозначным.
Упражнение 2. Определите, какие из следующих отношений являются исключительными, а какие – нет. Какие из них являются взаимно-однозначными?
а) отец
б) родитель
в) брат
г) жена
§2. Язык и семантика теории бинарных отношений.
Алфавит ТБО включает в себя следующие виды символов:
1) P, Q, R, S, … – реляционные переменные
2) , +, , –, /, –1, ! – реляционные связки
3) I, U, – реляционные константы
4) ( , ) – скобки
О
 пределение формулы. (1) реляционные константы и переменные являются формулами; (2) если А и В – формулы, то А!,А, А–1, А+В, АВ, А–В, и А/В также являются формулами; (3) ничто другое не является формулой.
пределение формулы. (1) реляционные константы и переменные являются формулами; (2) если А и В – формулы, то А!,А, А–1, А+В, АВ, А–В, и А/В также являются формулами; (3) ничто другое не является формулой.Формула, входящая в состав некоторой формулы, называется ее подформулой и выделяется скобками.
Реляционные связки позволяют производить различные операции над отношениями, связывая их в более сложные отношения.
-
Символ
Название
дополнение (отрицание)
–1
конверсия (обращение)
+
объединение (логическое сложение)
пересечение (логическое умножение)
–
вычитание
/
композиция
!
оператор исключительности
Зададим теперь семантику ТБО с помощью графов. Граф есть ориентированное ребро, исходящая врешина которого обозначает первый, а входящая – второй элемент бинарного отношения.
- Каждой реляционной переменной сопоставляется её объем – некое множество графов, определенных на предметной области U.
R
 a b
a b- Дополнением отношения является множество графов, которые не входят в его объем. Например: если R – интерес, то`R – безразличие (отсутствие интереса).
R `R


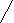 a b a b
a b a b- Конверсией отношения является множество графов, полученных из графов, входящих в объем данного отношения, путем замены входящей вершины на исходящую. Например: если R – старше, то R–1 – моложе (старше «наоброт»)
R R–1

 a b a b
a b a b- Пересечением двух отношений является множество графов, входящих в объем обоих этих отношений. Например: если R1 – получение, а R2 – дарение, то R1R2 – обмен (получение и дарение).
R1 R1R2


 a b a b
a b a bR2
- Объединением двух отношений является множество графов, входящих в объем по крайней мере одного из этих отношений. Например: если R1 – сын, а R2 – дочь, то R1+R2 – ребенок (сын или дочь)
R1
 a b R1+R2
a b R1+R2 или a b
или a b a b
a b R2
- Вычитанием из одного отношения другого является множество графов, которые входят в объем первого, но не входят в объем второго. Например: если R1 – ребенок, а R2 – сын, то R1 – R2 – дочь (ребенок, но не сын).
R1 R1–R2



 a b a b
a b a bR2
- Композицией двух отношений является множество графов, соединяющих исходящую вершину первого со входящей вершиной второго. Например: если R1 – брат, а R2 – жена, то R1/R2 – шурин (брат жены)
R1 R2 R1/R2


 a b с a с
a b с a с- Оператор исключительности запрещает проводить для данного отношения более одного графа, направленного к его входящей вершине. Например: если R – сын, то R! – единственный сын
R R
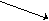
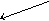
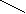 a d
a d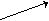
 b
b  c f
c f R R
Все эти операции естественным образом можно определить и с помощью логики предикатов, язык и семантика которой были изложены в главе IV. Пусть xRy означает, что R(x,y). Тогда


 x R y R(x,y)
x R y R(x,y)x R–1 y R(y,x)
x (R1+R2) y R1(x,y) R2(x,y)
x (R1R2) y R1(x,y) & R2(x,y)
x (R1–R2) y R1(x,y) & R2(x,y)
x (R1/R2) y z(R1(x,z) & R2(z,y))
x R! y "x,y,z (R(x,y) & R(z,y) É х=z)
Реляционные константы U и совпадают по смыслу с символами 1 и 0 пропозициональной логики, обозначая универсальное и пустое отношение соответственно.
У
 ниверсальным называется отношение, в котором состоит любая пара объектов универсума. Пустым называется отношение, в котором не состоит ни одна пара объектов универсума. Символ I обозначает отношение тождества, в котором каждый объект универсума находится только сам к себе.
ниверсальным называется отношение, в котором состоит любая пара объектов универсума. Пустым называется отношение, в котором не состоит ни одна пара объектов универсума. Символ I обозначает отношение тождества, в котором каждый объект универсума находится только сам к себе.На языке КЛП это выражается следующими определениями:


"x"y Ø(x,y)
"x"y U(x,y)
"x"y (I(x,y) º x=y)
Пример формализации. Примем исходные обозначения: Fr – друг, Bs – начальник. Тогда следующие отношения можно записать в виде таких формул:
- Друг начальника Fr / Bs
- Враждебный начальник Fr Bs
- Единственный подчиненный друга Bs–1! / Fr
- Враг начальника или подчиненного Fr / (Bs + Bs–1)
Упражнение 3. Пусть H – «муж», O – «старше», S – «сестра», а В – «брат». Запишите на языке ТБО следующие отношения:
а) единственная сестра мужа
б) старший брат жены
в) жена единственного младшего брата
§3. Основные законы теории бинарных отношений.

Используя определенные в прошлом параграфе операции, можно описать универсальные свойства бинарных отношений, выражаемые следующими законами:
R `R = Æ – закон непротиворечия
R +`R = U – закон исключенного третьего
R! / R–1 = I – закон конверсии
I
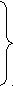 / R = R
/ R = RR / I = R – законы сокращения
U R = R
Æ + R = R
R1 – R2 = R1 `R2 – закон вычитания
R

 1 + R2 =`R1 `R2 – законы Де Моргана
1 + R2 =`R1 `R2 – законы Де МорганаR
 1 R2 =`R1 +`R2
1 R2 =`R1 +`R2R
 1 (R2+R3) = (R1R2) + (R1R3)
1 (R2+R3) = (R1R2) + (R1R3)R1 + (R2R3) = (R1+R2) (R1+R3) – законы дистрибутивности
R1 / (R2 +R3) = R1/R2 + R1/R3
Опираясь на эти законы, можно упрощать и преобразовывать различные отношения, например, отношения родства.
Возьмем базисную номенклатуру родства:
F – отец H – муж B – брат C – сын
М – мать W – жена S – сестра D – дочь
Тогда наиболее распространенные отношения родства можно представить с помощью композиции базисных отношений:
Тесть F/W Шурин B/W
Теща M/W Деверь B/H
Свекор F/H Сноха W/C
Свекровь M/H Свояченица S/W
Золовка S/H Свояк H/S/W
Общеизвестно, как нелегко человеку бывает разобраться в сложной системе отношений, связывающей его с ближними и дальними родственниками. Например, кем мне приходится единственный свояк единственного брата деверя сестры моей снохи? Запишем это отношение в виде формулы:
Единственный свояк единственного брата деверя сестры моей снохи
(H/S/W)! / B! / B/H / S / W/C
Разберем сначала первую часть формулы – «(H/S/W)!». Оператор исключительности следует пронести внутрь скобки и рапределить на все три переменные – «H!/S!/W!». Но поскольку H и W – отношения заведомо исключительные, знак «!» имеет смысл только возле S. Итак, мы получаем:
H/S!/W/B!/B/H/S/W/C
Теперь выделим и сократим конверсные отношения типа «единственный брат моего брата» или «муж моей жены».
H/S!/W/B!/B/H/S/W/C единственный брат брата мужа – сам муж
H/S!/W/H/S/W/C жена мужа сестры – сама сестра
H/S!/S/W/C единственная сестра сестры жены – она сама
H/W/C муж жены сына – сам сын
С сын
Ответ: этот родственник приходится говорящему сыном.
Упражнение 4. Составьте формулы для следующих отношений, упростите их и ответьте на поставленные вопросы.
а) Деверь единственной сестры моего шурина. Кто это?
б) Единственная сноха матери моего зятя. Кто это?
в) У деверя моей снохи родилась дочь. Кто она мне?
Упражнение 5. При помощи теории бинарных отношений решите следующую задачу:
Сын отца бухгалтера убил отца сына бухгалтера, но только бухгалтер здесь ни причем – это не убийца и не жертва. Самоубийство тоже исключено. Кто же кого убил?
§4. Логические свойства бинарных отношений
Кроме того, мы можем теперь выделить некоторые специфические свойства бинарных отношений и связанные с ними законы.
К наиболее важным своствам бинарных отношений причисляют рефлексивность, симметричность и транзитивность.
Р
 ефлексивность отношения означает его способность обращаться на исходный объект. Рефлексивным отношениям соответствуют графы, у которых входящая и исходящая вершины совпадают.
ефлексивность отношения означает его способность обращаться на исходный объект. Рефлексивным отношениям соответствуют графы, у которых входящая и исходящая вершины совпадают. С
 имметричность отношения заключается в его способности быть двусторонним, т.е. взаимным. Симметричным отношениям соответствуют двусторонние графы.
имметричность отношения заключается в его способности быть двусторонним, т.е. взаимным. Симметричным отношениям соответствуют двусторонние графы. Т
 ранзитивность отражает способность отношения передаваться «по цепочке»; такие отношения позволяют переходить от первого элемента цепочки к последнему минуя промежуточные звенья.
ранзитивность отражает способность отношения передаваться «по цепочке»; такие отношения позволяют переходить от первого элемента цепочки к последнему минуя промежуточные звенья.На основании данных трех свойств можно составить классификацию бинарных отношений:
| Свойство | Виды отношений | Определение на языке ТБО | Определение на языке КЛП |
| Рефлексивность | Рефлексивные | I – R = Æ | "x R(x,x) |
| Нерефлексивные | I – R ≠ Æ | $x RØ(x,x) | |
| Антирефлексивные | I – R = I | "x ØR(x,x) | |
| Симметричность | Симметричные | R – R–1 = Æ | "x,y (R(x,y) É R(y,x)) |
| Несимметричные | R – R–1 ≠ Æ | $x,y (R(x,y) & ØR(y,x)) | |
| Антисимметричные | R – R–1 = R | "x,y (R(x,y) É ØR(y,x)) | |
| Транзитивность | Транзитивные | (R/R) – R = Æ | "x,y,z (R(x,y) & R(y,z) É R(x,z)) |
| Нетранзитивные | (R/R) – R ≠ Æ | $x,y,z (R(x,y) & R(y,z) & ØR(x,z)) | |
| Антитранзитивные | (R/R) – R = R/R | "x,y,z (R(x,y) & R(y,z) É ØR(x,z)) |
Возмем, например, отношение однофамилец (другой человек с той же фамилией). К каким видам оно относится? Во-первых, оно антирефлексивное – ни один человек не может быть однофамильцем самому себе. Во-вторых, оно симетричное (для любых двух людей верно, что если первый из них однофамилец второго, то второй – однофамилец первого). Наконец, это отношение транзитивное (для любых трех людей верно, что если первый из них однофамилец второго, а второй – однофамилец третьего, то первый – однофамилец третьего).
Упражнение 6. Определите, к каким видам принадлежат следующие отношения:
а) знает
б) ровесник
в) сын
г) начальник
д) сосед
Н
 аконец, выделим наиболее важные типы отношений, которые встречаются практически во всех науках.
аконец, выделим наиболее важные типы отношений, которые встречаются практически во всех науках. 1) Тождество (рефлексивно, симметрично, транзитивно)
Например, в математике – отношение «=»
2) Подобие, или толерантность (рефлексивно, симметрично, нетранзитивно)
Например, в математике – отношение «»
3) Частичный порядок (рефлексивно, несимметрично, транзитивно)
Например, в математике – отношение «»
4) Линейный порядок (антирефлексивно, антисимметрично, транзитивно)
Например, в математике – отношение «»
Упражнение 7. Докажите следующие теоремы:
а) антитранзитивное отношение не может быть рефлексивным
б) антисимметричное отношение не может быть рефлексивным
в) любое транзитивное симметричное отношение рефлексивно
Тесты
- Реляционными называются высказывания о
- свойствах
- отношениях
- тождестве
- существовании
- Основы логики отношений заложил
- Аристотель
- Дунс Скот
- А. Де Морган
- Ф. Бэкон
- Аристотель
- Бинарными являются отношения
- любовь
- посредничество
- обмен
- предательство
- дружба
- знакомство
- любовь
- Тернарными являются отношения
- любовь
- посредничество
- обмен
- предательство
- дружба
- знакомство
- любовь
- Дополнение отношения "равно"
- больше или меньше
- больше или равно
- меньше или равно
- больше или меньше
- Дополнение отношения "друг"
- враг
- не друг
- доброжелатель
- подруга
- враг
- Объединение отношений "отец" и "мать"
- опекун
- предок
- семья
- родитель
- опекун
- Объединение отношений "сын" и "дочь"
- ребенок
- семья
- внук
- внучка
- ребенок
- Конверсия отношения "начальник"
- командир
- коллега
- деспот
- подчиненный
- командир
- Конверсия отношения "муж"
- холостяк
- супруг
- жена
- любовник
- Универсальным называется отношение, в котором
- состоит любая пара объектов
- не состоит ни одна пара объектов
- объект может состоять только к себе самому
- состоит любая пара объектов
- Пустым называется отношение, в котором
- состоит любая пара объектов
- не состоит ни одна пара объектов
- объект может состоять только к себе самому
- состоит любая пара объектов
- Отношение «друг» является
- рефлексивным
- нерефлексивным
- антирефлексивным
- рефлексивным
- Отношение «отец» является
- рефлексивным
- нерефлексивным
- антирефлексивным
- рефлексивным
- Отношение «сосед» является
- симметричным
- несимметричным
- антисимметричным
- симметричным
- Отношение «знаком с» является
- транзитивным
- нетранзитивным
- антиранзитивным
- транзитивным
- Отношение частичного порядка является
- рефлексивным, симметричным, транзитивным
- рефлексивным, несимметричным, транзитивным
- рефлексивным, симметричным, нетранзитивным
- антирефлексивным, антисимметричным, транзитивным
- рефлексивным, симметричным, транзитивным
- Отношение линейного порядка является
- рефлексивным, симметричным, транзитивным
- рефлексивным, несимметричным, транзитивным
- рефлексивным, симметричным, нетранзитивным
- антирефлексивным, антисимметричным, транзитивным
- рефлексивным, симметричным, транзитивным
- Отношение подобия является
- рефлексивным, симметричным, транзитивным
- рефлексивным, несимметричным, транзитивным
- рефлексивным, симметричным, нетранзитивным
- антирефлексивным, антисимметричным, транзитивным
- рефлексивным, симметричным, транзитивным
- Отношение тождества является
- рефлексивным, симметричным, транзитивным
- рефлексивным, несимметричным, транзитивным
- рефлексивным, симметричным, нетранзитивным
- антирефлексивным, антисимметричным, транзитивным
- рефлексивным, симметричным, транзитивным
Раздел III.
И
 Ндуктивная логика.
Ндуктивная логика.