Geum.ru

Логика – как наука. История развития логики. Формы человеческого мышления

Вид материалаДокументы

Содержание


Законы логики
Логическое умножение
Сумматор – это логическая электронная схема, выполняющая сложение двоичных чисел. Сумматор является главной частью процессора.
Подобный материал:
1   2   3   4   5   6

Задача 4 Представьте, что к приведенной схеме подключили источник питания и прибор для измерения тока, состояние контактов задается таблицей, определите показания прибора (есть ток или нет):




А В С А



1 0 0 В

0 1 0 С

1 1 1


Задание

а) б)


&

1



X

x
&
ch

1

У Y

Z Z


в)



&

1

X

Y


Задача 2. Судейская коллегия состоящая из трех членов, выносит решение большинством голосов при тайном голосовании. Постройте такую схему, чтобы голосование каждого члена «за» производилось нажатием кнопки (включением выключателя) и в случае принятия решения загоралась сигнальная лампа.


Задача 3. Представьте, что к приведенной схеме подключили источник питания и прибор для измерения тока, состояние контактов задается таблицей, определите показания прибора (есть ток или нет):


А неА В С


1 0 1 0

0 1 0 0

1 0 1 1


Законы логики


Если логическое выражение содержит большое число операций, то составлять для него таблицу истинности достаточно сложно, так как приходится перебирать большое количество вариантов. В таких случаях формулы удобно привести к нормальной короткой и понятной форме.

Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания.

Для приведения формулы к нормальной форме используют законы логики и правила логических преобразований.

Законы логики

№ п/п
Закон логики
Математическая запись
Название закона

1
А = А(А=А)



Закон тождества


2
__

А & А = 0

__

А * А = 0
Закон непротиворечия


3
__

А v A = 1
__

A + A = 1
Закон исключающего третьего


4
==

А = А



Закон двойного отрицания

5
А & 0 = 0; A v 0 = A
А * 0 = 0; А + 1 = А



6
A & 1 =A; A v 1 = 1
A * 1 = A; A + 1 = 1



7
A & A = A; A v A =A
A * A =A; A + A =A




8
__

A v A =1
__

A + A =1

Законы Моргана


9
________ __

(A B) =A & B







10
__

A B = A v B






11
A & (A v B) = A
A * (A + B) = A
Закон поглощения

12
A v A & B =A
A + A * B =A
Закон поглощения


13
__ __

A & (A v B) = A & B
__ __

A * (A +B) = A * B




14
__

A v A & = A v B

__

A + A * B = A + B



15
(A v B) v C = A v (B v C)

(A & B) & C = A & (B & C)
(A + B) + C = A + (B + C)

(A * B) * C = A * (B * C)
Правило ассоциативности

16
(A & B) v (A & C) = A & (B v C)

(A v B) & (A v C) = A v (B & C)
(A*B) + (A*C) = A*(B+C)

(A+B)*(A+C) = A+(B*C)
Правило дистрибутивности

17
A v A = A

A & A = A
A + A = A

A * A = A
Правило иденпотентности

18
A v B = B v A

A & B = B & A

A + B = B + A

A * B = B * A
Правило коммутативности


19
____ __ __

A = B=A&BvA&B = (A+B)&(A+B)







Пример:

________________

Упростите логическое выражение _____

F = (A v B) (B v C)

Это логическое выражение необходимо привести к нормальной форме, т.к. в нём присутствует импликация и отрицание логической операции.

  1. Избавимся от импликации и отрицания.

Воспользуемся формулой (9). Получится:

_________________

______ ========

(A v B) (B v C) = (A v B) & (B v C))
  1. Применим закон двойного отрицания (4). Получим:

=======

(A v B) & (B v C) = (A v B) & (B v C)
  1. Применим правило дистрибутивности (16). Получим:

(A v B) & (B v C) = (A v B) & B v (A v B) & C
  1. Применим закон коммутативности (18) и дистрибутивности (16). Получим:

(A v B) & B v (A v B) & C = A & B v B & B v A & C v B v C

5. Применим (7). Получим:

A & B v B & B v A & C v B & C = A & B v B v A & C v B & C


6.Применим (16), т.е. вынесем за скобки В. Получим:

A & B v B v A & C v B & C = B &(A v 1) v A & C v B & C


7. Применим (6). Получим:

B &(A v 1) v A & C v B & C =B v A & C v B & C


8. Переставим местами слагаемые, сгруппируем и вынесем В за скобки. Получим:

B v A & C v B & C = B & (1 v C) v A & C


9. Применим (6). и получим ответ:

B & (1 v C) v A & C = B v A & C.


Ответ: F = B v A & C

Закрепление изученного материала:

Упростите выражения:

_____ _____
  1. F = A & B v B v C;
  2. F = (A B) v (B A);

__
  1. F = A & C v A & C;

Ответы:

_____ _____ __ _ _ __ __ __ _ _ _
  1. F = A & B v B v C = A v B v B & C = B( 1v C) v A = A v B;



  1. F = ((A B) v (B A) = A v B v B v A = (A v A) v (B v B) = 1 v 1 =1;



  1. F = A & C v A & C = C &(A v A) = C;


Задание

Упростите логические выражения:

  1. F = A v ( не A & B );
  2. F = A & ( не A v B );


Использование логических устройств в вычислительной технике


Логические схемы имеют практическое применение в вычислительной технике. Они используются:
  1. Для реализации выполнения математических операций. Что это значит? А значит это следующее. Своё название ( «компьютер») компьютер получил не сразу. Сначала данное устройство называлось электронно-вычислительная машина, т. е. одним из главных назначений ЭВМ было выполнение вычислительных операций. Занималось этим специальное устройство, которое называется процессор. Процессор можно сравнить с умом человека и именно процессор (так же, как и человек в «уме») выполнял ( и выполняет) все математические операции. Как он это делает? Рассмотрим ниже.
  2. Для хранения информации. Как он это делает? Также рассмотрим ниже.

Итак, как процессор выполняет математические операции?

Прежде всего, обратите внимание на следующие компоненты:
  • Каким образом должна быть представлена информация, чтобы с ней мог работать компьютер? ( В двоичном коде, т.е. в виде 0 и 1).
  • Чтобы компьютер мог выполнять математические операции с числами, в какой системе счисления они должны быть представлены? ( В двоичной).
  • Почему ? (Потому что двоичную систему счисления наиболее просто реализовать в технических устройствах)
  • Какие сигналы подаются на входы логических вентилей? (0 и 1)


Вывод: таким образом в двоичной системе счисления и в алгебре логики информация представлена в виде двоичных кодов.

И второй момент. Для того чтобы максимально упростить работу компьютера, все математические операции (вычитание, деление, умножение и т . д.) сводятся к сложению.

Вспомнит таблицу сложения двоичных чисел. Запишем её в несколько иной форме.



А
В



S

0
0



0

0
1



1

1
0



1

1
1
1
0


Обратите внимание на дополнительный столбец. Его мы ввели потому, что при сложении происходит перенос в старший разряд. Обозначим его Р и закончим заполнение таблицы.

А
В
Р
S

0
0
0
0

0
1
0
1

1
0
0
1

1
1
1
0


Проанализируем полученный результат:
  • Таблице истинности какой логической функции аналогичен столбец Р? ( Логическое умножение).
  • Таблице истинности какой логической функции аналогичен столбец S? (Логическое сложения , кроме случая, когда на выходы подаются две единицы).

Логическое выражение, по которому можно определить сумму S, записывается следующим образом: _______

S=(A v B) & (A & B)

Построим к этому логическому выражению логическую схему:





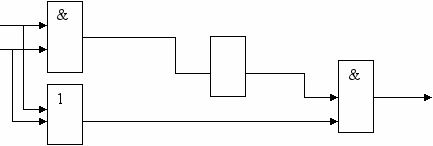
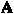
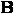
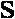
Проследим за прохождением сигнала через cхему:







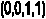
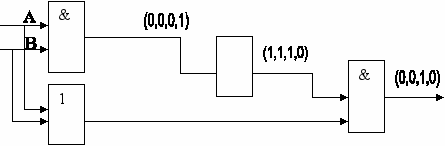
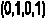
С какого элемента можно снимать сигнал Р, если мы выяснили, что результат Р соответствует логическому умножению? (С первого вентиля, реализующего операцию конъюнкции)





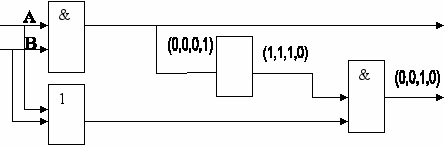
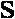
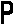
Полученная нами схема выполняет сложение двоичных одноразрядных чисел и называется полусумматором, т. к. не учитывает перенос из младшего разряда в старший (выход Р).

Для учёта переноса из младшего разряда необходимы два полусумматора.

Более «умным» является устройство, которое при сложении учитывает перенос из младшего разряда. Называется оно полный одноразрядный сумматор.


Сумматор – это логическая электронная схема, выполняющая сложение двоичных чисел. Сумматор является главной частью процессора.


Рассмотрим принц работы одноразрядного двоичного сумматора.

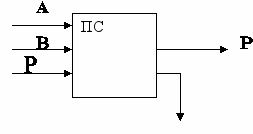
Одноразрядный сумматор должен иметь три входа: А, В – слагаемые и Р0 –перенос из предыдущего разряда и выходы: S – сумма и Р – перенос.

Нарисуем одноразрядный сумматор в виде единого функционального узла:





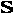
Построим таблицу сложения:



А
В
Р0
Р
S

0
0
0
0
0

0
1
0
0
1

1
0
0
0
1

1
1
0
1
0

0
0
1
0
1

0
1
1
1
0

1
0
1
1
0

1
1
1
1
1



Логические выражения для Р и S будут иметь следующий вид:

__

S = (A v B v P0 ) & P0 v (A & B & P0 )

P = (A & B) v (A & P0 ) v (B & P0 )


Но процессор, как правило, складывает многоразрядные двоичные числа. Например, 1012 + 1102 = 10112 . Для того чтобы вычислить сумму n - разрядных двоичных чисел, необходимо использовать многоразрядный сумматор, в котором на каждый разряд ставится одноразрядный сумматор и выход – перенос сумматора младшего разряда подключается к выходу сумматора старшего разряда.





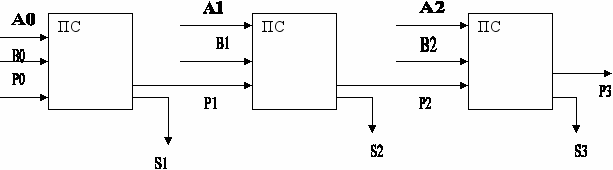
Пример:


Сложить числа 1012 + 1102 =10112





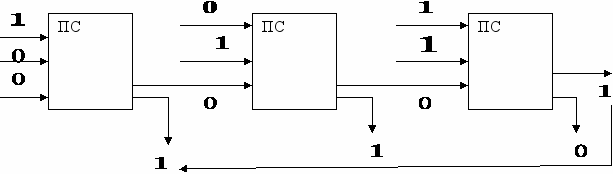
Ответ записывается с конца :


1012 +1102 =10112