< Предыдущая		Оглавление		Следующая >

6.2.2. Критерий Шарлье

Критерий Шарлье целесообразно применять лишь для рядов измерений, в котором п > 20. Если число результатов измерения п > 20, то по теореме Бернулли число результатов, превышающих по абсолютному значению Кшах, будет равно "[I - Ф(КШ)], где Ф(КШ) - значение нормированной функции Лапласа для Z = Кш.

Если сомнительным в ряду наблюдений является один результат, то

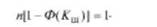
Отсюда щкт) = -.

Критические значения критерия Шарлье можно определить по формуле

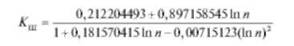
(для 5 <п< 100, /> = 0,95.)

Пользуясь критерием Шарлье, отбрасывают результат, значение которого превосходит по модулю Кшах

Порядок обнаружения и исключения грубых погрешностей и промахов с использованием критерия Шарлье сводится к следующему:

- определяется среднее значение результатов измерения

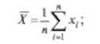
- определяется оценка среднего квадратичного отклонения ф:) по

- определяется расчетное (критическое) значение критерия Шарлье по уравнению (6.8);

- определяется абсолютное значение разности сомнительного

результата, т. е. -Х;

- сравниваются значения

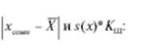
если 1*^,, - Х> то результат отбрасывают как содержащий грубую погрешность;

если хс<тн - Х < 5(х)АГш, то результат не содержит грубой ошибки.

6.2.3. Критерий Шовенэ

Критерий Шовенэ основан на тех же предпосылках, что и критерий Шарлье. Его можно использовать, если количество результатов измерения меньше 20.

Критическая область для этого критерия определяется неравенством

Результаты, значения которых в ряду из п наблюдений превосходят по модулю значение 2тох, отбрасываются как промахи. Исключение результатов выполняют в такой последовательности.

Сначала отбрасывают один результат с наибольшим по модулю отклонением от х и снова подсчитывают ах. Если и в этом случае критерий Шовенэ нарушается, то исключают следующий с наибольшим отклонением и т. д.

Критическое значение критерия Шовенэ можно определить по формуле

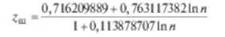
(для 2 <п <20).

Порядок обнаружения и исключения грубых ошибок и промахов с использованием критерия Шовенэ аналогичен проверке по критерию Шарлье.

Если -Х > 5<х)АГш, то результат отбрасывают как содержащий грубую погрешность;

если исоын - Х < то результат не содержит грубой ошибки.

6.2.4. Критерий Диксона

Критерий Диксона (Кд) - удобный и достаточно мощный критерий. Для использования критерия Диксона результаты измерений располагают в вариационный возрастающий рядх,<х,<... <х".

Критерий Диксона определяется по формуле

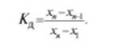
Критическая область для этого критерия

Значения 2ть(с(ду п) вычисляются по формулам

(где 4 < п < 30).

Порядок обнаружения и исключения грубых погрешностей и промахов с использованием критерия Диксона сводится к следующему:

- значения результатов измерений сортируются в порядке возрастания;

- определяется расчетное (критическое) значение критерия Диксона по формулам (6.13) - (6.16) для принятого уровня значимости

ч -ъ^М*");

- определяется значение критерия Диксона (Кд) по формуле (6.11);

- сравниваются значения АГД и п):

если Ад > 2,нкс(<7, я), то результат отбрасывают как содержащий грубую ошибку;

если АГД< 2ГДИК(^, я), то результат не содержит грубой погрешности (промаха) с вероятностью Р = I - а.

Если есть основание предполагать, что два наибольших (или два наименьших) результата являются "промахами", то можно воспользоваться методом, основанным на оценке максимальных различий полученных результатов измерения.

Для этого необходимо расположить результаты в порядке возрастания. Минимальное значение в ряду наблюдений будет у^ а максимальное - упУ где п - количество результатов измерений;

- если сомнительным результатом является упУ то вычисляют отношение

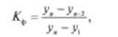
- если сомнительным результатом является уу, то вычисляют отношение

Критическое значение критерия определяется по формуле, которая одновременно учитывает количество наблюдений п и уровень значимости ц = 0,05(/> = 0,95), д = 0,01(/> = 0,99):

где х = In", у = щ.

Применение перечисленных выше критериев требует учета условий измерений. В сомнительных случаях следует стремиться выполнить дополнительные измерения (если это возможно), а затем использовать тот или иной критерий.

< Предыдущая		Оглавление		Следующая >