< Предыдущая		Оглавление		Следующая >

6. Грубые погрешности и промахи

Источниками промахов нередко бывают ошибки, допущенные оператором при измерении. Наиболее характерными из них являются: неправильный отсчет по шкале измерительного устройства, неправильная запись результата наблюдения (описка), неправильная запись значений отдельных мер использованного набора и т. п., ошибки при действиях с приборами, если они повторяются при измерениях.

Причинами грубых погрешностей могут быть внезапные или кратковременные изменения условий измерения или незамеченные неисправности в аппаратуре.

6.1. Обнаружение и исключение грубых погрешностей

Оценка наличия грубых погрешностей решается методами математической статистики - статистической проверкой гипотез. Суть метода сводится к следующему. Выдвигается нулевая гипотеза относительно результата измерения, который вызывает некоторое сомнение и рассматривается как грубый промах в связи с большим отклонением от других результатов измерения. При этом нулевая гипотеза заключается в утверждении, что "сомнительный" результат в действительности принадлежит к возможной совокупности полученных в данных условиях результатов измерений, и получение такого результата вероятно.

Пользуясь определенными статистическими критериями, пытаются опровергнуть нулевую гипотезу, т. е. пытаются доказать ее практическую невероятность. Если это удается, то промах исключают, если нет - то результат измерения оставляют.

Выбор того или иного критерия основан на принципе практической уверенности. Для этого задаются достаточно малой вероятностью ц того, что сомнительный результат действительно мог бы иметь место. Вероятность называется уровнем значимости и обычно выбирается из ряда: 0,10; 0,05; 0,01 и т. д.

Для данного ц определяют критическую область значений критерия проверки нулевой гипотезы. Если значение критерия попадает в эту область, то гипотеза отвергается.

6.2. Критерии грубых погрешностей

Известен ряд критериев, которые позволяют исключить грубые промахи. К ним, в частности, можно отнести критерий Греббса (Смирнова), Шарлье, Шовенэ, Диксона и др. Эти критерии основаны на статистических оценках параметров распределения, так как в большинстве случаев действительные значения параметров распределения неизвестны.

6.2.1. Критерий Греббса (Смирнова)

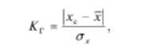
где хс - результат измерения, вызывающий сомнение; х - среднее арифметическое значение ряда измерений; ах - среднее квадратичное отклонение результатов измерения.

Критическая область значений этого критерия определяется как

Значение 2Я " для случая нормального закона распределения результатов измерения в зависимости от уровня значимости ц и количества наблюдений можно вычислить по формулам

(для 3 < п < 25).

Если при выбранном уровне значимости ц и числе наблюдений п критерий К,> Zv, то результат отбрасывают как содержащий грубую погрешность.

Порядок обнаружения и исключения грубых погрешностей и промахов с использованием критерия Греббса (Смирнова) сводится к следующему:

- определяется среднее значение результатов измерения

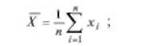
- определяется оценка среднего квадратичного отклонения 5(дг)

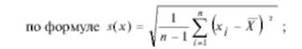
- принимается уровень значимости из ряда: 0,001; 0,025; 0,05; 0,1;

- определяется расчетное (критическое) значение критерия Греббса (Смирнова) по одному из уравнений (6.3) - (6.6) для принятого уровня значимости ц - Zff я;

- определяется критерий Греббса (Смирнова) по формуле (6.1)

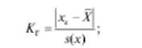
- сравниваются значения и Zч:

если К[> Zv, то результат отбрасывают как содержащий грубую погрешность;

если Кг< то результат не содержит грубой ошибки с принятой вероятностью Р = I - а.

< Предыдущая		Оглавление		Следующая >