Авторефераты по всем темам >> Авторефераты по техническим наукам

Создание перспективных электротехнических и энергетических комплексов судовых единых электроэнергетических систем

Автореферат докторской диссертации по техническим наукам

Страницы: | 1 | 2 | 3 |

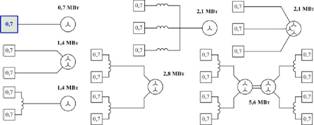
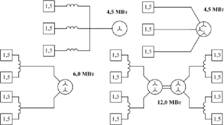
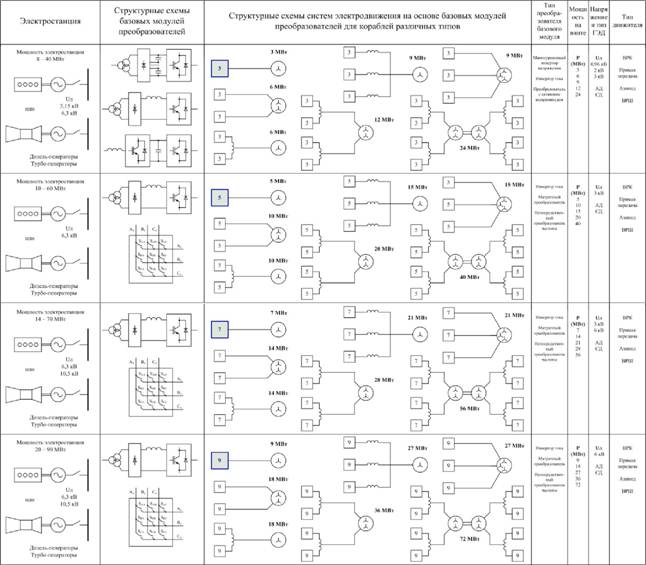
Таблица 1. Варианты структур различных типов судовых ЕЭЭС

Электростанция

Структурные схемы базовых модулей преобразователей

Структурные схемы систем злектролвижения на основе базовых модулей преобразователей для кораблей различных типов

I ни ?|???1?:?-

модуля

ХКнчг ОСТЬ

Н;ифя

Тип

[HSH--

эооо р=(ЧЛЧ""Ч

Д и кль-генер ато ры

Т н

Мощность злектростшщив

й-24 МВт

iHSK-

ОООО U^"\j)Ч-"'Ч

Лл ]ж: .!ж-; .???'.??^?'?

<ш

J.96 кВ

2 кВ ЗкЗ

Продолжение таблицы 1

Вторая глава содержит математическое обеспечение для исследования и расчётов режимов работы источников электроэнергии судовых ЕЭЭС - судовых электростанций. Приведённый в первой главе анализ показывает, что основным структурным набором любой СЭС является многообразие функциональных элементов, включающих в себя источники электроэнергии переменного тока и коммутационную аппаратуру, системы распределения активных и реактивных нагрузок, регуляторы возбуждения генераторов и регуляторы первичных двигателей генераторных агрегатов.

Значительное увеличением суммарной мощности потребителей СЭС потребованло увеличения напряжения на шинах главных распределительных щитов. Резко изменились параметры генераторных агрегатов СЭС. Потребовались ранее неизвестные структурные изменения конфигурации электромеханических систем. Последствия аварийных режимов стали более угрожающими для безопасности судов.

Отмечено, что СЭС отличаются большим разнообразием структур, а следовательнно, и процессов, происходящих в установившихся и переходных режимах. Исследование переходных процессов даже в отдельно взятом элементе СЭС уже представляют собой большие трудности, т.к. приходится иметь дело с решением систем нелинейных алгебраинческих и дифференциальных уравнений с переменными коэффициентами. Эти трудности усугубляются при объединении элементов в систему.

В работе представлены уровнения для моделирования различных режимов работы вариантов СЭС. Среди них расчёт динамических режимов работы синхронных генераторнных агрегатов СЭС в режимах подгонки частоты и синхронизации.

Ugi =?/? -xdJduUm = Va' 7Щi =U9Idi ~UJq^Un = K*Ugi +КпХ^т ~Jyu

In =C/,i +xJ^P^n ={UA -Ifi)/Tfi'PIyi=(-Iyi +K4Ui ~U* + *?? +0,1/>?/1))/?Д;

U = ? -xаа iаа ж U =?а iаа жа Iа =TJаа I -Tjаа Tаа ж

^q2L/2а A<fc2V2> ^ dlа д11д1'аа J relа ^ql1 dl ^dl1 ql'

Pl>2 =(-!* +Kk2(U2 -Un2 -krkr2dir+0,lpVf2))/Tk:

(1)

-kada>n))/Tp2;

P4>f2=(Uf2-if2)/T}

"/2а ^иГ^ q2 ~l~-^-i2^rf2-'rf2 -* y2 ' * flа "q2+Xd2ld2

мгх = UqXlqX + С/,/,,!; ??1 = (mPl -MA )/?? ; pmpl = {-mpl -kpl (?, - ?1? ))/Г; ме2 = Uq2lq2 + Ud2Id2; ??2 = (mp2 -Me2 )/TJ2; pmp2 = {-mp2 - Kp2 (?2 - ??2

dMД

-К (М, -М;аа d. =г, -/ ,;аа Uаа = dM ;аа Uаа =kа ;аа U =Uаа +Uа :

r \ ele2 / 'аа irre\rel 'а sne 'аа spаа р 'аа 5 snsp '

--??-?2; pds = kps3Us,; ? = kpsdss:, sd

= sin

(5ds).

<xi,x + хи >л - fo* cos^>i2 - x?2 sin^>?2 = % - У/2 cos(<5), (xqi +?л?? + fo,2 sm^i2 -?92 cos(S)iq2 = ?/2 sinfJJ, (?? + x* >л + r ,1 + (fa + xk + *?2 > cos ^ - rn sm(S))id2 + +(TXД + xt + x?2 > sin W + rД cos(3))iq2 = ?/2 cosfJ),

>; ''л - ft, + ** >?i + ((?? + *?2 + *J sin^j;+

+r cos( S))id2 ((rn ??(?) -(xn+xk+xq2) cos( S))iq2 = ?/2 sin(S).

(2)

где г/? - напряжение на серводвигателе; ит - сигнал по разности активной нагрузки; usp- сигнал, пропорциональный скольжению; ?? - частота вращения серводвигателя; dcos- изменение уставки регулятора частоты вращения; s<& - сигнал периодизатора угла между векторами напряжений; st- сигнал включения генераторов на параллельную работу.

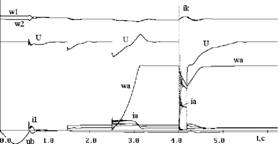
Результаты моделирования режима синхронизации на примере двух генераторных агрегатов СЭС приведены на рисунке 5.

Из рисунка видно, что после подачи

-------- командыа на синхронизациюа (0,6а с)

уавтоматик СЭС выполняетаа процедуру

?аа "Ь/

/l/V^-

подгонки частот, а в момент времени 2,8 с

-"аа происходитаа включение генератороваа ана

Ю00оо"р-

паралельнуюаа работу.аа Н 5-ойаа секунде

происходит включение нагрузки.

"~йГ Полученаа формализацияа расчета

электромагнитных процессов в многоагре-

_, ?аа гатных комплексах СЭС, позволяющая мо-

Рисунок 5. - Процесс подгонки частот

^ъг^а делировать в структурах судовых электро-

и синхронизации синхронных генераторов LJLаа r t-jjfjг

станции динамические режимы параллельнной работы генераторных агрегатов различных типов. На примере разработки математиченского описание для исследования динамических электромеханических процессов в системе

из двух синхронных дизель-генераторов СЭС переменного тока, процедуру формализации расчёта можно представить в следующем виде.

Дана исходная система уровнений синхронного генератора:

Uq = - rid + a>4>q + ??? /соъ,^d = if - *d 4 + Ь,

Ud = - riq + ???- p4q/a>b ,?1 =V* + lQ>

Uf = if + Tf p*еf,?/ = '/ ж md xd 'd + gib,

0=iD+ TD ???,??= *D+ 82'f - mds *d id,^

0 = iQа + Tq ??? ,?? = iQа + mqxqiq,

Me = xеdiq+Xеqid ж

где Uq, Ud- составляющие вектора напряжения статора по осям q и d; id, iq- составляющие вектора тока статора по осям; ?& Wq-составляющие вектора потокосцепления статора по осям; Wf- потокосцепление обмотки возбуждения; idJq-составляющие вектора тока демпферных контуров; ??, Wq- составляющие вектора потокосцепления демпферных контуров; Xd, xq- синхронные сопротивления статорных обмоток по осям; md,mds,mq-коэффициент магнитной связи обмоток статора и ротора по осям; gj, g2 - коэффициенты магнитной связи обмоток ротора по осям; Tf, Td, Tq- постоянные времени роторных обмоток по осям; г - активное сопротивление обмотки статора; <х>ь, со - базисная угловая и относительная частоты вращения ротора.

Уравнения систем возбуждения записаны в виде:

ufi= kuliudi- ku2iuqi+ ЬШ1Л + kI2iIqi- kkliIti,plh= -(\/Ть )lM+ (l/TJa )Uh,

ki\а dHiа di )qHi qi '\ /

где Ud, Uq- составляющие вектора напряжения статора по осям d и q; Uf, If- напряжение и ток обмотки возбуждения; Id, Iq- составляющие тока статора по осям d и q; Id, Iq- токи демпферных контуров; со - частота вращения осей d и q; Wd,Wq- потокосцепления статора по осям d и q; Wft?ц Tq- потокосцепления роторных контуров; г - активное сопротивленние обмоток статора; Xd, xq- индуктивное сопротивление обмоток статора; ??, ?4 , gi, gi-коэффициенты связи обмоток машины.

- уравнения приводного двигателя с АРЧ записаны в виде:

??? = (mpl-Мл )/??,ил = {Мл -Ме2 )/(хи + хк2 + ха) _

(5)

pmpl= (-mpl -kpfa-{??1 -???1)))/??1,

- уравнения асинхронного гребного электродвигателя:

1/d=aUd+co4/q+corId,

?,=???+???+???4?

pVD=-(\/Tr)4'D+(Mx/Tr)ld+a?еex{SM-<p),

??=(\?(\-?)?)??-(\?(\-?)?)??,

?9={\?{\-?)?)?9-{\?{\-?)?)??,

?^?^?^-?^-?^,(6)

p4>e=-{\/Tr)4>e+{Mx/Tr)lq+a>4>Dx(SM-<p),а 8д=\-сод.

где ? - отклонение частоты сети; сод - частота вращения асинхронного двигателя; ? - коэффициент связи обмоток ротора и статора; х - реактивность статора; Тг - постоянная времени обмоток двигателя; Wd, Tq, Td, Tq- потокосцепления обмоток, статора и ротора асинхронного двигателя; ?д - скольжение ГЭД.

- уравнений нагрузки:

Idi=SHiUdi+bHiU,

Я"

gmuqi -Ьнгиа-

и уравнении линии связи: Idce\=SceUd\ +bceUq\-SceUd2 cos(s) + bceUd2sin(s)-gceUq2sin(s)-bceUq2cos(s),

Iqce\ = -bceUd\ + 8ceUql+ bceUd2 Щ*(?) + 8ceUd2 Щ(?) + bceUq2 Щ(?) ~ 8ceUq2 Щ*(?)

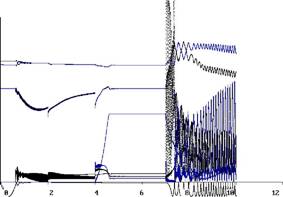
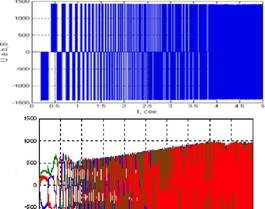
Результаты моделирования режима параллельной работы двух синхронных генеранторных агрегатов СЭС, аварийного режима короткого замыкания и срабатывания защиты приведены на рисунке 6. Из рисунка видно, что через 0,5 с. после подачи команды на синхронизацию, автоматика СЭС выполнила процедуру подгонки частоты и включила генераторы на паралельную работу. Затем в электростанции происходит включение общесудовых потребителей. На четвёртой секунде на шинах СЭС происходит короткое замыкание, отключаемое автоматическим выключателем.

Рисунок 6. - Моделирование режимов работы генераторов СЭС

Переходные процессы в режиме параллельной работы двух генераторов со сверхпроводящими обмотками приведены на рисунке 7. Следует отметить, что режим параллельной работы таких маншин неустойчив в связи с практически нулевыми диссипативными членами в синстеме дифференциальных уравнений гененраторов со сверхпроводящими обмотками. Как видно из рисунка, для режима параллельной работы сверхпроводниконвых генераторов характерно значительнное ухудшение качества регулирования напряжения и потеря устойчивости паралнлельной работы в режиме восстановления

синхронного состояния машин после короткого замыкания.

Рисунок 7. - Моделирование режимов параллель- Рисунок 8. - Моделированиев режимов па-

ной работы ВТСП-синхронных генераторова раллельной работы генератора обычной кон-

струкции и генератора со сверхпроводящими обмотками

Показано (рисунок 8), что при параллельной работе генераторов обычной коннструкции и сверхпроводниковых генераторов уровень устойчивости значительно повыншается в связи с внесением потерь в систему распределения.

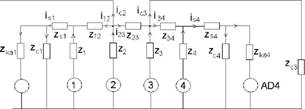
Составлены уравнения всей ЕЭЭС. Для расчета режима работы СЭС используем схему замещения, в которой все статические и асинхронные нагрузки объединены, при этом каждая из них питается от своей СЭС.

ГРЩ1 AC1

г------ 1Ч

/ АЛаа /А2

|-|Zll

РЩ1а I

РЩ2

,9"а ? /,/

ТН Iа Па 7

1___ ( (а (аа ???1

AD1

'РЩ2

(СГ2) (СГ2)

ДГ \fДГ

АД

(аа I. I

Sж_

АС2

_у____

А4 /а AS1

Т Iа I

^ мех

АД

?а {аа ?аа ( (

Рисунок 9. - Структурная схема ЕЭЭС с двумя СЭС

Рисунок 10. - Схема замещения ЕЭЭС с двумя СЭС

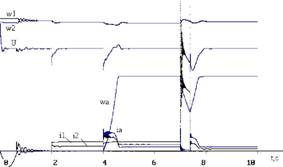
Результаты моделирования динамических процессов в многостанционных ЕЭЭС при параллельной работе четырёх генераторных агрегатов представлены на рисунке 11.

Из рисунка видно, что в начальный момент времени в структуре ЕЭЭС работает только один генераторный агрегат. Происходит его нагружение. Когда мощности одного генератора не хватает идет команда на включение второго генератора. Показан процесс синхронизации и распределения нагрузки. Когда не хватает мощности двух генераторов идет команда на включение третьего генератора и т.д.

r-f-

-/____ l^

ЧjlfW*-

1аа i = In

ж^

ра?

^^уууху^^^куу^^

Ф*=С

жж/*-

Рисунок 11. - Динамические процессы в многоагрегатных электростанциях

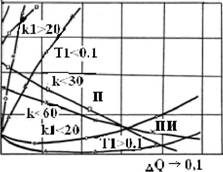
Разработана методика определения областей параметров системы распределения нагрузок между генераторными агрегатами СЭС, обеспечивающая получение наилучших или, по меньшей мере, отвечающих поставленным требованиям показатели функциониронвания проектируемой системы.

Так, исходная система уравнений, описывающая режим параллельной работы двух генераторов на судовую сеть, может быть записана в виде:

Задача обеспечения заданной точности системы распределения реактивной нагрузнки СЭС решается в процессе параметрического синтеза за счёт целенаправленного поиска в области основных и дополнительных параметров системы распределения при ограниченниях вида:

[К1], [К2], [F] > 0.(19)

После ввода системы в область заданного распределения, границы этой области становятся дополнительными ограничениями процедуры поиска и ищется оптимальное, для данных условий, соотношение параметров, минимизирующее целевую функцию вида:

F^I.+Ml/Cj+h^/Cj,(20)

где \ (УСх1), p (l/Cx2)аа - штрафные ограничения целевой функции, а

со

/, = ^AQe^ sm(k2зt)dty,

(21)

о. = Pimin - степень устойчивости системы; ? =| ?? max | /-J(pf+ caf )rmn- степень ее колебантельности; AQ =\QlЧQ2\ - ошибка распределения реактивных нагрузок в СЭС; Pi, cOi- вещественная и мнимые части z'-го комплексного корня характеристического уравннения системы; kitk2, - масштабные коэффициенты; hi, li2 - весовые коэффициенты.

CX1=0,\-AQ,аа Cx2=Po-pIimn.(22)

где р0 - запас устойчивости системы.

Допустимые границы переменных функционала для ошибки распределения реакнтивных нагрузок определяются из Классификационных требований, а степень и запас устойчивости, а также степень колебательности - исходя из желаемых качественных характеристик рассматриваемой системы.

О № i

0,001

0,01

0,005

l^	\H
\	^\		ПУ
				"*-???
		ПН

Kcy^ 90

Рисунок 12. - Выбор параметров настройки CAP

Рисунок 13. - Зависимость показателя качества

системы от параметров настройки и структуры

устройств согласования

Процедура поиска экстремума целевой функции организована с использованием классического метода оптимизации - метода Нелдера-Мида (рисунки 12, 13). Целевая функция связывает исходную математическую модель СЭС с показателями качества раснпределения через вектор параметров ошибки распределения реактивной нагрузки и ком-

бинацию параметров собственных чисел исследуемой системы. Такое сочетание позволянет в рамках критерия эффективности наложить на классическое понятие устойчивости синстемы реальныеаа технические ограничения.

Методика определения областей параметров искомой системы, удовлетворяюнщей требуемым показателям качества, выполняется на линеаризованной модели с дальнейшей проверкой полученных результатов на полной нелинейной модели СЭС.

В третьей главе изложены вопросы исследования и расчёта режимов работы синстемы электродвижения судовых ЕЭЭС. Показано, что разработка транзисторных и тири-сторных ГЭП связана с анализом новых схем и большим объемом расчетов как при выбонре структур и элементов силовой части, так и при выборе состава и алгоритмов системы управления.

Структура автоматической системы управления (САУ) режимами работы ГЭП напрямую зависит как от состава главной силовой цепи ГЭП, так и от алгоритмов реалинзации законов управления, в значительной степени определяемыми свойствами самого объекта управления - ГЭД.

В настоящее время разработано много сред моделирования, однако применение

универсальных, проверенных многолетним опытом известных программ и стандартных

библиотек обеспечивает эффективное решение задач при анализе сравнительно простых

схем. Работоспособность и надёжность реальных силовых машинно-вентильных комплекн

сов ЕЭЭС напрямую зависит от множества специфических факторов режимов работы и

параметров схем электрических машин и СПЧ. Поэтому использование стандартных бибн

лиотек известных сред моделирования не всегда приводит к желаемымаа результатам

из-за заложенных в них погрешностей. Возникающие погрешности должны оцениваться в

каждом конкретном случае и, если они недопустимы, то необходимо находить возн

можности более точного описания элементов или использования более подходящих вын

числительных методов и процедур.

В настоящее время в качестве ГЭД, входящих в состав САУ ГЭП, наиболее широко используются асинхронные ГЭД с трёхфазными (многофазными) статорными обмотками и синхронные ГЭД с электромагнитным возбуждением или с возбуждением на постояннных магнитах. Кроме того, в ближайшей перспективе, очень привлекательными могут стать вентильно-индукторные ГЭД и гребные электродвигатели на основе высокотемпенратурных сверхпроводящих технологий.

В работе представленыуравнения для синтеза систем управления асинхронным ГЭП с векторным регулированием.

^saа J-A'

i.p=-E'(ia+2Ib)

Тз"

!,? = !Sa cosy+ Isp sin?, IS2=IsPcosy-Isasiny,

(23)

(24)

L.а ..... аL.

Y = |(??

^т=/(-^т+-7-^-1.1)*.аа (25)

?аа ?

0а ^r Xim

ХIs2)dt, (26)

где ?№ - модуль вектора потокосцепления ротора, Isl, Is2 - проекции вектора тока статора, со - скорость вращения вала электродвигателя, р -число пар полюсов, ? - угловое полонжение вектора потокосцепления ротора, Rr ,Lа Lr - параметры ГЭД.

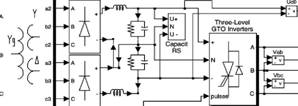
На основанииаа приведённых формул предложена модель ГЭП с векторной систенмой управления и датчиком скорости (рисунок 14).

№

transform kooramate2

l>u

Calc controljspeedа ?42??

???? Них

<Я

+fаа V-Unp lslz-+fаа V^lnpUslz

Uab Induction Motor

Demux js_abc

Ubz

gamma

2-3

Scope1

Step2аа ГП

Transform kordinatel

H Isl i gamma

FLUX	z
	Них
Flux_z	Is2i
	Wi

Powergui

-Discrete,

T5 = 4e-00Ss

Рисунок 14. Ч Схема модели векторной системы управления ГЭП с датчиком скорости

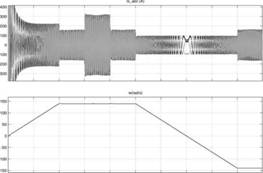
На рисунке 15. представлены графики переходных процессов в рассматриваемой модели ГЭП.

ЧJ
ЧJ	ца -

Из рисунка видно, что асинхронный ГЭД разгоняется с номинальным моментом до номинальной скорости за 2 секунды. Через 3 секунды набрасывается дополнительный момент равный номинальному моменту, через 4 секунды дополнительный момент сбрасыванется. Через 5 секунд производится реверс ГЭД. Общее время реверса составляет 4 секунды. Как видно из графиков, электропривод обладанет хорошей динамикой и может быть применен для судовых электроприводов, где требуется высокое быстродействие и большая перегрунзочная способность.

Рисунок 15. - Моделирование режимов ранботы ГЭП с векторной системой управленния и датчиком скорости

Ваа работеаа такжеаа приведены:аа система уравнений векторного управления синхронным ГЭД с датчиком положения ротора (27), комнпьютерная модель векторной системы управнления синхронным ГЭД (рисунок 16) и завинсимость изменения параметров режима работы синхронного ГЭП при разгоне ГЭД от нуля до номинальной частоты вращения (рисунок 17.). При этом угловое положение вектора по-токосцепления статора определяется относительно неподвижных осей с помощью направнляющих cosл>, sinл>:

??. (27)

оо

:\QJ

оаа е

XLf2-аа _|_ XLf2-

-IspRs)dt,

cos ? -

sin <5 =

-IsaRs)dt,аа ??

saа l^saаа 'sa'^s;"1' * $?а s^\а $?аа *??*^;^> * sm ^* sa ' * ??'?а 'а ?

smsm

Управляющий сигнал по току возбуждения формируется согласно выражению

ifo-

Даа 2а га Mz

___________ Ч Fnz1

2 , ,2аа Mz2

Fnz'

L^irwzаа +Lx

(28)

гдеаа F/izаа - заданиеа поа потокосцеплению,аа Mzаа - заданиеа поа моменту,аа L L^L^

параметры ГЭД.

А по известным проекциям вектора тока вычисляется его скорость вращения:

dip т_ dla

la---------- ??--------

dtdt

(29)

жfflh

Diode rec tiller

Diode rectifierl

жCS

Powerful

ж Discrete.

Тз = 2е-006з.

Vector control

*fаа Scope

Рисунок 16. - Компьютерная модель векторной системы управления синхронного ГЭП

0.5а 1аа 1.5

1.2
Фаа 0.8 аа 0.6 ш 4аа 0.4 5аа 0.2 0 -0.2


												<
	И											Б
												а
	3	0	5	1	5а 2	2	5 ек	?а 3	5	tа 4	5	-

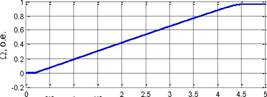
Рисунок 17. - Результаты моделирования пуска синхронного ГЭД при возрастающем потоке возбуждения

Представлены система уравнений векторного управления синхронным ГЭД без датчика положения ротора (30). Скорость и угловое положение ротора определяются на основании следующих выражений:

?аа ?

?1 = Ч2-й), cos?,а ?2 = Ч2-й), sin?,

со.

<Je\2 + ?22,а ? = arctan(г2 / ?1),

Страницы: | 1 | 2 | 3 |

Авторефераты по всем темам >> Авторефераты по техническим наукам

Blog

Создание перспективных электротехнических и энергетических комплексов судовых единых электроэнергетических систем