Авторефераты по всем темам  >>  Авторефераты по геологии-минералогии

Моделирование тепломассообменных процессов в мерзлых породах с подвижной ледовой компонентой

Автореферат докторской диссертации по геологии-минералогии

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 | 4 | 5 | 6 |

 

Для сравнения результатов измерений с теорией создана вычислительная программа по решению сопряженных тепловой задачи во внутренней области основного блока и задачи фильтрации в керамике. Входными параметрами являются температура теплообменников (5) и давление в трубках (7) (Рис. 13а). Программа находит скорость движения льда в полости ячейки, температуру латунных пластин (2), также величины потоков тепла и жидкости через основания образца.

В втором параграфе приведены результаты изучения тепломассопереноса через образец под действием градиента давления жидкости. Порядок измерения следующий. Перед началом опыта устанавливается одинаковая температура теплообменников (5) и, как следствие, латунных пластин (2) с точностью 0,01 градуса при нулевом перепаде давления. Затем последовательно в течение 1 суток поддерживается разность давлений в капиллярах (7) из следующего ряда значений: 0,37; 2,3; 12; 32; 64 кПа.

На рис. 14 представлены результаты измерений потока воды через образец под действием градиента давления жидкости при различных средних температурах образца.

Эксперимент показывает, что величина потока массы через образец уменьшается с понижением средней температуры. Это может быть объяснено гидравлическим сопротивлением пленки незамерзшей воды, разделяющей лед и каркас пористой среды. Однако сравнение с теорией, в которой этот фактор исключен из рассмотрения, показывает, что расчетная величина потока массы меньше наблюдаемой в эксперименте. Может быть истинное значение скорости движения льда выше теоретического?

В качестве индикатора скорости движения льда служит разность температур латунных пластин (2) (Рис. 15). При сближении со стенкой столбик льда плавится с поглощением тепла. На противоположной стороне включения происходит обратный процесс - замерзание воды и выделение тепла. Разделенные в пространстве источники и стоки тепла изменяют температурное поле окружающей среды и создают перепад температуры на пластинах, который пропорционален скорости движения льда. Экспериментальные данные на рис. 15 показывают, что с понижением средней температуры образца уменьшается перепад температуры на пластинах, а значит и скорость движения льда в полости. Такое поведение системы может быть объяснено зависимостью гидравлического сопротивления пленки незамерзшей воды от температуры. Не противоречит этому объяснению и то, что экспериментальные точки оказываются ниже расчетных - в теории гидравлическое сопротивление не принимается во внимание.

На основании результатов теплофизических измерений можно сделать вывод о том, что истинная скорость движения льда в полости не превышает теоретическую. В таком случае, чтобы объяснить более высокие значения потока жидкости в эксперименте по сравнению с теорией (Рис. 14) необходимо ввести в рассмотрение дополнительные факторы. На наш взгляд наиболее вероятной причиной расхождения данных эксперимента и теории является наличие незамерзающих каналов жидкости между стенками полости и столбиком льда. Так согласно расчетам, если убрать гидроизоляцию между керамическими кольцами (Рис. 13б, 13), поток массы в системе возрастает почти в 50 раз.

Нельзя также исключить возможность движения жидкости через лед по незамерзающим межзерновым каналам, свойства которых обсуждается в ряде работ [Ketcham, Hobbs, 1969; Mader, 1992].

Во третьем параграфе представлены результаты экспериментальных работ по изучению тепломассопереноса через образец под действием градиента температуры.

Градиент температуры инициирует движение льда в полости ячейки (Рис. 13б) и, как следствие, через образец устанавливается поток жидкости.

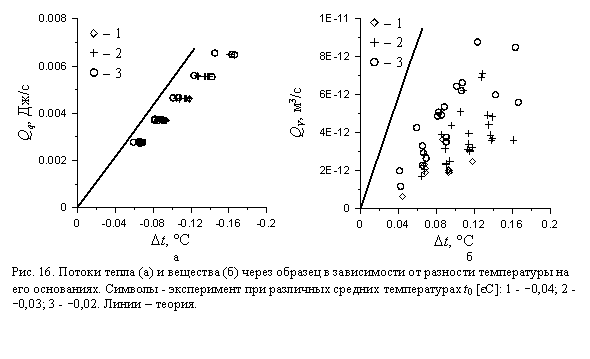
Экспериментальные величины потоков тепла и расхода жидкости в зависимости от перепада температуры на основаниях образца представлены на Рис. 16. Между величиной потоков и перепадом температуры на границах образца наблюдается примерно линейная зависимость. Понижение средней температуры при прочих равных условиях приводит к уменьшению величин потоков тепла и массы. Сравнение с теорией показывает, что в отличие от результатов опытов, в которых потоки создавались градиентом давления, на обоих графиках экспериментальные точки лежат ниже расчетных значений и обнаруживают значительно больший разброс данных.

В четвертом параграфе представлены результаты обработки экспериментальных данных по измерению потоков тепла и массы под действием различных термодинамических сил (градиентов давления и температуры).

Опыты, проведенные при различных граничных условиях (Рис. 15 и Рис. 16б), показывают, что система обладает термоосмотическими и баротермическими свойствами, т.е. градиент температуры создает поток массы через образец, а градиент давления - поток тепла. Поэтому в основу обработки экспериментальных данных положены уравнения переноса в общем виде:

а (27)

где jV - плотность объемного потока [мс-1] и jq - плотность потока тепла [Джм-2с-1] через основания образца; Dp, DT - перепады давления жидкости [Па] и температуры [К] на высоте образца Dx [м]; Cpp, Cpt, Ctp, Ctt - коэффициенты переноса; T0 = 273,15 K.

Результаты двух экспериментов, проведенных при различных граничных условиях, образуют два набора данных (экспериментальных точек). Первый набор получен в эксперименте, в котором потоки создавались градиентом давления жидкости при перепаде температуры на теплообменниках равном нулю. Точки второго набора - данные эксперимента, в котором в качестве движущей термодинамической силы выступает градиент температуры при нулевом перепаде давления жидкости. По двум экспериментальным точкам из первого и второго наборов на основании соотношений (27) определяются коэффициенты переноса.

Как можно видеть на рис. 14 - 16 потоки тепла и массы, а значит и C-коэффициенты, зависят от средней температуры образца, которая, по этой причине, включена в набор параметров результатов измерения. Экспериментальные точки неравномерно распределены на температурной шкале, поэтому вначале были найдены значения температур, вблизи которых концентрация точек из обоих наборов максимальна. Затем вблизи этих узловых температур образованы группы из экспериментальных точек. В каждой группе данных была решена система уравнений (1) для всех сочетаний точек из первого набора со вторым, а затем вычислены средние коэффициенты переноса.

Величины коэффициентов в зависимости от средней температуры образца приведены на Рис. 17 - 18. Можно видеть, что с понижением температуры абсолютные значения коэффициентов уменьшаются.

Весь цикл измерений включал семь серий. После каждой серии за исключением четвертой производилась промывка системы дистиллированной водой в течение от 1 до 7 суток. Необходимость в этом обнаружилась в ходе эксперимента. В 1 серии было замечено, что величины потоков массы через образец значительно меньше расчетных. В конце этой серии температура фазового равновесия лед-вода оказалось равной Ц0,017 ?С, что соответствует концентрации раствора неэлектролита примерно 0,01 моль/л. Величина концентрации попадает в диапазон значений от 0,001 до 0,01 моль/л, в пределах которого происходит, согласно теоретическим оценкам резкое уменьшение скорости движения льда относительно каркаса пористой среды.

С целью проверки предположения о попадании в воду посторонних примесей была осуществлена промывка всей системы дистиллированной водой в течение недели. После первой промывки значение коэффициента Cpt, увеличилось больше, чем 5 в раз.

Для вычисления экспериментальных значений коэффициентов переноса были взяты результаты измерений 6 и 7 серий.

Теоретическая модель дает величины коэффициентов переноса, представленные в таблице 2.

Таблица 2

Cpp, м2с-1Па-1	Cpt, м2с-1	Ctp, м2с-1	Ctt, Джм-1с-1
-8,6310-15	1,3210-6	1,2910-6	-524

Нарушение симметрии C-коэффициентов (Таблица 2) - следствие теплообмена образца с окружающей средой через боковую поверхность.

Сравнение коэффициентов переноса тепла Ctt (Рис. 17б и Таблица 2) показывает, что абсолютное значение теоретического коэффициента оказывается выше экспериментального практически по всем диапазоне температуры. Заметный вклад в величину коэффициента Ctt дает режеляционное движение льда. Так, если лед неподвижен относительно керамики, теоретическое значение коэффициента Ctt оказывается равным -326 Джм-1с-1.

Теория предсказывает более высокую скорость льда по сравнению с экспериментальной. Это различие может быть следствием двух причин: в теории не учитывается гидросопротивление пленки незамерзшей воды между основанием включения льда и стенками полости, а также предполагается отсутствие растворимых соединений в воде. Оба этих фактора уменьшают скорость льда относительно керамики.

Абсолютное значение коэффициента переноса вещества Cpp, найденное из теории (Таблица 2), оказывается меньше экспериментального (Рис. 17а) практически во всем диапазоне температур. С учетом предыдущего заключения наиболее вероятной причиной этого различия может быть течение жидкости между боковой поверхностью включения льда и стенками полости. Перенос жидкости по проводящим каналам увеличивает величину суммарного потока вещества под действием градиента давления, практически не меняя скорость льда.

В свою очередь оба фактора - уменьшение скорости режеляционного движения льда и наличие незамерзающих каналов между областями плавления льда и замерзания воды - приводят к тому, что величины недиагональных коэффициентов переноса Cpt и Ctp, измеренные в эксперименте, становятся заметно меньше теоретических. (Таблица 1 и Рис. 18).

Явные значения C-коэффициентов позволяют определить параметры процесса, при которых законы переноса тепла и массы необходимо применять в общей форме.

Слагаемые в законе переноса вещества (27) имеют один порядок, когда выполняется следующее соотношение:

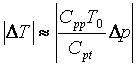(28)

Принимая Cpp = -210-14 м2с-1Па-1 и Cpt =  510-7 м2с-1 (Рис. 17 - 18), из равенства (28) следует, например, что при перепаде давления 105 Па, изменение температуры DT = 1 K. Таким образом, термоосмотический вклад в массоперенос через образец становится заметным при изменении температуры среды не менее 1 K на 1 атм перепада давления жидкости. В природе это условие выполняется довольно часто.

Аналогично для перепада давления жидкости, выше которого закон переноса тепла должен применяться в общем виде, имеем

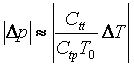(29)

Полагая Ctt = -420 Джм-1с-1 и Ctp =  510-7 м2с-1 (Рис. 3 - 4), из соотношения (29) получаем Dp/DT  3106 ПаK-1.

Представленные выше оценки получены для пористой среды с макровключениями. Величина коэффициентов Cpt и Ctp, входящих в соотношения (28) и (29), определяется во многом гидравлическими свойствами каналов между областями плавления и замерзания льда, а значит и размером включения. С уменьшением размера льда роль проводимости гидравлических каналов возрастает и, как результат, должна быть меньше величина недиагональных коэффициентов. Косвенным подтверждением этому могут служить результаты экспериментальной работы [Horiguchi, Miller, 1980] - баротермические свойства обнаруживает макровключение льда между мембранами, но не мерзлые грунты. Наиболее вероятная причина - доля макровключений в грунте была достаточно мала. Однако, в настоящее время отсутствует необходимое количество экспериментального материала, на основании которого можно обоснованно судить о значимости размерного фактора включений льда в тепломассообменных процессах.

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 | 4 | 5 | 6 |

     Авторефераты по всем темам  >>  Авторефераты по геологии-минералогии