Авторефераты по всем темам  >>  Авторефераты по геологии-минералогии

Моделирование тепломассообменных процессов в мерзлых породах с подвижной ледовой компонентой

Автореферат докторской диссертации по геологии-минералогии

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 | 4 | 5 | 6 |

 

ичный вклад соискателя. Основные результаты по теме диссертации получены лично автором.

Работа выполнена в соответствии с планами научных исследований ИКЗ СО РАН, включаяа интеграционные программы СО РАН №№ 13 и 122), и на отдельных этапах была поддержана грантами: РФФИ 05-05-64228-а; Губернатора Тюменской области 2007 г. УРежеляционный способ очистки водыФ; Губернской Академии 2007, 2008 гг.

аа Апробация работы. Результаты работы были представлены на следующих конференциях: 9 межотраслевой научно-методологический семинар (Тюмень, 2002); Международная конференция Permafrost (Zurich, Switzerland, 2003), Международная конференция УКриосфера Земли как среда жизнеобеспеченияФ (Пущино, 2003), Международная конференция Криосфера нефтегазоносных провинций (Тюмень, 2004), Международная конференция Теория и практика оценки состояния криосферы Земли и прогноз ее изменений (Тюмень, 2006), Международная конференция Криогенные ресурсы полярных и горных регионов. Состояние и перспективы инженерного мерзлотоведения (Тюмень, 2008).

Публикации. По результатам исследований опубликовано 15 работ, включая 1 книгу (в соавторстве), 9 статей в рецензируемых зарубежных (International Journal of Heat and Mass Transfer - 4 статьи) и отечественных журналах, в том числе из перечня ВАК - 5 статей.

Структура и объем диссертации. Диссертация состоит из введения, 5 глав, заключения и списка литературы. Общий объем диссертации составляет 262 страницы, в том числе 46 рисунков и 4 таблицы, список литературы содержит 205 наименований.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении обосновывается актуальность работы, сформулированы цель и задачи исследования, раскрывается научная новизна, отмечена практическая значимость полученных результатов.

Глава 1. Термодинамический аспект криогенного текстурообразования

Глава носит обзорный характер. В первом параграфе показано, что в современных моделях криогенного текстурообразования важную роль играет промерзающая зона - мерзлый грунт вблизи температуры начала замерзания. Лед участвует при тепломассопереносе в промерзающей зоне вследствие его движения относительно грунтовых частиц (режеляции).

Во втором параграфе дается обзор по режеляции льда в системах двух видов: движение твердых, жидких и газообразных включений через лед и движение льда внутри твердого тела. Несмотря на длительную историю изучению этого явления, внимание ко второй системе было привлечено сравнительно недавно работами Р.Д. Миллера (1978-1985гг.) по моделированию криогенного текстурообразования в промерзающих грунтах. Некоторые допущения модели относительно движения льда через скелет грунта требуют экспериментального и теоретического обоснования. Поэтому изучение особенностей движения льда в модельных системах следует рассматривать как этап в построении физически обоснованной теории криогенного текстурообразования промерзающих грунтов.

Перенос жидкой фазы в мерзлых грунтах вблизи температуры начала замерзания происходит через незамерзшие грунтовые агрегаты. Поэтому в третьем и четвертом параграфах дается обзор равновесных и неравновесных свойств пористых сред, насыщенных раствором неэлектролита и электролита.

Основные результаты работы:

Глава 2. Модель бипористой среды

В данной главе представлена модель бипористой среды, ее основные свойства и общая постановка задачи о стационарном тепломассопереносе.

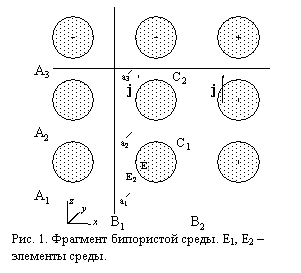Бипористая среда регулярной структуры состоит из двух однородных (гомогенных) элементов - водонасыщенной мелкопористой среды и льда (рис. 1).

Элементы среды обладают следующими свойствами. Мелкопористая часть среды насыщена бинарным раствором электролита и проницаема для текучей субстанции. Каркас пористой среды не деформируем и изготовлен из нейтрального вещества, которое не вступает в реакции обмена с раствором электролита. Газовая фаза отсутствует.

Лед полагается жестким телом, непроницаемым для флюида, и может двигаться относительно каркаса мелкопористой среды вследствие режеляции, т.е. плавиться при сближении с препятствием и восстанавливать свою форму при удалении от поверхности полости за счет замерзания воды. При кристаллизации лед полностью отторгает инородные примеси.

Термодинамические условия обеспечивают сохранение льда в крупных порах и запрещают его проникновение в мелкие поры.

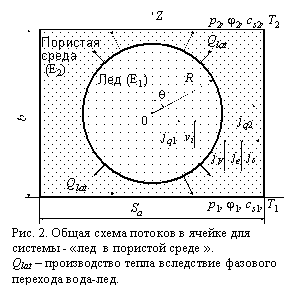Изучается одномерный стационарный процесс тепломассопереноса. В силу симметрии проблема решается для одной элементарной ячейки (Рис. 2), на горизонтальных гранях которой заданы постоянные значения термодинамических величин: температуры, давления жидкости, концентрации раствора и электрического потенциала. Потоки тепла и массы через боковые грани равны нулю. В градиентном поле термодинамических потенциалов лед может перемещаться относительно каркаса мелкопористой среды и в силу симметрии, скорость его движения параллельна оси Z.

Система координат привязана к каркасу пористой среды.

В пренебрежении конвективным переносом тепла, распределение температуры T в элементах ячейки E1 и E2 удовлетворяет уравнению Лапласа:

аа (1)

где D - оператор Лапласа.

В пренебрежении термоосмотическими свойствами микропористой среды плотности потоков массы через нее линейно связаны с движущими силами - градиентами давления жидкости, электрического потенциала и концентрации раствора:

jV = kppNp + kpeNj + kpsNcsа

je = kepNp + keeNj + kesNcs (2)

js = kspNp + kseNj + kssNcs,а

где jV, je, js - плотности объемного потока раствора, электрического тока и молярного потока растворенного вещества, p - давление жидкости, плотность, j - электрический потенциал, cs - молярная концентрация раствора, kpp, kpe,..., kss - коэффициенты переноса. Соотношения взаимности Онзагера для потоков и термодинамических сил (2) имеют следующий вид:

kpe = kep, 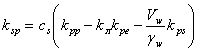, ,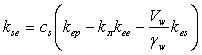а (3)

где Vw - парциальный молярный объем воды в растворе, kp - некоторый параметр, , mw - химический потенциал воды в растворе. Далее в тексте индекс w будет обозначать воду, i - лед.

В работе предложен способ, позволяющий связать феноменологические k-коэффициенты с опытными величинами.

Уравнения движения ионов в объемном растворе обобщаются на ограниченное пространство посредством введения коэффициентов торможения di:

, i = 1, 2аа (4)

где ci - молярная концентрация i-ионов в растворе; Di, ui - коэффициент диффузии и подвижность i-иона. Знак величины подвижности совпадает со знаком иона.

В эксперименте определяются коэффициенты гидропроводностиKh, осмоса Kos и электроосмоса Ke, которые связывают объемный поток jV c термодинамическими силами:

аа (5)

Коэффициенты, входящие в законы переноса массы (2) - (4), выражаются через опытные величины Kh, Kos, Ke:

kpp = -Kh; kpe = -Ke; kps = Kos аа (6)

kep = -Ke; ; kes = -kD а (7)

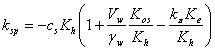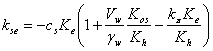;; kss = -Dn,а (8)

где ;;; , Dk, uk - коэффициент диффузии и подвижность k-иона, ; nk - число k-ионов при диссоциации молекулы растворенного вещества (k = 1, 2),F - постоянная Фарадея, Rg - универсальная газовая постоянная, zk - формальный заряд k-иона.

Будем полагать, что для раствора в пористой среде, также как и для объемного раствора, справедливо соотношение Эйнштейна, связывающее коэффициенты диффузии ионов и их подвижности:

Уравнения переноса (2) в совокупности с законом сохранения массы позволяют получить уравнения для термодинамических величин p, cs и j . В дальнейшем изучаются свойства системы вблизи состояния равновесия. В этом случае k-коэффициенты (6) - (8) можно положить константами, а уравнения для величин p, cs и j ав мелкопористой среде упрощаются и представляют собой уравнения Лапласа:

(9)

Уравнение для поиска электрического потенциала во льду (однородный диэлектрик) - также уравнение Лапласа:

(10)

Граничные условия

На основаниях ячейки в общем случае заданы постоянные значения термодинамических величин (Рис. 2):

на нижней грани (z = -b/2):

T = T1, p = p1, cs = cs1, j = j1аа (11)

на верхней грани (z = b/2):

T = T2, p = p2, cs = cs2, j = j2аа (12)

В силу пространственной симметрии потоки тепла и массы через боковые грани ячейки (Sl) равны нулю:

, , , , (13)

где через обозначены производные по направлению l, перпендикулярном боковой поверхности.

На поверхности включения (на контакте льда и мелкопористой среды) граничные условия задаются из следующих физических требований - непрерывность температуры и электрического потенциала. По отношению к потокам требуется выполнимость баланса тепла и массы воды, а также полное отторжение льдом примесей, содержащихся в поровом растворе.

При записи баланса тепла должно приниматься во внимание наличие тепловыделения на границе раздела лед-пористая среда.

Условия на границе включения имеют следующий вид:

- для температуры:

а(непрерывность температуры)а (14)

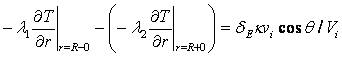а(условие Стефана)аа (15)

где k - молярная теплота плавления льда; vi - скорость движения льда; Vi - молярный объем льда; l1 и l2 - коэффициенты теплопроводности элементов ячейки E1 и E2; R - радиус включения; r, q - радиус и угол в сферической системе координат, dE - параметр конфигурации системы: dE = 1, если E1 - лед, E2 - мелкопористая среда, и dE = -1 для обратной конфигурации.

Граничные условия на поверхности включения следуют из законов переноса (1), закона сохранения массы для воды и условия отторжения примесей льдом:

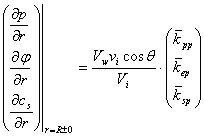, (16)

где а- элементы матрицы обратной матрице .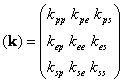

Для электрического потенциала на границе раздела лед - частица, помимо соотношения (16), задается условие непрерывности электрического потенциала:

а (17)

Скорость движения льда vi, входящая в граничные условия (15) - (16), находится из условий механического равновесия частицы и локального фазового равновесия льда и воды в растворе, которыеа в отсутствие внешних силовых полей дают следующее выражение:

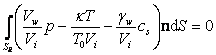,а (18)

где SR - поверхность, ограничивающая включение; n - внешняя нормаль к элементу поверхности dS; T0 = 273,15 K.

Совокупность уравнений (11) - (18) - граничные условия для задачи тепломассопереноса в ячейке, которая представляет собой систему уравнений (уравнения Лапласа): для температуры (1), электрического потенциала (9) и (10) в элементах ячейки E1 и E2, а также для давления и концентрации (10) в микропористой среде.

В пятом параграфе изложена суть метода анизотропной проводимости, при помощи которого решается задача тепломассопереноса для элементарной ячейки среды.

Изотропные элементы ячейки заменяются анизотропными. В направлении внешних градиентов величины коэффициентов переноса имеют реальные значения. В плоскости, перпендикулярной внешним градиентам, коэффициенты проводимости принимаются равными нулю или бесконечности. Таким образом, изучаются тепломассообменные свойства двух ячеек в предельными горизонтальными проводимостями. А их коэффициенты переноса дают границы интервала, в который попадают коэффициенты переноса ячейки с изотропными свойствами ее элементов.

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 | 4 | 5 | 6 |

     Авторефераты по всем темам  >>  Авторефераты по геологии-минералогии