Авторефераты по всем темам  >>  Авторефераты по техническим наукам

Разработка теоретических основ определения параметров поршневых двигателей как единой динамической системы для повышения эффективности их функционирования

Автореферат докторской диссертации по техническим наукам

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 |

 

В таблица 1-2 приведены данные, характеризующие объем вычислений, принходящихся на преобразование форматов данных при решении приведенных задач. В этих таблицах в процентах приведены результаты расчета отношения затрат машинного времени Ту-, приходящихся на преобразование форматов данных, к обнщим затратам машинного времени Т на выполнение задач с использованием 64 разрядного процессора.

Таблица 1 Результаты расчета Т//Т*100% в задаче сортировки #да-разрядных подслов данных

N	128	256	512	1024	2048	4096	8192	16384	32768	4194304
гп=4	86	76	67	61	55	50	48	42	42	29
гп=8	88	77	69	62	56	52	46	42	42	29
гп=1б	92	80	71	64	60	55	48	45	41	31

Таблица 2 Результаты расчета TflT

Виды обработки информации		7>/Г*100%
Медианная фильтрация изображений		78
Распознавание геометрических образов и символов на бинарных изображениях		50
Коррекция морфологии изображений		48
Упаковка и распаковка данных		60
LSB стеганография	Прямое преобразование	45
	Обратное преобразование	53
UUE (Uuencode)	Прямое преобразование	59
	Обратное преобразование	62
Биоинформатика (операция трансляции)		59
Формирование последовательностей перестановок в системах RPMA		91
Обработка данных в системах RPMA		90
Криптографический алгоритм DES		57
Криптографический алгоритм RC5		59
Защита файлов мультимедиа от нелицензионного копирования		91

На основе анализа алгоритмов различных задач показано, что можно выденлить два типа преобразований формата - статическое и динамическое. В первом случае задача сводится к выполнению фиксированных перестановок на уровне бит данных, во втором случае дескриптор формата данных меняется в процессе вынчислений и зависит от данных.

В главе 2 проведена формализация постановки задач и разработаны теорентико-множественные модели форматирующих преобразований. На основе требонваний к их реализации вводятся базовые форматирующие преобразования.

Структурные элементы обрабатываемых данных можно рассматривать как естественные кластеры данных в основной памяти компьютера. При представленнии данных в ячейках основной (оперативной) памяти компьютераа производится

11

их упаковка в машинные слова определенной длины, в пределах которых они раснсматриваются как бинарные векторы A = (bl,b2,...,bn). Блок ячеек памяти компьюнтера можно рассматривать как набор переменных. Отношение бинарного набора данных и набора переменных определяет формат представления данных.

В настоящем изложении принят ряд терминов, смысл которых интерпретинруется следующим образом:

под транспозицией понимается отображение элемента bj вектора А, опренделенного в /-й позиции исходной бинарной строки S, в j-ю позицию результинрующей строки D, или обратное представление;

под дескриптором формата понимается совокупное описание транспозинций всех элементов исходной бинарной строки при их представлениях в результинрующей строке, или при обратном представлении.

Будем обозначать А - представление компонент бинарного вектора А в иснходной строке и Ч их образ в результирующей строке.

Конкретный вид отображения (R :А ^>А ) определяется в декартовом произведении множеств Аа а : (As X AD).

Теоретико-множественная модель представлений структурных элементов данных, определяющая прямое преобразование исходного формата, имеет вид:

P = {AS,AD,ASXAD}.(1)

Для обратного преобразования формата

P-1 = {AD,AS,ADXAS}.(2)

При исследовании способов построения и принципов функционирования преобразователей форматов данных основное внимание уделялось следующим понложениям:

1. скорость преобразования;
2. размер дескрипторов формата;
3. число логических вентилей преобразователя.

На основе анализа практических задач, исследованных в первой главе, в канчестве базовых преобразований форматов данных в диссертации предложено иснпользовать упорядоченные и неупорядоченные разбиения входных данных. Такой выбор определялся следующими положениями:

1.а Ва общем случаеа мощность множества форматов представлений вектора

А = (Ьг,Ь2,...,Ьп)определяется числом возможных перестановок его компонент и сонставляет п\. С увеличением п быстро возрастает размер дескрипторов формата, понэтому для сокращения ресурсов, отводимых под описание операции, необходимо использовать более простые форматирующие преобразования.

1. В большинстве рассмотренных в первой главе приложений не требуется вынполнения произвольных преобразований форматов данных. Обычно используются операции выделения определенных бит данных и их группировка или обратные операции установки группы бит данных в заданные позиции.
2. Произвольная перестановка компонент вектора А является частным случанем упорядоченного разбиения, когда множество {bl,b2,...,bn}разбивается на п ненпустых подмножеств.

12

Глава 3 посвящена разработке и обоснованию теоретических положений, обеспечивающих структурный синтез устройств базовых форматирующих преобнразований. В главе исследованы способы построения ряда устройств последовантельного и параллельного преобразования формата данных, имеющих аппаратур-

9аа 9

ную сложность O(w), 0(wlog2w), 0(w(log2w) ), 0(w ). Проведена сравнительная оценнка их производительности. Точные данные, характеризующие производительность предлагаемых устройств, получены на основе анализа имитационных моделей устройств и приведены в шестой главе.

Предложена и обоснована модель ВСТА устройства последовательного формирования упорядоченных разбиений. Устройство осуществляет упорядоченнные разбиения компонент вектора данных A= (bl,b2,...,bn)а на 2а подмножеств

мощности 2й , где п=2 , и=0,1,2,...,к-1, к - положительное целое число. Аппарантурная сложность устройств последовательного действия составляет Тв Ч п/2и Ч 1. Для параллельной обработки в модели ВСТАР используется п устройств послендовательного действия. Задержка выполнения преобразования определяется чиснлом последовательно соединенных уровней дешифратора устройства и имеет знанчение 2(log2n-u)t3, где t3 - задержка на одном логическом инверторе, нагруженном на четыре входа. Аппаратурная сложность при этом составляет ТРВ Ч п(п/2и Ч 1) и быстро возрастает с увеличением п.

Для упрощения формирователя упорядоченных и неупорядоченных разбиенний в диссертации предложены и обоснованы теоретические положения, обеспенчивающие структурный синтез коммутационной матрицы, формирующей упоряндоченные и неупорядоченные разбиения компонент вектора данных А = (Ьг,Ь2,...,Ьп)

на 2к~и подмножеств мощности 2й , где п=2 , и=0,1,2,...,&-1. На базе данной матнрицы разработана имитационная модель устройства ВСТАМ.

Соединения переключателей коммутационной матрицы устройства ВСТАМ

можно представить в виде орграфа G^(S,T,V,D,A), где S = (sl,s2,...,sn) - множестнво входных вершин, Т Ч множество промежуточных вершин входной части оргранфа,а V- множество промежуточных вершин выходной части орграфа,

D = (dl,d2,...,dn)- множество выходных вершин, а А - множество дуг орграфа. Сонгласно теореме о композиции переключателей для осуществления упорядоченных и неупорядоченных разбиений данных промежуточные вершины графа можно представить в виде матрицы с п/2 иниями (строками) и 21og2W-л-l уровнями (столбцами), причем log2W-1 уровень образован вершинами множества Т, a log2W-иаа уровень образован вершинами множества V. Каждая вершина Tim е Т уровня

m = (\,к Ч 2) входной части является смежной вершинам Th>m+i, Tp>m+\ уровня m+\.

Каждая вершина Vim е Vуровня m = (\,k Ч u-Y) выходной части является смежной

вершинам Vh,m+i, Vp>m+\ уровня m+\. Причем на отношение смежности накладыванются ограничения

1 Bit Cluster Transposition Accelerator

13

i-\

i-\ ж\kЧmЧ\

+ 1

2*-",-1int

\k-m-l

J

(3)

+ \<h<2k-m-lint

\k-m-\

(1 + 2к-т-'-\)тоап

k-m-l

2^"-1int

+ \<p<2

+ 1

lllt

Г0 + 2к-т-1-\)тоапЛ

\kЧmЧ\

V k-m-1

\kЧmЧ\

где int - функция выделения целой части, (j + 2аа т Ч\)modп Ч операция вычис

i+ 2k-m-i_x

ления остатка от частного

п

Промежуточные вершины интерпретируются как переключатели коммутанционной матрицы. Каждый переключатель имеет два входа, два выхода данных и бинарный вход управляющего кода с е {0,1}. Данные на входах переставляются местами (при значении управляющего кода с=1), либо не переставляются (при с=0). Множество ребер графа описывает соединения между переключателями. Конды управления переключателями являются битовыми атрибутами промежуточных вершин орграфа. В зависимости от их значений формируются разрешенные пути прохождения вершин графа.

В диссертации развита методика управления переключателями для осущестнвления заданного разбиения.

На рис. 2 приведена диаграмма орграфа одного из вариантов коммутационнной матрицы устройства ВСТАМ для случая w=16, и=\. Вершины входной части орграфа образуют уровни Fj, F2, F3, вершины выходной части орграфа образуют уровни GhG2, G3.

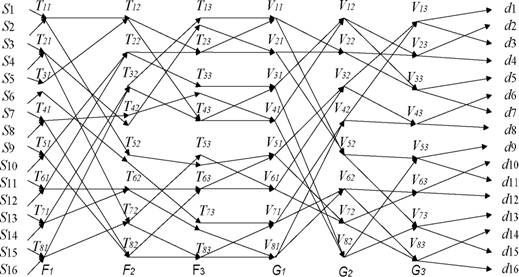
Рис. 2. Диаграмма орграфа одного из вариантов матрицы формирователя разбиений для слунчая и=16, и=\

Число переключателей коммутационной матрицы устройства ВСТАМ сонставляет п (log2 (п) Ч и/2 Ч 1) +1 и растет практически линейно с ростом п, что денлает технически возможной реализацию функционального формирователя разбиенний при больших значениях п. Быстродействие устройства определяется числом последовательно соединенных уровней коммутационной матрицы устройства и составляет не более 2(2log2n-u-l)t3, так как задержка на уровне составляет 2t3. Та-

14

ким образом, разработанные устройства ВСТАМ обладают достаточно высоким быстродействием при выполнении фиксированных преобразований. Проблемой является то, что время настройки переключателей коммутационной матрицы устнройства возрастает с ростом п как wlog2W, что приводит к существенному сниженнию производительности при решении задач с динамическим преобразованием форматов данных. Попытки организовать процесс настройки параллельно привондят к необоснованно сложным техническим решениям.

Для ускорения настройки устройства формирования упорядоченных разбиенний при смене дескрипторов формата в диссертации предложен способ структурнного синтеза формирователей перестановок и упорядоченных разбиений на оснонве топологии сортирующей сети. Если дескриптор формата задан в виде перестанновки ?(1,2,...,?),а Р - преобразование, осуществляемое сортирующей сетью, при подачеаа н ееаа входыаа перестановкиаа ?(\,2,...,?),тоаа справедливоаа выражение:

я"(1,2,...,л) = Р~ (1,2,3,...,и) , где Р~ - преобразование, обратное Р. Для выполнения

обратного преобразования у преобразователя, реализующего перестановку Р доснтаточно поменять выходы и входы. Поэтому, если на сортирующую сеть Р нало-

D-iа ~

жить сеть Раа с аналогичной топологией, у которой входы заменены на выходы,

получим устройство, реализующее заданную перестановку л"(0,1,2,...,и). Имитанционная модель разработанного устройства получила название BCTAS. В диссернтации показано, что с использованием топологии сортирующей среды нетрудно построитьаа преобразователь,аа осуществляющийаа обратноеаа преобразование

?аа (0,1,2,...,и). Аппаратурная сложность предложенного устройства составляет

0\m-\og2n) I, что хуже, чем у модели ВСТАМ. При этом скорость настройки перенключателей коммутационной матрицы значительно выше и определяется числом последовательно соединенных компараторов используемой сортирующей сети. Число двоичных разрядов чисел, сравниваемых компараторами, составляет log2W. При использовании компараторов с пирамидальной структурой оценка задержки выполнения преобразований составляет 4(log2w) t3, где t3 - задержка на одном лонгическом инверторе, нагруженном на четыре входа. Недостатком устройства BCTAS является низкая производительность осуществления фиксированных пренобразований форматов данных, время выполнения которых в устройствах ВСТАМ составляет не более (41og2w) t3.

В связи с этим на базе устройства ВСТАМ, формирующего упорядоченные разбиения входных данных на два подмножества, были разработаны принципы построения и функционирования универсального устройства, осуществляющего статические и динамические преобразования форматов данных. Разработанные принципы включают теоремы о композиции формирователей упорядоченных разнбиений, о формировании сигналов управления переключателями формирователей, о декодировании битов управления. Теоремы о композиции формирователей упонрядоченных разбиений обеспечивает ряд способов структурного синтеза матрицы

15

устройства. На основе теорем о формировании сигналов управления переключантелями матрицы и о декодировании битов управления показано, что наиболее пернспективным решением является коммутационная матрица на базе сети baseline, которая удовлетворяет уравнению (3). В результате было разработано устройство, осуществляющее две новые инструкции: bsnг\=Г2, ar.b\, ar.bi, ar.bi, и grpmг\=Г2, г-}, где Г2 Ч регистр входных данных, г\ Ч регистр выходных данных, аг.Ъ\, аг.Ъ2, аг.Ьз, г-}Ч регистры, хранящие код управления перестановкой.

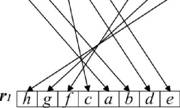
На рис. 3 приведена диаграмма, иллюстрирующая преобразования, осущестнвляемые с использованием инструкций bsn, grp, grpmдля случая w=8, где в верхнней части рисунков расположены регистр управляющих кодов гт, и регистр входнных данных 7*2, а в нижней части рисунков изображен регистр выходных данных г\. Отличие инструкции grpmот grpзаключается в том, что при использовании иннструкции grpсгруппированные данные сохраняют свой первичный порядок, а при использовании инструкции grpmпорядок данных, выбранных с использованием битов управления с низким логическим уровнем, меняется на обратный. Инструкнция bsnпредназначена для статического преобразования форматов данных, а иннструкция grpmЧ для динамического, так как настройка коммутационной матрицы при использовании этой инструкции выполняется значительно быстрее с испольнзованием разработанных средств аппаратурной поддержки. В диссертации показанно, что произвольное преобразование форматов данных формируется с использонванием последовательно log2W инструкций grpmили двух инструкций bsn, которые осуществляют преобразование входной и выходной частей коммутационной матнрицы модели ВСТАМ.

 

ar.bi	1100
ar.b2	1111
ar.bi	1001

bsn п =Г2,ar. hi,ar. bi,ar. Ьз Г2

а

п

gdbechfa

grpП=Г2,ГЗ

~й~\ гзаа о | I | оаа 1 | 1 | о | о | оаа гз 1'2

grpm п=Г2,гз

0

1

0

110 0 0

b\c\d\e\f \J\J\Г2 \q\b\c\d\e\r\s\h

п\a\c\f\g\h\b\d\e

0-7

0-7

Нумерация разрядов

регистраа "аа 'а 0-7

Рис. 3. Диаграмма преобразований, осуществляемых с использованием инструкций bsn,

grpm, grp

На рис. 4 представлена структурно-функциональная схема разработанного устройства GRPM-64, выполняющего преобразования данных длиной п=64 бит с использованием инструкций grpmи bsn. Коммутационная матрица устройства включает 6 уровней преобразования bsnj-bsng. В зависимости выполняемой инстнрукции bsnили grpmблок FPосуществляет одну из двух фиксированных перестанновок.

16

/2

Ш32

bsrh

Ш32

ar.th

Ш32

bsrn

2Ш16

Ш32

bsib

4Ш8

ar.bi

Ш32

bsn

8Ш4

Декодер ( Ш64аа /j

Ш32

bsn

16Ш2

ar.bi

Ш32

Z?s/fc

32Ш1

/=P

bsn/

Я

Рис. 4. Структурно-функциональная организация устройства формирования преобразований форматов данных, осуществляющего инструкции bsnи grpm

Декодер бит управления, помещаемых в регистр ri, процессора, включает сумматоры, осуществляющие вычисление порядковых номеров следования бит с высоким и низким логическим уровнем, и формирующие биты управления перенключателями коммутационной матрицы устройства.

Предложены и обоснованы способы синтеза сумматоров декодера. Согласно одному способу сумматоры образуют пирамидальную структуру. Число сумматонров в декодере определяется выражением Ъ12п. Задержка преобразования составнляет 2?slog2W, где ts- задержка, создаваемая сумматором. Исследована возможнность использования в декодере структур параллельных префиксных сумматоров Ладнера-Фишера (Ladner-Fischer), Кога-Стоуна (Kogge-Stone), Брента-Кунга (Brent-Kung), Хана-Карлсона (Han-Carlson). С их использованием удалось сокрантить общую задержку выполнения инструкции grpmдо 28 задержек на инверторе, нагруженном на четыре входа.

Устройство GRPM-64 позволило объединить преимущества быстрого вынполнения статических преобразований форматов данных с использованием моденли ВСТАМ и обеспечения динамического преобразования форматов данных в мондели BCTAS. При этом аппаратурная сложность устройства составляет 0(wlog2w).

17

Доказаны следующие утверждения:

1. юбые параллельные инструкции рех выделения и группировки с сохраненнием начального порядка бит данных могут быть осуществлены с использованием наложения битовой маски на входные данные и однократного преобразования упорядоченного разбиения входных данных на два подмножества с использованинем устройства ВСТАМ;
2. юбые параллельные инструкции depositразмещения бит данных в заданнных позициях машинного слова могут быть осуществлены с использованием одннократного преобразования, обратного упорядоченному разбиению входных даннных, на два подмножества с использованием устройства ВСТАМ и наложения бинтовой маски на выходные данные;

Ч инструкции grpмогут быть осуществлены путем однократного параллельн

ного использования двух устройств ВСТАМ, обеспечивающих упорядоченные разн

биения входных данных на два подмножества;

Чаа инструкции логического сдвига могут быть осуществлены путем однократн

ного преобразования упорядоченного разбиения входных данных на два подмнон

жества с использованием устройства ВСТАМ.

На основании проведенных исследований разработаны варианты структурнно-функциональной организации и модели устройств, осуществляющих инструкнции bsn, grpm, grp, pex.v, pdep.v, рех, pdep, rotate, shift. Показано, что для реализанции перечисленных инструкций устройство ВСТАМ следует выполнять на базе многоуровневой коммутационной сети baseline. Возможно также использование любых коммутационных сетей, изоморфных baseline.

В главе 4 описаны принципы построения и модели устройств, формируюнщих перестановки с заданной структурой циклов и устройств для перечисления упорядоченных разбиений входных данных.

В основу работы устройств, формирующих перестановки и упорядоченные разбиения с заданной структурой циклов, положен метод формирования сопрянженных перестановок. Перестановки А, В, являются сопряженными, если сущенствует перестановка ? такая, что ?~??? Ч В, где ?-1 - перестановка, обратная ?. Из теории групп известно, что перестановки являются сопряженными в том и только том случае, если их цикловые структуры одинаковы. Таким образом, если А Ч фиксированная перестановка с заданной цикловой структурой, то для любой перестановки В с аналогичной цикловой структурой существует перестановка ?, такая что ?~??? Ч В. Используя различные перестановки ?, можно перечислить

весь класс сопряженных элементов с заданной цикловой структурой. Цикловая

/аа к-,аа к2а ks\ структура записывается в виде \С1 с2аа ...cs), где s- количество различных длин

циклов в циклической записи перестановки, с,- длина у'-го цикла, а к,Ч количество циклов длины Cj, входящих в перестановку. В диссертации показано, что для форнмирования перестановки с заданной цикловой структуройаа перестановки ?, ?_1

-1

можно представить в виде произведения двух перестановок ? = пгпс, ? Ч Пг1Пс1,а где 7ГГ, щх - прямая и обратная перестановки, формирующие неупоря-

18

доченные разбиения входных данных на подмножества c\,..,cs, пс,пс - перестанновки с фиксированной неподвижной точкой, которые осуществляют полноциклонвые преобразования подмножеств с1 , с2 ,..., cs .

На основе проведенных исследований в данной главе представлены резульнтаты разработки аппаратурных формирователей перестановок с заданной циклонвой структурой. Синтез матриц формирователей перестановок 7ГГ, ?^1,?(:,?^1 осуществлен с использованием переключателей, осуществляющих прямое и обнратное преобразования одновременно. Показано, что аппаратурная сложность разнработанных устройств составляет 0(wlog2w), а задержка формирования перестанновки с заданной цикловой структурой не превосходит (81og2w)?3, что вдвое больнше, чем в моделях ВСТАМ, так как в данных устройствах последовательно выполнняются прямая и обратная перестановки. Для увеличения производительности формирования перестановок с заданной цикловой структурой предложено ис-пользовать устройства ВСТАР, имеющие аппаратурную сложность 0(w ). Разрабонтаны и обоснованы модели устройств, осуществляющих прямые и обратные перенстановки под управлением одинаковых кодов. Показано, что в этом случае время формирования перестановки составляет не более (21og2w)?3, так как задержка опренделяется временем работы дешифраторов, одновременно используемых для форнмирования прямой и обратной перестановок.

Комбинаторные процедуры перебора перестановок, сочетаний и разбиений различных элементов представляют собой трудоемкие процессы, значительно снижающие производительность вычислительной техники. Предложен метод понстроения комбинаторных формирователей упорядоченных разбиений чисел (0,l,2,...,w) с использованием преобразований, обратных упорядоченным разбиенниям входных данных на два подмножества и формирующих сочетания бинарных наборов. Формирование упорядоченных разбиений осуществляется поразрядно, с использованием формирователей сочетаний бинарных наборов.

Различные устройства для перечисления перестановок и сочетаний предлангались в работах Курейчика, Щербакова и др., однако предложенное в диссертанции решение позволило упростить конструкцию формирователя,а аппаратурная

сложность которого составляет О ( [nlog2 п)а ), в отличие от 0(п2).

Глава 5 посвящена исследованию принципов построения и разработке унинверсальных вероятностных формирователей упорядоченных разбиений и перестанновок с произвольной и заданной структурой циклов, увеличивающих производинтельность вычислительной техники при решении задач, связанных с обработкой данных в системах RPMA, тестированием, защитой данных от нелицензионного копирования, обеспечением защиты информации. Проведены исследования научнно-технических принципов построения цифровых генераторов случайных сигнанлов (ГСС) на базе систем с хаотической динамикой.

Разработке алгоритмов формирования случайных перестановок с произнвольной и заданной структурой циклов посвящено большое количество работ разнных авторов. В диссертации были разработаны модель и устройство синхронного формирователя перестановок последовательного действия, работа которого оснонвана на аппаратурной реализации модифицированного алгоритма Фишера-Йетса. Исследования данного устройства показали, что аппаратурная поддержка после-

19

довательных алгоритмов не приводит к существенному увеличению производинтельности системы.

На основе разработанных формирователей базовых преобразований формантов данных в диссертации были разработаны принципы построения и функционинрования высокопроизводительных вероятностных устройств параллельного дейстнвия для формирования упорядоченных разбиений и перестановок с произвольной и заданной структурой циклов.

На рис. 5 приведена структурная схема вероятностного формирователя

упорядоченных разбиений, для случая w=16, и=0. Устройство состоит из блока рен

гистров данных и многоуровневой коммутационной сети baseline. Где D\ - DnЧ

параллельные qразрядные входы блока регистра данных и выходы коммутационн

ной матрицы; Q\-Qn Ч параллельные qразрядные выходы блока регистров данных

и выходы формирователя; S\ - SД Ч qразрядные входы коммутационной матрин

цы; С\ - Ст Ч бинарные входы формирователя для подачи управляющих сигнан

лов от внешних источников случайных сигналов; А\ - Ап Ч начальная строка qразн

рядных данных, загружаемая в блок регистров данных;аа Vi. - переключатели

коммутационной матрицы; РЕ Ч бинарный вход управления последовательной и

параллельной записью данных; SЧ последовательный qразрядный вход блока

регистров данных для записи элементов начальной строки данных А\ - Ап; elkЧ вход тактовых импульсов.

Преимуществом данного формирователя является быстрый рост энтропии Нт распределения вероятностей генерируемых последовательностей, где т Ч чиснло импульсов на входе elk. В диссертации показано, что для рассматриваемых устнройств энтропия Нт достигает значения более 50% от максимальной величины за один тактовый импульс.

Приведенный пример иллюстрирует метод построения высокопроизводинтельных вероятностных формирователей упорядоченных разбиений и перестанонвок с произвольной и заданной структурой циклов, и равномерным распределенинем вероятностей. Согласно разработанной методике вероятностные формироватенли строятся на основе описанных в третьей главе диссертации преобразователей форматов данных, выходы которых соединены с входами через буферный регистр. В диссертации показано, что процессы, протекающие в разрабатываемых устройнствах, описываются однородными цепями Маркова с конечным числом состояний. Поэтому последовательность вероятностных распределений {??,?2...,??)? форминруемых разбиений определяется выражениемаа (??,?2...,??)?+? = (??,?2...,??)\???, где

матрица \\р1 оказывается дважды стохастической с отсутствием нулевых элеменнтов, что приводит к быстрой экспоненциальной сходимости последовательности {??,?2...,??)?к равновероятному распределению ??=?2=... = ??.

20

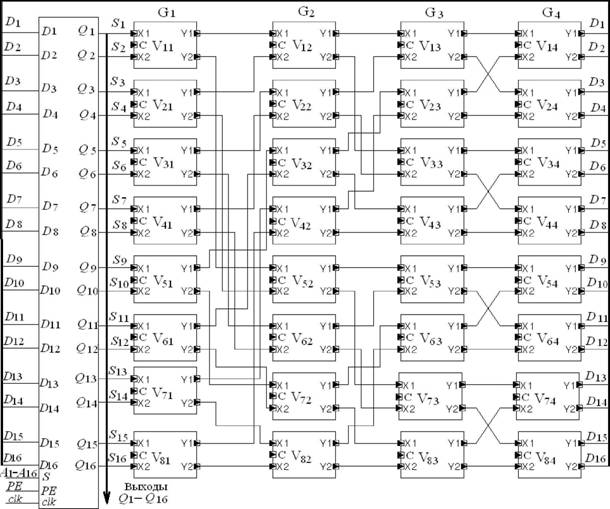
Рис. 5. Структурная схема стохастического формирователя дескрипторов формата упорядонченных разбиений для случая и=16, и=0

Основными компонентами разработанных вероятностных устройств являнются физические генераторы случайных сигналов (ГСС). В качестве источников случайных сигналов предложено использовать генераторы динамического хаоса. В диссертации сформулированы и обоснованы условия непредсказуемости испольнзуемых генераторов. Предложена модель хаотического формирователя случайных чисел и временных интервалов, удовлетворяющего сформулированным условиям. Предложенный в диссертации метод построения ГСС обеспечивает построение формирователей импульсов случайной длительности и случайных бинарных кодов с равномерной функцией распределения вероятностей, устойчивых к внешним воздействиям. Возможность исполнения разработанных ГСС в виде интегральной микросхемы с использованием только стандартных цифровых элементов позволянет без дополнительных исследований использовать при их производстве различнные технологические процессы, а также реализовать ГСС на ПЛИС. Перечисленнные свойства являются очень важными для практических применений.

21

Согласно модели функционирования ГСС по запросу системы в некоторые моменты времени Tf на основе внутреннего состояния Х(Т{) генератора формирунется цифровой сигнал {DS}T . Система определяет состояние ?(?]) с погрешнонстью ? , таким образом, {DS}T генерируется на основе любого значения Xиз ? -окрестности ?(?]) в фазовом пространстве системы {X}ST = {X: \/Х, X-XЗTJ <?}. Цифровой сигнал {DS}T генерируется системой по известному наблюдателю алгонритму S для \/Х(1]) g {Х}т S(X(TJ) ^> {DS}T . ГСС будет непредсказуемым, если нанблюдатель не сможет определить его состояние с погрешностью, не превышаюнщей ? в требуемые моменты времени Tf даже в том случае, если некоторые значенния из последовательности Х(Т{) ему известны.

Утверждение. Генератор динамического хаоса вычислительно непредсказунем, если погрешность ?? определения его состояния Хп экспоненциально возраснтает при моделировании в прямом и обратном времени.

В диссертации рассмотрены два типа систем с дискретным и непрерывным временем, для которых доказываются следующие утверждения.

Генератор динамического хаоса на базе отображения Xn+l = F(Xn) вычиснлительноаа непредсказуем, еслиаа в спектре собственныхаа значенийаа матрицы [А (Xп) J х [А (Xп)] присутствуют два собственных значения %Xs, %ls, одно из конторых хи > 1, а другое x2s < 1, где |/?(?Д)] - матрица Якоби для F(XД).

dXа -а -Генератор динамического хаоса на базе потоковой системы Ч = F(X) вы-

dt

числительно непредсказуем, если в каждой точке фазовой траектории ГСС в спекнтре собственных значений ?5 матрицы [yj=|/4j \А\ присутствуют положительнные и отрицательные значения, где [А\Ч матрица Якоби F(X) .

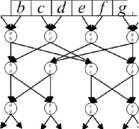
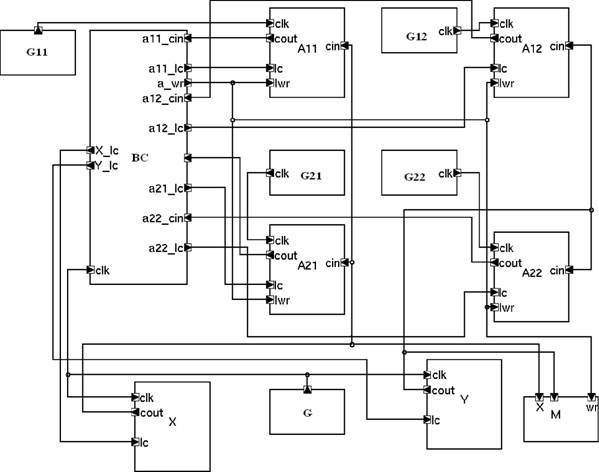
Приведенным условиям вычислительной непредсказуемости удовлетворяет предложенный и исследованный в диссертации формирователь случайных бинарнных последовательностей, моделируемый системой с хаотической динамикой. Структурно-функциональная схема разработанного формирователя представлена на рис. 6. Его работа описывается двухмерным отображением

J яа J я

к Л

Кmod^),аа (4)

/ll JY1

\mn+lJ

\mnj

J я . J я

ч У 21 У 22 J

где fg,fij- частоты задающих генераторов G, Gil, G12, G21, G22. Таким образом, частоты задающих генераторов являются параметрами управления в модели преднложенного формирователя.

22

Выход

Рис. 6. Структурно-функциональная схема генератора случайных временных интервалов

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 |

     Авторефераты по всем темам  >>  Авторефераты по техническим наукам