Авторефераты по всем темам  >>  Авторефераты по математике

Адгезионное взаимодействие между застеклованными аморфными полимерами

Автореферат докторской диссертации по физико-математическим наукам

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 |

 

Таблица 1

Исследованные полимеры и их некоторые характеристики

Полимер	Обозначение полимера	w а(h), г/моль	n, г/моль	Тс об, оС
ПС ПС ПС ПС ПС ПС ПС ПФО ПММА ПММА ПЭТФ ПЭТФ* ПЭТФ ПЭТФ* ПС+ПФО ПС+ПФО	ПС-230 ПС-225 ПС-103 ПС-450 ПС-1111 ПС-210 ПС-200 ПФО ПММА-55 ПММА-87 амПЭТФ-15 амПЭТФ-76 крПЭТФ-15 крПЭТФ-300 смесь1:1 смесь3:1	аа 230 000 225 000 102 500 450 000 1 110 500 210 000 200 000 44 000 55 100 87 000 (15 000) (76 000) (15 000) (300 000) 230 000/44 000 230 000/44 000	а 81 000 75 000 97 000 402 000 965 600 200 000 192 000 23 000 51 900 43 500 - - - - 81 000/23 000 81 000/23 000	103 97 105 105 106 105 105 216 109 109 81 82 - - 149 121

*Синтезированы в лаборатории физики прочности ФТИ им. А.Ф. Иоффе РАН методом твёрдофазной дополиконденсации в высоком вакууме.

Значения Тсоб, определённые с помощью метода ДМТА [температура a-пика модуля потерь (Тaоб) при скорости нагревания 2оС/мин и частоте 3.5 Гц] для амПЭТФ-76, крПЭТФ-15 и крПЭТФ-300 составили 90, 100 и 105оС, соответственно. Из вышеуказанных полимеров при использовании методов прессования расплава, экструзии расплава и полива были получены образцы с гладкой поверхностью. Для формирования АС полученные образцы попарно выдерживались в контакте в прессе или термокамере при рк ? 0.8 МПа. Выбор величины рк аргументируется отсутствием вязкого течения в зоне контакта. Температуры и времена контактирования выбирались таким образом, чтобы соблюдалось условие Тк < Тсоб и tк < taоб (taоб - время a-релаксации в объёме), т.е. чтобы Тк была ниже фактической Тсоб в используемом интервале tк. Механические испытания АС проводили при комнатной температуре и скорости перемещения подвижного захвата 5 мм/мин. Значение прочности при сдвиге (s)для АС внахлёстку (см. рис. 1-а) рассчитывали общепринятым способом - делением разрушающей нагрузки (Fразр) на площадь контакта, допуская равномерность распределения напряжения вдоль зоны контакта (см., например, ГОСТ 14759-69 или ASTM D3163).

а)а б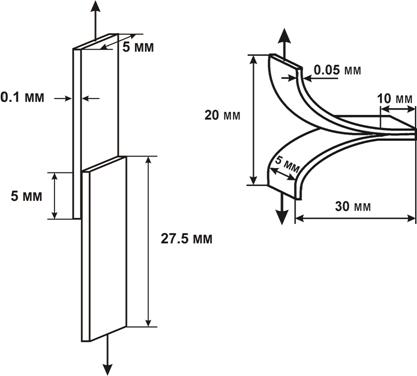)а

а

Рис. 1. Геометрия адгезионных соединений при деформировании в модах сдвига (а) и расслаивания (б) в момент приложения нагрузки.

Значение работы разрушения (G) при расслаивании (см. рис. 1-б) определяли какG = 2Fмакс/b, где Fмакс - максимальное усилие расслаивания, b - ширина образца. Каждое значение sи G получено усреднением 10-20 измерений. Рассматривается предложенная автором аддитивная модель деформирования, позволяющая определять не только прочностные, но и вязкоупругие свойства (модуль упругости) на границе раздела. Топография свободных поверхностей и поверхностей разрушенных АС исследовалась методами СЭМ и АСМ. Выбор вышеперечисленных объектов исследования позволил охватить широкий круг возможных зон контакта двух полимерных образцов (см. рис. 2) с точки зрения (а) нахождения в контакте одного и того же [симметричные границы раздела ПС-ПС, ПФО-ПФО, ПММА-ПММА, ПЭТФ-ПЭТФ и смесь(ПС+ПФО)-смесь(ПС+ПФО)] или различных полимерных материалов [асимметричные границы раздела ПС-ПФО, ПС-ПММА, ПС-ПЭТФ, амПЭТФ-крПЭТФ, ПС-смесь(ПС+ПФО)], (б) термодинамической совместимости полимеров (совместимые границы раздела ПС-ПФО и амПЭТФ-крПЭТФ, и несовместимые границы раздела ПС-ПММА и ПС-ПЭТФ), (в) фазового состояния {границы раздела аморфный полимер - аморфный полимер [ПС-ПС, ПФО-ПФО, ПММА-ПММА, ПЭТФ-ПЭТФ, ПС-ПФО, ПС-ПММА, ПС-ПЭТФ и ПС-смесь(ПС+ПФО)], аморфный полимер - частично-кристаллический полимер (амПЭТФ-крПЭТФ) и частично-кристаллический полимер - частично-кристаллический полимер (крПЭТФ-крПЭТФ)} и (г) композиционного состава (границы раздела гомополимер-гомополимер, гомополимер-смесь и смесь-смесь).

В третьей главе представлены результаты исследования механических свойств адгезионных соединений в условиях сдвигового деформирования.

В разделе 3.1 рассматриваются кривые деформирования для ряда АС, сформированных при Тк < Тсоб. Показано, что все они имеют линейный характер. Регистрация значений Fразр = 1-20 Н связывается с диффузионной природой эволюции механических свойств в зоне контакта и её расстеклованным состоянием. Отмечается нелинейный характер зависимости s как от tк (см. рис. 3-а), так и от Тка (см. рис. 3-б).

В разделе 3.2 экспериментальные зависимости sот tк для ряда аморфных симметричных границ раздела ПСЦПС и ПФОЦПФО в диапазонах температур контактирования (Тсоб - 48)оС ? Тк ?(Тсоб - 13)оС и (Тсоб - 126)оС ? Тк ?(Тсоб - 60)оС, соответственно, исследуются на соответствие теоретическим кинетическим законам различных диффузионных механизмов.

част.-кристаллическая

а

ПС-ПС, ПФО-ПФО, ПММА-ПММА, ПЭТФ-ПЭТФ

а

ПЭТФ-ПЭТФ

а

симметричная граница раздела

(гомо-адгезионное соединение)

а

асимметричная граница раздела

(гетеро-адгезионное соединение)

а

аморфная

а

аморфно Ц част.-кристаллическая

а

аморфная

а

смесь-смесь (ПС+ПФО)

а

совместимая

а

несовместимая

а

совместимая

а

ПС-смесь (ПС+ПФО)

а

ПС-ПФО

а

аморфная

а

ПЭТФ-ПЭТФ

а

ПС-ПММА,

ПС-ПЭТФ

а

Рис. 2. Исследованные в работе границы раздела линейных аморфных и частично-кристаллических гомополимеров и их смесей.

Рис. 3. Зависимости прочности при сдвиге длягомо-адгезионного соединения ПС-225-ПС-225 от tк при Тк = 64оС =(Тсоб - 33)оС (а) и от Тк при tк = 1 час (б). Вертикальными линиями на экспериментальных точках (как и во всех случаях, рассмотренных ниже) показано стандартное отклонение.

Установлено, что наиболее корректным значением показателя степени х, при котором линейная зависимость s(tкх) имеет максимальное значение коэффициента корреляции в рамках метода наименьших квадратов, является значение х = 1/4 (см. рис. 4-а и 4-в), которое является характерным для симметричных границ раздела полимерЦполимер и в области Тк > Тсоб [2]. Делается вывод, что эволюция адгезионной прочности на симметричных границах раздела аморфных полимеров при Тк < Тсоб контролируется механизмом сегментальной диффузии рептирующей цепи [2, 6, 7]. Проводится эмпирический анализ кинетики эволюции адгезионной прочности для широкого круга симметричных и асимметричных границ раздела полимерЦполимер путём определения показателя степени х для абсциссыtкх по углу наклона кривых s(tк), рассмотренных в двойных логарифмических координатах. Отмечается удовлетворительное соответствие экспериментальных кривых кинетическому закону s~tк1/4 на границах раздела ПСЦПС и ПС-ПММА.

а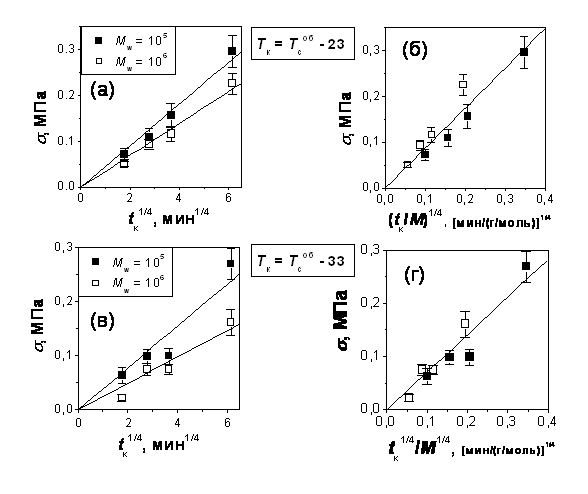а а

Рис. 4. Зависимости прочности при сдвиге длягомо-адгезионных соединений ПС-103-ПС-103 и ПС-1111-ПС-1111 (монодисперсные полимеры) от tк1/4 (а, в) и (tк /Mn)1/4 (б, г) при Тк = (Тсоб - 23)оС (а, б) и (Тсоб - 33)оС (в, г).

В разделе 3.3 исследуется влияние молекулярной массы (М) на прочность при сдвиге s на симметричных границах раздела ПСЦПС (M = 105-106) и амПЭТФ-амПЭТФ [М = (15-76) ? 103] в диапазонах Тк от (Тсоб - 67)оС до(Тсоб - 13)оС и от (Тсоб - 7)оС до (Тсоб + 13)оС, соответственно. Установлено, что величина s гомо-адгезионных соединений ПС-ПС и амПЭТФ-амПЭТФ уменьшается несущественно, в 1.1-3.3 раза и 1.2-1.7 раза, соответственно, при существенном увеличении М, в 10 раз (ПС) и 5 раз (амПЭТФ). Показано, что зависимости sот М имеют вид s~ 1/М0.02-0.55 (ПСЦПС) и s~ 1/М0.12-0.35 (амПЭТФ-амПЭТФ). Отмечается, что такое поведение находится в удовлетворительном согласии с моделью глубины диффузии (s~ 1/M1/4) и в противоречии с моделью числа цепей (s~ 1/M5/4) рептационой теории Вула [2]. Констатируется, что полученные экспериментальные зависимости sот tк и M при Тк < Тсоб наиболее адекватно описываются соотношением s~tк1/4/M1/4 (см. рис. 4-б и 4-г). Делается вывод, что в условиях стеклообразного состояния образца линейного аморфного полимера в объёме процесс изменения адгезионной прочности контролируется глубиной взаимной диффузии сегментов цепей, совершающих рептационное перемещение через зону контакта.

В разделе 3.4 исследуется зависимость кинетики процесса изменения адгезионной прочностиот температуры контактирования и выясняется её соответствие термоактивационному процессу аррениусовского типа при помощи уравнения (3.1):

D = D0exp[-Еа/(RТк)] (3.1),

где D - коэффициент диффузии рептирующей цепи, D0 - предэкспоненциальный множитель, R- универсальная газовая постоянная и Еа - энергия активации. Проводится анализ кинетики sпутём выражения sчерез D [2]:

D1/4 = с(ds/dtк1/4)а (3.2),

где с - постоянная. Возведение левой и правой частей уравнения (3.1) в степень 1/4 и подстановка {D0exp[-Еа/(RТк)]}1/4 вместо D1/4 в уравнение (3.2) даёт уравнение (3.3):

ds/dtк1/4 = с-1{D0exp[-Еа/(RТк)]}1/4а (3.3).

После логарифмирования левой и правой частей уравнения (3.3) и несложных преобразований получено уравнение (3.4), которое и использовалось для расчёта значений Еа процесса сегментальной диффузии [Еа(D)]:

Еа(D) = 4R? [Dln(ds/dtк1/4) / D(1/Тк)]аа (3.4).

Для определения значений Еа(D) при Тк < Тсоб с помощью уравнения (3.4), зависимости s(tк) для 9-ти границ раздела полимер-полимер были сначала рассмотрены в координатах s- tк1/4 в широких диапазонах Тк < Тсоб, и на основании удовлетворительной линейности экспериментальных данных в этих координатах не только на симметричных (совместимых) (см. рис. 5-а), но и на асимметричных (несовместимых) границах раздела (см. рис. 6-а), наклон зависимостей s- tк1/4 был использован для построения аррениусовских графиков логарифм ds/dtк1/4 - 1/Тк (см. рис. 5-б и 6-б). В свою очередь, полученные аррениусовские графики также представляют собой зависимости линейного типа, что позволяет использовать их для расчёта значений Еа(D) с помощью уравнения (3.4). Определённые таким образом значения Еа(D) анализируются ниже в данной главе, а также в Главе 6. Показано, что величина Еа(D) практически не зависитот молекулярной массы ПС. Такое поведение интерпретируется активированием в элементарном акте процесса диффузии субцепной кинетической единицы движения (участка цепи коррелированного движения - сегмента Куна).

В разделе 3.5 исследуются зависимости кажущегося модуля упругости при сдвиге Ес* от tк и Тк при Тк < Тcоб. Значения Ес* на симметричных и асимметричных границах раздела полимерЦполимер рассчитывались по предложенной автором методике, основаннойа на аддитивной модели деформирования, при использовании уравнений (3.5) и (3.6), соответственно:

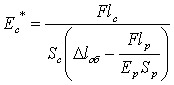аа аа(3.5),

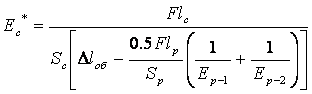а (3.6),

где F - усилие,lс - длина перекрытия двух образцов, Sс - площадь контакта, Dlоб -общее удлинение АС, lр- исходная длина двух образцов АС, деформируемых только в моде растяжения, Ер - модуль упругости при растяжении образца, Sр - площадь поперечного сечения образца. В уравнении (3.6) индексы Ур-1Ф и Ур-2Ф относятся к деформированию в моде растяжения соответственно первого и второго образцов при соблюдении условий lр-1 = lр-2 = 0.5lр и Sр-1 = Sр-2 =Sр. Процесс залечиванияа границ раздела впервые проанализирован при использовании предложенной автором нормированной характеристики адгезионного соединения Ес*/s.

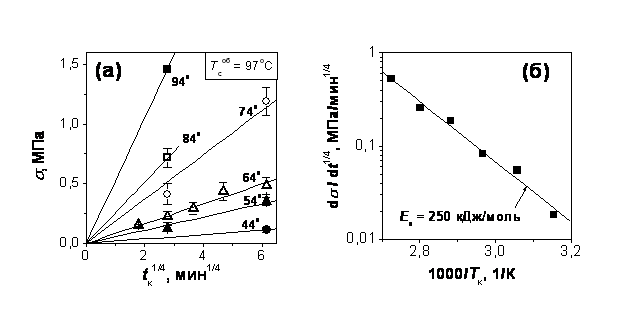
Рис. 5. Зависимость прочности при сдвиге от tк1/4 при нескольких Тк < Тсоб (указаны у кривых) (а) и аррениусовский график наклона этих кривых (б) для симметричной (совместимой) границы раздела ПС-225-ПС-225; Тсоб = 97оС.

Рис. 6. Зависимость прочности при сдвиге от tк1/4 при нескольких Тк < Тсоб (указаны у кривых) (а) и аррениусовский график наклона этих кривых (б) для асимметричной несовместимой границы раздела ПС-225-ПММА; Тсоб = 97оС (ПС) и 109оС (ПММА).

В разделе 3.6 исследуется возможность обобщённого описания процесса изменения адгезионных механических свойств в зоне контакта аморфных полимеров с застеклованным объёмом в зависимости от Утехнологических параметровФ, Тк и tк. Для серии границ раздела полимерЦполимер построены обобщённые кривые s - lg(tк?аТ) и Ес* - lg(tк?аТ), где аТ - фактор сдвига, позволяющие прогнозировать значения sи Ес* в широких интервалах tк (от 2 до 1016 минут) и Тк, а также определить значения энергии активации Еа(аТ) по наклону аррениусовских графиков lnаТа - 1/Тк. Констатируется полезность привлечения классического принципа температурно-временной суперпозиции, традиционно используемого для прогнозирования величины механической характеристики полимера в зависимости от температуры или времени испытаний, применительно к прогнозированию эволюции адгезионных механических свойств при использовании в качестве приведённых переменных Тк и tк при проведении механических измерений при одних и тех же температурно-временных условиях.

В разделе 3.7 исследуются зависимости прочности при сдвиге от температуры контактирования для серии границ раздела при нескольких постоянных значениях tк в интервале от 2 мин до 24 час. Выявлено соответствие эволюции s от Тк при Тк < Тсоб термоактивационному механизму для всех исследованных значений tк. При использовании уравнения аррениусовского типа (3.7):

lns = lns0 - Еа(s)/(RTк )аа (3.7),

где s0а - константа, определены значения энергии активации процессов аутогезии и адгезии [Еа(s)] на симметричных и асимметричных границах раздела полимер-полимер, соответственно. Отмечается хорошее соответствие между значениями Еа(D) и 4Еа(s), которое ожидается при определении значений Еа с помощью уравнений (3.4) и (3.7) при использовании экспериментальных значений s.

В разделе 3.8 исследуется влияние донорно-акцепторного межмолекулярного взаимодействия на адгезию застеклованных аморфных полимеров. Для этих целей сопоставляется эволюция адгезионной прочности на симметричных границах раздела ПСЦПС, ПФОЦПФО и смесь(ПС+ПФО)Цсмесь(ПС+ПФО) при Тк, равно удалённых от Тсоб каждой из контактных систем, а также на границах раздела ПСЦПС, ПФОЦПФО и ПСЦсмесь(ПС+ПФО) при одной и той же Тк = 90оС. Показано, что присутствие в зоне контакта молекул ПС и ПФО по сравнению с присутствием в зоне контакта только молекул ПС является благоприятным фактором, приводящим к достижению более высоких значений s.

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 |

     Авторефераты по всем темам  >>  Авторефераты по математике