 Авторефераты по всем темам >>
Авторефераты по математике
Авторефераты по всем темам >>
Авторефераты по математике
Математическое моделирование процессов мезосферы, термосферы и ионосферы
Автореферат докторской диссертации по физико-математическим наукам
|
Страницы: | 1 | 2 | 3 | |
В главе 2 приведена математическая постановка задачи моделирования среднеширотной верхней атмосферы и ионосферы (в системе координат, связанной с местной вертикалью), которая основывается на решении двух групп взаимосвязных уравнений движения, непрерывности и теплового баланса для нейтрального и электронно-ионного газа в интервале высот 50-500 км. Такая постановка задачи позволяет исследовать взаимное влияние нетрально-ионно-электронного газа, а также мезосферно-термосферные связи и связи между D-E-F областями ионосферы и особенно межслоевые области. Основной интерес вызывает область перехода от мезосферы к термосфере (область турбопаузы), которая характеризуется переходом от турбулентности к молекулярной диффузии. В этой области существенную роль играет конвективный перенос. В связи с этим и возникает задача с малым параметром при старшей производной.
Система гидродинамических уравнений была разработана автором на основании ранее полученных моделей. Она состоит из восьми нелинейных связных дифференциальных уравнений, описывающих высотно-временное поведение параметров нейтрального, ион-электронного газа, которые могут быть решены лишь численными методами.
Высотно-временное распределение нейтрального и ионного состава описывается системой уравнений непрерывности вида:
![]()
![]() .
.
Для короткоживущих компонент и ионов расчет проводится без учета члена переноса:
![]() .
.
Уравнение теплопроводности для электронного и нейтрального газа рассчитывается по уравнению:
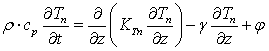 .
.
В уравнении учитываются следующие физические процессы:
- нагревание за счет фотоионизации нейтральных компонент Qi;
- нагревание за счет фотодиссоциации O3 и O2 в континууме и полосах Шумана-Рунге QSR;
- нагревание за счет фотоэлектронов Qf;
- нагрев за счет рекомбинации кислородных составляющих QH;
- нагревание за счет диссоциативной рекомбинации (химическая энергия) Qr;
- нагревание за счет диссипации турбулентной энергии;
- охлаждение за счет инфракрасного излучения молекул СО2 на длине волны 15 мкм LCO2;
- охлаждение за счет излучения О на длине волны 63 мкм L0;
- охлаждение за счет излучения NО на длине волны 5.3 мкм LNO;
Уравнение теплопроводности для электронного и ионного (H+, O+) газа:
![]() ,
,
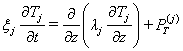 ,
,
где PG - прибыль тепла за счёт энергии фотонов и фотоэлектронов, РT - член теплообмена с газом, находящимся при другой температуре, ![]() .
.
Составляющие макроскопические скорости нейтрального ветра рассчитывались по уравнению:
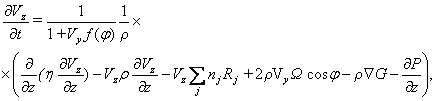

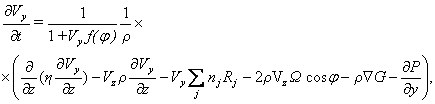
Граничные и начальные условия:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
Выше отмеченные уравнения представляет собой нелинейную связную систему дифференциальных уравнений, которая может быть решена только численными методами.
В главе 3 рассматриваются различные варианты разностных схем, аппроксимирующих уравнение модели. Построен контрольный пример. Приведены результаты тестирования, разработанных разностных схем на этом примере. Построен алгоритм модели.
Как показал вычислительный эксперимент для построения абсолютно устойчивой консервативной разностной схемы необходимо преобразовать уравнение с конвективным членом, записанным в дивергентной форме, к виду:
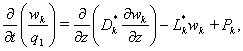
где  ,
, ![]() ,
, ![]() ,
, ![]() .
.
Уравнение непрерывности для ионного состава записывается аналогичным образом:
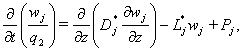 а
а
где  ,
, ![]() ,
, ![]() ,
, ![]() .
.
Аналогичным образом преобразуется уравнение с конвективным членом, записанным в недивергетной форме, к виду:
 ,
,
где 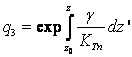 ,
, ![]() ,
, ![]() ,
, ![]() .
.
Уравнение теплопроводности для ионного и электронного газа оставляем без изменений. Система уравнений макроскопического движения скорости нейтрального газа преобразуется по выше отмеченной схеме к виду:
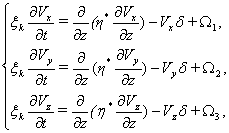
где 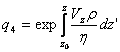 ,
, ![]() ,
, ![]() ,
, ![]() , аа
, аа ![]() ,
,
![]() ,
,![]() .
.
Тогда система уравнений, описывающая высотно-временное распределение нейтрального, ионного и электронного состава имеет вид:
|
Граничные и начальные условия:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
В разностном виде уравнения данной системы можно представить по единой схеме. Неизвестные функции обозначаем за y.
![]() ,
,
где ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Линеаризация разностных уравнений проводилась путем расчета коэффициентов и правых частей по значениям неизвестных функций с предыдущего временного слоя или предыдущей итерации. Линеаризованные итерационные разностные уравнения записывались в виде:
![]() ,
,
где S - номер итерации. За нулевое приближение ![]() абрались значения
абрались значения ![]() ас предыдущего временного слоя. Линейная относительно
ас предыдущего временного слоя. Линейная относительно ![]() асистема разностных уравнений, дополненная при
асистема разностных уравнений, дополненная при ![]() акраевыми условиями, решалась методом прогонки
акраевыми условиями, решалась методом прогонки
![]() ,
, ![]() ,
, ![]() ,
,
или различными его модификациями, рассмотренными в работе. При решении уравнений методом итераций задается число итераций или точность их сходимости ?, когда требуют выполнение неравенства
![]() .
.
В главе 4приводятся результаты вычислительного эксперимента на основе построенной модели.
В модели рассчитывается фотодиссоциация следующих компонент N2, O2, О3, Н2О, Н2О2, NO, NO2, N2O, СО2 и ионизация О, О2, NO, N2, O2(1Dg).
Основными источниками ионизации в дневное время являются: La-излучение с длиной волны 121,5 нм; солнечные Х-лучи (0,1-0,8 нм); фотоионизация O2(1Dg) в интервале длин волн 102,7 < l < 111,8 нм; солнечное излучение в диапазоне (3-102,7 нм); галактические космические лучи. В ночное время: HLa, HLp, Hel(50,4 нм), Hell (30,4 нм).
Алгоритм модели строился с учётом фотохимических и диффузионных-времён жизни компонент и их связанности в фотохимических процессах. Шаги интегрирования по высоте и времени выбирались в зависимости от характеристик этих процессов: шкалы высот и времён жизни компонент.
На основании результатов проведённого на данной модели вычислительного эксперимента установлено существование фотохимического равно версия N иNO в области высот 70-95 км и объяснено стационарное распределение окиси азота.
Получены новые аналитические выражения высотного поведения [NO] и Neза висящее от высотного распределения основных компонент N2, O2, потокаLa-излучения, а также Тп с учётом современных представлений о зависимости температуры мезопаузы от уровня солнечной активности и года.
Получено, что введение дополнительной фотохимической реакции горячих атомов электронно-возбуждённого кислорода O(1D*)(с кинетической энергией большей 1,27 ЭВ), образующихся при фотодиссоциации О2 с длиной волны, не превосходящей 121,7 нм, приводит к лучшему согласию с экспериментальными данными.
Показано в области D неучёт NOприводит к уменьшению [Ne] примерно на порядок в области 80 км. Представлены результаты вычислительного эксперимента, подтверждающего необходимость учёта окиси азота в фотохимических процессах области Е и что малые азотные составляющие существенно влияют на пере распределение [О2+] и [NO+] в области 110-140 км и не влияют на электронную концентрацию.
Разработано новое возможное объяснение зимней аномалии области D. На основе реакции горячих O(1D) с N2, образующей N(4S) и NO, увеличения Тn, и последующего роста коэффициента реакции N(4S) с О2 (при сильной его температурной зависимости), приводящей к образованию NO.
Представлены результаты вычислительного эксперимента по её исследованию. Полученные результаты расчётов удовлетворительно согласуются с экспериментально измеренными значениями [О], [O2(1Dg)] и [NO] для условий ЗА. Максимум высотного распределения О находится в области 98-104 км и его величина равна 1,2 1012 см-3. Показано, что для условий ЗА скорость ионизации O2(1Dg) составляет около 50% от qN0 в области 90 км. Учёт qo,(1Dg) приводит к увеличению электронной концентрации на фактор 1,5 в области 85-95 км.
|
Страницы: | 1 | 2 | 3 | |
 Авторефераты по всем темам >>
Авторефераты по математике
Авторефераты по всем темам >>
Авторефераты по математике

 СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА
СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА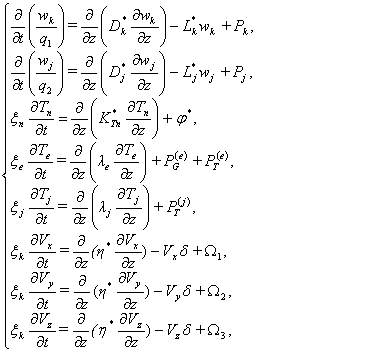 а
а