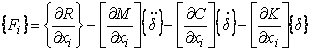Geum.ru
   Авторефераты по всем темам  >>  Авторефераты по техническим наукам

Многоуровневые методы и их программно-алгоритмическая реализация в задачах оптимизации механических систем при статических и динамических воздействиях

Автореферат докторской диссертации по техническим наукам

  Страницы: | 1 | 2 | 3 |
 

Вариант 3. На внешних итерациях алгоритма строились аинейные аппроксимации функции ограничений, что требовалоа ngаобращений к прямому вычислению ограничений (ng=2nx+1). Таким образом, общее число решений задачи КЭ анализа было сокращено. На внутренних итерациях алгоритма задача поиска условногоа экстремума с использованием линеаризованной функции ограниченийа производилась по асхеме 3. Как уже отмечалось, такой подход не требовала точности в поиске прямых переменных X , поэтому предельноеа число внутренних итераций было ограничено до 5-ти.

Таблица 3. Сопоставление результатов расчёта

Объем, аin 3

? (%)

Число итераций

Источник

3,600

ANSYS

Метод аппроксимации подзадачи

3,616

0,434

12

ANSYS

Метод первого апорядка

3,609

0,261

17

РОСК

в. 1

3,60332

0,092

9

в. 2

3,60218

3,6026

0,061

0,072

6

7

в. 3

3,60826

0,229

8

Рассмотренные примеры показали высокую робастность алгоритмов оптимизации, заложенных в ПК РОСК. При решении задачи безусловной минимизации была отмеченаа высокая устойчивость метода деформируемого многогранника. Метод Ньютона показал устойчивую работу на последних итерациях только в варианте 1, ачто позволило получить высокую точность в невязках ограничений (10-5). аВо всех вариантах была продемонстрирована быстрая сходимость к решениям близким к оптимальным уже на 2-3 итерации (рис. 6). аПоследующие итерации доводили результат до требуемой степени точности.

В главе приведены также примеры решения практических задач оптимизации стальных конструкций.

  1. Оптимизация стальной балки составного двутаврового сечения, аработающей на изгиб в плоскости стенки

Целевая функцияа f(x) в этой задаче представляла площадь поперечного сечения балки, где варьировалось 4 параметра.а В качестве ограничений были принятыапроверки по прочностиа иа устойчивостиа ва соответствииа са требованиямиа СП 16.13330.201 Стальные конструкции.а Было выполнено исследование результатов задачи на единственность путема решения с 5-ти начальных проектов.а Максимальная разница в варьируемых параметрах при этом составила 0,03%, т. е. решения практически совпали.а Число итераций колебалось от 7 до 8,а невязки ограничений имела порядока а10-4. аВ качестве методов безусловной минимизации были использованы метод деформируемого многогранника и градиентный метод 1-го порядка. На этой задаче было исследовано влияние параметров методов на сходимость алгоритма.а

  1. Оптимальное проектирование ферм

Решено несколько примеров оптимального проектированияа ферм, в которых предусмотрено варьирование геометрией сечений, а также координатами узлов расчетной модели. Учтено несколькоа случаев загружения. Минимизировался объем при соблюдении нормативных требований по прочности, устойчивости и жесткости.

Для оценки эффективностиа результатов было выполненоа их сравнение с параметрами равнопрочной фермы с параллельными поясами, площади сечений элементов которой были пропорционально умножены на коэффициент k, что обеспечивало перемещения узлов в допустимых пределах. Результаты решений приведены в таблице 4.

а Один из вариантов оптимизируемых ферм показан на рис. 7. Эта задача была решена при различных типах сечений, меняющихся как непрерывно, так и дискретно (по сортаментам).

Рис. 7. а) исходный;а б) оптимальный проектаа

а



Таблица 4. Варианты решений при оптимизации 23-ти стержневой фермы

Непрерывные параметры

Дискретныеаа параметры

Показатели

Равнопрочная ферма

№ 1

№ 2

№а 3

ГОСТ 10704-91

№ 4

ТУ 36-2287-80

Сечения

h1 (см)

200

300

300

300

300

h2 (см)

200

250

260

250

260

h3 (см)

200

150

150

140

160

Объём (см3)

329433

168400

169117

168925

173037

Объём %

100 %

51,1 %

51,3 %

51,3 %

52,53 %

Решение задачи оптимизации фермы подтвердило, что на сходимость алгоритмов существенное влияние оказывают параметры методов, в частности, минимальное значение коэффициента штрафа, коэффициента нормировки ограничений и др., что делает затруднительным применение алгоритмов оптимизации пользователем, который не знаком с их особенностями.а Эти исследования подтвердили аактуальность разработки эвристических подходов, обеспечивающих автоматическую настройку параметров поисковых методов, что было сделано в дальнейшем при решении задач оптимизации конструкций более сложной конфигурации с большим числом элементов. Пример такой конструкции показан на рис. 8.

 


Элементы фермы были сгруппированы по типу сечений и материалу, что апозволилоа сократить число варьируемых параметров, время вычисленийа и ав конечном итоге повысило сходимость алгоритма. Оптимальные результаты были проверены на единственность путем выполненияа расчётов с нескольких начальных проектов. При непрерывном изменении параметров все решения практически совпали (разница в объёме до 0,0012 %).а В случае дискретных изменений сечений согласно сортаментам было получено несколько локальных оптимумов, дающих разницу в объёме до 4,3 %. В качестве оптимального в таком случае может быть выбран проект, имеющий лучшие показатели (наименьшее значение целевой функции и точность в невязках ограничений и т.д.).

  • Оптимальное проектирование рам

Рассмотрены примеры оптимизацииа рам.а Одна из таких конструкций аизображена на рис. 9. Приняты различные типы сечений: аадля стоек; адля аригелей ; адля связей.а Задано 2 случая загружения. аНазначены анормативные ограничения по прочности и местной устойчивости в элементах рамы. Ограничение по жесткости задано в виде допуска на горизонтальное перемещениеа узла 9. Варьировались параметры сечений, а также высота h с шагом 10 см. Задача была решена в 2-ха вариантах. В первом случае параметры сечений менялись непрерывно (1 параметр кольцевого и коробчатого сечения, 2 параметра двутаврового сечения). Число варьируемых параметров с учетом того, что элементы рамы объединены в группы, равнялось 10-ти. аИмело место 42 ограничения, включая ограничение по жесткости. Во второма случае параметры сечений менялись дискретно по сортаментам. Число варьируемых параметров сократилось доа 8, число ограничений - 38.

В случае непрерывного изменения параметров результаты во всех примерах практически совпали, уже на 2-й итерации были получены решения близкие к оптимальному, а на 5-й - глобальный оптимум. При дискретных изменениях параметров наблюдалось 2 локальных оптимума с разницей в объёме до 2,8%.а

а

Рис. 9. Оптимизируемая рам

аа


Был отмечен ещё один эффект. Если варьировались 2 параметра сечений, например, адиаметр и толщина кольцевого сечения, то с разных начальных проектов были получены разные оптимальные решения для параметров сечений (с отличием до 30%), в то время как разницы в площадях были существенно меньше (10-2 %), а значение объёмаа практически совпадало.а Таким образом, при задании избыточного количества параметров варьирования имеет место множество локальных решений при одинаковом значении целевой функции а(плато целевой функции).аа

Рассмотренные примеры показали высокую робастность алгоритма оптимизации, заложенного в ПК РОСК. При решении задачи безусловной минимизации была отмеченаа высокая устойчивость методов деформируемого многогранника и покоординатного спуска (во всех примерах). Градиентный методаа а1-го порядка дал быструю сходимость в задаче оптимизации балки. Метод Ньютона показал устойчивую работу на последних итерациях вблизи оптимума в задачах оптимизации балок и ферм.

Шестая глава посвящена построению явных задач оптимизации механических систем при нестационарных динамических воздействиях:

найтиа аа minf(x, P(x,t)),аа xIEnx

(16)

при ограничениях

(17)

(18)

Здесь целевая функция и ограничения, накладываемые наа систему, связаны с варьируемыми параметрами через динамические параметры состояния Р(x,t) :

(19)

Принята КЭ динамическая модель системы ав линейной постановке

(20)

с начальными условиями , не зависящими от x. Таким образом, параметры состояния Р(x,t) являются неявными функциями варьируемых параметров. Рассмотрено несколькоа подходов к построению явной задачи НМП. Дляа исключения фактора времени отслеживались моменты времени (tCR), где функции ограничений принимали экстремальные значения на заданном временном интервале. Эти моменты времениа определялись из условия

,

(21)

где функция hj может быть определена, например, следующим образом:

.

(22)

Размерность задачи при этом существенно возрастает. Для ее сокращения была установлена полоса отбора ограничений.

Явной зависимость функций ограничений от переменных x была получена на основе аппроксимаций. Скорость сходимости при этом сущестнвенно зависит от нелинейности ограничительных функций, которая обусловлена, во-первых, сложной зависимостью параметров соснтояния от варьируемых параметров, связанной со структурой механических систем. Во-вторых, сами ограничения, как правило, нелинейны относительно параметров состояния. Тогда аппрокнсимация параметров состояния может дать более качественные приближения, чем аппрокнсимация самих функций {g}, поскольку в последних сохраняются нелинейности второго типа. Это позволяет использовать полученные аппроксимации на более широкой области варьируемых параметров, что в конечном итоге принводит к сокращению числа итераций для поиска оптимума. С учетом этого разработана методикаа построенияа аппроксимаций параметров состояния системы, выполненных путём разложения функций в ряд Тейлора в окрестности пробной точки. Были получены выражения чувствительностей дляа частных случаев, когда параметры состояния являются функциями динамических перемещений, скоростей и ускорений. Приведем выражение производнойа k-го параметра состояния, связанного с перемещениями системы:аа

Предложено 2 схемы анализа чувствительности 1-го порядка.

а). Прямое дифференцирование: ,аа аагде производные 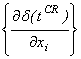аопределяются из условия:

,

(23)

а вектор псевдонагрузкиа находится по выражению

(24)

с начальными условиями 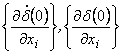ааравными нулю.

Трудоемкость прямого метода пропорциональна числу варьирунемых параметров. Между тем, в задачах оптимизации механических систем число активных ограничений значительно меньше числа варьируемых параметров. Это обусловлено нелинейностью целевой и ограничитенльных функций, а также выходом некоторых варьируемых параметров на границу параметрических ограничений (18). В силу этого, при станбилизации числа активных ограничений более эффективным становитнся метод сопряженных переменных.

б). аДифференцирование через сопряженные переменные адля k-го параметра состояния выполняется по следующей схеме:

(25)

где вектор аопределяется решением системы уравнений

(26)

Рассмотрено 2 способа формирования аппроксимаций 2-го порядка:а прямое дифференцирование и комбинированный способ, которыйа позволяета сократить число решений уравнения состояния системы. Во всех случаях решение задачи динамического анализа и анализа чувствительности совмещено. Для изменения знака у второго слагаемого в выражении (26) была произведена замена переменных.

Отдельно исследован случай, когда уравнение движения сначала раскладывается по собственным формам колебаний, а затем выполняется покомпонентный синтез чувствительностей по требуемому числу форм. Так как матрица демпфирования не является пропорциональной матрице масс и жесткости, такой переход приводит к разделённым уравнениям удвоенного порядка.

Выбор того или иного метода анализа чувствительности зависит от аконкретной задачи. Наиболее рационально на первых итерациях, когда множество активных ограничений не выявлено, использовать метод прямого дифференцирования. На последующих итерациях, если число активных ограничений невелико, целесообразно перейти к определению чувствительностей через сопряженные переменные. Таким образом, эти два подхода могут хорошо дополнять друг друга.

Седьмаяа глава.а Для решенияа практических задач оптимального проектирования механических систем при нестационарных динамических воздействиях было разработано специализированное программное обеспечение. Приведём описание основных блоков алгоритма, который был положен в основу программного комплекса оптимизации а(рис. 10).

В блоке аDiransаформируются коэффициенты аппроксимации на основе прямого метода анализа чувствительности. Для решения системы дифференциальныха уравнений состояния (20) и (23) использовался метод прямого интегрирования (?-метод Вилсона). Блок Aprox включает построение приближенной задачи оптимизации. Здесьа строятся линейные аппроксимации параметров состояния по варьируемым параметрам. Блок NMPackа предназначен для решения задачи условной минимизации по алгоритмам, которые изложены в главе 3.

 


Дляа апробации программного комплекса были решены задачи оптимизации асистемы виброударозащиты балочного типа, где установлены присоединенные массы, которые необходимо отстроить от кинематических воздействий на балку. Задача оптимизации была поставлена следующим образом: минимизировались ускорения верхних присоединённых масс. Ограничения накладывались на перемещения точек системы, а также на напряжения, возникающие в результате действия статических и динамических нагрузок. Варьировались геометрические и физические параметры: размеры поперечного сечения, величины масс, демпфирования иа жесткости.

На рис. 11 показана расчетная схема амортизатора, имеющаяаа l степеней свободы.а Поперечное сечение балки принято в виде составного двутавра. Задано кинематическое воздействие на опоры ?оп в виде кратковременного импульса на временном интервале tp.

 


Рис. 11. Схема амортизатораа балочного типа с l степенями свободы.

а

а Ниже приведены результаты для наиболее простого случая, когда на балке имеют место только две массыа и а,аа расположенные посередине пролёта. Было принято несколько вариантов воздействий на опорыа .а В таблице 4 показаны результаты решения задачи, когда внешнее воздействие задано симметричным в виде импульса: (t??p).

Таблица 5 . Сравнение исходных и оптимальных параметров

(т)

(кН?с/м)

(кН/м)

B

(м)

h

(м)

b

(м)

(м/с2)

Начальные параметры системы

0,3

40

1000

0,2

0,5

0,01

122,2

Оптимальные параметры системы

0,8

11

98

0,12

0,244

0,006

2,056

d2 (мм)

а

б)

а

t (с)

а

t (с)

а

 


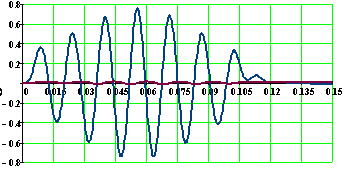
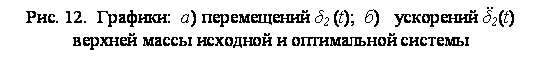
В примере были использованы прянмые методы анализа чувствительности, что для решения задач такого класса целесообразно вследствие их небольшой размерности, а также того обстоятельства, что число ограничений здесь соразмеримо с числом варьируемых параметров. Кроме того, кратковременнный характер импульсной нагрузки позволяет исследовать поведение конструкции за малый промежуток времени (хотя число временных шагов при этом может быть достаточно большим). Совмещение процендур динамического КЭ анализа и анализа чувствительности позволило существенно сократить вычислительный процесс оптимизации. Для повышения точности и надежности решения приближенной задачи могут быть реализованы аппроксимации второго порядка.

Задачи оптимизации механических систем при нестационарных динамических воздействиях решались с нескольких начальных проектов. В результате было выявлено, что в ряде случаев различные начальные проекты приводят к разным направлениям поиска по отдельным переменным. Для того, чтобы исследовать эту особенность были построены графики зависимости функций ограничений от варьируемых параметров. Было выявлено, что функции ограничений в большинстве своем существенно нелинейные, невыпуклые функции. Таким образом, апроблема поиска глобального оптинмума в задачах оптимизации динамически систем является достаточно сложной. Для её численного решения можно выделить два основных подхода. Первый заключается в получении хороншего начального приближения путем прямого вычисления функций ограничений (например, методом случайного поиска). Второй предполагает исслендование нескольких случайных точек в области поиска, из которых осуществляется спуск с помощью локальных методов. В случае, если сущестнвует несколько локальных решений, в качестве оптимального берется проект, имеющий лучшие показатели (наименьшее значение целевой функции и точность в невязках ограничений и т.д.). Следующая проблема при решении задачи оптимизации азаключалась в том, что вследствие аппроксимации задача на условный экстремум часто становилась несовместной (особенно в области тончек перегиба ограничительных функций, где градиенты ограничений близки к нулю, что существенно ухудшает сходимость задачи). Для того, чтобы добиться сходимости, на каждой итерации поиска регунлировалась величина шага изменения варьируемых параметров (обычнно 1/5-1/15 всего интервала). В случае, если нанблюдалась монотонная сходимость, этот шаг увеличивался, если же в ходе поискового процесса варьируемые параметры ударялись в разные границы, шаг уменьшался. В результате такой постановки приближенной задачи допустимое решение на итерации часто отсутствовало (особенно на первых итенрациях). Однако применение методов модифицированных функций Лагранжа позволило осуществлять поиск в направлении оптимума и за пределами допустимой области. При этом имело место резкое увелинчение двойственных переменных на внутренних итерациях условно-экстремальной задачи (уровень R). Для того, чтобы ограничить их значения, задавалось всего две итерации этого уровня (ближе к оптимуму число этих итераций было увеличено).

ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ

    • Разработана эффективная комплексная методика оптимизации механических систем на основе численных методов конечно-элементного анализа и нелинейного математическогоа программирования (НМП), позволяющая варьировать физическими и геометрическими параметрами расчетных моделей этих систем,а решать рекурсивные задачи оптимизации.
    • На основе этой методики разработан алгоритм оптимизации ав статической постановке, который реализован в двух вариантах: при оптимизации сложных пластинчато-стержневых конструкций строится приближенная задача на основе аппроксимации статических апараметров состояния с использованиема методов анализа чувствительности первого и второго порядка. В задачах оптимизации стержневых систем предложена схема прямого вычисления функций ограничений. Модули КЭ при этом разработаны с учётом того, что матрица жесткости является функцией варьируемых физических и геометрических параметров оптимизируемой системы.а
    • В алгоритм оптимизации встроеныа требования по прочности иа устойчивостиа в соответствии с нормативным документома СП 16.13330.201 Стальные конструкции. Эти требования формализованы в виде функций ограничений задачи НМП. Для надёжной работы алгоритма оптимизации апроизведена корректировка этих функций таким образом, чтобы они были сглажены и обеспечивали сходимость к оптимальныма результатам, как в пределах, така и за пределами допустимых решений. Таким образом, задача оптимизации стальных конструкций реализована наиболее полно с включением нормативных требований и библиотеки стандартных сечений.а аа
    • Разработана многоуровневая концепцияа решения стандартной задачи НМП с использованием модифицированных функций Лагранжа первого и второго порядка, позволяющая работать с функциямиа произвольного видаа на широком диапазоне непрерывных и дискретных параметров расчётной модели. В рамках этого концепции развиты двойственные и комбинированные подходы,а работающие в редуцированном пространстве потенциально-активных ограничений.
    • Реализована эвристический механизм переключения методов условной и безусловной минимизации на основе анализа состояния вычислительного процесса оптимизации, позволяющий автоматически настраивать алгоритм на наиболее эффективный поисковый метод.
    • Рассмотрено несколькоа подходов к построению явной задачи НМП при решении задач оптимизации механических систем в условиях нестационарных динамических воздействий. Разработана методикаа построенияа аппроксимации на основе прямого дифференцирования иа дифференцирование через сопряжённые переменные дляа частных случаев, когда параметры состояния системы являются функциями динамических перемещений, скоростей и ускорений. Отдельно исследован аслучай покомпонентного синтеза чувствительностей по требуемому числу форм колебаний. Так как в алгоритме использована динамическая модель с матрицей демпфирования не пропорциональной матрице масс и жесткости, такой переход приводит к разделённым уравнениям удвоенного порядка. Предложенные подходы могут хорошо дополнять друг друга на различных стадиях вычислительного процесса оптимизации.
    • Алгоритм реализована в видеа программного комплекса расчета и оптимизации стальных конструкцийа РОСК, состоящий из 3-ха основных блоков, каждый из которых может функционировать автономно: блок конструктивного расчета стальных конструкций, блок оптимизации и блок КЭ анализа. Такая структураа ПК дает возможностьа его расширения, как в пополнении нормативной базы, так и в добавлении новыха КЭ модулей.
    • Произведена апробация программного комплекса РОСКа посредствомаа решенияа тестовых и практических задачи оптимизации конструкций:а балок, рам, ферм, пластин при статических и нестационарных динамических воздействиях. На этих задачах выполнено исследование сходимости алгоритма оптимизации. Определены параметры поисковых методов, влияющие на сходимость.а Даны рекомендации их настройке,а что позволило повыситьа устойчивостьа алгоритма. Выявлено, что в задачах, где варьируемые параметры меняются непрерывно, имеет место один глобальный оптимум. В задачах адискретной оптимизации присутствует несколько локальных решений, из которых выбирается проект, имеющий лучшие показатели.
    • Решение верификационных тестов аподтвердило эффективность алгоритмов, на основе которых разработан ПК, как в части вычислительных затрат, так и по степени точности полученных результатов. При решении практических примеров в большинстве случаев сходимость к проектам близким к оптимальным, была получена уже на 2-3 итерации с последующим доведением ана последующих итерациях до требуемой степени точности.

    Основное содержание диссертации отражено в следующих аапубликациях в изданиях,а рекомендованных ВАК РФ

    1. Дмитриева Т.Л.а Аппроксимация параметров состояния в задачах оптимизации систем, подверженных нестационарным динамическим воздействиям. //Современные технологии. Системный анализ. Моделирование. Иркутск: Из-воа ИрГупс, 2008, № 1.а С. 110-114.
    2. Соболев В.В., Дмитриева Т.Л. Вибрационная защита промышленных конструкцийа на основе параметрической оптимизации дискретно-континуальных математических моделейа Уконструкции - виброактивное оборудованиеФ // аСовременные технологии. Системный анализ. Моделирование. Иркутск:Из-во ИрГупс, 2009,а № 4.а С. 149-158.
    3. Безделев В.В., Дмитриева Т.Л. Использование многометодной стратегии оптимизации в проектированииа строительных конструкций// Известия вузов. Строительство, 2010, № 2. С. 90-95.
    4. Дмитриева Т.Л.Алгоритм аавтоматизированного проектированияаа ферма минимального веса // Известия вузов. Строительство, а2010, № 3. С. 98-105.
    5. Дмитриева Т.Л.Оптимизация ферм с дискретными параметрами // Известия вузов. Строительство, 2010,а № 8. аС. 86-94.
    6. Дмитриева Т.Л.К вопросу оптимизации однопролётной балкиа двутаврового сечения // Вестник Иркутского государственного технического университета, 2010,а № 5.а С. 88-94.
    7. Дмитриева Т.Л.Алгоритм решения условно-экстремальных задач, использующий методы модифицированных функций Лагранжа первого и второго порядка // Современные технологии. Системный анализ. Моделирование, № 4, Иркутск: Из-воаа ИрГупс, 2010.а С. 115-121.
    8. Дмитриева Т.Л., Безделев В.В. аАлгоритм автоматизированногоа проектирования механических система са оптимальными параметрамиаа приа импульсных воздействиях //а InternationalJournalforComputationCivilandStructuralEngineering/ Международный журнал по расчету гражданских и строительных конструкций, 2011, v. 7,а № 1.а P. 85-94.аа
    Дмитриева Т.Л.а Программный комплекс лOPTIDEST и егоа использование в задачаха расчёта и оптимизации стальныха конструкций // Вестник МГСУ , 2011,а т.1, № 1.аа C. 100-105.
    1. аДмитриева Т.Л.а Решение тестовых задач оптимального проектированияа стержневых систем // Вестник Иркутского государственного технического университета, 2011,а № 7 (54), C. 40-46.
    2. аДмитриева Т.Л.Оптимизация геометрических параметрова стальных рам // Academia. Архитектура и строительство, 2011,а № 3.а C. 114-119.

    СВИДЕТЕЛЬСТВА

    о государственной регистрации в федеральной службе апо интеллектуальной собственности, патентам и товарным знакам аа(РОСПАТЕНТ) программ для ЭВМ

      • Свидетельство № 2011617406 от 23.09.2011 о государственной регистрации программы для ЭВМ Программный комплекс для решения задач нелинейного математического программирования (НМПак). Авторы: Дмитриева Т.Л.,а Безделев В.В.
      • Свидетельство № 2011617407 от 23.09.2011 о государственной регистрации программы для ЭВМ Расчет и оптимизация стальных конструкций (РОСК). Автор: Дмитриева Т.Л.
      • Свидетельство № 2011617408 от 23.09.2011 о государственной регистрации программы для ЭВМ Конструктивный расчет стальных конструкций (КРаСК). Автор: Дмитриева Т.Л.
        Страницы: | 1 | 2 | 3 |
           Авторефераты по всем темам  >>  Авторефераты по техническим наукам