 Авторефераты по всем темам >>
Авторефераты по техническим наукам
Авторефераты по всем темам >>
Авторефераты по техническим наукам
Многоуровневые методы и их программно-алгоритмическая реализация в задачах оптимизации механических систем при статических и динамических воздействиях
Автореферат докторской диссертации по техническим наукам
| Страницы: | 1 | 2 | 3 | |
В первой главеа представлена аналитический обзор подходов, используемых при решении проблемы оптимизации конструкций различного вида. Отмечено, что методология численной оптимизации базируется как на методах оптимизации (или синтеза), так и на методах расчета (или анализа) конструкций. Таким образом, снижения вычислительных затрат ва задачах оптимального проектирования можно добиться как приемами, заложенными в алгоритмы КЭ анализа, так и эффективной реализацией поисковых алгоритмов синтеза инженерных объектов. Перечислены подходы, используемые при оптимизации сложных крупногабаритных сооружений. Большинство их ниха используют поэтапный подход к рассматриваемой проблеме. Кроме того, часто используется прием, основанный на построение приближенной задачи путем ааппроксимации параметров состояния системы (перемещений, усилий, частот и форм колебаний и др.), когда задача КЭ анализа решается на внешних итерациях алгоритма оптимизации, а поиск оптимальных решений осуществляетсяа для приближенной задачи. аРассмотрена авторский вклад отечественных и зарубежных исследователей ва разработку теории оптимизации конструкций. Показано, что фундаментальные основы большинства направлений оптимального проектирования на основе методов нелинейного математического программирования (НМП) были заложены в 60-80 годы прошлого века. К настоящему времени накоплен немалый опыт решения прикладных задач оптимизации в различных инженерных областях, которые можно классифицировать по материалу конструкций, по вопросам оптимизации топологии и формы, разделить на оптимизацию конструкций определенного вида: ферм, рам, пластин, балок на упругом основании, контактные задачи, вопросы дискретной оптимизации и др. аВ отдельную группу относят задачи оптимизации механических систем при динамических воздействиях. Заа последние 10-15 лет аинтенсивное развитие получили аматематические подходы, основанные на имитации биологических или физических явлений, наиболее известные среди которых - генетические и эволюционные алгоритмы, которые удобны тем, что не накладывает математических требований к характеру целевой и ограничительных функций. Этиа алгоритмы используют стохастические методы поиска в многомерных пространствах, их параметры влияют друг на друга сложным образом, а их эффективность во многом зависят от выбранной модели.
Отмечено, что большинство алгоритмов оптимизации требуют вычисления не только значений функций, описывающих поведение системы, но их производных. Такая задача может быть востребована при использовании градиентных поисковых методов, либо при построении аппроксимаций.а Но и помимо этого, исследованиеа свойств оптимизируемой системы при малом варьировании параметров в окрестности заданной точки (так называемая задача анализа чувствительности) анесет важную информацию, т.к.а позволяет выявить те параметры, которые оказывают наибольшее влияние на поведение конструкции. Таким образом, анализ чувствительности, представляет собой один из важных этапов численной оптимизации и должен осуществляться эффективно. Для задач статики методы анализа чувствительности аразработаны достаточно полно. Исследования в области оптимизации динамических систем ограничиваются в основном чувствительностями первого порядка.
Приведен обзор методов решения условно-экстремальных задач, поставленных ва форме НМП. Одним из часто используемых здесь является подход, сводящий задачу поиска экстремума при наличии ограничений к задаче на безусловный экстремум, на основе использования методов штрафных функций, либо методы множителей Лагранжа. Показано, что одним из существенных недостатков методов множителей Лагранжа является их применимость к ограниченному классу задач сепарабельного программирования, где функция Лагранжа выпукла по исходным переменным, и допускает вычислениеа производныха по двойственным переменным в явном виде. Для построения методов, применимых для отыскания локального экстремума в невыпуклых задачах, целесообразно воспользоваться модифицированными функциями Лагранжа (МФЛ). В результате этого множество седловых точек функции Лагранжа остается неизменным, но обеспечивается сходимость для более широкого класса задач и с большей скоростью. Фундаментальные исследования методов МФЛ приведены в работах А.С. Антипина, Д. Бертсекаса, Е.Г. Гольштейна, Ю.Г.Евтушенко,а Б.Т.Поляка,а Н.В. Третьякова и др. Однако в целом МФЛ в задачах оптимизации конструкций не имеют широкого использования. Нет четких рекомендаций по назначению параметров этих методов, с целью повышения их эффективности.
Рассмотрен вопрос оптимизации механических систем апри динамических воздействиях. Такая задача может быть решена только на основе аппроксимаций функций ограничений, либо динамических параметров состояния, входящих в эти функции. Приведены особенности реализации МКЭ в задачах анализа, где динамическая модель строится с учётом демпфирования, изложены известные методики анализ чувствительности.
В отдельном разделе дается характеристика отечественных и зарубежных программных комплексов, реализующиеа алгоритмыаа оптимизацииа инженерных систем.
Вторая глава посвящена построению алгоритма автоматизированногоа проектирования астальных конструкций минимального веса апри статических авоздействиях:
найти аа minаа f (x, P(x)),аа xI Enx |
(1) |
|
при ограниченияхаа |
(2) |
|
аа |
(3) |
Здесь целевая функция и ограничена системы, связаны с варьируемыми параметрами через параметры состояния
|
(4) |
которые определяются решением КЭ уравнения состояния в линейнойа поста-
новке: |
а (5) |
В качестве минимизируемой функции f(x) использован объём (вес) аконструкции. Варьируются её геометрические и физические параметры, которые могут меняться непрерывно либо дискретно. В задачах оптимизации пластин, варьируется толщины в узлах конечно-элементной сетки. При дискретном изменении сечений согласно сортаментам варьируются позиции сортамента, включающие выборочные значения параметров, обеспечивающиеа монотонное возрастаниеа площадей и моментов инерции сечений. Отдельный случай представляет рекурсивная задача оптимизации, когда варьируется положение груза (ищется его невыгодное положение), при одновременном варьировании параметров сечений.
Функции ограничений (2) представляют собой ограничения по прочности, жесткости, устойчивости. К параметрическим ограничениям (3), можно отнести ограничения по габаритам,а свариваемости и др. Возможно также задание пользовательских вариантов ограничительных функций.
Вектор ограничений всей системы содержит вклады по элементам, которые могут быть объединены в группы по типоразмерам и материалу. Такой подход позволяет независимо задавать физические и геометрические свойства каждой группе. При этом вектор ограничений аэлемента (или группы элементов) формируется с учётом нескольких случаев загружения, а также нескольких характерных сечений в элементе. Задаётся массив выборки ограничений, c помощью которого любое ограничений может быть отключено.
Для решения поставленной задачи оптимизации (1-3) было разработано 2 подхода.а Впервом случаеа для получения явных зависимостейа функций (2) от варьируемых параметров формировалась приближенная задача путём построения аппроксимаций самих функций, либоа параметров состояния, входящих в них, в окрестности пробной точки аx*:аа аа
|
(6) |
|
(7) |
Коэффициенты аппроксимации при этом вычисляются на основе методов анализа чувствительности 1-го и 2-го порядка. Взаимосвязь основных блоков алгоритма на основе аппроксимаций показана на рис. 1.

Эффективность такого подхода связана ещё и с тем,а что даёт возможность реализовать двусторонние связи с известными конечно-элементными программными комплексами, что существенно расширяет область исследуемых объектов оптимизации.
Второй режим работы предполагает, что блок оптимизации обращается к вычислению целевой и ограничительной функциям напрямую (рис. 2). Такой подход может быть реализован при решении задач ограниченной размерности, когда мощности вычислительных средств позволяют находить значения усилий и перемещений прямым КЭ расчётом при каждом обращении к функциям ограничений (наиболее часто такой прием был использован при оптимальном проектировании стержневых систем).а При этом было отмечено, что прямое вычисление этих функций даёт лучшую сходимость алгоритма и позволяет использовать более тонкие поисковые методы оптимизации (например,а градиентные методы 1-го и 2-го порядка).
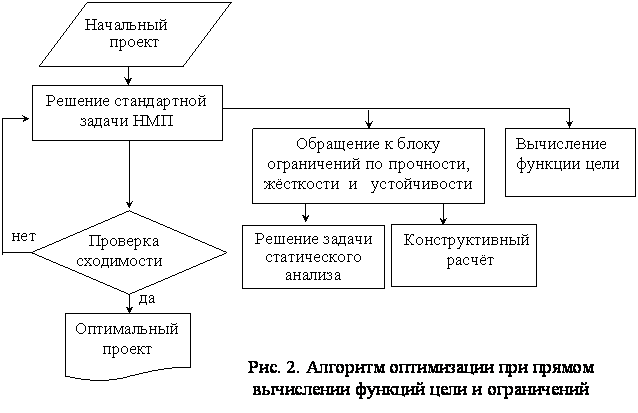
аа
Блок конструктивного расчёта ориентирован на расчет стальных конструкций. Здесь реализованы аапроверкиа по прочности и устойчивости согласно нормативному документу СП 16.13330.2011 Стальные конструкции. Предусмотрено 6 вариантов напряжённо-деформированного состояния (НДС) конструкций, перечисленных в таблице 1.
Таблица 1. Виды напряженно-деформированного состояния |
||
№ |
Вид НДС |
Ссылка на апараграфа СП |
Центральное растяжение-сжатие |
7.1Ц7.3 |
|
Изгиб в одной плоскости |
8.2, 8.4, 8.5 |
|
Изгиб в двух плоскостях |
||
Изгиб в одной плоскости с учётома пластическиха деформаций |
||
Изгиб в двух плоскостях с учётома пластическиха деформаций |
||
Действие осевой силы ас изгибом |
9.1-9.4 |
|
Блок конструктивного расчета может функционировать также в режиме тестирования функций ограничений, для чего было выполнено построение их графиков на широком диапазоне изменения варьируемых параметров. Результаты тестирования дают возможность, во-первых, выявить ошибки в формировании функций g(x), во-вторых, подобная информация может быть полезна проектировщику, поскольку позволяет оценить чувствительность этих функций к изменению того или иного параметра, аи наконец, на графиках были отслежены аслучаи, когда функции ограничений имеют скачки и изломы. Для встраивания этих функций в алгоритм оптимизации в ряде случаев в аих выражения были внесены акорректировки, направленные на то, чтобы обеспечить их непрерывность за пределами областей допустимых значений. Проведенные исследования показали, что при решении задач оптимального проектирования стальных конструкций наибольшую устойчивость могут обеспечить прямые методы безусловной минимизации (метод случайного поиска, метод деформируемого многогранника, метод покоординатного спуска и др.). Здесь не требуется выполнение таких условий как гладкость и дифференцируемость функций (1), (2). Однако эти методы требуют большого числа обращений к их вычислению, а соответственно большого числа перерасчетов задачи КЭ анализа (5). Градиентные методы 1-го и 2-го порядка могут дать лучшую сходимость при большей точности в невязках ограничений, однако не всегда устойчивы в работе. На основании перечисленных особенностей можно сформулировать такоеа требование к разработке поисковых алгоритмов оптимизации,а как многометодность, которая позволяла бы получать устойчивую сходимость в решении условно-экстремальных задач (1), (2) с функциями произвольного авида на широком диапазоне непрерывных и дискретных параметров варьирования при меньших вычислительных затратах. Отмечено, что эффективность такого подхода может быть усилена, если в программной реализации алгоритма выбор того или иного поискового метода осуществляется не в диалоговом режиме,а где вычислительным процессом управляета пользователь, аа на основе эвристического механизма переключения методов и эффективной настройки апараметров этих методов.
В третьей главе приведён многоуровневый алгоритм решения задачи нелинейного математического программирования с использованием методов модифицированных функций Лагранжа. Преимущество такого подхода состоит в том, что он позволяет рассматривать широкий класс условно-экстремальных задач как выпуклого, так и невыпуклого программирования.
В алгоритме аиспользуютсяа 2 модифицированные функции Лагранжа:
|
а (8) |
|
(9) |
где ![]() ааЦа функцияа Лагранжа, {Y} - вектор двойственных переменных (или множителей Лагранжа) размерностью m. В выражении (8)а [K] Цдиагональная матрица штрафных коэффициентов. Элементы матрицы [d] аопределяются из условия: еслиа а
ааЦа функцияа Лагранжа, {Y} - вектор двойственных переменных (или множителей Лагранжа) размерностью m. В выражении (8)а [K] Цдиагональная матрица штрафных коэффициентов. Элементы матрицы [d] аопределяются из условия: еслиа а![]() аиначеа
аиначеа ![]()
?Zj Ц величина сдвига j-го ограничения в допустимую область. аПараметры kf и t , входящие в функции (8), (9) арегулируют сходимость алгоритма.
Численный алгоритм решения задачи НМП основан на двух попеременных процедурах. аНа первом шаге при определенных {Xt}, {Yt} арешается задача на безусловный экстремум при наличии параметрических ограничений:
|
(10) |
в результате чего вычисляется вектор {Xt+1}. Для решения этой задачи могут быть реализованы методы безусловной минимизации различных классов. На первых итерациях при отсутствии хорошего начального приближения используется метод случайного поиска. Метод деформируемого многогранника обладает высокой надежностью и позволяет получать оптимальные решения для функций произвольного вида, но при этом требует большого числа обращений к вычислению целевой и ограничительных функций.а В методе наискорейшего спуска поиск ведется вдоль градиента минимизируемой функции. Скоростьа этого метода на порядок выше, но он применим для гладких дифференцируемых функций. Метод покоординатного спуска предполагает спуск вдоль соответствующей координаты при фиксированных значениях других переменных. Этот метод аиспользуется в задачах дискретного программирования. На последних итерациях для получения результатов высокой точности, возможно переключение на метод Ньютона. Однако метода может быть реализован только для континуальных задач, если функция Fp выпукла и дифференцируема. В градиентных методах для определения длины вектора, вдоль которого осуществлялся спуск к экстремуму, используются методы одномерного поиска. В этом случае сначала выявлялся интервал, где расположена выпуклая тройка точек, а далее методом золотого сечения, либо методом квадратичной интерполяции этот интервал исследовался на экстремум.
Второй шаг итерационного процесса заключается в определении двойственных переменныха {Yt+1}, для чего апредусмотрено 3 способа.
Способ 1 предполагает, что вектор двойственных переменных определяется из сравнения условий стационарности функции Fp и функции Лагранжа FL. Этот способ дает линейную скорость сходимости по Y:аа
|
(11) |
В способе 2 приращение двойственныха переменных вычисляется путем максимизации Fp методом Ньютона в редуцированном пространстве потенциально-активных ограничений ![]() , что дает квадратичную сходимость по Y.
, что дает квадратичную сходимость по Y.
В 3-м способе вектор ![]() аопределяется непосредственно через прямые переменныеа путем максимизации функции FM аапо Y.
аопределяется непосредственно через прямые переменныеа путем максимизации функции FM аапо Y.
|
(12) |
Этот способ не требует выполнения условий стационарности функции Fp по исходным переменным X.
В соответствие этим способам было поставлено 3 схемы решения задачи НМП:а
В схеме 1 реализуютсяа прямые поисковые методы либо градиентный метод 1-го порядка для решения задачи (10) в сочетании с 1-м способом пересчёта переменных Y . Этот приём был использован на 1-х итерациях алгоритма.
Схема 2 даёт квадратичную сходимость по прямым и двойственным переменным.
|
а(13) |
|
а(14) |
гдеа |
|
Добавкиа а[D] и {V} учитываюта влияниеа параметрических ограничений. Сочетание задач (13), (14) дает существенное сокращение вычислительных операций за счет того, ачто треугольное разложение матрицы вторых производных [A] здесь выполняется 1 раз. Практические расчёты показали высокую эффективность метода Ньютона и по времени вычислений, и в точности невязок ограничений, которая была на 5-7 порядков выше. Однако устойчивая работа этого метода имеет место лишь в том случае, еслиа установилось множество потенциально активных ограничений, то есть на последних итерациях поискового процесса. а
В схеме 3а был применен комбинированный подход с использованием сразу 2-х функций. Прямые переменные определялись их условия (10), однако, итерационный процесс при этом мог не достигать точности в её решении, а двойственные переменные вычислялисьа через функцию FM по выражению (12). Такой подход оказалсяа эффективен в задачах на основе линейных аппроксимаций. В этом случае (особенно на первых итерациях) не всегда существует допустимое оптимальное решение, т.к.а задача часто становится несовместной.а
При решении задач дискретной минимизации поиск безусловного оптимума осуществляется методом покоординатного спуска в сочетании с 1-м либо 3-м способом пересчета двойственных переменных. а
Алгоритм решения задачи НМП связан системой уровней, на каждом из которых используется своя группа методов (многоуровневая модель алгоритма приведена в главе 4).а Комплексная реализация предложенных схем делает этот алгоритм надежным и устойчивым, т. к. если не срабатывают градиентные методы, то автоматически производится переключение к прямым поисковым методам. аРешение тестовых задач показало эффективность многометодного, многоуровневого аподхода. Была отмечена аширокая области сходимости алгоритма, его устойчивость, а также в возможностьа получения результатов требуемой точности.
В четвёртой главе даётся описание программного комплекса расчета и оптимизации стальных конструкций РОСК, разработанного на основе алгоритмов, изложенных в главах 2-4. Этот комплекс может функционировать в двух режимах: на основе построения приближенной задачи и при прямом обращении к вычислениюа целевой и ограничительной функций.
Приведена общая архитектура ПК, включающая следующие блоки:
- Блок построения приближенной задачиа Aprox.
- Блока статического анализа Statics.
- Блокаа конструктивногоа расчета стальных конструкцийа Steel.
- Блок решения задачи нелинейного математического программирования аNMPack.
- Библиотека сечений Section.
Показана взаимосвязь программных процедур каждого блока, дано описание основных процедур. а
Выходными параметрами блока Aprox являются коэффициенты аппроксимации. В зависимости от заданного режима это могут быть аппроксимации первого либо второго порядка. При этом программы блока NMPackаавтоматически настраиваются на режим аппроксимаций.а
Блок статического КЭ анализа Statics реализован в перемещениях для пластинчато-стержневых систем.
Блок поверочного конструктивного расчёта стальных конструкций включает в себя проверки на прочность и устойчивость соответственно нормативным требованиям СП 16.13330.2011а Стальные конструкции.
Блокрешения задачи НМПа NMPackрассмотрен наиболее подробно, как блок, обеспечивающий надежную работу всего алгоритма оптимизации. Здесь реализованы алгоритмы условной и безусловной минимизации, которые былиа приведены в главе 3. БлокиNMPackа и Aproxсвязаны между собойа системойа уровней (рис. 3).а
Уровень С (Control) Ц уровень контроля исходных данных.
На уровне R(Restrict)исходная условно-экстремальная задача преобразуется в задачу на безусловный экстремум. Здесь производится пересчет двойственныхаа переменных, проверка сходимости алгоритма, а также переключение методов безусловной минимизации. Управление процессом переключения осуществляется при помощи массива Method, который может задаваться пользователем на этапе подготовки данных. Если массив не задан, в процессе расчёта происходит настройка на тот или иной метод автоматически на основе анализа состояния вычислительного процесса оптимизации. Предполагается также автоматическая настройка параметров поисковых методов, таких как штрафные коэффициенты, коэффициенты нормировки целевой и ограниченных функций, которая обеспечивает устойчивую работу программного комплекса.
аУровень А (Aprox) предназначен для построения приближенной задачи оптимизации.
![]()
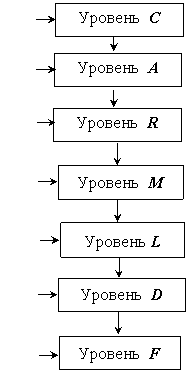
Рис. 3. Взаимосвязь уровнейа в программном комплексе оптимизации
ааУровень М (Minimum) включает методы безусловной минимизации ана интервале изменения варьируемых параметров, обозначенном параметрическими ограничениями.
Уровень L (Line)предназначен для решения задач одномерного поиска.
Уровни D (Derive) Ц уровень вычисления производных, где используются как аналитические методы, так и методы численного дифференцирования.
На Уровне аFа (Fun) - авычисляются значения целевой и ограничительных функций, а также значения модифицированных функций Лагранжа.
Приведен интерфейс ПК РОСК. Для ввода данных разработан табличный редактор,а где задаются физические и геометрические параметры конструкции.а Выходные данные выводятся в текстовые и графическиеа файлы:
- текстовый файл, куда выводятся параметры алгоритма оптимизации на каждой итерации (используемые методы, значения варьируемых параметров, целевой функции и невязок ограничений, штрафные коэффициенты и т.д.);
- атекстовый файл, где приведены исходные и оптимальные геометрические и физическиеа параметры конструкции;
- текстовый файл, где приведены данные КЭ анализа исходной и оптимальной системы;
- графический файл, куда выведена расчетная схема исходной и оптимальной конструкции.
В данной версии ПК реализованы задачи расчёта и оптимизации стальных конструкций. Однако архитектура комплекса позволяет расширять его возможности. Предусмотрено встраивание пользовательских процедур, реализующих требования к поведению конструкции.а Так, добавление модулей в блок КЭ анализа дает возможность для оптимизации конструкций с физическими, либо геометрическими нелинейностями. Блок конструктивного расчета может быть пополнен нормативными требованиями к расчету алюминиевых, ж/б и др. конструкций.а Особого внимания заслуживает тот факт, что данные, передаваемые в различные блоки ПК, помещены в специальный модуль GlobalControl (таким образом, данные отделены от программного кода). Такая конструкция позволяет решать рекурсивные задачи оптимизации любой степени вложенности.
В пятой главе выполнена апробация ПК аРОСК. Для этого были решеныа тестовые и практические задачи оптимального проектирования конструкций в статической постановке. аНиже приведены а2а верификационных теста.
- Оптимизация 10-стержневой статически неопределимой фермы.
Минимизируется объем фермы (рис. 4). Варьировались площади сечений.
![]()
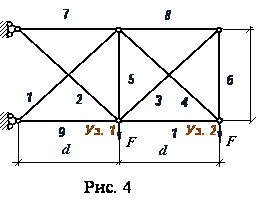
Заданы ограничения: на напряжения вэлементах иа на перемещения узлов 1 и 2. аРешено 3 варианта задачи: а1)а площадиа стержней 3, 5, 6, 8 имеют нижний предел;а 2) площади этих стержней фиксированы; 3) нижний предел площадей отсутствует.а аа
ааДано сравнение решений, которые были получены в вариантах 1, 2, 3, са известным решением, приведенным ав монографииа Э. Xoга и Я. Ароры Прикладное оптимальное проектирование: Механические системы и конструкции. Точность результатов оценивалась по невязкам ограничений при условии, что они нормированы к единице.
В варианте 1 устойчивую работу показал метод деформируемого многогранника. В варианте 2 хорошая сходимость была полученаа методом деформируемого многогранника с переходом на метод Ньютона, что обеспечило получение результатов высокой точности. В оптимальном проекте варианта 3 площади стержней 3, 5, 6, 8 стремились к нулю (ферма близка к статически определимой). Невязки в активных ограничениях при этом были несколько выше. Сходимость к решению заданной точности (10-4), таким образом, не была достигнута, и итерационный процесс был остановлен по максимальному числу итераций (20). Метод Ньютона в этом варианте не показал сходимости, т.к. функция Fp была не выпукла по ряду переменных даже вблизи оптимума.
Таблица 2. Сравнение результатов расчетов |
||||||
Вариант 1 |
Вариант 2 |
Вариант 3 |
Э. Xoг, Я. Арора |
|||
Значение целевой функции (м3) |
||||||
0,82340573 |
0,82311129 |
0,81689703 |
0,8294476 |
|||
Максимальные невязки ограничений |
||||||
0,23601010-3 |
0,61839410-12 |
0,47482310-3 |
0,2710-4 |
|||
Число итерций |
||||||
7 |
6 |
20 |
15 |
|||
В целом, сравнивая результаты варианта 2 с решением, приведенным в монографии аЭ. Xoга и Я. Ароры, аследует отметить, что метод Ньютона в данной задаче дал большую точность в невязках ограничений при более низкома значении целевой функции (на 0,77%). Число итераций алгоритма здесь также самое низкое.
- Оптимизация консольной пластины
 Приведено сопоставление решений задачи оптимизации консольной пластины (рис. 5), выполненных в ПК ANSYSMechanicalи в ПК РОСК. аВарьировались значения полутолщин в четырех сечениях пластины. Были приняты ограничения по напряжениям и на максимальное перемещение точек пластины. Минимизировался её объем.а
Приведено сопоставление решений задачи оптимизации консольной пластины (рис. 5), выполненных в ПК ANSYSMechanicalи в ПК РОСК. аВарьировались значения полутолщин в четырех сечениях пластины. Были приняты ограничения по напряжениям и на максимальное перемещение точек пластины. Минимизировался её объем.а
а
Рис. 5.а Оптимизируемая консольная пластина
ааВ ПК ANSYS конструкция рассчитывалась как пластина, работающая в условиях плоского напряженного состояния (к расчету была взята верхняя ее часть).а КЭ схема моделировалась плоскимиа четырехузловыми элементами, что позволило получить хорошее приближение в задаче анализа на достаточно разряженной сетке (было использовано 16 элементов). а
С помощью ПК РОСКа задача была решена в нескольких вариантах.а
Вариант 1.аа Расчетная схема принята в виде стержня переменного сечения. Так как размеры сечения на порядок меньше длины консоли, то это решение в дальнейшем рассматривается как точное.
Вариант 2.а Расчетная схема принята в виде консольной пластиныа ломаного очертания, работающей в условиях плоского напряженного состояния с треугольной КЭ сеткой, имеющей шаг а2?192.а Погрешность в решении задачи анализа в перемещениях при этом составилаа 14%. На рис. 6 показана сходимость алгоритма с 2-х начальных проектов на всех поисковых итерациях (рис. 6,а) и в более крупном масштабе на последних четырех (рис. 6,б).
![]()
![]()

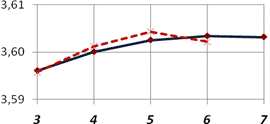
Рис. 6.а Изменение целевой функции на итерациях са двух начальных проектов (вариант 2)
ааИспользование густой КЭ сетки в этом варианте привело к достаточно громоздким вычислениям в задаче анализа, решение которой занимало основное время счета.а С этой точки зрения существенным показателем эффективности алгоритма явилось число обращений к функции ограничений, вычисление которой включало КЭ расчет. В вариантах 1,2 число таких обращений составило от 320 до 425. Сокращения вычислений при решении подобных задач можно добиться, если ослабить требование к точности в невязках ограничений, например, до 1% (оптимальное решение при этом абудет получено уже на 2-3 итерации), либо использовать режим построения аппроксимаций.
| Страницы: | 1 | 2 | 3 | |
 Авторефераты по всем темам >>
Авторефераты по техническим наукам
Авторефераты по всем темам >>
Авторефераты по техническим наукам

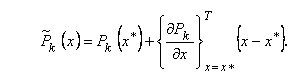
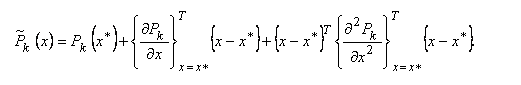
 аа
аа 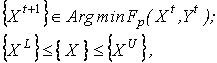
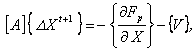
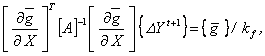
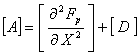 ,
,