Авторефераты по всем темам  >>  Авторефераты по геологии-минералогии

Методы количественной оценки перспектив нефтегазоносности (на примере седиментационных бассейнов Сибири)

Автореферат докторской диссертации по геологии-минералогии

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 | 4 | 5 | 6 |

 

Приведенные зависимости однозначно указывают на устойчивую связь между индексом успешности и плотностью ресурсов. Подобные зависимости можно получить и для других НТК ЗСНГП. В тех случаях, когда удается установить зависимость индекса успешности от каких-либо картируемых геологических параметров, данные соотношения могут быть использованы для прогноза плотности ресурсов на сравнительно менее изученной части НТК.

Для учета влияния совокупности прогностических параметров на вероятность положительного результата при испытаниях может быть применена комбинация анализа условных вероятностей и линейного дискриминантного анализа (Галкин, 1992; Галкин и др., 1997; Харбух, Давтон, Дэвис, 1981; Rastirolla et al., 2003).

Логарифм индекса успешности

Рис.

. 7. Зависимость логарифма плотности начальных геологических ресурсов от логарифма вероятности успеха при поисково-разведочном бурении.

Нижнемеловые НГК ЗСНГП. Например, для верхнеюрского (васюганского) НГК юго-востока Западной Сибири по данным о более чем 1100 поисково-разведочных скважинах удалось выявить частные зависимости успешности поисково-разведочного бурения от геологических характеристик разреза. Некоторые из полученных результатов этого анализа представлены на рис. 8-9 (см. вкл.).

24

Наилучшее разделение скважин на продуктивные и остальные обеспечила следующая дискриминантная функция (параметры значимы с доверительной вероятностью не ниже 0.95):

/= -0.461 + 0.0184 ж Xl+ 0.0265 -х2- 0.0074 -х,+ 0.00086 -х4-а (2?)

-0.00059-х5+0.0130-х6-0.00033-х7+0.00296-х8.

Здесь Ху - суммарные толщины песчаных пачек К^ и К^ (м), х2 -оценка возможных масштабов аккумуляции (у.е.), х3 - толщины глин подстилающих баженовскую свиту (георгиевская свита) (м), х4 -расстояние до ближайшего гипсометрического максимума (у.е.), х5 -абсолютные отметки подошвы баженовской свиты (м), х6 - структурные остатки по подошве баженовской свиты (м), х7 -абсолютные отметки подошвы мезозойского чехла (м), х8 -толщины нижневасюганской подсвиты (м).

Процедура анализа условных вероятностей реализовывалась для комплексного параметра, совпадающего со значением дискриминантной функции.

Аналогичным образом для среднеюрского НГК юго-восточных районов Западно-Сибирского бассейна, по данным о более чем 730 скважинах наилучшее их разделение на продуктивные и не давшие промышленного притока УВ обеспечила следующая дискриминантная функция (параметры значимы с доверительной вероятностью не ниже 0.85):

/ = 0.815 + 0.00455 ж хх -0.00519 ж х2 -0.179 ж х, +а (2g)

+ 0.00234-х4-0.00204-х5.

Здесь хх - суммарные толщины песчаников среднеюрского НГК (м), х2 - суммарные толщины верхневасюганской подсвиты (м), х3 - современный средний температурный градиент (С/100 м), х4 - структурные остатки по подошве нижневасюганской подсвиты, х5 - толщины баженовской свиты (м).

Далее, как и для верхнеюрского НГК, реализовывалась процедура условного анализа для одной переменной.

Следует отметить, что все многообразие возможных зависимостей индекса успешности от геологических характеристик (примеры на рис. 8-9) не может быть описано на основе введения комплексного параметра в виде линейной дискриминантной функции Фишера. Однако для довольно широкого класса ситуаций, когда геолого-геофизические параметры, влияющие на вероятность успеха испытаний, взаимно независимы, данная проблема может быть решена. Случай частично зависимых параметров может быть сведен к рассматриваемому ниже с помощью специальных процедур (например, факторного анализа). Излагаемый ниже подход был развит автором совместно с Л.С. Грековой и И.В. Жилиной (2006).

Под взаимной независимостью параметров хну будем понимать, независимость вероятности р появления пары любых их допустимых значений как для любой точки всего исследуемого НГК, так и для всех

25

входящих в эталонную выборку скважин, для которых известен результат испытания:

р(х,у) = р(х)-р(у), p{x,y\q) = p{x\q)-p{y\q).(29)

Здесь q - результат испытания, принимающий значения 0 или 1.

Выполнение условий (29) для пар переменных может быть проверено с использованием критерия ? (Неймана-Пирсона) (Дэвис, 1990; Крамер, 1975). Используя формулу Байеса (Корн Г., Корн Т., 1984) можно показать, что для любого числа TV независимых в этом смысле параметров условная вероятность результата испытания факторизуется:

p(q\xv...,xN) = p{q\xl)-...-p(qI xN) -(p(q))^Nж(30)

Выражение (30) позволяет существенно облегчить проведение условного анализа. В частности, для анализа влияния на результаты испытаний двух независимых переменных можно использовать не полностью пересекающиеся эталонные выборки. Сходная по идеологии методика построения прогнозных карт для некоторых видов минерального сырья, но с использованием аппарата нечетких множеств была описана в работах (Ткачев, Амосов, 2003; Qiuming, Agterberg, 1999). Определение всякого рода нечетких объектов неизбежно содержит существенные элементы экспертизы, что, с нашей точки зрения, вносит избыточный произвол в процедуру прогноза и неоправданно ее усложняет.

Как и выше, рассмотрим в качестве примера прогноз успешности испытаний в верхнеюрском и среднеюрском нефтегазоносных комплексах юго-востока Западно-Сибирской нефтегазоносной провинции. При анализе вероятности успеха использовалась та же, что и в первом случае, база данных.

Далее приведен аналитический вид зависимости вероятности успеха от некоторых конкретных прогностических параметров. Вид зависимостей выбирался с учетом естественных формальных (0<р<1) и физических ограничений.

Верхнеюрский НГК.

p{qI х) = ехр(-0.057 ж х-0.874),

х - толщины аргиллитов георгиевской свиты (м);

р(#1х) = ехр(-8.16-х2+8.52-х-3.03),

х - коэффициент песчанистости горизонта Ю] (доли единицы);

p{qI х) = 0.423 - 0.555 /(1 + ехр((х- 0.922) /1.04)),

х - натуральный логарифм нормированной оценки масштабов аккумуляции (условные единицы);

p{qI х) = 0.51-25.51/(1 + ехр((х + 23.34) /5.44)),

х-суммарные толщины песчаных пачек Ю] иЮ]а (м).

26

Среднеюрский НГК

p(q\x) =0.148 + (0.059-0.148) /(1 + ехр((х-43.5)/3.05)),

х - общие толщины песчаников верхнетюменской подсвиты (м);

М#1х) = ехр(-1.819 + (1.819-3.024)/(1 + ехр((х-19.5)/4.0))),

х - толщины нижневасюганской подсвиты (м);

p{qI х) = ехр(0.0304 + (0.1834-0.0304) /(1 + ехр((х- 68.52)/9.03))),

х - толщины васюганской свиты (м);

p(q I х) = ехр(-0.628-(1п(х + 0.001))2 + 6.834 -1п(х + 0.001) -20.59),

х - суммарные толщины нижне- и среднеюрских отложений (м).

На основе полученных частных зависимостей, карт входящих в них геологических параметров и с учетом соотношения (30) были построены карты успешности поисково-разведочного бурения, примеры которых приведены на рис. 10, 11 (см. вкл.). Карты прогноза успешности могут использоваться самостоятельно при планировании поисково-разведочных работ. Использование зависимостей между успешностью поисково-разведочного бурения и плотностью ресурсов или более точных зависимостей, которые теоретически можно построить на основе статистики о геометрической форме скоплений, характерной для целевого комплекса, позволяет перейти от карт индекса успешности к картам плотности ресурсов. В рассматриваемом подходе локальную плотность ресурсов естественно рассматривать как еще одну форму меры успешности поисково-разведочного бурения.

Основным достоинством рассматриваемого подхода является возможность придания операционного смысла понятию локальная плотность ресурсов. Что в свою очередь позволяет выполнять оценки участков территории произвольной формы. Последнее существенно при решении задач геолого-экономической оценки при лицензировании недр. Метод прогноза перспектив нефтегазоносности на основе анализа условной вероятности успеха при поисково-разведочном бурении может быть хорошим дополнением или в ряде случаев альтернативой традиционным вариантам метода внутренних аналогий.

В главе 5 построен комплекс эмпирических прогностических моделей, обоснована методика количественного прогноза нефтегазоносности сравнительно хорошо изученных объектов ранга НГК на основе связи успешности поисково-разведочного бурения с плотностью начальных суммарных ресурсов и с использованием аппарата анализа условных вероятностей, что и представляет собой шестой и седьмой защищаемые результаты.

27

Глава 6. Прогноз уникальных и крупных скоплений углеводородов в нефтегазоносных системах различного масштаба

Анализа закономерностей локализации гигантских месторождений нефти и газа играет большую роль в теоретической и прикладной геологии нефти и газа. Их освоение обеспечивает наибольшую эффективность геологоразведочных работ, с ними связана большая часть разведанных на сегодняшний день запасов углеводородного сырья и объемов его добычи в мире.

Проблеме прогноза крупнейших скоплений посвящено значительное число работ отечественных и зарубежных специалистов (Вышемирский и др., 1971; Нестеров и др., 1975; Конторович, Демин, 1979; Конторович и др., 1981; Краснов, 1980; Белонин, 1982, 1997; Шпильман, 1982; Лившиц, 2003; Klemme, 1983 и др.). Обстоятельные сводки по этой проблеме с 70-х годов прошлого века публикуются под редакцией М.Т. Хэлбути (1970, 1980, 1992, 2003).

Наиболее общий подход к вероятностному прогнозу количества месторождений в определенных классах крупности основан на анализе их распределения по величине запасов (Шпильман, 1972, 1982; Конторович, Демин, 1977, 1979; Конторович, Лившиц, 1988; Лившиц, 2003, 2004). Подход имеет некоторые ограничения. Оценки, полученные на его основе, будут локализованы с точностью до размеров нефтегазоносной системы, а параметры распределения скоплений УВ по величине запасов наиболее надежно определяются по информации об уже открытых, как правило, самых крупных скоплениях в системе.

Альтернативой для получения локализованных оценок числа крупнейших скоплений и их размеров является подход на основе анализа стохастических зависимостей величин скоплений УВ от характеристик нефтегазоносной системы. Соответствующая группа методов разрабатывалась АЭ. Конторовичем, О.С. Красновым (1980, 1984), В.И. Шпильманом (1982) и в наиболее законченной форме М.Д. Белониным (1982, 1997).

Для случаев, когда есть основания предполагать, что в нефтегазоносной системе выявлено достаточно большое число скоплений известно несколько методик оценки параметров УРП (Конторович, Демин, 1977; Лившиц, 2003, 2004). Хотя при современном развитии компьютерной техники реализация этих методик не представляет больших проблем, для практического применения при оперативных оценках можно воспользоваться более простым и наглядным подходом.

Введем понятие ненормированной интегральной функции распределения, равной числу скоплений, размеры которых превосходят величину ?'-

?(?) = ?- ]з{x)dx.

в

28

Будемаа считать,аа чтоаа выявлено,аа поаа крайнейа мере,аа таа крупнейших скоплений - 0 > 0 > ... > 0 .

Исходяаа изаа смысл функции ?(?),аа ясно,аа чтоаа еслиаа природная

совокупность скоплений описывается УРП, то существуют такие параметры ,аа 0 иаа jV,аа ааприа которыха значениеа ненормированной интегральной

функции распределения от величины г'-го скопления близко к его номеру г:

0(0; )~i, i = l...m.

Тогдаа задачуа отыскания ,аа 0 иаа ??аа можноаа свестиа ка обычной минимизации суммы квадратов отклонений:

(31)

Х(Ф^;-if-min.

Поиск параметров распределения формально можно выполнить по любому поднабору из т (ш>3) крупнейших выявленных скоплений. В рамках описываемого подхода нет необходимости знать величину начальных ресурсов Q. При известных параметрах , 0а и N она может быть оценена

с использованием выражения (3). Однако на практике ее независимая оценка часто позволяет регуляризовать полученные результаты.

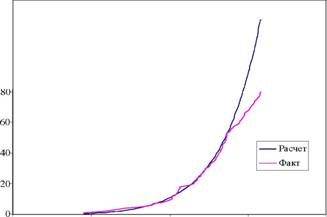
На основе предложенной методики был выполнен многовариантный прогноз возможного количества крупных и уникальных месторождений нефти и газа для Западно-Сибирской нефтегазоносной провинции. Примеры фактической и модельной ненормированных интегральных функций распределения приведены на рис. 12, 13.

120т

1а 0Л 0.01

Запасы месторождения, (у.е.)

Рис. 12. Эмпирическое и расчетное ненормированные интегральные распределения месторождений нефти ЗСНГП по запасам.

29

120

100-

140

100

10аа 1а 0Л

Запасы месторождения, (трлн м3)

0.01

Рис. 13. Эмпирическое и расчетное ненормированные интегральные распределения месторождений газа ЗСНГП по запасам.

В вариантах, давших наилучшее соответствие фактической и модельной функций распределения без учета соответствия оценок ресурсов, можно ожидать выявления не более 2 крупных и уникальных месторождений нефти, и не более 43 крупных (из них не более 1 уникального) месторождения газа. При этом оценка извлекаемых ресурсов нефти ЗСНГП оказывается на 17% выше официально принятой, а газа на 40% ниже. В вариантах, в которых прогнозируемая оценка начальных извлекаемых ресурсов нефти ближе всего к принятой, число прогнозируемых невыявленных месторождений минимально.

Естественно, полученные результаты следует рассматривать как рамочные, накладывающие лишь самые общие ограничения на результаты локализованного прогноза.

Для прогноза количества и величины месторождений нефти и газа в единицах нефтегазогеологического районирования ранга области или района подход на основе анализа распределения по крупности применим не всегда. Часто методически проще построить статистические зависимости для размеров и-го месторождения или числа месторождений определенного размера.

Из общих соображений ясно, что на количество и размеры месторождений в единице нефтегазоносного районирования любого ранга должны влиять и плотность и величина начальных ресурсов (Белонин, 1997). Поиск зависимости величин месторождений в каком-либо нефтегазоносном объектеа следуета вести ота величины ресурсова и иха плотности или,а что

30

эквивалентно, от величины ресурсов и размеров объекта. В качестве размеров объекта может быть использована площадь или объем осадков в его пределах. Продемонстрируем этот подход на примере нефтегазоносных районов ЗСНГП.

В соответствии с принятым при оценке перспектив нефтегазоносности по состоянию на 01.01.2002 г. нефтегазогеологическим районированием на территории ЗСНГП выделены 61 НГР и 3 самостоятельных НТО, в пределах которых НГР еще не выделены.

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 | 4 | 5 | 6 |

     Авторефераты по всем темам  >>  Авторефераты по геологии-минералогии