Авторефераты по всем темам  >>  Авторефераты по геологии-минералогии

Методы количественной оценки перспектив нефтегазоносности (на примере седиментационных бассейнов Сибири)

Автореферат докторской диссертации по геологии-минералогии

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 | 4 | 5 | 6 |

 

После стандартной замены переменных w = {k1lk4)-Qa,u = {k2lk4)-Qm,v = {k2lkl)-Qk,T = k4-t,a = k4lkl,

P = k5lkv ?= к6/к2^=к4/к7,?= {к2 ж /)/(&! ж к4)

система (1) примет вид:

dwсаа dudvДfj\

?----- = Чw+ о -и,а------- = Чи + v-и,Ч = ЧV Ч v-и + р -u + ?.\?)

??????

Исследование фазового портрета системы (2) стандартными методами (Амелькин, 1987; Арнольд, 2000) в предположении ее автономности показывает, что она имеет два стационарных решения:

{w0=S, и0=0, ?0=?}; {w0=S, Ug=S{<p-l)/(l-fi), vД=l}.

При значениях управляющего параметра ?<\ первый стационар (узел) устойчив, т.е. является аттрактором, и расположен на границе физически допустимых решений, второй стационар (седло) неустойчив и расположен в физически запрещенной части фазовой плоскости. Следовательно, если параметр ? имеет значение ниже критического ?=\, система при любых начальных условиях будет стремиться к состоянию с фиксированной положительной массой немигрантоспособных, рассеянных в коллекторах УВ и нулевой массой мигрантоспособных и аккумулированных УВ.

При переходе через критическое значение физический смысл имеют оба стационара, но первый из них теряет устойчивость (превращается в седло), а второй приобретает (фокус) и становится аттрактором. Характер поведения системы меняется. При начальном состоянии с суммарной массой УВ, близкой к нулю, в системе некоторое время будет происходить накопление немигрантоспособных УВ, а лишь затем, при достижении окрестности первого стационара процессы вторичной миграции и аккумуляции интенсифицируются, и величины w и и (и соответствующие им Qaи Qm) станут возрастать. При этом величина v (соответствующая Qk) будет уменьшаться до стационарного значения. Фазовые портреты системы в координатах и и v при разных значениях управляющего параметра ? представлены на рис. 1.

Анализ системы (2) показывает, что малые неконтролируемые вариации начальных условий могут приводить к существенным временным сдвигам в фазовом портрете тождественных в остальном систем. Этим обстоятельством, наряду с другими факторами, может объясняться

значительный разброс в наблюдаемых плотностях ресурсов, близких по своим характеристикам НГС, что в свою очередь может привести к плохо устранимым погрешностям прогноза при использовании упрощенных моделей, параметры которых определяются на основе эмпирических данных.

Рис. 1. Фазовые портреты нефтегазоносной системы при различных значениях управнляющего параметра: (а) ? = 0.2;(б) ? = 0.6;(в) ? = 0.99;(г) ? = \5;{?)? = 3.0;(е) ? = 5.0.

Из графиков на рис. 1 видно, что при некоторых значениях параметров и начальных условий в системе возможны затухающие колебания масс УВ. Возникновение осцилляции связано с нелинейностью системы и характером второго, основного стационара - устойчивого фокуса.

Выше предполагалась автономность системы (1) и постоянство входного сигнала - интенсивности эмиграции. Естественно, в реальных системах это условие в общем случае не выполняется. Интересно выяснить, в какой мере на поведении системы скажется отказ от условия стационарности. Интенсивность процессов генерации зависит от температурного режима и динамики погружения нефтематеринских толщ (Конторович, 1978; Тиссо, Велте, 1981). Достаточно реалистичным выглядит сценарий, при котором интенсивность процессов эмиграции сначала плавно возрастает, а затем уменьшается до нуля, что соответствует равномерному или затухающему погружению единственной нефтематеринской толщи. Трехмерный фазовый портрет системы и зависимости от времени массы УВ в различных формах, приведены на рис. 2. Количество УВ в системе во всех формах имеет два максимума, при одном максимуме управляющего параметра - интенсивности эмиграции.

9

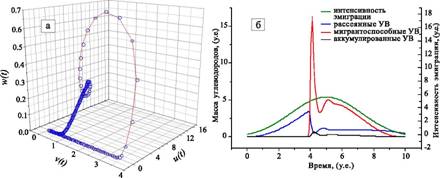
Рис. 2. Фазовый портрет нефтегазоносной системы (а) и временные зависимости фазовых переменных (б) при одномодальном изменении управляющего параметра.

При более сложном поведении управляющего параметра, соответствующем неравномерному погружению с периодическими инверсиями, количество мигрирующих и аккумулированных УВ в системе изменяется практически синхронно и с некоторым сдвигом по фазе по отношению к интенсивности эмиграции и количеству рассеянных УВ. Квазициклический характер поведения системы, проявлявшийся для постоянной и одномодальной функций интенсивности эмиграции, нивелируется за счет влияния периодической компоненты в управляющем параметре. В то же время сохраняется основной эффект, связанный с учетом возможной нелинейности процессов нафтидогенеза - процессы миграции и аккумуляции в системе не протекают, пока не накоплена некоторая критическая масса рассеянных УВ.

Таким образом, материалы главы 1, изложенные выше обосновывают первое из защищаемых положений.

Одной из надежно установленных в геологии нефти и газа количественных закономерностей является закон распределения скоплений УВ по крупности. Закон распределения для месторождений УВ изучался многими специалистами (Arps, Roberts, 1958; Kaufman, 1963; Шпильман, 1972, 1982; Буялов и др., 1975; Конторович и др., 1977, 1979, 1980, 1986, 1988, 1989; Лившиц, 2004; Харбух, Давтон, Дэвис, 1982; Крылов, 2009; и др.). Продолжительное время преобладала точка зрения о логарифмически нормальном законе распределения скоплений УВ по крупности. В.И. Шпильман (1972) показал, что логарифмически нормальный закон справедлив только для совокупностей выявленных скоплений УВ. Для описания РСК в природных системах им бьшо предложено использовать амодальный закон распределения с функцией плотности вероятности вида -?[?) = ?0??2 (? - запасы скопления УВ; ?0 - запасы минимального учитываемого скопления).

10

А.Э. Конторовичем и В.И. Деминым (1977, 1979) на основе эмпирического анализа данных по хорошо изученным бассейнам России и Северной Америки, была развита теория анализа РСК при произвольном виде этого распределения сформулированы общие ограничения на вид функции плотности вероятности и предложено аппроксимировать РСК усеченным распределением Парето:

?(?)=?^-(?-?)-(?-?-?-^)?(?-?^ + ?0-(?-?-(?^??0)?)).О)

Здесь бЦх - максимально возможные размеры скопления УВ. Выражение (3) обобщает классическое распределение Парето и стремится к нему при вщас->со.

Отметим, что сходные идеи об ограничениях на вид функции плотности вероятности в общем виде высказывал и В.И. Шпильман (1982).

Природа формирования РСК для УВ и иных полезных ископаемых анализировались в работах (Булкин, Неженский, 1981; Харбух, Давтон, Дэвис, 1982; Конторович и др., 1988; и др.) Анализ механизмов или общих принципов, приводящих к распределению объектов по классическому распределению Парето, можно найти в работах (Шрейдер, 1963; Яблонский, 1986; Федер, 1991; и др.). К сожалению, эти модели исходят из общих, часто физически не очевидных принципов и, как следствие, не дают возможности связать характеристики нефтегазоносной системы с параметрами РСК.

Естественно рассматривать запасы ? юбого скопления УВ в НГС как следствие процессов аккумуляции и диссипации. В первом приближении изменения величины ? во времени можно представить в виде уравнения:

^- = а-Ъв.(4)

dt

Здесь t - время, а - скорость поступления УВ в ловушку, Ъ -относительная скорость разрушения скопления.

Скорость поступления УВ в ловушку и относительная скорость

диссипации УВ из ловушки могут интерпретироваться как случайные

величины (Конторович, 1976; Вистелиус, 1980). Для достаточно длительных

этапов развития устойчиво погружающихся нефтегазоносных систем можно

допустить, что а и Ъ для конкретного скопления не зависят от времени. Тогда

решение уравнения (4), при условии б^0)=0, описывает динамику изменения

величины запасов единичного скопления УВ на этапе его формирования

после начала активной аккумуляции: ? = (аIЬ) ж (\- е~ы).(5)

При достаточной длительности процессов нафтидогенеза, размеры

скопления ? могут достичь стационара - предельно достижимой (при

фиксированных anb) величины ?: ??Idt = 0 , ? = albж(6)

После завершения процессов аккумуляции изменение размеров

скопления будет происходить по закону: в = (а1Ъ) е~ы ж(7)

11

При статистически независимых а и Ъ, и достижении стационарности (6) для плотности вероятности РСК ?(?) можно получить:

?(?) = Ч?\?2(?)-?^)-?-??.(8)

Здесь ?? - область интегрирования, зависящая от ?; ?2{?) и ?,?) -

плотности вероятности для распределений скоплений УВ в системе по скоростям аккумуляции и относительным скоростям диссипации.

В частном случае, когда параметры а и Ъ равномерно распределены на конечных интервалах [а^, ашях] и [Ь^, Ьшях], из (8) легко получить явный вид плотностиа ?(?). При достаточно больших ^ (^>max(andn/fcndll,iiniax/fcmax))

модельная плотность вероятности тождественна УРП (3) с показателем Я=2. Естественно, трудно ожидать, что в реальных системах параметры а и Ъ будут распределяться равномерно. Однако численное моделирование вида функцииа ?{?)аа при различных формах^ (д)аа иа зJb)аа показывает, что для

широкого спектра форм распределения <р2(а) и зJb)а УРП апроксимирует

правые хвосты полученных модельных распределений с очень высокой точностью.

Модельные РСК могут быть и амодальными, и унимодальными. В общем случае характер поведения модельных распределений на левом хвосте (то есть, в области мелких и мельчайших скоплений) отличается от характера его поведения на правом хвосте в сторону уменьшения доли скоплений по сравнению с УРП. Естественно, это обстоятельство существенно, только если изменение наблюдается для значений ?>?0.

Для анализа влияния времени на форму РСК была построена серия специальных модельных распределений. Принималось, что эволюция размеров каждого скопления происходит до момента времени г=100 у.е. и состояния, близкого к стационарному (6), затем аккумуляция прекращается и начинается распад сформировавшихся скоплений по закону (7). Для полученных модельных распределений правые хвосты аппроксимировались УРП для оценки параметра Я. Пример зависимости параметра Я от времени с начала интенсивной аккумуляции для одного из модельных распределений представлен на рис. 3.

Картина изменения параметра Я, представленная на рис. 3, качественно сохраняется при любых правдоподобных формах распределений параметров а и Ъ. Косвенное подтверждение этой закономерности можно получить, сравнив значения параметра Я для совокупностей месторождений в бассейнах или нефтегазоносных комплексах с различным преимущественным возрастом осадочного выполнения.

12

20

40

60а 100

t, (ye.)

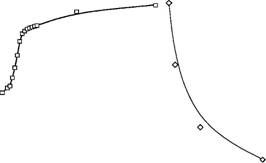
Рис. 3. Зависимость параметра от времени с начала интенсивной аккумуляции. На рис. 4 оценки значений параметра ? (Конторович, Демин, 1979) для совокупностей нефтяных месторождений в 18 СБ Северной Америки сопоставлены с преимущественным возрастом их осадочного выполнения. Параметр ? минимален для кайнозойских и мезо-кайнозойских бассейнов, возрастает для мезозойских и несколько снижается для палеозойских. Очевидно качественное совпадение наблюдаемой закономерности с полученной на основе модельных построений. ?

2.5

2.3

Преимущественный возраст осадочного выполнения, Т Рис.аа 4.аа Параметраа аа дляаа бассейноваа саа преимущественноаа кайнозойским, мезозойско-кайнозойским, мезозойским и палеозойским возрастом осадочного выполнения.

Результатыаа анализ предложеннойаа модели, изложенныеаа выше, обосновывают второе, третье и четвертое защищаемые положения.

13

Глава 2. Оценка ресурсов углеводородов слабоизученных седиментационных бассейнов

При выполненииа количественнойаа оценкиа перспектив

нефтегазоносности на первых этапах геологоразведочных работ приходится иметь дело с объектами, характеристики которых определены с невысокой степенью точности. Чаще всего такими объектами являются седиментационные бассейны или их крупные части. Развитие теории и практики геологии нефти и газа показало, что их скопления естественным образом связаны с относительно крупными депрессиями со значительными объемами неметаморфизованных осадков, испытавших погружение на глубины, превосходящие некоторую критическую величину. Наиболее последовательно это положение выражено в учении о нефтегазоносных бассейнах (НГБ), развитом в трудах большой группы исследователей (И.О. Брод, Н.Б. Вассоевич, И.В. Высоцкий, А.Э. Конторович, М.С. Моделевский, В.А. Оленин, Б.А. Соколов, А.А. Трофимук, В.Е. Хаин и др.).

На этой основе возникла обширная группа методов, базирующихся на

наличии стохастических связей между величиной НГР УВ и некоторыми

характеристиками осадочного выполнения СБ или его крупных частей.

Элементы такого подхода к прогнозу НГР слабоизученных территорий

можно найти еще в работах Л.Г. Уикса (Weeks, 1949, 1950). Впервые СБ как

объект оценки был выделен М.Ф. Двали и Т.П. Дмитриевой (1976). Они же

предложили название лобъемно-статистический метод (ОСМ). Данный

подход к оценке НГР УВ крупных нефтегазоносных систем развивался в

основном в работах отечественных исследователей (А.А. Арбатов,

А.В. Кондаков, А.Э. Конторович, В.Д. Наливкин, М.С. Напольский,

И.И. Нестеров,аа М.С. Моделевский,аа А.А. Растегин,аа B.C. Резник,

А.А. Трофимук и др.). Наиболее последовательным критиком рассматриваемого подхода был Х.Д. Хедберг (1978).

Совершенствование ОСМ шло по пути расширения набора прогнозируемых величин и прогностических параметров, усложнения вида математических моделей прогноза. С одной стороны, усложнение математических моделей и увеличения числа учитываемых параметров требует увеличения объемов эталонных выборок и более детального описания геологического строения входящих в них СБ. С другой стороны, чем больше объем выборки, тем менее изученные СБ приходится в нее включать, тем ниже относительная точность анализируемых параметров и тем больше связанные с этим ошибки прогноза. В ряде работ функциональные преобразования прогностических параметров не учитывают характер их распределения, что приводит к завышению формальной точности полученных математических моделей. Все эти обстоятельства накладывают естественные ограничения на применение ОСМ.

В то же время при количественной оценке слабоизученных СБ подходы ОСМ не имеют альтернативы. Необходимость оценки величины

14

НГР УВ в условиях, когда об объекте оценки имеется лишь самая общая информация, вынуждает использовать для прогноза достаточно простые и максимально устойчивые в статистическом смысле зависимости и параметры. Анализ выборки из чуть менее 100 сравнительно хорошо изученных НГБ, для которых известны основные геометрические характеристики осадочного выполнения, его преимущественный возраст и относительно точные оценки НГР УВ, позволил построить серию прогностических моделей, в определенной мере учитывающих приведенные выше ограничения.

Для подвыборки, содержащей 38 бассейнов с преимущественно кайнозойским и мезозойско-кайнозойским возрастом осадочного выполнения, были получены следующее уравнения:

ln6 = 1.699 + 0.588-lntf-0.776-lnS+1.474-lnV, Я2 =0.581, <7 = 0.997,а (9)

InQ= 4.632 + 0.686-InV^, г =2.65, R2 =0.546, ? = 1.010. (Ю)

Здесь и ниже Q - начальные геологические ресурсы в млн т условных углеводородов (УУВ); V- объем осадочного выполнения в тыс. км ; S -площадь осадочного выполнения в тыс. км ; Я - мощность осадочного выполнения в км; Vef - эффективный объем осадочного выполнения в тыс. км ; ? - мощность неэффективного слоя пород в км; R - коэффициент детерминации; <т- стандартное остаточное отклонение величины In Q.

Для подвыборки, содержащей 33 бассейна с преимущественно мезозойским возрастом осадочного выполнения:

InQ = -1.197 ж In S + 2.257 -\nV, R2 = 0.872, ? = 0.693,аа (11)

In Q = 2.463 + 1.036- InVef, e = 23,R2= 0.873, ? = 0.689. (12)

Для подвыборки, содержащей 26 бассейнов с преимущественно палеозойским возрастом осадочного выполнения:

In Q = 1.727 ж In Я + 0.506 ж In S + 0.318 -In V, R2 = 0.88, ? = 0.593,а (13)

In Q = 4.168 + 0.809- In ?? ? = 3.3, Я2 = 0.846, ? = 0.657.а (14)

Для смешанной подвыборки, содержащей 71 бассейн с преимущественно кайнозойским или мезозойским возрастом осадочного выполнения:

In? = 0.665 ж InЯ-1.087-InS+ 1.965-In V, Я2 =0.729, ? = 0.886, (15)

??? = 3.766 + 0.844 ж lnV^, ? = 2.7, R2 = 0.711, ? = 0.908.аа (16)

Для смешанной подвыборки, содержащей 59 бассейнов с преимущественно мезозойским или палеозойским возрастом осадочного выполнения:

In Q = 1.069 ж In Я + 0.943 -lnV, Я2 = 0.853, ? = 0.690,а (17)

??? = 3.163 + 0.947 ж In У., ? = 2.8,tf2 = 0.858, ? = 0.679.а (18)

15

И, наконец, для объединенной выборки, содержащей 98 бассейнов разного возраста, были получены следующее уравнения:

??? = 0.717 + 1.25 -lntf+ 0.841-lnV- 0.191 T,R2 =0.725, ? = 0.875, (19)

??? = 3.955 + 0.823 ж In Ve/, f = 3.0,tf2 = 0.725, ? = 0.882.а (20)

Здесь и ниже Г - индекс преимущественного возраста осадочного выполнения, принимающий следующие значения: 1 - для СБ с преимущественно кайнозойским, 2 - преимущественно мезозойским и 3 -преимущественно палеозойским возрастами осадочного выполнения.

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 | 4 | 5 | 6 |

     Авторефераты по всем темам  >>  Авторефераты по геологии-минералогии