«злп и Динамическое программирование» Методы, используемые в состояниях определенности, неопределенности, риска, конфликта

Вид материала

Документы

Подобный материал:

• Рабочей программы дисциплины «Экономико-математические методы» (наименование) по направлению, 26.59kb.
• Программа профилирующей дисциплины "теория игр и исследование операций" Содержание, 69.55kb.
• Особенности преподавания элементов теории риска на экономических специальностях вузов, 48.21kb.
• Аттестационное тестирование в сфере профессионального образования, 72.49kb.
• Татьяна Георгиевна Шешукова. Молодые ученые разрабатывают методы наблюдения и анализируют, 6.61kb.
• Формы и методы индивидуальной и профилактической работы, используемые социальным педагогом, 61.33kb.
• Оценка инвестиционного проекта в условиях неопределенности и риска, 113.02kb.
• Примерная тематика рефератов (курсовых работ), 10.16kb.
• Курс является базовым как для изучения других математических дисциплин, так и для более, 36.89kb.
• Программа вступительного экзамена по специальности 05. 13. 18 Математическое моделирование,, 115.33kb.

Коллоквиум 7

«ЗЛП и Динамическое программирование»


Методы, используемые в состояниях определенности, неопределенности, риска, конфликта:

1. Качества работы системы по ее результатам и затратам.
   
2. Отношений (функционального или конструктивного), т.е. зависимостей между построением системы и ее результатом.
   

Для первого используют методы:

Состояние определенности

1. прямой расчет, если количество исходов может ≤ 2.;
   
2. методы математического моделирования функционирования экономической системы при условии, когда количество исходов > 2, и нужно выбрать тот способ функционирования системы, когда результата будет наилучшим, используя методы линейного, нелинейного, параметрического, целочисленного и динамического программирования.
   

Если это линейное программирование, то зависимость в ЦФ линейная. Сначала фиксируются значения ограничений и выбираются из всеч значений максимальные. Затем меняется одно из значений ограничений и т.д. Полеченные значения минимума или максимума представляют либо в графическом виде, либо в виде вектора.

График-интерполяция. Графики либо совмещают между собой и в поле пересечения находят значения ограничений, при которых функция устойчива.

Имитационное моделирование.

Метод двойного дифференцирования.

F*max=ЗЛП d(d( I ( ЗЛП))).

Получаем вектор точек и опять находим максимум или минимум.

Метод параметрического программирования отличается от метода линейного/ нелинейного программирования только тем, что в ограничения и в ЦФ вносятся коррективы на время.










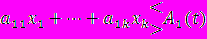
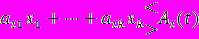
Динамическое программирование:





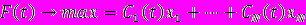
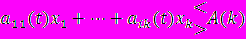
вычисляются a₁₁(t)=f₁(t), …, a_1k(t)=f_k(t).


Метод имитационного программирования использует различные математические методы по определению технологии, связанные с имитацией реального состояния экономической системы с учетом воздействующих на нее факторов.

Математико-статистическое моделирование – это моделирование функционирования системы с использованием математических методов (любых) при учете воздействия внешних и внутренних возмущений на результаты работы системы. То есть, производственная функция объекта (системы) строится с учетом (статистическим) наличия внутренних и внешних факторов, влияющих на устойчивое функционирование объекта (системы). Наиболее применительные методы статистического моделирования: метод Монте-Карло, метод Марковских сетей (деревьев).



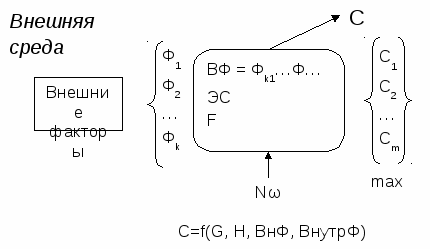
Цель:

1)определить зависимость С от внешних факторов;

2) построить статистические ряды внешних и внутренних факторов и связать их с выборкой общественных благ.

Классический подход

Факторный анализ: выявляют те факторы, которые непосредственно связаны с максимальной функцией;

Корреляционный анализ: минимизирует множество влияющих факторов. Определяют пары факторов, которые связаны между собой;

Дисперсионный анализ: позволяют описать функцию, по которой меняются значения факторов