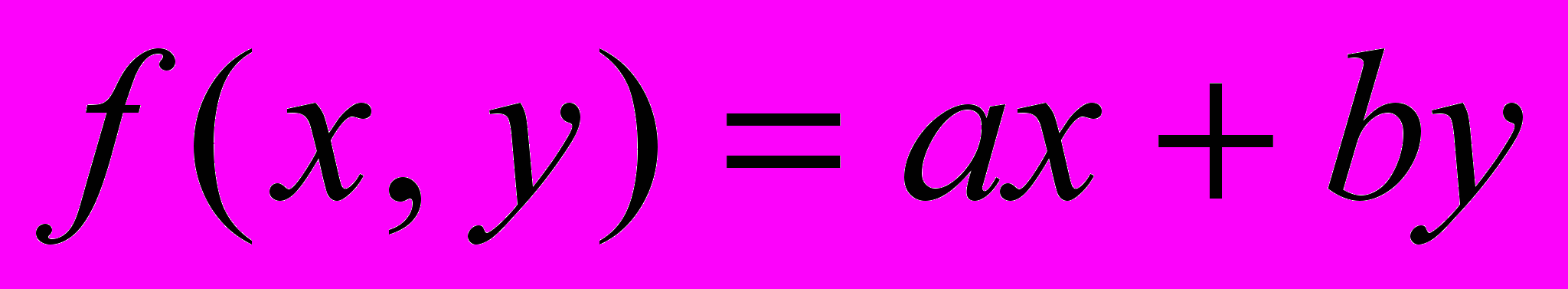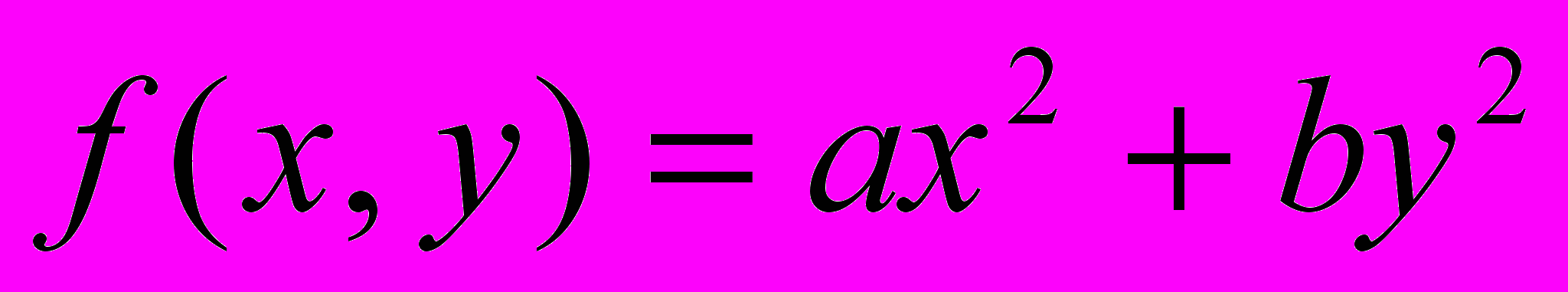I. Пояснительная записка Требования к студентам
| Вид материала | Пояснительная записка |
СодержаниеII. Содержание программы III. Тематика Темы семинарских занятий Базовый учебник Основная литература Дополнительная литература |
- Пояснительная записка Требования к студентам: Учебная, 146.96kb.
- Пояснительная записка Требования к студентам, 653.17kb.
- Пояснительная записка 1 Требования к студентам, 264.49kb.
- Пояснительная записка 1 Требования к студентам, 237.35kb.
- Пояснительная записка 1 Требования к студентам, 232.02kb.
- Пояснительная записка Автор программы : д э. н., профессор Дыбская Валентина Владимировна, 101.31kb.
- Пояснительная записка Автор программы: к э. н., доцент Проценко Инга Олеговна. Требования, 113.29kb.
- Пояснительная записка Автор программы: доцент кафедры теории права и сравнительного, 340.95kb.
- Пояснительная записка Требования к студентам, 139.5kb.
- Пояснительная записка. Требования к студентам, 336.56kb.

I. Пояснительная записка
Требования к студентам: Учебная дисциплина «Исследование операций» в менеджменте (3-й – 4-й модули второго курса) использует материал предшествующих ей дисциплин «Высшая математика» для менеджеров и «Теория вероятностей и математическая статистика» для менеджеров учебного плана факультета Менеджмента.
Аннотация: Дисциплина вводит студентов в круг понятий исследования операций – науки, доказавшей свою полезность в анализе социально - экономических явлений и ситуаций, в управлении социально – экономическими системами и процессами, при принятии организационных и производственных решений. Программа учебной дисциплины содержит как основные математические разделы – например, элементы теории графов, линейное и выпуклое программирование, динамическое программирование, многокритериальную оптимизацию, оптимальное управление, игры, так и прикладные разделы, которые необходимы современному менеджеру для профессиональной работы. Внимание в курсе сосредоточено на математических определениях понятий и на описании математических моделей наиболее важных типовых операций, которые реализует ЛПР – лицо, принимающее решение. Основные математические результаты доказываются строго. Учебный материал сопровождается примерами из управленческой практики, что дает возможность иллюстрировать плодотворность использования математической теории для решения прикладных задач. Программа курса предусматривает проведение семинарских занятий, цель которых – научить студентов решать конкретные оптимизационные задачи, грамотно проводить необходимые вычисления. Самостоятельная работа студента заключается в освоении теоретического материала по конспекту лекций и по рекомендуемой к изучению литературе, а также в решении задач, предлагаемых преподавателями.
Учебная задача курса: Материал учебной дисциплины используется при изучении последующих дисциплин учебного плана: «Статистический анализ данных в менеджменте», «Разработка управленческих решений», «Производственный и операционный менеджмент», «Управление рисками», «Теория организаций» и др. Материал учебной дисциплины «Исследование операций» в менеджменте дает студенту – будущему менеджеру, инструментарий, позволяющий на научной основе принимать достаточно обоснованные, а в идеале – и оптимальные, решения для достижения поставленных целей.
Формы контроля: По курсу предусмотрены три контрольных работы, как форма промежуточного контроля. Форма итогового контроля – письменный экзамен в конце 4 модуля второго курса. Каждая форма контроля оценивается в 10-балльной шкале. Итоговая оценка складывается:
- из оценки за контрольную работу – 60% итоговой оценки
- из оценки за письменный экзамен – 40% итоговой оценки
Итоговая оценка выставляется в пятибалльной и в 10-балльной системах в ведомость и в зачетную книжку студента (оценкам 1, 2, 3 в 10-балльной системе соответствует оценка «неудовлетворительно» в пятибалльной системе, оценкам 4, 5 – «удовлетворительно», оценкам 6, 7 – «хорошо», оценкам 8, 9, 10 – «отлично»).
^
II. Содержание программы
Тема 1. Обзор задач оптимизации решений в менеджменте (формализация и математические модели).
О возможностях применения математики для решения управленческих задач. Математическое описание социально - экономических объектов. О важности информированности лица, принимающего решения (ЛПР). Схемы принятия управленческих решений.
Иллюстративные примеры: задача о наборе в штат фирмы столичных и местных сотрудников; задача о кредите.
Типовые этапы построения математических моделей. Классификация математических задач принятия решений.
Тема 2. Задачи математического программирования.
Необходимые и достаточные условия оптимальности в задачах безусловной оптимизации, условной оптимизации с ограничениями типа равенств, условной оптимизации с ограничениями типа неравенств. Выпуклые задачи оптимизации. Теорема Куна – Таккера. Экономический смысл множителей Лагранжа.
Иллюстративный пример: задача об оптимальном портфеле ценных бумаг.
Тема 3. Линейное программирование и некоторые классические задачи.
Примеры задач линейного программирования (ЛП): распределение ресурсов, многосторонний коммерческий арбитраж. Алгебраическая формулировка задачи. Геометрическая интерпретация. Теория двойственности. Экономический смысл двойственных переменных. Анализ чувствительности решений к коэффициентам ограничений. Графическое решение задач малой размерности. Симплекс - метод. Транспортная задача. Сведение транспортной задачи к задаче ЛП. Задача о назначениях. Теорема Фалкерсона о максимальном потоке и минимальном разрезе. Метод построения максимального потока в сети.
Тема 4. Некоторые примеры моделей динамического программирования.
Принцип оптимальности Р. Беллмана и построение математической модели динамического программирования. Примеры задач динамического программирования: модель распределения усилий (инвестиций), модель замены оборудования, поиск кратчайшего пути в сети, задачи календарного планирования, поиск критического пути, вычисление ранних и поздних сроков наступления событий.
Тема 5. Элементы теории оптимального управления.
Некоторые необходимые сведения из теории обыкновенных дифференциальных уравнений. Постановка задачи оптимального управления. Формулировка принципа максимума Л.С.Понтрягина.
Иллюстративный пример: неоклассическая модель оптимального экономического роста.
Тема 6. Основные сведения о многокритериальной оптимизации.
Постановка многокритериальной задачи принятия решений. Понятие эффективного решения. Решения, оптимальные по Парето, по Слейтеру. Теорема Фана для вогнутых задач многокритериальной оптимизации. Линейные задачи многокритериальной оптимизации. Внутренняя и внешняя устойчивость решений. Свёртка критериев. Лексикографическая оптимизация.
Тема 7. Основы теории антагонистических игр.
Определение антагонистической игры. Чистые и смешанные стратегии. Игры с конечным числом чистых стратегий (матричные игры), примеры матричных игр. Ситуации равновесия и седловые точки. Принцип минимакса. Основная теорема теории матричных игр. Теоремы о доминировании стратегий. Сведение решения матричной игры к паре двойственных задач линейного программирования.
Иллюстративные примеры: игра полковника Блотто; PR-операция по завоеванию голосов избирателей.
Тема 8. Элементы теории неантагонистических игр.
Игра многих лиц в нормальной форме. Ситуации равновесия по Нэшу и по Парето в бескоалиционной игре. О существовании ситуаций равновесия. Биматричные игры. Использование свойства дополняющей нежёсткости для решения биматричных игр.
^
III. Тематика
Темы семинарских занятий
Тема 1.
Обзор задач оптимизации решений в менеджменте.
Тема 2.
Типовые этапы построения математических моделей. Классификация математических задач принятия решений.
Тема 3.
Задачи математического программирования.
Тема 4.
Линейное программирование и некоторые классические задачи.
Тема 5.
Некоторые примеры моделей динамического программирования.
Тема 6.
Элементы теории оптимального управления.
Тема 7.
Основные сведения о многокритериальной оптимизации.
Тема 8.
Основы теории антагонистических игр.
Тема 9.
Элементы теории неантагонистических игр.
Тема 10.
Игра многих лиц в нормальной форме.
Тема 11.
Ситуации равновесия по Нэшу и по Парето в бескоалиционной игре.
Тема 12.
Биматричные игры. Использование свойства дополняющей не жесткости для решения биматричных игр.
Тематика контрольных работ:
- Изобразить на плоскости
 линии уровня
линии уровня  , где
, где 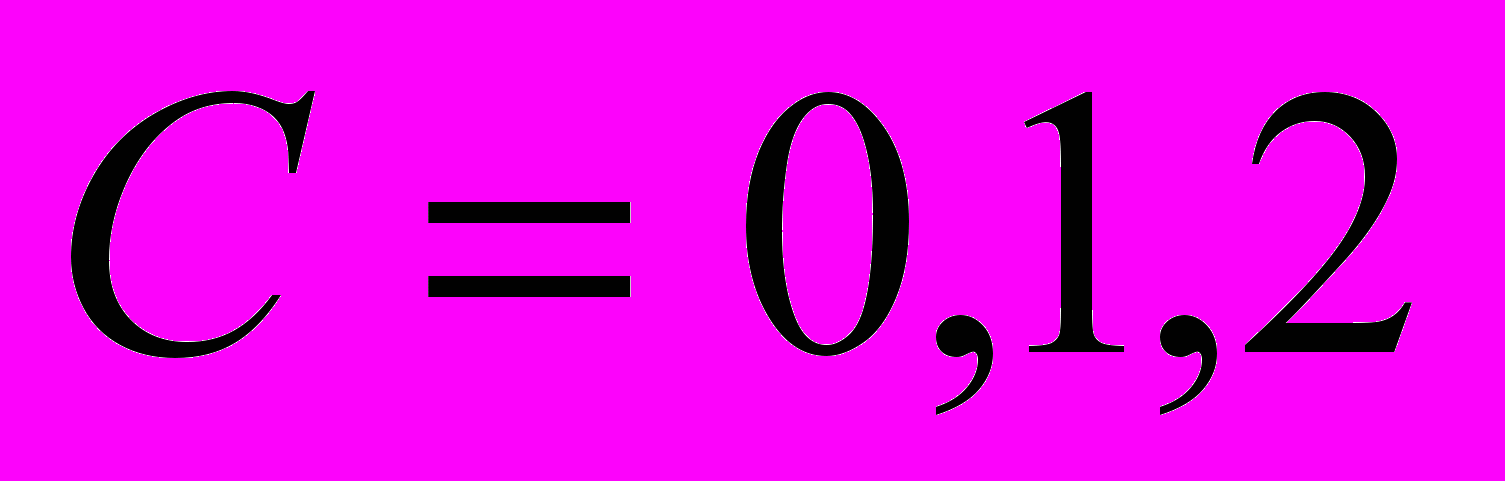 , следующих функций (
, следующих функций (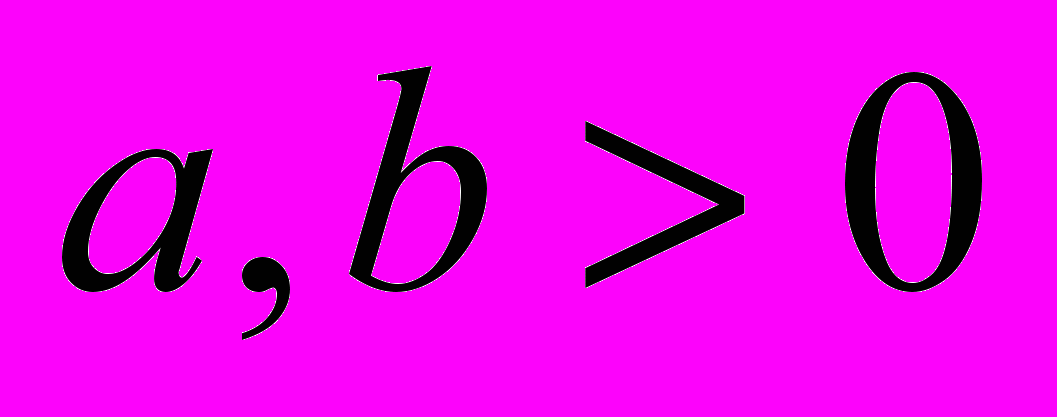 ):
):
-
- Построить линии уровня следующих функций двух переменных:
a)
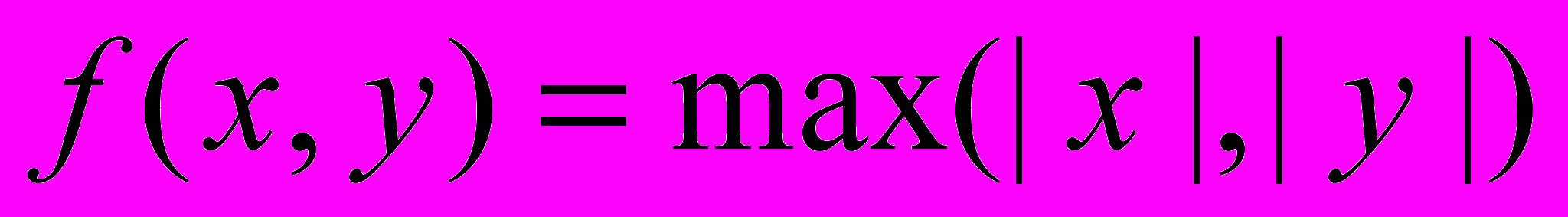
b)
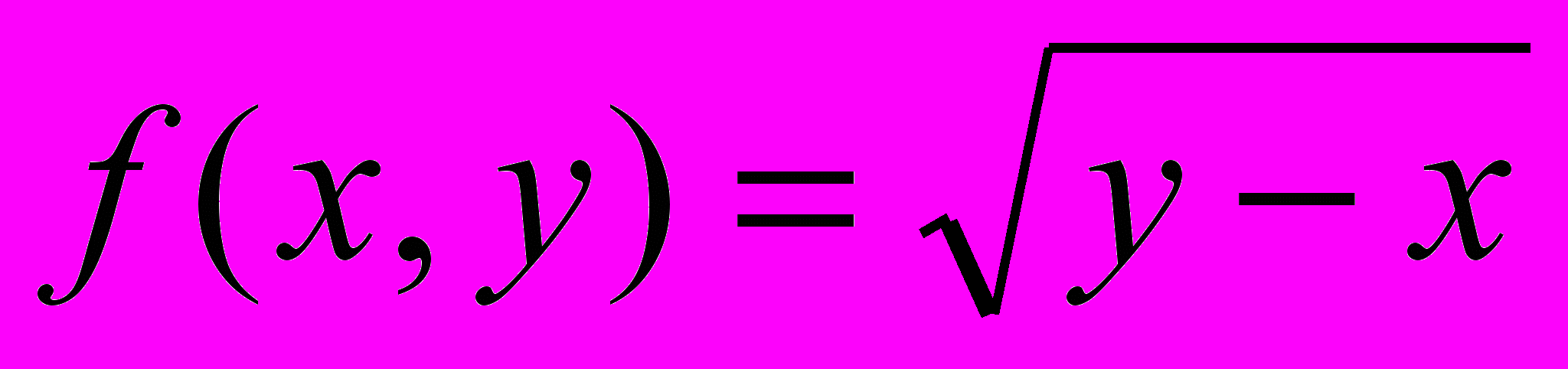
c)
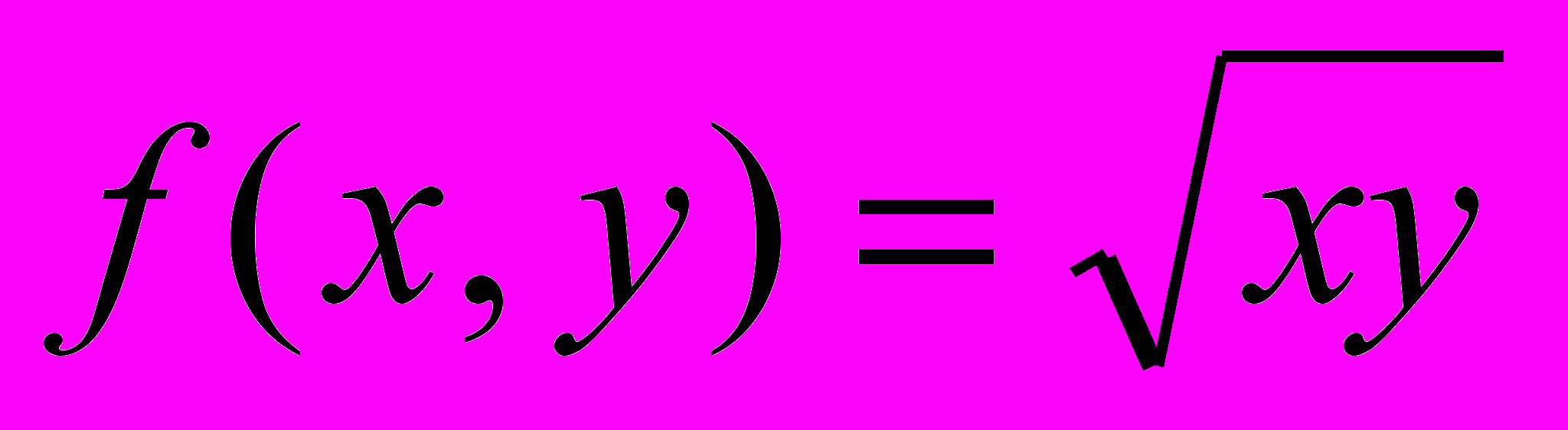
- Вычислить градиент
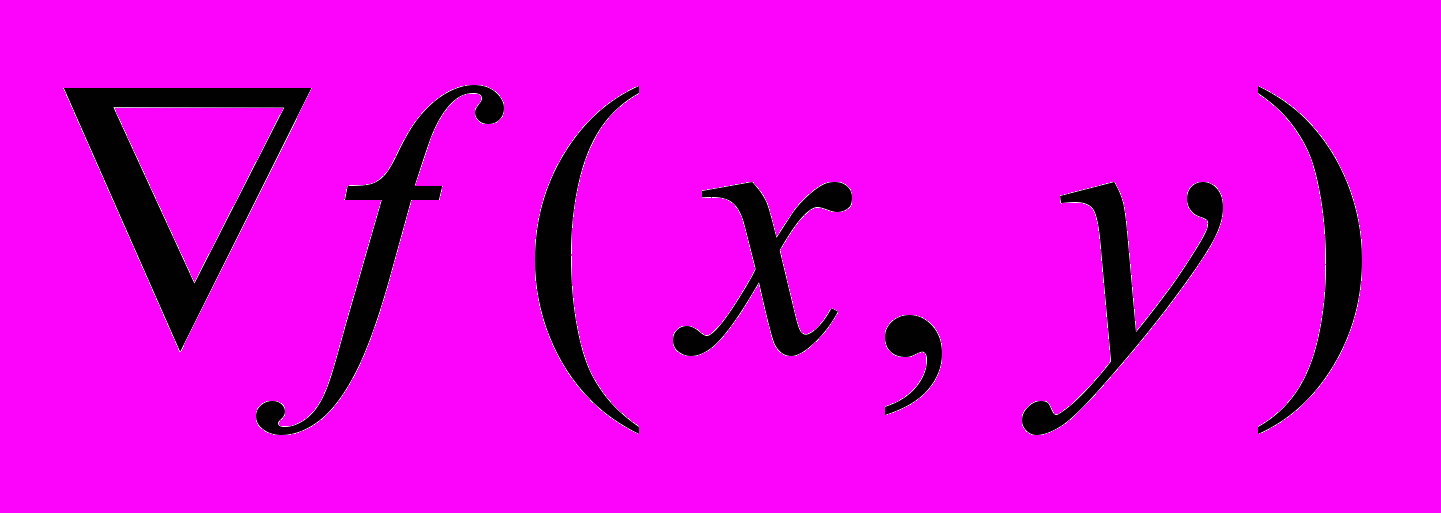 и матрицу Гессе
и матрицу Гессе 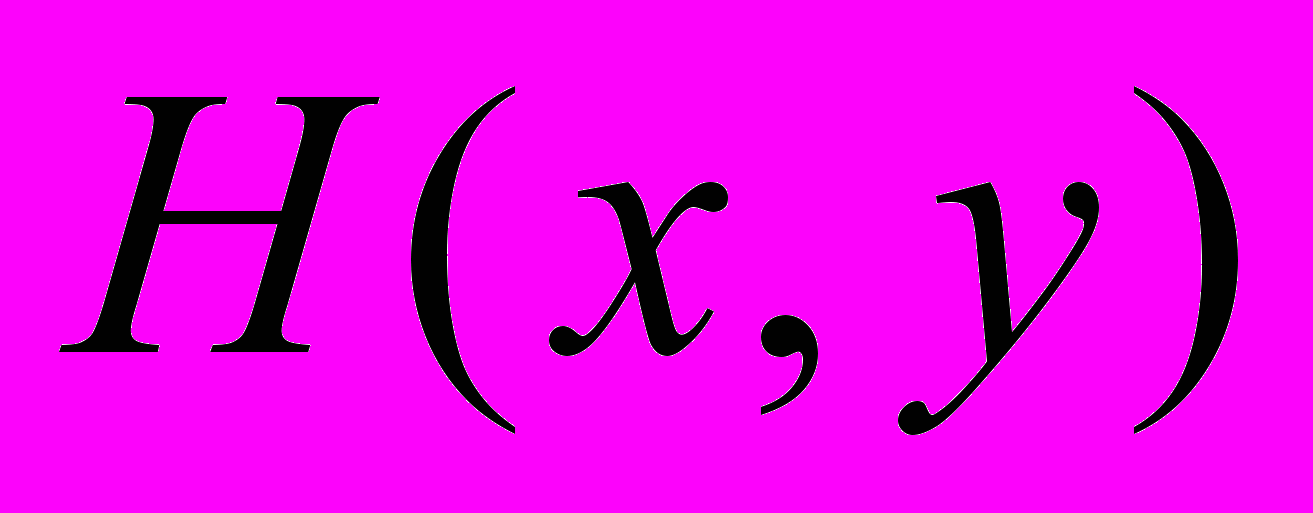 функции
функции 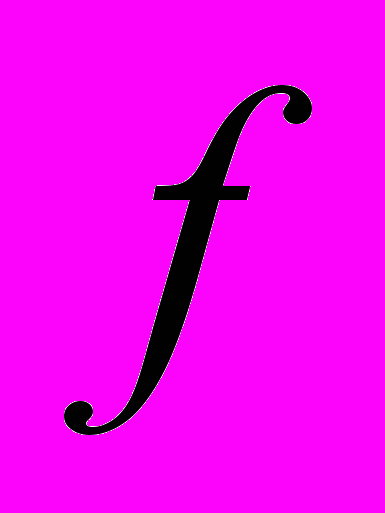 в точке
в точке 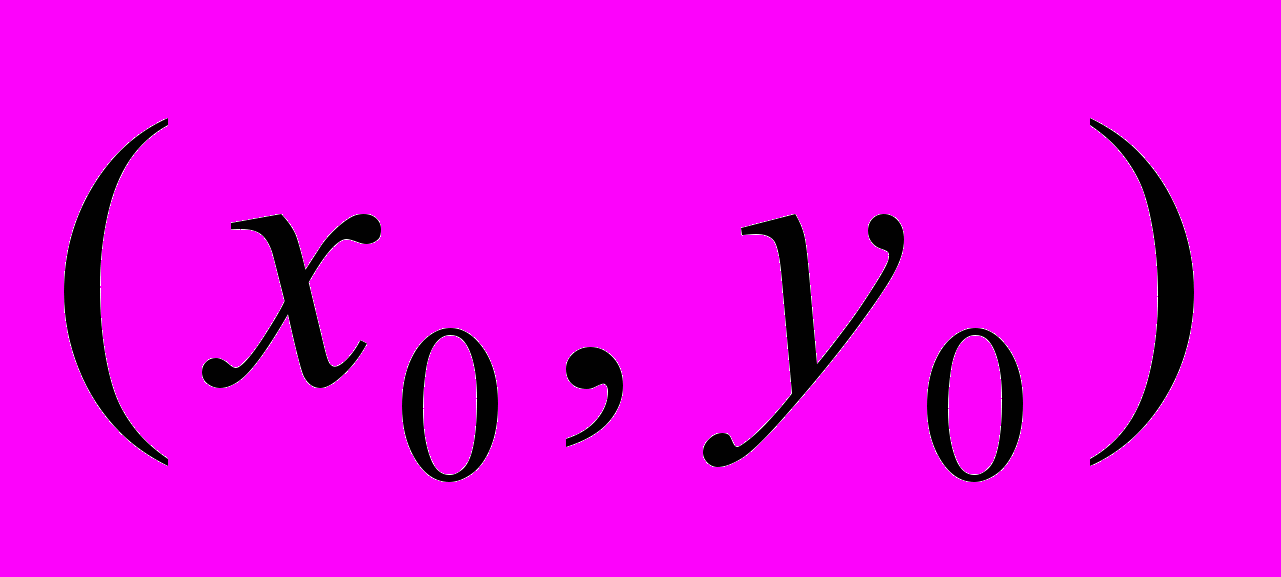 для следующих функций:
для следующих функций:
a)

b)
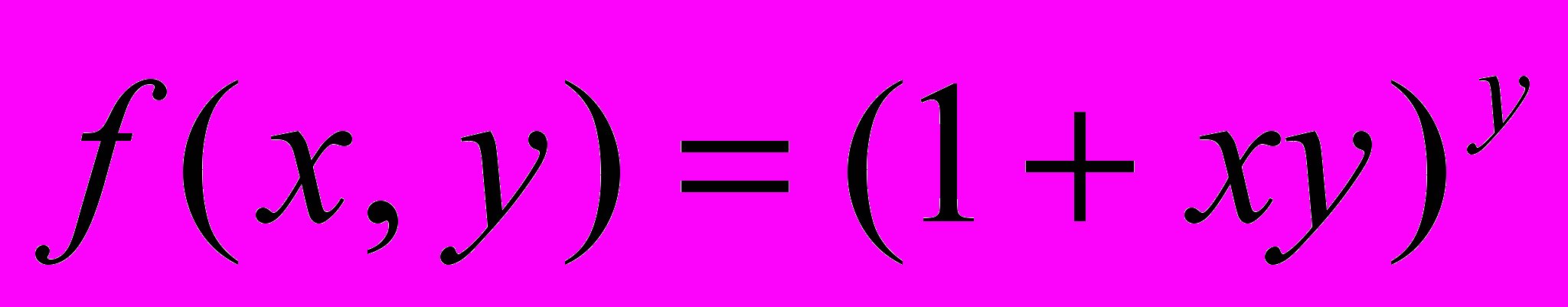
- Выписать общий вид квадратичной функции двух переменных и определить ее градиент и матрицу Гессе.
- Пусть
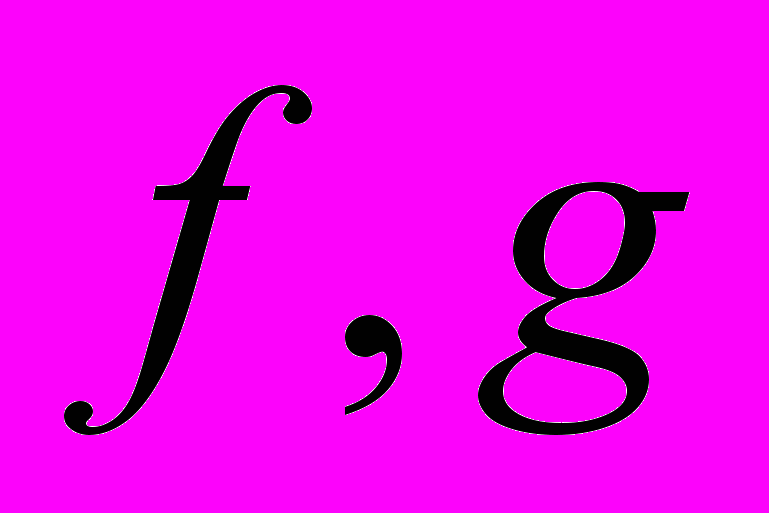 – числовые функции, заданные на множестве
– числовые функции, заданные на множестве 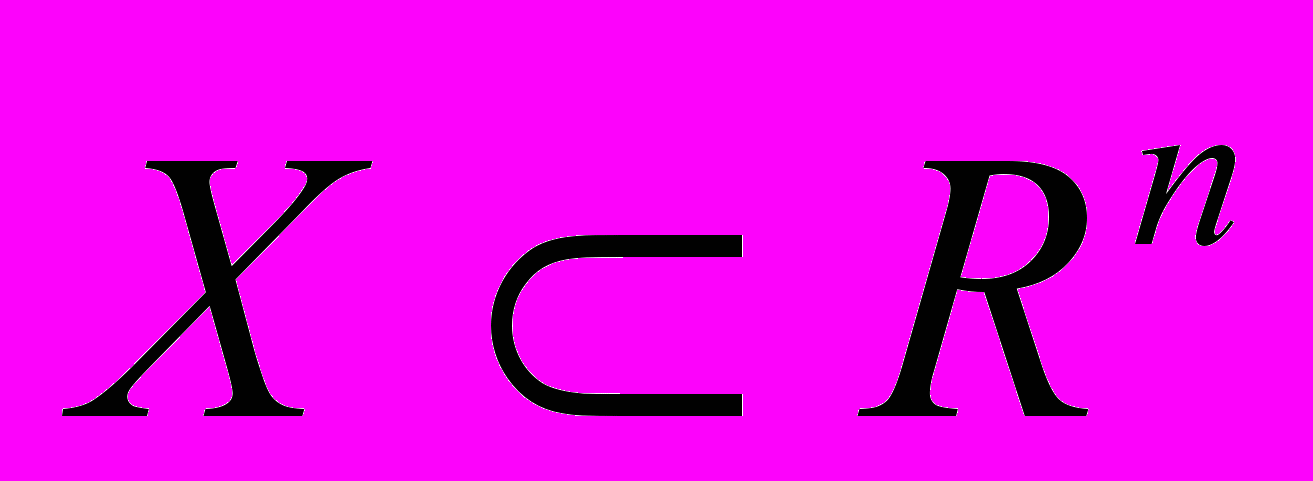 . Доказать следующие равенства и неравенства:
. Доказать следующие равенства и неравенства:
a)
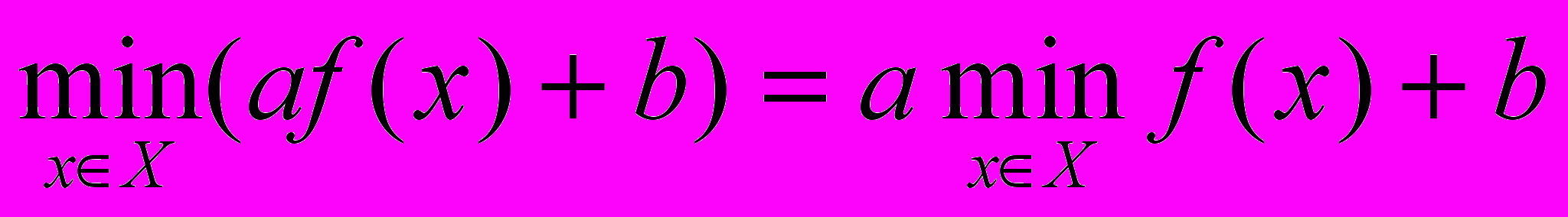 , где
, где 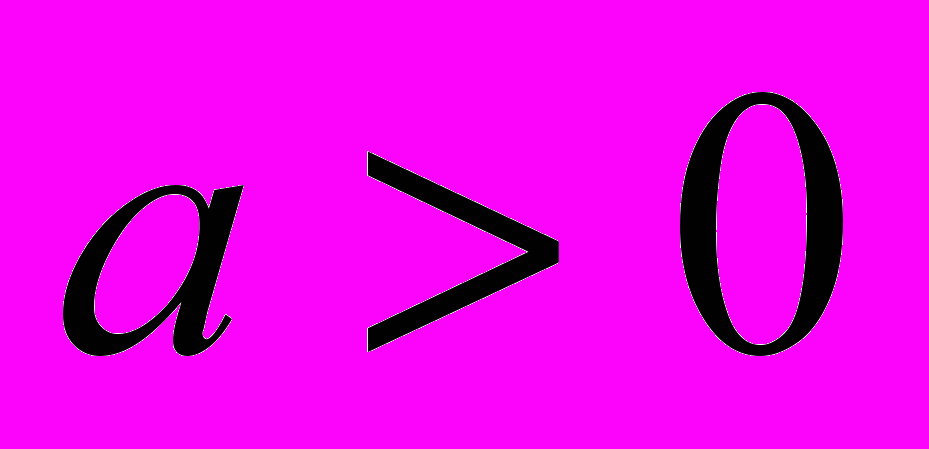 и
и 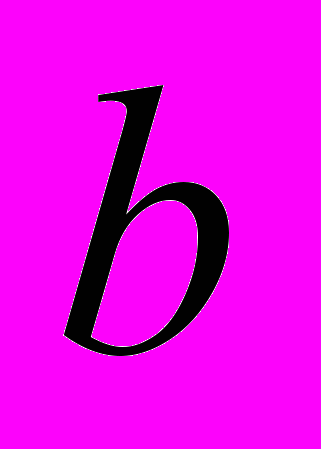 – любое число
– любое числоb)
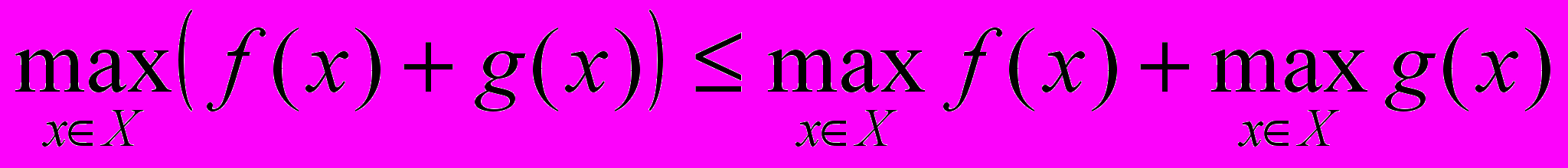
- Доказать, что пересечение двух (а также любого конечного числа) замкнутых множеств в
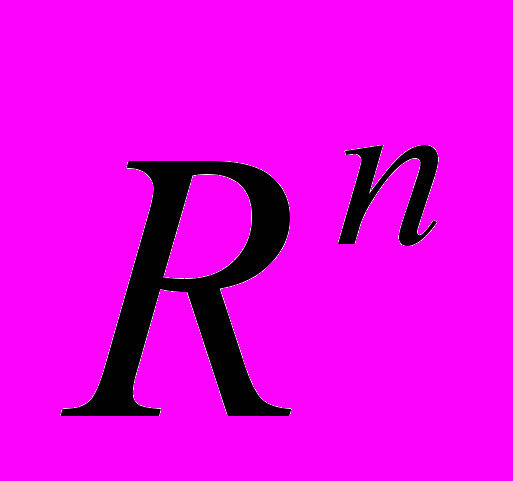 замкнуто, а пересечение двух (а также любого конечного числа) открытых множеств открыто.
замкнуто, а пересечение двух (а также любого конечного числа) открытых множеств открыто.
- Доказать, что пересечение любого числа выпуклых множеств в
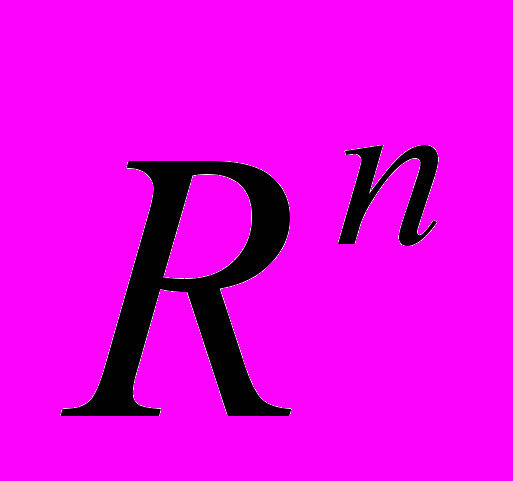 является выпуклым множеством.
является выпуклым множеством.
- Доказать, что
 -окрестность точки
-окрестность точки  является выпуклым множеством.
является выпуклым множеством.
- Задача о прокладке шоссе. Завод А нужно соединить шоссейной дорогой с прямолинейной железной дорогой, на которой расположен поселок В. Расстояние АС от завода до железной дороги равно а, а расстояние ВС по железной дороге равно b. Стоимость перевозок грузов по шоссе в k раз ( k>1) выше стоимости перевозок по железной дороге. В какую точку D отрезка ВС следует провести шоссе от завода, чтобы стоимость перевозок грузов от завода А к поселку В была наименьшей?
- Исследовать функцию
 на экстремум:
на экстремум:
a)
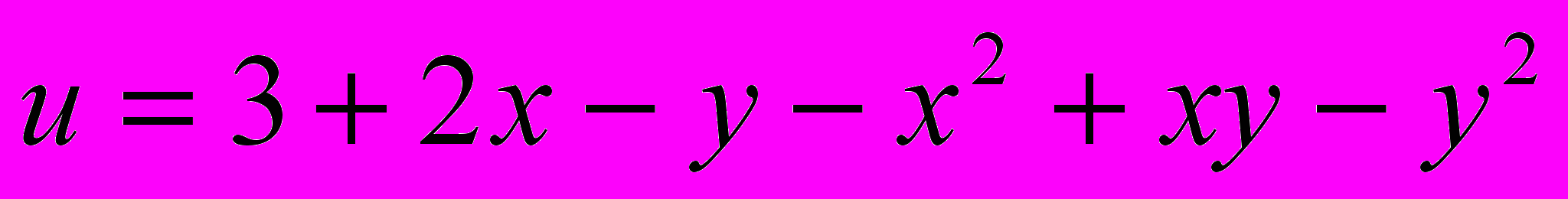
b)
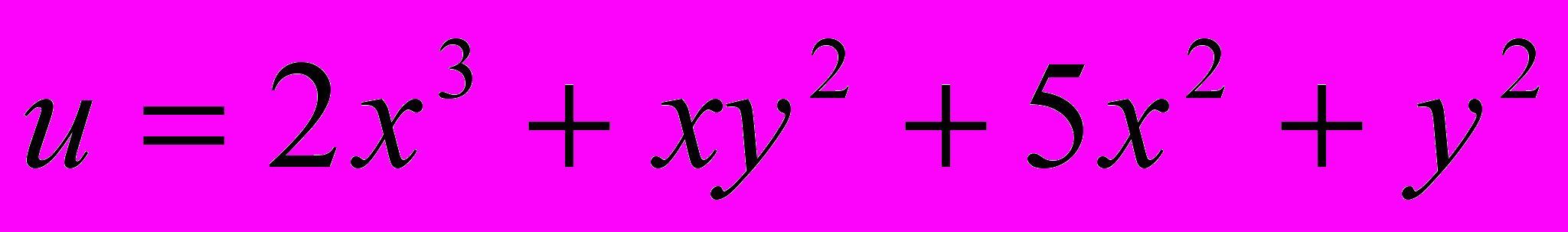
c)
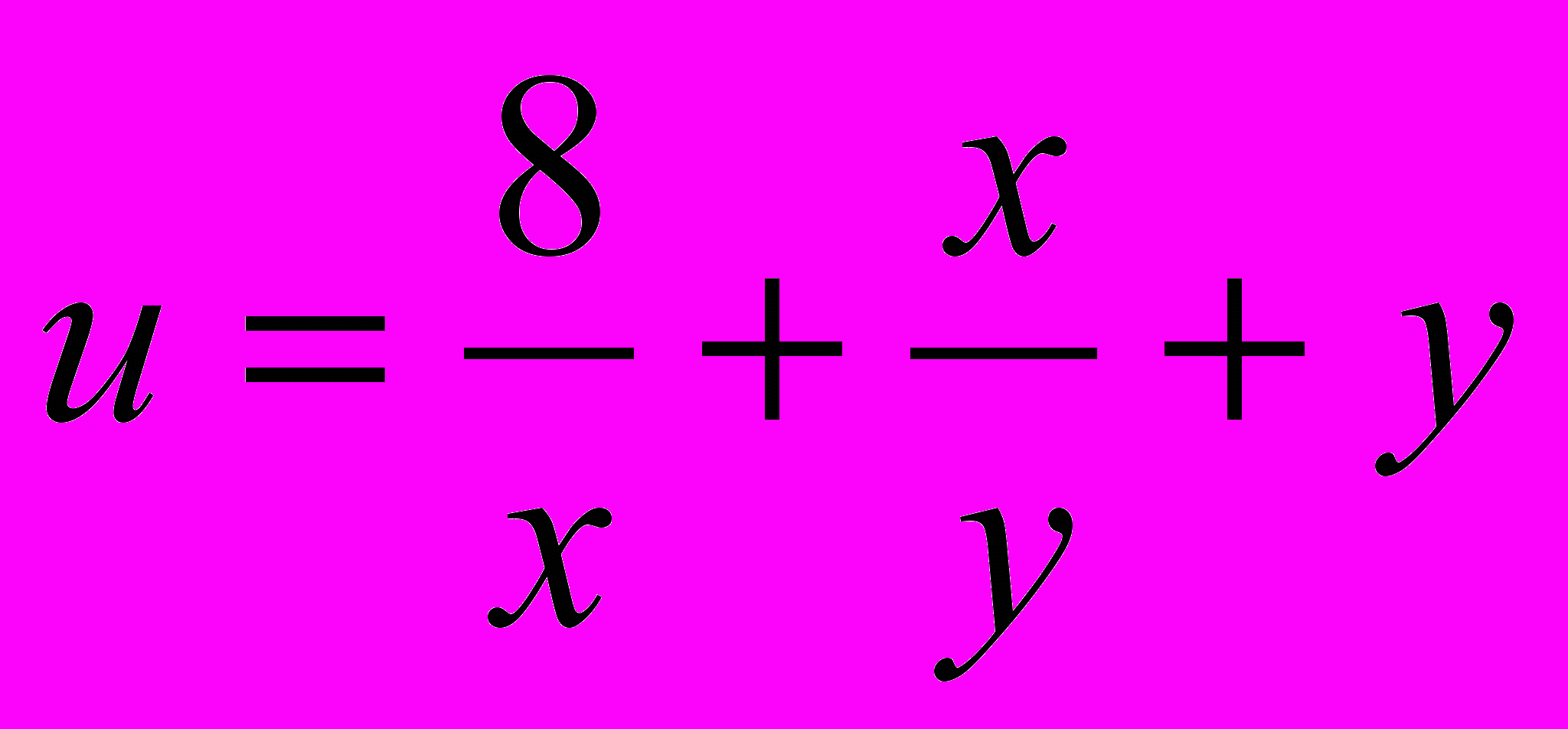
Экзаменационные вопросы:
- Математическое программирование: постановка задачи, этапы ее решения. Классификация задач математического программирования.
- Задача линейного программирования, ее различные формулировки. Геометрический метод решения. Выводы.
- Общий случай задачи ЛП. Базисные и свободные переменные. Каноническая форма задачи ЛП.
- Алгоритм симплекс – метода. Симплекс – таблицы.
- Нахождение первого базиса.
- Постановка задачи нелинейного программирования. Условный и безусловный экстремум. Сравнение с задачей ЛП.
- Градиентные методы нахождения стационарных точек:
- Метод с дроблением шага;
- Метод наискорейшего подъема (спуска).
- Метод с дроблением шага;
- Метод Лагранжа решения задачи оптимизации.
- Дискретное программирование: постановка задачи, методы решения.
- Метод ветвей и границ: идея метода, два основных положения.
- Алгоритм метода ветвей границ, его реализация для решения задачи целочисленного линейного программирования.
- Динамическое программирование: особенность задач ДП, постановка задачи, общая задача оптимального управления в терминах фазового пространства.
- Условия применения схемы ДП. Вычислительные схемы в прямом и обратном направлениях.
- Основные типы задач:
- Задача о смене режимов работы;
- Задача об увеличении высоты и скорости.
- Задача о смене режимов работы;
- Задачи, решаемые в теории игр. Антогинистическая игра двух игроков, стратегии игроков, платежная матрица, оптимальная стратегия, понятие устойчивого решения игры.
- Верхняя и нижняя цена. Игры I ( = ) и II ( < ) класса. Игры с Седловой точкой, ее нахождение.
- Смешанные стратегии, применение смешанных стратегий. Основная теорема матричных игр с нулевой суммой. Оптимальные смешанные стратегии, цена игры.
- Свойства оптимальных смешанных стратегий, их нахождение путем сведения к задаче ЛП.
- Принципы доминирования и его применение к задаче нахождения оптимальных смешанных стратегий.
- Элементы теории графов. Теоремы Эйлера.
- Задача о минимальном соединении.
- Матричный способ задания графов.
- Максимальный поток в сети.
- Истолкование суммы, произведения и степени матриц смежности вершин.
IV. Учебно - методическое обеспечение дисциплины.
^
Базовый учебник
Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели для менеджмента. Серия «Учебники для ВУЗов». – СПб.: Лань, 2000.
^
Основная литература
1. Аронович А.Б., Афанасьев М.Ю., Суворов Б.П. Сборник задач по исследованию операций. – М.: Изд - во МГУ, 1997.
2. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. Учебное пособие для студентов ВУЗов. – М.: Высшая школа, 2001.
3. Дубров А.М. , Лагоша Б.А., Хрусталев Е.Ю. Моделирование рисковых ситуаций в экономике и бизнесе: Учебное пособие. – М.: Финансы и статистика, 1999, 2002.
4. Таха Хэмди А. Введение в исследование операций. – М.: ИД «Вильямс», 2001.
5. Томас Ричард. Количественные методы анализа хозяйственной деятельности. – М.: Дело и Сервис, 1999.
6. Томас Ричард. Количественный анализ хозяйственных операций и управленческих решений. – М.: Дело и сервис, 2003.
7. Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. – М.: Финансы и статистика, 2001.
8. Фролькис В.А. Введение в теорию и методы оптимизации для экономистов. – СПб.: Питер, 2002.
9. Хазанова Л.Э. Математические методы в экономике: Учебное пособие. – М.: Изд - во БЕК, 2002.
10. Чейз Ричард Б., Эквилайн Николас Дж., Якобс Роберт Ф. Производственный и операционный менеджмент. – М.: ИД «Вильямс», 2003.
^
Дополнительная литература
1. Байе Майкл Р. Управленческая экономика и стратегия бизнеса. – М.: ЮНИТИ - ДАНА, 1999.
2. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учебное пособие. – М.: Финансы и статистика, 2002.
3. Губко М.В., Новиков Д.А. Теория игр в управлении организационными системами. Учебное пособие. – М.: СИНТЕГ, 2002.
4. Интрилигатор Майкл. Математические методы оптимизации и экономическая теория. – М.: Айрис - пресс, 2002.
5. Карманов В.Г. Математическое программирование. – М.: Физматлит, 2001.
6. Карманов В.Г., Фёдоров В.В. Моделирование в исследовании операций. – М.: Твема, 1996.
7. Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика: Математическое программирование: Учебник. – Минск: Вышэйшая школа, 2001.
8. Курбатов В.И., Угольницкий Г.А. Математические методы социальных технологий: Учебное пособие. – М.: Вузовская книга, 1998.
9. Лабскер Л.Г., Бабешко Л.О. Игровые методы управления экономикой и бизнесом: Учебное пособие. – М.: Дело, 2001.
10. Лесин В.В., Лисовец Ю.П. Основы методов оптимизации. – М.: Изд - во МАИ, 1998.
11. Льюс Р. Дункан, Райфа Ховард. Игры и решения. Введение и критический обзор. – М.: ИЛ, 1961.
12. Морозов В.В. Основы теории игр: Учебное пособие. – М.: Изд - во МГУ, 2002.
13. Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях. – М.: Высшая школа, 1986.
14. Мулен Э. Теория игр (с примерами из математической экономики). – М.: Мир, 1985.
15. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр: Учебное пособие для университетов. – М.: Высшая школа, 1998.
16. Плаус Скотт. Психология оценки и принятия решений. – М.: ИИД «Филинъ», 1998.
17. Протасов И.Д. Теория игр и исследование операций: Учебное пособие. – М.: Гелиос АРВ, 2003.
18. Розен В.В. Математические модели принятия решений в экономике: Учебное пособие. – М.: Книжный дом «Университет», Высшая школа, 2002.
19. Саати Томас Л. Математические методы исследования операций. – М.: Воениздат, 1963.
20. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. – М.: Физматлит, 2002.
21. Сио К.К. Управленческая экономика. – М.: ИНФРА - М, 2000.
22. Черноруцкий И.Г. Методы оптимизации и принятия решений: Учебное пособие. – СПб.: Лань, 2001.
23. Шикин Е.В. От игр к играм. Математическое введение. – М.: Эдиториал УРСС, 1998.
24. Эддоус М., Стэнсфилд Р. Методы принятия решений. – М.: Аудит, ЮНИТИ, 1997.
25. Cook Wade D., Kress Moshe. Ordinal Information and Preference Structures: Decision Models and Applications. – USA: Prentice-Hall – Englewood Cliffs, 1992.
26. Joyce James. The Foundations of Causal Decision Theory. – UK: Cambridge University Press, 2000.
27. Sundaram Rangarajan K. A First Course in Optimization Theory, 2 nd edition. – UK: Cambridge University Press, 1999.
V. Тематический расчет часов
| № темы | Название темы | Всего часов | Количество часов лекций | Количество часов семинаров | Количество часов самостоятельной работы |
| 1. | Обзор задач оптимизации решений в менеджменте (формализация и математические модели) | 11 | 2 | 2 | 7 |
| 2. | Задачи математического программирования | 15 | 4 | 4 | 7 |
| 3. | Линейное программирование и некоторые классические задачи | 15 | 4 | 4 | 7 |
| 4. | Некоторые примеры моделей динамического программирования | 15 | 4 | 4 | 7 |
| 5. | Элементы теории оптимального управления | 15 | 4 | 4 | 7 |
| 6. | Основные сведения о многокритериальной оптимизации | 15 | 4 | 4 | 7 |
| 7. | Основы теории антагонистических игр | 13 | 4 | 2 | 7 |
| 8. | Элементы теории неантагонистических игр | 9 | 2 | 2 | 5 |
| | ИТОГО: | 108 | 28 | 26 | 54 |
Авторы программы: ________________ Рейнов Ю.И.
________________ Рыбакин А.С.