А. А. Хамухин. Информатика для направления «Нефтегазовое дело»

Вид материала

Лекции

Содержание Задан ряд экспериментальных данных, состоящий из пар чисел (Xi, Yi), i =1,…,NТребуется Решение (метод МНК) Общая постановка задачи Решение задачи

Подобный материал:

• А. А. Хамухин. Информатика для направления «Нефтегазовое дело». Лекция, 120.87kb.
• Mathcad 0, 50.56kb.
• Компьютерные сети, 257.11kb.
• Пример программы чтения/записи на диск (на 10 точек) 5 Массивы, 155.38kb.
• Выполнение программы по шагам 4 Кнопка Точка останова (Toggle Breakpoint), 195.44kb.
• Основные принципы действия и характеристики аппаратного и программного обеспечения, 260.2kb.
• Рабочая программа для направления «Нефтегазовое дело», 240.95kb.
• Учебно-методический комплекс по дисциплине опд. Ф. 01" Начертательная геометрия. Инженерная, 796.72kb.
• Рабочая программа для магистров направления 650700 "Нефтегазовое дело" специальности, 220.38kb.
• Ло» в учебный процесс по дисциплине «Графика» внедрена рабочая тетрадь по разделу «Начертательная, 34.69kb.

Модели решения функциональных и вычислительных задач

(в нефтегазовом деле)

Для нефтегазового дела характерным является наличие огромного количества информации из разных источников, которую нужно быстро обрабатывать с помощью современных компьютерных средств, чтобы эффективно использовать.

Первым этапом получения информации является процесс измерения интересующих нас величин (примеры). Если наблюдаемая (измеряемая) величина распределена в пространстве (и/или во времени - примеры), то еще до начала измерений необходимо решить вопрос: сколько делать измерений по каждой координате, с каким шагом, с какой точностью измерять. Все эти вопросы рассматриваются в теории измерений, но и в информатике имеется похожая задача, которая возникает при оцифровке некоторых данных, заданных графически (или аналитически). Фундаментальное решение этой задаче сформулировано в теореме Шеннона-Котельникова. Предварительно рассмотрим пример оцифровки некоторой величины (сигнала), распределенной по одной координате.

1. Оцифровка

Сигнал, несущий информацию о некоторой измеряемой величине называется аналоговым, если он представлен в виде другой подобной ей величины (например, измеряемая величина высота представляется в виде отклонения стрелки прибора)

Сигнал, несущий информацию о некоторой измеряемой величине называется цифровым, если он представлен в виде последовательности чисел (или одного числа), отображающей значения наблюдаемой величины (например, та же высота, представленная в цифровом приборе)

Преобразование аналогового сигнала в цифровой сигнал называется оцифровкой

Пример


Рисунок 1. Пример аналогового сигнала

Во-первых, аналоговый сигнал (Рисунок 1) преобразуется в сигнал разделённый по времени, посредством периодической выборки (Рисунок 2). Временной интервал между двумя выборками называется периодом выборки, а его обратная величина называется частотой дискретизации. Согласно теореме о дискретном представлении (теорема Шеннона-Котельникова), частота дискретизации должна быть, по крайней мере, в два раза больше наивысшей частоты сигнала. В противном случае такой сигнал не может быть однозначно восстановлен из выборки.


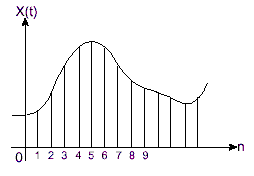
Рисунок 2. Временная дискретизация сигнала

Квантованием называется определение цифровых значений, соответствующих аналоговым выборкам, взятым на частоте дискретизации. Аналоговый сигнал квантуется путём приписывания аналоговой величине ближайшего «допустимого» цифрового значения (Рисунок 3). Количество цифровых значений называется разрешением и всегда ограничивается. Например, 256 значений для 8-битного цифрового сигнала или 10 значений в этом примере. Поэтому квантование аналоговых сигналов всегда приводит к потере информации. Эта ошибка квантования» обратно пропорциональна разрешению цифрового сигнала. Она также обратно пропорциональна динамическому диапазону сигнала, т.е. интервалу между минимальным и максимальным значениями (3 и 8 в этом примере).


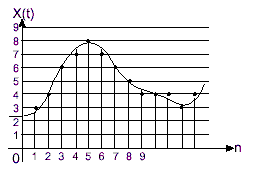
Рисунок 3. Квантованный сигнал

На рисунке 4 показаны цифровые значения, которые соответствуют аналоговому сигналу. Эти значения сняты с выхода АЦП.


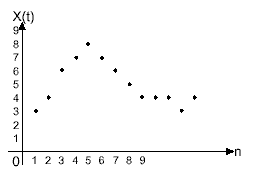
Рисунок 4. Цифровой сигнал

Итак, все необходимые величины измерены, данные оцифрованы и введены в компьютер.

Прежде чем начинать анализ данных и извлекать из них ценную информацию предстоит выявить и обработать погрешности, внесенные на этапе измерения и оцифровки.


2. Обработка ошибок измерений


Все измерительные приборы имеют некоторый класс точности, значит, все данные измеряются с некоторой погрешностью, которая при передаче может усиливаться случайным образом из-за помех. Кроме того, возможны просто грубые ошибки при проведении измерений в силу разных обстоятельств (примеры). А в некоторых значениях координат искомую величину просто невозможно измерить (пример).

Снижение этих погрешностей при обработке информации выполняется с помощью методов интерполяции и аппроксимации.


(Дать определения и пояснить рисунками)


Фундаментальной математическую основу для решения задач в этой области дает теорема Вейерштрасса, которая гласит, что любую непрерывную функцию на заданном интервале всегда можно аппроксимировать полиномом некоторой степени, причем, чем выше степень полинома, тем меньше будет погрешность аппроксимации. Еще одна фундаментальная теорема в этой области гласит, что построения полинома n-ой степени требуется не менее n+1 заданных точек (пар координат)


Аппроксимацией (приближением) функции 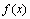называется нахождение такой функции 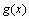(аппроксимирующей функции), которая была бы близка заданной. Критерии близости функци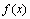й и 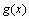могут быть различные.

В том случае, когда приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной.

В том случае, когда аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция (в широком смысле).

Пусть задан дискретный набор точек 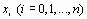, называемых узлами интерполяции, причем среди этих точек нет совпадающих, а также значения функции 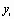в этих точках. Требуется построить функцию 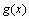, проходящую через все заданные узлы. Таким образом, критерием близости функции является .

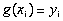В качестве функции 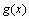обычно выбирается полином, который называют интерполяционным полиномом.

В том случае, когда полином един для всей области интерполяции, говорят, что интерполяция глобальная.

В тех случаях, когда между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции 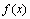между узлами (провести интерполяцию в узком смысле слова), а также определить значение функции 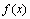даже за пределами заданного интервала (провести экстраполяцию).

Следует иметь в виду, что точность экстраполяции обычно очень невелика особенно при удалении от заданного интервала.


Локальная интерполяция

 Простейшим случаем локальной интерполяции является линейная интерполяция, когда в качестве интерполяционной функции выбирается полином первой степени, то есть узловые точки соединяются прямой линией (показать пример)

При линейной интерполяции используется полином 1-ой степени, стало быть для его построения необходимо знать 2 точки (узла интерполяции)

(показать расчетные формулы)

Линейная интерполяция самая простая и имеет самую большую погрешность. На практике чаще используется интерполяция полиномом более высокого порядка, например, квадратичная интерполяция

(показать примеры и формулы).

В настоящее время среди методов локальной интерполяции наибольшее распространение получила интерполяция сплайнами (от английского слова spline – гибкая линейка). При этом строится интерполяционный полином третьей степени, проходящий через все заданные узлы и имеющий непрерывные первую и вторую производные. На каждом интервале 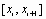интерполирующая функция является полиномом третьей степени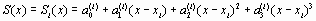



и удовлетворяет условиям

.

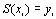Если всего n узлов, то интервалов – 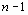. Значит, требуется определить 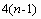неизвестных коэффициентов полиномов. Условие дает нам n уравнений. Условие непрерывности функции и ее первых двух производных во внутренних узлах интервала дает дополнительно 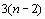уравнений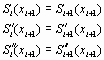



Всего имеем различных уравнений. Два недостающих уравнения можно получить, задавая условия на краях интервала. В частности, можно потребовать нулевой кривизны функции на краях интервала, то есть .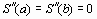

Задавая различные условия на концах интервала, можно получить разные сплайны.

Рассмотрим пример интерполяции синуса с помощью сплайнов (примеры выполнены в пакете MathCad). Обратите внимание, что результаты интерполяции различными типами кубических сплайнов практически не отличаются во внутренних точках интервала и совпадают с точными значениями функции. Вблизи краев интервала отличие становится более заметным, а при экстраполяции за пределы заданного интервала различные типы сплайнов дают существенно разные результаты. Для большей наглядности представим результаты на графиках











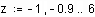
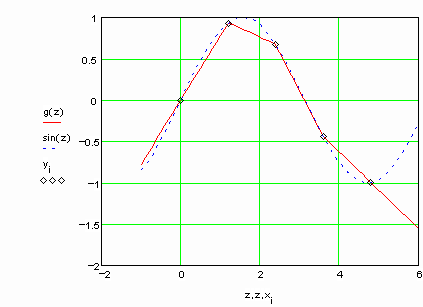
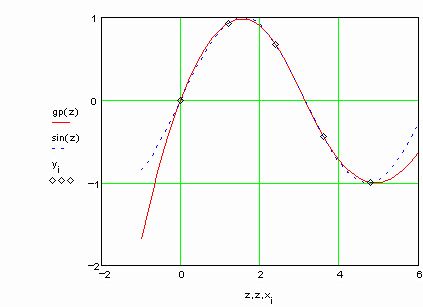
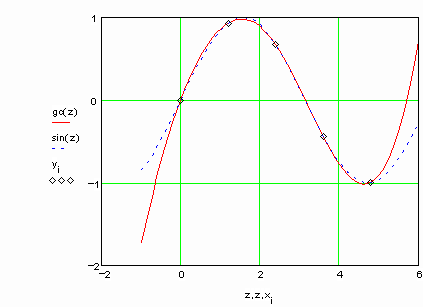
Убедимся в том, что первые и вторые производные сплайна непрерывны





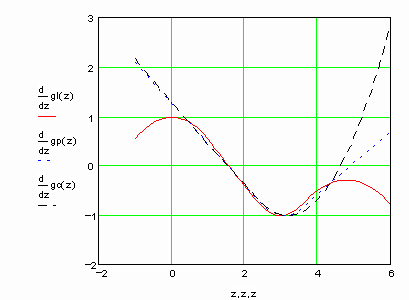
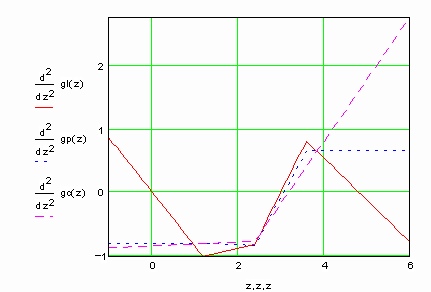
Но производные более высоких порядков уже не являются непрерывными

Глобальная интерполяция

 При глобальной интерполяции ищется единый полином для всего интервала. Если среди узлов {x_i,y_i} нет совпадающих, то такой полином будет единственным, и его степень не будет превышать n.

Запишем систему уравнений для определения коэффициентов полинома



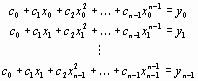
Определим матрицу коэффициентов системы уравнений

 

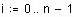
Решим систему уравнений матричным методом

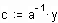
Определим интерполяционный полином

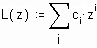
Представим результаты на графике



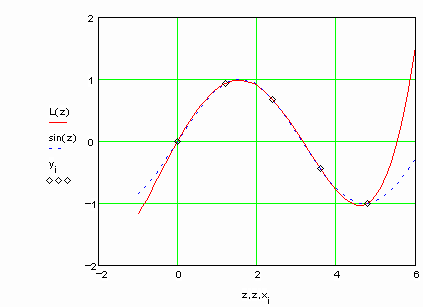
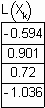
Вычислим значения интерполяционного полинома в заданных точках и сравним их с точными значениями

 

Коэффициенты интерполяционного полинома следующие:



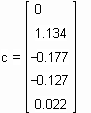
Внимание! Из-за накопления вычислительной погрешности (ошибок округления) при большом числе узлов (n>10) возможно резкое ухудшение результатов интерполяции. Кроме того, для целого ряда функций глобальная интерполяция полиномом вообще не дает удовлетворительного результата. Рассмотрим в качестве примера две таких функции. Для этих функций точность интерполяции с ростом числа узлов не увеличивается, а уменьшается. Первым примером является функция .

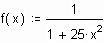Построим для нее интерполяционный полином на интервале [–1;1], используя 9 точек.

 



 

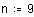
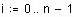
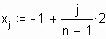
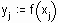
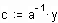
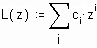
Представим результаты на графике.





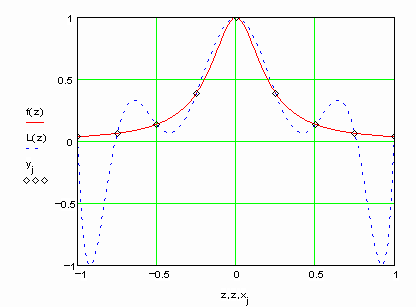
Второй пример – функция .

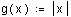Найдем интерполяционный полином, используя заданные выше точки.

 



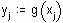
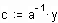
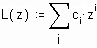
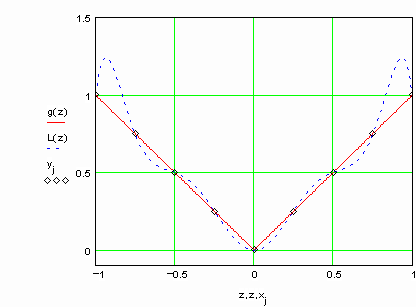
Убедитесь самостоятельно, что при увеличении числа узлов интерполяции, результаты интерполирования вблизи концов интервала ухудшаются.

На практике для инженерных расчетов наиболее удобно использовать интерполяционную формулу Лагранжа. Она не требует предварительного вычисления коэффициентов полинома, а позволяет сразу вычислять искомое значение функции Y(X) по N заданным точкам {Xi, Yi}. В модельной задаче ответы (Y точное) заранее известны, для того, чтобы Вы могли рассчитать погрешность интерполяции и по ней сделать вывод.




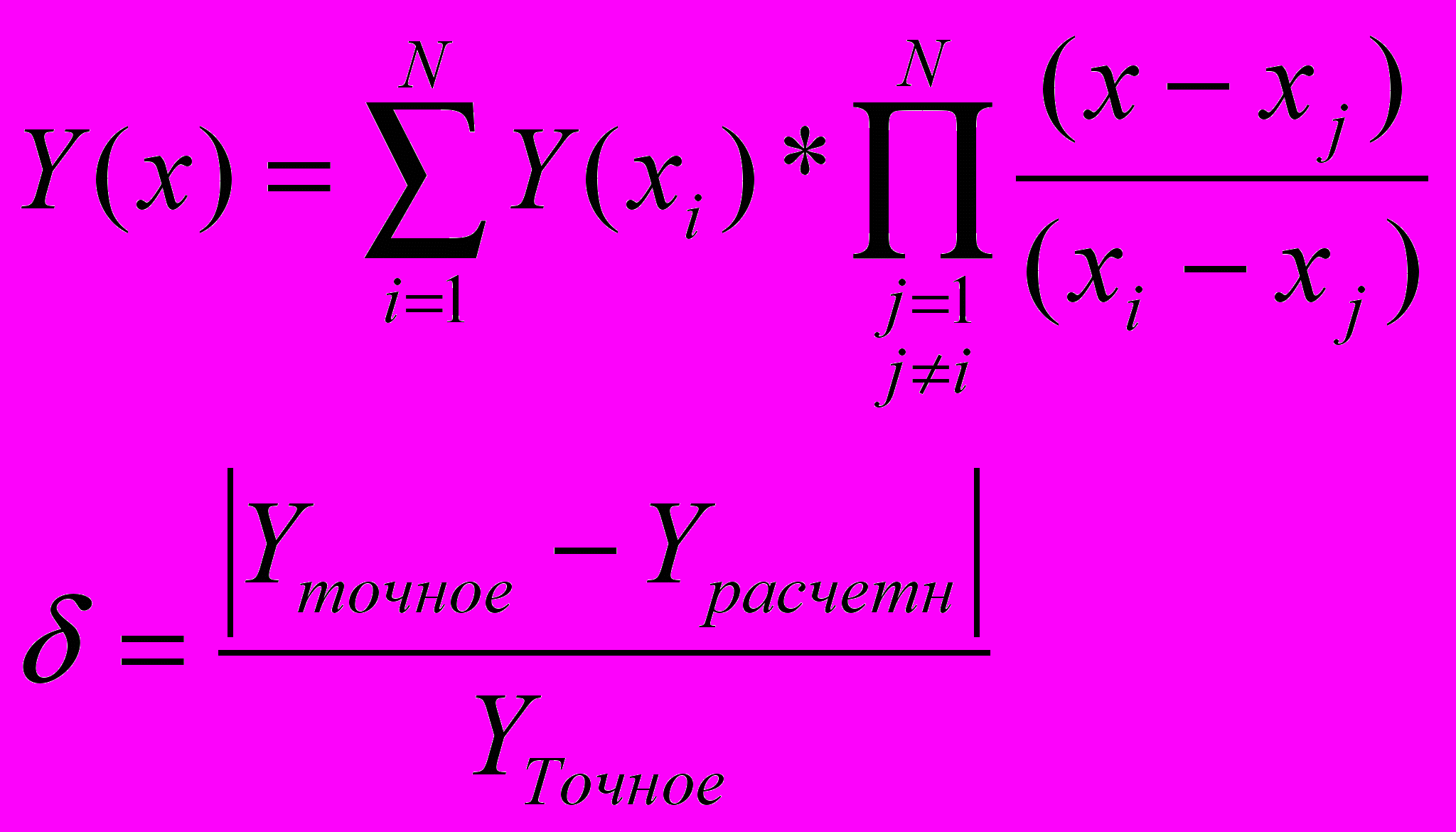
Фрагмент программы расчета по формуле Лагранжа для глобальной интерполяции


S = 0

For i = 1 To N

p = 1

For j = 1 To N

If j <> i And j <> Nz Then p = p * ((X(Nz) - X(j)) / (X(i) - X(j)))

Next j

If i <> Nz Then S = S + Y(i) * p

Next i

Y(Nz) = S


Где N – это общее количество точек в ряде, Nz – номер дефектной точки


Фрагмент программы расчета для локальной интерполяции (в т.ч. сплайнами)


S = 0

For i = Nz - Nleft To Nz + Nright

p = 1

For j = Nz - Nleft To Nz + Nright

If j <> i And j <> Nz Then p = p * ((X(Nz) - X(j)) / (X(i) - X(j)))

Next j

If i <> Nz Then S = S + Y(i) * p

Next i

Y(Nz) = S


Где Nleft, Nright – количество точек (узлов интерполяции) слева и справа от расчетной (дефектной) точки, участвующих в ее восстановлении


(показать пример ЭКСТРАПОЛЯЦИИ и ее отличие от интерполяции)

Аппроксимация

Наиболее распространенным методом аппроксимации экспериментальных данных является метод наименьших квадратов. Метод позволяет использовать аппроксимирующие функции произвольного вида и относится к группе глобальных методов. Простейшим вариантом метода наименьших квадратов является аппроксимация прямой линией (полиномом первой степени). Этот вариант метода наименьших квадратов носит также название линейной регрессии.

Критерием близости в методе наименьших квадратов является требование минимальности суммы квадратов отклонений от аппроксимирующей функции до экспериментальных точек:



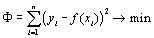
Таким образом, не требуется, чтобы аппроксимирующая функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих погрешности.

Важной особенностью метода является то, что аппроксимирующая функция может быть произвольной. Ее вид определяется особенностями решаемой задачи, например, физическими соображениями, если проводится аппроксимация результатов физического эксперимента. Наиболее часто встречаются аппроксимация прямой линией (линейная регрессия), аппроксимация полиномом (полиномиальная регрессия), аппроксимация линейной комбинацией произвольных функций.

Кроме того, часто возможно путем замены переменных свести задачу к линейной (провести линеаризацию). Например, пусть аппроксимирующая функция ищется в виде 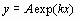. Прологарифмируем это выражение и введем обозначения 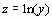, 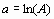. Тогда в новых обозначениях задача сводится к отысканию коэффициентов линейной функции .

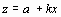Аппроксимация линейной функцией

Задан ряд экспериментальных данных, состоящий из пар чисел (Xi, Yi), i =1,…,N. Где Xi – независимая координата, заданная обычно с некоторым (постоянным) шагом, Yi – результат измерения некоторой величины (высоты рельефа местности, глубины верхней границы нефтяного пласта и т.п.).

Требуется по этим данным построить линейную аппроксимирующую функцию вида

,

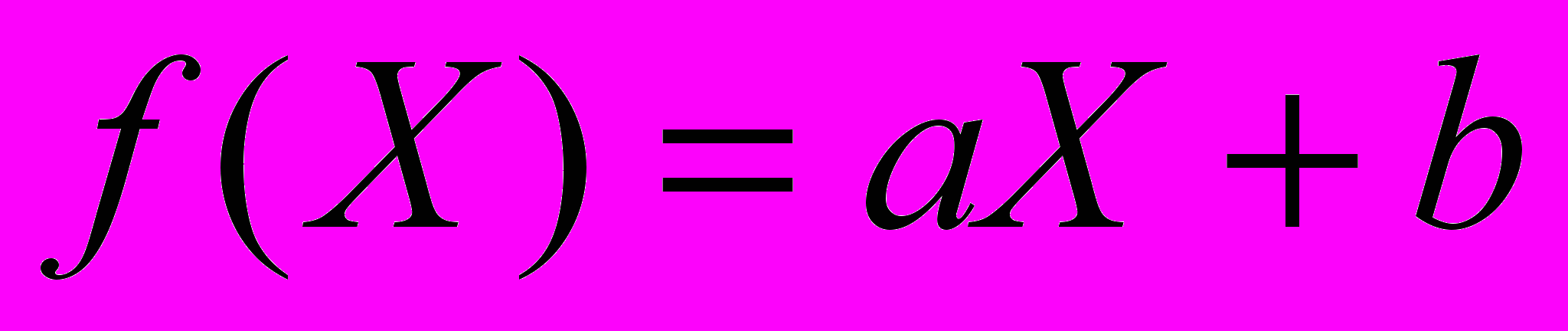такую, чтобы сумма квадратов отклонений экспериментальных данных от расчетных в заданных точках была минимальна.

Неизвестными параметрами в этой задаче являются коэффициенты a b аппроксимирующей функции.

Решение

Запишем указанный выше функционал для заданной аппроксимирующей функции:




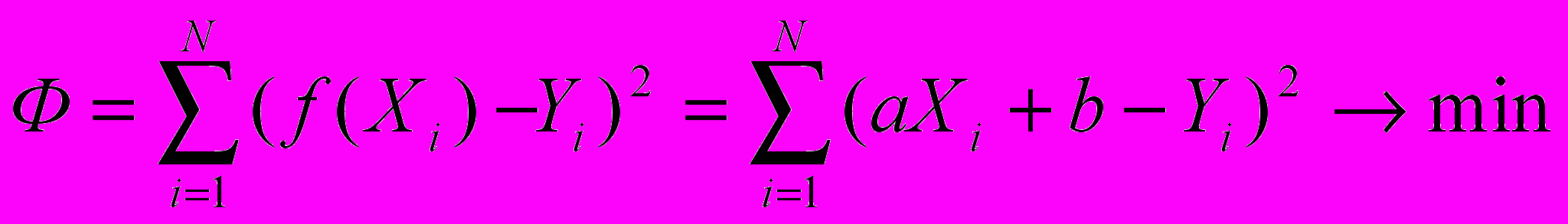
Из математического анализа известно, что минимум функционала достигается при равенстве нулю всех его частных производных по независимым переменным. Таким образом, запишем условие минимума нашего функционала:



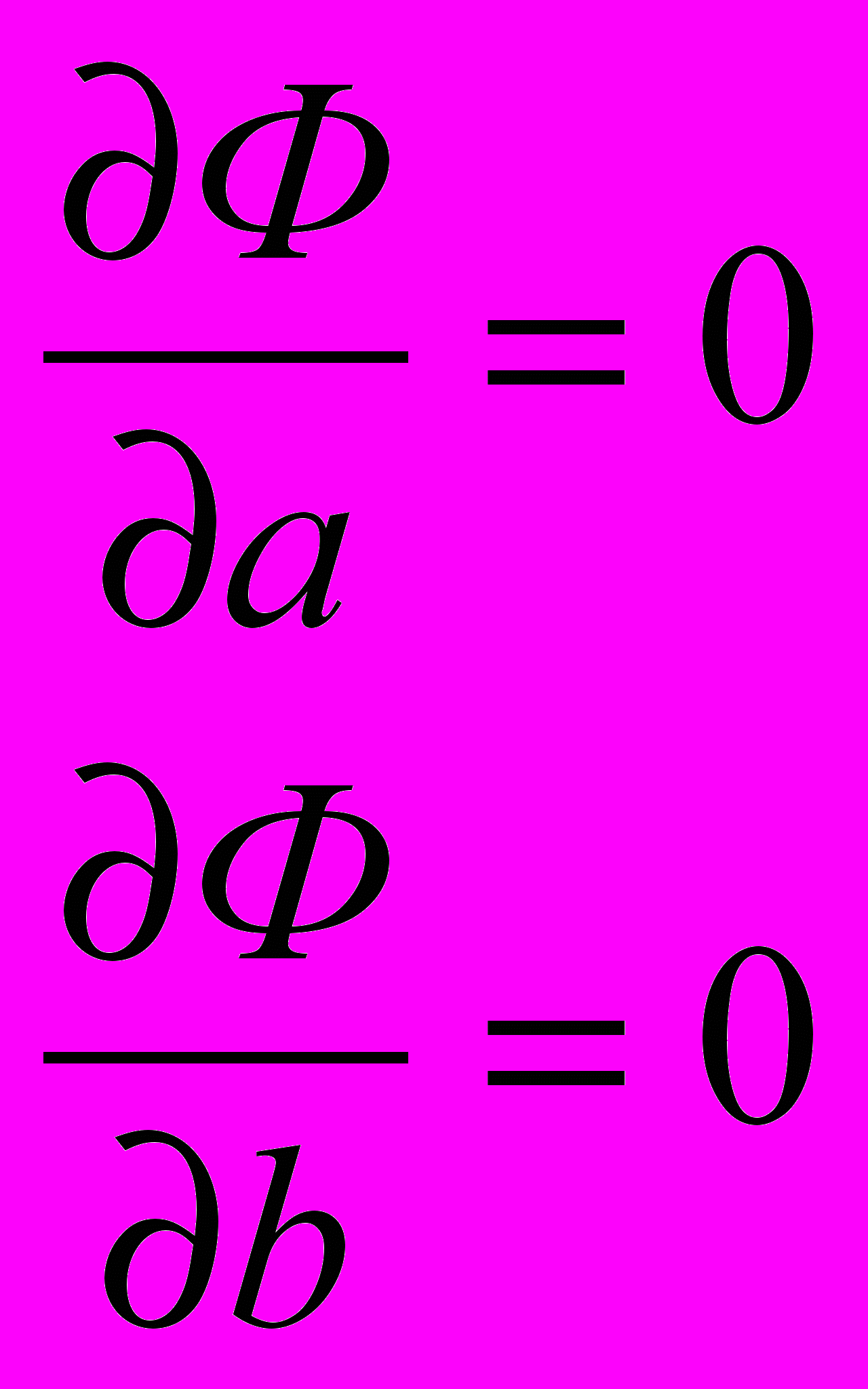
Или, после подстановки и взятия частной производной:




Таким образом, получаем систему из двух линейных уравнений с двумя неизвестными (a b), из которой с помощью преобразований получаем:




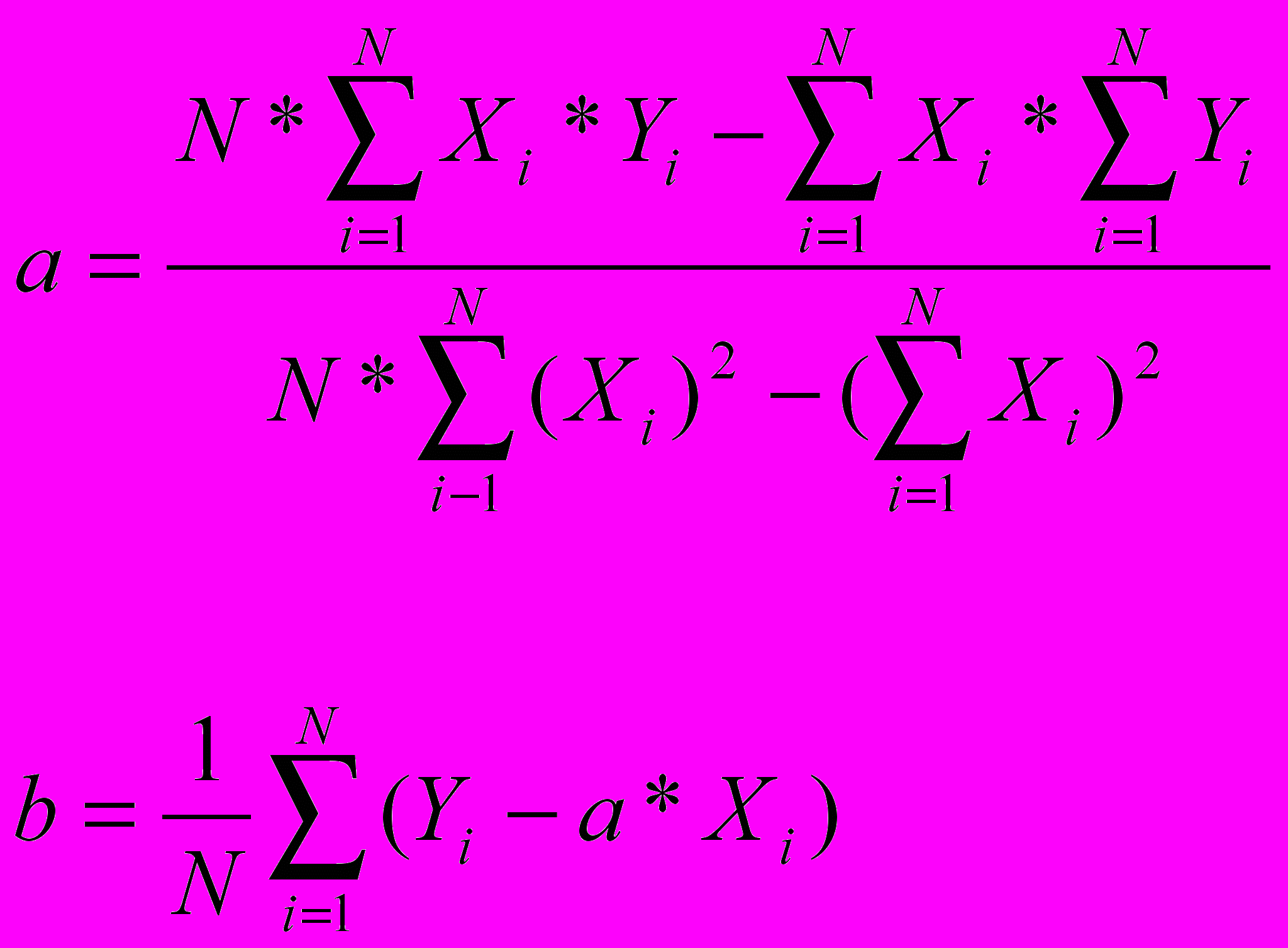
Далее, задавая значения Xi с некоторым шагом, вычисляем по найденным коэффициентам f(Xi) и строим график:




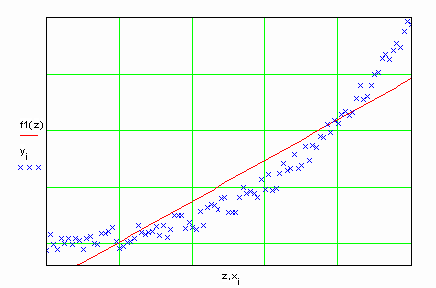
Как видно из графика, точность прогноза с помощью линейной аппроксимации относительно невысока, поэтому ее используют хотя и часто, но только для предварительных оценок и выявления тенденций изменения экспериментальных данных. Для повышения точности расчета используют более сложные аппроксимирующие функции, например, полиномы второго и выше порядка.

(Далее рассказать о постановке и выполнении лабораторной работы по аппроксимации)

(Для студентов элитного отделения дать задание по квадратичной аппроксимации)


Аппроксимация квадратичной функцией и другими функциями


Для повышения точности расчета используют более сложные аппроксимирующие функции, например, полиномы второго порядка:





Порядок решения таких задач полностью аналогичен рассмотренному выше, только меняется вид выражений. Например, рассмотрим аппроксимацию квадратичной функцией.


^ Задан ряд экспериментальных данных, состоящий из пар чисел (Xi, Yi), i =1,…,N


Требуется по этим данным построить квадратичную аппроксимирующую функцию вида




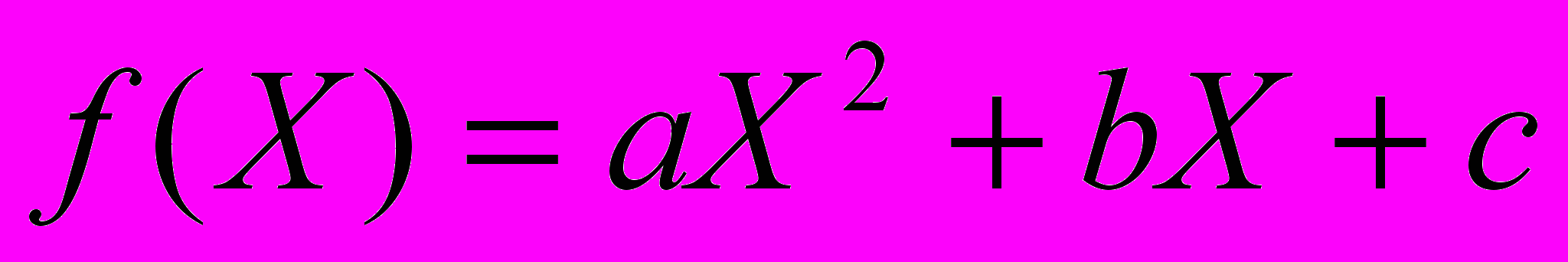
Неизвестными параметрами в этой задаче являются коэффициенты a b с аппроксимирующей функции.

^ Решение (метод МНК)

Запишем указанный выше функционал для заданной аппроксимирующей функции:





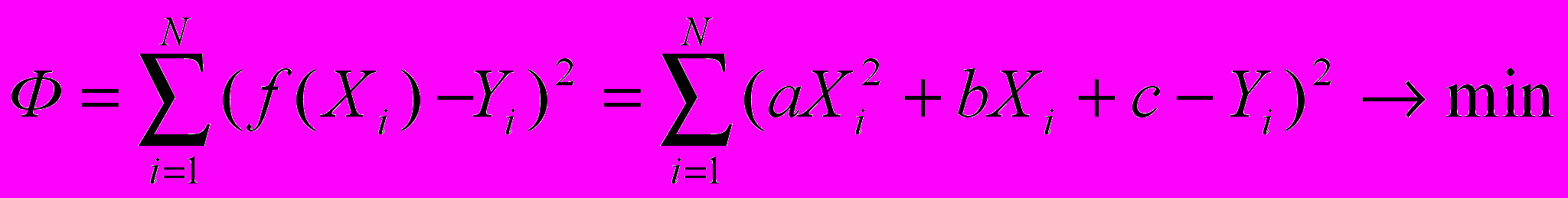
Из математического анализа известно, что минимум функционала достигается при равенстве нулю всех его частных производных по независимым переменным. Таким образом, запишем условие минимума нашего функционала:



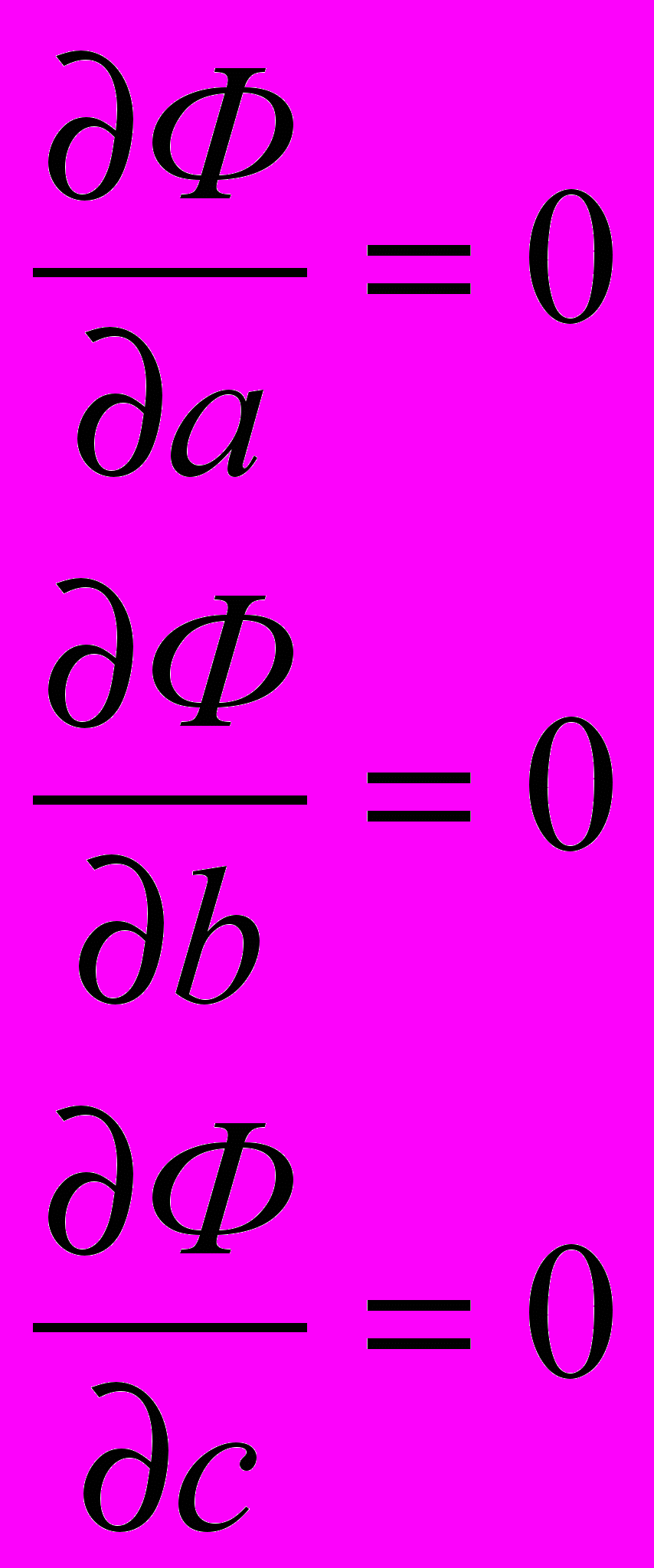
Подставляем выражение функционала Ф и вычисляя производные получим систему из трех уравнений для трех неизвестных, из которой можно записать выражения для искомых коэффициентов (a b c):





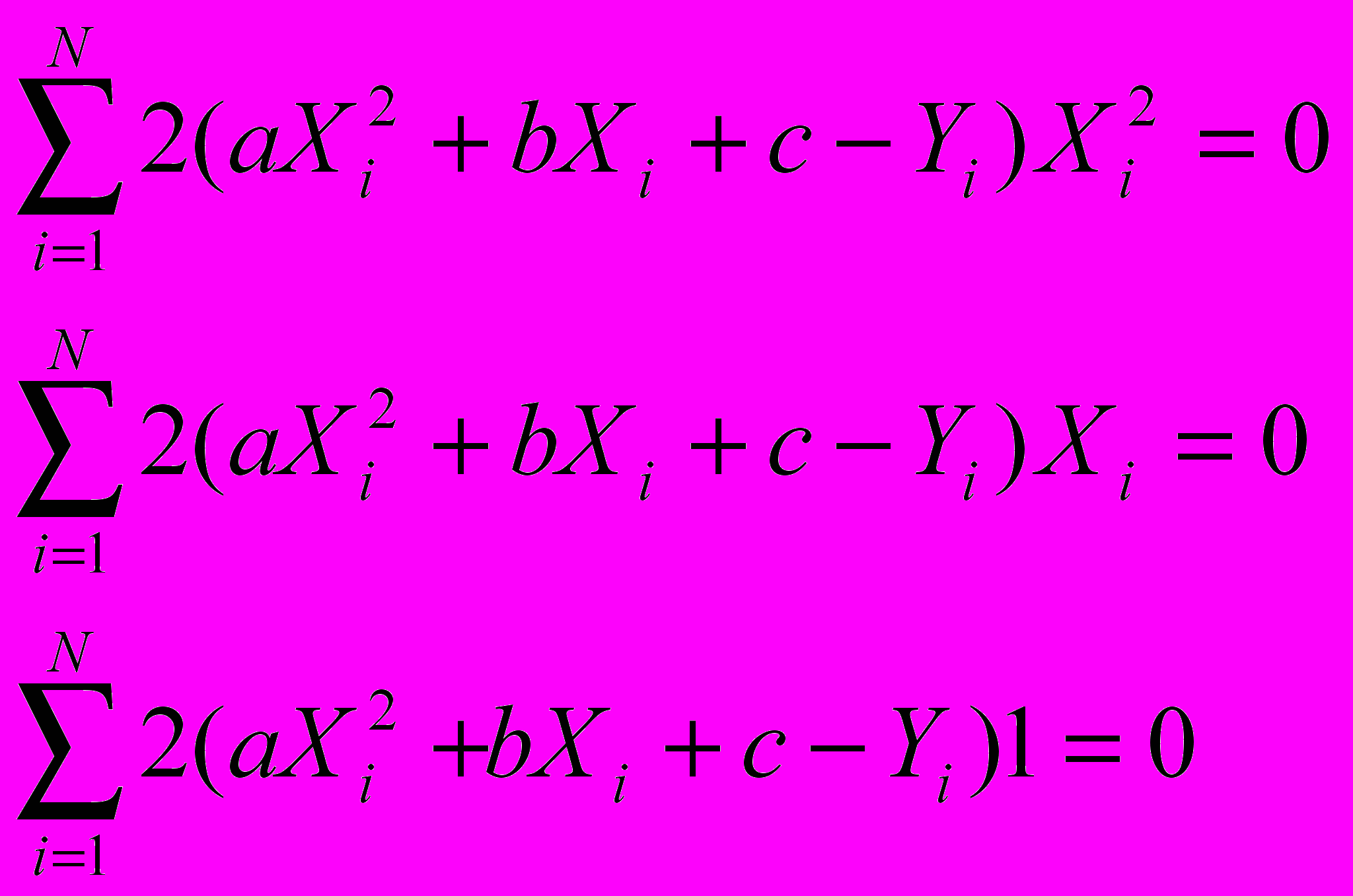
Аналогично строятся аппроксимирующие функции и более сложного вида.


Модели решения функциональных и вычислительных задач

в нефтегазовом деле (продолжение). Численное интегрирование


Одной из главных задач нефтегазогеологии является оценка запасов разведанных месторождений. Для этого они экспериментально «оконтуриваются», то есть определяются координаты (на плоскости и в пространстве) границ залежей. Затем по найденным координатам вычисляются их площади и объемы. Математически эта задача известна как вычисление интеграла по контуру, но аналитическое решение получить невозможно, так как неизвестен вид подынтегральной функции. Поэтому для решения подобных задач применят методы численного интегрирования.


^ Общая постановка задачи

Пусть требуется вычислить определенный интеграл на интервале [a;b].



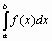
Далеко не всегда задача может быть решена аналитически. В частности, численное решение требуется в том случае, когда подынтегральная функция задана таблично. Для численного интегрирования подынтегральную функцию аппроксимируют какой-либо более простой функцией, интеграл от которой может быть вычислен. Обычно в качестве аппроксимирующей функции используют полином. В случае полинома нулевой степени метод численного интегрирования называют методом прямоугольников, в случае полинома первой степени – методом трапеций, в случае полинома второй степени – методом Симпсона. Все эти методы являются частными случаями квадратурных формул Ньютона-Котеса.

(показать примеры на графиках)

^ Решение задачи

Метод прямоугольников, как наиболее простой здесь не рассматривается и в лабораторной работе его будем применять только для демонстрации снижения погрешности расчета с помощью более точных методов на одном и том же наборе экспериментальных данных

В методе трапеций подынтегральную функцию аппроксимируют полиномом первой степени, то есть прямой линией. Это значит, что вместо площади криволинейной трапеции мы будем искать площадь прямоугольной трапеции. Приближенное значение интеграла равно



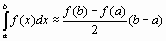
Погрешность этой формулы равна .

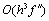Обозначим , где 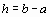. Смысл введенного обозначения станет ясен несколько позже.

Оценку значения интеграла можно сделать более точной, если разбить интервал на n частей и применить формулу трапеций для каждого такого интервала

.

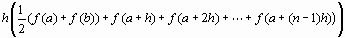Если разбить интервал на две части, то есть уменьшит шаг в два раза 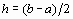, то оценка для величины интеграла будет иметь вид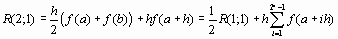



В данном случае суммирование включает только один элемент. Обратите внимание, в новую оценку вошла старая оценка. Нам потребовалось определять значение функции только в новых узлах.

Если имеется 2ⁿ подынтервалов, то





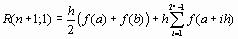
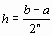
Если n=0, то



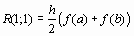
Если n=1, то



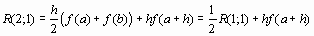
Если n=2, то



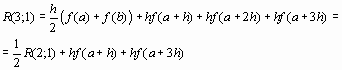
Вообще, справедливо рекуррентное соотношение



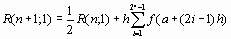
Полученное соотношение называют рекурсивной формулой трапеций и часто применяют для вычисления определенных интегралов. Преимущество этой формулы состоит в том, что при увеличении числа подынтервалов функцию нужно вычислять только во вновь добавленных точках. К сожалению, с помощью этой формулы нельзя получить сколь угодно точное значение интеграла. Во-первых, при увеличении числа разбиений объем вычислений стремительно возрастает; во-вторых, на каждом шаге накапливается ошибка округлений. Для дальнейшего уточнения значения интеграла можно сделать следующий шаг – экстраполировать полученную последовательность значений на случай бесконечного числа точек или что то же самое, на случай нулевого шага. Такой подход называется методом Ромберга.

Метод Ромберга заключается в том, что полученные оценки значения интеграла экстраполируют на случай бесконечного числа разбиений (величины шага равной нулю) по рекуррентной формуле



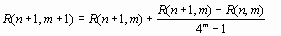
То есть строится следующий треугольник

R(1,1)

R(2,1) R(2,2)

R(3,1) R(3,2) R(3,3)

R(4,1) R(4,2) R(4,3) R(4,4)

R(5,1) R(5,2) R(5,3) R(5,4) R(5,5) ,

в котором первый столбец состоит из значений интеграла, полученных при последовательном удвоении числа интервалов. Второй столбец – результат уточнения значений первого столбца по рекуррентной формуле . Третий столбец – уточненные значения интеграла на основе второго столбца и т.д.

Формула может быть получена различными способами. Можно, например, воспользоваться методом Невиля. Пусть имеется набор точек . Обозначим полином нулевой степени, проходящий через i-ю точку. Обозначим полином первой степени, проходящий через точки i и i+1. Совершенно аналогично будет означать полином n–1 степени, проходящий через все n точек. Легко убедиться, что



В нашем случае 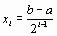. В качестве 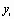выступают 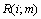. Мы хотим получить значение интеграла в пределе 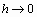, поэтому .

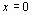( далее продемонстрировать лабораторную работу)

Вычисление определенных интегралов в системе Mathcad

 Для вычисления определенного интеграла необходимо выбрать знак интеграла из палитры или набрать его нажатием клавиши &. После этого следует вписать пределы интегрирования, подынтегральную функцию и переменную интегрирования. Mathcad успешно справляется с большинством интегралов, в том числе, с несобственными. Точность вычислений регулируется встроенной переменной TOL. По умолчанию ее значение установлено 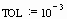. Ниже приводится несколько примеров успешного вычисления несобственных интегралов, интеграла от быстро осциллирующей функции и интеграла от ступенчатой функции.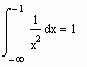





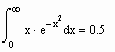
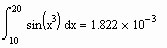
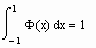
Здесь

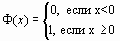
Зависимость результата от заданной точности вычислений представлена ниже







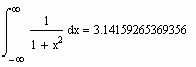
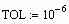
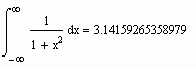
Для этого примера результат может быть получен также в символьном виде. Для этого вместо знака равенства необходимо нажать знак символического равенства Ctrl+.



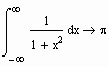
В то же время в некоторых случаях несобственные интегралы вычисляются неправильно.



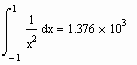
Хотя очевидно, что




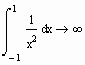
Модели решения функциональных и вычислительных задач

в нефтегазовом деле (продолжение). Поиск особых точек


Не менее важной задачей в нефтегазогеологии является поиск так называемых «особых точек» в экспериментальных данных. Это могут быть минимумы или максимумы в профилях контуров нефтяных залежей, точки пересечения различных линий уровня и т. п. Визуализация этих данных в графическом виде до некоторых пор была едва ли не единственным способом поиска таких точек. Однако в связи со значительным ростом количества экспериментальных данных и применением компьютерных методов обработки поиск особых точек также стали выполнять с помощью алгоритмизации. Существует множество методов поиска, рассмотрим три фундаментальных метода, наиболее ярко демонстрирующие те или иные подходы к решению подобных задач. Это метод дихотомии (деления пополам), метод хорд-касательных (Ньютона), и метод Монте-Карло (случайного поиска). В качестве «особых точек» будем рассматривать только точки пересечения некоторой функцией (заданной таблично или аналитически) оси ОХ (нули функции). К такой постановке могут быть сведены задачи поиска и других видов особых точек. Напомним (из математики), что точки пересечения графика функции f(x)=0 оси ОХ называются корнями этого уравнения.

( Дать определения: итерации, последовательное приближение, сходимость, скорость сходимости, условия сходимости)


Метод дихотомии (деления пополам)


(пояснить рисунками)




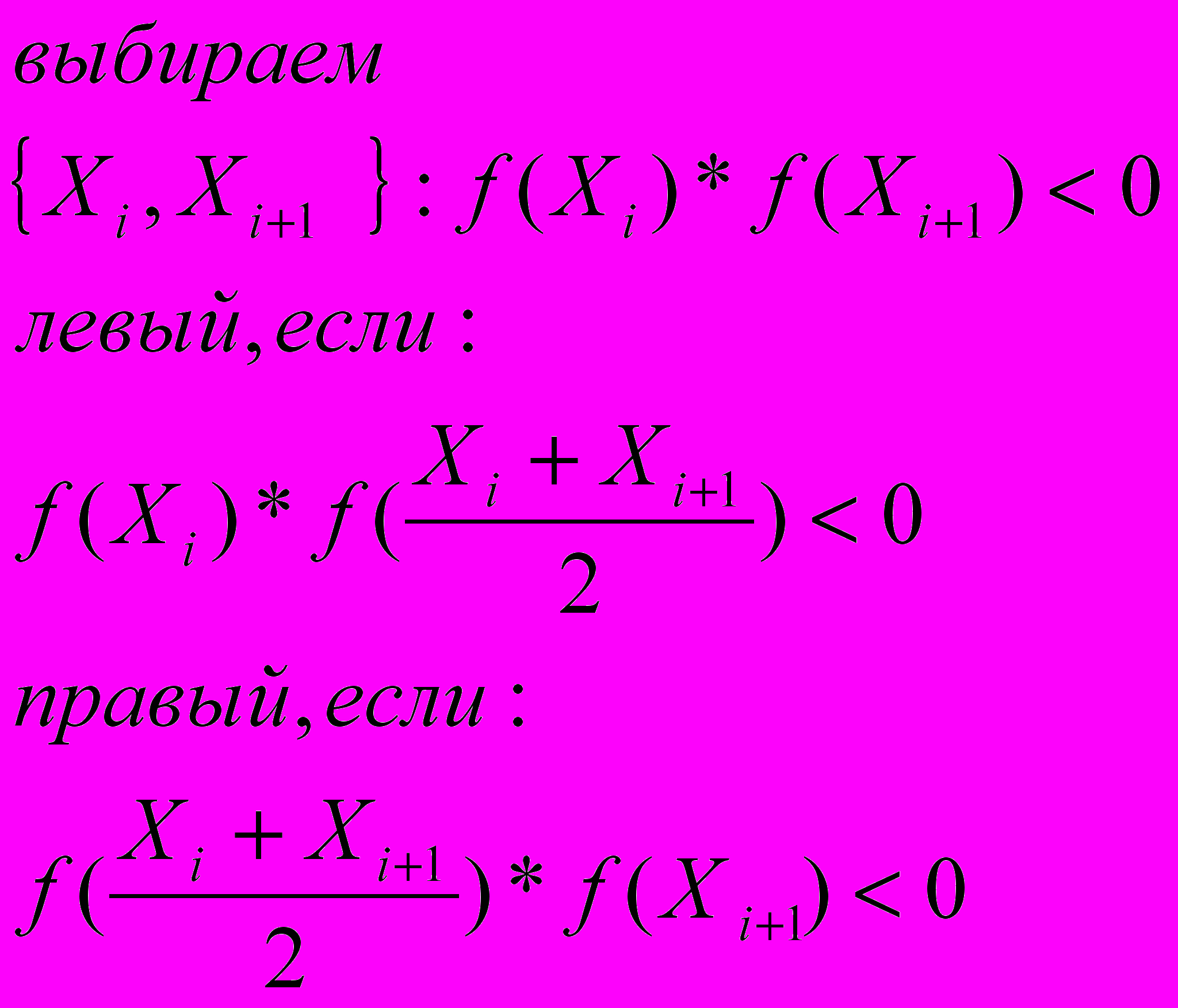
Модификация – метод золотого сечения, который применяют для поиска экстремумов. Метод золотого сечения позволяет исключать интервалы, вычисляя только одно значение функции на каждой итерации. В результате двух рассмотренных значений функции определяется интервал, который должен использоваться в дальнейшем. Этот интервал будет содержать одну из предыдущих точек и следующую точку, помещаемую симметрично ей. Точка делит интервал на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т. е. равно так называемому «золотому сечению».

Метод хорд-касательных (Ньютона)


В чистом виде метод Ньютона (или метод касательных) формулируется следующим образом:

Действительный корень x' уравнения f(x) = 0 вычисляется методом Ньютона по итерационному уравнению:

x_k+1  = x_k  - f(x_k )/f'(x_k )

Процесс сходится к точному значению корня, если начальное приближение x₁  выбрано так, что

|f(x₁ )f''(x₁ )| < |f'(x₁ )| ²

Оценка погрешности k-го приближения производится по приближенной формуле

|f(x_k )f'(x_k )| < e


( пояснить рисунками)

Недостатком этого метода является необходимость вычислять производную на каждой итерации, поэтому на практике чаще используют модификации этого метода, известные, как метод хорд, метод секущих, комбинированные методы хорд-касательных-секущих.



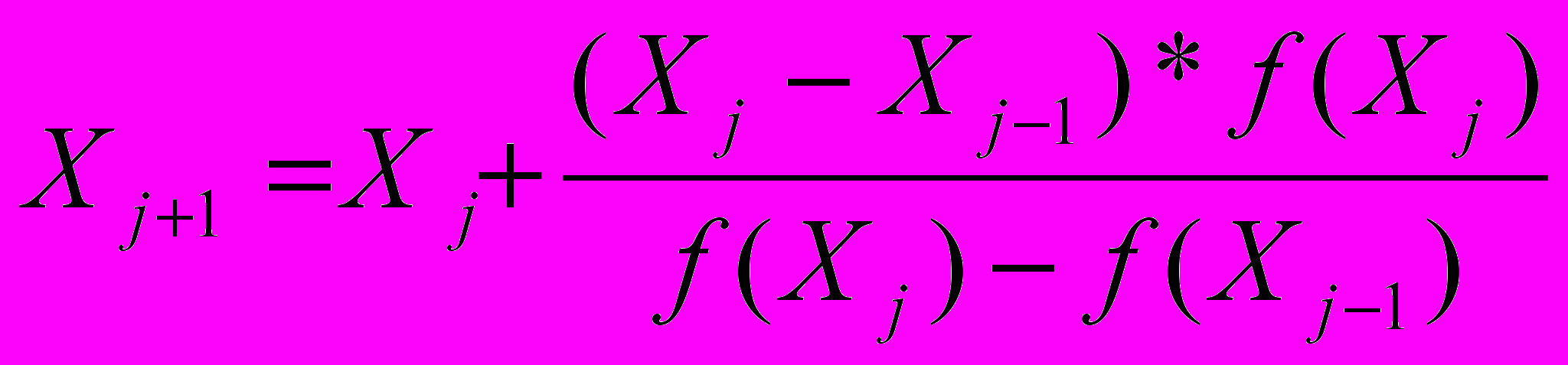
( пояснить рисунками)


( далее продемонстрировать лабораторную работу и фрагменты программ)


Метод Монте-Карло (случайного поиска)


Датой рождения метода Монте-Карло принято считать 1949 год, когда американские ученые Н. Метрополис и С. Услам впервые опубликовали статью с аналогичным названием «Метод Монте-Карло», в которой были изложены принципы этого метода. Свое название метод получил в честь города Монте-Карло, славящимся своими игорными заведениями, непременным атрибутом которых является рулетка -- одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых и основан этот метод.

Метод Монте-Карло -- это статистический метод, его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации и массового обслуживания, при исследовании сложных систем (экономических, биологических и т. д.).

Сущность метода состоит в том, что в решаемую задачу вводят случайную величину , изменяющуюся по какому-то закону 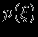. Как правило, случайную величину выбирают таким образом, чтобы искомая в задаче величина 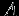стала математическим ожиданием от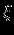



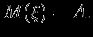
Таким образом мы определяем искомую величину 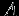лишь теоретически. А вот чтобы найти ее численно, пользуются статистическими методами: берут выборку случайной величины 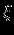объемом 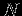элементов. В результате получают 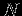вариант случайной величины 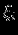, для которых вычисляют их среднее арифметическое (выборочное среднее)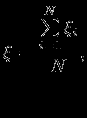



которое и принимают в качестве приближенного значения (оценки) искомой величины :



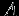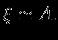
Для получения результата приемлемой точности по методу Монте-Карло требуется большое число статистических испытаний. Именно поэтому этот метод иногда так и называют: метод статистических испытаний.

При поиске экстремумов, часто возникает проблема «ловушки локального экстремума», которую многие алгоритмы не могут преодолеть. Метод Монте-Карло один из немногих, который позволяет находить глобальный экстремум. Существует множество модификаций этого метода, в частности метод «моделируемого отжига», который применяют для поиска глобальных экстремумов. Метод «моделируемого отжига» строится на аналогии постепенного охлаждения нагретого до температуры плавления металла, при которой атомы, первоначально находящиеся в беспорядочном движении, последовательно занимают все более низкоэнергетическое состояние, пока не будет достигнуто наименьшее из возможных энергетических состояний – глобальный минимум.

При реализации этой аналогии в виде алгоритма «закон» понижения «температуры» должен быть таким, чтобы каждый атом Аi имел достаточно «энергии» для преодоления «потенциального барьера» и перехода в более «низкоэнергетическое состояние», но недостаточно «энергии» для возврата в более «высокоэнергетическое состояние». В терминах поиска глобального минимума это означает обеспечение выхода из текущей ловушки локального минимума, и не возвращение в предыдущую ловушку локального минимума.


( далее продемонстрировать работу программы ММК)