Нашей основной целью является изучение подходов для построения синтаксического анализатора языка программирования высокого уровня

Вид материала

Документы

Содержание Любая КС-грамматика эквивалентна такой КС-грамматике в нормальной форме Хомского, где в правых частях продукций не встречается н

Подобный материал:

• Рабочая программа по курсу "Программирование на языках высокого уровня" Факультет экономический, 113.19kb.
• Аннотация рабочей программы учебной дисциплины языки программирования Направление подготовки, 135.09kb.
• Сборник заданий по методам программирования, 665.7kb.
• Сборник заданий по методам программирования, 665.53kb.
• Программа курса «Программирование на языке высокого уровня», 126.66kb.
• Рабочая программа по дисциплине Программирование на языке высокого уровня для специальности, 182.97kb.
• Рекурсивно-логическое программирование, 48.32kb.
• Пояснительная записка к курсовой работе по предмету «Языки и технологии программирования», 353.31kb.
• Тематика курсовых работ по курсу «проектирование информационных систем», 13.87kb.
• Краткий курс по изучению языка программирования Visual Basic, 357.37kb.

17. МП-автоматы


Нашей основной целью является изучение подходов для построения синтаксического анализатора языка программирования высокого уровня. Основная работа при этом заключается в построении дерева разбора. Практически все языки полностью описываются в помощью нотации Бэкуса-Наура, т.е. посредством контекстно-свободной грамматики. Как мы увидим, не любая КС-грамматика годится для того, чтобы на ее основе строить систаксический анализатор. Тем не менее мы начнем с дальнейшего изучения КС-грамматик в общем виде. На очереди описание КС-языков с помощью автоматов с магазинной памятью (МП-автоматов).


Автомат с магазинной памятью (МП-автомат) это структура

A = < Q,T, M ,  , s, F>


где:

Q,T, M – конечные множества (состояний, терминалов, магазинных символов),

 : Q (T {})(M {})  P(Q(M {})) – функция,

s  Q – начальное состояние,

F  Q. – множество заключительных (конечных) состояний,

 – символ, обозначающий пустое место.

P(S) – множество всех подмножеств множества S, включая пустое.

Общая схема МП-автомата представлена на рисунке



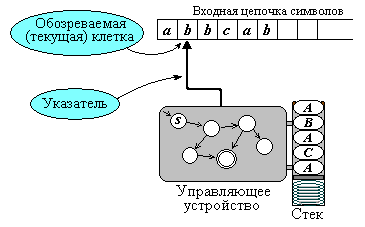
 – это функция переходов. Если (q,B)   (p,a,A), то это понимается как команда, согласно которой:

1) автомат из состояния p переходит в состояние q;

2) если a и a – символ входной цепочки в обозреваемой клетке, то указатель с этой клетки переходит на соседнюю клетку справа (обработка символа a); при a= указатель остается на месте;

3) если A и A - верхний символ стека, то:

• при B символ A в вершине стека заменяется символом B;
  
• при B= символ A из стека выкидывается;
  

4) если A=, то:

• при B в стек кладется символ B;
  
• при B= стек не меняется.
  

При изображении управляющего устройства МП-автомата в виде графа описанная выше команда изображается на стрелке, идущей из состояния r в состояние p, в виде метки a/AB



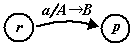
Для изображения меток используем соглашения: /AB пишем как AB;B пишем как B;  не пишем вовсе;

Конфигурация – это информация о состоянии автомата, которая полностью определяет возможности его дальнейшего поведения. Конфигурация включает нформацию о текущем состояни, о непрочитанном еще содержимом ленты и о содержимом стека. Записывается конфигурация в виде тройки

, , >,

где p - состояние,  - цепочка терминалов на ленте от текущего указателя (непрочитанная часть),  - содержимое стека (при  =a₁a₂…a_n a₁– верхний символ стека, a₂ - символ под ним и т.д.)

Если согласно какому-то (q,B)   (p,a,A) автомат из конфигурации , , > может перейти в конфигурацию , ’, ’>, то пишем , , >  , ’, ’>. Транзитивное замыкание этого отношения обозначаем как _*.


Начальной или стартовой конфигурацией МП-автомата является конфигурация , , >. Конечной или заключительной называется любая конфигурация вида , , > при условии, что p – одно из заключительных состояний.

Говорим, что цепочка  терминалов воспринимается автоматом, если

, , > _* , , >

для некоторой заключительной конфигурации , , >.

Множество всех цепочек, воспринимаемых автоматом A, называется языком, который распознает A, и обозначается L(A). Если для языка L существует такой автомат A, что L = L(A), то язык L называется МП-автоматным.

Два МП-автомата A₁ и A₂ называются эквивалентными, если L(A₁)= L(A₂).


Теорема. Класс языков, распознаваемых МП-автоматами, совпадает с классом контекстно-свободных языков.

Для того, чтобы доказать эту теорему, нам надо установить истинность таких двух фактов.

Лемма 1. Любая КС-грамматика эквивалентна такой КС-грамматике в нормальной форме Хомского, где в правых частях продукций не встречается начальный нетерминал грамматики.

Доказательство. Приведем данную КС-грамматику к нормальной форме Хомского бех дополнительного условия в лемме. Если в полученной грамматике есть правила вида ABС, где или B или С совпадает с S – начальным нетерминалом, то делаем следующее.

1) Вводим в множество нетерминалов новый символ T.

2) Во всех продукциях ABС заменяем в правой части символ S на T.

3) Для каждой продукции S добавляем правило T.

Легко видеть, что новая грамматика эквивалентна прежней. Получаем результат.


Лемма 2. Любой МП-автомат эквивалентен такому МП-автомату в котором:

• единственное заключительное состояние;
  
• для функции переходов  при любых (q,B)   (p,a,A) равно один из символов A, B равен  (т.е. при операциях со стеком либо только один символ кладется в стек и ничего не выкидывается, либо только один символ из стека выкидывается и ничего не кладется) .
  
• если автомат воспринимает какую-то цепочку, то в момент остановки его стек пуст.
  

Доказательство. Cделаем заключительное состояние единственным и сразу обеспечим третье условие. Для этого:

1) введем новое состояние на роль стартового и проведем из него переход в прежнее стартовое с меткой , где  - новый магазинный символ, который будет играть роль маркера дна стека.

2) введем новое состояние f на роль заключительного и добавим еще одно состояние g – очиститель стека. Из g в f проведем связь с меткой . Для каждого из магазинных символов Z, не равных , на состояние g навесим петлю c меткой Z, Все прежние элементы из множества заключительных выкинем. но проведем из них связь в g с меткой .



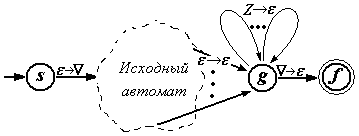
Для обеспечения второго условия в каждый переход a/ встраиваем новое состояние с переходами a/U и U для нового магазинного символа U, а в каждый переход a/AB встраиваем новое состояние с переходами a/A и B.


Доказательство теоремы. Доказываем, что любой КС-язык является МП-автоматным. Берем такой язык и рассматриваем грамматику G в нормальной форме Хомского, которая его определеяет. Считаем по лемме 1, что начальный символ S грамматики G не входит ни в одну из правых частей ее продукций. Для начала считаем, что пустое слово не выводится в этой грамматике.

Итак, G – грамматика указанного вида. Строим по ней МП-автомат A.

Состояниями автомата A являются: s, w, g, f и q_ для каждой продукции  вида ABC.

Терминалы A - это терминалы G.

Магазинный алфавит M состоит из всех нетерминалов G и одного дополнительного символа , который будет лежать на дне стека.

Состояние w – стартовое, f - заключительное.


Схематический вид автомата



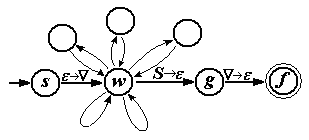
Каждый лепесток сверху соответствует одной продукции вида A  BC. В более крупном масштабе его можно изобразить



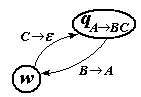
Смысл путешествия из w в q_{A  BC} и обратно в том только, что верхушка стека из двух символов CB заменяется одним символом A.

Каждая петля снизу соответствует одной продукции вида A  a. В более крупном масштабе ее можно изобразить



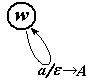
Эта петля означает, что автомат обрабатывает текущий символ a и одновременно заносит в стек символ A, ничего из него не вынимая. Эти петли – единственные места, передвигающие головку автомата вправо.

Продемонстрируем работу автомата и суть доказательства эквивалентности с помощью примера грамматики:

S  AB |AC | a, A  AB | a, B  BC | b, C  b | c

Автомат для этой грамматики есть



Например, для цепочки abbc можно найти два разных вывода

S  AB  ABB  ABBC  aBBC  abBC  abbC  abbc

с деревом разбора



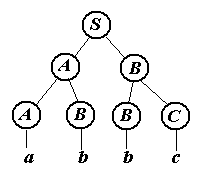
и

S  AC  ABC  ABCC  ABBc  ABbc  Abbc  abbc

с деревом разбора



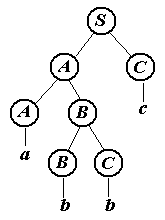
Распознавание этой цепочки автоматом будет идти, параллельно обрезанию у дерева либо листа с терминалом, либо пары смежных листьев с нетерминалами. Каждое такое действие определяет траекторию на переходах автомата. Отрезание терминала a под нетерминалом A, например, - это движение по петле с меткой a/A - читается символ a, а A заносится в стек. Обрезание пары нетерминалов, например A, B под A для автомата означает путешествие в состояние q_AAB с выкидывание из стека символов B, A и с занесением A. Покажем последовательность обрезаний на каждом из деревьев и состояния стека при этих действиях..


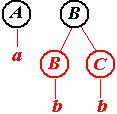
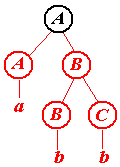
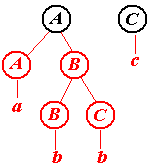
Первое дерево



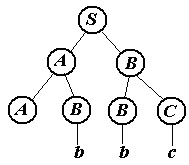
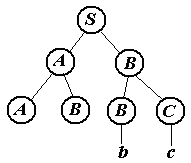
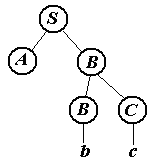
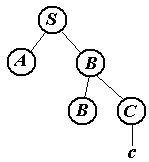
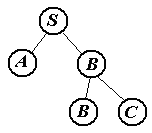
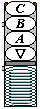
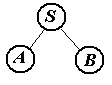
Обрезаемые части (нарисованы красным цветом).

^{}

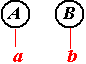
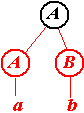
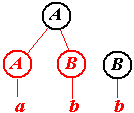
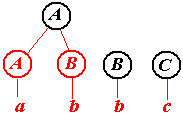
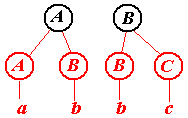
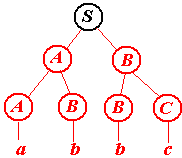
Нетрудно догадаться, что последняя серия рисунков иллюстрирует построение дерева вывода снизу вверх. По этой причине говорят, что построенный нами автомат осуществляет разбор слева направо и снизу вверх. Этот же автомат может строить дерево и иначе (хотя все-равно слева направо и снизу вверх).

Второе дерево.



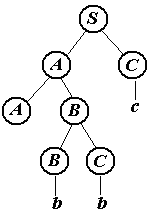
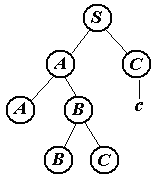
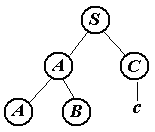
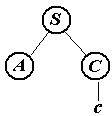
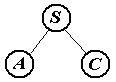
Обрезаемые части (нарисованы красным цветом).

^{}.


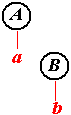
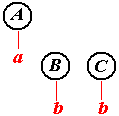
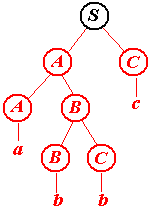Как видим, в любом случае конец один – автомат считал входную цепочку и оказался в состоянии w имея символы S, в стеке. Теперь ему остается только перейти в состояние g и далее – в заключительное. Продемонстрированная работа автомата синхронно с обрезанием дерева вполне убеждает в том, что автомат воспринимает любую выводимую в грамматике цепочку. Желающие иметь более строгое доказательство должны индукцией проверить такое утверждение: на каждом шаге последовательность листьев дерева, прослеживаемая слева направо, сначала содержит одни нетерминалы, затем только терминалы; нетерминалы в обратном порялке – содержимое стека (без ), терминалы – непрочитанная часть. При этом надо иметь ввиду, что алгоритм обрезания состоит в просмотре листьев текущего дерева слева направо и в поиске либо первого терминала, либо первой пары смежных нетерминалов.

Теперь надо понять, что построенный автомат не может воспринять лишнюю цепочку, т.е. то, что он воспринимает, выводится в грамматике. Допустим, что автомат воспринял некую цепочку. Совершенно ясно, что после перехода в заключительное состояние его стек пуст. А перед переходом в состояние g в стеке лежит S. В силу того, что левые части правил вывода буквы S не содержат, до перехода в состояние g у автомата нет возможности выкинуть из стека символ S однажды туда попавший. S может оказаться в стеке только при переходе в w. Более того, если после этого S в стек попадет еще какой-нибудь символ, то при переходах по петлям автомата этот S никак не сможет оказаться на вершине стека. Значит после появления в стеке первого S есть одна дорога – только в g и в f.

Отдельно стоит рассмотреть случай, когда символ S попадает в стек благодаря продукции S a, т.е. при переходе 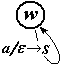. Этот случай просто означает, что автомат имел на входе цепочку из одного единственного терминала a, которую благополучно распознал. Естественно a выводится в грамматике.

Таким образом считаем что S проник в стек при переходе из верхней части диаграммы. Рассмотрим теперь траекторию переходов автомата, пока он бегает из состояния w и обратно до момента появления этого первого S в стеке. В конце пути вся входная цепочка считана. Расположим все переходы траектории в обратном порядке. Вот еще пример:



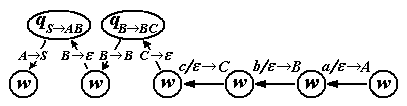
Это соответствует считыванию цепочки abc. И тут же мы видим ее вывод в грамматике: S  AB  ABC  ABc  Abc  abc.

Строгое доказательство можно получить как и в предыдущем случае сформулировав соответствующий инвариант для движения по таким последовательностям и доказав его по индукции.

Последнее замечание касается случая, когда исходная грамматика имеет продукцию S, т.е. распознает пустую цепочку. В этом случае надо в нашей конструкции автомата просто сделать стартовое состояние s еще и заключительным.


Для доказательства теоремы в обратную сторону надо по МП-автомату построить эквивалентную ему грамматику. По лемме 2 существует МП-автомат, эквивалентный данному с единственным заключительным состоянием, у которого на каждом шаге либо один символ кладется в стек, либо один символ выкидывается из стека. Кроме того этот автомат устроен таким образом, что если он воспринял какую-то цепочку, то в момент остановки его стек становится пустым. По этому автомату КС-грамматика строится так.

Для любой пары состояний <p,q> вводится нетерминал A_p,q. Далее в грамматику заносятся:

продукции A_p,p для всех состояний p автомата;

продукции A_p,w aA_q,r bA_v,w для всех состояний p,q,r,v,w автомата, переходов

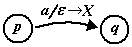и .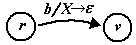

и магазинных символов X. Здесь a,b либо терминалы, либо пустые цепочки.


Начальным нетерминалом грамматики является символ A_s,f, где s – начальное состояние автомата, f – конечное.

Нетерминал A_p,q обозначает множество всех терминальных цепочек, которые может прочитать автомат при переходе из состояния p в состояние q при условии, что он начинает с пустого стека и заканчивает пустым стеком. Суть рассуждения, которое мы не будем проводить в деталях, заключается в следующем. Предположим, что автомат совершил путешествие из состояния p в состояние q и по пути распознал цепочку  в указанном выше смысле. Т.к. он начинает с пустого стека, то на первом шаге он с стек кладет какой- символ X. Это переход 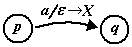. А т.к. автомат заканчивает пустым стеком, этот X должен удалиться на каком то переходе 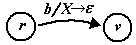. На пути от q до r автомат работает, начиная с X в стеке и так же заканчивает и прочитывает какую-то терминальную цепочку . Если бы этого X в стеке не было, то поведение автомата на этом участке никак бы не изменилось, т.е. он начиная с пустого стека прочитал бы на этом пути от q до r ту же цепочку и оказался бы в q при пустом стеке. Значит  из тех, совокупность которых обозначает нетерминал A_q,r. Далее автомат выкидывает X из стека, считывая b, и как то из состояния v добирается до w опять начиная и заканчивая пустым стеком. Значит считанная на этом участке цепочка  лежит в классе A_v,w. Теперь понятно, почему  = ab соответствует aA_q,r bA_v,w.