Geum.ru

3. Классификация систем автоматического управления

Вид материалаДокументы

Содержание


Система стабилизации
Пример 3-1.
Подобный материал:
3.Классификация систем автоматического управления.


3.1. Классификационные признаки.


Автоматические системы можно классифицировать по многим признакам: по назначению (системы управления станками, летательными аппаратами, антеннами радиолокационной станции и т.п.); по характеру управляемых величин (системы регулирования напряжения, частоты, скорости, ускорения, температуры, давления и др.); по виду используемой для управления энергией (электрические, электронные, гидравлические, пневматические и др.) и т.п. [1.2].

В зависимости от числа регулируемых величин системы подразделяются на одномерные и многомерные.

Одномерной АСР называется система с одной регулируемой величиной.

Многомерными называются системы с несколькими регулируемыми величинами.

Многомерные системы в свою очередь подразделяются на системы несвязанного и связанного регулирования.

Системами несвязанного регулирования называются такие, в которых регуляторы непосредственно не связаны и могут взаимодействовать только через общий для них объект регулирования.

Системами связанного регулирования называются системы, в которых регуляторы различных параметров одного и того же технологического процесса связаны между собой вне объекта регулирования. Если этими связями исключается влияние регулируемых величин друг на друга, система связанного регулирования называется автономной.

Кроме того, автоматические системы подразделяются на разомкнутые и замкнутые; подразделяются по характеру изменения задающего воздействия Xвых.(t) (т.е. по виду закона управления); по величине установившейся ошибки; по способу, передачи и преобразования сигналов; по виду дифференциальных уравнений. Рассмотрим классификацию автоматических систем по основным классификационным признакам.


3.2. Разомкнутые и замкнутые автоматические системы.


При изучении принципов автоматического управления отмечалось, что в зависимости от примененного при построении системы принципа автоматического управления, системы автоматического управления могут разомкнутые и замкнутые.

Если при построении системы был использован принцип управления по возмущению, то такая автоматическая система работает по разомкнутой цепи, т.е. является разомкнутой.

При использовании принципа управления по отклонению автоматическая система строится с применением О.С. и работает по замкнутой цепи, т. е. является замкнутой.

Как уже отмечалось, наиболее широкое применение в технике получили замкнутые системы, т.е. системы с О. С. . Их изучению будет уделено основное внимание в нашем курсе лекций.


3.3. Классификация автоматических систем по характеру изменения задающего воздействия

Xвх. (t) (по виду законов управления).


По характеру изменения задающего воздействия Xвх.(t) автоматические системы разделяются на три типа: системы стабилизации, программные системы и следящие системы [Л.2.].

Система стабилизации – это автоматическая система, предназначенная для поддержания с заданной точностью постоянного значения управляемой величины.

В
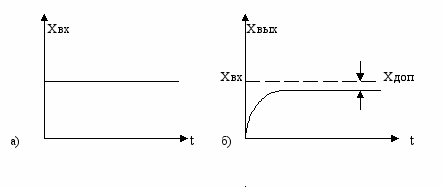
этой системе требуемое значение управляемой величины постоянно, а ошибка (рассогласование) в установившемся режиме  X уст. не должна превосходить допустимой величины  X доп.:

X вх. = const;  X уст. = X вх. – X вых.  X доп.


Рис. 3-1

Влияние возмущающих воздействий в системе стабилизации резко снижается или полностью устраняется. Примерами систем стабилизации являются системы стабилизации напряжения, частоты, скорости, температуры, давления и др.


Пример 3-1. Рассмотрим систему стабилизации температуры. [Л.5].






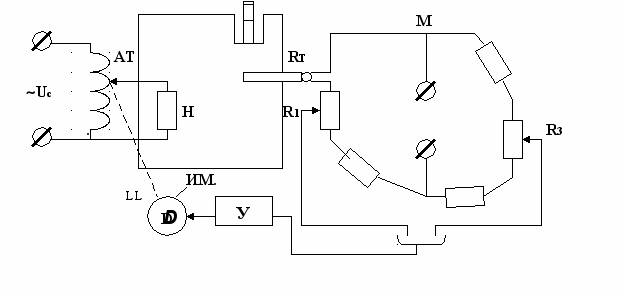
Рис. 3 –1 а)

Р
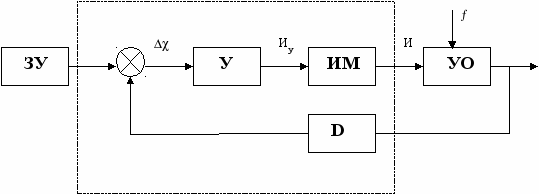
ис. 3 –1 б)

При температуре УО, равной заданной, измерительный мостик М уравновешен, на вход электронного усилителя У сигнал не поступает и система находится в равновесии. При отклонении температуры (н-р, в результате изменения напряжения сети) изменяется сопротивление термометра RT и равновесие мостика нарушается. На входе усилителя У появляется напряжение, фаза которого зависит от знака отклонения температуры объекта от заданной. Напряжение, усиленное в блоке У, подается на электродвигатель D, который начинает вращаться со скоростью, пропорциональной этому напряжению. Направление вращения двигателя зависит от фазы подаваемого напряжения.

Двигатель будет перемещать движок автотрансформатора АТ или в сторону увеличения напряжения, подаваемого на нагревательный элемент Н при уменьшении температуры объекта, или в сторону уменьшения напряжения при ее увеличении. По достижении заданной температуры измерительный мостик сбалансируется и двигатель отключится. При установившемся режиме и отсутствии возмущающих воздействий на объект подается ровно столько энергии, сколько ее необходимо для поддержания заданной температуры, и система находится в равновесии. Величина заданного значения температуры устанавливается перемещением движка резистора R3. (Другие примеры см. 6[Л.2 стр.46], 6[Л.4. стр.36- 38]).

Программная система – это автоматическая система, задача которой заключается в изменении управляемой величины по заранее составленной программе, определяемой задающим воздействием:

Хвх.(t) = Fп.(t); Хуст. = Хвх. – Хвых.  Хдоп.,

где Fп.(t) – программа, заранее известная функция времени. [Л2]

Примеры программных автоматических систем: системы программного управления станками, системы программного управления полетом космических кораблей, системы программного вывода спутников Земли на расчетные орбиты и т. п.

Пример 3- 2. Рассмотрим программную систему управления температуры. За основу возьмем схему (рис. 3-1 а). [Л5]. Если необходимо, чтобы температура нагревательной печи после загрузки ее материалами или изделиями медленно поднималась до определенной величины, которая далее выдерживалась некоторое время постоянной и затем медленно снижалась, то, чтобы автоматизировать технологический процесс по этому закону, следует менять во времени задающее

воздействие на регулятор. Этот закон управления (программа) может быть задан с помощью следующего устройства (рис. 3-3)






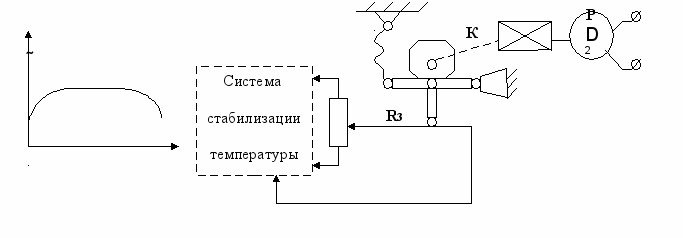
Рис. 3 – 2. Рис. 3 – 3.


Двигатель D2 вращает с определенной скоростью через редуктор Р кулачок К, профиль которого соответствует программе регулирования; кулачок изменяет задающее воздействие в соответствии с этой программой, перемещая движок резистора R3.

Следящая система – это автоматическая система, задача которой заключается в изменении управляемой величины в соответствии с заранее неизвестной функцией времени, определяемой задающим воздействием:

Хвх. (t) = F(t); Хуст. = Хвх.(t) – Хвых.(t)  Хдоп.

где F(t) - заранее неизвестная функция времени [Л. 5.]

В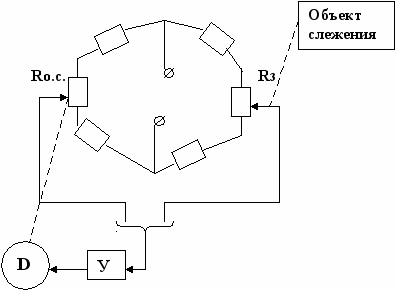ходом системы является перемещение движка резистора R3, а выходом – перемещение движка резистора Rо.с. При сбалансированном измерительном мостике система находится в равновесии. При перемещении движка по любому заранее неизвестному закону нарушается равновесие измерительного мостика и двигатель D будет перемещать движок резистора Rо.с. в сторону восстановления этого равновесия. Таким образом, движок резистора Rо.с. будет повторять все перемещения движка резистора R3.

Пример 3 – 4.

Следящая система отработки угла [Л.2.]. В состав данной следящей системы входят следующие элементы (рис. 3- 5.): сельсины СД и СП, работающие в трансформаторном режиме; фазовый дискриминатор ФА; электромашинный усилитель мощности ЭМУ; исполнительный двигатель Д; редуктор Р и объект управления ОУ, вал которого ПВ должен следить за поворотом командного вала КВ.

Сельсины в трансформаторном режиме выполняют функции элемента сравнения. Ротор сельсин датчика механически связан с командным (ведущим) валом КВ, а ротор сельсин приемника – с приемным (ведомым) валом ПВ. Поэтому на сельсины как на элемент сравнения поступают задающее воздействие (угол  поворота командного вала) и регулируемая величина (угол  поворота приемного вала).

Сельсины выявляют угол рассогласования между командным и приемным валами и преобразуют его в напряжение несущей частоты, величина огибающей которого при малых угла рассогласования пропорциональна углу рассогласования, а фаза несущей частоты определяется знаком этого угла. Если угол рассогласования относительно согласованного положения является положительным, то напряжение несущей частоты совпадает с напряжением питания. При отрицательном угле рассогласования напряжение несущей частоты находится в противофазе с напряжением питания (рис 3-5, б)

Б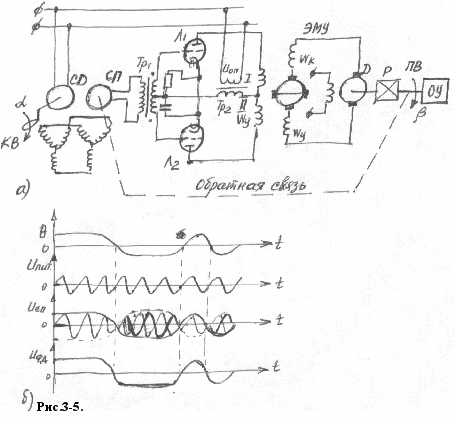удем считать, что положительное значение огибающей модулированного напряжения несущей частоты соответствует случаю, когда напряжение несущей совпадает по фазе с напряжением питания, а отрицательное значение огибающей случаю, когда напряжение несущей частоты находится в противофазе с напряжением питания. Тогда можно сказать , что сигнал рассогласования следящей системы на выходе сельсин- приемника выражен огибающей модулированного напряжения несущей частоты (рис 3-5,б).

Напряжение сигнала рассогласования в следящей системе усиливается. Для этого применен электромагнитный усилитель мощности ЭМУ, т.е. усилитель с входом на постоянном токе. Поскольку на вход ЭМУ необходимо подавать сигнал постоянного тока, то модулированное напряжение несущей частоты с выхода СП нужно предварительно демодулировать, т.е. получить огибающую без её заполнения несущей частоты. Для этой цели служит фазовый дискриминатор ФД.

ФД преобразует напряжение несущей частоты в напряжение постоянного тока, величина которого пропорциональна огибающей входного напряжения, а полярность определяется фазой напряжения несущей частоты (в отличие от обычного детектора), т.е. для демодуляции сигнала (рис. 3-5,б).

С выхода ЭМУ напряжение подается на исполнительный двигатель постоянного тока, который через редуктор связан с приёмным валом сельсин приемника.

Рассмотрим работу следящей системы. При идентичном положении командного и приемного валов угол рассогласования между ними равен нулю. Роторы СД и СП находятся во взаимно-перпендикулярном, т.е. в согласованном положении. Выходное напряжение СП равно нулю. В этом случае потенциалы сеток ламп Л1 и Л2 фазового дискриминатора одинаковы, следовательно, равны между собой и анодные токи этих ламп. Поскольку токи протекают через оба плеча (I и II) обмотки управления ЭМУ в противоположных направлениях, то результирующий магнитный поток обмотки управления равен нулю. Также равно нулю и выходное напряжение ЭМУ. Двигатель и вся система находится в покое.

Допустим, что командный вал повернулся на угол . В результате этого появился угол рассогласования =-, где  - угол поворота приемного вала.

В однофазной обмотке СП возникло напряжение сигнала ошибки переменного тока. Поскольку напряжение сигнала ошибки на сетке ламп Л1 и Л2 поступает в противофазе, то при угле рассогласовании данного знака анодный ток лампы, у которого анодное и сеточное напряжение в фазе, возрастает, а анодный ток другой лампы, у которой анодное и сеточное напряжение находятся в противофазе, уменьшается. Магнитные потоки, создаваемые анодными токами в плечах I и II обмотки управления, будучи неравны, и возникнет результирующий магнитный поток управления, а, следовательно, и напряжение на выходе ЭМУ. Направление результирующего магнитного потока и полярность напряжения ЭМУ зависят от фазы несущей частоты напряжения сигнала ошибки на выходе ФД, т.е., в конечном счете от знака угла рассогласования.

Напряжение с ЭМУ, являющееся управляющим воздействием, поступает на двигатель Д, который вращает через редуктор приемный вал и ротор СП в сторону уменьшения угла рассогласования до тех пор, пока этот угол не станет равным нулю.

В данной следящей системе использован принцип по отклонению. Регулируемая величина  через обратную связь подается на элемент сравнения с задающим воздействием , в результате чего выявляются отклонения между величинами  и . Последнее используется для управления работой системы.


3.4. Статические и астатические системы.


По величине установившейся ошибки автоматические системы подразделяют на статические и астатические [Л.2].

Если при постоянном полезном (Хвх=const) или вредном (Fk=const) воздействии на систему устанавливается отличное от нуля значение ошибки Хуст., то такую систему по отношению к рассматриваемому воздействию называется статической.

Если же при постоянном воздействии устанавливается равное нулю значение ошибки, то такую систему по отношению к данному воздействию называют астатической.

П.3.5


Рассмотрим простейшую автоматического прямого регулирования уровня воды в резервуаре посредством поплавкового регулятора (рис 3-6) [Л.1]. Поплавок в этой схеме жестко связан с регулирующим органом – задвижкой, которая изменяет количество воды , поступающий в единицу времени по питающей трубе Т1. Нагрузкой объекта, резервуара, в данном случае является расход воды q по трубе Т2 . При увеличении расхода уровень воды в резервуарах начинает понижаться, поплавок опускается и переставляет задвижку, увеличивая её открытие. Количество воды, поступающее по трубе T1 в единицу времени, увеличивается, и уровень начинает повышаться. Равновесие наступит тогда, когда приход воды будет равен её расходу. Чем больше нагрузка, т.е. расход, тем больше будет открыта задвижка и, следовательно, тем ниже будет находится поплавок в состоянии равновесия. А это значит, что с возрастанием нагрузки в данной схеме значение уровня воды, т.е. регулированной величины, будет уменьшаться. График зависимости установившихся значений регулируемой величины H от нагрузки q имеет следующий вид:





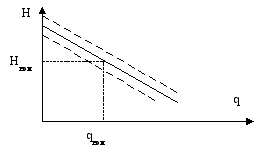
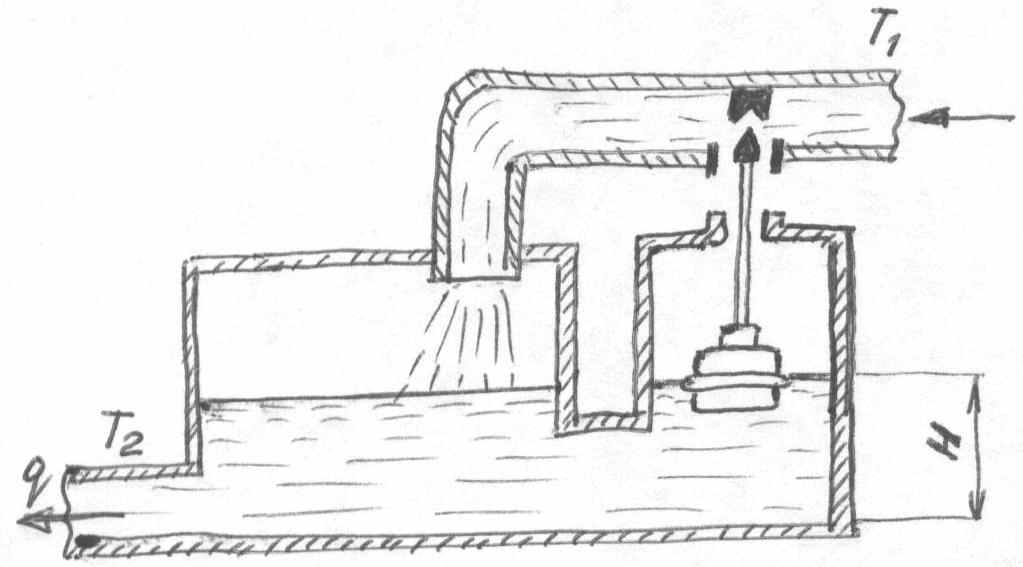
Рис. 3-6 Рис. 3-7


* Из графика видно, что только при одном значении нагрузки, равном qном, регулируемая величина H=H ном, т.е. установившаяся ошибка xуст=0. При всех же других значениях нагрузки регулируемая величина будет иметь различные значения, следовательно, xуст0 . Т.о., статистическая система по своему принципу действия работает с ошибкой. *

Пример 3-6.

В некоторых системах статическая ошибка нежелательна. В этих случаях строят астатические системы, в которых статическая ошибка равна 0.

Р
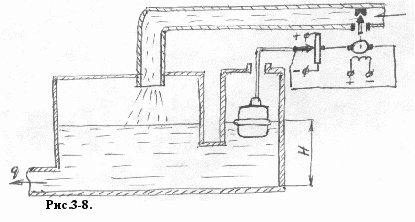
ассмотрим астатическую систему регулирования уровня (Рис. 3-8)

Поплавок в этой схеме перемещает поплавок реостата, при помощи которого двигатель всякий раз, как ползунок сместится вверх или вниз от среднего положения, начинает вращаться и перемещает регулирующий орган до тех пор, пока не восстановится заданный уровень.

График зависимости установившихся значений регулируемой величины H от нагрузки q имеет следующий вид (Рис.3-9):

Т.е. представляет собой прямую линию,

п
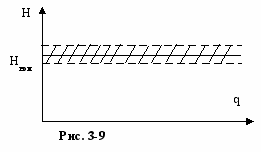
араллельную оси нагрузки. Установившаяся ошибка при астатическом регулировании теоретически равна 0, практически вследствие неточности регулятора она возможна, но не будет зависеть от нагрузки. В результате ошибки регулируемая величина может принять любое значение внутри некоторой зоны (заштрихованной на Рис. 3-9).

Для получения астатического регулирования нужно устранить в регуляторе жёсткую зависимость между положением регулирующего органа и значением регулируемой величины с тем, чтобы заданное значение регулируемой величины можно было поддерживать при любой нагрузке, т. е. при любом положении регулирующего органа. С этой целью в цепь регулирования вводят так называемое астатическое звено. Примером астатического звена является элементарный двигатель с идеальной чувствительностью. Когда напряжение на зажимах двигателя равно нулю, он неподвижен, т. е. находится в положении равновесия; при этом его вал может быть повернут на любой угол. При появлении напряжения двигатель начинает вращаться. Вращение прекратиться лишь тогда, когда подведенное к двигателю напряжение станет равным нулю.

* В нашем примере это возможно только при значении регулируемой величины Н1 равном заданному, т. е. при среднем положении ползунка.* Астатические системы могут быть первого, второго, и т.д. порядков.

[Л5.стр. 108.]


3.5 Непрерывные и дискретные системы


По способу передачи и преобразования сигналов автоматические системы подразделяются на непрерывные и дискретные [Л2].

В непрерывных системах передается и преобразуется каждое мгновенное значение сигнала, т. е. сигнал является непрерывной функцией времени.

В дискретных системах передается и преобразуется сигнал, квантованный по времени, по уровню или одновременно по времени по уровню.

3.6 Линейные и нелинейные системы.

По виду дифференциальных уравнений, которыми описываются автоматизированные системы, их можно подразделить на линейные и нелинейные [Л2].

Автоматические системы, динамика которых, описывается нелинейными уравнениями, называются нелинейными системами. Большинство автоматизированных систем являются нелинейными. Нелинейности возникают по различным причинам: из-за наличия зон нечувствительности и зон насыщения в статистических характеристиках отдельных элементов, при включении в управляющее устройство системы нелинейных элементов (реле) и т. п. Если нелинейности сильно влияют на динамические свойства системы, то их учитывают и исследуют систему как нелинейную. Однако во многих случаях, особенно в системах с обратными связями при малых отклонениях, нелинейности оказывают несущественное влияние, и такие системы можно считать линейными.

Линейными автоматизированными системами называются такие системы, которые можно описать с достаточной точностью линейными уравнениями (алгебраическими, дифференциальными, уравнениями в конечных разностях и т.д.) Линейные системы подразделяют на стационарные и нестационарные. Параметры линейных стационарных систем неизменны во времени, эти системы описываются линейными уравнениями с постоянными коэффициентами. Линейные нестационарные системы имеют переменные во времени параметры и описываются линейными уравнениями с переменным коэффициентами

3.7 Одноконтурные и многоконтурные системы [Л5]