Котельников Ю. П

Вид материала

Документы

Содержание Исходные данные График моделирования

Подобный материал:

• Ф. Попов, И. С. Гро-мека, П. С. Порецкий, П. С. Назимов, Ф. М. Су-воров, Д. М. Синцов,, 50.97kb.
• В. С. Котельников, Н. П. Алёшин, Э. А. Гладков, А. А. Шельпяков, В. Ф. Лукьянов,, 1128.77kb.
• В. С. Котельников, Н. П. Алёшин, Г. Г. Чернышов, А. А. Шельпяков, В. Ф. Лукьянов,, 1262.71kb.
• Г. П. Щедровицкий, С. И. Котельников, 511.11kb.
• Хххvii самарская областная студенческая научная конференция 12 22 апреля 2011 года, 1774.74kb.
• П. П. Котельников Не судимы, но осуждены книга, 2891.33kb.
• Технологический регламент, 1659.01kb.
• Пригласительный билет и программа часть 2 Гуманитарные дисциплины самара 2011 сопредседатели, 1127.78kb.
• С. И. Котельников Организационно-деятельностная игра как новая форма организации, 473.36kb.
• А. А. Котельников Проблемы российско-монгольского сотрудничества, 167.62kb.

Санкт-Петербургский Государственный Университет Информационных Технологий, Механики и Оптики


Кафедра Систем Управления и Информатики


Расчетная работа №1 (этап 2)

"Инженерные методы оптимизированной динамической настройки регуляторов"

по курсу "Основы системной автоматизации"

Вариант №27





Санкт-Петербург

2008 г.

Исходные данные:




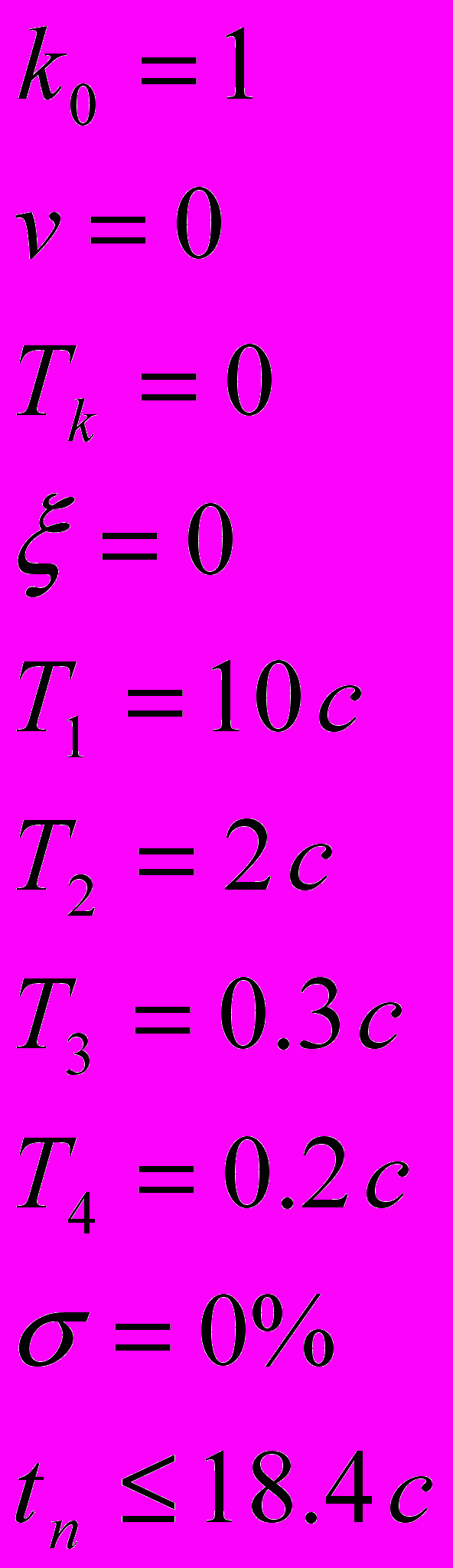
Настройка на симметричный оптимум подразумевает «пригонку» модуля частотной передаточной функции к 1, так же как и для модульного оптимума, только с разницей в виде передаточной функции замкнутой системы:


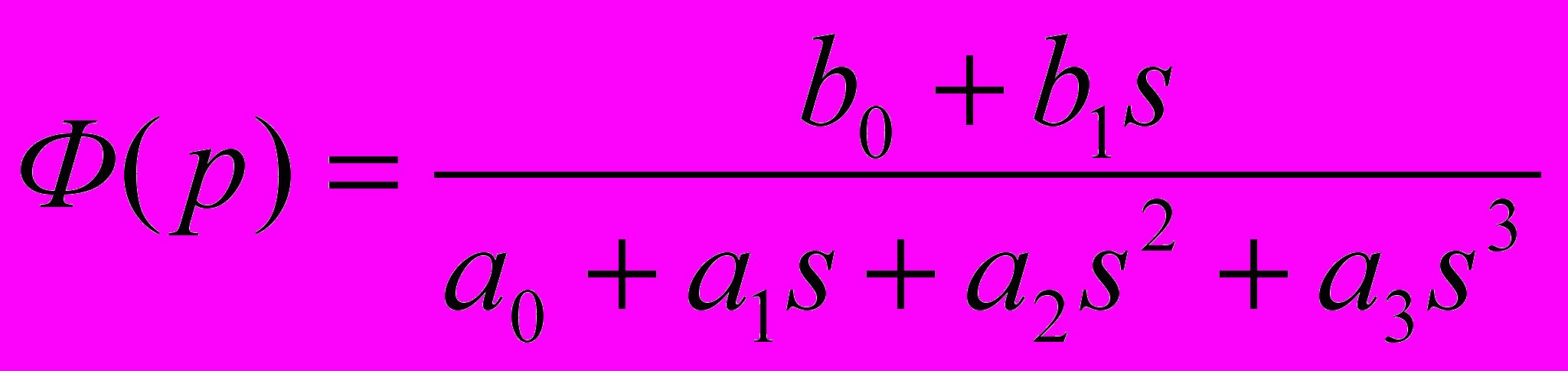
Дана статическая система:

.


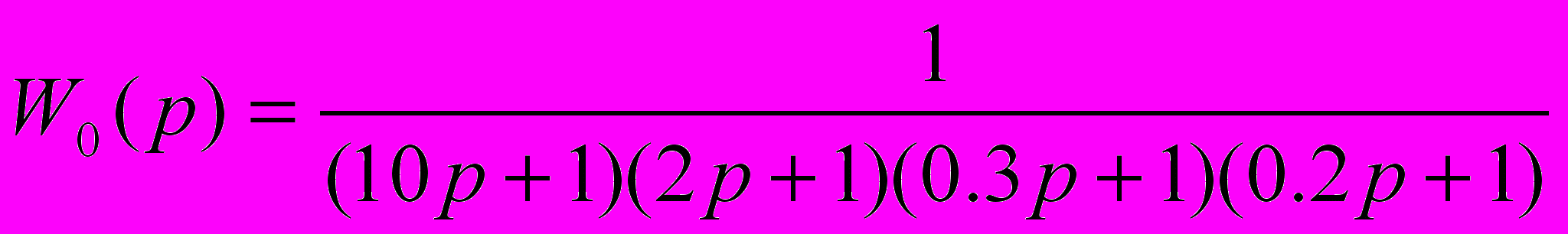Можно попробовать использовать регулятор с астатизмом первого порядка, например ПИ-регулятор:



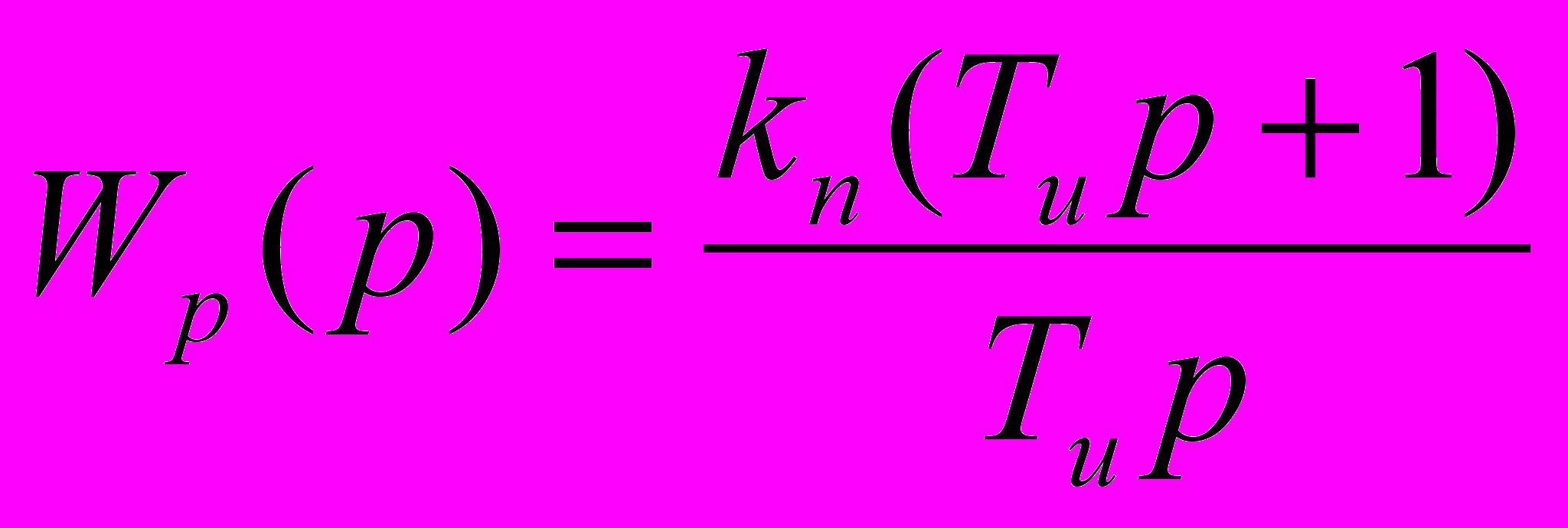
Упрощенный ОУ:




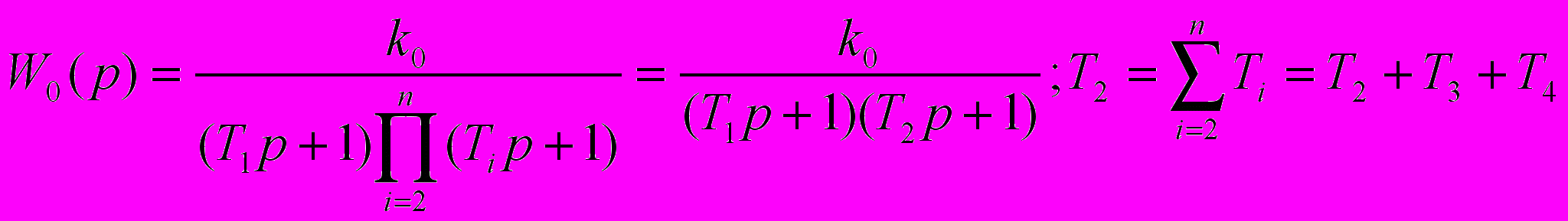
ПФ разомкнутого контура:



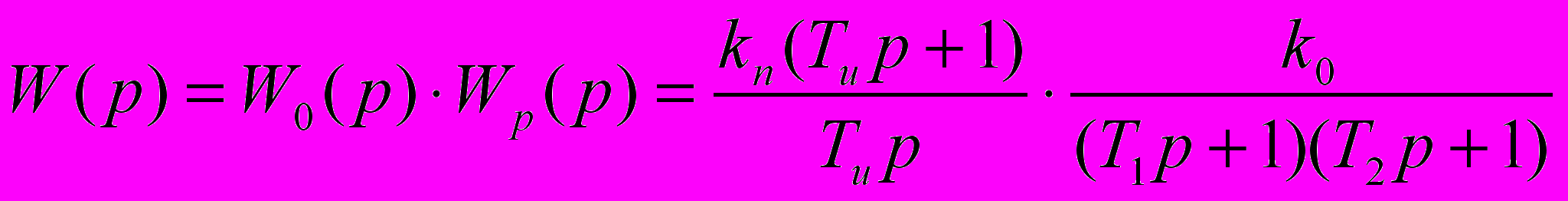
ПФ замкнутой системы:



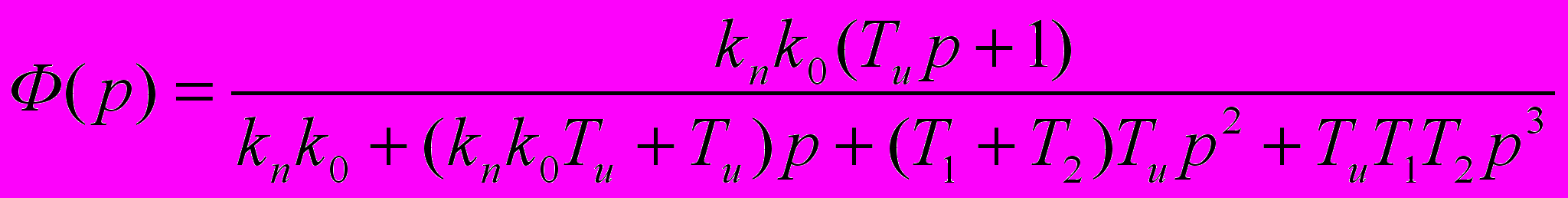
Вид ПФ замкнутой системы удовлетворяет виду замкнутой системы для которых применима настройка на СО:




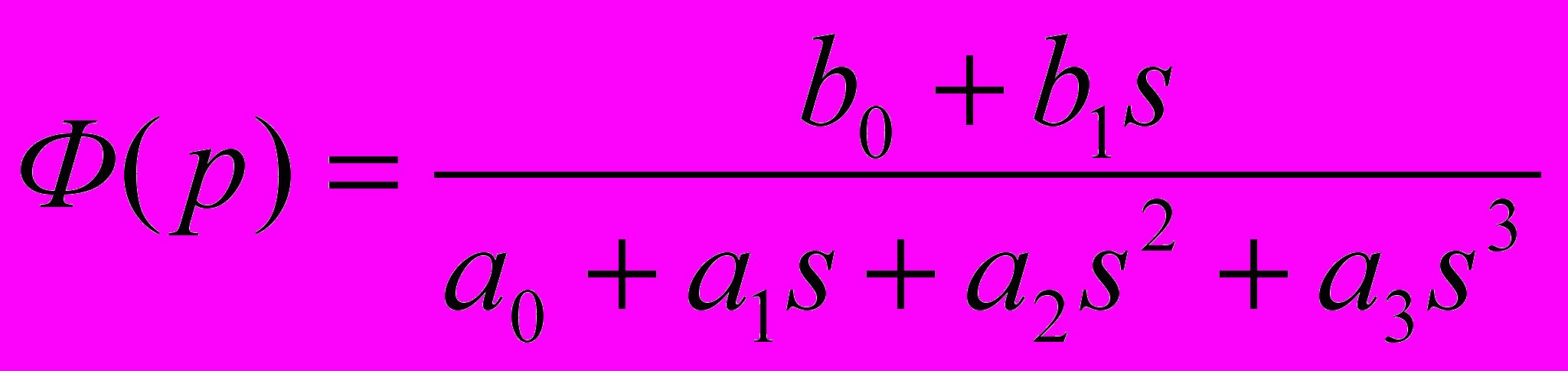
Применим условие настройки на симметричной оптимум:

,


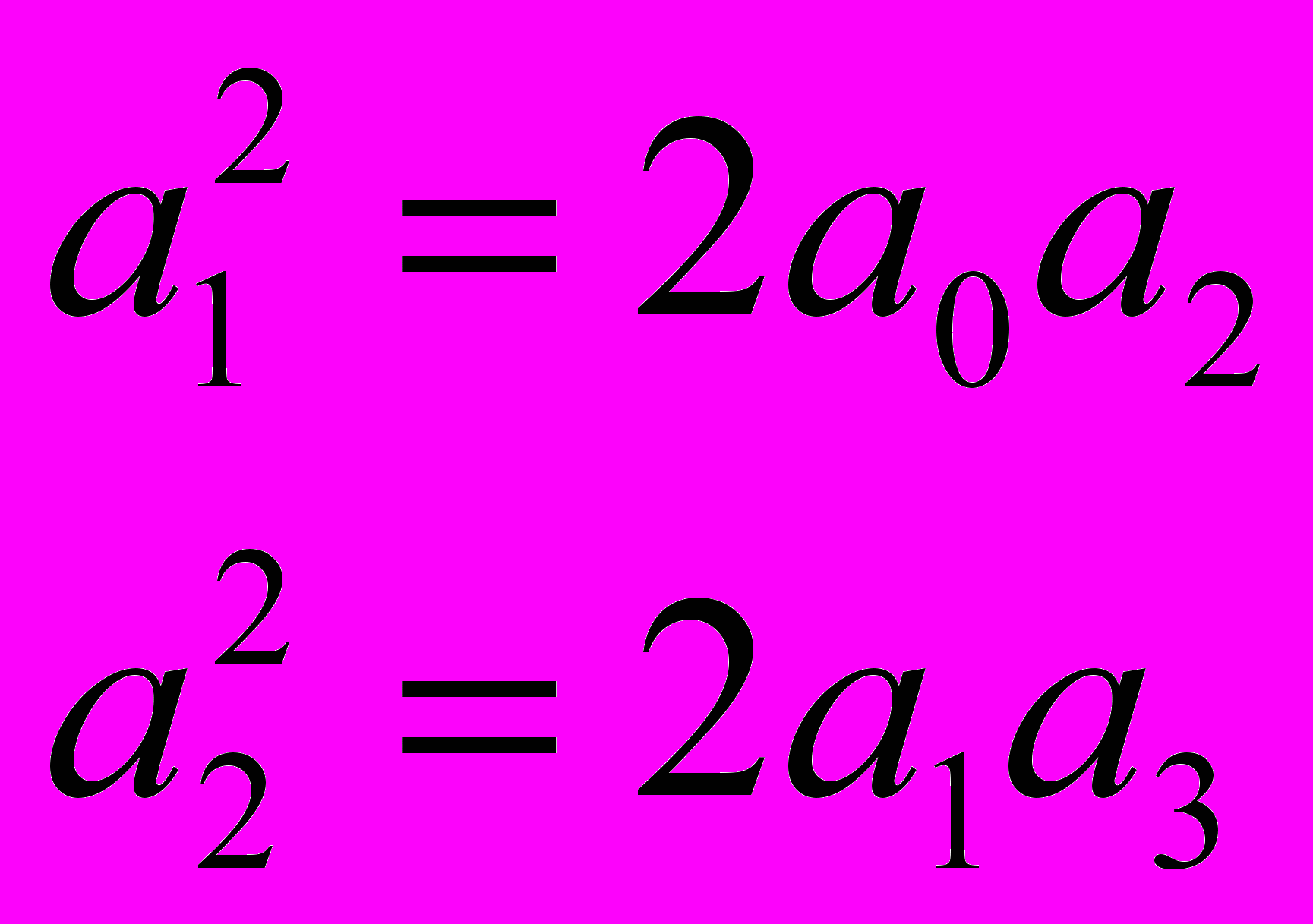Условие настройки симметричного оптимума для данной системы:

;

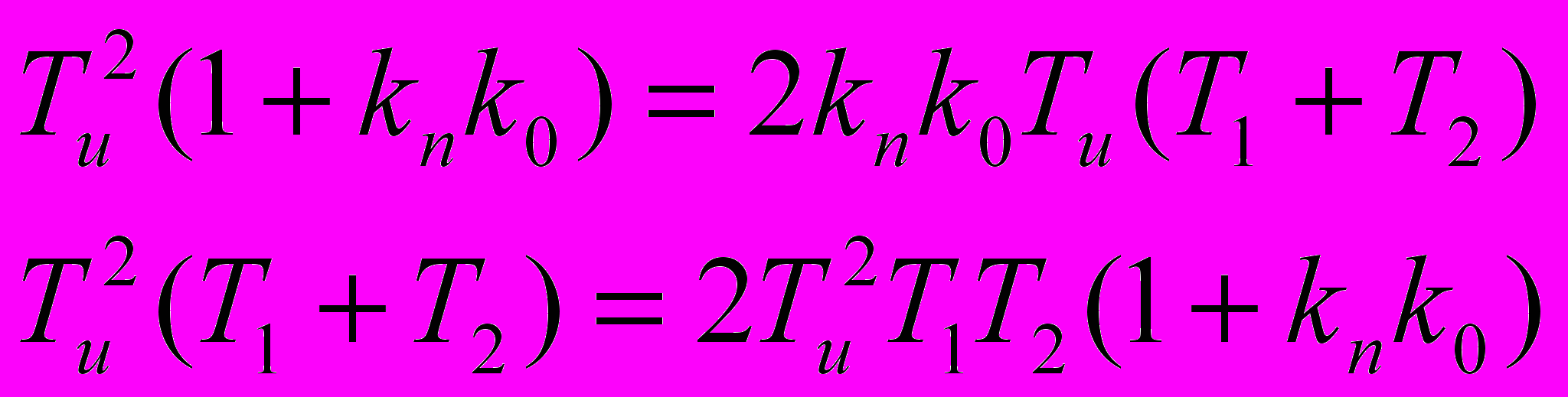Отсюда получаем постоянную времени Пи-регулятора и пропорциональный коэффициент:



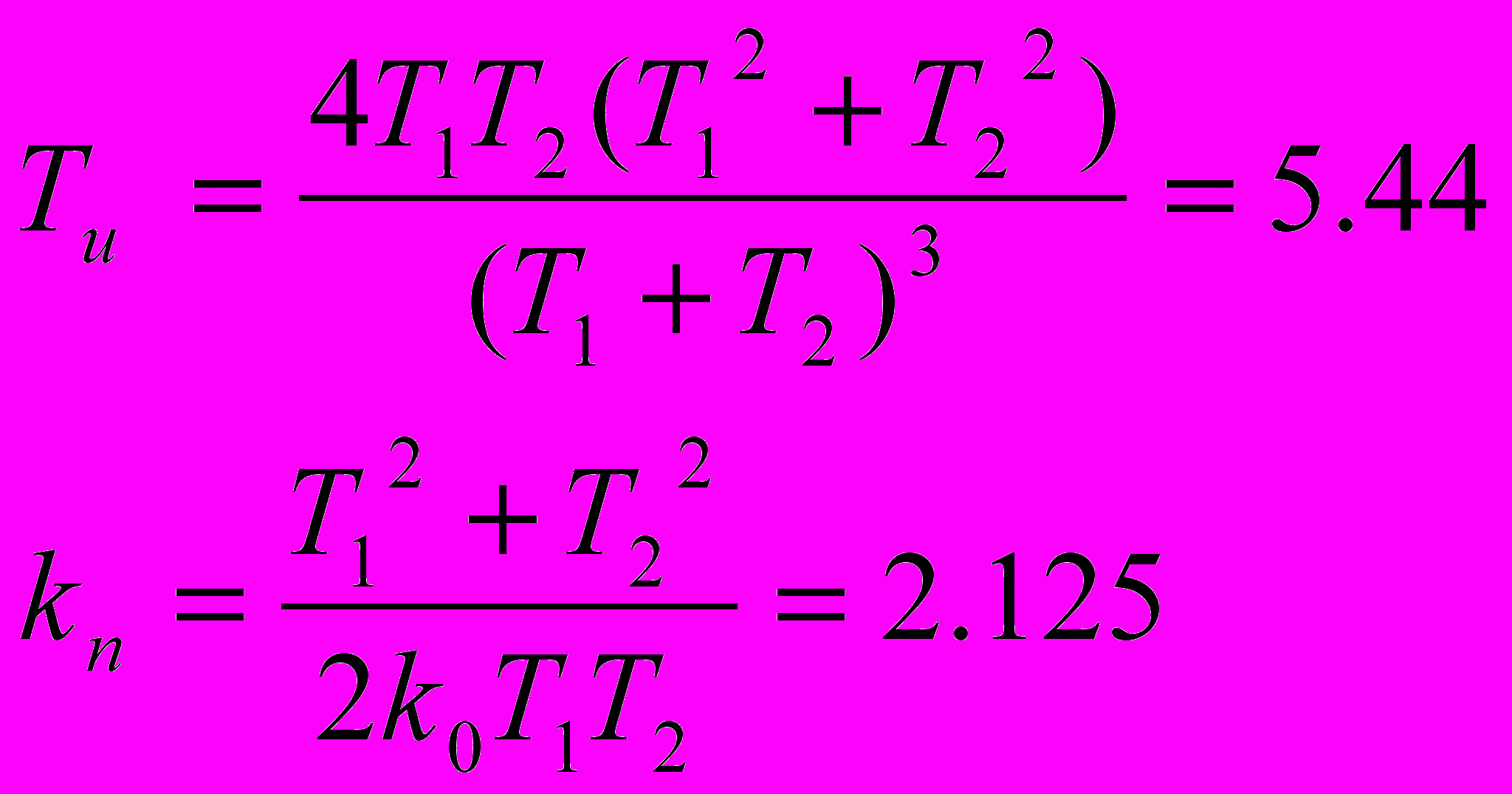
Для проверки правильности расчетов введем нормирующую постоянную времени и параметр r:



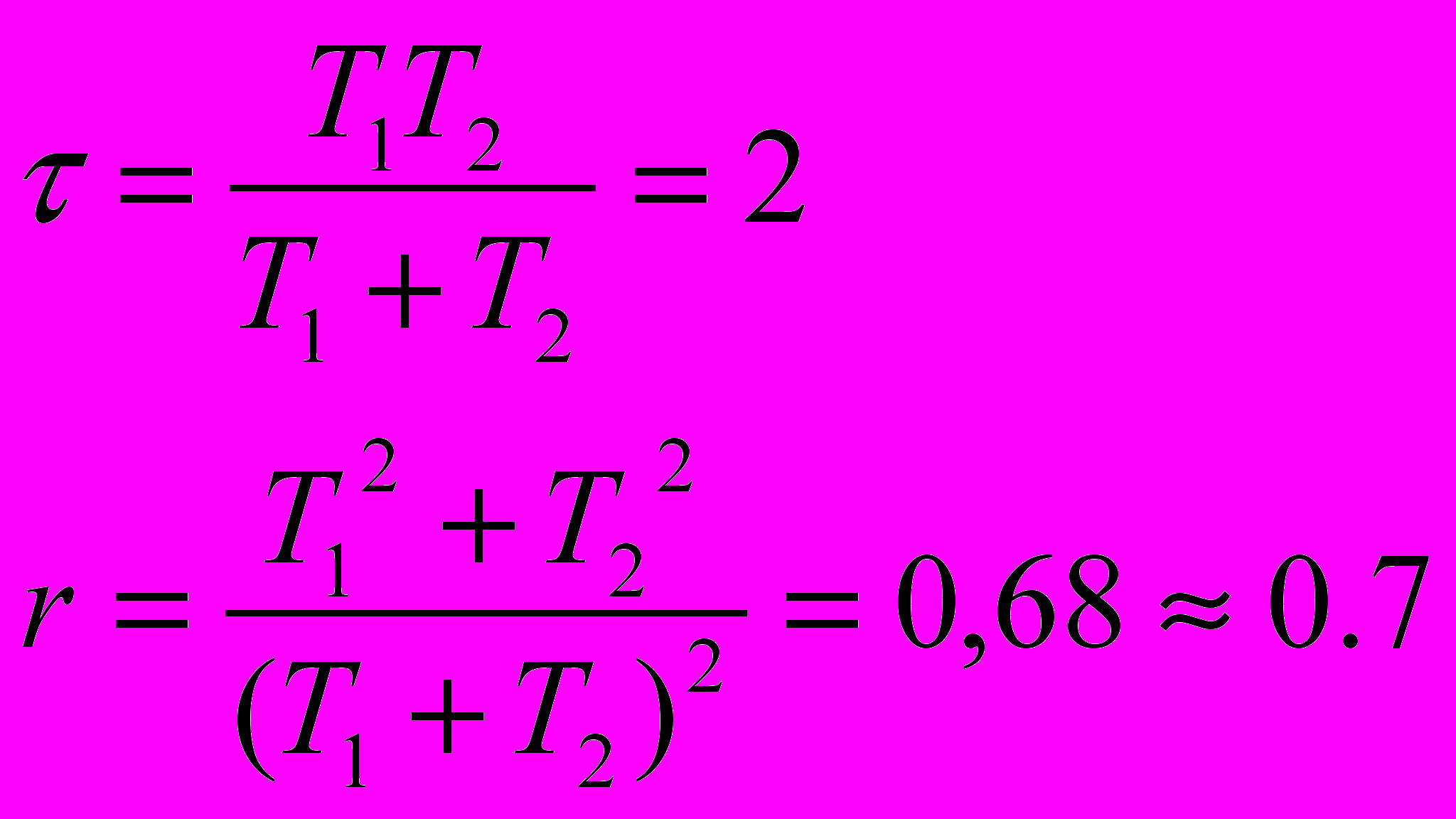
Подставляя постоянную времени ПИ-регулятора, пропорциональный коэффициент, нормирующую постоянную времени и параметр r в передаточную функцию замкнутой системы, получим ПФ замкнутой системы, настроенную на симметричный оптимум:



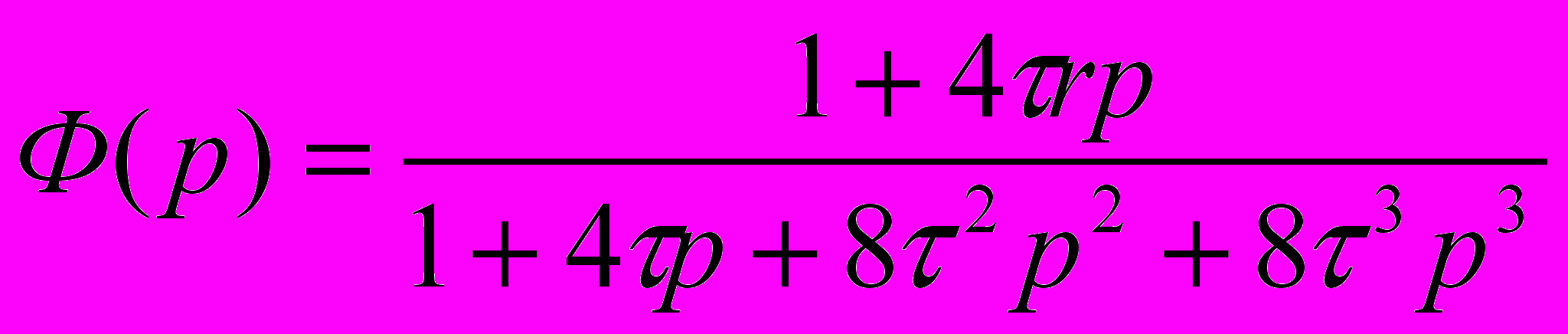
Качественные показатели системы имеют значения при r=0.7




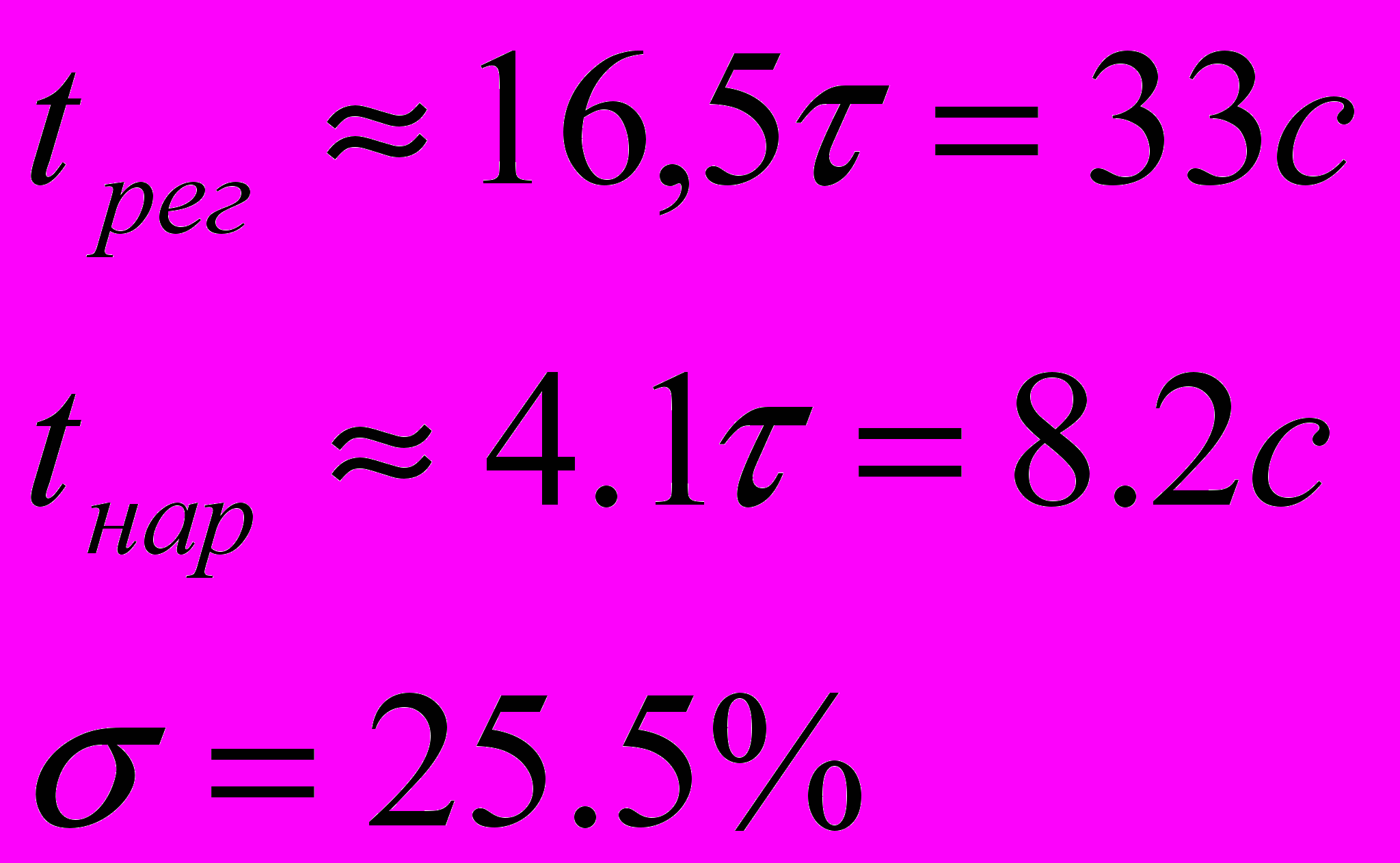
Схема моделирования:



График:




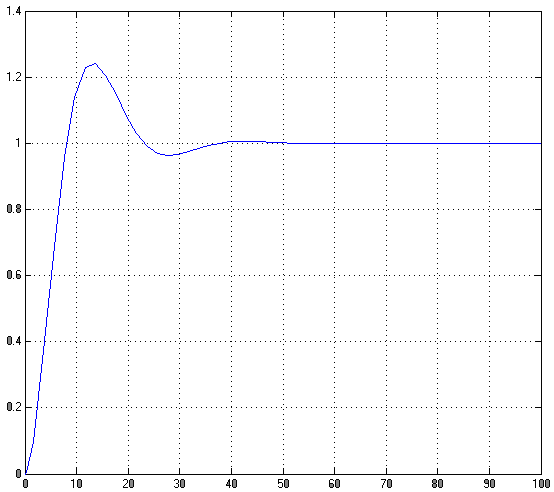
Полученные параметры:



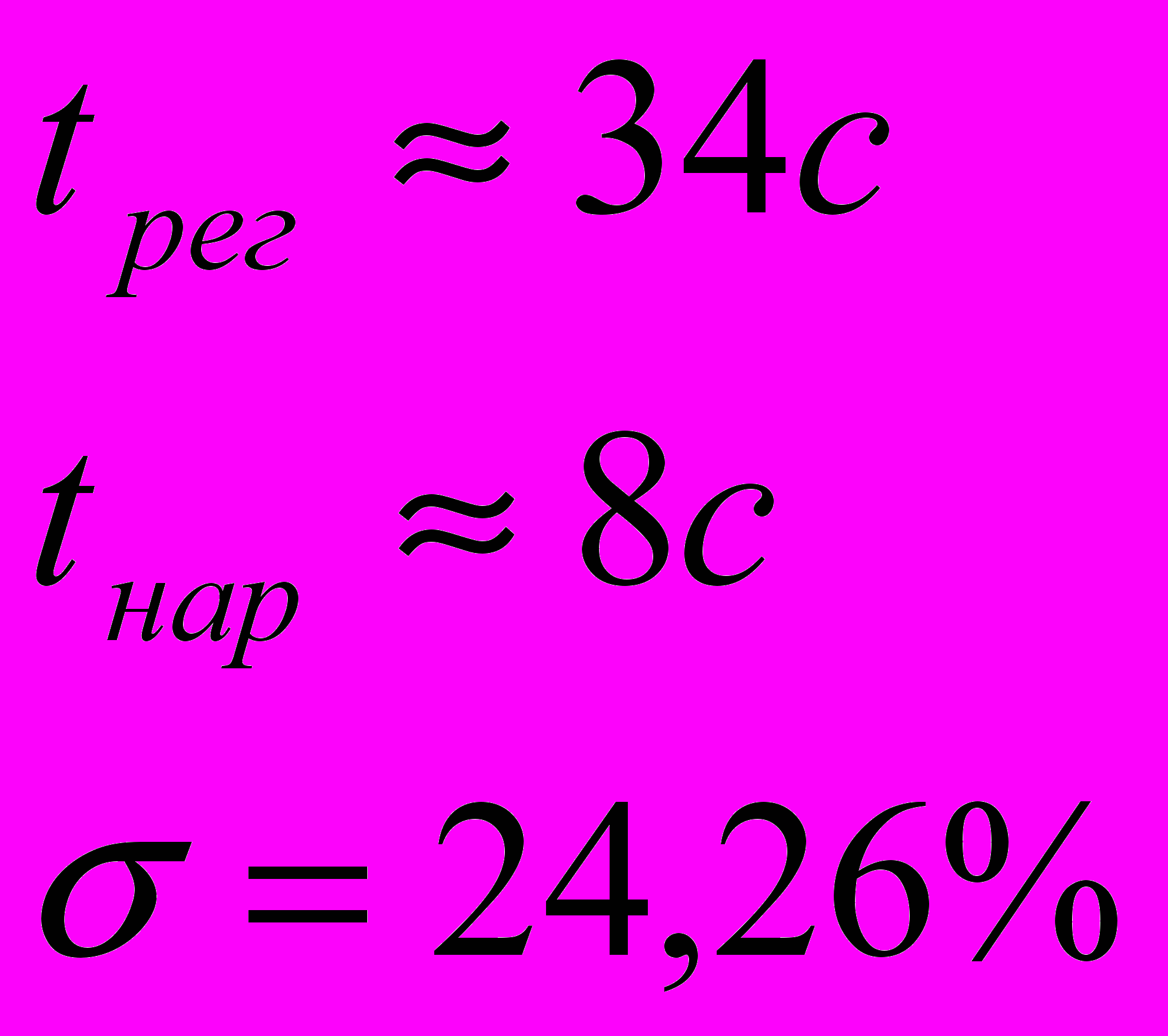
Теоретические значения и значения полученные из графика совпадают с допустимой погрешностью.

Исследуем влияние изменения параметров настройки в широких пределах.

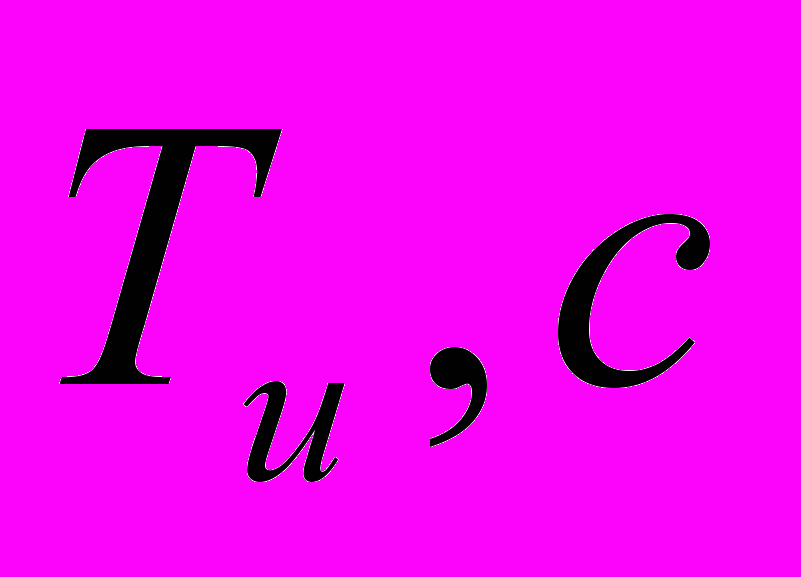	0.1	1	5.44	10	50
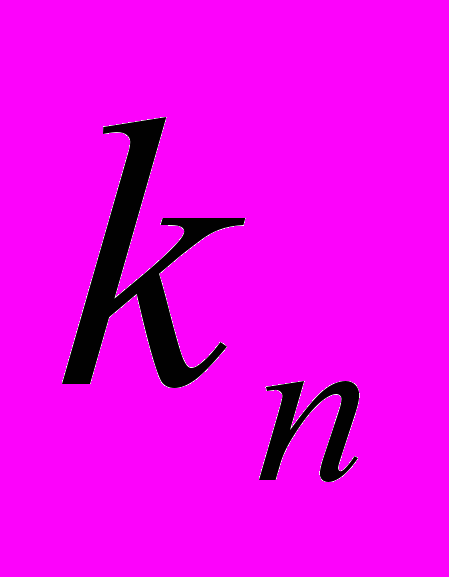	2,12	2,12	2,12	2,12	2,12
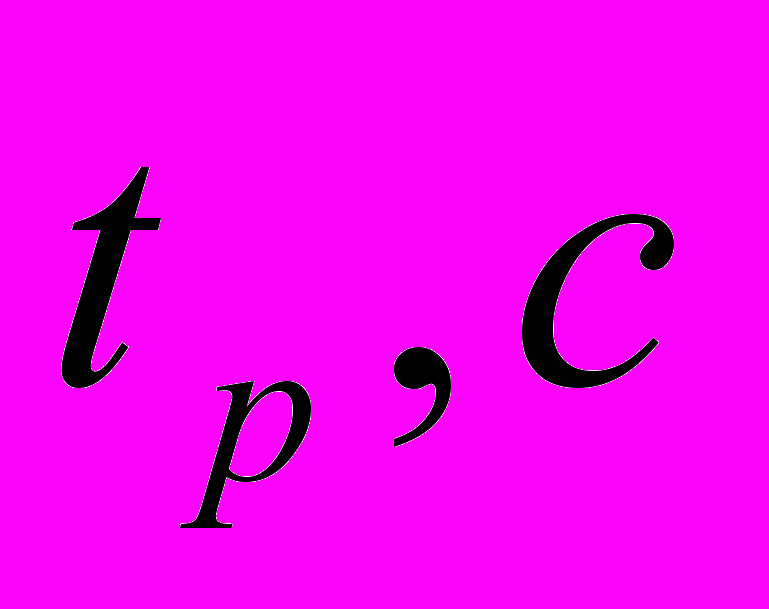	неуст	неуст	34	21	185
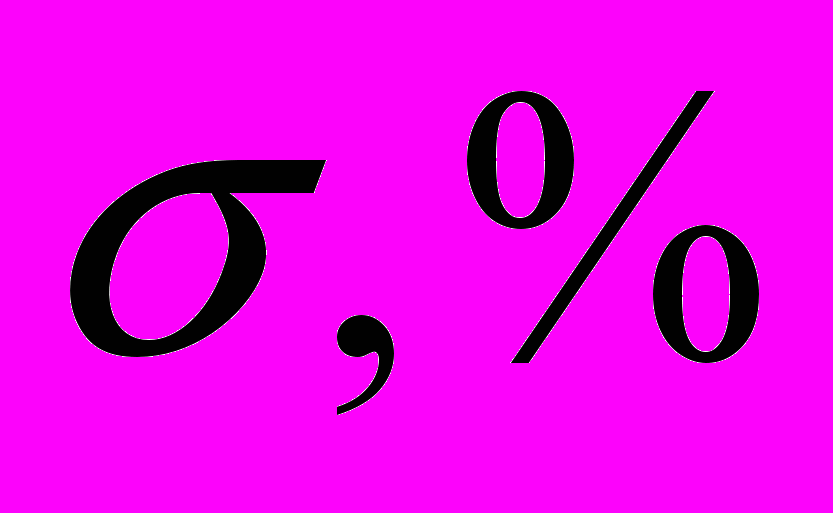			24,26	5	0

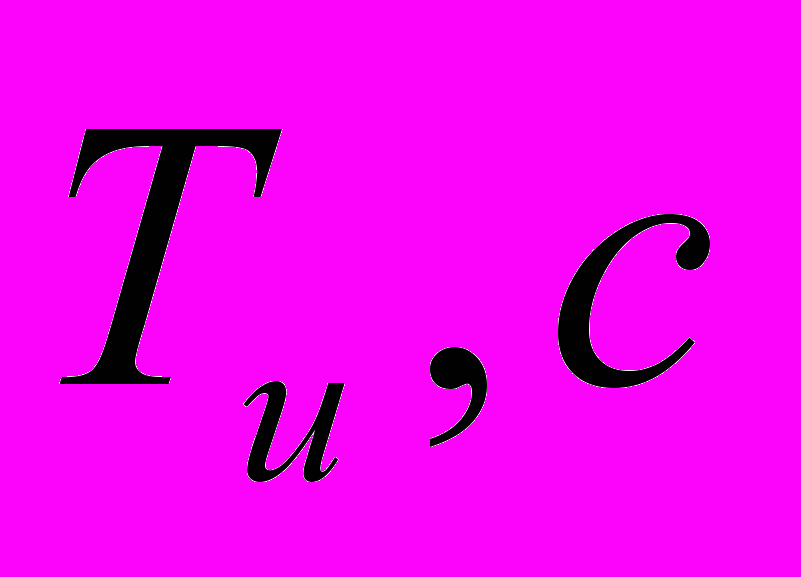	5.44	5.44	5.44	5.44	5.44
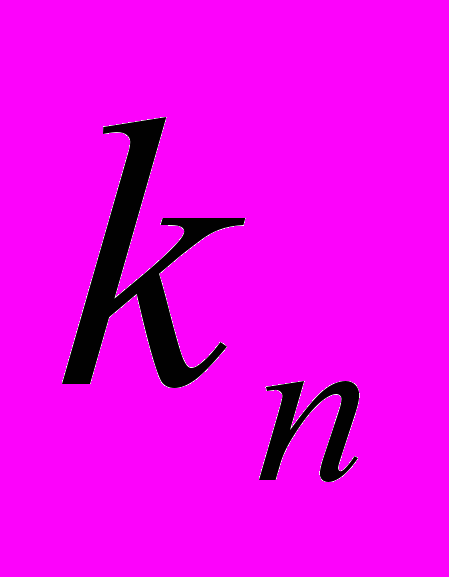	0.1	1	2,12	10	30
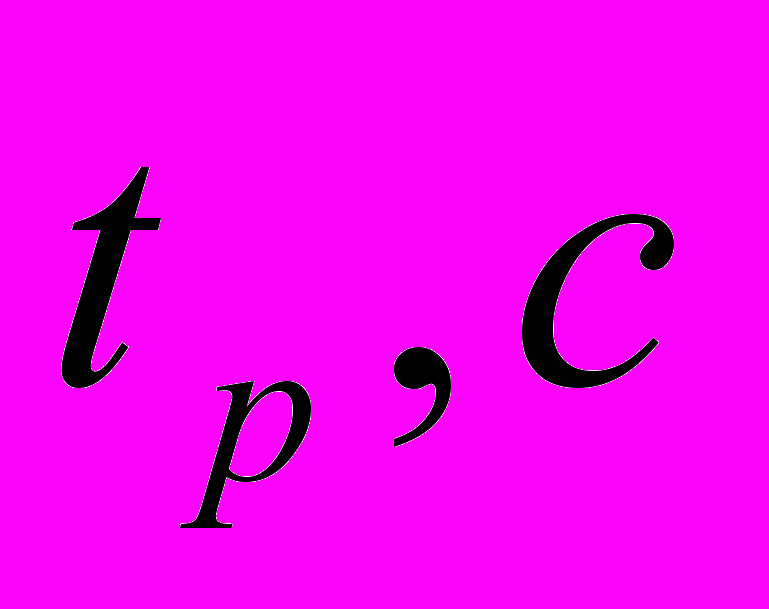	188	38	34	28	25
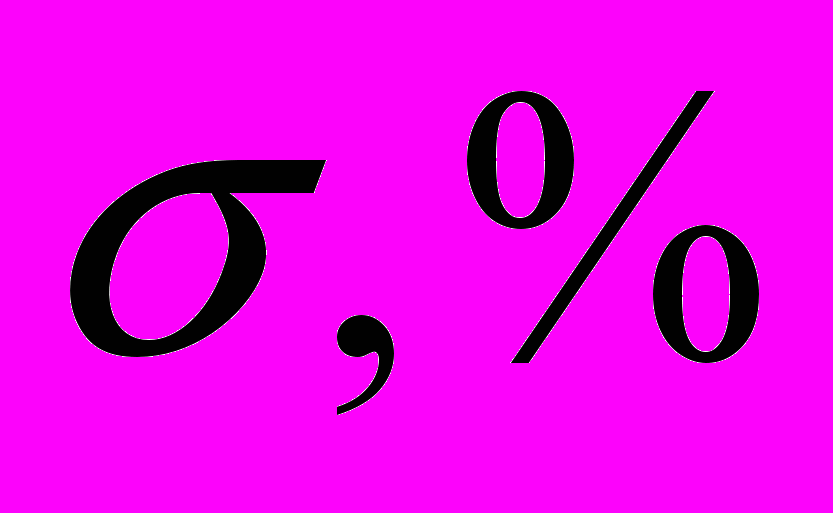	0	14,4	24,26	47	60

Использование фильтров

Для переходных характеристик систем, настроенных на ОСО характерно значительное перерегулирование, что в ряде случаев может быть недопустимо

Значительное перерегулирование связано с наличием в числителе передаточной функции замкнутой системы. Для того, чтобы компенсировать влияние этого значения в числителе необходимо использовать фильтр и, поскольку, фильтр будет располагаться на входе системы по задающему воздействию, то будем говорить о сглаживании задающего сигнала.


Выбирая фильтр с передаточной функцией:



можно добиться следующих качественных показателей:




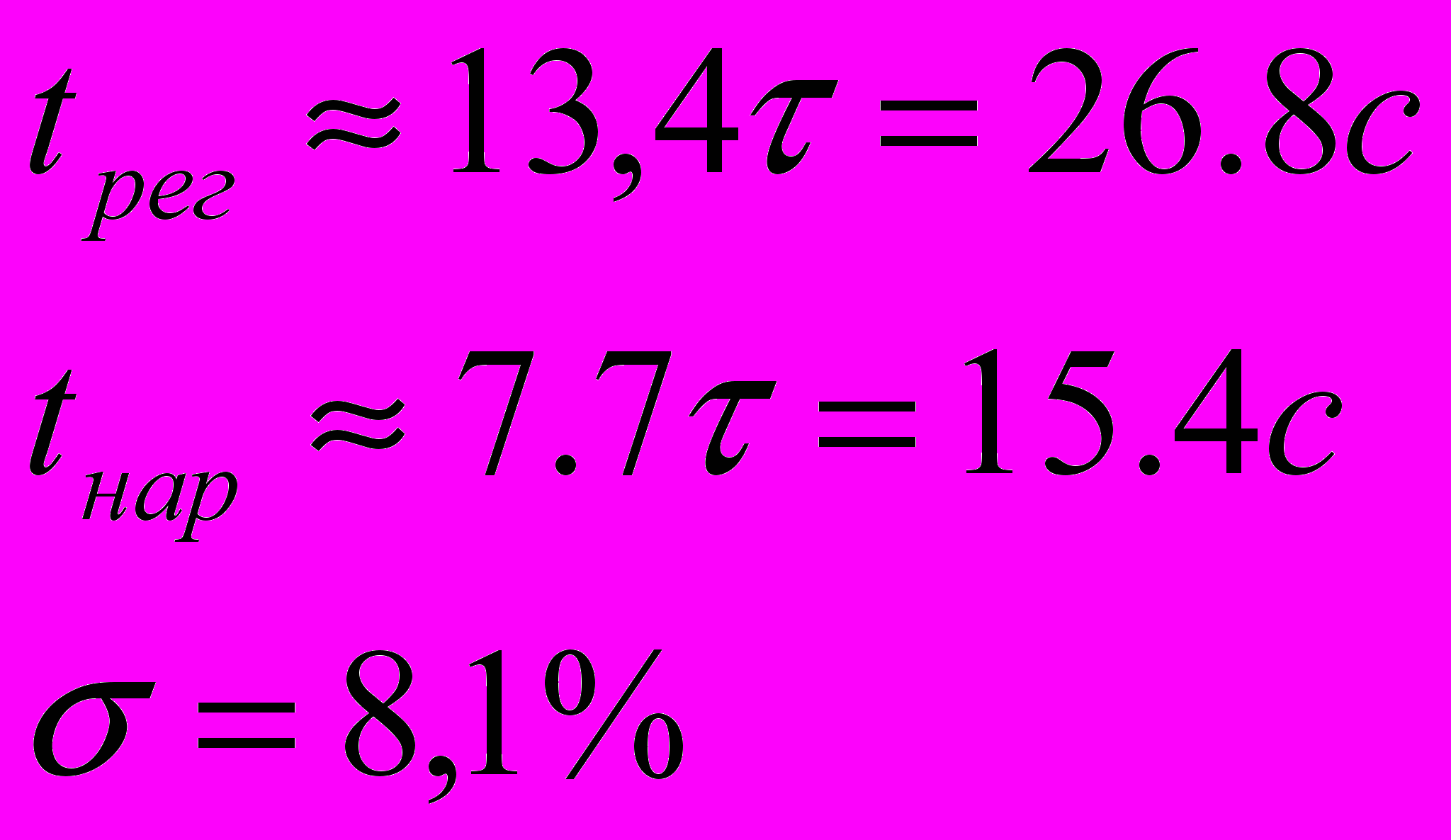
Схема моделирования:




График:



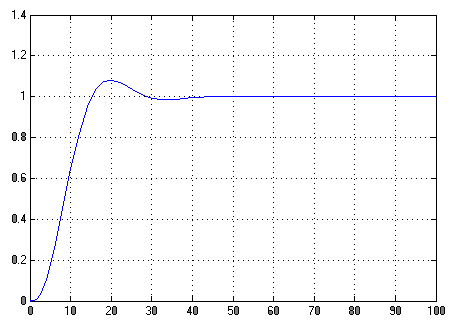
Полученные параметры:



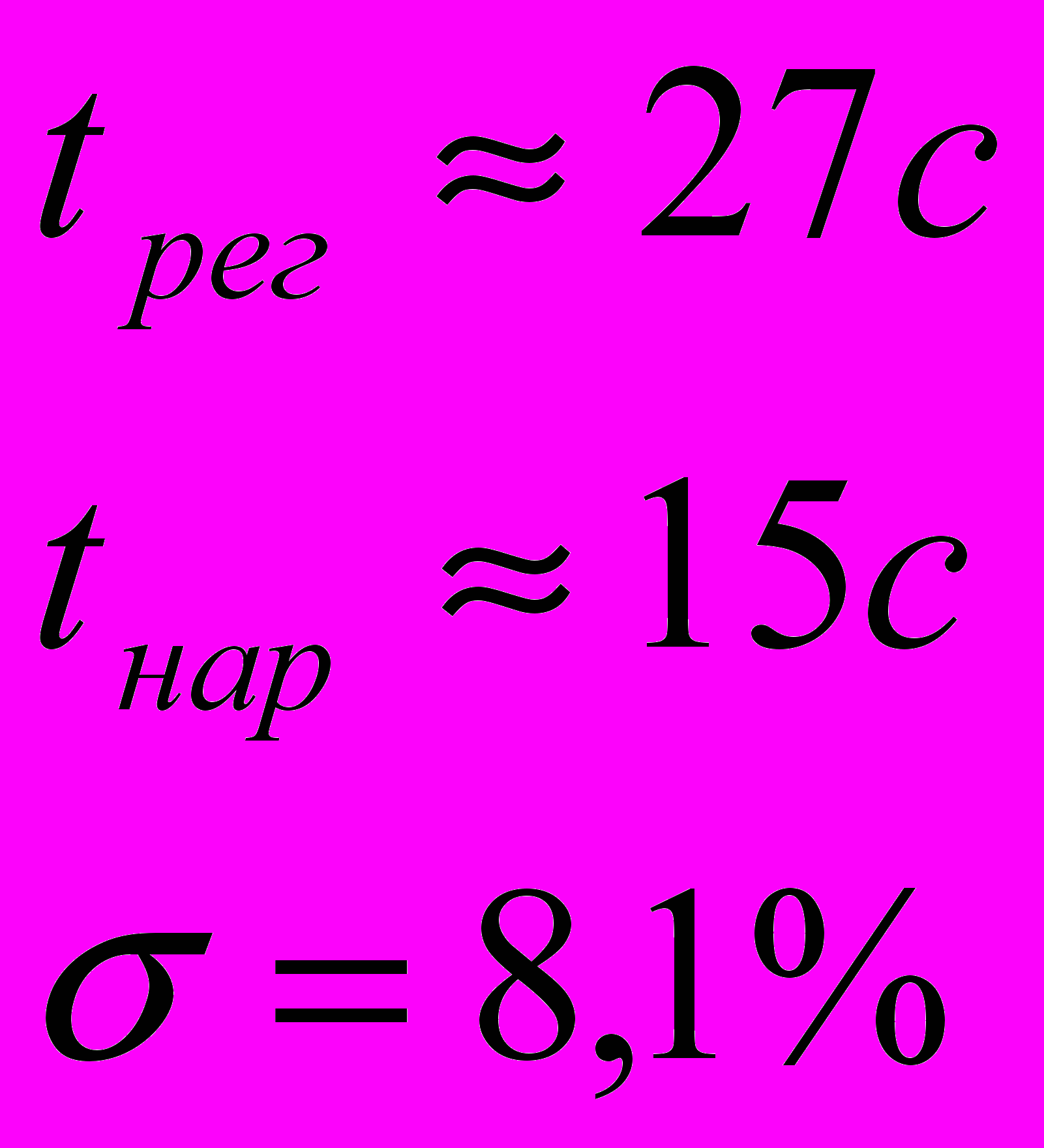
Как видно из графика качественные показатели соответствуют теоретическим, поэтому если требуется уменьшить перерегулирование до 0, необходимо применить фильтр сглаживания-дифференцирования:



Параметры фильтра:



Тогда передаточная функция системы примет вид:

, a фильтр примет вид: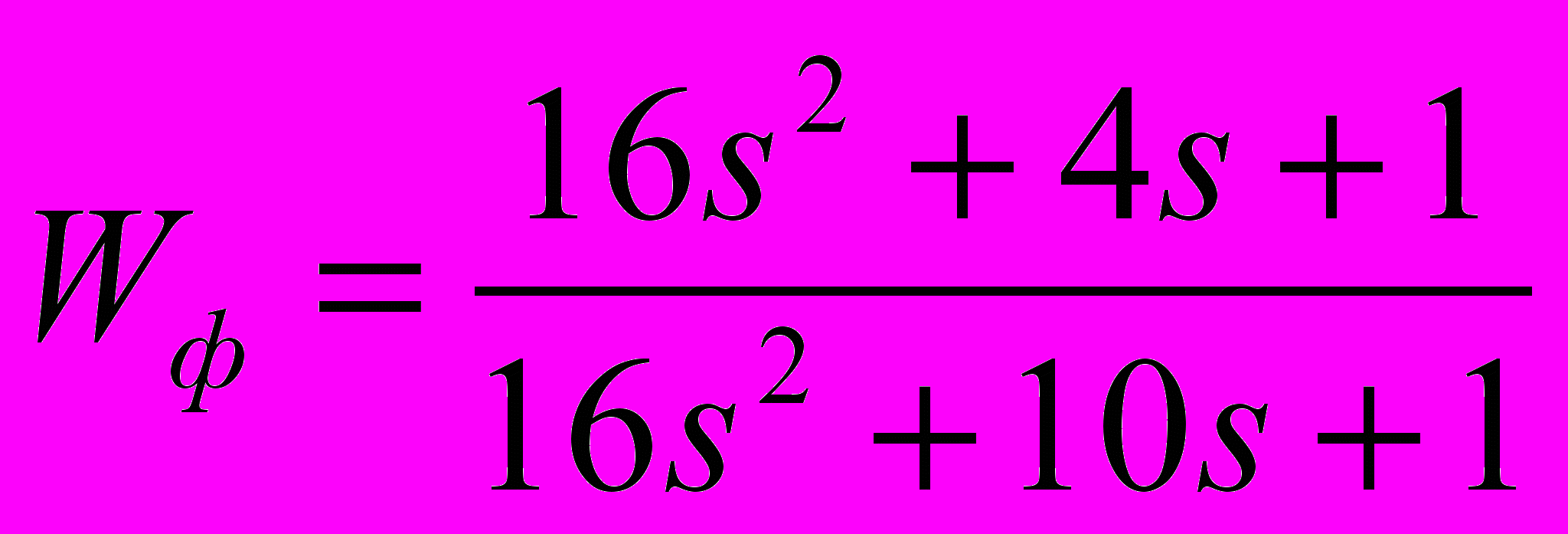

Соответствующие качественные показатели системы:




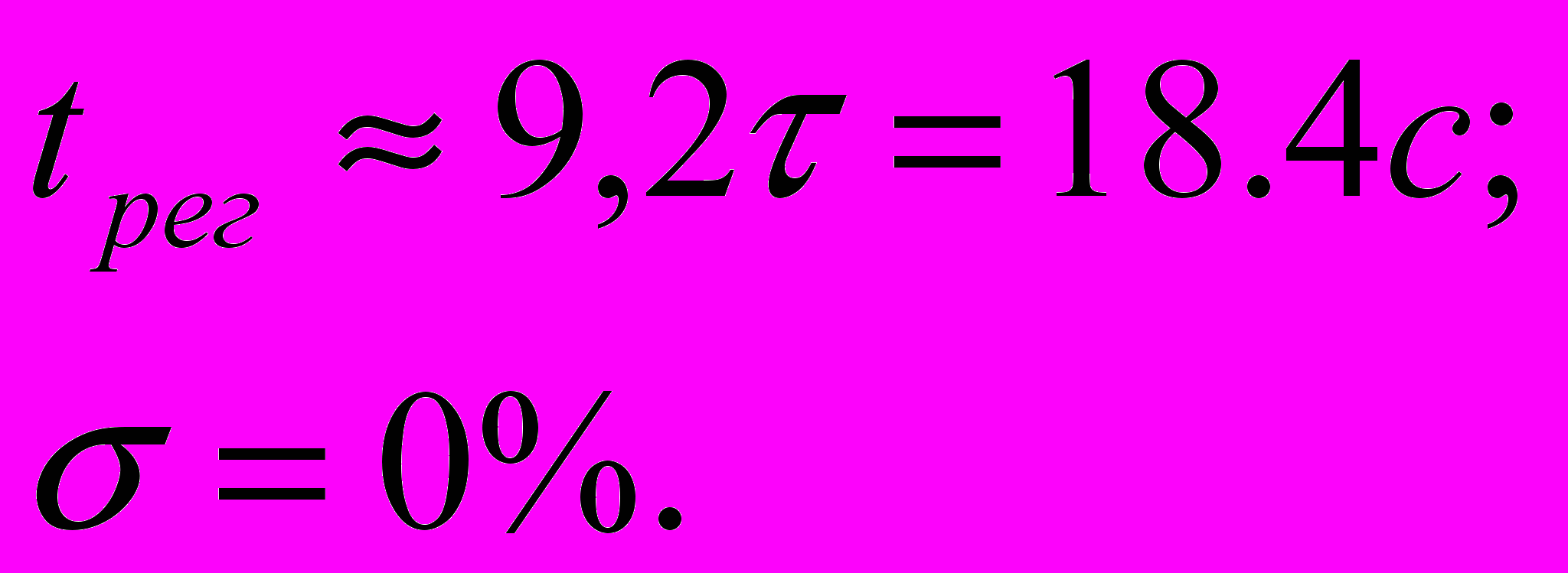
Схема моделирования:




График моделирования:



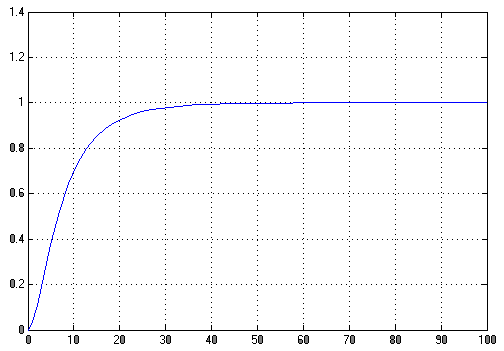
Полученные параметры:



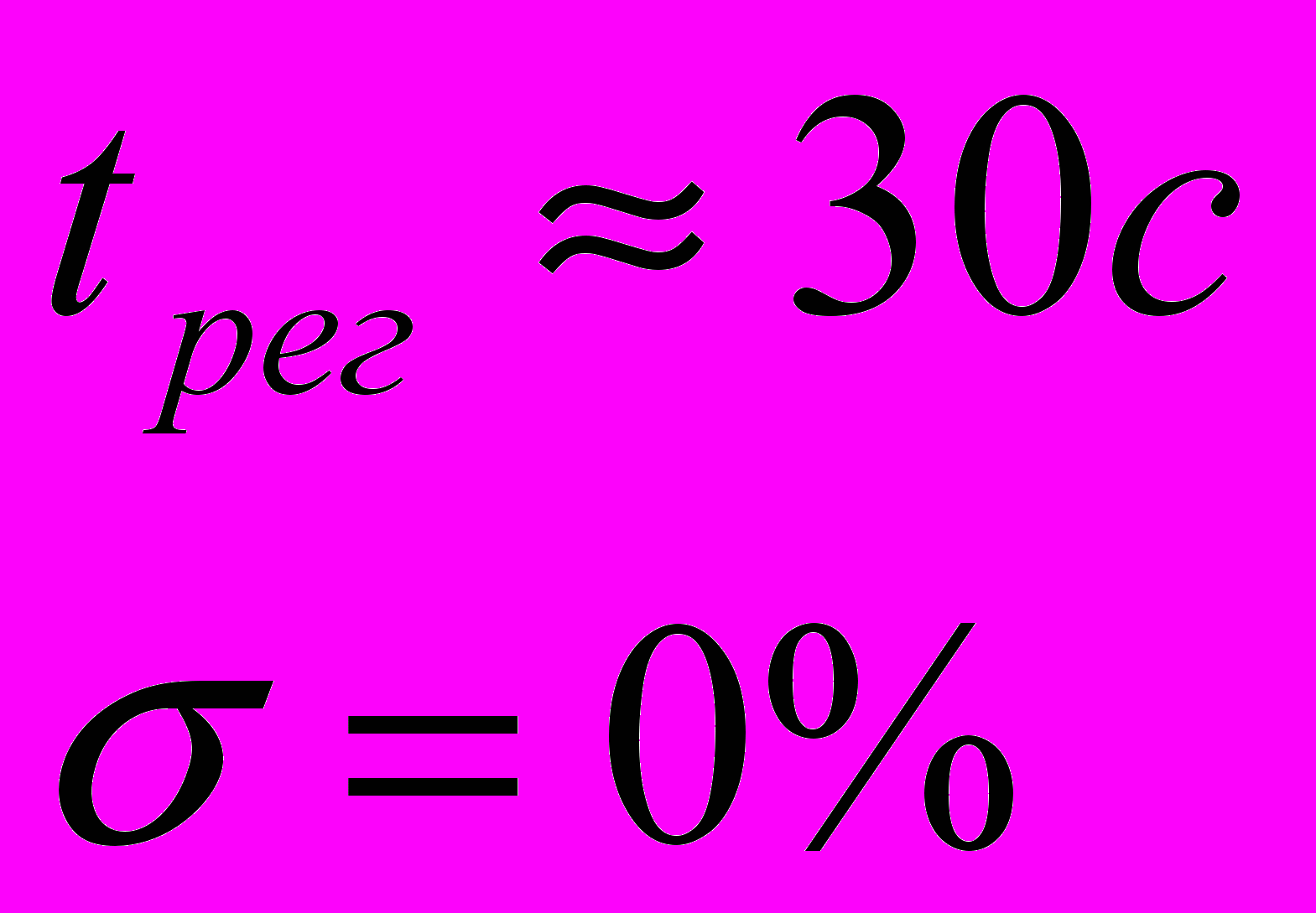
Из графика видно, что перерегулирование уменьшилось до нуля, хотя время регулирования немного возросло.

Полученное время переходного процесса не укладывается в допустимые пределы (30с>18,4), попробуем использовать ПД-регулятор.


ПД-регулятор имеет вид:



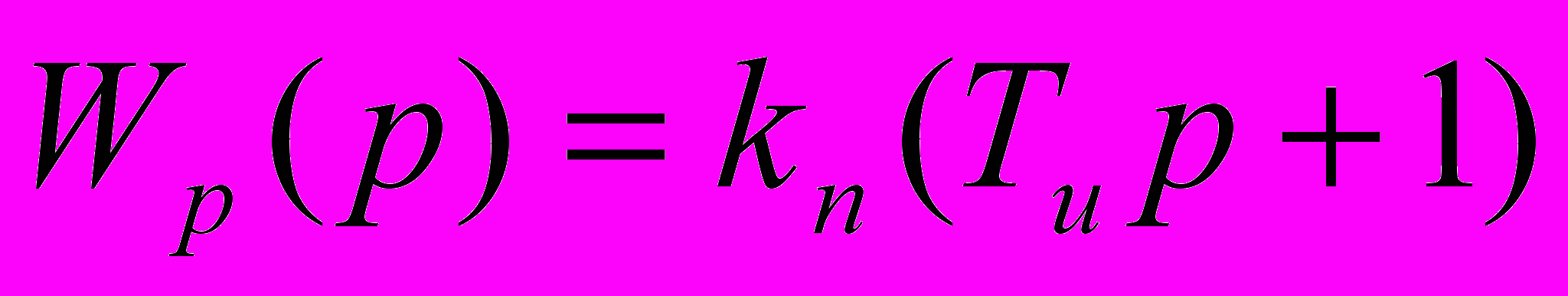
Упрощенный ОУ:




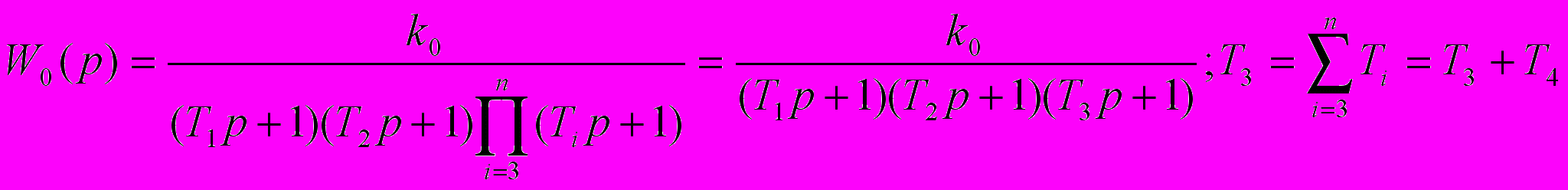
ПФ разомкнутого контура:



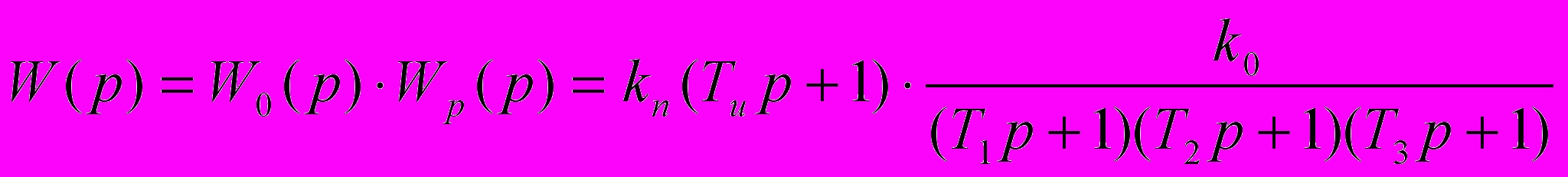
ПФ замкнутой системы:




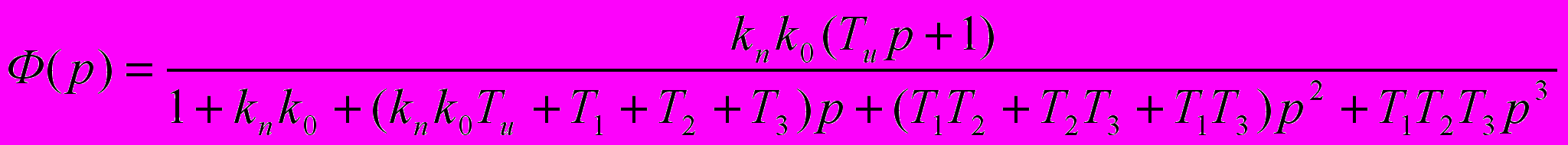
Применим условие настройки на симметричной оптимум:

,


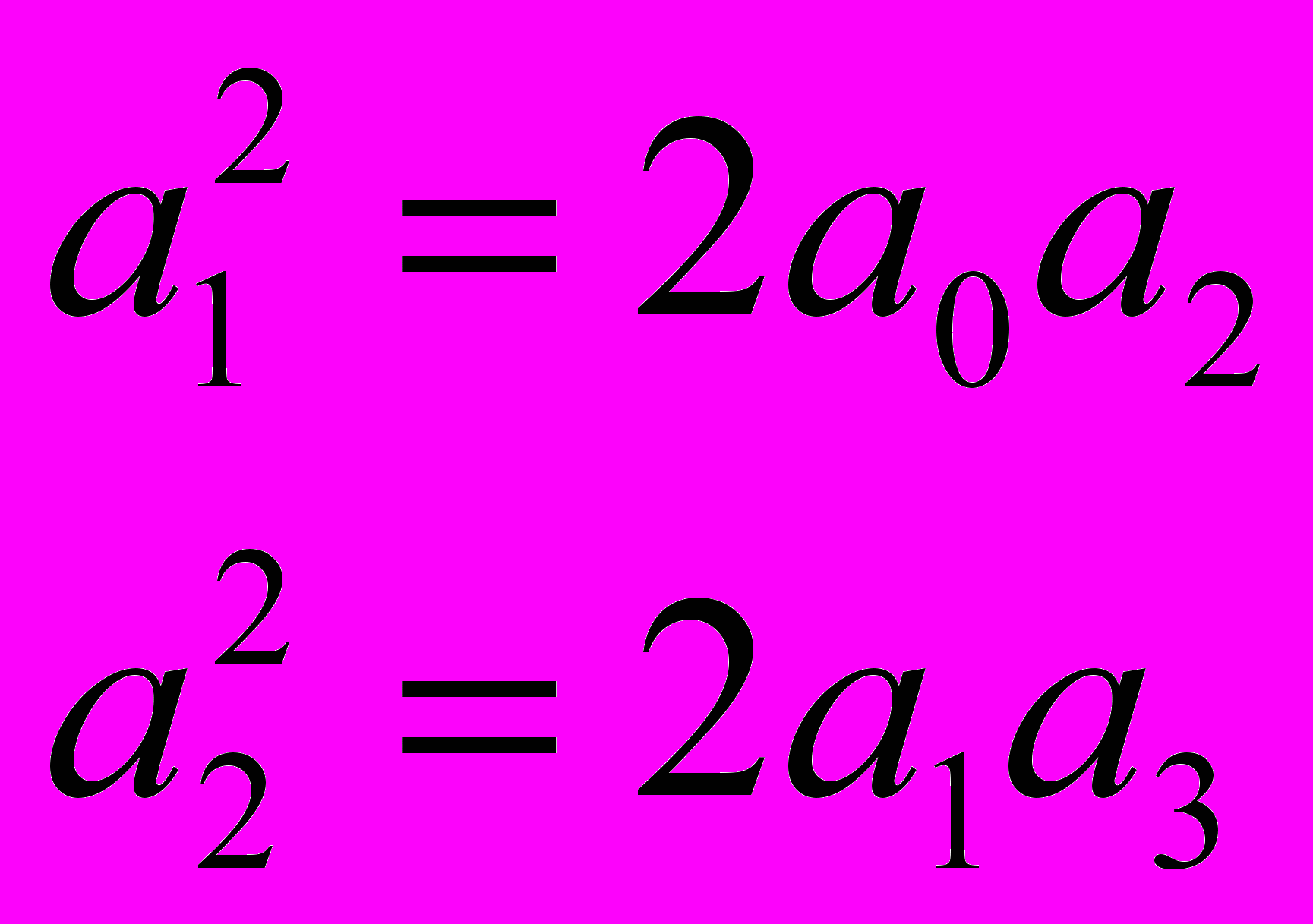Условие настройки симметричного оптимума для данной системы:

;


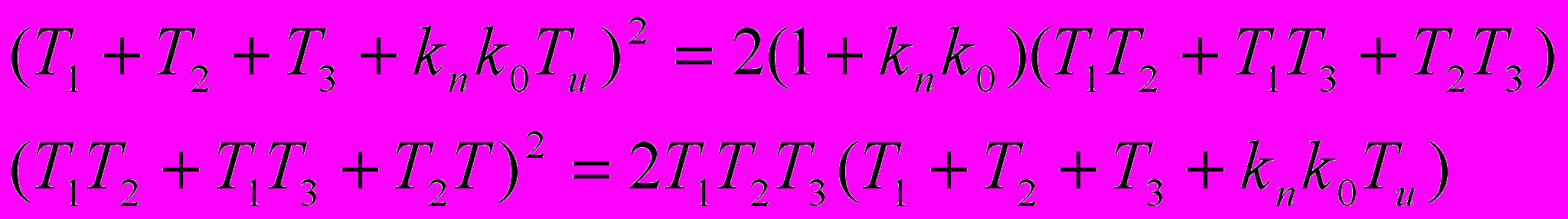Вводя нормирующую постоянную времени



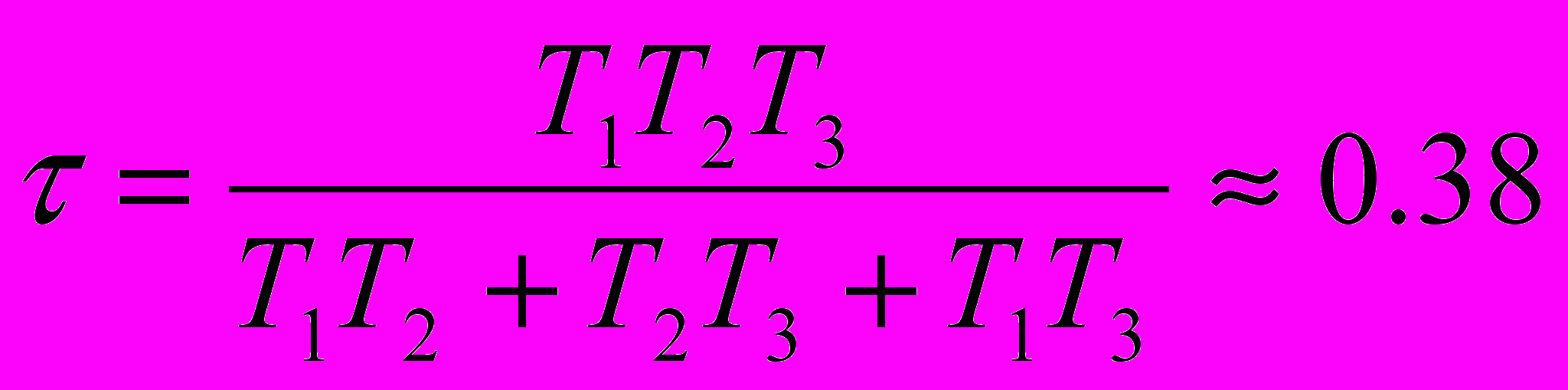
получаем соотношения для выбора параметров регулятора:



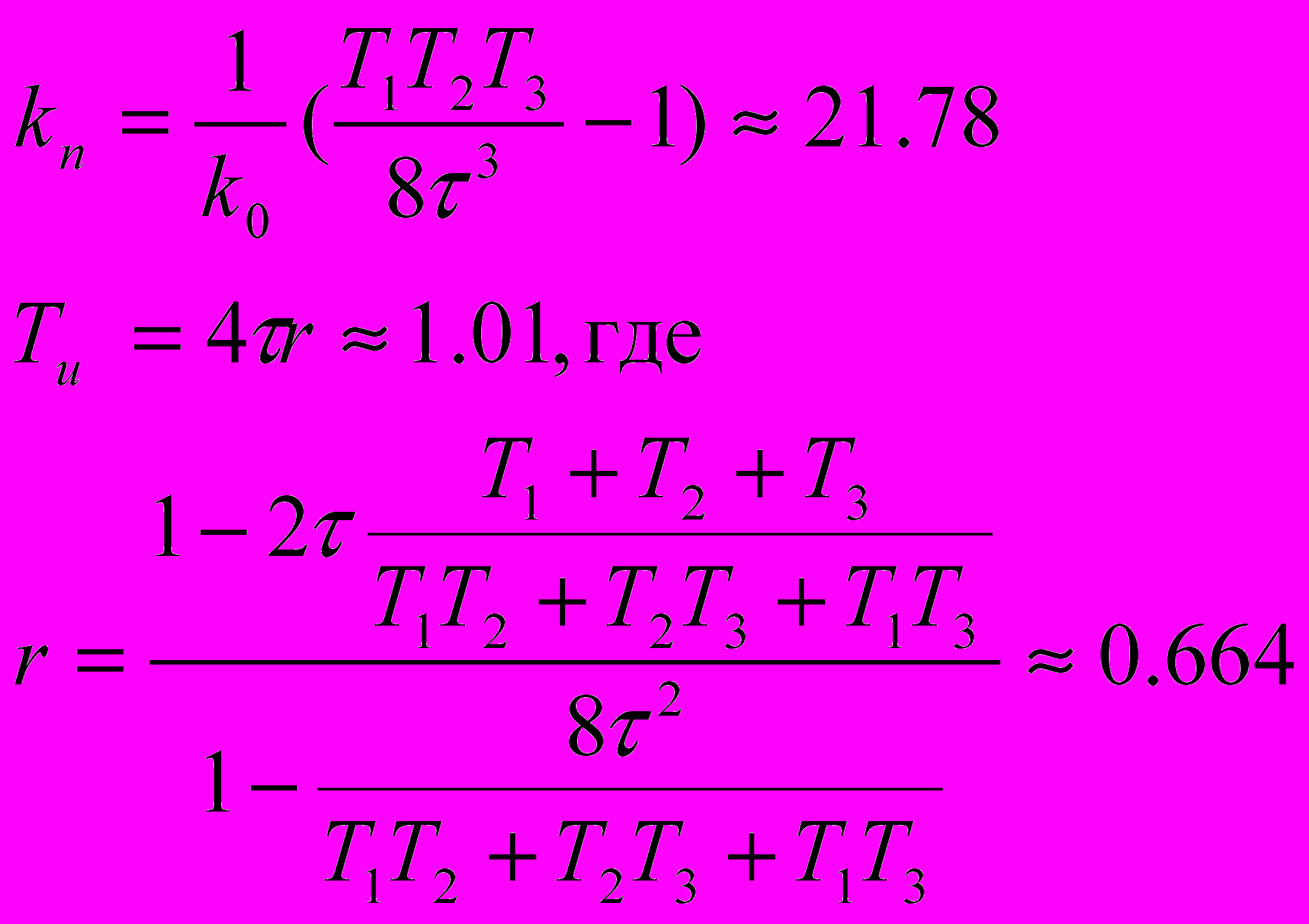
Получаем ПФ замкнутой системы, настроенную на симметричный оптимум:




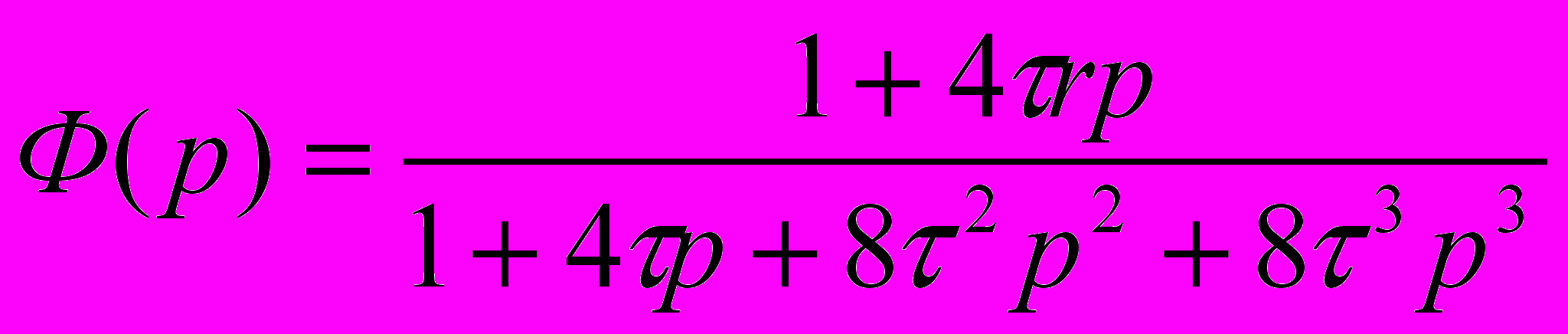
График моделирования:



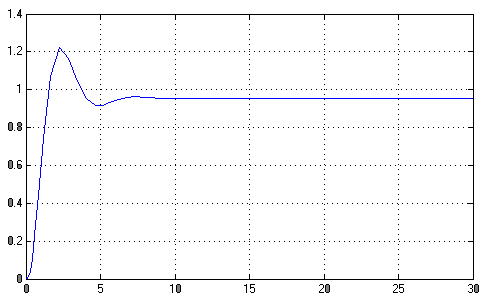
Полученные параметры:



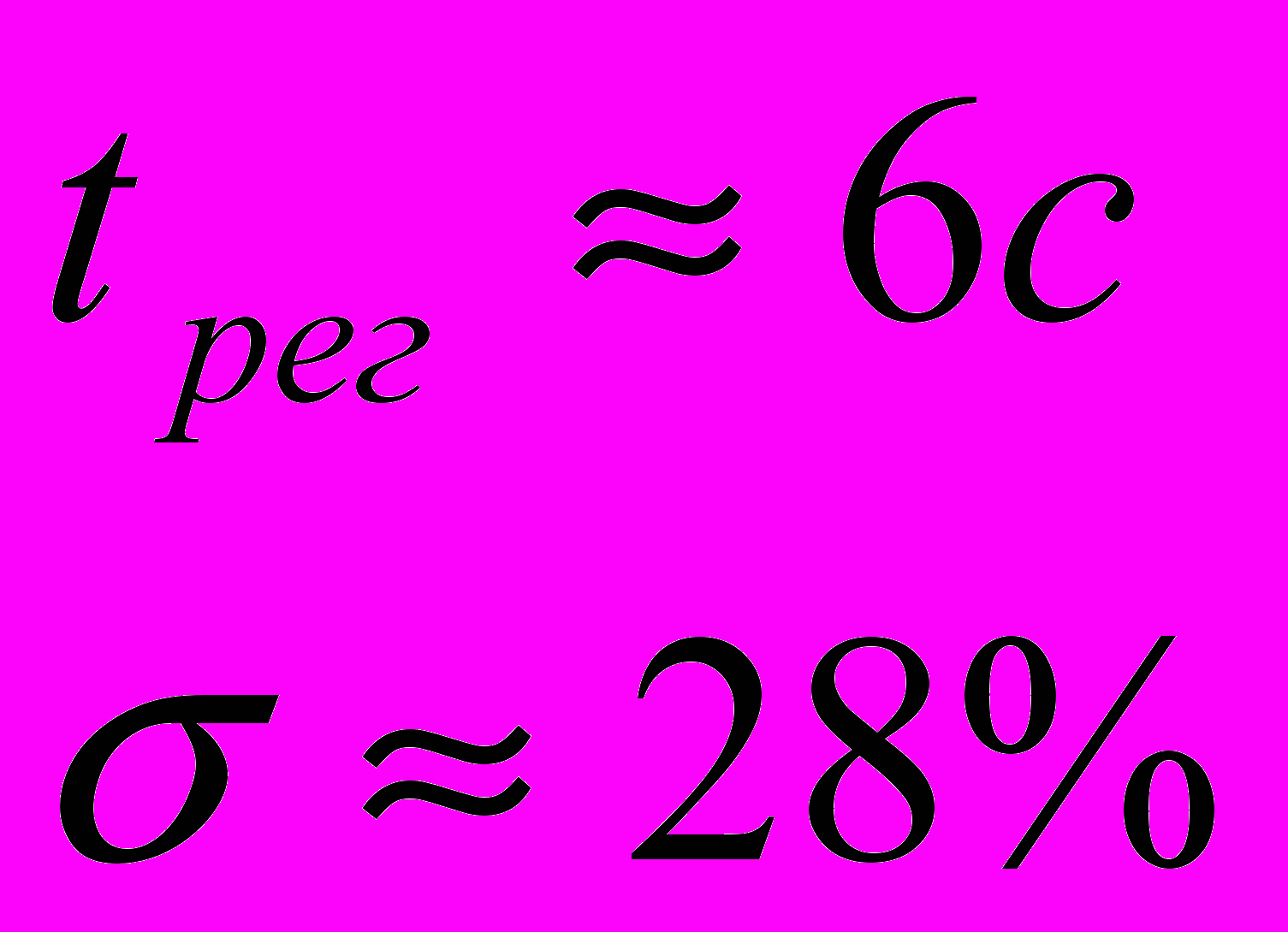
Перрегулирование нас не устраивает, значит применим фильтр сглаживания-дифференцирования:



Параметры фильтра:



Тогда передаточная функция системы примет вид:

, a фильтр примет вид: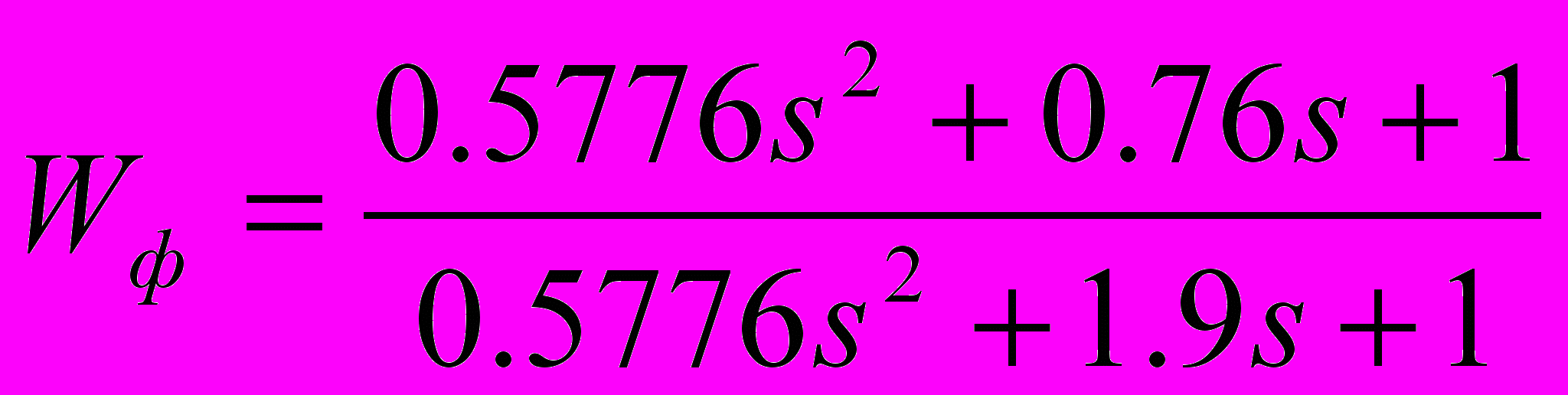


Схема:



График:





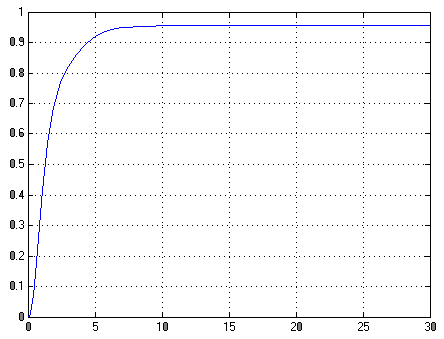
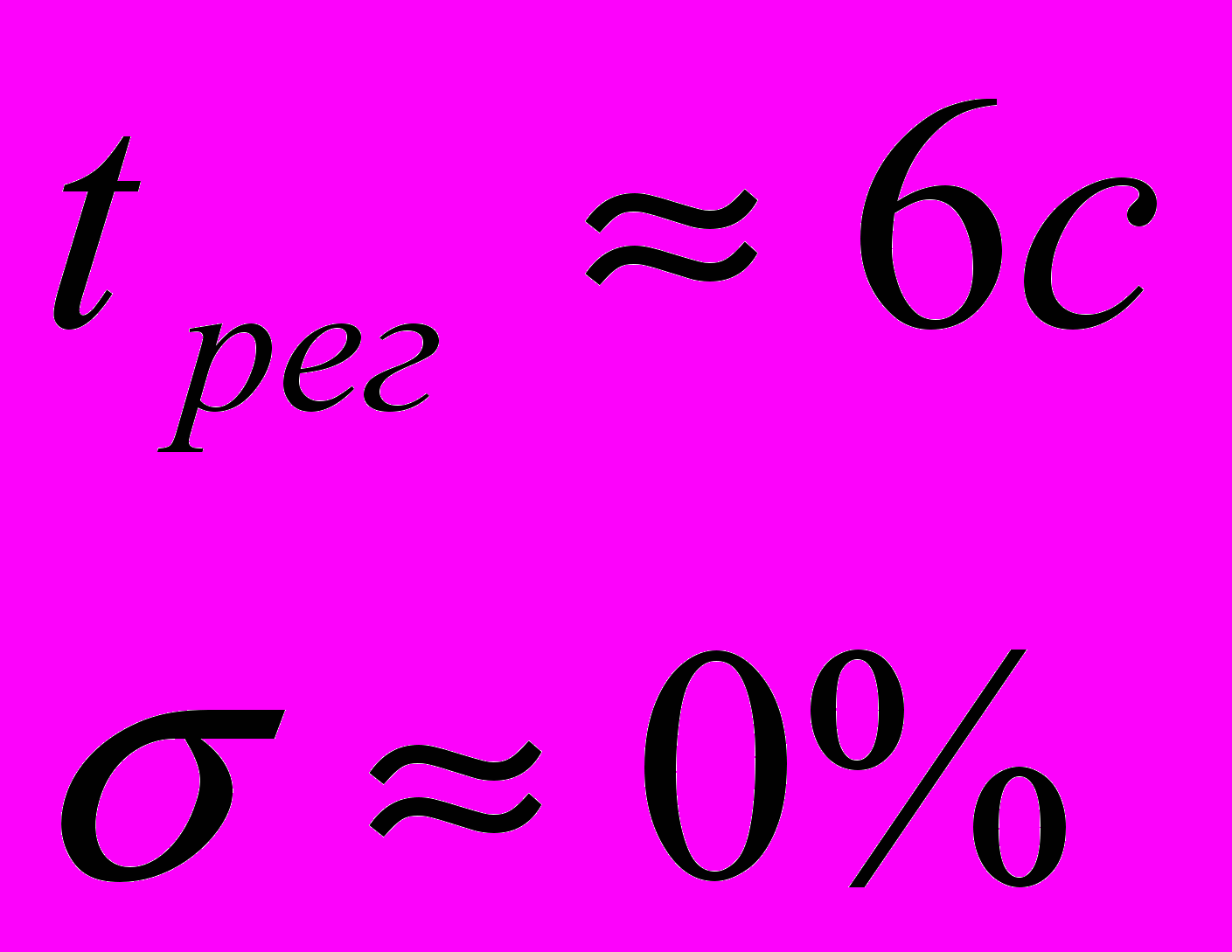
Вывод: Настройка на симметричный оптимум в сочетании со сглаживанием-дифференцированием по достигаемым качественным показателям практически не уступает настройке на модульный оптимум.