"Компьютерные методы в химии. Современное состояние" летняя школа по методам компьютерного моделирования

Вид материала

Документы

Содержание Разработка новых моделей для “Классического” компьютерноного моделирования жидких систем Density Functional Theory of solvation: from simple solutes to self-assemblies of macromolecules Микроскопическая структура молекулярных и ион-молекулярных систем: комплиментарность экспериментальных методов и методов молекул О. Н. Калугин E-mail: Oleg.N.Kalugin@univer.kharkov.ua Компьютерное моделирование фазовых переходов воды Компьютерное моделирование процессов сольватации

Подобный материал:

• Тема Методика обучения химии как наука и учебный предмет в педвузе, 398.5kb.
• Рабочая программа компьютерное моделирование в материаловедении Специальность (направление):, 40.83kb.
• Применение информационных технологий в процессе обучения химии, 213.65kb.
• Iii международный симпозиум актуальные проблемы компьютерного моделирования конструкций, 77.34kb.
• Основы компьютерного проектирования и моделирования рэс, 34.5kb.
• 1. понятие компьютерного моделирования, 110.25kb.
• О Конкурса асов компьютерного 3D-моделирования среди предприятий, использующих в проектных, 9.87kb.
• Курс 3 Семестр -5 Количество кредитов 3 Трудоемкость 135 часов, 91.32kb.
• Аннотация примерной программы учебной дисциплины «Планирование, обработка и анализ, 71.54kb.
• Рабочая программа дисциплины основы компьютерного проектирования и моделирования радиоэлектронных, 255.77kb.

"Компьютерные методы в химии. Современное состояние"

летняя школа по методам компьютерного моделирования

28.06-02.07, Плес


В настоящее время методы компьютерной химии (квантово-химические методы, методы молекулярной динамики, Монте-Карло и т. д.) являются неотъемлемой составной частью теории растворов. Широкое применение компьютерных методов для исследований многокомпонентных конденсированных систем связано с возможностью расчета как любых экспериментальных измеряемых величин, так и величин, экспериментально не определяемых, но используемых для теоретического описания (например, потенциалы средних сил, различные автокорреляционные функции и т. д.). Стремительный прогресс в области вычислительной техники обусловил успешное применение численных методов в биологической и супрамолекулярной химии (исследование сольвофобных эффектов в растворах белков, определение механизма транспорта ионов через биомембраны, изучение структуры растворителей на поверхности раздела фаз и макромолекул). Крайне важным, ввиду бурного развития сверхкритических технологий, является использование ab initio расчетов и методов компьютерного моделирования для изучения растворов в экстремальных условиях.

Уровень современного специалиста в области физической, органической, координационной химии предполагает, с одной стороны, знание основных расчетных схем квантовой химии, с другой – умение применять методы компьютерного моделирования (методы молекулярной динамики и Монте-Карло). Это позволяет критически оценить уровень теоретических работ в конкретной, интересующей исследователя области.

Для проведения школы приглашены известные высококвалифицированные специалисты в области компьютерного моделирования и квантово-химических расчетов из ведущих научно-исследовательских и образовательных центров России:

1. акад. Леонтьев Л.И., ИМ РАН, Екатеринбург
   
2. проф. Маленков Г.Г., ИХФ РАН, Москва
   
3. доц. Калугин О.Н., ХГУ, Харьков
   
4. проф. Чуев Г.Н., ИТЭБ РАН, Пущино
   
5. проф. Назмутдинов Р.Р., КГТУ, Казань
   
6. с.н.с. Пуховский Ю. П., ИХР РАН, Иваново
   
7. с.н.с. Киселев М.Г., ИХР РАН, Иваново
   
8. доц. Бушуев Ю.Г., ИгХТУ, Иваново
   

В рамках школы будут проведены практические занятия по обучению работы с программными продуктами такими как (GROMACS, CHARMM, MODYS, GAUSSIAN 2003).

Тезисы лекций приведены ниже:

Разработка новых моделей для “Классического” компьютерноного моделирования жидких систем

Пуховский Ю.П.


Институт химии растворов РАН, 153045, г. Иваново, ул. Академическая, 1


В настоящее время исследование жидкостей на молекулярном уровне стало возможным благодаря бурному развитию методов статистической геометрии совместно с методами компьютерного моделирования, среди которых наиболее приспособленными для конденсированного состояния являются метод молекулярной динамики (МД) и метод Монте-Карло (МК). Эти методы моделирования появились около полувека назад и на смену им идут новые методы: ab initio МД, QM/MM, QM/MD, развитие и применение которых, однако сдерживается современным состоянием компьютерной техники. Поэтому методы «классического» моделирования, получившие достаточное развитие и вошедшие в состав в ряд коммерческих и некоммерческих пакетов программ, стали стандартным методом исследования не только теоретиков, но и экспериментаторов.

Выбор оптимальных молекулярных моделей исследуемых жидких систем по-прежнему является важнейшей задачей, так как адекватная эмпирическая модель позволяет с высокой точностью воспроизводить с помощью численного моделирования целый ряд экспериментально наблюдаемых термодинамических, структурных и динамических свойств. Однако к началу 90-х годов уже полностью исчезла первоначальная эйфория от успехов методов компьютерного моделирования, поскольку исследователи стали ставить задачи, которые уже нельзя было решить с использованием эффективных парных потенциалов (ЭПП). Эти задачи связаны, прежде всего, с изучением растворов макромолекул, особенно биологически значимых, с изучением жидкостей под влиянием внешних полей, жидкостей у поверхности раздела фаз, а в последние годы исследование сверхкритического состояния вещества. Стали понятны ограничения подхода ЭПП, которые можно преодолеть, учитывая в явном виде многочастичные взаимодействия молекул и неаддитивные эффекты.

В докладе рассмотрены базисные принципы, которые лежат в основе квантовой теории молекул и межмолекулярного взаимодействия в конденсированной среде и которые приводят к представлению о жидкости, как о «супермолекуле» и квантовой природе коллективных эффектов в жидкостях. Описываются общие физические принципы построения ЭПП. Показано, что методика использования ЭПП в МД и МК моделировании является вынужденным вычислительным приемом, который применяется из-за невозможности явно учитывать многочастичные взаимодействия в жидкости. Отмечены принципы, которые лежат в основе построения поляризуемых моделей воды и дают достаточно хорошее приближение квантовой природы коллективных эффектов. Показано, что ПМ лишены недостатков ЭПП и могут применяться для описания воды при внешних воздействиях.

Рассмотрен ряд вопросов, связанных с созданием ЭПП на основе квантово-химических расчетов: начиная от общетеоретических предположений, используемых при конструировании ЭПП и кончая практическими рекомендациями, связанные с проведением расчетов, выбором аналитической функции, процедурой аппроксимации и последующим уточнением полученной модели.


Density Functional Theory of solvation: from simple solutes to self-assemblies of macromolecules”


Chuev. G.N.


Institute of Theoretical and Experimental Biophysics, Russian Academy of Sciences, 142292 Pushchino, Moscow Region, Russia E-mail: genchuev@rambler.ru

.


The state-of-art density functional theory (DFT) is considered within the context of current approaches to solvation effects. The key concept and numerical scheme of DFT is outlined. The schemes based on the correlation function formalism and the integral equation method are described. The main attention is focused on the application of the DFT to solvated quantum solutes, molecular complexes and self-assembled nanostructures.

1. Introduction
   

Statement of the problem. Current treatment of solvation phenomena. Continumm models, molecular simulations, and density functional theory. The key concept of DFT. Advantages of DFT. Integral Equation Theory (IET) and DFT.

2. DFT formalism.
   

Density functionals. Combined DFT for solvated molecular complexes. Correlation function formalism. Numerical schemes of IET and DFT. Multiscale nature of solvation effects. Wavelet algorithm for solving IET. Wavelet DFT technique.

3. Applications.
   

Solvated quantum solutes. Simple and molecular liquids. Solvated molecular complexes. Colloids and self-assembled nanostructures. Polymer liquids. Biomacromolecules.

Микроскопическая структура молекулярных и
ион-молекулярных систем: комплиментарность экспериментальных методов и методов молекулярного моделирования

О. Н. Калугин

Харьковский национальный университет им. В. Н. Каразина,

кафедра неорганической химии, химический факультет,

пл. Свободы, 4, г. Харьков, 61077, Украина

E-mail: Oleg.N.Kalugin@univer.kharkov.ua

Настоящее сообщение посвящено сравнительному анализу возможностей современных экспериментальных методов и методов молекулярного моделирования в исследовании структуры молекулярных жидкостей и электролитных растворов на микроскопическом уровне. Основное внимание уделяется методологическим вопросам исследования микроскопической структуры. В частности, подробно рассмотрена статистико-механическая концепция пространственных корреляционных функций для описания конденсированных неупорядоченных систем – жидкостей и растворов, а также ограничения классического ассоциативно-координационного подхода в применении к многоатомным молекулярным жидкостям и ионным сольватам в неводных электролитных растворах. Рассмотрены возможности и ограничения квантово-химических расчетов и молекулярно-динамического моделирования в исследовании структурной организации молекулярных и ион-молекулярных систем. Показана плодотворность комплиментарного использования экспериментальных методов и методов молекулярного моделирования. Последнее продемонстрировано авторскими результатами исследования микроструктуры чистых метанола, диметилсульфоксида и ацетонитрила, а также растворов NiCl₂ в метаноле и 1-1 электролитов в некоторых неводных растворителях.

Компьютерное моделирование фазовых переходов воды


Ю.Г. Бушуев


ГОУВПО «Ивановский государственный химико-технологический университет», 153460, Иваново, пр. Ф. Энгельса, 7, bushiuev@isuct.ru

Институт химии растворов РАН, 153045, Иваново, ул. Академическая, 1.


Исследованию процессов кристаллизации методами компьютерного моделирования посвящено относительно мало работ [1]. Решение подобных задач требует огромных затрат компьютерных ресурсов. В работах [2,3] описаны фазовые переходы вода-лед, полученные в больших элементарных ячейках моделирования (N~500).

Нами разработана методика моделирования процессов кристаллизации воды, позволяющая получать структуры льдов за короткие интервалы времени моделирования. Мы проводили моделирование воды с потенциалами TIP5P и 6 points методом МК в NpT ансамбле при N=125, T=298 K и давлении до 1 ГПа. Было получено несколько кристаллических фаз воды, в частности, лед 1с.






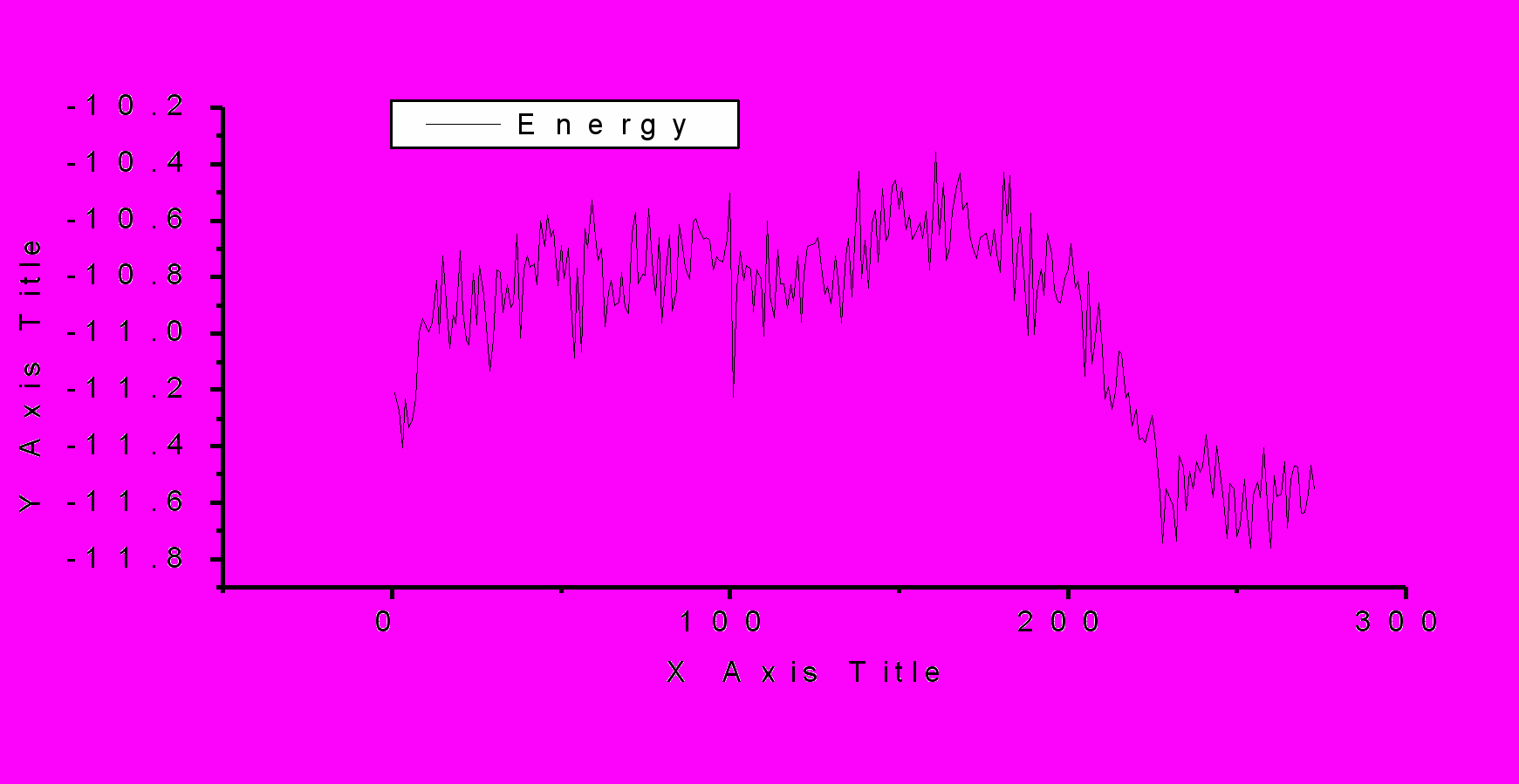
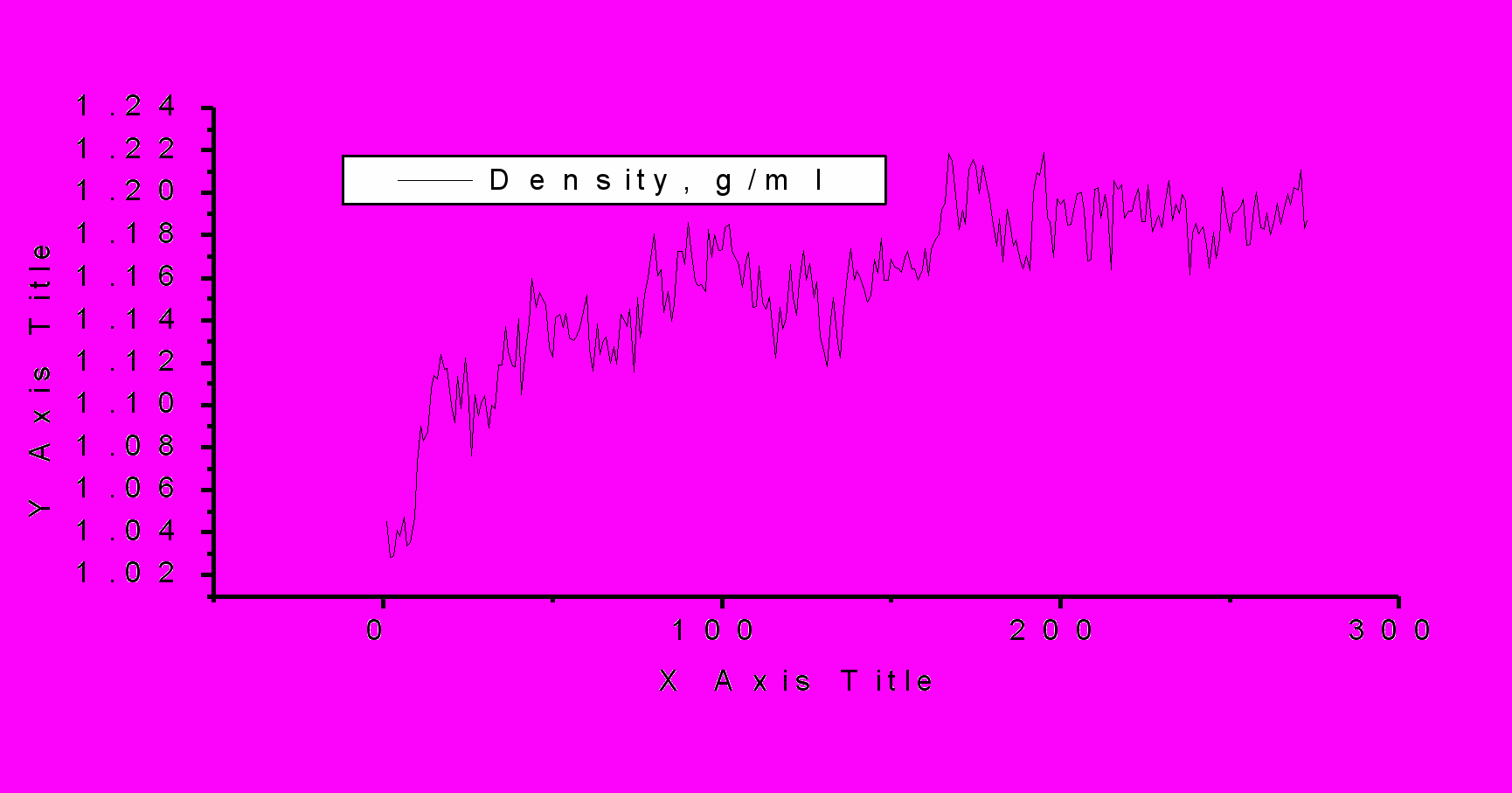
Р


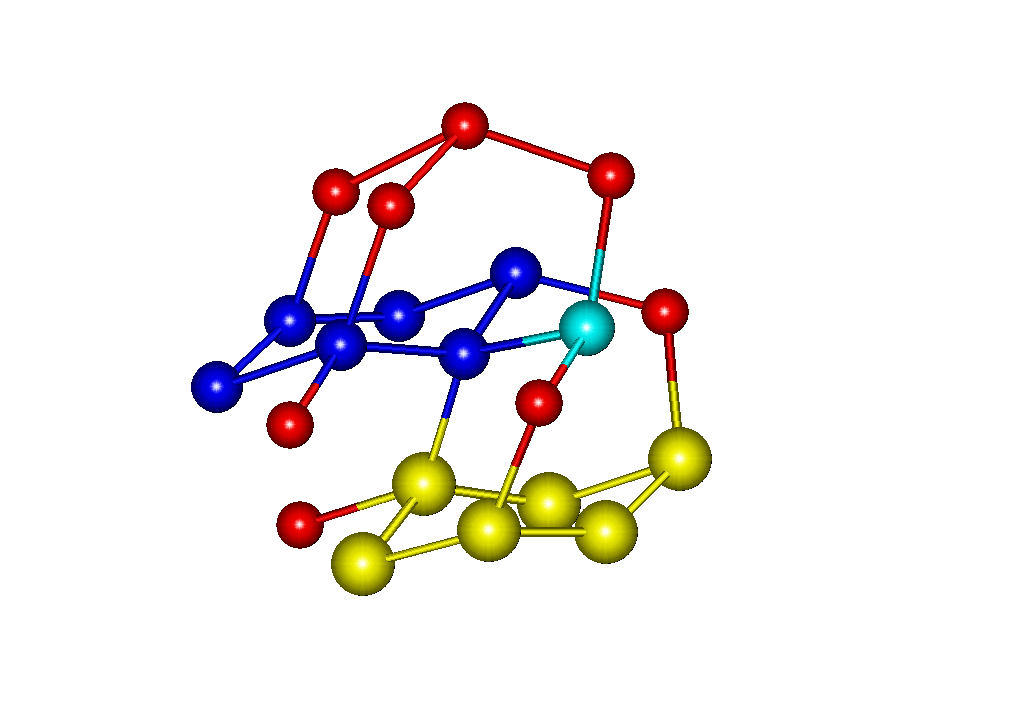
Рис.2. Кристалл новой формы льда
ис.1. Изменение плотности и энергии в процессе фазового перехода. По оси ординат – сохраненная конфигурация на отрезке цепи Маркова. P=0.5 ГПа, Т=298К, TIP5P.

Обсуждается методика моделирования, открывающая возможность практического, детального исследования процессов кристаллизации воды на молекулярном уровне. Другой способ получения структур льдов основан на использовании информации о геометрических параметрах кристаллических ячеек льдов. Мы модифицировали программу, реализующую метод МК для получения кристаллов в NVT –ансамбле. Детально обсуждаются методические аспекты моделирования фазовых переходов. Приводятся примеры (рис.1, 2), даются практические рекомендации использования пользования новых методик. Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 04-03-32363а).

[1] P. Verwer, F.Leusen. Rew. Comput. Chem. 12 (1998) 327.

[2] M. Matsumoto, S. Saito, I. Ohmine. Nature. 416 (2002) 409.

[3] M. Yamada, S. Mossa, H. Eu. Stanley, F. Sciortino. Phys.Rev.Lett. 88 (2002) 195701-1.

Современные проблемы микроскопического моделирования электрохимических межфазных границ


Р.Р. Назмутдинов


Казанский государственный технологический университет

ул. К. Маркса, 68 420015 г. Казань, Республика Татарстан, Россия

(e-mail: nazmutdi@kstu.ru)


В настоящей лекции дается критический анализ современных подходов к описанию микроскопического строения межфазной границы металлический электрод/водный раствор электролита. Подчеркивается, что наиболее перспективным является комбинированный способ, основанный на предельно тесном взаимодействии (сращивании) методов квантовой химии, компьютерного моделирования, теории и эксперимента. Обсуждаются принципиальные микроскопические детали структуры водных растворов в плотной части двойного электрического слоя. Приводятся основные способы описания взаимодействия молекул растворителя и ионов с поверхностью металла (“кластерный” и “твердотельный”) и дискутируются их сильные и слабые стороны. Центральное внимание уделено описанию на молекулярном уровне процессов переноса заряда (электрона, протона или иона) через межфазную границу электрод/раствор. Раскрывается физический смысл неравновесной (коллективной) координаты растворителя; обсуждаются различные способы расчета энергии реорганизации растворителя. Разбираются два предельных режима реакций переноса электрона (адиабатический и неадиабатический) и основные подходы к моделированию эффектов орбитального перекрывания “металлический электрод” - ”частица реагента”. Акцентируется внимание на проблеме корректного описания влияния растворителя на величину одного из ключевых кинетических параметров - резонансного расщепления реакционных термов. Подробно обсуждается один из эффективных способов построения адиабатических поверхностей свободной энергии для реакций межфазного переноса электрона. Особое место в лекции занимают проблемы микроскопического описания специфической адсорбции ионов, сопровождающейся частичным переносом заряда на металл. Анализируются современные подходы к изучению молекулярных аспектов влияния динамики растворителя (вязкости) на кинетику электрохимических реакций. Фундаментальные основы используемых моделей и общие принципы микроскопического моделирования иллюстрируются большим количеством как литературных, так и оригинальных результатов. Приводится ряд примеров, демонстрирующих новую интерпретацию наиболее интересных эффектов, наблюдаемых в эксперименте.


Компьютерное моделирование процессов сольватации.

М. Г. Киселев

Институт химии растворов РАН, 153045, г. Иваново, ул. Академическая, 1, mgk@isc-ras.ru


Численное моделирование жидкостей возникло почти одновременно с появлением компьютерной техники в начале 60-х годов и с тех пор прочно заняло одно из первых мест в арсенале исследователей. Из двух существующих методов: Монте-Карло (МК) и молекулярная динамика (МД), последний выглядит наиболее привлекательным при исследовании сольватации, поскольку наряду со структурными и термодинамическими свойствами растворов позволяет рассчитывать и их кинетические свойства, в то время как МК ограничен лишь расчетом статических свойств жидкостей. Суть метода МД моделирования состоит в численном интегрировании уравнений движений молекул исследуемой системы, взаимодействующих посредством заданного парного потенциала. В результате получается полная информация о микросостоянии системы (координатах и скоростях всех частиц) на некотором участке ее траектории. Использование основных соотношений статистической физики позволяет из этой информации получить макроскопические (термодинамические, структурные и кинетические) свойства исследуемой системы, часть из которых наблюдаема в физическом эксперименте. Выбор и особенности расчета тех или иных макроскопических свойств определяется конкретными целями исследования.

В лекции рассматриваются различные сольватационные характеристики, одной из которых является потенциал средней силы (ПСС) W(r), позволяющий оценить работу по переносу молекул растворенного вещества друг к другу. Кроме этого обсуждается современное состояние проблемы расчета свободной энергии сольватации на основе комбинации классического МД моделирования и квантово-химического расчета энергий конфигураций. Непосредственно о возникновении клатрато-подобных структур в растворе можно судить, рассчитав такие функции, как локальный состав 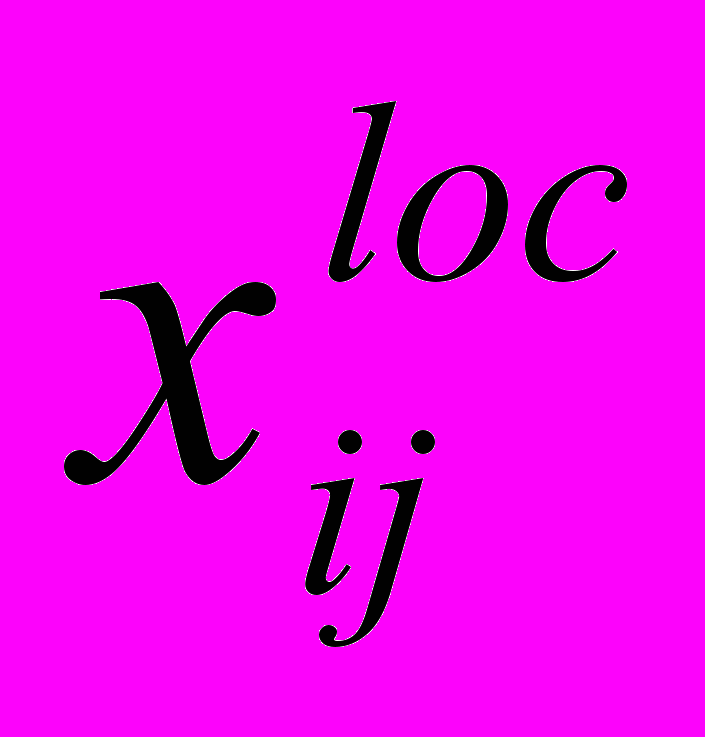компонента i вблизи компонента j в зависимости от состава смеси x₂ , парные корреляционные функции ближайших соседей и т.д.

Изучение сетки водородных связей дает дополнительную информацию о сольватации в смесях ассоциированных жидкостей. Рассматриваются как классические так и квантовые подходы к описанию сетки Н-связей. Другой плодотворный подход к изучению структуры жидкостей может быть осуществлен в рамках статистической геометрии на основе описания свойств симплексов Делоне. Структура водных растворов может быть описана с помощью распределения вероятности искажения так называемых координационных симплексов. Особое внимание в лекции уделено методам неэмпирического МД. Рассмотрены основные принципы и некоторые приложения.