Учебное пособие, Пер с англ. М.: Апрель Пресс, Изд-во эксмо-пресс, 2001. 752 с. (Серия «Кафедра психологии»). Перевод с английского
| Вид материала | Учебное пособие |
СодержаниеРаспределение индивидуальных различий |
- Анастази А. А 64 Дифференциальная психология. Индивидуальные и групповые разли- чия, 11288.93kb.
- Кафедра психологии, 11232.1kb.
- Франкл В. Воля к смыслу/Пер с англ. М.: Апрель-Пресс, Изд-во эксмо-пресс, 2000. 368, 2242.15kb.
- Пол вацлавик джанет бивин дон джексон прагматика человеческих коммуникаций, 10972.83kb.
- Джон дилeo детский рисунок, 1281.21kb.
- Экскурс в психологию семьи и семейных отношений от древности до наших дней 10 Проблематика, 6419.83kb.
- Ялом И. Когда Ницше плакал/ Пер с англ. М. Будыниной, 4547.16kb.
- Ялом И. Когда Ницше плакал/ Пер с англ. М. Будыниной, 4547.52kb.
- Tales of psychotherapy basic books, 2957.8kb.
- Ирвин Ялом. Мамочка и смысл жизни, 2766.77kb.
РАСПРЕДЕЛЕНИЕ ИНДИВИДУАЛЬНЫХ РАЗЛИЧИЙ
Поскольку индивидуальные различия в обозначенном выше смысле носят количественный характер, возникает вопрос, как различные степени каждого качества распределяются среди людей. Происходит ли распределение индивидов равномерно по всему ряду этих степеней, или они как бы группируются вокруг одного или нескольких пунктов? Какова относительная частота проявления различных степеней? На эти вопросы лучше всего отвечать, анализируя частотные распределения и графики частоты.
Подобно другим методам статистики, частотное распределение представляет собой суммирование и обработку количественных данных, которые производятся для понимания общей картины и выявления существенных тенденций. Результаты тестирования или любые другие серии измерений группируются в классы, и все случаи, лежащие внутри каждого класса, заносятся в таблицу. Таблица 1 представляет собой пример та-
распределение индивидуальных различий 35
кого частотного распределения. В ней приводятся результаты тестирования 1000 студентов колледжа на умение применять код, в котором необходимо было один набор бессмысленных слогов заменить на другой. Данные, показывающие количество правильно замененных за две минуты слогов, находились в интервале от 8 до 52. Они были сгруппированы по интервалам (по 4 пункта в каждом), начиная с 52—55 на верхней точке распределения и заканчивая 8—11 на нижней. Колонка под названием «частота» в таблице 1 показывает количество людей, чьи результаты лежат в этих интервалах. Например, показатели, находящиеся в пределах 52 и 55, зафиксированы только у одного человека, значения между 48 и 51 — тоже у одного, а значения между 44 и 47 — у двадцати и так далее. Очевидно, что результаты данного теста гораздо легче увидеть при помощи такого распределения, чем рассматривая лист, содержащий 1000 первичных результатов.
Еще удобнее иметь дело с показателями частотного распределения, если изобразить их графически. Рисунок 2 представляет данные таблицы 1 в графической форме. На горизонтальной оси даны результаты, сгруппированные в интервалы; числа на вертикальной оси означают количество случаев внутри каждого интервала.
График сделан в двух формах, которые обычно широко используются. Одна графическая форма называется полигоном частот, в котором число индивидов внутри каждого интервала обозначено точкой, расположенной напротив центра интервала; последовательность точек затем была соединена прямыми линиями. Другая графическая форма образуется прямыми колонками, или прямоугольниками, основаниями которых служат интервалы высота каждой колонки зависит от числа случаев в данном интервале. Такая графическая форма называется гистограммой. Если взглянуть, например, на интервал 44—47 в таблице 1, то можно найти 20 случаев результирующих значений, находящихся в его пределах. Соответственно на рисунке 2 точка ставится на пересечении проекции от 20 и проекции центра интервала 44—47. Мы получаем одну из точек, необходимых для построения частотного полигона. В гистограмме те же 20 случаев представлены колонкой 44—47 интервала, ограниченной сверху проекцией числа 20, находящегося на вертикальной оси.
36 Дифференциальная психология *
Таблица 1 Частотное распределение данных 1000 студентов колледжа, тестирование умения применять код. (Данные из Анастази, 2, с. 34.)
| Класс—интервал | Частота |
| 52-55 48-51 44-47 40-43 36-39 32-35 28-31 24-27 20-23 16-19 12-15 8-11 | 1 1 20 73 156 328 244 136 28 8 3 2 |
| | N = 1000 |
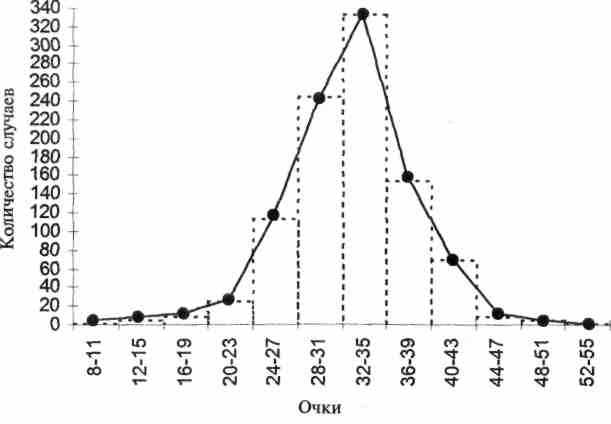
Рис. 2. График распределения: полигон частот и гистограмма. (Данные из таблицы 1.)
Распределение индивидуальных различий 37
Мы можем продолжить описание группы, определив ее центральную тенденцию. Если мы захотим получить наиболее типичное значение, которое характеризовало бы группу в целом, то необходимо определение главной тенденции. Одним из наиболее известных способов является вычисление средней величины, получаемой при сложении всех показателей и делении полученной суммы на число случаев. Такая величина называется средним арифметическим.
Другим способом определения главной тенденции, часто используемым в психологии, является медианный. Если все результирующие значения расположить по порядку в соответствии со своей величиной, то медианой будет результат, расположенный ровно посередине ряда. Для больших групп гораздо легче вычислить медиану непосредственно на основе частотного распределения. В этом случае медианная точка разделяет распределяемое множество таким образом, что половина случаев будет находиться выше нее, а другая половина — ниже. Еще одним способом измерения главной тенденции, иногда встречающимся в психологических исследованиях, является определение моды, или наиболее часто встречающегося показателя. Его так же можно найти на основе частотного распределения, выявив ту точку интервала, которая имеет самую большую частоту. Заметим, что мода соответствует самой высокой точке графика. Для распределения, данного в таблице 1 и на рисунке 2, среднеарифметическое значение составляет 32,37, медианное — 32,46 и значение моды — 33,5.
