Рабочая программа дисциплины Комплексный анализ Направление подготовки
| Вид материала | Рабочая программа |
- Рабочая программа дисциплины «Комплексный анализ хозяйственной деятельности» Рекомендуется, 199.12kb.
- Рабочая программа дисциплины «Математический анализ» Направление подготовки, 180.51kb.
- Рабочая программа дисциплины Системный анализ и принятие решений Направление подготовки, 138.22kb.
- Рабочая программа дисциплины «теоретические основы теплотехники» Направление подготовки, 554.69kb.
- Рабочая программа дисциплины «Техническая термодинамитка» Направление подготовки, 804.99kb.
- Рабочая программа учебной дисциплины «Математический анализ» Направление подготовки, 275.11kb.
- Рабочая программа дисциплины Физика, ен. Ф. 03 направление подготовки, 491.56kb.
- Рабочая программа дисциплины «Математический анализ ii» Направление, 132.24kb.
- Рабочая программа учебной дисциплины «комплексный экономический анализ хозяйственной, 285.64kb.
- Рабочая программа дисциплины «Компьютерная диагностика» Направление подготовки, 209.63kb.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Томский государственный университет
Факультет прикладной математики и кибернетики
Декан ФПМК
___________________ А.М.Горцев
"1" марта 2011 г.
Рабочая программа дисциплины
Комплексный анализ
Направление подготовки
010400– Прикладная математики и информатика
Квалификация выпускника
Бакалавр
Форма обучения: очная
Томск
2011
- Цели освоения дисциплины
Целью освоения дисциплины «Комплексный анализ» является изучение методов, задач и теорем комплексного анализа, их применение к решению задач прикладной математики и информатики.
Задачи:
• дать студентам знания по теории функций комплексного переменного, необходимые для понимания ее приложений к математическому анализу, алгебре, дифференциальным уравнениям и другим математическим дисциплинам теоретическое освоение студентами современных концепций и моделей комплексного анализа;
• снабдить студентов математическим аппаратом, необходимым для применения математических методов в практической деятельности и в исследованиях;
• познакомить студентов с понятиями, фактами и методами, составляющими теоретические основы комплексного анализа;
Учебный материал дисциплины «Комплексный анализ» сгруппирован вокруг следующих тем: комплексные числа, дифференциальное исчисление функций комплексных переменных, комплексные ряды, аналитические функции, интегрирование функций комплексной переменной, разложение в ряд Лорана, теорема Лиувилля и ее приложения, приложения теории вычетов к вычислению интегралов. Изучение дисциплины в значительной мере опирается на курсы «Математический анализ 1-3», Линейная алгебра» и в свою очередь доставляет необходимый аппарат для решения проблем и задач упомянутых дисциплин. Многие теоремы и утверждения дисциплины «Комплексный анализ» напрямую заимствуются из теории функций действительного переменного. Методической особенностью курса является то обстоятельство, что при переходе в комплексную область многие привычные факты становятся просто неверными. так, например, довольно сложно построить в действительной области непрерывную функцию, которая не является дифференцируемой ни в одной точке. В комплексном анализе такие примеры может построить любой студент. Для аналитических и мероморфных функций их область значений - это почти все комплексные числа, за исключением нескольких точек. Другой особенностью курса является существенное расширение запаса возможных действий. Особое значение имеет комплексный анализ для дифференциальных уравнений. Многие типы дифференциальных уравнений получают при этом чисто алгебраическое решение.
2.Место дисциплины в структуре ООП бакалавриата
Дисциплина «Комплексный анализ» является базовой дисциплиной математического и естественнонаучного цикла Б.2 дисциплин Федерального государственного образовательного стандарта высшего профессионального образования (ФГОС ВПО) по направлению «Прикладная математика и информатика» (бакалавриат).
Дисциплина «Комплексный анализ» базируется на знаниях, полученных в рамках курса «Математический анализ».
Дисциплина «Комплексный анализ» является общим теоретическим и методологическим основанием для всех математических дисциплин и дисциплин информационного блока, входящих в ООП бакалавра прикладной математики и информатики.
3 Компетенции обучающегося, формируемые в результате освоения дисциплины «Комплексный анализ
В совокупности с другими дисциплинами базовой части математического цикла ФГОС ВПО дисциплина «Комплексный анализ» обеспечивает инструментарий формирования следующих компетенций бакалавра прикладной математики и информатики.
а) Общекультурные компетенции (ОК):
• владение культурой мышления, умение аргументировано и ясно строить устную и письменную речь (ОК-1);
• способность и готовность к письменной и устной коммуникации на родном языке (ОК-2);
• способность к интеллектуальному, культурному, нравственному, физическому и профессиональному саморазвитию, стремление к повышению своей квалификации и мастерства (ОК-3);
• демонстрация общенаучных базовых знаний естественных наук, математики и информатики, понимание основных фактов, концепций, принципов теорий, связанных с комплексным анализом (ОК-10);
• владение навыками работы с компьютером как средством управления информацией (ОК-11);
• способность работать с информацией в глобальных компьютерных сетях (ОК-12);
• способность использовать в научной и познавательной деятельности, а также в социальной сфере профессиональные навыки работы с информационными и компьютерными технологиями (ОК-14);
• умение использовать навыки поиска и работы с информацией из различных источников, включая сетевые ресурсы сети Интернет, для решения профессиональных и социальных задач (ОК-15);
• умение приобретать новые научные и профессиональные знания, используя современные образовательные и информационные технологии (ОК-16);
б) Профессиональные компетенции (ПК) (по видам деятельности):
1) научно-исследовательская деятельность:
• способность собирать, обрабатывать и интерпретировать данные современных научных исследований, необходимые для формирования выводов по соответствующим научным, профессиональным, социальным и этическим проблемам (ПК-1);
• способность понимать и применять в исследовательской и прикладной деятельности современный математический аппарат (ПК-2);
• способность применять в профессиональной деятельности современные языки программирования и языки баз данных, операционные системы, электронные библиотеки и пакеты программ, сетевые технологии (ПК-3);
2) проектная и производственно-технологическая деятельность:
• способность осуществлять целенаправленный поиск информации о новейших научных и технологических достижениях в сети Интернет и из других источников (ПК-6);
• понимание сущности и значения информации в развитии современного общества; владение основными методами, способами и средствами получения, хранения, ереработки информации (ПК-9);
3) организационно-управленческая деятельность:
• способность составлять и контролировать план выполняемой работы, планировать необходимые для выполнения работы ресурсы, оценивать результаты собственной работы (ПК-12);
В результате освоения содержания дисциплины «Комплексный анализ» студент должен:
знать
- основы комплексного анализа (поле комплексных чисел, аналитические функции, разложение в ряд Тейлора и Лорана, продолжение аналитической функции, вычеты и их применение для вычисления интегралов), необходимые для успешного изучения математических и теоретико-информационных дисциплин, решения задач, возникающих в профессиональной сфере; задач, возникающих в информатике;
уметь
- применять методы комплексного анализа для решения математических задач, построения и анализа моделей в технических и экономических системах и информатике;
владеть
- навыками применения современного математического инструментария для решения задач прикладной математики и информатики; методикой построения, анализа и применения математических моделей в различных областях техники и информатики.
4. Структура и содержание дисциплины «Комплексный анализ»
Общая трудоемкость дисциплины составляет 6,6 зачетных единиц 237часов.
Вид промежуточной аттестации – зачет, экзамен
| № п/п | Раздел Дисциплины | Семестр | Неделя семестра | Виды учебной работы, включая самостоятельную работу студентов и трудоемкость (в часах) | Формы текущего контроля успеваемости (по неделям семестра) Форма промежуточной аттестации (по семестрам) | ||
| | | | | лекции | практики | Сам. раб | |
| 1 | Комплексные числа | 4 | | 6 | 6 | 8 | |
| 2 | Дифференциальное исчисление функций комплексных переменных | 4 | | 6 | 6 | 8 | Контрольная работа, коллоквиум |
| 3 | Разложение в ряд функции комплексной переменной | 4 | | 6 | 6 | 8 | |
| 4 | Аналитические функции | 4 | | 4 | 4 | 8 | |
| 5 | Интегрирование функций комплексной переменной | 4 | | 6 | 6 | 8 | Контрольная работа, коллоквиум |
| 6 | Разложение в ряд Лорана | 4 | | 8 | 8 | 8 | |
| 7 | Теорема Лиувилля и ее приложения | 4 | | 4 | 4 | 8 | |
| 8 | Приложения теории вычетов к вычислению интегралов | 4 | | 6 | 6 | 8 | Контрольная работа, коллоквиум |
| 9 | Интегралы, зависящие от параметра | 4 | | 8 | 8 | 8 | |
| 10 | Основные понятия операционного исчисления | 4 | | 6 | 6 | 8 | Контрольная работа, коллоквиум Зачет, экзамен |
| | | | | 60 | 60 | 80 | 37 |
- Содержание курса
Тема 1. Комплексные числа
Комплексные числа и действия над ними, алгебраическая форма комплексного числа. Сопряженные комплексные числа, модуль комплексного числа. Геометрическая интерпретация комплексных чисел. Неравенство треугольника. Тригонометрическая форма комплексного числа. Формулы Эйлера и Муавра. Показательная форма комплексного числа. Извлечение корня. Расширенная плоскость, сфера Римана.
Тема 2. Дифференциальное исчисление функций комплексных переменных
Последовательности и ряды комплексных чисел. Функции комплексной переменной, ведение к функциям действительной переменной. Элементарные функции. Предел функции комплексной переменной в точке, на бесконечности, бесконечный предел. Непрерывность функции комплексной переменной. Дифференцируемость функции комплексной переменной. Геометрический смысл производной. Условия Коши - Римана.
Тема 3. Разложение в ряд функции комплексной переменной
Степенные ряды в комплексной области. Теорема Абеля, круг и радиус сходимости. Свойства степенного ряда внутри его круга сходимости: равномерная сходимость, почленное дифференцирование и интегрирование. Разложение в ряд Тейлора. Примеры разложения в ряд Тейлора основных элементарных функций.
Тема 4. Аналитические функции
Аналитические функции. Теорема единственности. Понятие об аналитическом продолжении. Элементарные аналитические функции: линейная, дробно-линейная, степенная функция с натуральным показателем, показательная, тригонометрические и гиперболические функции, логарифмическая функция. Формула Эйлера.
Тема 5. Интегрирование функций комплексной переменной
Интеграл от функции комплексной переменной. Интегральная теорема Коши для непрерывно дифференцируемой функции. Интегральная формула Коши. Теорема о среднем. Аналитичность непрерывно дифференцируемой функции.
Тема 6. Разложение в ряд Лорана
Ряды Лорана и их область сходимости. Разложение в ряд Лорана функции, аналитической в кольце. Единственность разложения в ряд Лорана. Неравенства Коши для коэффициентов ряда Лорана. Изолированные особые точки, их классификация. Ряд Лорана в окрестности изолированной особой точки.
Тема 7. Теорема Лиувилля и ее приложения
Теорема о максимуме модуля. Теорема Лиувилля. Основная теорема алгебры. Представление мероморфной функции с конечным числом полюсов. Теорема Пикара.
Тема 8. Приложения теории вычетов к вычислению интегралов
Понятие вычета. Вычисление вычета в конечной точке. Вычет в бесконечности. Основная теорема теории вычетов. Примеры вычисления интегралов с помощью вычетов.
Тема 9. Интегралы, зависящие от параметра
Изучаются свойства и способы преобразования интегралов, зависящих от параметров. В качестве частного случая таких интегралов изучаются преобразования Фурье и Лапласа. В лекциях рассматриваются вопросы: равномерная сходимость функций, непрерывность предельной функции; перестановка двух пределов, предельный переход под знаком интеграла, дифференцирование и интегрирование под знаком интеграла; равномерная сходимость несобственных интегралов; признаки равномерной сходимости; Г и В – функции Эйлера; интеграл Фурье; признаки сходимости интеграла Фурье; преобразование Фурье, его свойства и применение; преобразование Лапласа, его свойства и применение.
Тема 10. Основные понятия операционного исчисления
Основные свойства преобразования Фурье и Лапласа. Изображение элементарных функций. Применение операционного исчисления к решеню обыкновенных дифференциальных уравнений
5. Образовательные технологии
В качестве образовательной технологии выбрана традиционная - лекционно-семинарская система обучения, которая является наиболее информационноемкой. Она пригодна для решения таких задач как передача большого объема информации, развития памяти, внимания, некоторых логических умений обучающихся (выделять главное и существенное, структурировать учебный материал, подбирать доказательство). Составляющие технологии:
- поточно-групповая организация занятий;
- еженедельная передача информации небольшими порциями;
- постановка преподавателем четких целей обучения;
- фронтальная и индивидуальная работа преподавателя со студентами;
- индивидуальная работа студентов с учебной литературой;
- фрагментарная проверка выполнения самостоятельной работы студентов;
Условием эффективного усвоения содержания курса является обязательное сочетание теоретических занятий с практическими, на которых отрабатываются выделенные общие умения, входящие в них знания.
Занятия лекционного типа составляют 50% аудиторных занятий
6. Учебно-методическое обеспечение самостоятельной работы студентов. Оценочные средства для текущего контроля успеваемости, промежуточной
Самостоятельная работа студентов заключается в выполнении домашних практических работ, индивидуальных работ, подготовке теоретических вопросов, в том числе систематизации знаний.
Обязательными при изучении дисциплины «Комплексный анализ» являются следующие виды самостоятельной работы:
— разбор теоретического материала по пособиям и конспектам лекций;
— самостоятельное изучение указанных теоретических вопросов;
— решение задач по темам практических занятий;
— выполнение домашних контрольных работ.
Для текущего контроля самостоятельной работы в каждом семестре предусмотрено проведение контрольных работ и коллоквиумов по основным разделам дисциплины
Контрольные вопросы по курсу «Комплексный анализ»
1. Комплексные числа и действия над ними.
2. Алгебраическая форма комплексного числа.
3. Сопряженные комплексные числа, модуль комплексного числа.
4. Геометрическая интерпретация комплексных чисел.
5. Неравенство треугольника.
6. Тригонометрическая форма комплексного числа.
7. Формула Эйлера.
8. Формула Муавра.
9. Показательная форма комплексного числа.
10. Извлечение корня.
11. Расширенная плоскость, сфера Римана.
12. Предел последовательности комплексных чисел и его свойства.
13. Ряды комплексных чисел. Их сходимость, признаки сходимости.
14. Функции комплексной переменной, сведение к функциям действительной переменной.
15. Предел функции комплексной переменной в точке, на бесконечности, бесконечный предел.
16. Непрерывность функции комплексной переменной.
17. Дифференцируемость функции комплексной переменной.
18. Геометрический смысл производной.
19. Условия Коши - Римана дифференцируемости функции комплексной переменной.
20. Понятие о конформном отображении.
21. Степенные ряды в комплексной области.
22. Теорема Абеля, круг и радиус сходимости.
23. Равномерная сходимость степенного ряда внутри его круга сходимости.
24. Почленное дифференцирование степенного ряда внутри его круга сходимости.
25. Почленное интегрирование степенного ряда внутри его круга сходимости.
26. Разложение в ряд Тейлора.
27. Примеры разложения в ряд Тейлора основных элементарных функций.
28. Аналитические функции.
29. Теорема единственности для аналитических функций.
30. Понятие об аналитическом продолжении.
31. Линейная функция
32. Дробно-линейная функция.
33. Степенная функция с натуральным показателем.
34. Показательная функция.
35. Тригонометрические функции.
36. Гиперболические функции.
37. Логарифмическая функция.
38. Формула Эйлера.
39. Интеграл от функции комплексной переменной.
40. Интегральная теорема Коши для непрерывно дифференцируемой функции.
41. Интегральная формула Коши. Формула Коши для высших производных
42. Неравенство Коши, теорема Лиувилля, теорема Мореры.
43. Аналитичность непрерывно дифференцируемой функции.
44. Ряды Лорана и их область сходимости.
45. Разложение в ряд Лорана функции, аналитической в кольце.
46. Единственность разложения в ряд Лорана.
47. Неравенства Коши для коэффициентов ряда Лорана.
48. Типы особых точек функции. Связь типа особой точки функции с видом ее ряда Лорана.
49. Ряд Лорана в окрестности изолированной особой точки.
50. Понятие вычета. Вычеты: определение, основная теорема о вычетах, вычисление вычетов (без вычисления интеграла).
51. Вычисление вычета в конечной точке.
52. Вычисление вычета в бесконечности.
53. Основная теорема теории вычетов.
54. Вычисление с помощью вычетов интегралов:
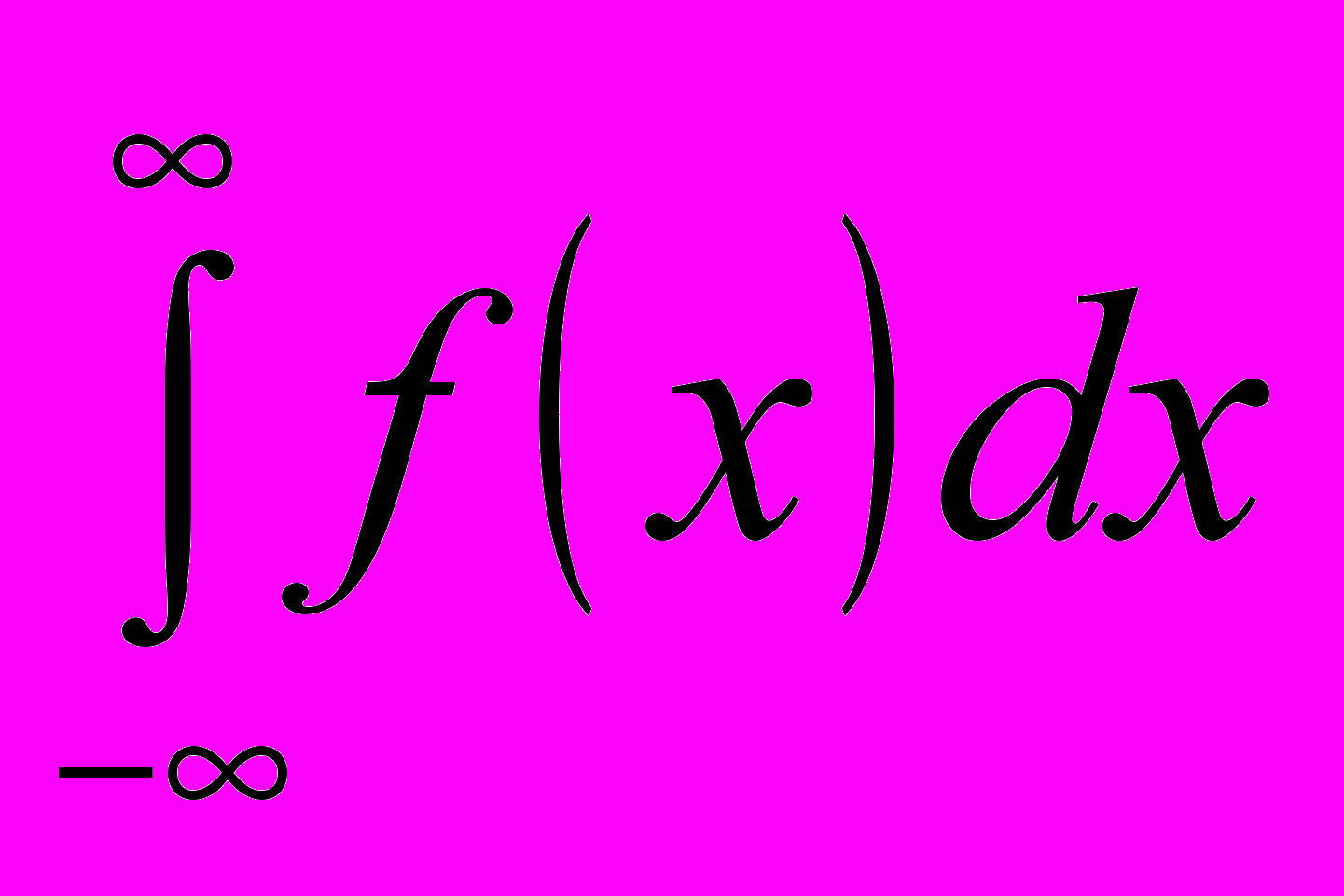 и
и 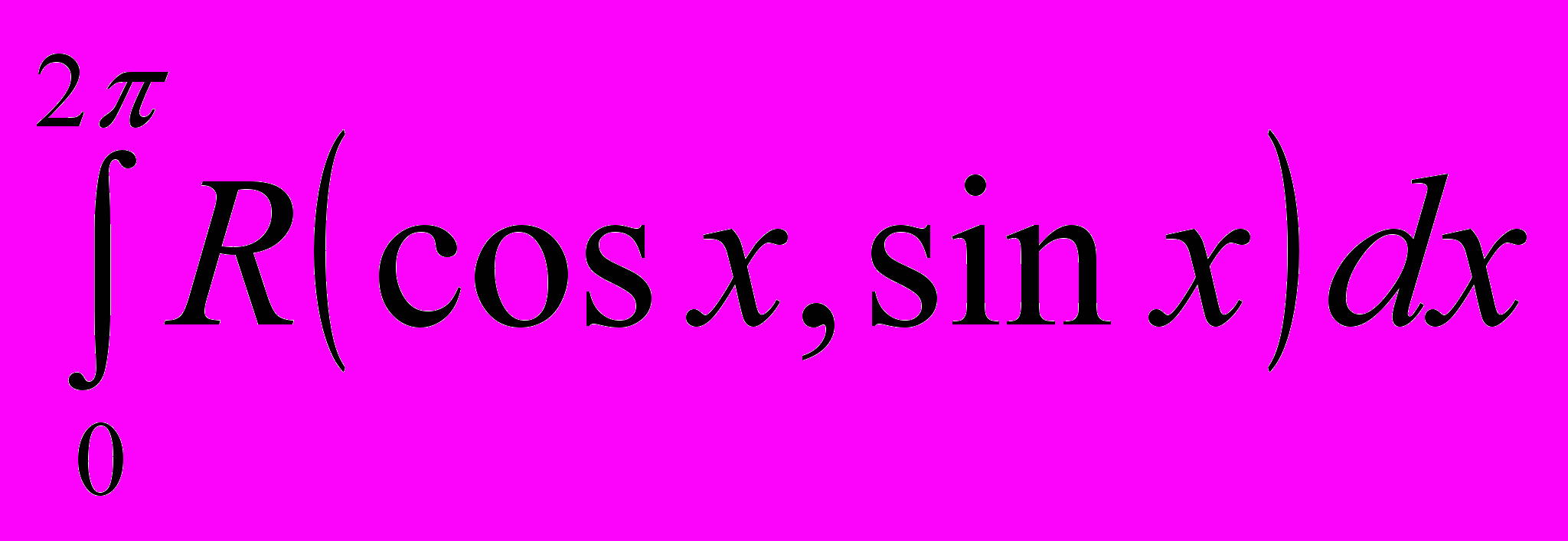 .
.55.Вычисление с помощью вычетов интеграла
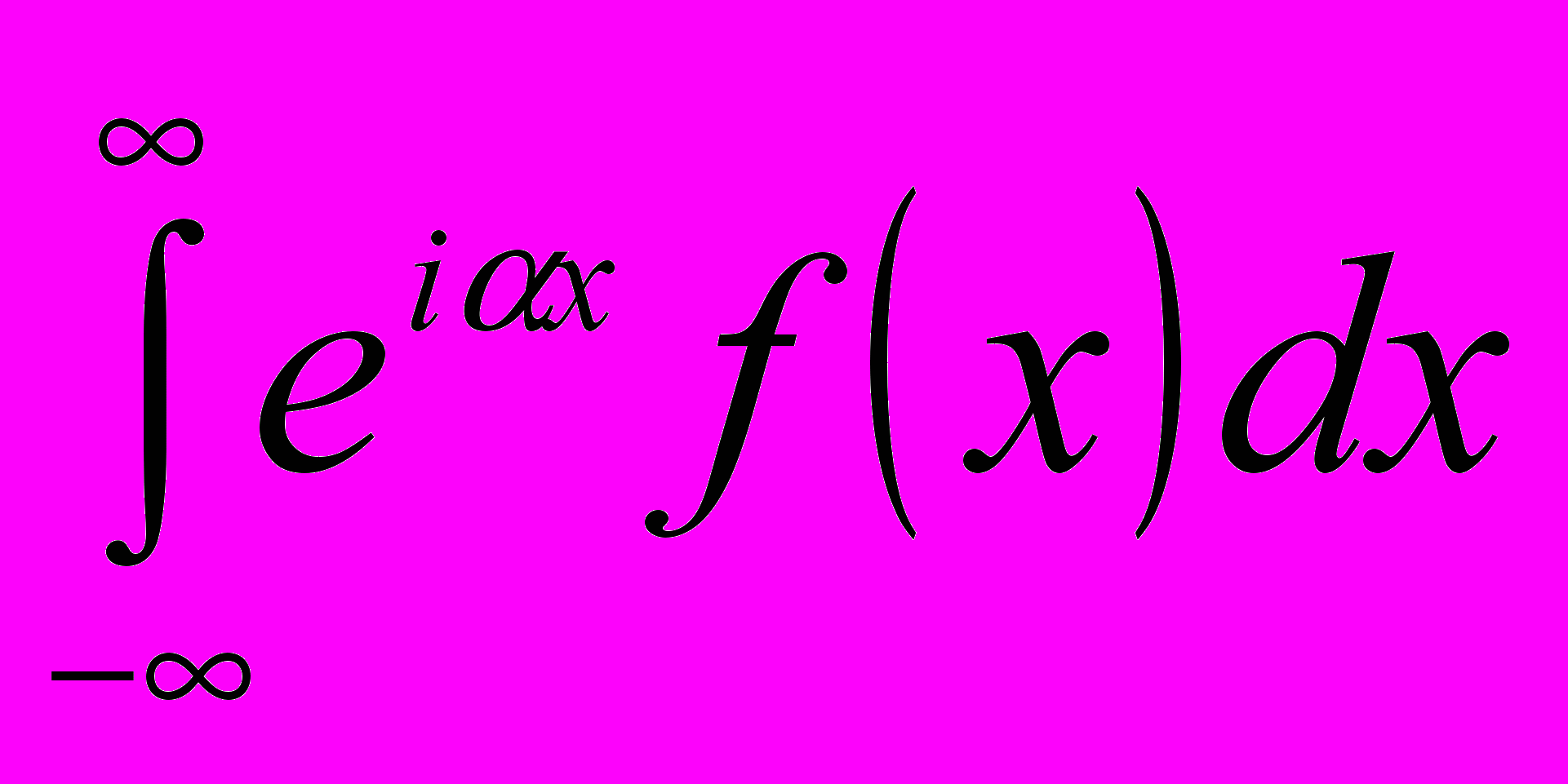 .
.56.Интегралы от многозначных функций:
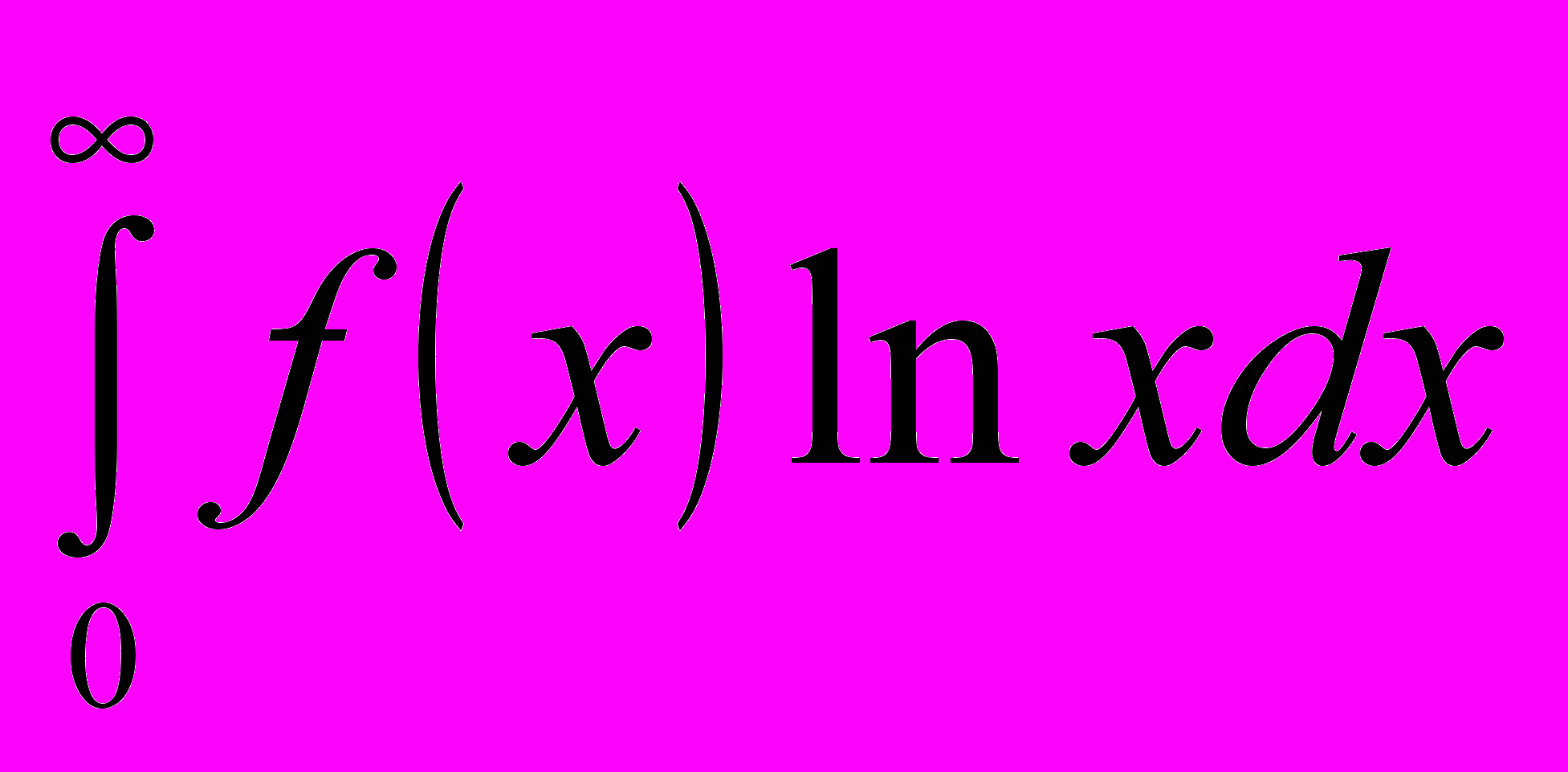 ,
, 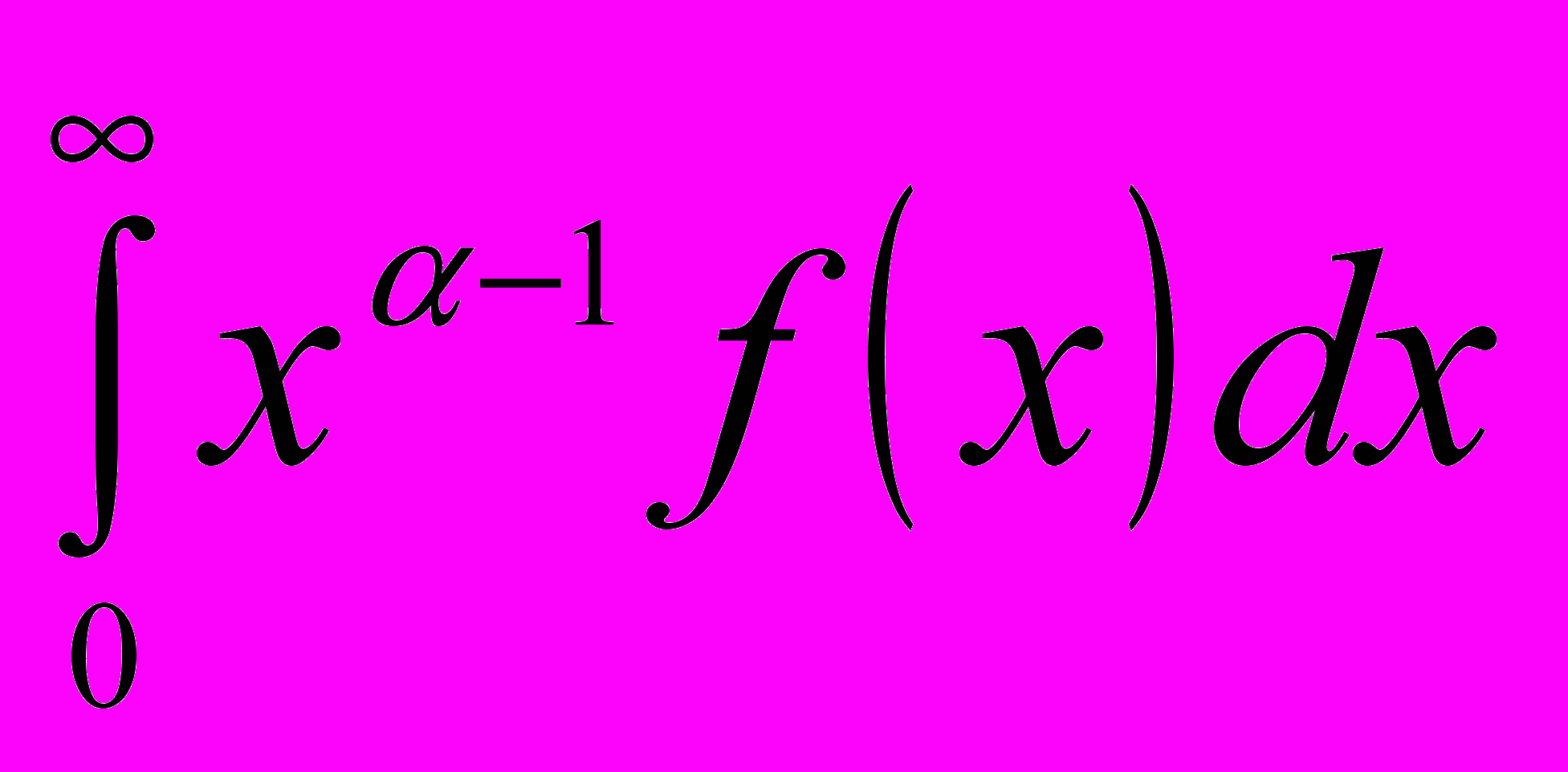
57.Теоремы о предельном переходе под знаком собственного интеграла, зависящего от параметра, и о непрерывности этого интеграла.
58.
 Теоремы о дифференцировании по параметру собственного интеграла с постоянными и переменными пределами интегрирования.
Теоремы о дифференцировании по параметру собственного интеграла с постоянными и переменными пределами интегрирования.59. Интегрирование по параметру в конечном промежутке собственного и несобственного интегралов.
60. Достаточные признаки сходимости несобственного интеграла, зависящего от параметра.
61. Теорема о предельном переходе по параметру под знаком несобственного интеграла и два следствия из него.
62. Теорема о дифференцировании несобственного интеграла по параметру.
63. Теорема об интегрировании несобственного интеграла по параметру в бесконечном промежутке.
64. В-функция Эйлера и ее свойства.
65. Г-функция Эйлера и ее свойства.
66. Интеграл Фурье и аналог интеграла Дирихле для него.
67. Достаточные признаки сходимости интеграла Фурье.
68. Преобразование Фурье и его свойства.
69. Преобразование Лапласа. Теорема об его аналитичности и замечания к ней.
70. Формула обращения преобразования Лапласа.
71. Свойства преобразования Лапласа.
7. Учебно-методическое и информационное обеспечение дисциплины (модуля)
а) основная литература:
- Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: Наука – все издания для физико-математических факультетов университетов.
- Кудрявцев Л.Д. Курс математического анализа. Т.1,2 – М.: Наука, 1981.
- Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. – М.: Наука, 1973.
- Малышева Н.Б., Розендорн Э.Р. Функции комплексного переменного. - М.: Физматлит, 2010, 168 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. - М.: Наука, 1974, 336 с.
- Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций комплексного переменного. М.: Наука, 1976, 480 с.
- Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, тт. I-III. – М.: Наука, 1970.
- Шабунин М.И., Половинкин Е.С., Карлов М.И. Сборник задач по теории функций комплексного переменного. М.: Бином, 2009, 368 с.
б) дополнительная литература:
- Василевская Т.П., Колосова О.А. Интегралы и ряды в комплексной области. – Изд-во ТГУ, 2001 г.
- Василевская Т.П., Колосова О.А. интегралв и ряды в комплексной области (Методические указания к решению задач по курсу «Математический анализ»). Изд-во ТГУ, 2001
- Василевская Т.П., Завгородняя М.Е., Колосова О.А. Вычеты и их применение к вычислению интегралов (Учебно-методическое пособие) Изд-во ТГУ, 2005
- Гендрина И.Ю., Завгородняя М.Е., Колосова О.А. Интегралы , зависящие от параметра (Учебно-методическое пособие) Изд-во ООО «Лито-принт», 2009
-
- Марголис Н.Ю. Вычисление интегралов с помощью вычетов. – Изд-во ТГУ, 1991 г.
- Марголис Н.Ю. Ряды Лорана. Вычеты. – Изд-во ТГУ, 1991 г.
- Натансон И.П. Теория функций вещественной переменной. – М.: Наука, 1974.
- Очан Ю.С. Сборник задач по математическому анализу. – М.: Просвещение, 1981.
- Туренова Е.Л. Преобразование Лапласа. – Изд-во ТГУ, 2003 г.
в) программное обеспечение и Интернет-ресурсы
- el="nofollow" href=" " onclick="return false">ссылка скрыта – «Образовательный математический сайт Exponenta.ru».
- el="nofollow" href=" " onclick="return false">ссылка скрыта – Лекции, примеры решения задач, интегралы и производные, дифференцирование, ТФКП, Электронные учебники. Типовой расчет из задачника Кузнецова.
- el="nofollow" href=" " onclick="return false">ссылка скрыта – «Образовательный математический сайт Math.ru».
8. Материально-техническое обеспечение дисциплины
В распоряжении преподавателей и обучающихся имеется основное необходимое материально-техническое оборудование, а именно компьютеры с соответствующим компьютерным и программным обеспечением, Интернет-ресурсы, доступ к полнотекстовым электронным базам, книжный фонд (3,8 млн. экземпляров) Научной библиотеки Томского университета.
Программа составлена в соответствии с требованиями ФГОС ВПО с учетом рекомендаций и ПрООП ВПО по направлению «Прикладная математика и информатика».
Авторы
Колосова Ольга Андреевна – кандидат физико-математических наук, доцент кафедры исследования операций
Моисеева Светлана Петровна – кандидат технических наук, доцент кафедры теории вероятностей и математической статистики
Рецензент: д.техн.н., профессор А.А. Назаров
Программа одобрена на заседании Ученого Совета ФПМК
от «24» февраля 2011года, протокол №. 282
