Программа курса «эконометрика»

Вид материала

Программа курса

Содержание 1. Организационно-методический раздел 2. Распределение учебных часов по дисциплине (дневное отделение) Итого по курсу 3. Содержание дисциплины (темы и их содержание) 3.1. Лекции Тема 1. Введение Тема 2. Линейная модель парной регрессии Тема 4. Нелинейные регрессионные модели Тема 5. Обобщенная линейная регрессионная модель. Тема 6. Временные ряды Тема 7. Системы линейных одновременных уравнений Тема 8. Дискретные зависимые переменные 3.2. Практические занятия (семинары) Семинары 1-2: Основные положения модели парной регрессии Семинары 3-4: Статистические свойства МНК-оценок параметров модели парной регрессии Семинары 5-7: Основные положения модели множественной регрессии Семинары 8-11: Статистические свойства МНК-оценок параметров модели множественной регрессии Семинар 12: Регрессионные модели с переменной структурой Семинар 13: Мультиколлинеарность, частная корреляция и спецификация модели множественной регрессии Семинары 15-16: Линейные регрессионные модели с гетероскедастичностью Семинары 17-19: Линейные регрессионные модели с авторегрессией Семинары 20-21: Временные ряды Семинары 22-24: Системы линейных одновременных уравнений ... Полное содержание

Подобный материал:

• Программа дисциплины Эконометрика Для направления 080102. 65 Мировая экономика подготовки, 121.81kb.
• Программа по дисциплине эконометрика для студентов 3 курса дневного отделения факультета, 134.08kb.
• Контрольная работа по дисциплине «Эконометрика», 755.12kb.
• «Эконометрика» вводный курс для лиц с высшим образованием, проходящих программу дополнительной, 30.15kb.
• Программа и контрольные задания по учебной дисциплине «эконометрика» для студентов, 555.04kb.
• Учебная программа название дисциплины Эконометрика для специальности (ей)/ специализации, 231.63kb.
• Программа дисциплины дн. Ф "Эконометрика" для студентов 4 курса направления 080100, 150.65kb.
• Примерная программа наименование дисциплины Эконометрика Рекомендуется для направления, 196.23kb.
• Задачи данного курса включают, 112.73kb.
• Задачи данного курса включают, 83.9kb.

ИНСТИТУТ МЕЖДУНАРОДНЫХ ЭКОНОМИЧЕСКИХ СВЯЗЕЙ




Программа курса


«ЭКОНОМЕТРИКА»


Москва

2010

Обсуждено и рекомендовано

к изданию на заседании

Ученого Совета ИМЭС

(Протокол № 11 от 24.06.10)


Данную программу разработал доктор физико-математических наук, профессор кафедры экономики Института международных экономических связей Коренман Григорий Яковлевич.


© Коренман Г.Я., 2010

© ИМЭС, 2010

Содержание

1. Организационно-методический раздел

Эконометрика относится к общепрофессиональным дисциплинам в образовательной программе подготовки современных экономистов. Она находит применение в практической работе экономиста в самых различных сферах хозяйственной, финансовой и торговой деятельности.

Целью изучения этой дисциплины студентами является освоение основных положений и методов эконометрики, понимание содержания и области применимости эконометрических моделей, получение навыков использования прикладной эконометрики на примерах анализа простейших задач, в том числе с использованием специальных компьютерных программ.

Настоящая программа курса «Эконометрика» как по тематике, так и по объему материала полностью соответствует требованиям государственного образовательного стандарта второго поколения по направлению экономика. Программа рассчитана на студентов 3-го года обучения (пятый шестой семестры). К этому времени студенты прослушали курс математики, включающий математический анализ с элементами аналитической геометрии, линейную алгебру, теорию вероятностей и математическую статистику. Указанный курс содержит все математические сведения, необходимые для понимания эконометрики. Тем не менее в лекциях и на семинарах по мере необходимости мы напоминаем наиболее часто используемые понятия теории вероятностей, математической статистики и линейной алгебры.

Последовательность изложения материала, в основном, совпадает с принятым в начальных курсах эконометрики (см., например, учебники [1,2]), за исключением того, что вопросы прогнозирования в разных моделях не выделяются в специальный раздел, а обсуждаются непосредственно при рассмотрении той или иной модели. Весь материал курса можно, несколько условно, разделить на две части, на изучение каждой из которых приходится около половины времени, выделяемого на весь курс. К первой части относятся основные положения и детальный анализ классических линейных моделей парной и множественной регрессии, а ко второй – более сложные модели (модели с гетероскедастичностью и с автокорреляциями, нелинейные модели, системы регрессионных уравнений, временные ряды и др.). Модель парной регрессии представляет собой, по существу, частный случай модели множественной регрессии, однако в данном курсе, как и во многих пособиях по эконометрике, ей посвящена отдельная тема. Математический аппарат, необходимый для анализа этой модели, проще, чем в других разделах, поэтому линейная модель парной регрессии удобна для первоначального знакомства с предметом эконометрики. На примере этой модели можно детально рассмотреть и обсудить основные понятия эконометрики, методику эконометрического подхода, постановку простейших задач, методы оценивания параметров модели, статистические свойства оценок, прогнозирование и т.д., что значительно облегчает студентам понимание последующих разделов, в которых используется более сложный математический аппарат.

Обучение по курсу эконометрики предполагает посещение студентами лекций и семинаров, самостоятельную работу над теоретическим материалом и практическими задачами, выполнение контрольных работ. Студенты сдают зачет по первой части курса и экзамен по всему курсу. Основные требования при сдаче зачета: знание основных понятий, теоретических положений, формулировок и методов классических эконометрических моделей, понимание смысла соответствующих расчетных формул, умение их использовать для решения простых задач. При сдаче экзамена эти же требования распространяются на все разделы курса, с более пристальным вниманием к теоретическим вопросам.

2. Распределение учебных часов по дисциплине

(дневное отделение)

№ темы	Наименование темы	Количество часов
		всего	из них по видам учебной работы
			лекции	практ. занятия	самост. работа
1	Введение	4	2	-	2
2	Линейная модель парной регрессии	32	8	8	16
3	Линейная модель множественной регрессии	48	12	12	24
4	Нелинейные регрессионные модели	8	2	2	4
5	Обобщенная линейная регрессионная модель	36	8	10	18
6	Временные ряды	40	10	10	20
7	Системы линейных одновременных уравнений	24	6	6	12
8	Дискретные зависимые переменные	8	2	2	4
	Итого по курсу:	200	50	50	100

Для вечернего отделения количество аудиторных часов (лекций и семинаров) по каждой теме вдвое меньше (в сумме 50 часов), а количество часов самостоятельной работы увеличивается, так что общее число часов остается таким же, как для дневного отделения.

Для заочного отделения количество аудиторных часов в четыре раза меньше (в сумме 25 часов), а количество часов самостоятельной работы соответственно увеличивается до того же полного числа часов.

3. Содержание дисциплины (темы и их содержание)

3.1. Лекции

Тема 1. Введение

Предмет эконометрики. Основные вехи истории возникновения и развития эконометрики. Специфика измерений в экономике. Стохастические особенности исходных данных и взаимосвязей между характеристиками экономических процессов. Цели и задачи прикладных эконометрических исследований. Теоретические основания и методология эконометрического анализа.

Общая постановка задачи о нахождении количественной взаимосвязи разных величин по эмпирическим данным. Общие черты и различия количественных моделей в эконометрике и в естественных науках. Разделы и специальные вопросы математики, наиболее часто используемые в эконометрике.


Литература по теме: [1], введение, глава 1; [2], глава 1.

Тема 2. Линейная модель парной регрессии

Исходные предположения (гипотезы) линейной модели парной регрессии. Стохастическая (случайная) составляющая зависимой переменной. Гомоскедастичность и гетероскедастичность. Нормальная линейная модель парной регрессии. Требования к оценке параметров регрессии (несмещенность, эффективность, состоятельность). Оценка параметров линейной модели парной регрессии по методу наименьших квадратов (МНК). Несмещенность МНК-оценок параметров модели. Дисперсия МНК-оценок параметров модели и ее связь с дисперсией случайной составляющей зависимой переменной (дисперсией ошибок). Теорема Гаусса Маркова. Уравнения в отклонениях. Оценка дисперсии ошибок .

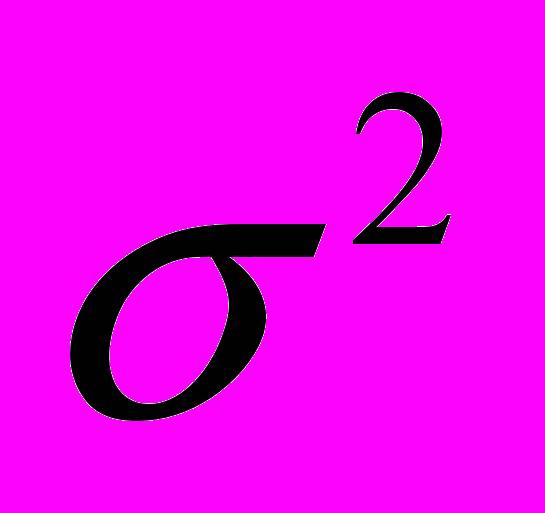Статистические свойства МНК-оценок параметров регрессии. Распределение МНК-оценок коэффициентов регрессии и распределение оценки дисперсии ошибок 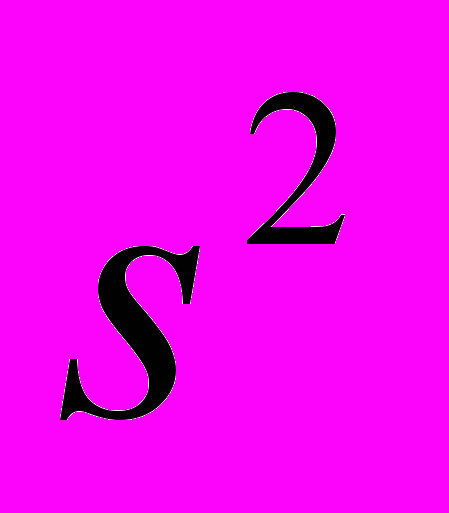для нормальной линейной модели. Независимость 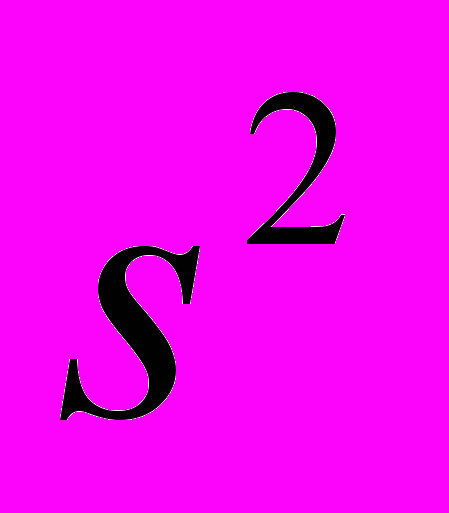и МНК-оценок линейных параметров. Проверка статистических гипотез и доверительные интервалы для коэффициентов регрессии. Показатели качества регрессии. Коэффициент детерминации (доля объясненной дисперсии) 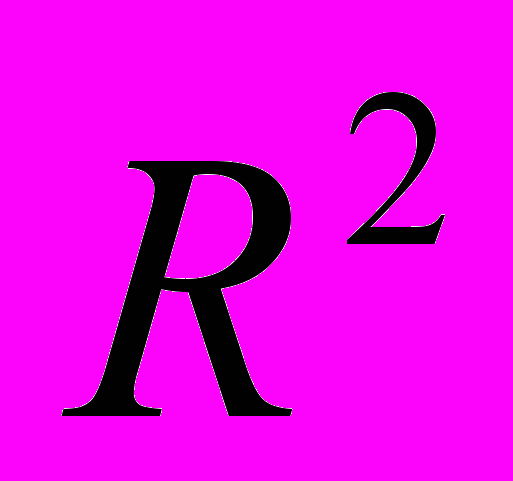и его геометрическая интерпретация. F-статистика. Векторно-матричная форма линейной модели парной регрессии.

Оценка параметров линейной модели парной регрессии по методу максимального правдоподобия.

Применение линейной модели парной регрессии для анализа рынка акций (модель Шарпа).

Прогнозирование в линейной модели парной регрессии. Точечный и интервальный прогноз. Среднеквадратичная ошибка и доверительный интервал прогноза.


Литература по теме: [1], глава 3; [2], глава 2, [3], глава 2, параграфы 2.1–2.4.

Тема 3. Линейная модель множественной регрессии

Исходные предположения линейной модели множественной регрессии. Нормальная линейная модель регрессии. Векторно-матричная форма линейной модели множественной регрессии. Оценка параметров модели по методу наименьших квадратов (МНК). Редукция общих (матричных) формул множественной регрессии в случае парной регрессии. Уравнения в отклонениях. Несмещенность МНК-оценок параметров модели. Матрица ковариаций (матрица дисперсии) МНК-оценок параметров модели множественной регрессии. Теорема Гаусса Маркова. Уравнения в отклонениях. Оценка дисперсии ошибок .

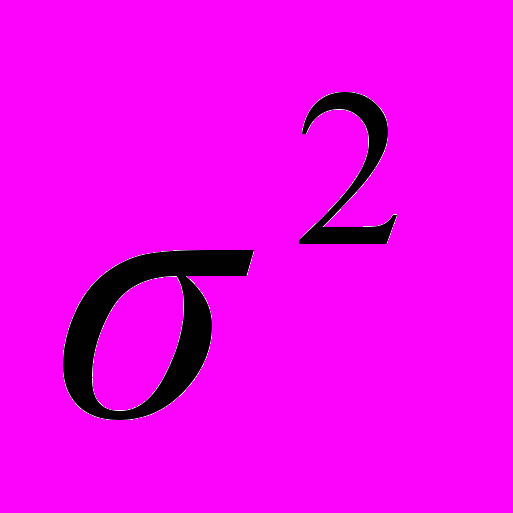Статистические свойства МНК-оценок параметров регрессии. Распределение МНК-оценок коэффициентов множественной регрессии и распределение оценки дисперсии ошибок 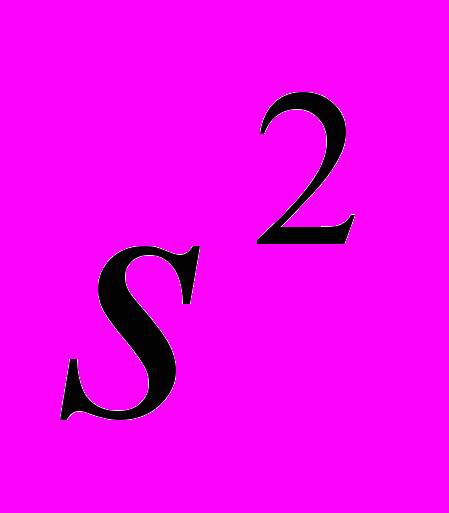для нормальной линейной модели. Независимость 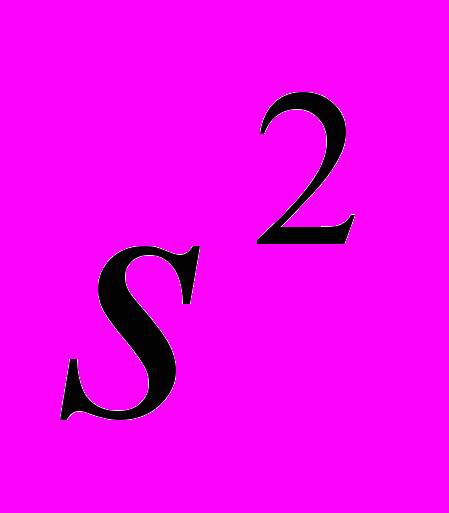и МНК-оценок линейных параметров.

Показатели качества регрессии и анализ вариации зависимой переменной в регрессии. Коэффициент детерминации 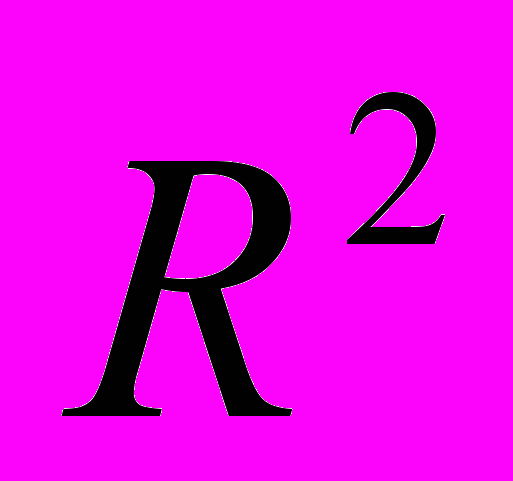и улучшенный коэффициент детерминации. Проверка статистических гипотез, доверительные интервалы и доверительные области для коэффициентов регрессии. F-статистика.

Оценка коэффициентов множественной регрессии по методу максимального правдоподобия.

Фиктивные (дискретные) переменные и регрессионные модели с переменной структурой и их использование для учета сезонных изменений и дискретных признаков. Проверка гипотезы о структурных изменениях с помощью дискретных переменных.

Проблемы выбора переменных и спецификации модели множественной регрессии. Проблема мультиколлинеарности. Частная корреляция и ее использование для спецификации модели. Исключение существенных переменных. Включение несущественных переменных. Сравнение моделей с ограничениями и без ограничений.

Прогнозирование в линейной модели множественной регрессии. Среднеквадратичная ошибка и доверительный интервал прогноза.


Литература по теме: [1], глава 4, [2], главы 3, 4; [3], глава 3.

Тема 4. Нелинейные регрессионные модели

Природа нелинейных моделей. Методы выбора вида нелинейных моделей. Два класса нелинейных моделей регрессии. Линеаризация. Коэффициенты эластичности. Корреляция для нелинейной регрессии.


Литература по теме: [3], глава 2, параграфы 2.5, 2.6.

Тема 5. Обобщенная линейная регрессионная модель.

Матрица ковариаций в обобщенной линейной регрессионной модели, смысл диагональных и недиагональных элементов этой матрицы. Обобщенный метод наименьших квадратов (ОМНК). Теорема Айткена.

Доступный обобщенный метод наименьших квадратов. Оценки по методу максимального правдоподобия.

Линейная модель множественной регрессии с гетероскедастичностью. Метод взвешенных наименьших квадратов как частный случай ОМНК. Коррекция на гетероскедастичность. Формы стандартных ошибок в моделях с гетероскедастичностью. Тесты на гетероскедастичность.

Линейная модель с автокорреляциями. Авторегрессионный процесс первого порядка. Коэффициент авторегрессии. Методы оценивания в модели с авторегрессией. Тест Дарбина Уотсона на наличие или отсутствие автокорреляций.


Литература по теме: [1], глава 7, [2], глава 5, параграф 5.1, глава 6, параграфы 6.1, 6.2.

Тема 6. Временные ряды

Характеристики временных рядов. Модели распределенных лагов. Авторегрессионные модели распределенных лагов (динамические модели). Авторегрессионная модель при наличии автокорреляции ошибок. Оценка моделей с распределенными лагами по методу инструментальных переменных и по методу максимального правдоподобия. Нелинейный метод наименьших квадратов. Тест на автокорреляцию ошибок. Модель частичной корректировки. Модель адаптивных ожиданий. GARCH-модели. Нестационарные временные ряды.


Литература по теме: [1], глава 8, [2],глава 11; [3], глава 7.

Тема 7. Системы линейных одновременных уравнений

Системы одновременных уравнений. Экзогенные и эндогенные переменные. Внешне не связанные уравнения. Структурная и приведенная формы модели. Косвенный метод наименьших квадратов. Проблемы идентифицируемости. Оценивание систем одновременных уравнений. Двухшаговый и трехшаговый метод наименьших квадратов.


Литература по теме: [1] глава 9, [2], глава 9; [3], глава 4.

Тема 8. Дискретные зависимые переменные

Модели бинарного выбора. Линейная модель вероятности, probit- и logit- модели. Модели множественного выбора для номинальных и порядковых переменных. Модели с урезанными и цензурированными выборками.


Литература по теме: [2], глава 12.

3.2. Практические занятия (семинары)

Семинары 1-2: Основные положения модели парной регрессии

Решение задач на оценивание параметров a, b и дисперсии ошибок 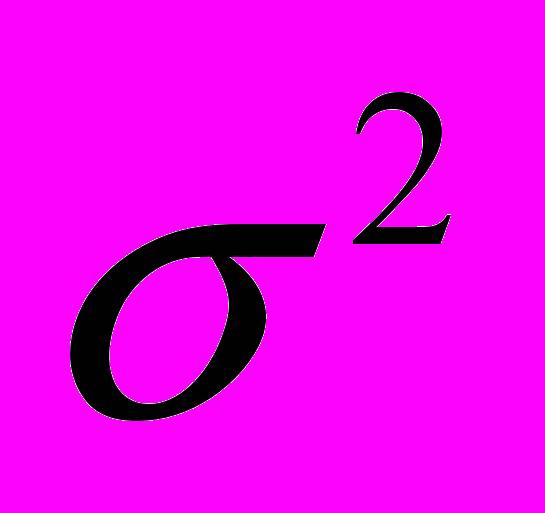в модели парной регрессии. Основные статистические распределения, используемые в эконометрике.

Типовые задачи: № 2.1, 2.2, 2.7, 2.9 (1-я часть: определение параметров), 2.10, 2.14 (a) из [4].

Семинары 3-4: Статистические свойства МНК-оценок параметров модели парной регрессии

Решение задач на проверку гипотез и определение доверительных интервалов для параметров a и b модели парной регрессии, расчет коэффициента детерминации и F-статистики, анализ показателей качества регрессии по этим величинам. Прогнозирование в модели парной регрессии.

Типовые задачи: № 2.9 (2-я часть) 2.10, 2.14 (b), 2.15, 2.17, 2.18 из [4].

Семинары 5-7: Основные положения модели множественной регрессии

Матричная формулировка модели и основные правила работы с матрицами. Решение задач на оценивание вектора коэффициентов b и дисперсии ошибок 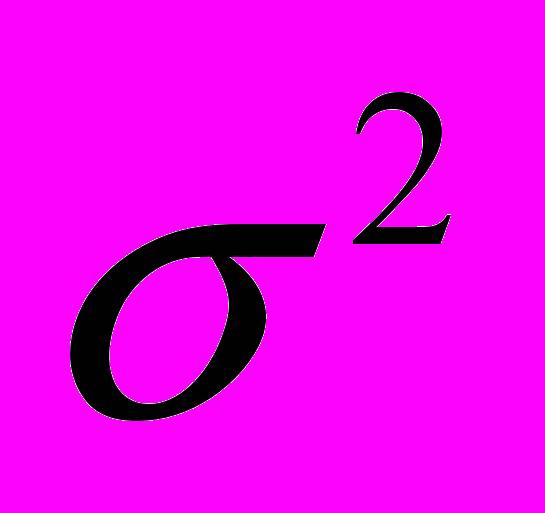в модели множественной регрессии.

Типовые задачи: № 3.1, 3.2, 3.5 (a, b), 3.11 (a-e) из [4].

Семинары 8-11: Статистические свойства МНК-оценок параметров модели множественной регрессии

Решение задач на проверку гипотез и определение доверительных интервалов для отдельных параметров модели множественной регрессии. Определение доверительной области для совокупности параметров модели. Расчет коэффициента детерминации и F-статистики, анализ показателей качества регрессии. Прогнозирование в модели множественной регрессии.

Типовые задачи: № 3.4, 3.5 (c-e), 3.6 из [4].

Семинар 12: Регрессионные модели с переменной структурой

Решение задач для линейных регрессионных моделей с переменной структурой. Использование фиктивных переменных для учета сезонных изменений.

Типовые задачи: № 4.4, 4.5, 4.6, 4.13, 4.14 из [4].

Семинар 13: Мультиколлинеарность, частная корреляция и спецификация модели множественной регрессии

Решение задач и анализ результатов в случае возникновения коллинеарности Решение задач на расчет коэффициента частной корреляции и его использование для спецификации модели множественной регрессии. Матрица корреляций регрессоров. Примеры включения и исключения существенных переменных при спецификация модели.

Типовые задачи: № 4.7, 4.8, 4.9, 4.10, 4.11, 4.12, 4.17, 4.18, 4.21 из [4].

Семинар 14: Нелинейные модели регрессии

Решение задач на линеаризацию нелинейных моделей, определение коэффициента эластичности и индекса корреляции нелинейных моделей.

Типовые задачи: № 2.5 из [4], № 1.17, 1.18, 1.19 из [5].

Семинары 15-16: Линейные регрессионные модели с гетероскедастичностью

Решение задач на определение параметров линейных регрессионных моделей с коррекцией на гетероскедастичность, проведение тестов на гетероскедастичность, определение типа гетероскедастичности.

Типовые задачи: № 6.1, 6.2, 6.7, 6.8 из [4].

Семинары 17-19: Линейные регрессионные модели с авторегрессией

Решение задач на оценивание параметров модели с авторегрессией для случаев известного и неизвестного коэффициента авторегрессии. Проведение теста на наличие или отсутствие корреляции во времени.

Типовые задачи: № 6.4, 6.6, 6.9, 6.10 из [4].

Семинары 20-21: Временные ряды

Классификация моделей временных рядов. Тест на причинно-следственную связь. ARIMA- и GARCH-модели.

Типовые задачи: № 11.1–11.3, 11.10, 11.13 из [4].

Семинары 22-24: Системы линейных одновременных уравнений

Упражнения на преобразование структурной формы системы одновременных уравнений к приведенной форме, анализ идентифицируемости каждого из уравнений системы, составление схемы расчета по двухшаговому методу наименьших квадратов.

Типовые задачи: № 9.1, 9.2, 9.3, 9.4 из [4].

Семинар 25: Дискретные зависимые переменные

Модели бинарного выбора. Линейная модель вероятности, probit- и logit- модели.

Типовые задачи: № 12.5, 12.7, 12.8 из [4].

4. Текущий контроль знаний

1. В первом семестре проводятся контрольные работы по темам 2 и 3 в пределах почасового тематического плана семинарских занятий.
   
2. Зачет в конце первого семестра по пройденным темам.
   
3. Во втором семестре проводятся контрольные работы по темам 5 и 7 в пределах почасового тематического плана семинарских занятий.
   
4. Экзамен в конце второго семестра по всему курсу.
   

5. Перечень вопросов к зачету (вопросы 1-25 ) и к экзамену (1–35)

1. Исходные предположения линейной модели парной регрессии.
   
2. Оценка параметров модели парной регрессии по методу наименьших квадратов.
   
3. Несмещенность МНК-оценок параметров линейной модели парной регрессии.
   
4. Дисперсия МНК-оценок параметров линейной модели парной регрессии.
   
5. Теорема Гаусса-Маркова для модели парной регрессии.
   
6. Оценка дисперсии случайных составляющих 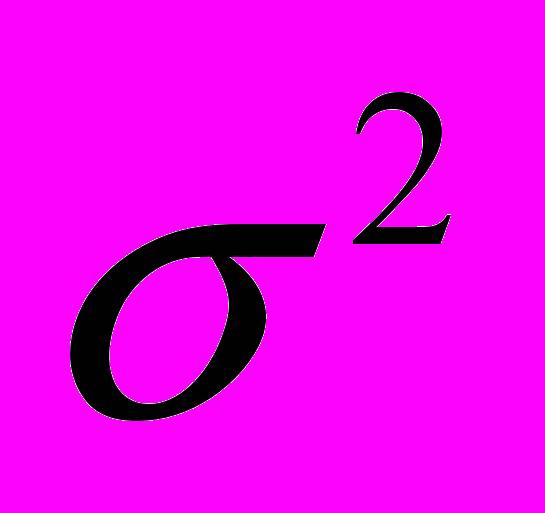в модели парной регрессии.
   
7. Статистические свойства МНК-оценок параметров модели парной регрессии.
   
8. Распределение оценки дисперсии ошибок 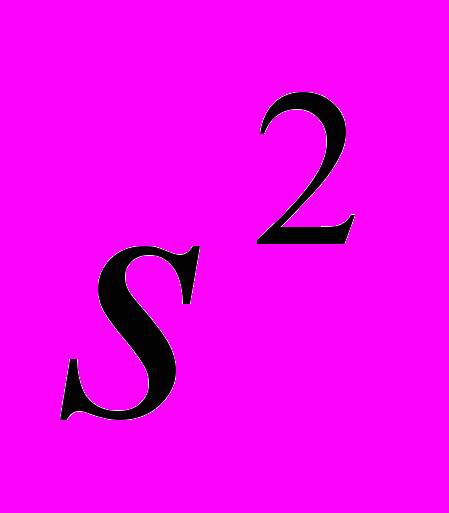модели парной регрессии.
   
9. Проверка нулевой гипотезы и доверительные интервалы для коэффициентов парной регрессии.
   
10. Анализ вариации зависимой переменной, коэффициент детерминации 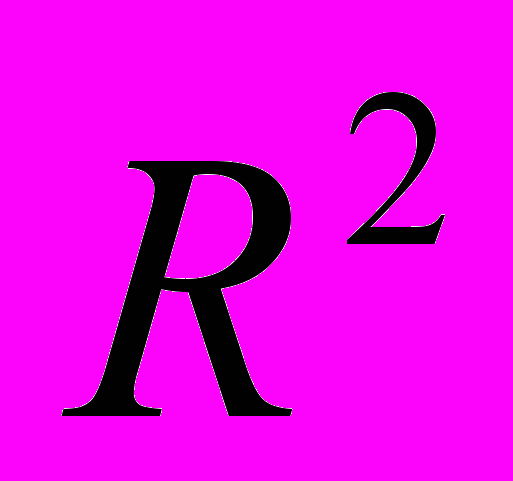и F-статистика в линейной модели парной регрессии.
    
11. Прогнозирование в линейной модели парной регрессии.
    
12. Исходные предположения линейной модели множественной регрессии.
    
13. Матричная форма записи линейной модели множественной регрессии.
    
14. Оценка параметров линейной модели множественной регрессии по методу наименьших квадратов.
    
15. Несмещенность МНК-оценок параметров линейной модели множественной регрессии.
    
16. Матрица ковариаций и дисперсия МНК-оценок параметров линейной модели множественной регрессии.
    
17. Теорема Гаусса-Маркова для линейной модели множественной регрессии.
    
18. Оценка дисперсии ошибок 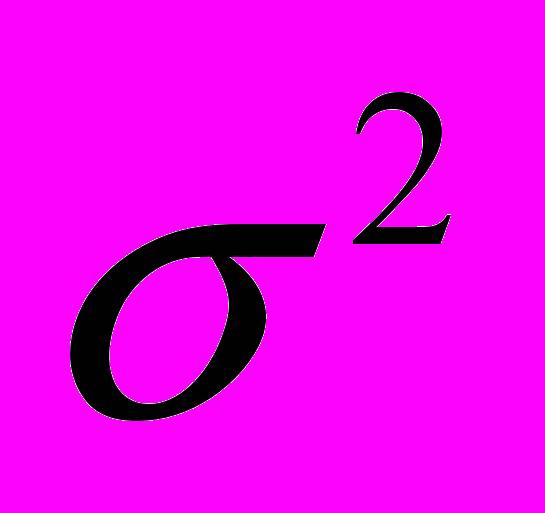в линейной модели множественной регрессии.
    
19. Распределение оценки дисперсии ошибок 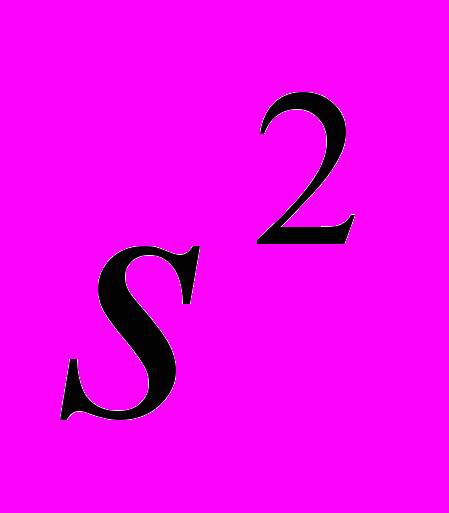в линейной модели множественной регрессии.
    
20. Анализ вариации зависимой переменной и коэффициент детерминации 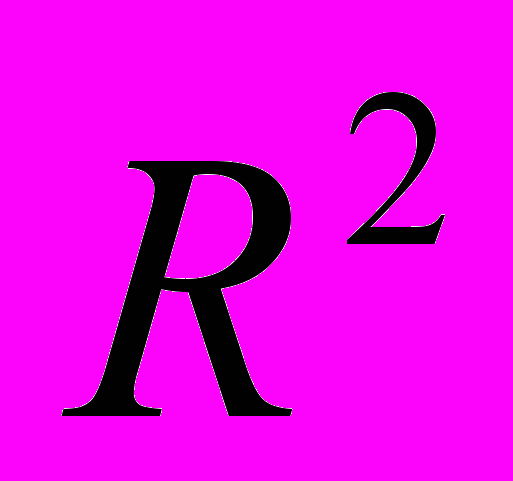в линейной модели множественной регрессии.
    
21. Проверка нулевой гипотезы и доверительные интервалы для одного из коэффициентов линейной модели множественной регрессии.
    
22. Проверка многомерной нулевой гипотезы в линейной модели множественной регрессии.
    
23. Проблема мультиколлинеарности в линейной модели множественной регрессии.
    
24. Фиктивные (дискретные) переменные (модель множественной регрессии с переменной структурой).
    
25. Прогнозирование в линейной модели множественной регрессии.
    
26. Линейная модель множественной регрессии с гетероскедастичностью.
    
27. Линейная модель множественной регрессии с автокорреляцией.
    
28. Нелинейные модели регрессии.
    
29. Обобщенный метод наименьших квадратов.
    
30. Доступный обобщенный метод наименьших квадратов.
    
31. Внешне не связанные системы регрессионных уравнений.
    
32. Структурная и приведенная формы системы одновременных регрессионных уравнений.
    
33. Модели распределенных лагов.
    
34. Авторегрессионные модели распределенных лагов.
    
35. Дискретные зависимые переменные. Модели logit и probit.
    

6. Типовые задачи для контрольных работ

Контрольная работа № 1

В таблице приведены результаты 10 наблюдений пар величин x и y (каждому студенту выдается своя таблица).

1. Оценить регрессию 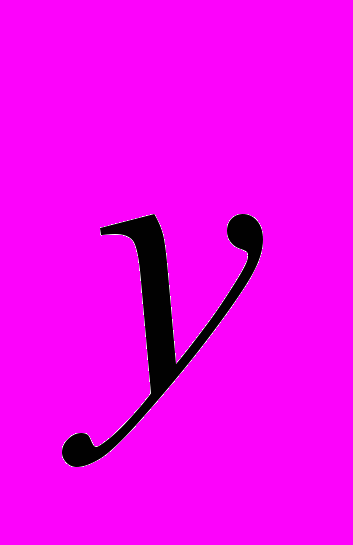на 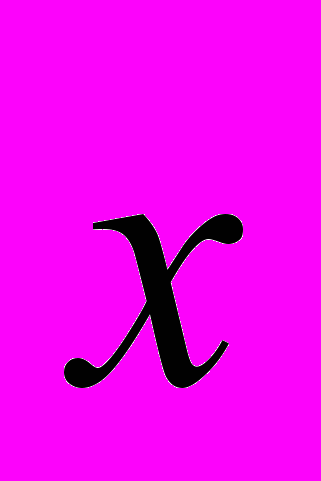(найт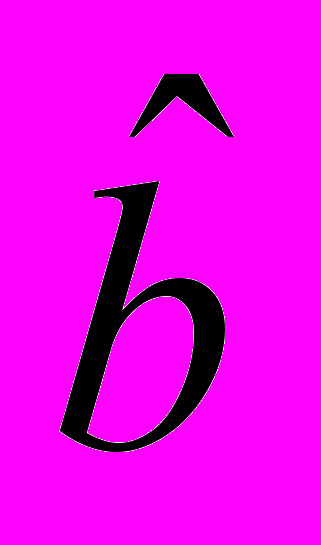и , и ).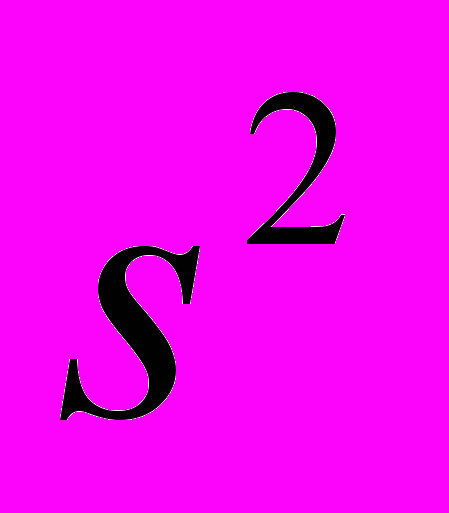

2. Найти коэффициент детерминации .

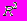3. Проверить гипотезу 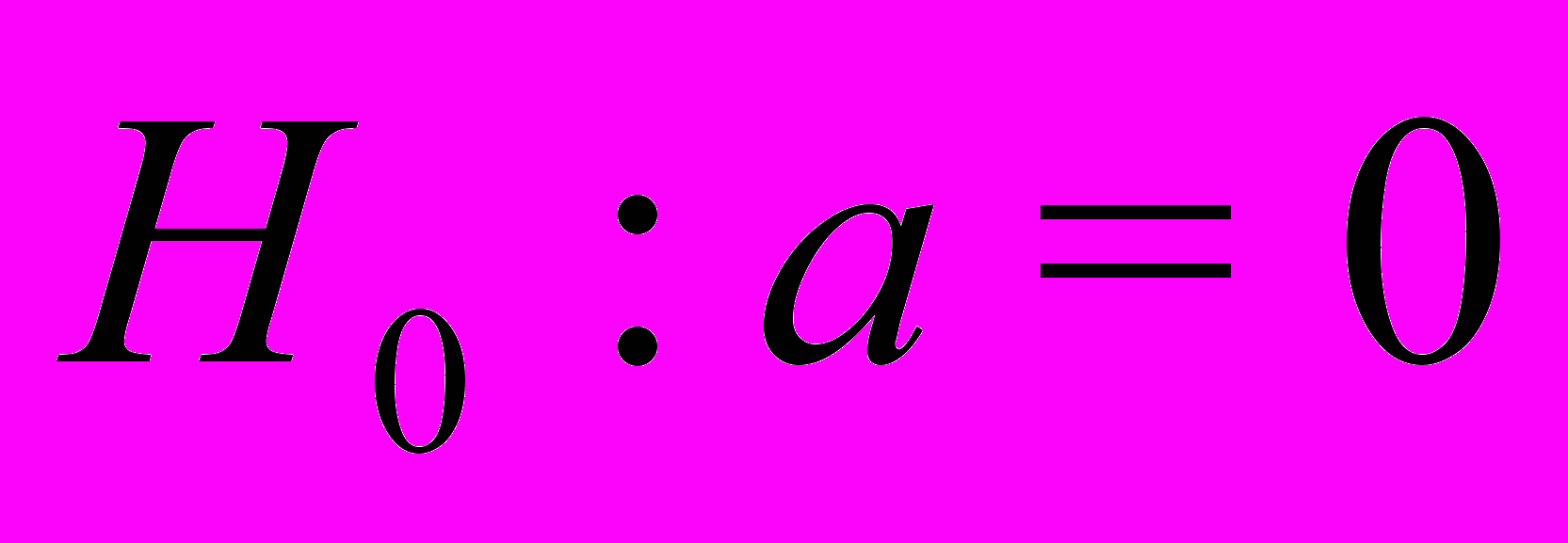на 10%-ом уровне значимости.

4. Найти 95%-ый доверительный интервал значений .

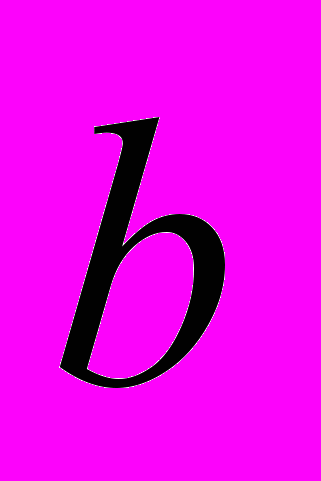5. Получить прогноз значения 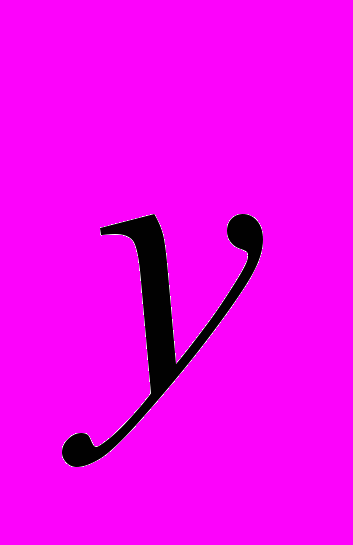при 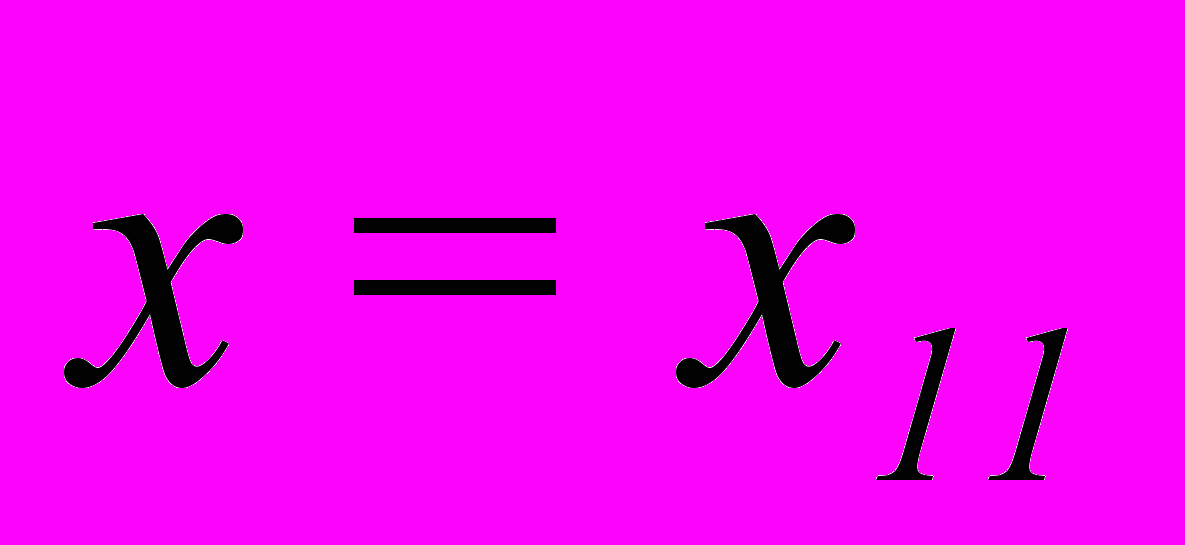(значение 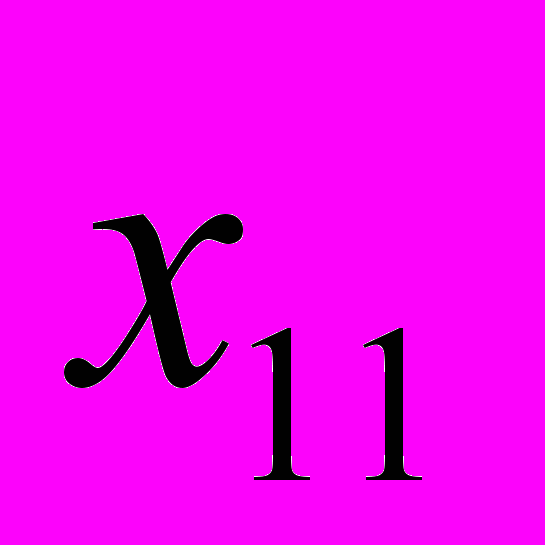дано в таблице) и 95%-ый доверительный интервал значений 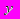в этой точке.

Контрольная работа № 2

В таблице даны пять наборов величин 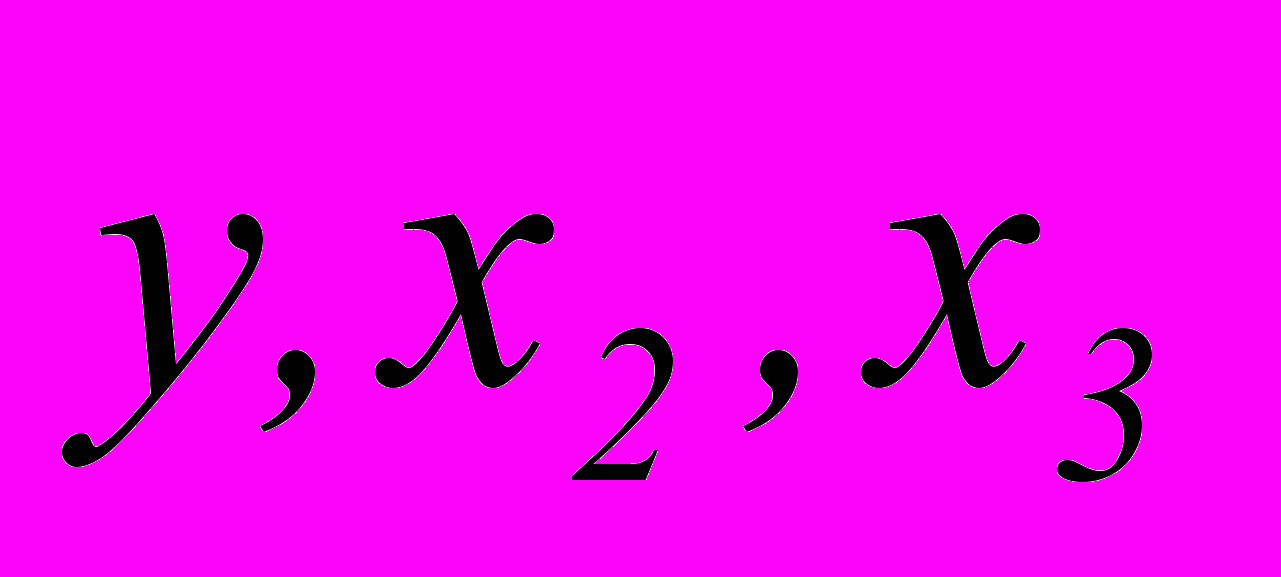(каждому студенту выдается своя таблица)

1. Оценить регрессию 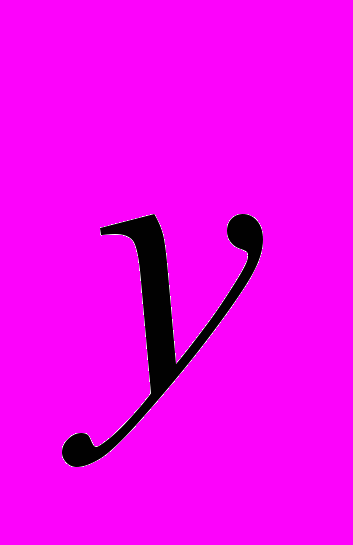на константу 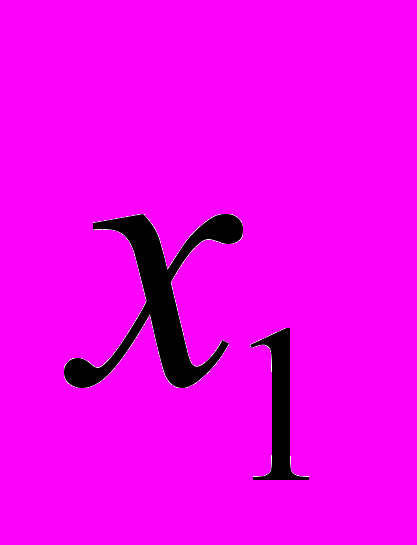и переменные 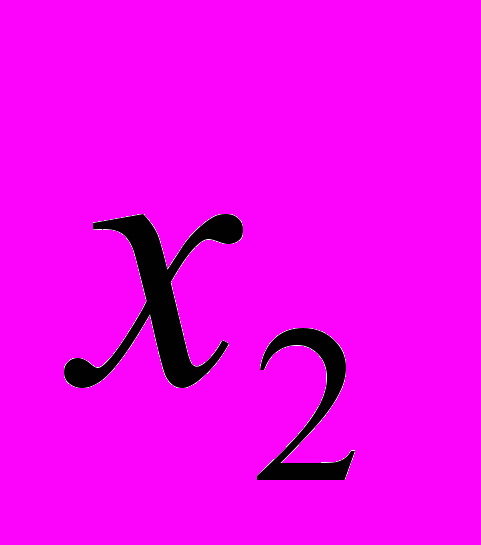, 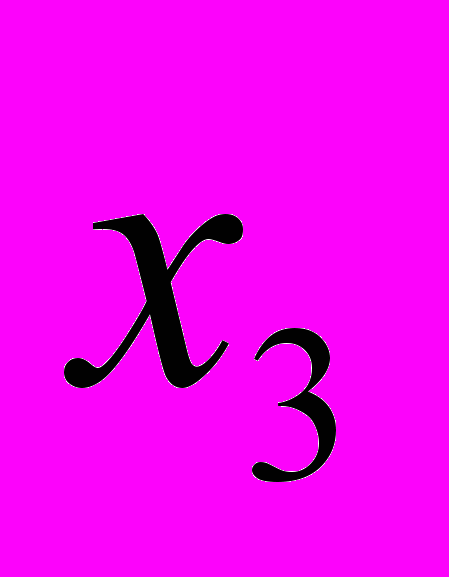(получить вектор ).

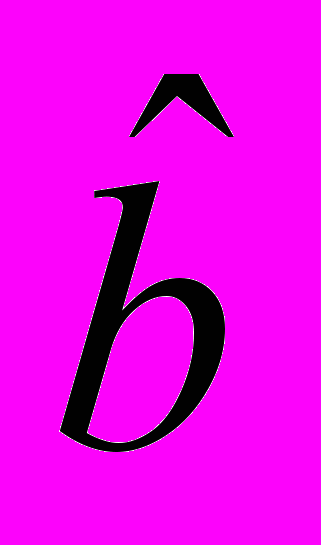2. Найти оценку дисперсии случайных составляющих .

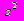3. Проверить гипотезу 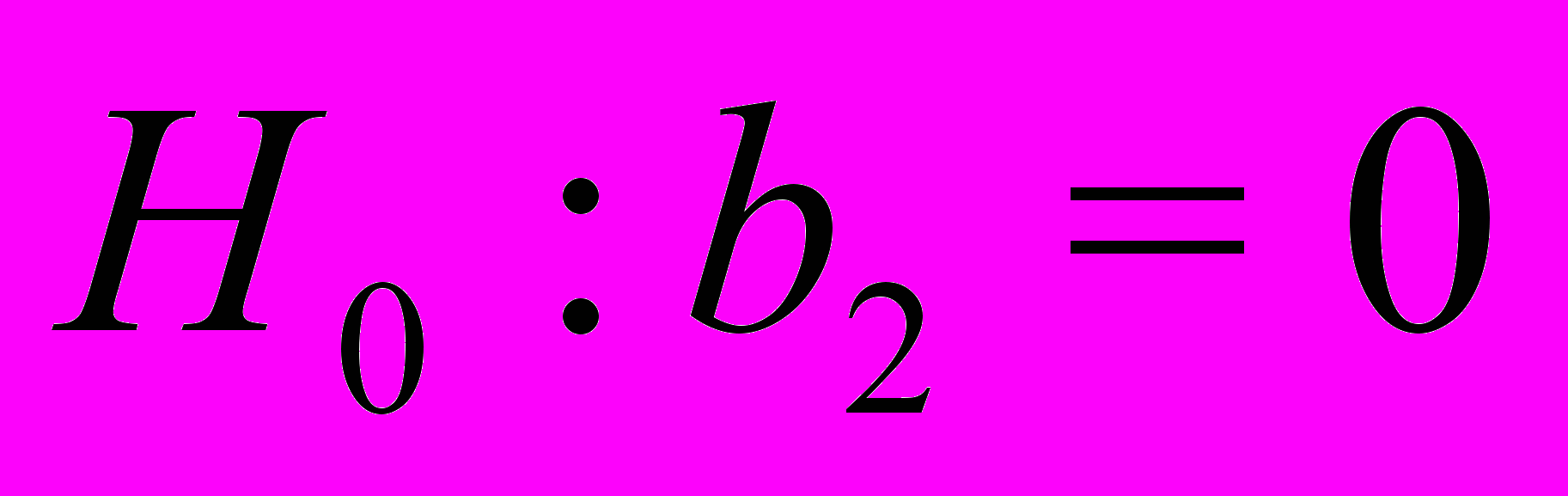и найти 95%-ый доверительный интервал .

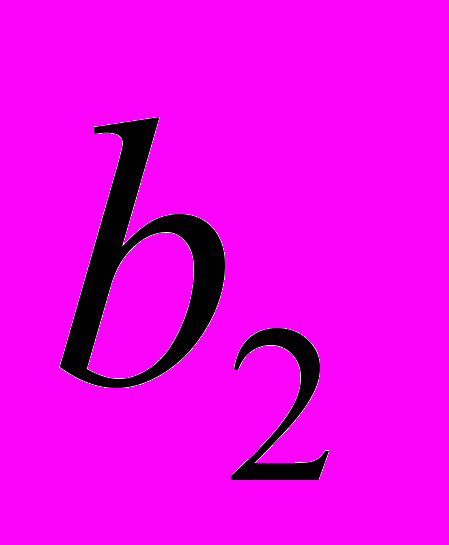4. Получить прогноз величины 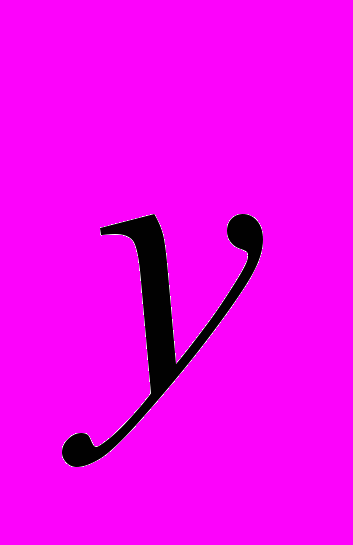при 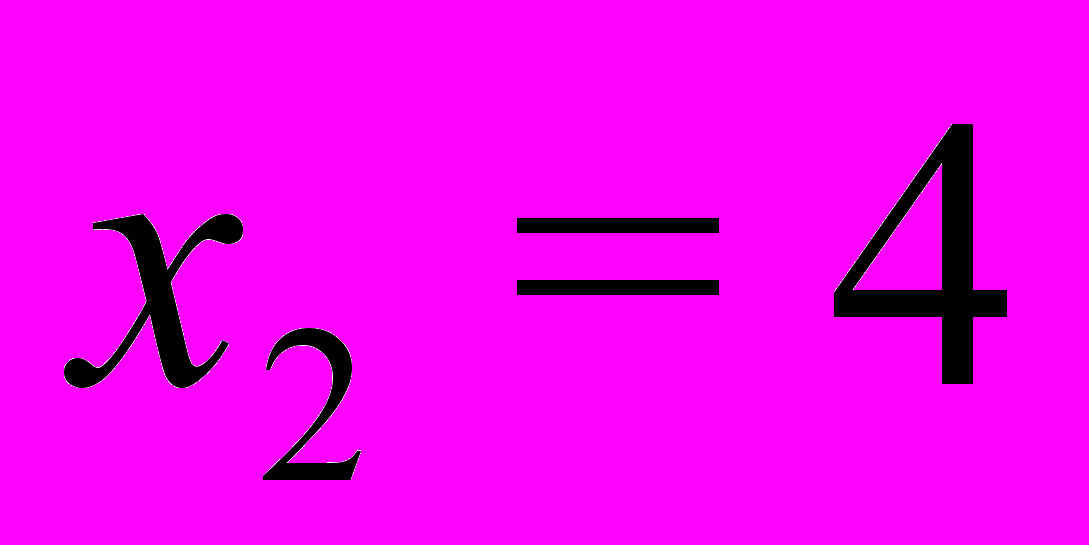, 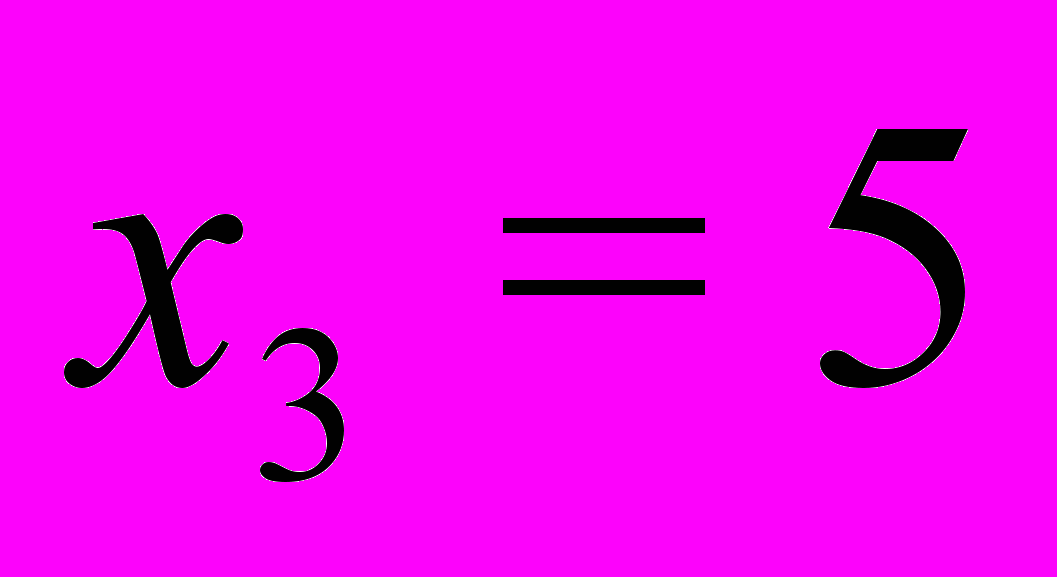и найти 95%-ый доверительный интервал значений 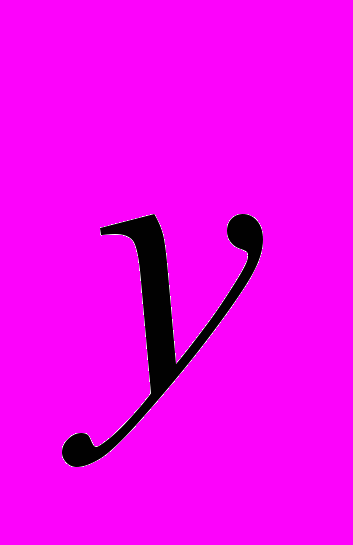при этих .

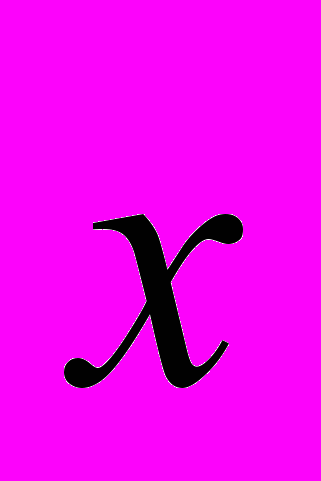Контрольная работа № 3

Задача № 1. В результате регрессии n значений 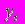на k переменных получены остатки регрессии 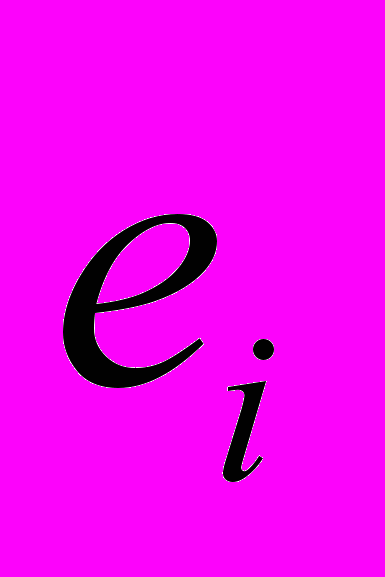, приведенные в прилагаемой таблице. Проверить гипотезу об отсутствии автокорреляций и оценить величину параметра автокорреляции .

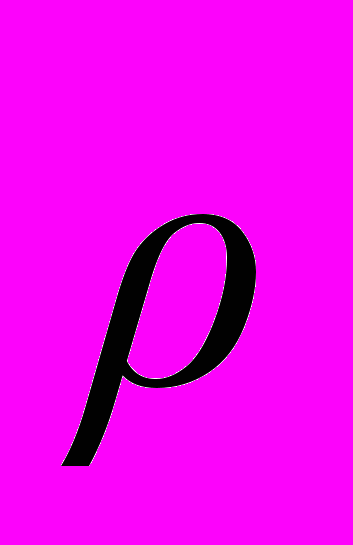Задача № 2. В прилагаемой таблице приведены значения числа работающих 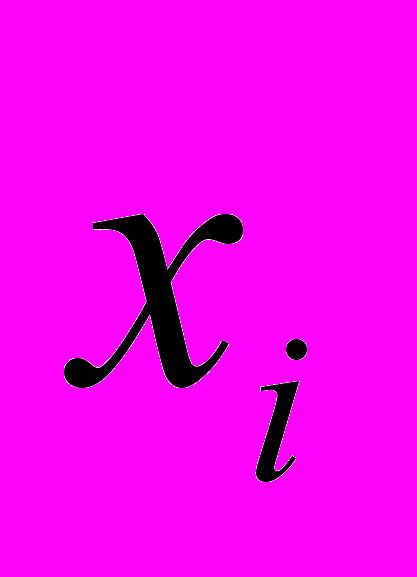(в тыс. чел.) и поступлений в бюджет 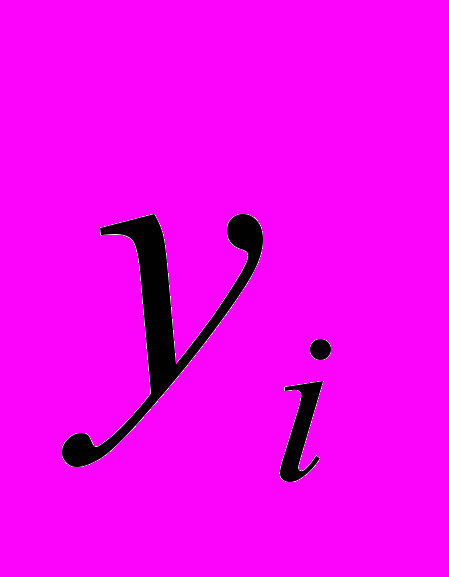(в млрд руб.) для 15 районов крупного города, упорядоченные по возрастанию 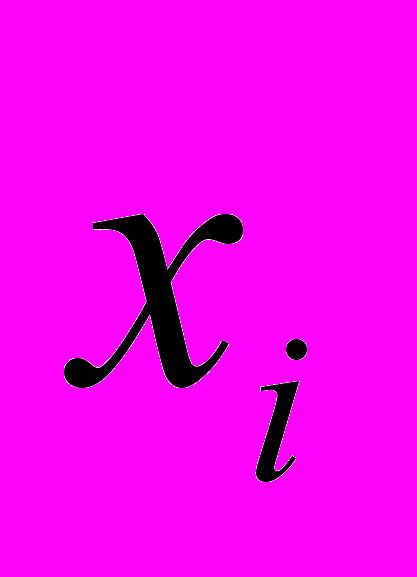. Выбирая первые 6 и последние 6 пар 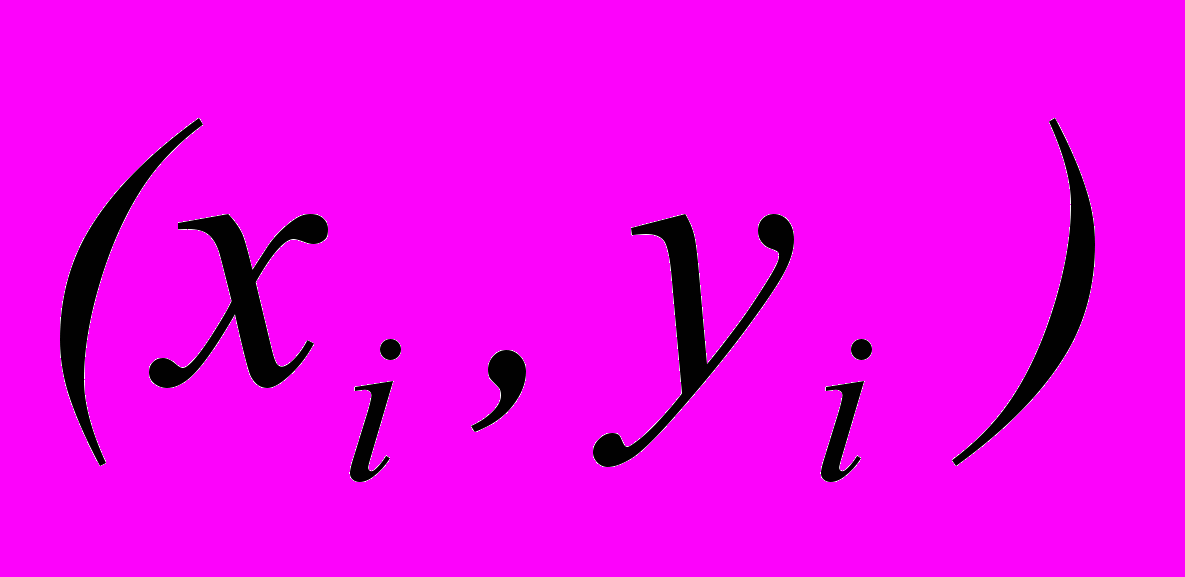в качестве двух групп данных, проверить гипотезу об отсутствии гетероскедастичности с помощью теста Голдфелда Куандта.

Контрольная работа № 4

Структурная форма системы линейных одновременных уравнений для объясняемых переменных 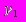и 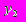переменных имеет вид:

,

.

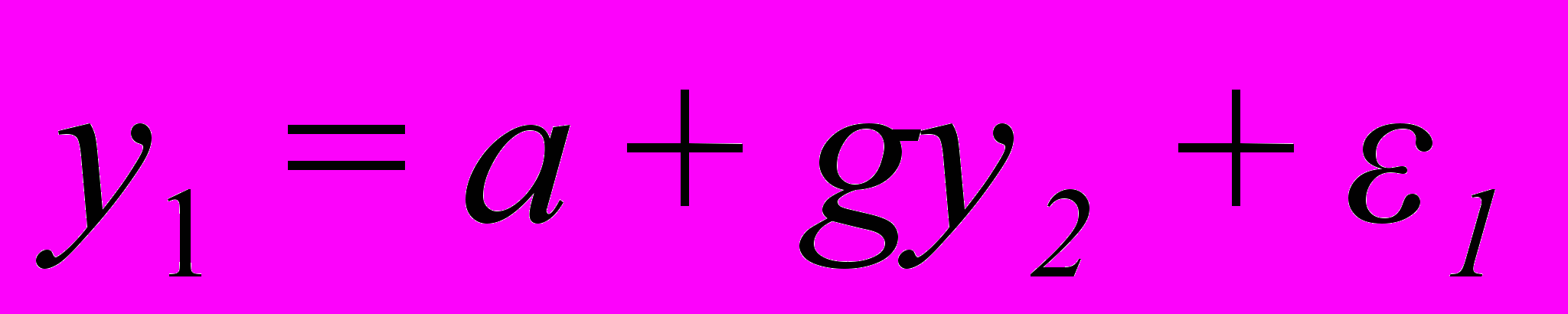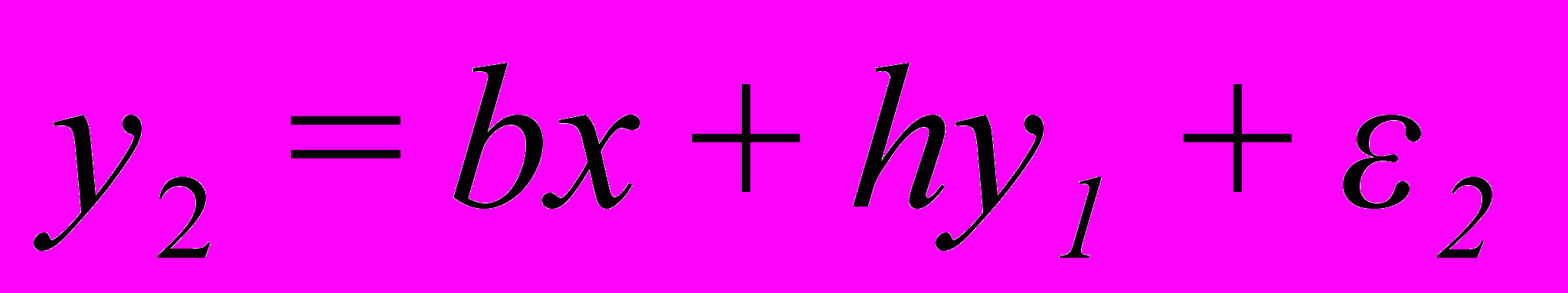Вводя «векторы» 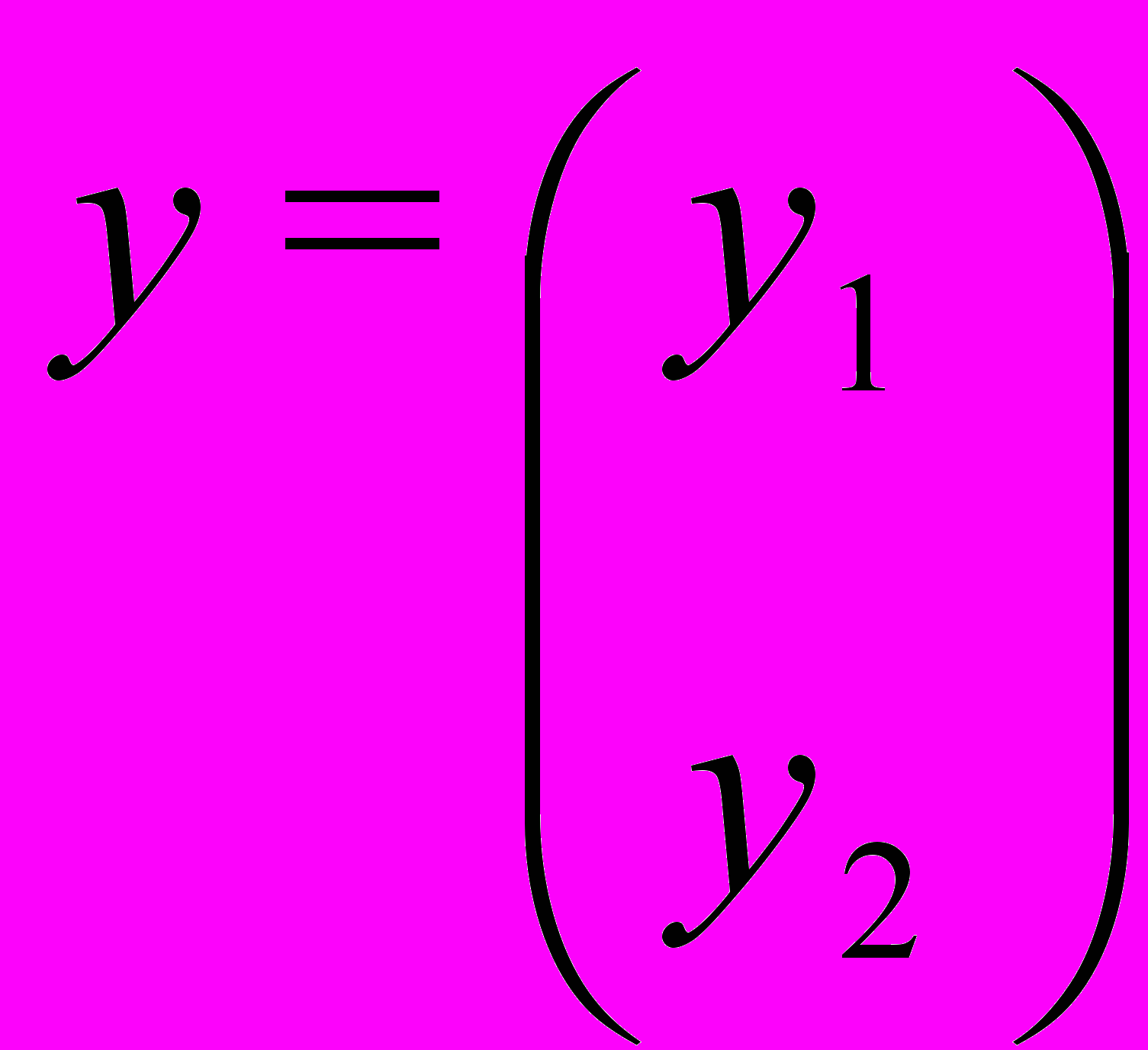, , 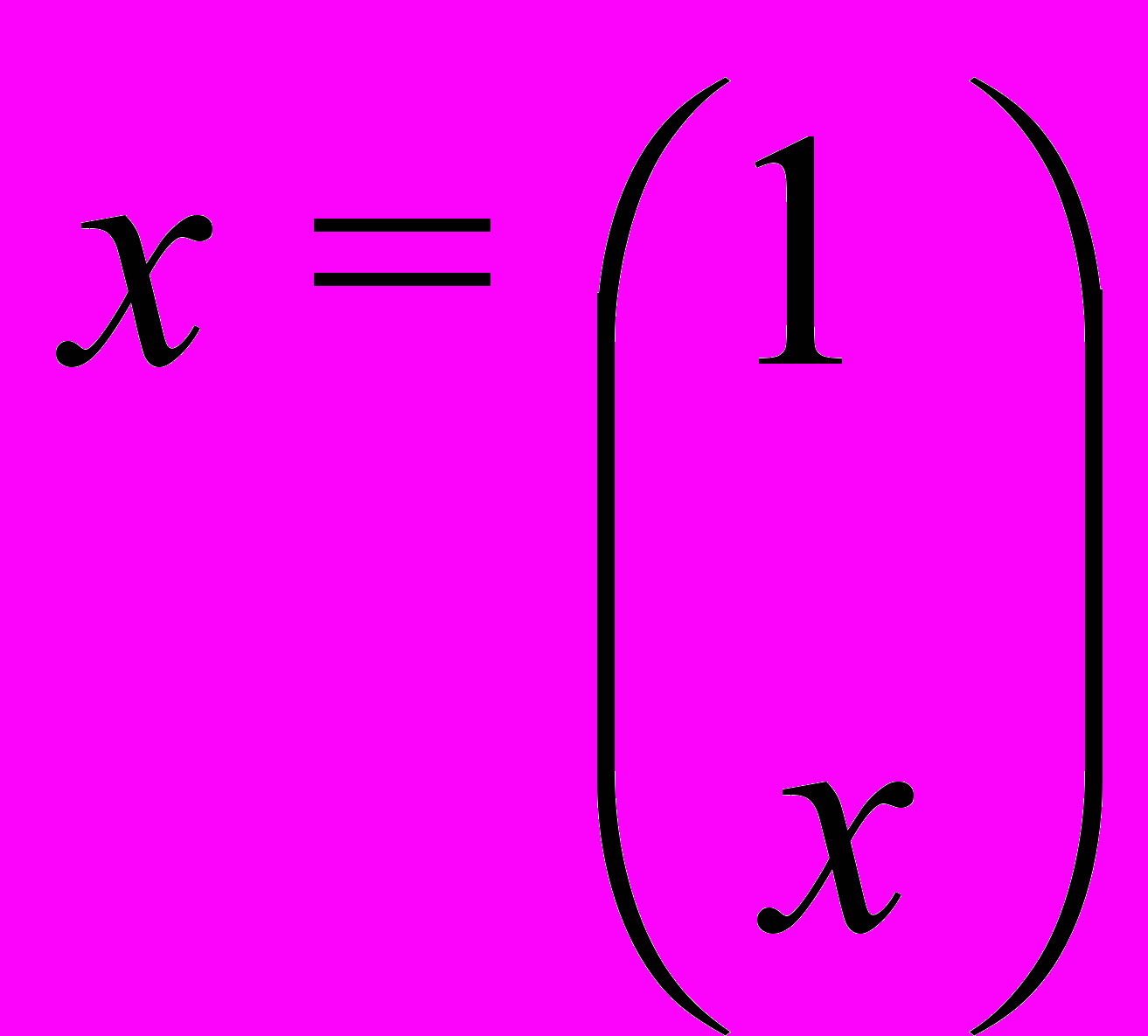, 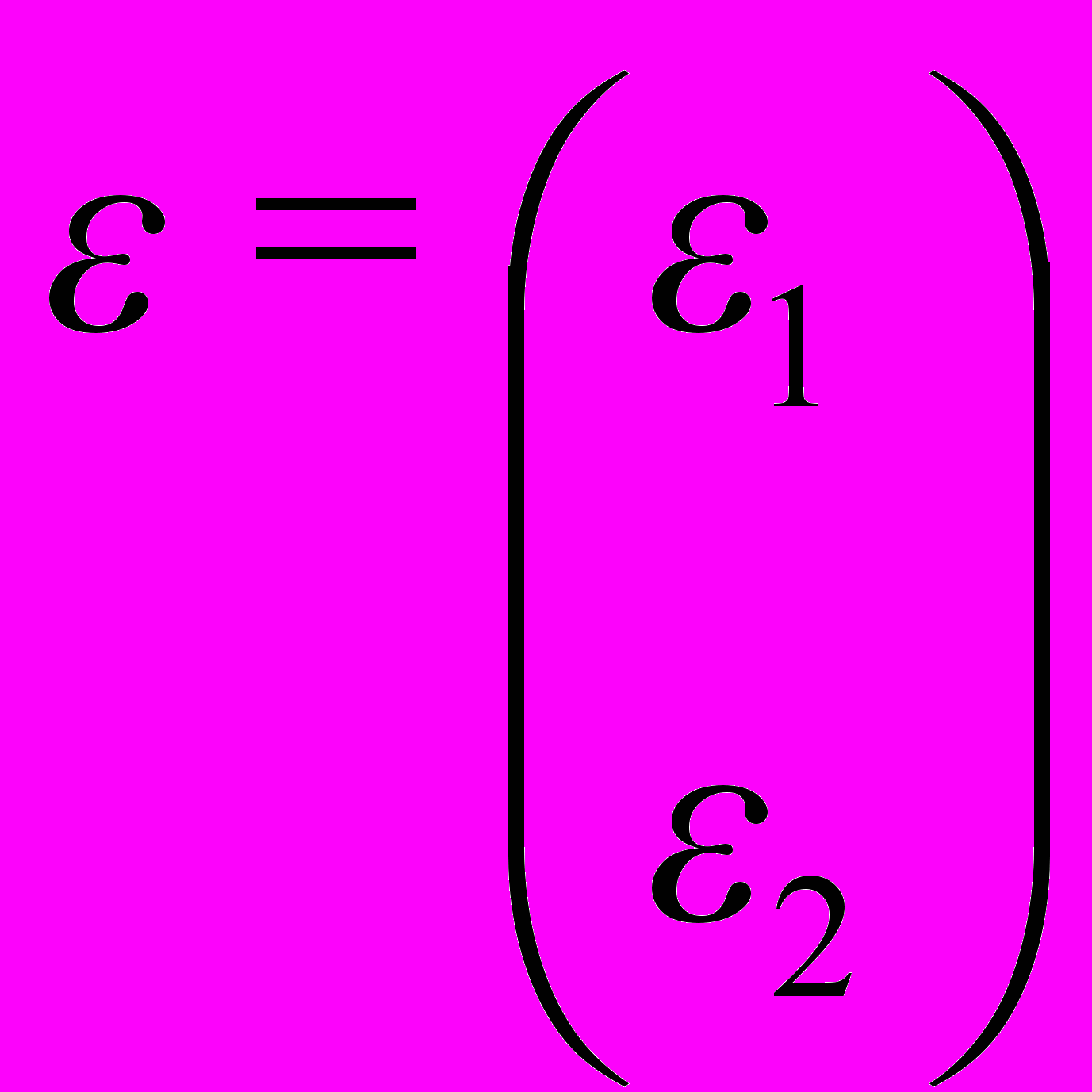можно записать эту систему в виде

.

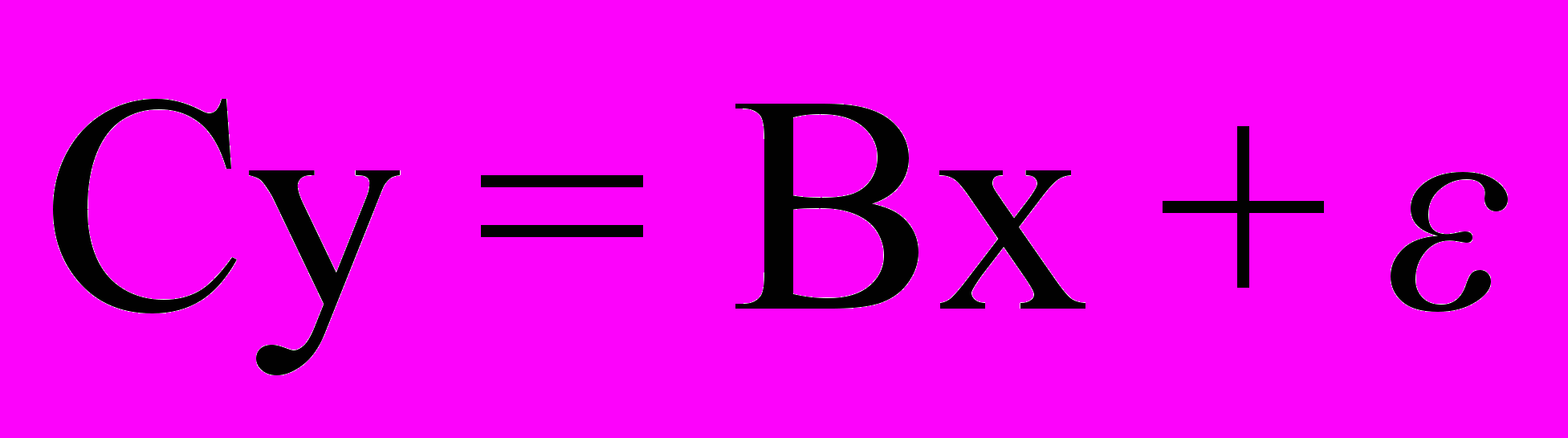1. Выразите матрицы и 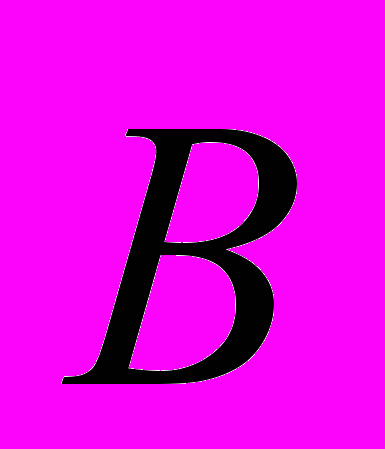через параметры исходной системы.
   
2. Перейдите к приведенной форме системы 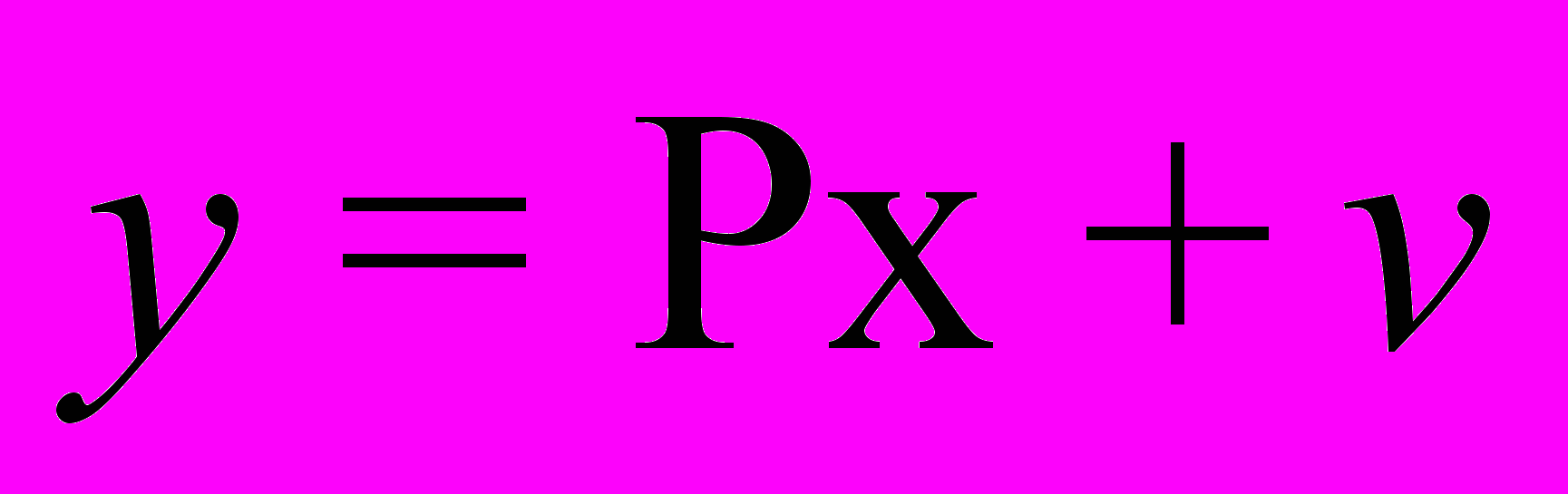и выразите матрицу 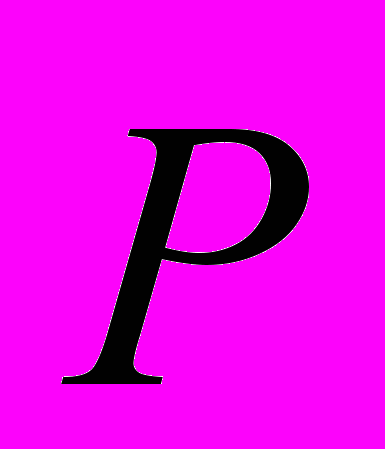и вектор 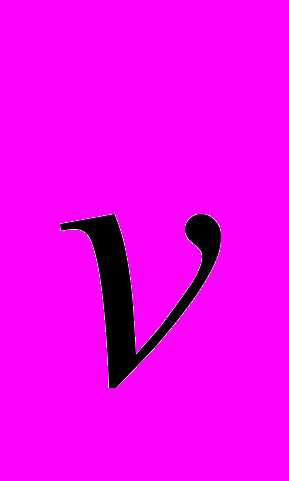через величины, входящие в исходную систему. Найдите связь между дисперсиями величин 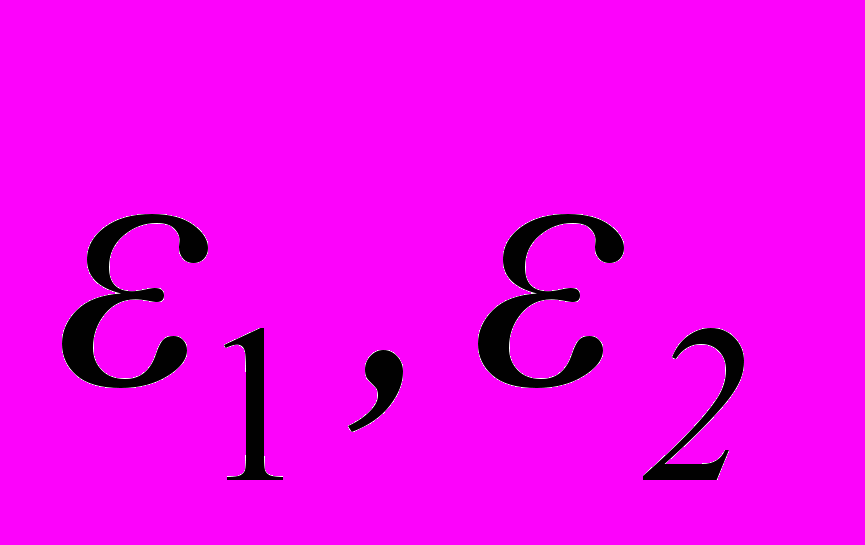и .
   
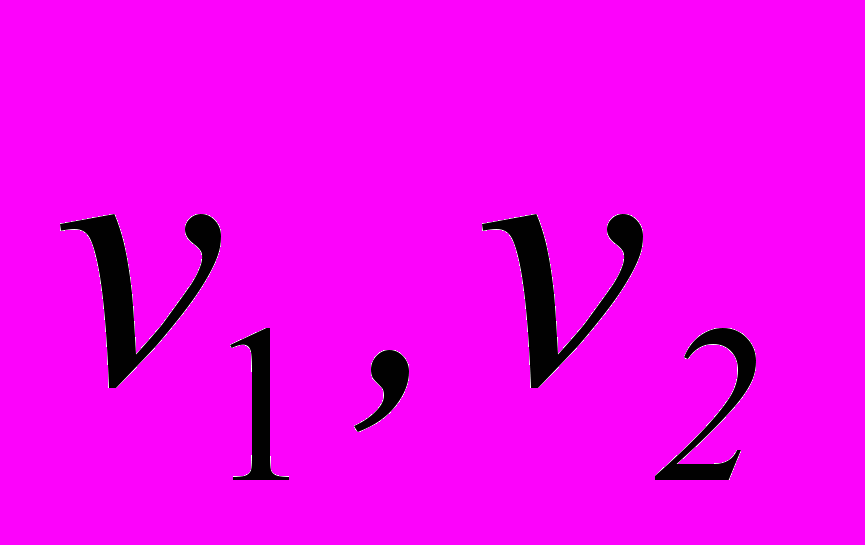3. Составьте систему уравнений, связывающих параметры исходной системы с элементами матрицы 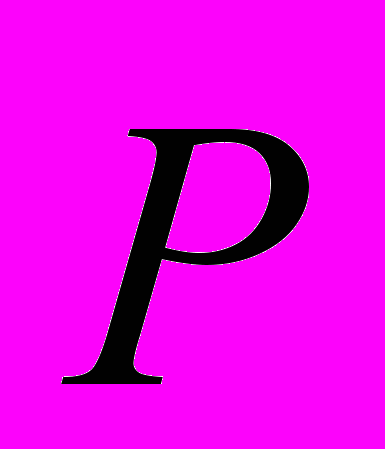и проанализируйте вопрос об идентифицируемости исходных параметров и системы в целом. Найдите явные выражения для всех идентифицируемых параметров через элементы матрицы .
   
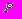4. Применение МНК к приведенной системе дало следующие оценки: 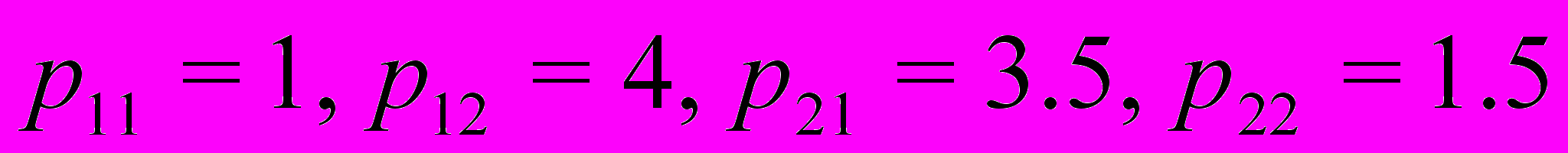, . Получить оценки идентифицируемых параметров и дисперсий случайных составляющих структурной формы.
   

7. Литература по дисциплине (основная и дополнительная)


Основная литература

1. Кремер Н.Ш., Путко Б.А. Эконометрика.   3-е изд., перераб. и доп.   М.: Юнити, 2010.
   
2. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс.   М.: Дело, 2007.   504 с.
   
3. Елисеева И.И. Эконометрика.   М.: Проспект, 2010.
   
4. Катышев П.К., Магнус Я.Р., Пересецкий А.А., Головань С.В. Сборник задач к начальному курсу эконометрики.   4-е изд., доп. и перераб.   M.: Дело, 2007.   368 с.
   

Дополнительная литература

5. Практикум по эконометрике / И.И. Елисеева, С.В. Курышева, И.М. Гордеенко и др. / Под ред. И.И. Елисеевой.   М.: Финансы и статистика, 2003.
   
6. Налимов В.Н. Элементы теории вероятностей и математической статистики для экономистов и менеджеров.   М.: ИМЭС, 2003.
   

7Гмурман В.Е. Теория вероятностей и математическая статистика.   М.: Высшая школа, 2000.

8. Замков О.О., Толстопятенко А.В., Черемнин Ю.Н. Математические методы в экономике / Под общей ред. А.В. Сидоровича.   4-е изд.   М.: Дело и Сервис, 2004.   (Учебники МГУ им. М.В. Ломоносова).
   
9. Берндт Э.Р. Практика эконометрики: классика и современность / Пер. с англ.   М.: ЮНИТИ, 2005.
   
10. Доугерти К. Введение в эконометрику / Пер. с англ.  М.: ИНФРА-М, 1999.   402 с.
    
11. Чураков Е.П. Прогнозирование эконометрических временных рядов. ­ М.: Финансы и статистика, 2008.
    

12. Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование.   М.: Инфра-М, 2010.