Список профилей направления подготовки бакалавра

Вид материала

Содержание

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 15

Раздел 3. Электричество и магнетизм

Электростатическое поле в вакууме. Закон Кулона. Принцип суперпозиции для вектора напряженности электрического поля. Поле системы точечных зарядов.
Поток вектора напряженности электрического поля. Теорема Гаусса для вектора напряженности.
Циркуляция вектора напряженности электрического поля. Потенциал.
Эквипотенциальные поверхности. Связь напряженности поля и потенциала.
Проводники в электростатическом поле.
Теорема о единственности решения задач электростатики (заданы расположения проводников и их заряды).
Теорема о единственности решения задач электростатики (заданы расположения проводников и их потенциалы).
Связь между плотностью заряда на поверхности проводника и полем вблизи него.
Решение электростатических задач методом электрических изображений.
Конденсаторы.
Энергия системы точечных зарядов. Энергия заряженного проводника и конденсатора. Плотность энергии электрического поля.
Дипольный момент молекул. Вектор поляризации.
Теорема Гаусса для вектора поляризации.
Вектор электрической индукции. Теорема Гаусса для вектора электрической индукции.
Линейные среды. Связь между векторами поляризации и напряженности, напряженности и индукции электрического поля.
Механизмы поляризации диэлектриков с неполярными и полярными молекулами.
Граничные условия для векторов напряженности и индукции электрического поля.
Энергия электрического поля при наличии диэлектриков. Плотность энергии электрического поля.
Поверхностная плотность силы, действующей на границе металла.
Объемная плотность силы, действующей на диэлектрик в электрических полях.
Закон Био-Савара-Лапласа.
Поле прямого провода.
Поле на оси соленоида.
Сила Лоренца и сила Ампера.
Момент сил, действующих на рамку с током в магнитном поле.
Теорема о циркуляции вектора индукции магнитного поля.
Теорема о циркуляции вектора намагничения.
Напряженность магнитного поля. Теорема о циркуляции вектора напряженности магнитного поля.
Линейные среды. Связь векторов индукции, напряженности и намагничения.
Граничные условия для векторов индукции и напряженности магнитного поля.
Механизм намагничения диамагнетиков.
Механизм намагничения парамагнетиков.
Ферромагнетики.
Явление электромагнитной индукции в движущихся проводниках. Примеры.
Энергетика динамомашины.
Энергетика электромотора.
Явление электромагнитной индукции в неподвижных проводниках. Вихревое электрическое поле.
Индукционный ускоритель электронов (бетатрон).
Баллистические измерения магнитной индукции.
Измерение циркуляции вектора индукции магнитного поля при помощи пояса Роговского.
Индуктивность (коэффициент самоиндукции). Примеры вычисления.
Процессы установления в контуре с индуктивностью.
Магнитная энергия.
Коэффициент взаимоиндукции. Примеры вычисления.
Магнитная энергия двух связанных контуров.
Работа при перемещении витка в магнитном поле.
Свободные контуры.
Теорема о циркуляции вектора индукции магнитного поля с учетом тока смещения.
Система уравнений Максвелла в вакууме.
Система уравнений Максвелла в веществе.
Граничные условия для векторов напряженности и индукции электрического поля, индукции и напряженности магнитного поля.
Волновое уравнение. Электромагнитные волны.
Энергия и импульс электромагнитного поля.
Метод векторных диаграмм для сложения гармонических колебаний. Примеры.
Метод комплексных амплитуд для сложения гармонических колебаний. Примеры.
Сложение гармонических векторных колебаний.
Свойства идеальных элементов в цепях квазистационарных токов.
Работа и мощность в цепях переменного тока.
Механизм проводимости металлов. Классическая модель.
Механизм проводимости металлов. Представление об энергетических зонах.
Эффективная масса электрона в кристалле. Дырки.

Раздел 4. Колебания и волны, оптика

Свободные колебания гармонического осциллятора. Фазовый портрет. Превращения энергии при колебаниях.
Затухающие свободные колебания линейного осциллятора. Характеристики затухания. Фазовый портрет.
Апериодический и критический режимы свободных колебаний линейного осциллятора. Фазовые портреты.
Линейный осциллятор с «отрицательным» трением (с примером). Фазовые портреты.
Вынужденные колебания линейного осциллятора. Явление резонанса, резонансные кривые (пример - колебательный контур).
Фазовые соотношения при вынужденных колебаниях линейного осциллятора.
Сложение двух скалярных гармонических колебаний с близкими частотами. Биения.
Сложение двух взаимно-перпендикулярных гармонических колебаний с близкими частотами.
Процесс установления колебаний: резонансный случай.
Процесс установления колебаний: нерезонансный случай.
Решение уравнения гармонического осциллятора при произвольной вынуждающей силе (с примером).
Разложение периодических функций в ряд Фурье (с примером).
Представление непериодических функций интегралом Фурье (с примером). Соотношение неопределенностей.
Отклик линейного осциллятора на произвольное внешнее воздействие. Колебательный контур как спектральный прибор. Опыт Мандельштама.
Амплитудно-модулированный сигнал и его спектр. Колебательный контур как селективный приемник радиосигналов.
Свободные колебания в системе двух связанных контуров. Нормальные колебания.
Вынужденные колебания в системе двух связанных контуров. Резонансная кривая. Динамическое демпфирование.
Энергетика параметрических колебательных систем. Параметрический резонанс.
Особенности свободных и вынужденных колебаний нелинейного осциллятора.
Автоколебания. Пример – генератор Ван-дер-Поля. Предельный цикл.
Волновое уравнение (одномерное и трехмерное). Бегущие недеформирующиеся волны: плоские, сферические, цилиндрические.
Дисперсия. Распространение сигналов (волновых пакетов) на примере тригармонической волны. Фазовая и групповая скорости. Условие пренебрежения дисперсионным искажением сигнала.
Явление интерференции. Интерференция двух встречных плоских волн. Стоячая волна.
Интерференция двух сферических волн.
Особенности интерференции в оптике. Классические опыты с раздвоением источника.
Интерференция света в тонких пленках. Просветление оптики. Полосы равного наклона и равной толщины.
Вывод волнового уравнения из уравнений Максвелла. Плоские электромагнитные волны. Импеданс.
Синусоидальные электромагнитные волны (бегущая и стоячая). Поляризация.
Энергетические соотношения для электромагнитных волн: теорема Пойнтинга с примерами (бегущая и стоячая волна).
Излучение электромагнитных волн элементарным вибратором. Диаграмма направленности, сопротивление излучения.
Решетки из вибраторов. Условия острой направленности излучения.
Нормальное падение электромагнитной волны на границу раздела двух диэлектрических сред.
Наклонное падение электромагнитной волны на границу раздела двух диэлектрических сред. Закон Снелля. Формулы Френеля.
Явления Брюстера и полного (внутреннего) отражения.
Дисперсионные свойства нормальных волн в одноосном кристалле. Поверхности нормалей.
Поляризационная структура нормальных волн в одноосном кристалле. Лучи, лучевые поверхности.
Преломление на границе одноосного кристалла. Построение Гюйгенса.
Фазовые пластинки.
Интерференция поляризованных лучей. Хроматическая поляризация.
Принцип Гюйгенса-Френеля как метод решения дифракционных задач.
Дифракция на круглом отверстии. Зоны Френеля.
Зонные пластинки (амплитудная и фазовая).
Дифракция на узкой щели. Спираль Корню.
Дифракция на прямоугольном отверстии.
Дифракция на крае экрана.
Дифракция на бесконечно длинной щели произвольной ширины. Предельные случаи дифракции Френеля.
Дифракция Фраунгофера на бесконечно длинной щели.
Дифракция Фраунгофера на прямоугольном отверстии.
Амплитудная дифракционная решетка.
Дифракционная решетка как спектральный прибор.

Раздел 5. Атомная и ядерная физика

Опыты Штерна-Герлаха. Гипотеза Гаудсмита-Уленбека.
Тепловое излучение. Законы теплового излучения. Спектр равновесного излучения.
Квантовые переходы. Коэффициенты Эйнштейна и формула Планка. Корпускулярная и волновая теория света.
Фотоэффект. Законы фотоэффекта.
Парадокс Эйнштейна-Подольского-Розена. Неравенства Белла.
Измерения в классической физике и квантовой механике. Сущность измерительного процесса.
Пси-функция, ее амплитуда и фаза. Физический смысл пси-функции.
Волновые свойства частиц. Гипотеза де Бройля. Волна де Бройля.
Условие измеримости динамических переменных. Принцип дополнительности.
Типы состояний квантовой системы и результаты измерений динамических переменных.
Квантовая система и прибор. Роль прибора в процессе измерения.
Редукция волновой функции в процессе измерений. Декогеренция.
Принцип неопределенности. Соотношения неопределенностей.
Теорема о квантовом клонировании. Квантовая телепортация.
Квантовая информация, квантовая криптография, квантовый компьютер.
Фотон и его свойства.
Вычисление средних значений динамических переменных. Оператор произвольной функции динамических переменных.
Физические величины и динамические переменные. Представление динамических переменных посредством операторов. Постулаты квантовой механики.
Чистые и смешанные состояния квантовой системы. Запутанные состояния квантовой системы.
Квантовая суперпозиция. Принцип суперпозиции.
Операторы координаты, импульса, момента импульса, энергии.
Серии спектральных линий, формула Бальмера. Спектральные термы. Модель атома водорода Бора-Зоммерфельда.
Электроны в кристаллах. Зонная структура энергии электронов в твердых телах. Электроны проводимости и дырки. Дисперсия энергии электронов в твердых телах.
Потенциальные ямы. Потенциальные барьеры. Туннельный эффект.
Квантовый осциллятор.
Момент импульса. Квантование момента импульса. Сложение моментов.
Уравнение Шредингера для водородоподобных атомов: решение уравнения в сферической системе координат. Собственные значения и собственные функции. Их физический смысл.
Энергетические уровни атома водорода. Спектр водородоподобных атомов. Спектры изотопов водорода и водородоподобных ионов.
Момент импульса электрона водородоподобного атома. Спин-орбитальное взаимодействие.
Магнитный момент атома.
Эффект Комптона.
Тонкая структура энергетических уровней и спектральных линий. Мультиплетность.
Результирующий (суммарный) механический и магнитный момент многоэлектронных атомов.
Терм атома. Спектры излучения и поглощения света. Правила отбора.
Эффект Зеемана. Эффект Пашена-Бака.
Эффект Штарка.
Спектральные серии поглощения и излучения щелочных металлов. Экспериментальные данные и эмпирическая формула Ридберга. Энергетическая структура атомов щелочных металлов. Квантовый дефект. Тонкая структура спектров щелочных металлов.
Атом гелия. Энергия электронов в атоме гелия. Обобщенное уравнение Шредингера. Его решение.
Принцип Паули. Электронные оболочки. Периодическая система элементов Менделеева.
Обобщенная пси-функция электронов атома гелия. Обменная энергия.

Фундаментальные взаимодействия. Виртуальные частицы. Обменный характер взаимодействий.
Элементарные частицы. Их классы, свойства и описание. Квазичастицы.
Законы сохранения в физике элементарных частиц.
Масса атомных ядер и энергия связи нуклонов в ядре. Формула Вейцзеккера.
Атомное ядро. Его основные характеристики.
Капельная и оболочечная модель атомных ядер.
Кварковая модель элементарных частиц. Особенности взаимодействия кварков, их описание.
Радиоактивность. Закон радиоактивного распада. Распад атомных ядер и элементарных частиц.

ПРИМЕРНАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Рекомендуется для направления подготовки

011800 «РАДИОФИЗИКА»

Квалификация (степень) выпускника бакалавр

1. Цели и задачи дисциплины

Содержание дисциплины «Математический анализ» направлено на обучение студентов основам дифференциального и интегрального исчисления функций одного и многих переменных, включая теорию пределов, числовых и функциональных рядов.

2. Место дисциплины в структуре программы бакалавра:

Дисциплина «Математический анализ» относится к дисциплинам базовой части математического и естественнонаучного цикла основной образовательной программы по направлению 011800 – Радиофизика.

3. Требования к уровню освоения содержания дисциплины

В результате освоения дисциплины «Математический анализ» формируются следующие компетенции:

способность к овладению базовыми знаниями в области математики, их использованию в профессиональной деятельности (ОК -8);
способность самостоятельно приобретать новые знания, используя современные образовательные информационные технологии (ОК -10);
способность к правильному использованию общенаучной и специальной терминологии (ОК-12).

В результате изучения студенты должны:

знать основные понятия теории пределов, дифференциального и интегрального исчисления, функции многих переменных, теории кратных интегралов, теории рядов;
уметь строить графики функций, как элементарными приемами, так и с использованием методов высшей математики, вычислять пределы последовательностей и функций, вычислять производные и применять их к исследованию функций, вычислять как неопределенные, так и определенные интегралы и применять их к решению геометрических, механических и физических задач, исследовать ряды на сходимость;
иметь представление об основных понятиях теории множеств, о представлении функции в виде степенных рядов.

4. Объем дисциплины и виды учебной работы

Общая трудоемкость дисциплины составляет 8 зачетных единиц 288 часов.

Виды учебной работы	Всего часов	Семестры
Общая трудоемкость дисциплины	288	1	2
Аудиторные занятия	136	68	68
Лекции	68	34	34
Практические занятия (ПЗ)	68	34	34
Самостоятельная работа	80	40	40
Вид итогового контроля (зачет, экзамен)	72 экзамен	36 экзамен	36 экзамен

5. Содержание дисциплины

5.1. Разделы дисциплины и виды занятий

№п/п	Раздел дисциплины	Лекции	ПЗ	ЛР
1	Предмет математики. Введение в анализ.	*	*
2	Пределы последовательности и функции.	*	*
3	Непрерывность функции. Точки разрыва.	*	*
4	Дифференциальное исчисление функций одной переменной.	*	*
5	Интегральное исчисление функций одной переменной	*	*
6	Функции многих переменных.	*	*
7	Кратные интегралы.	*	*
8	Криволинейные и поверхностные интегралы.	*	*
9	Ряды. Числовые, функциональные и степенные ряды.	*	*
10	Несобственные интегралы, интегралы, зависящие от параметра.	*	*
11	Ряд и интеграл Фурье.
12	Элементы теории обобщенных функций.

5.2. Содержание разделов дисциплины

1. Предмет математики. Введение в анализ

Предмет математики. Связь с другими науками. Историческая справка.

Понятие множества. Операции с множествами. Общее определение функции. Область определения и область изменения. Функция действительного переменного. Способы задания функции. Определение графика функции. Графики элементарных функций (прямая, парабола, кубическая парабола, окружность, гипербола, показательная и логарифмическая функции, тригонометрические функции). Обратные тригонометрические функции и их свойства. Преобразование графиков. Построение графиков с помощью цепочки преобразований. Действия с графиками. График сложной функции. График функции, заданной параметрически. Полярные координаты.

2. Пределы последовательности и функции

Понятие последовательности действительных чисел. Предел последовательности. Геометрический смысл предела последовательности. Теорема о единственности предела. Ограниченность сходящейся последовательности. Предельные переходы в равенствах и неравенствах. Монотонные последовательности. Подпоследовательность, частичные пределы, верхний и нижний пределы последовательности действительных чисел. Лемма о вложенных промежутках. Теорема Больцано-Вейерштрасса. Критерий Коши сходимости последовательности.

Предел функции действительного переменного по Коши и по Гейне. Геометрический смысл предела функции действительного переменного. Арифметические операции над функциями, имеющими предел. Односторонние пределы. Классификация бесконечно малых и бесконечно больших величин. Эквивалентные бесконечно малые и бесконечно большие величины. Первый и второй замечательные пределы.

3. Непрерывность функции

Непрерывность функции действительного переменного. Арифметические действия с непрерывными функциями. Непрерывность сложной функции. Односторонняя непрерывность. Теорема о существовании и непрерывности обратной функции. Сохранение знака непрерывной функции. Равномерная непрерывность. Теорема Кантора. Классификация точек разрыва.

4. Дифференциальное исчисление функций одной переменной.

Производные и односторонние производные, бесконечные производные. Геометрический и физический смысл производной. Правила дифференцирования и таблица производных. Дифференциал и его геометрический смысл. Производная сложной функции. Производные и дифференциалы высших порядков. Формула Лейбница. Инвариантность формы первого и неинвариантность формы высших дифференциалов. Параметрически заданные функции и их дифференцирование. Основные теоремы дифференциального исчисления Ролля, Лагранжа, Коши. Правило Лопиталя раскрытия неопределенностей. Формула Тейлора и ее связь с задачей приближенного вычисления значений функции. Признаки монотонности. Экстремумы и правила их нахождения. Выпуклость, вогнутость и точки перегиба. Асимптоты. Применение дифференциального исчисления к исследованию функций и построению графиков.

5. Интегральное исчисление функций одной переменной.

Понятие первообразной и неопределенного интеграла. Свойства неопределенного интеграла. Таблица неопределенных интегралов. Техника интегрирования (непосредственное интегрирование с помощью таблиц, метод разложения, замена переменной, интегрирование по частям, приведение квадратного трехчлена к каноническому виду). Примеры. Разложение многочлена с действительными коэффициентами на множители. Представление правильной рациональной дроби в виде суммы простейших рациональных дробей. Интегрирование простейших дробей. Интегрирование рациональных функций. Сведение интегралов от иррациональных и тригонометрических функций к интегрированию рациональных функций.

Определенный интеграл. Условие существования определенного интеграла. Классы интегрируемых функций. Свойства определенного интеграла. Интеграл как функция верхнего предела. Формула Ньютона-Лейбница. Теорема о среднем. Приложение определенного интеграла к вычислению площадей плоских фигур, площадей поверхности тел вращения и некоторых объемов. Параметрически заданные кривые. Длина дуги кривой.

6. Функции многих переменных

Основные понятия на плоскости (расстояние между точками, окрестность точки, внутренняя точка, изолированная точка, граничная точка, открытое множество, связное и несвязное множества, область, замкнутая область, ограниченное множество). Аналогия с пространством. Предел последовательности векторов. Теорема о покоординатной сходимости. Пределы и непрерывность. Двойные и повторные пределы. Примеры. Непрерывность по совокупности переменных и по отдельной переменной. Дифференциальное исчисление функций многих переменных. Частные производные. Дифференцируемость функции многих переменных. Необходимые условия дифференцируемости. Достаточные условия дифференцируемости функции многих переменных. Теоремы о взаимосвязи между дифференцируемостью, непрерывностью и существованием частных производных функции многих переменных. Производная сложной функции. Дифференциал функции многих переменных. Производная по направлению. Градиент. Связь производной по направлению с градиентом. Условие возрастания (убывания) функции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных. Исследование функций многих переменных, условие постоянства, условие монотонности в указанном направлении. Формула Тейлора. Экстремум. Неявные функции. Теоремы о существовании неявной функции. Функциональные определители. Существование системы неявных функций. Взаимнооднозначное отображение двух множеств векторного пространства. Условный экстремум. Правило множителей Лагранжа. Примеры.

7. Кратные интегралы.

Кратные интегралы. Площадь многоугольной фигуры. Мера Жордана. Измеримые множества. Необходимое и достаточное условие измеримости множества на плоскости. Свойства меры Жордана. Определение двойного интеграла. Суммы Дарбу и их свойства. Критерий существования двойного интеграла. Классы интегрируемых функций. Свойства двойного интеграла. Приведение двойного интеграла к повторному. Криволинейные координаты на плоскости. Полярные и эллиптические координаты. Замена переменных в двойном интеграле. Тройной интеграл. Сведение тройного интеграла к повторному. Замена переменных в тройном интеграле. Сферические и цилиндрические координаты.

8. Криволинейные и поверхностные интегралы

Определение криволинейных интегралов. Основные формулы вычисления криволинейных интегралов. Определения поверхностных интегралов первого и второго рода. Вычисление поверхностных интегралов. Математические и физические приложения криволинейных и поверхностных интегралов.

9. Ряды. Числовые, функциональные и степенные ряды

Числовые ряды. Сходящиеся и расходящиеся ряды. Критерий Коши сходимости числового ряда. Необходимое условие сходимости. Достаточные признаки сходимости: мажорантный и предельный признаки сравнения, Даламбера, Коши, Дирихле, Абеля. Абсолютная и условная сходимость. Умножение рядов. Перестановка членов ряда. Функциональные последовательности и ряды функций. Поточечная и равномерная сходимость. Признаки равномерной сходимости (критерий Коши, мажорантный признак для последовательности, мажорантный признак Вейерштрасса для ряда). Равномерная сходимость и непрерывность, равномерная сходимость и интегрирование, равномерная сходимость и дифференцирование. Степенной ряд. Радиус сходимости. Дифференцирование и интегрирование степенного ряда. Ряд Тейлора.

10. Несобственные интегралы, интегралы, зависящие от параметра

Определение несобственных интегралов первого типа. Определение несобственных интегралов второго типа. Эталонные интегралы. Свойства сходящихся интегралов. Критерий Коши сходимости несобственных интегралов. Достаточные признаки сходимости несобственных интегралов. Мажорантный признак сравнения. Предельный признак сравнения. Абсолютная и условная сходимость несобственных интегралов. Признак Абеля. Признак Дирихле. Расширение методов интегрирования на несобственные интегралы. Замена переменных. Интегрирование по частям. Главное значение несобственного интеграла. Интегралы, зависящие от параметра. Непрерывность по параметру. Дифференцирование и интегрирование по параметру. Несобственные интегралы от параметра.

11. Ряд и интеграл Фурье

Постановка задачи. Пространство со скалярным произведением. Нормированное пространство. Сходимость в среднем. Гильбертово пространство. Скалярное произведение и норма функции. Поточечная, равномерная сходимость и сходимость в среднем последовательностей и рядов. Ортогональные и ортонормированные элементы пространства со скалярным произведением. Обобщенный ряд Фурье. Свойства остатка ряда Фурье. Неравенство Бесселя. Условие сходимости ряда Фурье. Равенство Парсеваля. Замкнутые и полные ортонормальные системы элементов в пространстве со скалярным произведением. Теоремы о связи между замкнутой и полной системой. Ряд Фурье по ортогональной и ортонормированной системам функций. Неравенство Бесселя и равенство Парсеваля для этих рядов. Тригонометрический ряд Фурье. Разложение четной и нечетной функции в тригонометрический ряд Фурье. Комплексная форма ряда Фурье. Точечная и равномерная сходимость тригонометрического ряда Фурье. Полнота тригонометрической системы функций. Двойные и тройные ряды Фурье.

Интеграл Фурье как предельный случай ряда Фурье. Достаточные признаки сходимости интеграла Фурье. Представление функции интегралом Фурье. Представление четной и нечетной функции интегралом Фурье. Комплексное прямое и обратное преобразования Фурье. Синус и косинус преобразования Фурье.

12. Элементы теории обобщенных функций

Класс основных (пробных) функций. Функциональное определение обобщенной функции. Регулярные и сингулярные обобщенные функции. Дельта функция. Действия с обобщенными функциями. Секвенциальный подход к определению обобщенной функции.

6. Лабораторный практикум

Не предусмотрен.

7. Учебно-методическое обеспечение дисциплины

7.1. Рекомендуемая литература.

а) основная литература:

Ильин В.А., Позняк Э.Г. Основы математического анализа.- Части 1,2.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления.- т.т. 1,2,3.
Будак Б.М., Фомин С.В. Кратные интегралы и ряды.

б) дополнительная литература:

Фихтенгольц Г.М. Основы математического анализа.- т.т. 1,2.
Кудрявцев Л.Д. Курс математического анализа. - т.т. 1,2.
Соболев И.И. Лекции по дополнительным главам математического анализа. - М.1968.

8. Вопросы для контроля

Подмножество множества.
Собственное подмножество.
Равенство множеств.
Объединение множеств.
Пересечение множеств.
Разность множеств.
Дополнение множества.
Верхние и нижние границы числовых множеств.
Точная верхняя граница.
Точная нижняя граница.
Действительно значная функция.
Функция действительного переменного.
Точная верхняя граница действительно значной функции.
Точная нижняя граница действительно значной функции.
Расширенная система действительных чисел.
Определение комплексного числа.
Алгебраическая, тригонометрическая формы комплексного числа.
Показательные формы комплексного числа.
Определение последовательности.
Предел числовой последовательности.
Бесконечно большие последовательности.
Бесконечно малые последовательности.
Монотонные последовательности.
Определение подпоследовательности.
Частичный предел.
Верхний и нижний пределы.
Критерий Коши сходимости числовой последовательности.
Предел функции действительного переменного по Коши.
Предел функции действительного переменного по Гейне.
Односторонние пределы.
Понятие бесконечно малой и бесконечно большой величины.
Бесконечно малая более высокого порядка.
Бесконечно малые величины одного порядка.
Эквивалентные бесконечно малые.
Главная часть бесконечно малой.
Порядок бесконечно малой (бесконечно большой величины).
Теорема об умножении и делении комплексных чисел в тригонометрической форме. Формула Муавра.
Извлечение корня из комплексного числа. Геометрическая интерпретация корня.
Теорема о единственности предела.
Теорема об ограниченности сходящейся последовательности.
Арифметические действия над сходящимися числовыми последовательностями.
Предельный переход в неравенствах.
Теорема о пределе монотонной последовательности.
Доказать, что .
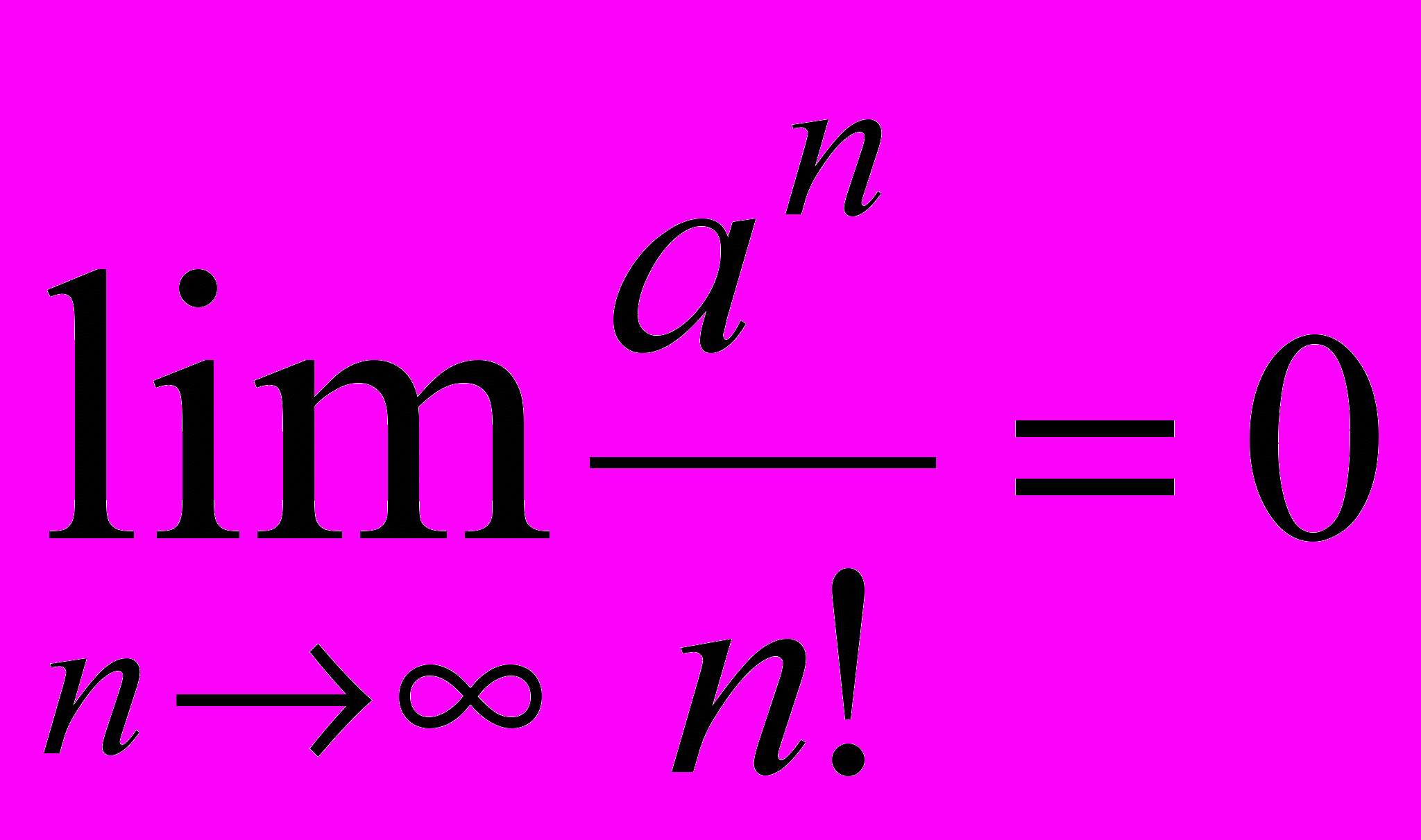Доказать, что
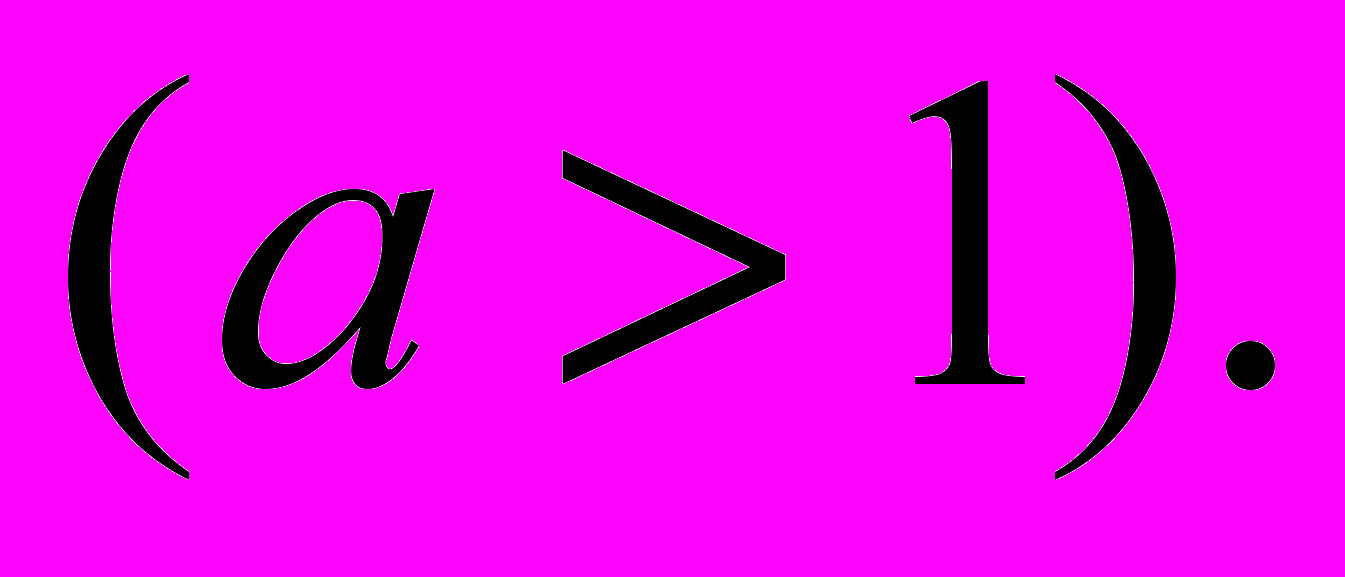
Доказать, что .
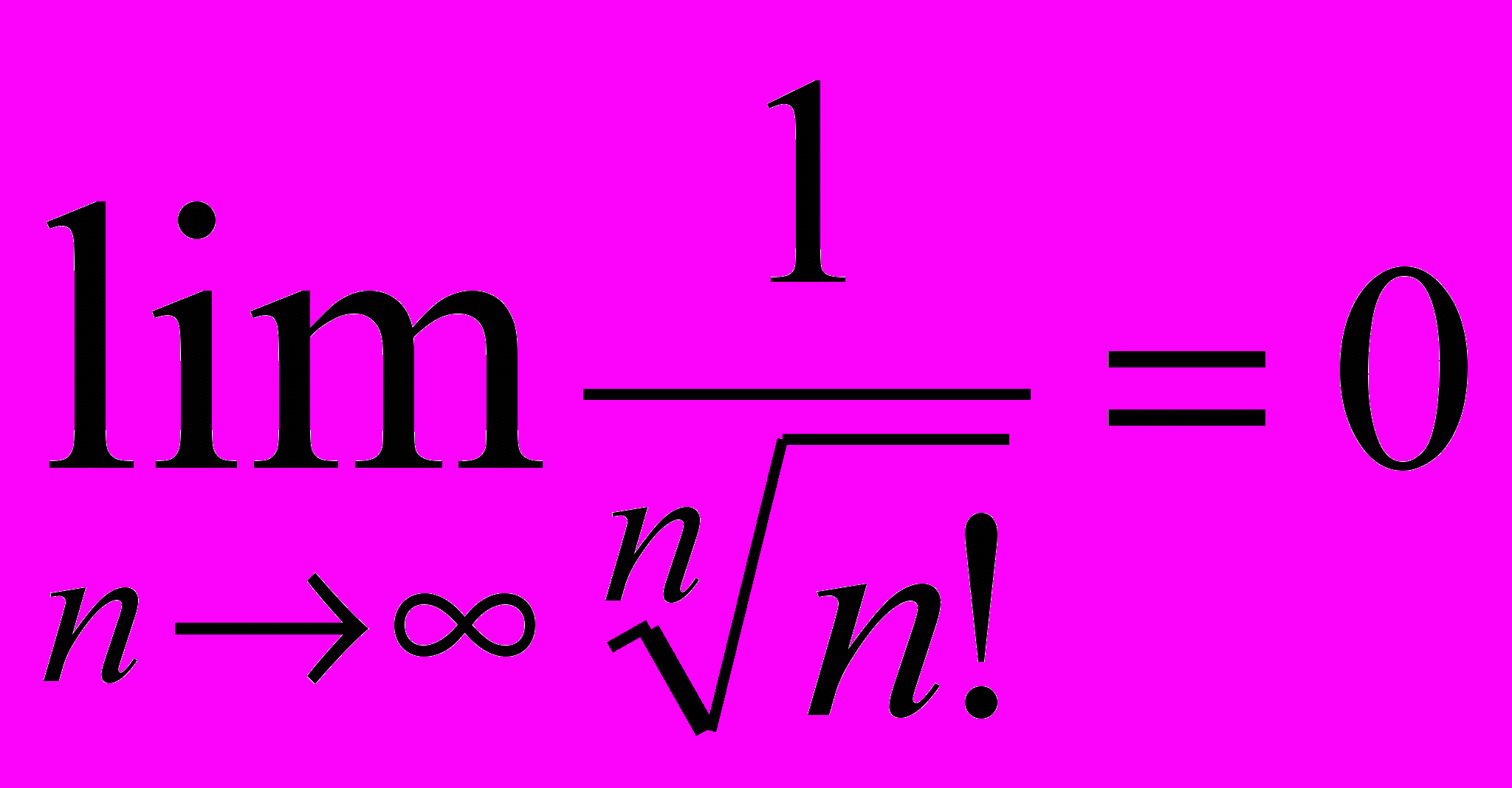Доказать, что .
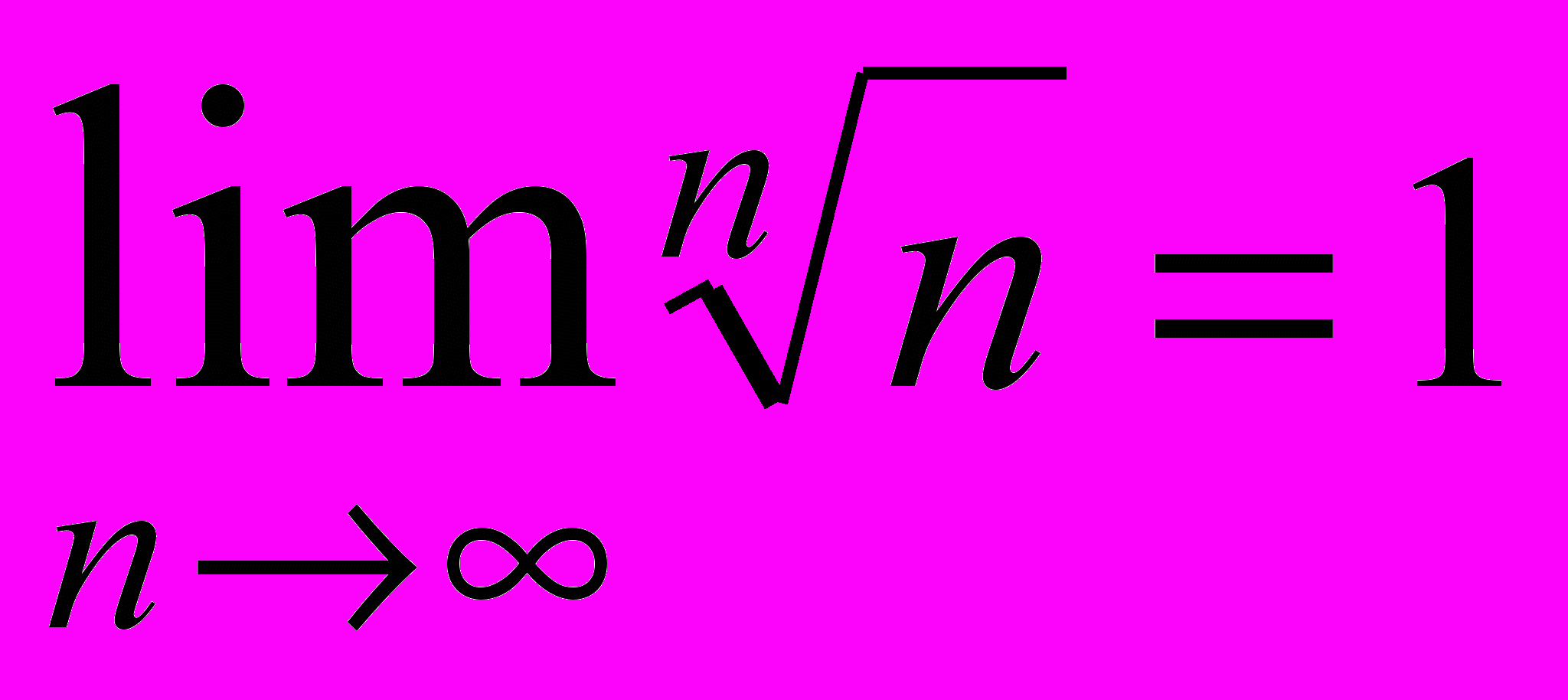Доказать, что .
Лемма о вложенных промежутках.
Теорема Больцано-Вейерштрасса.
Теорема об эквивалентности двух определений предела функции.
Теорема об односторонних пределах.
Критерий Коши существования предела функции.
Теорема о представлении бесконечно малой величины.
Производная, односторонние производные, бесконечная производная.
Односторонние касательные, касательная. Геометрический смысл производных.
Определение дифференцируемой функции и дифференциала.
Непрерывность дифференцируемой функции.
Необходимое и достаточное условие дифференцируемой функции.
Свойства дифференциала функции одного переменного.
Свойства дифференцируемых функций: теорема Ролля, теорема Коши, теорема Лагранжа, формула конечных приращений Лагранжа, формула Коши.
Правило Лопиталя.
Производные и дифференциалы высших порядков. Нарушение инвариантности формулы высших дифференциалов.
Правила отыскания высших производных.
Правила дифференцирования в дифференциалах (для первого дифференциала и для дифференциалов высших порядков).
Классы непрерывно дифференцируемых функций.
Теорема Тейлора. Формула Тейлора с остаточным членом в форме Лагранжа или Пеано. Формула Лагранжа как частный случай формулы Тейлора.
Разложения основных функций по формуле Тейлора.
Условие монотонности функции.
Понятие стационарной и критической точки. Определение максимума и минимума функции.
Необходимое условие экстремума.
Достаточные условия экстремума.
Выпуклость и вогнутость кривой. Определение выпуклой и вогнутой функции. Геометрический смысл выпуклости функции. Вторая запись условия выпуклости функции.
Необходимые и достаточные условия выпуклости (вогнутости) функции.
Определение точки перегиба. Необходимое и достаточное условия для точки перегиба.
Понятие первообразной функции и неопределенного интеграла. Теорема о первообразных.
Свойства неопределенного интеграла.
Замена переменных в неопределенном интеграле.
Интегрирование по частям.
Разложение многочлена на простейшие множители.
Разложение правильной рациональной дроби на простейшие.
Интегрирование простейших дробей. Вывод рекурентной формулы.
Определение верхнего и нижнего интегралов Римана. Интеграл Римана.
Теорема о существовании верхнего и нижнего интегралов Римана.
Определение интеграла Римана (разбиение сегмента, нижняя и верхняя суммы Дарбу, верхний и нижний интегралы, определенный интеграл).
Измельчение разбиения. Общее измельчение двух разбиений. Теорема об измельчении разбиения. Следствие.
Критерий существования определенного интеграла.
Классы интегрируемых функций.
Определенный интеграл как предел интегральных сумм.
Понятие колебания функции. Формулы для его вычисления. Лемма о колебаниях функции.
Свойства интеграла Римана, выражаемые равенствами.
Свойства интеграла Римана, выражаемые неравенствами.
Интеграл как функция верхнего предела. Теорема о его непрерывности и дифференцируемости.
Основная теорема интегрального исчисления.
Теорема о среднем для интегрального исчисления.
Определение абсолютной и условной сходимости несобственного интеграла. Признак Абеля. Признак Дирихле.
Расширение методов интегрирования на несобственные интегралы.
Главные значения несобственных интегралов.
Двойные и повторные пределы.
Непрерывность функции многих переменных по совокупности и по отдельной переменной.
Определение дифференцируемости функции многих переменных. Понятие градиента функции многих переменных.
Необходимое условие дифференцируемости.
Достаточное условие дифференцируемости функции многих переменных.
Теорема о производной сложной функции.
Определение и вычисление первого дифференциала функции многих переменных.
Теорема об инвариантности формы первого дифференциала.
Определение производной по направлению. Теорема о связи производной по направлению с градиентом.
Смысл градиента функции многих переменных.
Определение производных высших порядков.
Равенство смешанных производных.
Условие постоянства функции многих переменных.
Условие монотонности функции многих переменных.
Теорема Тейлора для функции многих переменных.
Определение экстремума функции многих.
Вывод необходимого условия экстремума функции многих переменных.
Достаточное условие экстремума функции многих переменных.
Теорема существования неявной функции.
Теорема о дифференцируемости неявной функции.
Определение функционального определителя.
Теорема об умножении якобианов.
Теорема о существовании системы неявных функций.
Взаимно однозначное отображение двух множеств векторного пространства.
Определение условного (относительного) экстремума. Два способа отыскания условного экстремума.
Площадь многоугольной фигуры. Мера Жордана. Измеримые множества.
Определение множества меры нуль.
Необходимое и достаточное условие измеримости множества на плоскости. Следствие (критерий измеримости области).
Измеримость области с кусочно-гладкой границей.
Определение двойного интеграла.
Определение сумм Дарбу. Их свойства.
Критерий Коши существования двойного интеграла.
Классы интегрируемых функций (для двойного интеграла).
Свойства двойного интеграла.
Теорема о приведении двойного интеграла к повторному в случае прямоугольной области.
Теорема о приведении двойного интеграла к повторному в случае криволинейной области.
Определение криволинейных координат на плоскости. Полярные и эллиптические координаты.
Теорема о замене переменных в двойном интеграле.
Объем многогранного тела. Понятие кубируемой (измеримой по Жордану) области трехмерного пространства.
Определение тройного интеграла.
Сведение тройного интеграла к повторному.
Формула замены переменных в тройном интеграле.
Сферические и цилиндрические координаты.
Определение числового ряда. Частичная сумма, остаток, отрезок числового ряда. Понятие сходимости и расходимости числового ряда.
Критерий Коши сходимости числового ряда.
Необходимое условие сходимости числового ряда.
Действия с числовыми рядами.
Мажорантный признак сравнения.
Предельный признак сравнения.
Интегральный признак.
Гармонический ряд с любым показателем.
Признак Коши.
Признак Даламбера.
Тождество Абеля. Признак Дирихле.
Признак Абеля.
Признак Лейбница.
Абсолютная и условная сходимость числового ряда.
Определение поточечной и равномерной сходимости функциональной последовательности и функционального ряда.
Критерий Коши равномерной сходимости функциональной последовательности и функционального ряда.
Мажорантный признак равномерной сходимости функциональной последовательности.
Признак Вейерштрасса равномерной сходимости функционального ряда.
Равномерная сходимость и непрерывность.
Равномерная сходимость и интегрирование.
Равномерная сходимость и дифференцирование.
Степенные ряды. Радиус сходимости.
Теорема о почленном дифференцировании степенного ряда.
Определение ряда Тейлора.
Разложения элементарных функций в степенной ряд.
Дифференцирование интеграла, зависящего от параметра.
Ряд Фурье от периодической функции.
Ряды Фурье от четной и нечетной функции.
Представление функции интегралом Фурье.
Определение обобщенной функции.
Определение Дельта функции.
Дифференцирование обобщенных функций.

ПРИМЕРНАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Рекомендуется для направления подготовки

011800 «РАДИОФИЗИКА»

Квалификация (степень) выпускника бакалавр

1. Цели и задачи дисциплины

Содержание дисциплины направлено на изучение разделов аналитической геометрии, необходимых для понимания других разделов математики и физики.

2. Место дисциплины в структуре программы бакалавра:

Дисциплина «Аналитическая геометрия» относится к дисциплинам базовой части математического и естественнонаучного цикла основной образовательной программы по направлению 011800 – Радиофизика.

3. Требования к уровню освоения содержания дисциплины

В результате освоения дисциплины «Аналитическая геометрия» формируются следующие компетенции:

способность к овладению базовыми знаниями в области математики, их использованию в профессиональной деятельности (ОК -8);
способность самостоятельно приобретать новые знания, используя современные образовательные информационные технологии (ОК -10);
способность к правильному использованию общенаучной и специальной терминологии (ОК-12).

В результате изучения студенты должны:

знать аппарат векторной алгебры, уравнения прямой и плоскости, уравнения и классификацию кривых и поверхностей 2-го порядка;
уметь решать задачи из указанных разделов курса;
иметь представление о приложениях разделов курса к решению практических задач.

4.Объем дисциплины и виды учебной работы

Общая трудоемкость дисциплины составляет 4 зачетные единицы 144 часа.

Виды учебной работы	Всего часов	Семестры
Общая трудоемкость дисциплины	144	1
Аудиторные занятия	68	1
Лекции	34	1
Практические занятия (ПЗ)	34	1
Самостоятельная работа	34	1
Вид итогового контроля (зачет, экзамен)	36 (экзамен)	1

5. Содержание дисциплины

5.1. Разделы дисциплины и виды занятий

№ п/п	Раздел дисциплины	Лекции	ПЗ (или С)	ЛР
1	Векторная алгебра.	*	*
2	Прямая и плоскость.	*	*
3	Кривые и поверхности 2-го порядка.	*	*

5.2. Содержание разделов дисциплины

Blog

Список профилей направления подготовки бакалавра

Содержание