Метод уменьшения размера таблиц маршрутизации в ip-сетях

Вид материала

Автореферат диссертации

Содержание Смагин Алексей Аркадьевич Угаров Владимир Васильевич Общая характеристика работы Объектом исследования Цели и задачи исследования. Научная новизна Основные положения, выносимые на защиту Практическая и теоретическая значимость исследований. Достоверность результатов Личный вклад автора. Апробация работы Структура и объем диссертации. Содержание работы Первая глава Вторая глава Рисунок 4. Схема приближенного алгоритма минимизации ДЕФ Список публикаций по теме диссертации

Подобный материал:

• Применение алгоритмов адаптивной маршрутизации в протоколе igrp, 37.51kb.
• Примеры тем дипломных проектов и работ, 73.48kb.
• Исследование эффективности алгоритмов маршрутизации в сетях с кп в датаграммном режиме, 394kb.
• Реферат По дисциплине: «Сети ЭВМ и средства коммуникаций» На тему: «Маршрутизация, 283.88kb.
• Протоколы маршрутизации, 61.97kb.
• А. А. Берестов московский инженерно-физический институт (государственный университет), 32.63kb.
• Название курса, 32.54kb.
• Курсовая работа тема: Разработка Архиватора, 95.11kb.
• Лекция 5 Базовые знания об atm, 109.54kb.
• Истолковывать понятие "добросовестные налогоплательщики" как возлагающее на налогоплательщиков, 53.88kb.

На правах рукописи


Шиготаров Андрей Владимирович


Метод уменьшения размера таблиц маршрутизации в IP-сетях


Специальность 05.13.18 - «Математическое моделирование, численные

методы и комплексы программ»


Автореферат

диссертации на соискание ученой степени

кандидата технических наук


Ульяновск -2009




Работа выполнена на кафедре «Телекоммуникационные технологии и сети» в государственном образовательном учреждении высшего профессионального образования Ульяновский государственный университет


Научный руководитель: доктор технических наук, профессор

Смагин Алексей Аркадьевич


Официальные оппоненты: доктор физико-математических наук, профессор

Ишмухаметов Шамиль Талгатович

кандидат технических наук

Угаров Владимир Васильевич


Ведущая организация: ГОУ ВПО Ульяновский государственный технический университет


Защита состоится 11 ноября 2009 года в 10⁰⁰ часов на заседании диссертационного совета Д 212.278.02 при Ульяновском государственном университете по адресу: Набережная р. Свияги, 106, корпус 1, ауд. 703.


С диссертацией можно ознакомиться в научной библиотеке Ульяновского государственного университета, с авторефератом на сайте ВУЗа www.uni.ulsu.ru.


Автореферат разослан « » октября 2009 года.


Просим прислать отзыв на автореферат по адресу: 432000, г. Ульяновск, ул. Л. Толстого, д. 42, УлГУ, Управление научных исследований.


Ученый секретарь М. А. Волков

диссертационного совета




ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность исследования. Неотъемлемой частью процесса построения быстродействующих сетей является разработка эффективных схем хранения и поиска записей в таблицах маршрутизации. Одним из следствий быстрого роста Internet стало значительное увеличение размера таблиц маршрутизации. Данный факт, а также ограниченность ресурсов программного и аппаратного обеспечения, существенно затрудняют возможность их эффективной обработки. Исследователями было предложено большое количество схем для увеличения скорости поиска в таблицах маршрутизации. Алгоритмические методы включают в себя: локальный поиск, двоичный поиск, использование специальных структур данных (бинарные деревья, трие), хеширование и ряд других. Основным недостатком данных подходов является то, что они требуют нескольких обращений к памяти. Требования к производительности современных сетей являются очень высокими, в то время как время отклика современных архитектур памяти ограничивают возможное количество обращений к памяти. Одним из наиболее распространенных и перспективных аппаратных решений является тернарная ассоциативная память (TCAM). Главной особенностью TCAM является то, что адресация осуществляется на основе содержания данных, поиск нужной записи, при этом, может быть осуществлен за одно обращение к памяти. Значительное число исследований, посвященных проблеме повышения эффективности обработки таблиц маршрутизации, ориентировано на использование данной аппаратной реализации и основано на методах сжатия таблиц маршрутизации¹. Уменьшение таблиц маршрутизации позволяет повысить скорость поиска нужной записи, использовать память меньшего размера, а также снизить энергопотребление маршрутизатора. Современное состояние дел в данной области знаний во многом основано на работах Х. Лиу (H.Liu)², В. Равикумара (V. Ravikumar)³, Р. Гуо (R.Guo) и Ж. Дельгадо-Фриаса (J. Delgado-Frias)⁴. Отечественные авторы, например, В. Г. Олифер и Н. А. Олифер⁵, внесли вклад в развитие теоретических основ проблем эффективной маршрутизации. Большинство существующих методов сжатия таблиц маршрутизации основано на сведении данной проблемы к задаче минимизации булевых функций в классе дизъюнктивных нормальных форм. При этом используются алгоритмы минимизации, которые были разработаны в первую очередь для оптимизации интегральных схем и не учитывают специфику данной задачи. В связи с этим, возможность их практического применения ограничена задачами небольшой размерности.

Объектом исследования в работе является обработка таблиц маршрутизации в IP-сетях. Предметом исследования являются методы сокращения размеров таблиц маршрутизации, как средства повышения скорости обработки пакетов и снижения затрат памяти для хранения информации о маршрутах в сети.

Цели и задачи исследования. Целью настоящей работы является разработка быстродействующего метода уменьшения размера таблиц маршрутизации, позволяющего уменьшить время поиска записей, снизить энергопотребление маршрутизатора и сократить аппаратные затраты. Для выполнения данной цели необходимо решить следующие задачи:

• анализ существующих методов сокращения таблиц маршрутизации;
  
• построение математической модели таблиц маршрутизации;
  
• разработка быстродействующих методов сокращения таблиц маршрутизации;
  
• экспериментальное исследование эффективности предлагаемых алгоритмов.
  

Методы исследования. При решении поставленных задач использовались методы математического моделирования, дискретной оптимизации, теории графов, линейного программирования.

Научная новизна

1. Предложен подход к решению задачи оптимизации размеров таблиц маршрутизации, использующий для представления ip-адресов термы булевых функций. В основу подхода положено применение:
   

• двоичных диаграмм решения для совместной обработки термов,
  
• метода ветвей и границ для ограничения перебора в пространстве возможных решений,
  
• двухуровневого представления термов для повышения скорости поиска в множестве всех исходных термов,
  
• эвристического алгоритма выборочной генерации простых импликант булевых функций.
  

Сочетание составных частей подхода по определенным правилам позволяет строить эффективные алгоритмы уменьшения размера таблиц маршрутизации.

2. Разработан точный алгоритм построения минимальной дизъюнктивной нормальной формы булевых функций, соответствующих множествам записей таблицы маршрутизации, основанный на использовании двоичных диаграмм решения и метода ветвей и границ, отличающийся более высокой скоростью работы, по сравнению с известными подходами.
   
3. Разработан приближенный алгоритм построения минимальной дизъюнктивной нормальной формы булевых функций, соответствующих множествам записей таблицы маршрутизации, основанный на двухуровневом представлении множества термов функции и эвристическом алгоритме генерации простых импликант. Показана возможность применения предложенного алгоритма для сокращения размера таблиц маршрутизации большой размерности в режиме реального времени.
   

Основные положения, выносимые на защиту

1. Алгоритмическая модель процесса уменьшения размера таблиц маршрутизации, основанная на использовании разработанных алгоритмов минимизации булевых функций и метода ветвей и границ.
   
2. Метод уменьшения таблиц маршрутизации, основанный на использовании эвристического алгоритма выборочной генерации простых импликант булевых функций, который обладает большей скоростью вычислений, по сравнению с известными подходами, и позволяет обрабатывать таблицы большой размерности в режиме реального времени.
   
3. Программный комплекс, реализующий разработанные алгоритмы, компьютерное моделирование и экспериментальная оценка эффективности методов уменьшения таблиц маршрутизации.
   

Практическая и теоретическая значимость исследований. Результаты диссертационной работы могут найти применение при разработке программных систем, предназначенных для повышения экономичности маршрутизаторов. Разработанные алгоритмы также могут быть использованы в системах автоматизации проектирования интегральных схем.

Достоверность результатов обеспечивается строгостью постановок задач, корректностью выбранного математического аппарата и подтверждается результатами компьютерного моделирования.

Личный вклад автора. Постановка задач исследования осуществлена совместно с научным руководителем А.А.Смагиным. Основные теоретические и практические исследования проведены автором самостоятельно.

Апробация работы проведена на шестой всероссийской научно-практической конференции (с участием стран СНГ) «Современные проблемы создания и эксплуатации радиотехнических систем» (Ульяновск, 2009) и ежегодных научно-технических семинарах кафедры «Телекоммуникационные технологии и сети» УлГУ.

Публикации. По теме диссертации опубликовано 7 работ, в том числе 2 – в изданиях из списка ВАК.

Структура и объем диссертации. Диссертация состоит из введения, трех глав, заключения, списка используемой литературы из 89 наименований и одного приложения. Основной текст диссертации изложен на 97 страницах.


СОДЕРЖАНИЕ РАБОТЫ

Во введении обоснована актуальность исследования, сформулированы цели и задачи исследования, дана общая характеристика работы.

Первая глава посвящена обзору и анализу существующих методов уменьшения размера таблиц маршрутизации. Показано, что большинство методов, приводимых в литературе, основано на минимизации булевых функций.

Построена классификация методов сжатия таблиц маршрутизации. По применимости к различным типам аппаратной реализации таблиц маршрутизации алгоритмы можно разделить на следующие типы:

1. применимые к любой аппаратной реализации ТМ;
   
2. ориентированные на использование TCAM.
   

По способу реализации методы оптимизации ТМ можно разделить на:

1. встраиваемые в маршрутизатор;
   
2. требующие отдельную рабочую станцию для выполнения вычислений;
   

В зависимости от используемых математических методов можно выделить типы, основанные на применении:

1. методов минимизации булевых функций;
   
2. методов теории графов;
   
3. прочих методов.
   

По соответствию исходной и сокращенной таблиц маршрутизации можно выделить методы уменьшения размера таблиц маршрутизации

1. с потерями;
   
2. без потерь.
   

На основе проведенного анализа показано, что возможность использования существующих схем уменьшения размера таблиц маршрутизации ограничена задачами небольшой размерности. Нужно также отметить, что все методы, приводимые в литературе, позволяющие оптимизировать размер таблиц маршрутизации в режиме реального времени, основаны на использовании специальных аппаратных архитектур, построение которых требует дополнительных расходов.

Вторая глава посвящена разработке метода уменьшения размера таблиц маршрутизации в IP-сетях. Базовым методом маршрутизации в IP-сетях является сопоставление по наиболее длинному префиксу. При этом для отправки трафика выбирается запись, префикс которой дает наибольшее совпадение разрядов с адресом назначения входящего пакета. В основе предлагаемого метода лежит представление таблиц маршрутизации с помощью систем булевых функций. При этом префиксам из таблицы маршрутизации сопоставляются элементарные конъюнкции, а каждому множеству записей, имеющих одинаковые длины префиксов k и следующий узел u, ставится в соответствие отдельная булева функция.

Таблица 1. Фрагмент таблицы маршрутизации

Префикс	Узел
172.68.20.16/24	1
172.68.0.0/16	2
67.118.0.0/16	2
128.116.0.0/16	3

Так, например, записи, соответствующие фрагменту таблицы маршрутизации, который приведен в таблице 1, могут быть представлены совокупностью следующих функций:



=

=

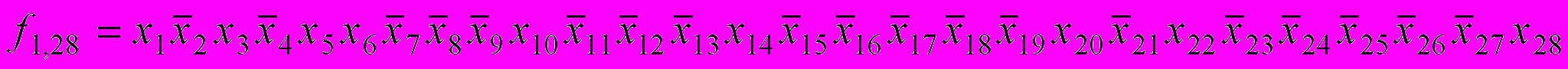
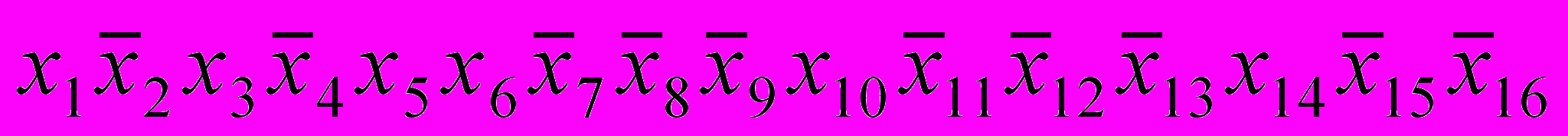
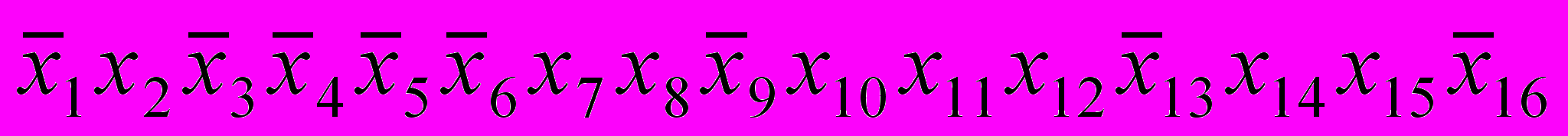
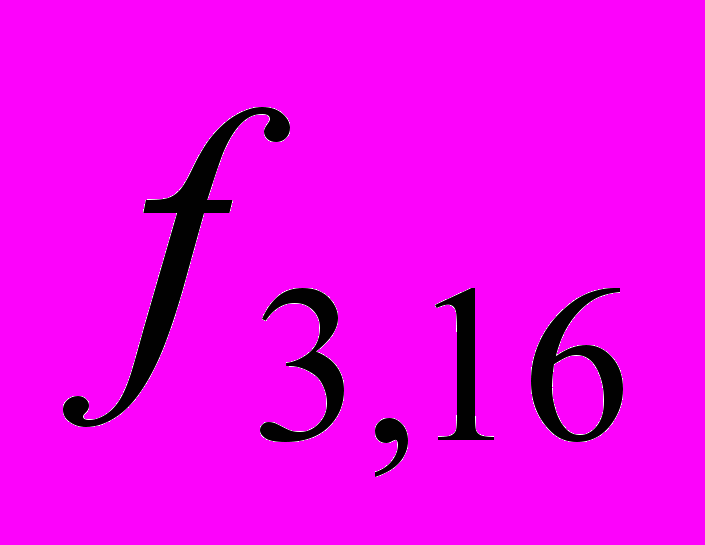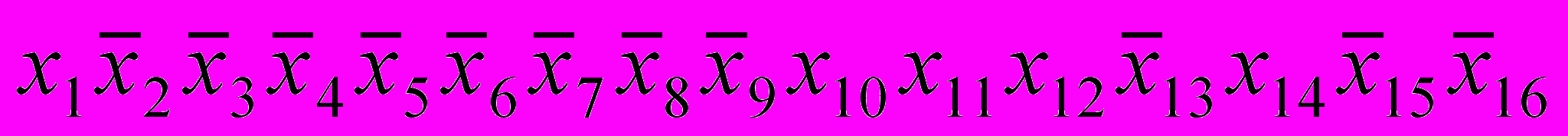
Предлагаемый метод уменьшения размера таблиц маршрутизации основан на объединении записей, отличающихся значением одного бита и имеющих один и тот же следующий узел. Метод может быть реализован с помощью использования тернарной ассоциативной памяти. Помимо индекса, являющегося побитовой записью префикса, TCAM хранят также отдельную маску для каждой записи. Маска определяет, какие из битов индекса являются активными (см. таблицу 2). Заметим, что записи 1 и 2 отличаются только значением 4-го бита и могут быть скомбинированы в запись (10100000, 11100000, 1)

Таблица 2. Таблица префиксов, хранящаяся в TCAM

Запись	Префикс	Маска	Следующий узел
1	10100000	11110000	1
2	10110000	11110000	1
3	11011000	11111000	2
4	10001000	11111000	3
5	10111000	11111000	2

Операции объединения записей осуществляются посредством запуска процедуры минимизации ДНФ (относительно количества конъюнкций) для каждой функции 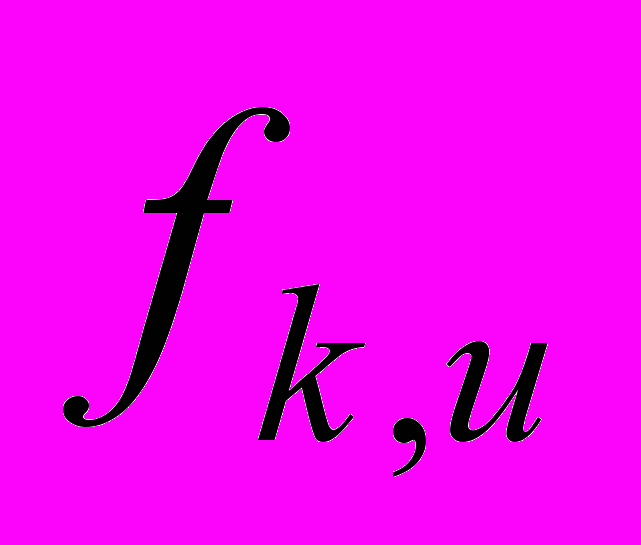. Такие преобразования, очевидно, не влияют на процесс маршрутизации, то есть выбор узла, на который необходимо отправлять трафик.

В диссертации был разработан ряд алгоритмов минимизации булевых функций в классе ДНФ, которые позволяют получить точное и приближенное решение задачи. Точный алгоритм использует классическую схему минимизации, предложенную Квайном и Маккласки⁶, которая состоит из двух этапов:

1. Генерация всех простых импликант функции;
   
2. Поиск минимального покрытия множества точек, в которых функция принимает значение 1, множеством простых импликант.
   

В зависимости от способа представления булевых функций и покрытий, существующие алгоритмы можно разбить на две группы – явные и неявные методы. Первые обрабатывают дискретные объекты последовательно, храня каждый из них в отдельной области памяти. При этом количество таких объектов может достигать значительных величин, например, верхняя граница количества всех простых импликант - 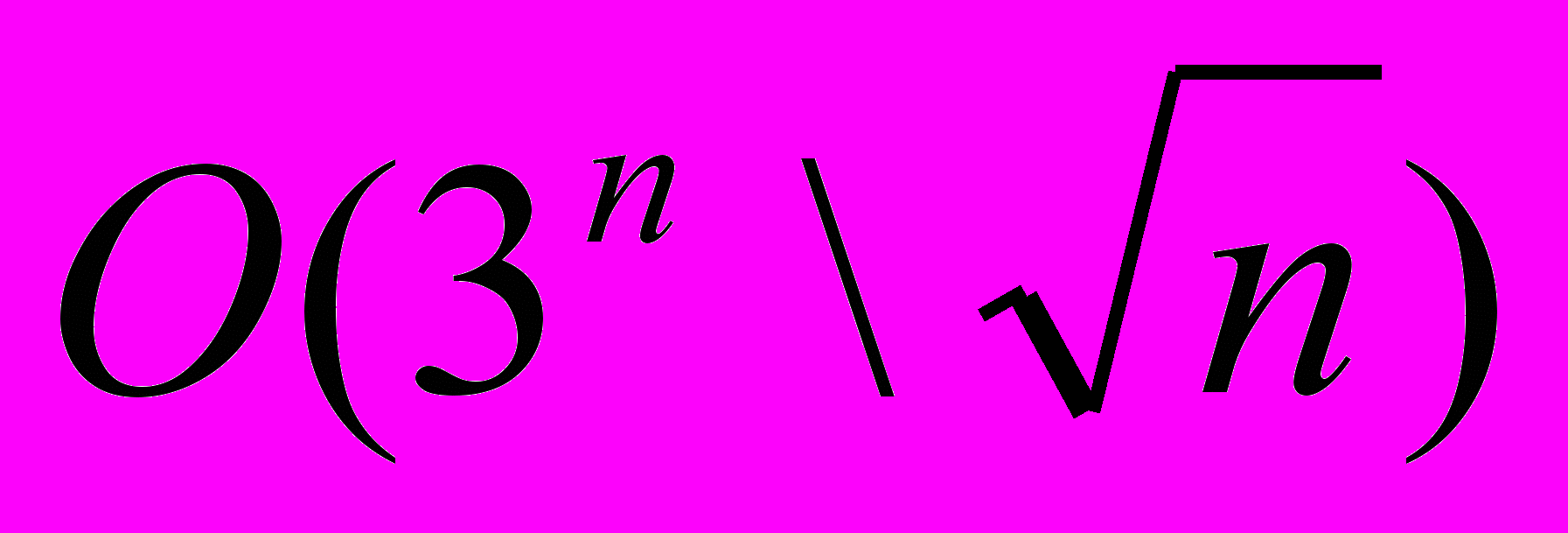⁷, что ограничивает сферу применения таких алгоритмов задачами небольшой размерности. Неявные же алгоритмы используют разделяемое представление для дискретных объектов, размер которого не зависит линейно от их количества. Традиционно в качестве такого представления используются двоичные диаграммы решения.

Предлагаемый в диссертационной работе алгоритм минимизации использует для представления булевых функций упорядоченные двоичные диаграммы решения (OBDD), а для покрытий – двоичные диаграммы с отбрасыванием незначащих нулей (ZDD)⁸.

Двоичные диаграммы решения (BDD) были выбраны в связи с тем, что они сочетают в себе два полезных качества – приемлемый расход памяти и, как правило, быстрое выполнение операций над реализуемыми функциями. Упорядоченная двоичная диаграмма решений (OBDD) для заданных функции 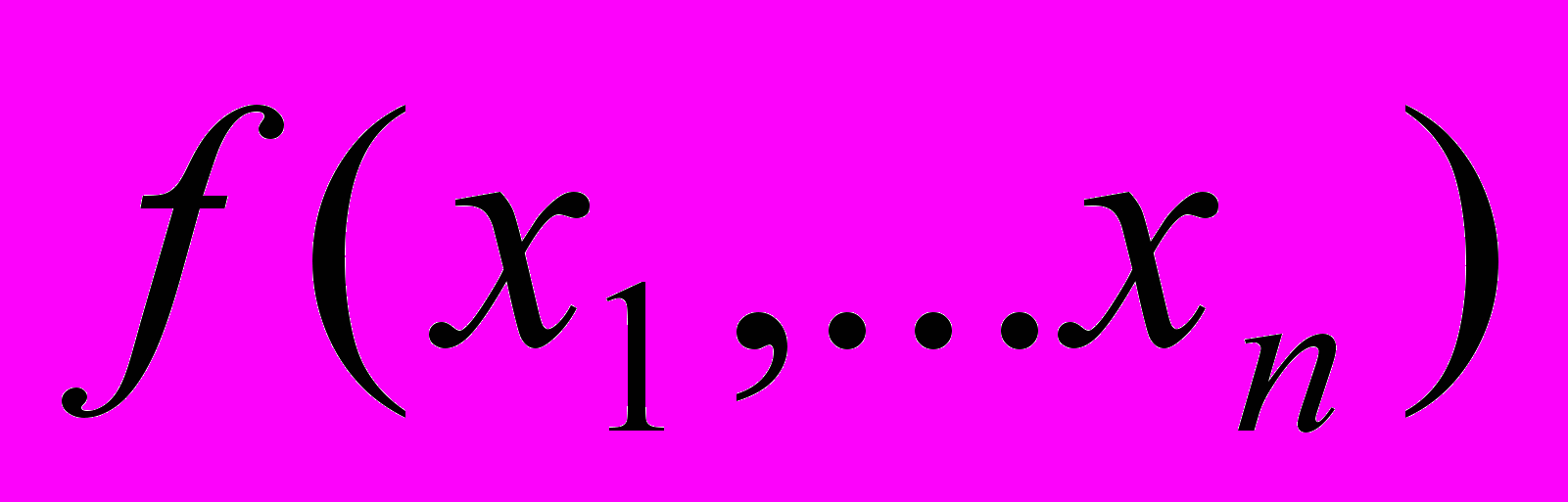и отношения порядка 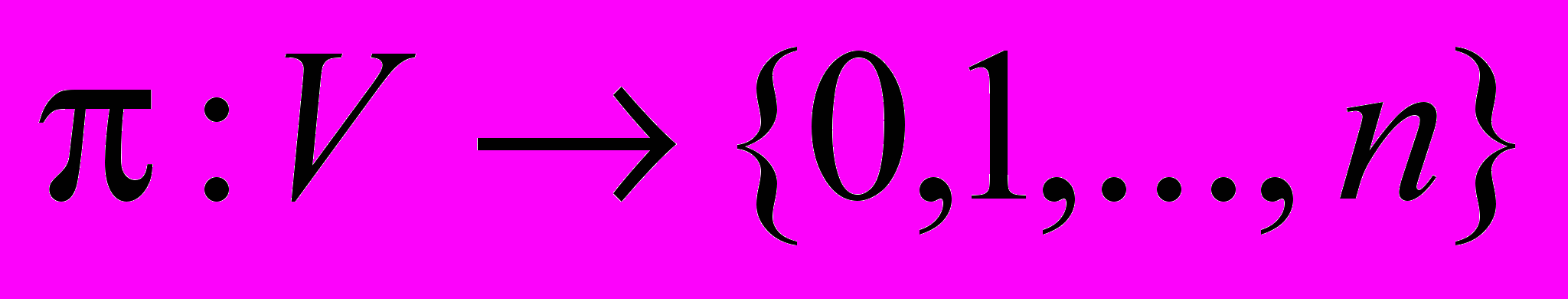, где 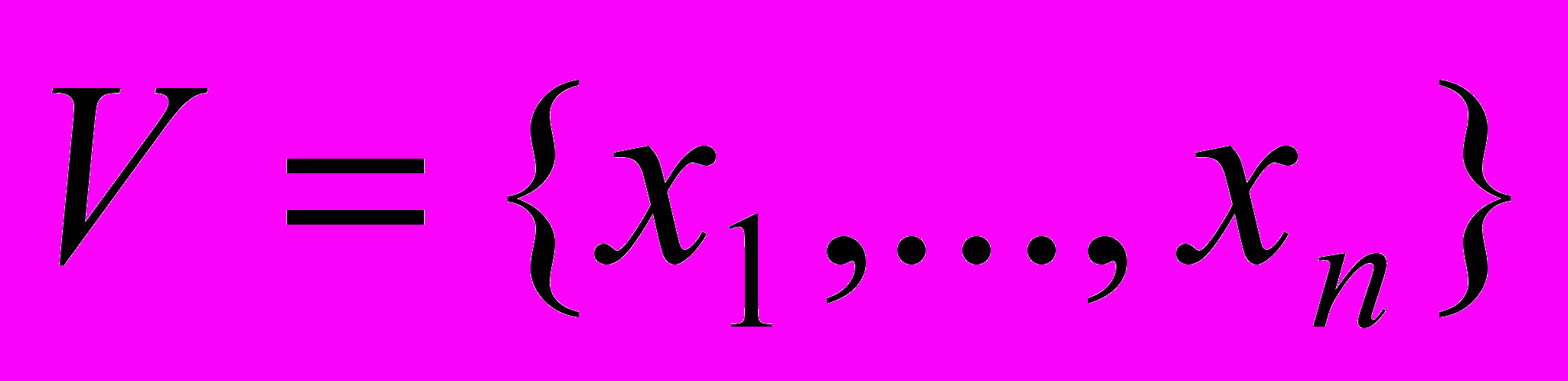– это направленный ацикличный граф, состоящий из нетерминальных вершин, отмеченных переменными из V и терминальными вершинами, отмеченными булевыми константами 1 и 0. Каждая нетерминальная вершина имеет два исходящих ребра – 1-ребро и 0-ребро. Начальный узел OBDD называется корнем. Для вычисления значения функции на заданном наборе значений переменных формируется путь от корня к терминальной вершине следующим образом: если переменная соответствующая текущей вершине принимает значение 1, то выбирается 1-ребро, в противном случае – 0-ребро. В сформированном пути каждая переменная встречается не более одного раза. На пути от корня к терминальной вершине, переменные встречаются в соответствии с заданным отношением порядка .

Двоичные диаграммы решения реализуют разделяемое представление для дискретных объектов, размер которого не зависит линейно от их количества. Пример OBDD-представления приведен на рис. 1, на котором 0-ребра изображены заштрихованной линией, а 1-ребра – обычной.

Для уменьшения размера OBDD применяют следующие правила:

1. совмещение изоморфных подграфов;
   
2. удаление узлов, оба исходящих узла которых указывают на один и тот же узел.
   

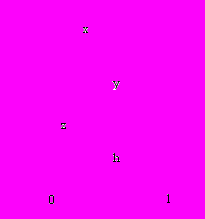
Рис 1. OBDD–представление для функции

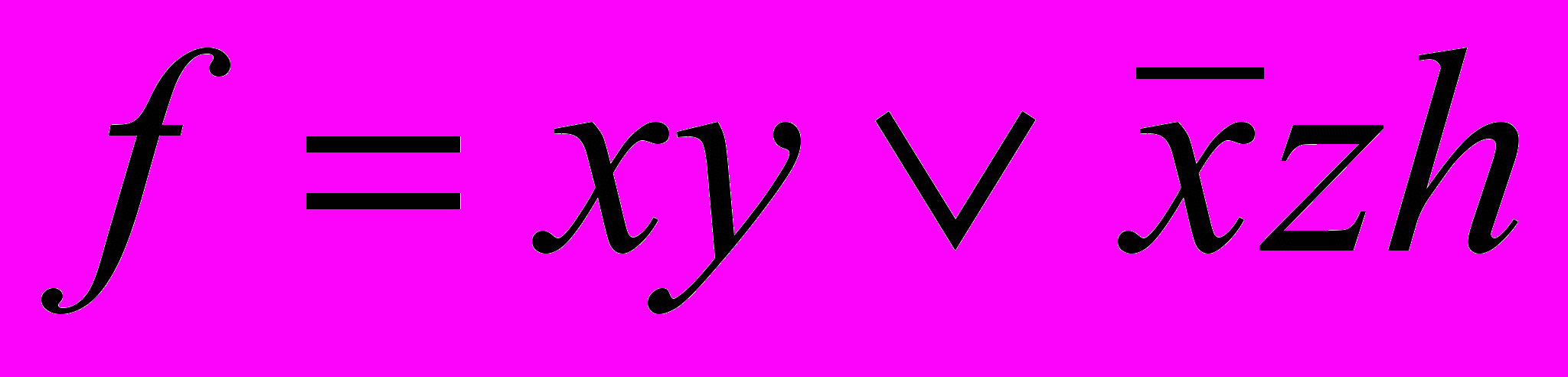
В случае двоичных диаграмм с отбрасыванием незначащих нулей (ZDD), первое правило сохраняется, а вместо удаления вершин, исходящие ветви которых указывают на один узел, удаляются узлы с единичным выходом, указывающим на 0. Данная разновидность диаграмм решения более эффективна, по сравнению с OBDD, для представления разреженных множеств, в частности, покрытий булевых функций.

Задача построения минимальной ДНФ рассматривается как задача о покрытии. Пусть M обозначает множество всех точек 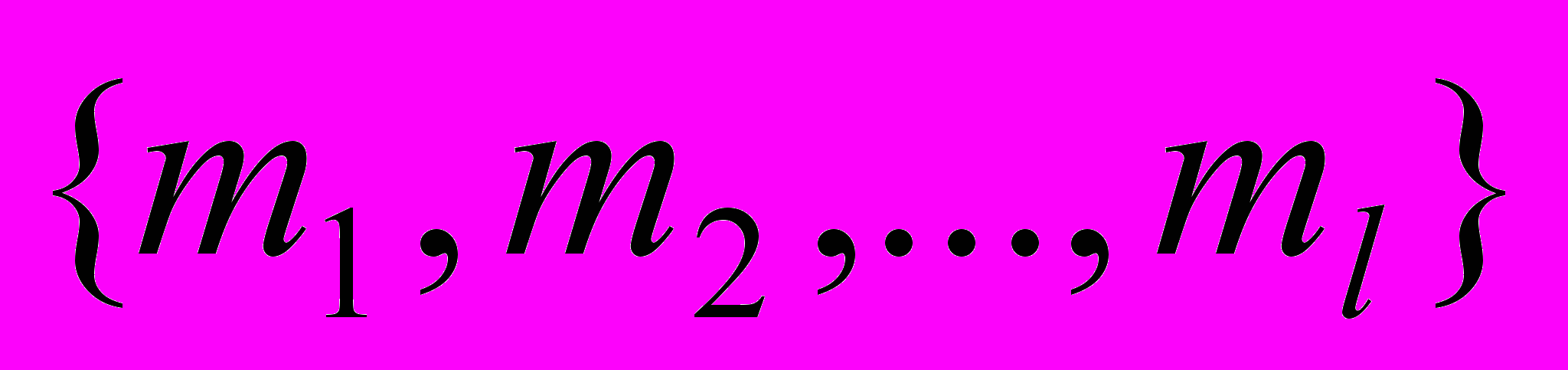, на которых заданная функция f принимает значение 1, а 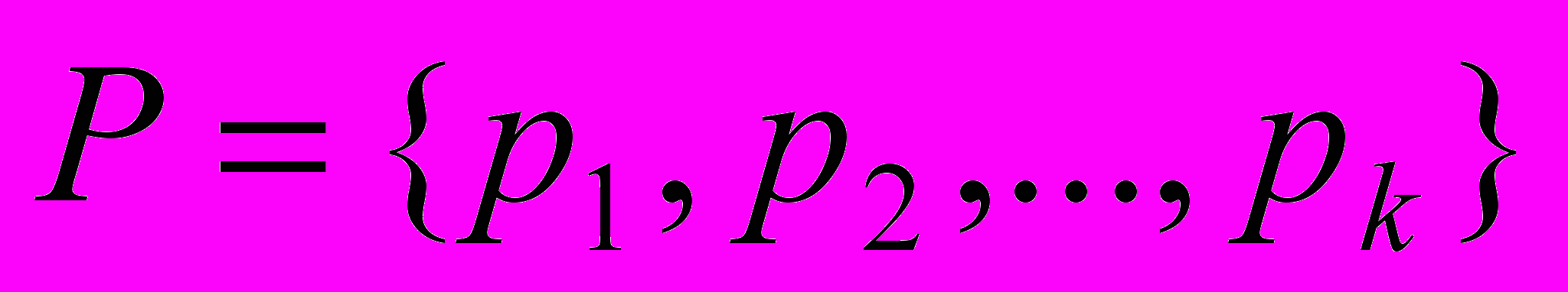– множество всех простых импликант f. Матрицей покрытия будем называть бинарную матрицу A размерности 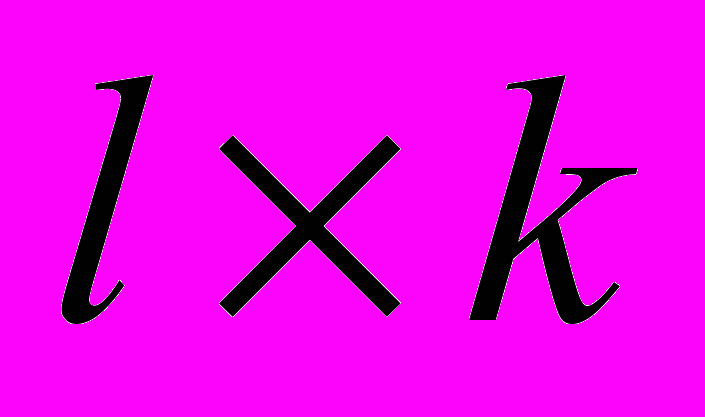такую, что A_ij=1 (при этом будем говорить, что j-й столбец покрывает i-ю строку), 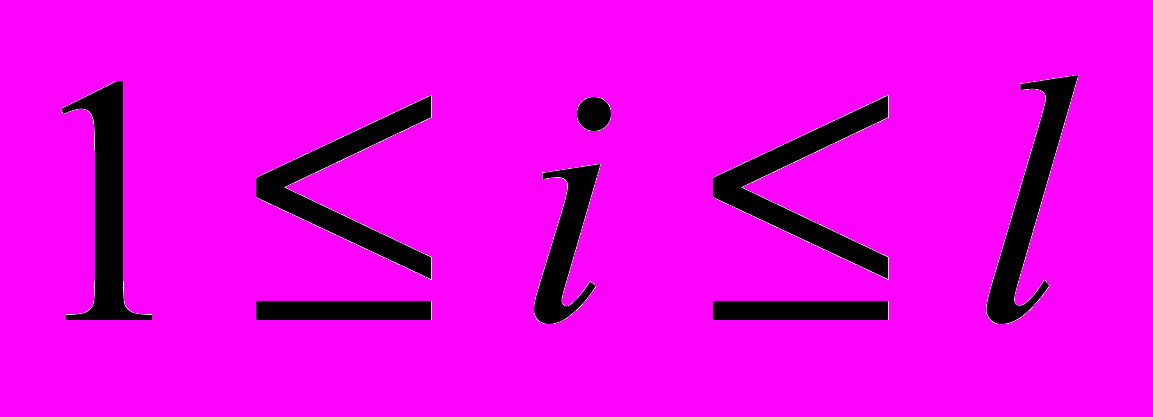, , 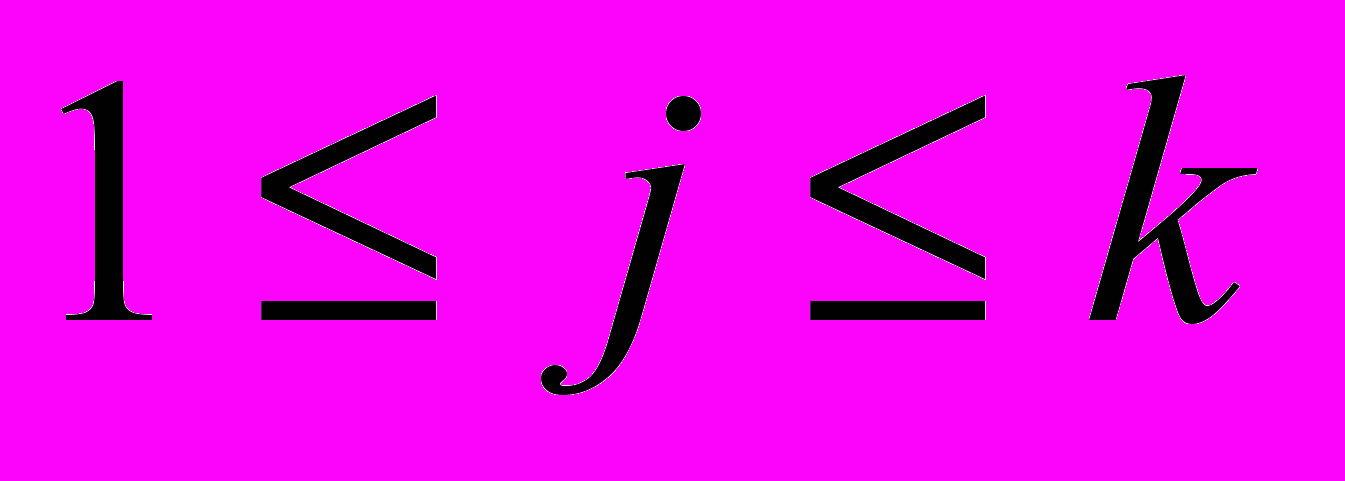если 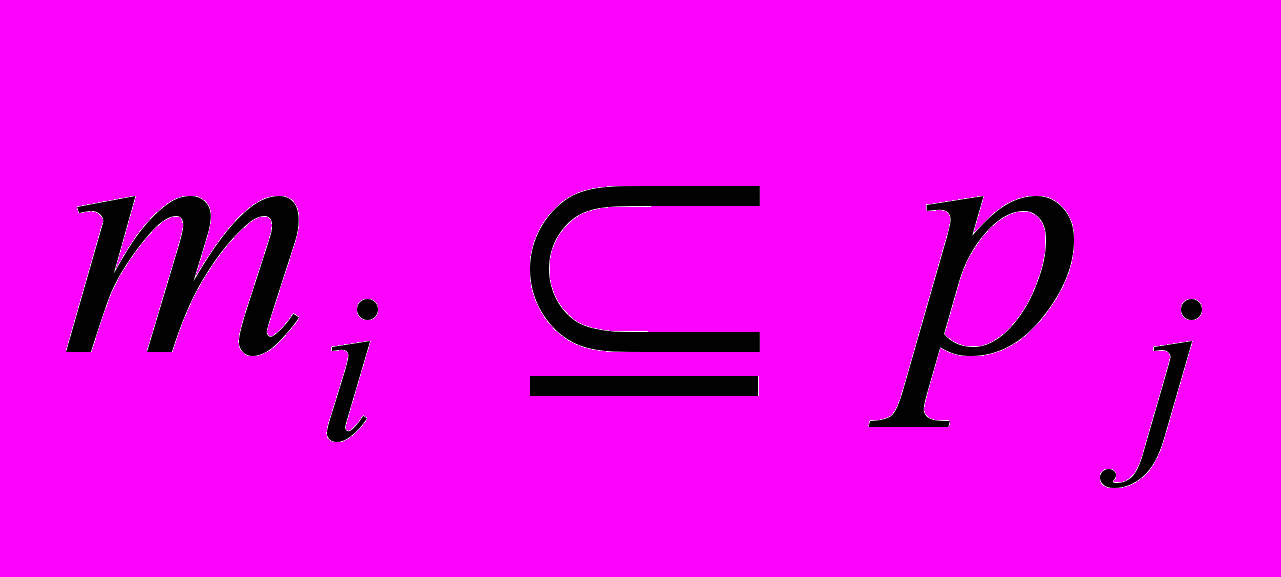, в противном случае A_ij=0. Требуется найти минимальное количество столбцов, покрывающих все строки матрицы A. В диссертации был использован ряд методов, позволяющих уменьшить размерность решаемой задачи о покрытии за счет удаления доминируемых строк и столбцов, а также выделения ядра. При этом, строка m_i доминирует строку m_j, если любой столбец матрицы A покрывающий m_i, покрывает также m_j, столбец p_k доминирует столбец p_l, если p_k покрывает все строки, покрываемые p_l. Ядру минимизируемой булевой функции соответствует множество столбцов K, таких, что 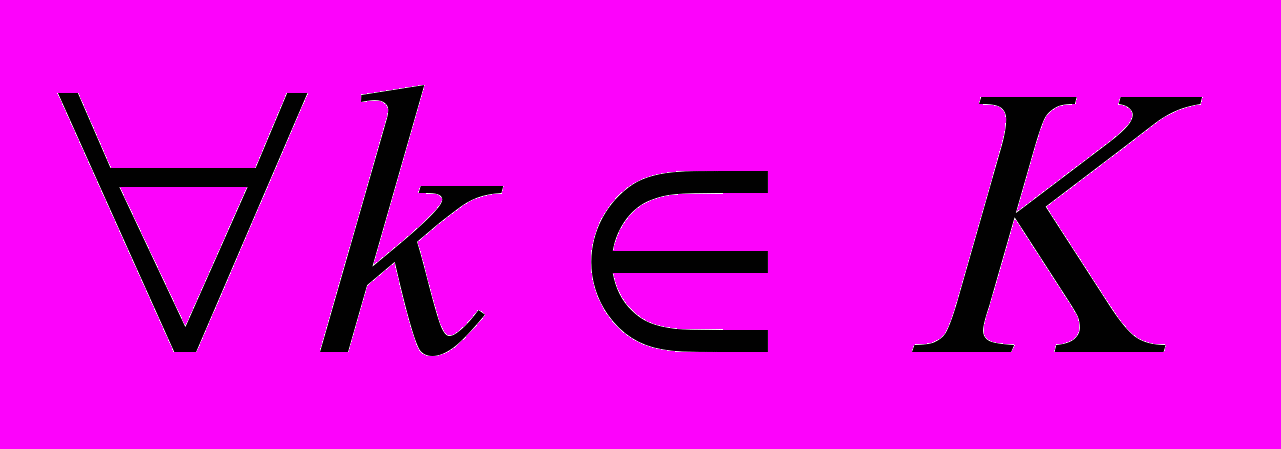найдется строка 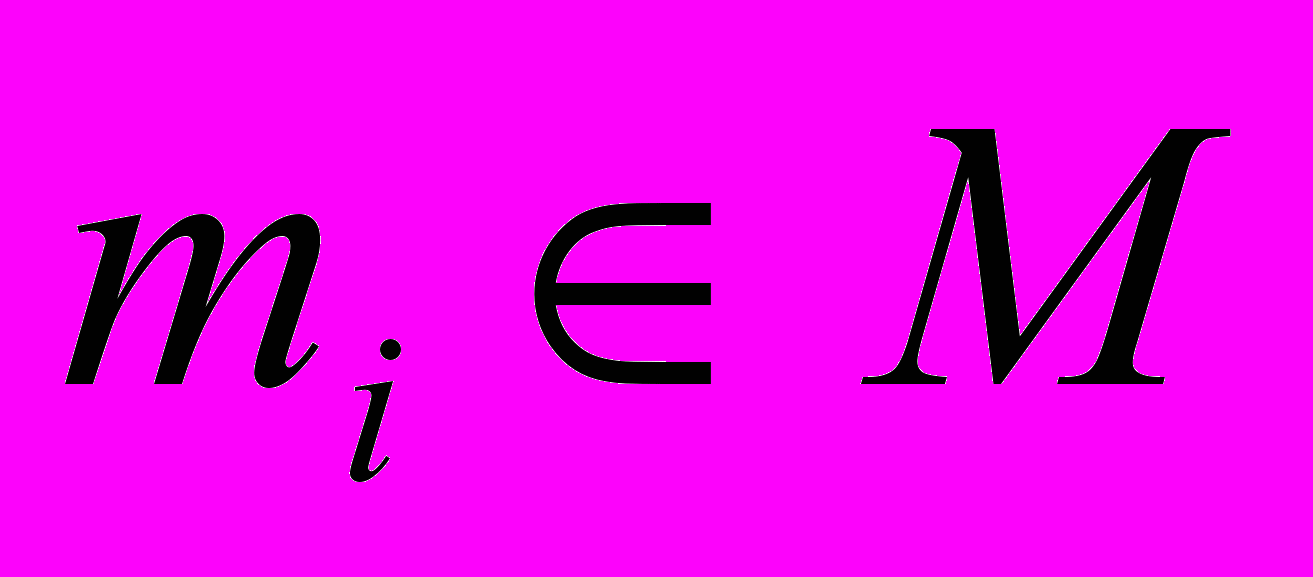, которая покрывается только k.

Генерация простых импликант, а также удаление доминируемых строк и столбцов осуществлялись с помощью методов, предложенных Коудертом и Мадре⁹. Обобщенная схема разработанного алгоритма приведена на рис. 2.



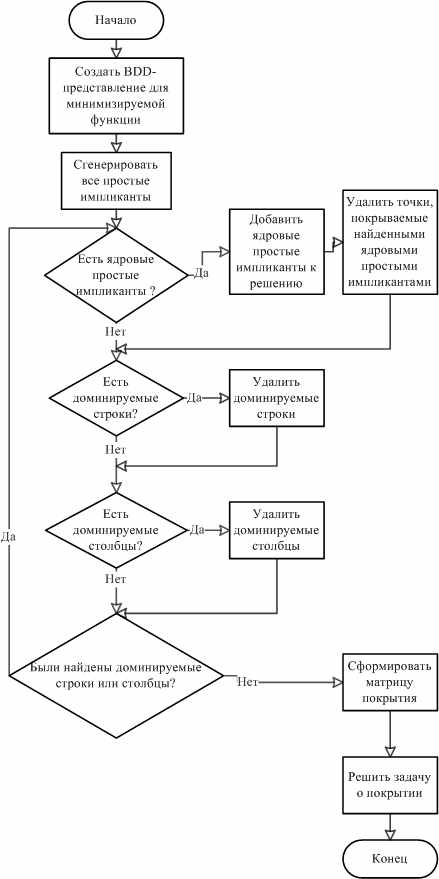
Рис. 2. Схема точного алгоритма минимизации ДНФ

Процесс построения минимального покрытия основан на применении метода ветвей и границ. Данный алгоритм исследует древовидную модель пространства решений. Корень R поискового дерева соответствует множеству всех возможных покрытий. Ветви, выходящие из корня, определяются выбором одного столбца матрицы покрытия, обозначим его y. Важнейшим этапом метода ветвей и границ является процедура ветвления, заключающаяся разделении исходного множества R на два подмножества, одно из которых состоит из решений, содержащих y, другое – из решений, не содержащих y. В поисковом дереве, каждому из этих подмножеств соответствует вершина ( 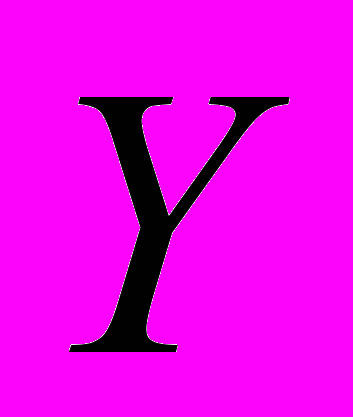и 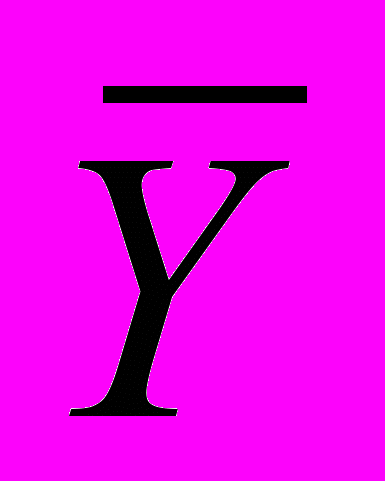, соответственно), для которой R является родителем. Далее процедура запускается для обеих сгенерированных вершин. С каждой вершиной связывается нижняя граница стоимости w любого покрытия из множества, представленного вершиной. Вычисление этих нижних границ – основной фактор, дающий экономию в вычислениях. Предположим, что стоимость текущего оптимального решения равна m. Если нижняя граница, связанная с множеством покрытий, представленных вершиной v_k, w(v_k)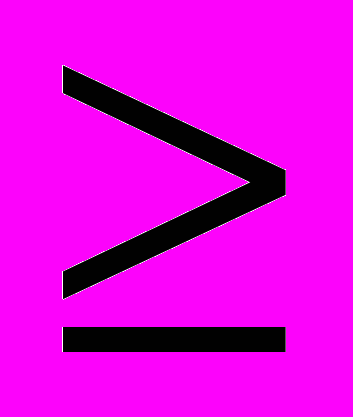m, то до конца процесса поиска минимального покрытия не нужно рассматривать вершину v_k и все следующие за ней. Основными факторами, влияющими на эффективность метода ветвей и границ, являются: выбор столбца для ветвления, способ получения нижних и верхних границ.

Столбец для ветвления выбирается в соответствии с эвристическим алгоритмом¹⁰, позволяющим быстрее находить оптимальные решения, по сравнению с альтернативными подходами, рассматриваемыми в литературе:


.


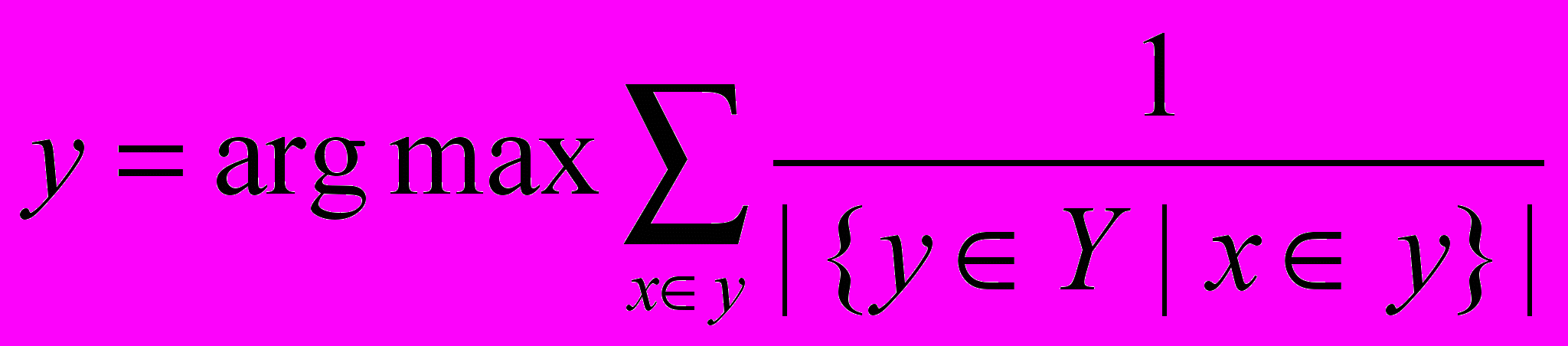Для вычисления нижних границ, задача построения минимального покрытия рассматривается, как задача целочисленного линейного программирования:




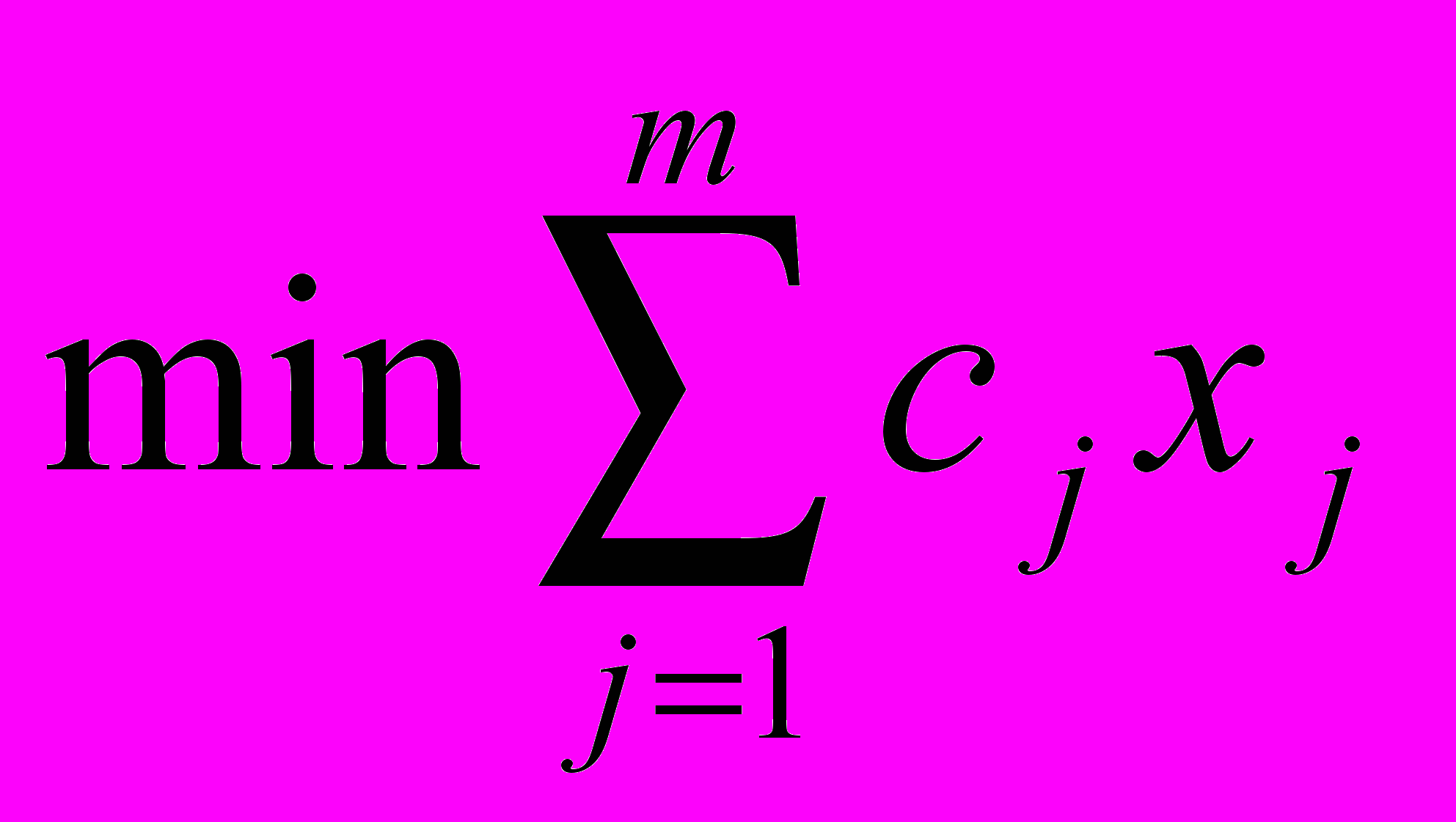
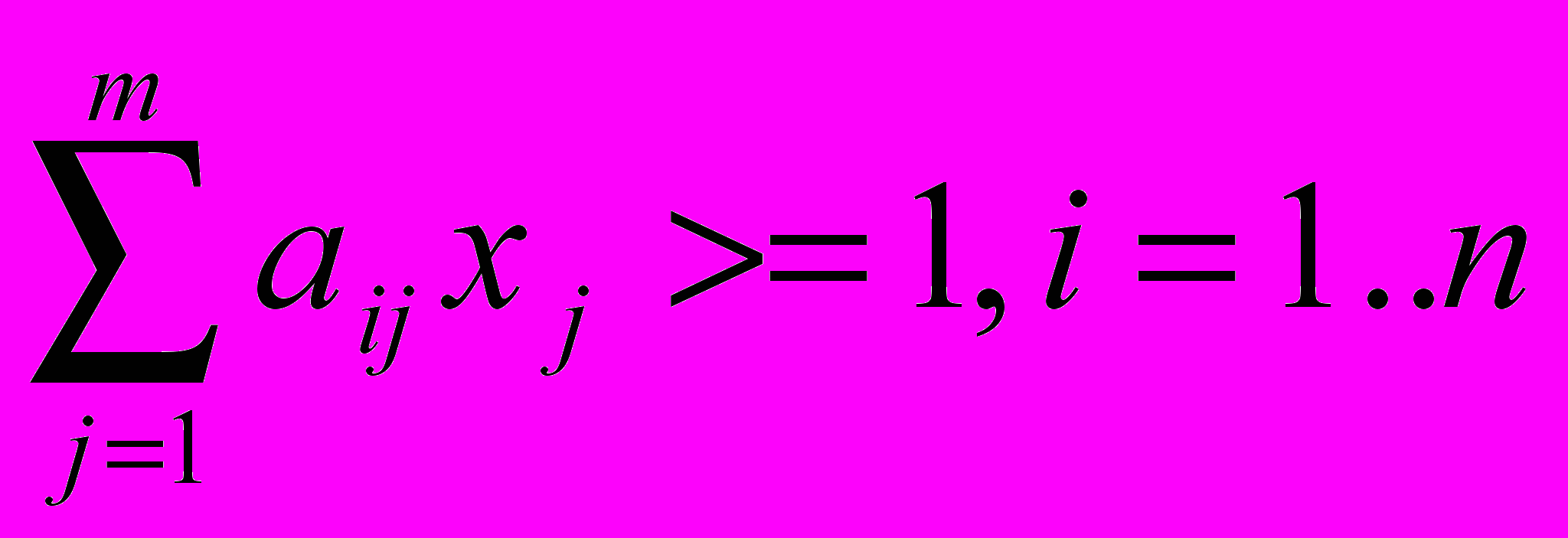(1)




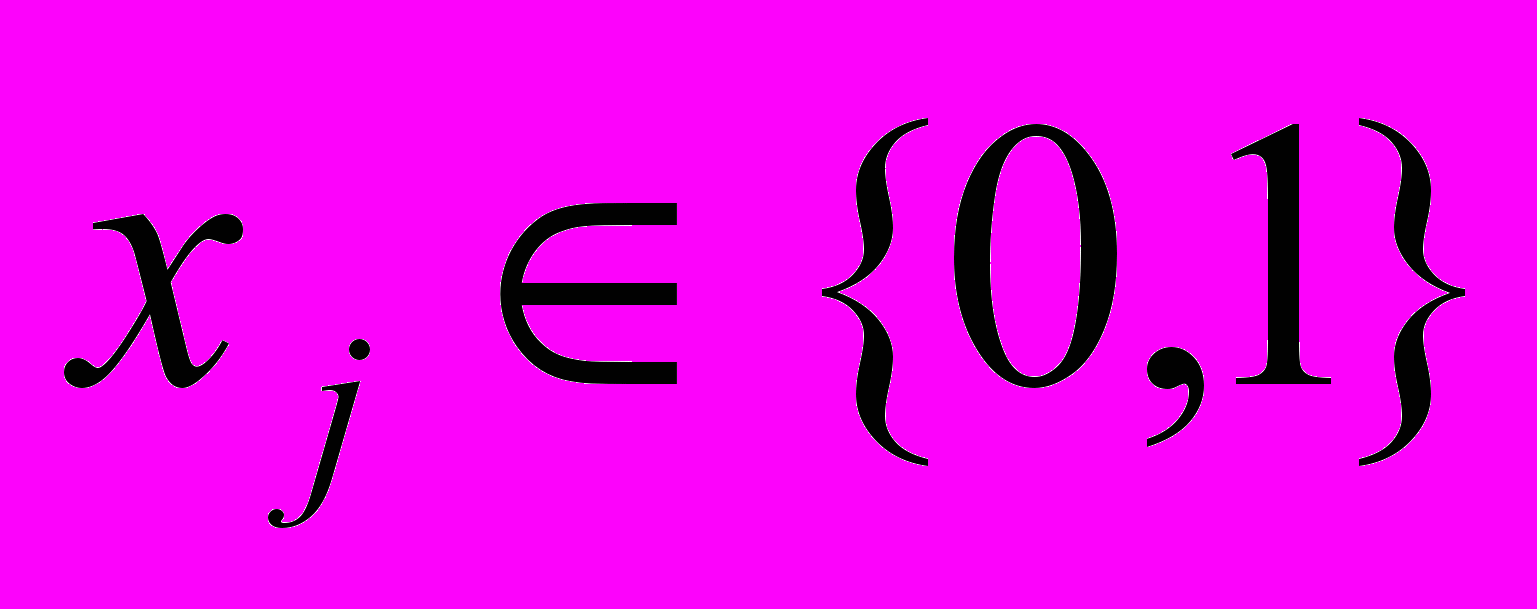
Очевидно, что решение релаксированной задачи

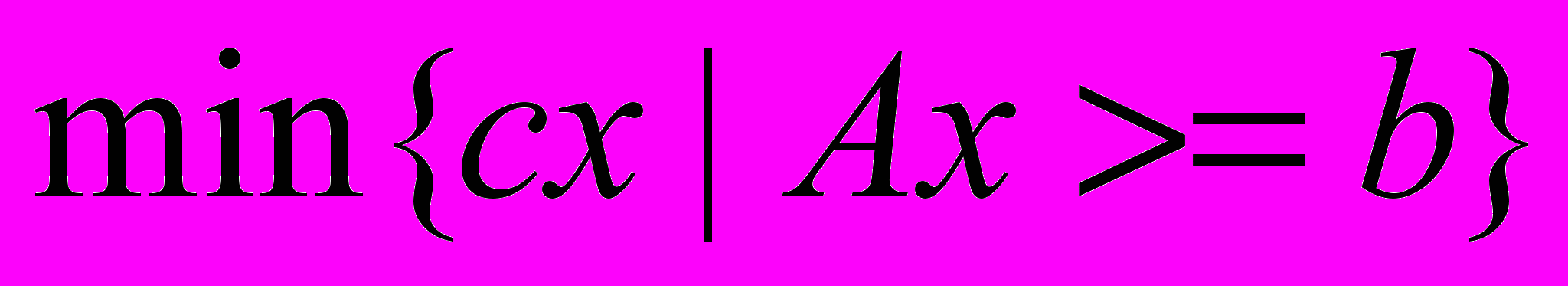, (2)

где b – единичный вектор, дает нижнюю границу для (1).

Для решения релаксированной задачи был использован двойственный симплекс-метод. Необходимо заметить, что в процессе работы алгоритма ветвей и границ, не нужно решать (2) для каждой новой вершины заново. Вместо этого к симплекс-таблице, соответствующей родительскому узлу, добавляется ограничение x_j=1, либо x_j=0, а двойственный симплекс-метод применяется к обновленной таблице.

Схема метода ветвей и границ, основанная на получении нижних границ с помощью решения релаксированной задачи была предложена в работе¹¹. Тем не менее, алгоритмы минимизации ДНФ, разработанные в данных работах, используют явную технику оперирования с дискретными объектами, которая во многих случаях не позволяет сгенерировать все простые импликанты и построить упрощенную матрицу покрытия. Предлагаемый алгоритм использует те же алгоритмы для вычисления нижних границ, однако для представления булевых функций и множеств объектов используются двоичные диаграммы решения.

Следующий важный фактор, влияющий на объем вычислений – это получение точных верхних границ. Для исходной задачи верхняя граница может быть найдена, например, с помощью алгоритмов локального поиска¹², либо на основе использовании релаксации Лагранжа¹³. В процессе работы алгоритма ветвей и границ верхняя граница не возрастает, на конкретном шаге она равна стоимости лучшего найденного решения. Основываясь на данном факте, был разработан модифицированный метод ветвей и границ. На первом шаге вычисляется нижняя граница задачи k и запускается метод ветвей и границ с установленной верхней границей, равной k. Если будет найдено решение, то оно является оптимальным и алгоритм останавливается, в противном случае, снова запускается метод ветвей и границ с верхней границей, равной k+1 и т.д. Разработанный алгоритм построения минимального покрытия minCP приведен на рис. 3.



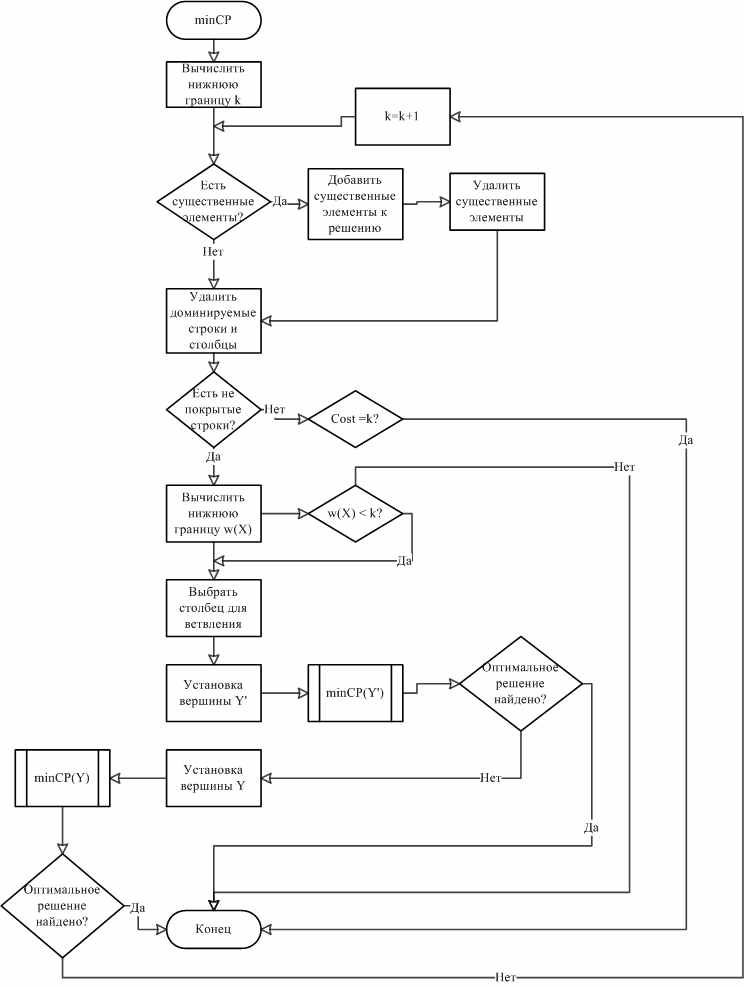
Рис. 3. Схема алгоритма построения минимального покрытия

Во второй главе описывается разработанный приближенный алгоритм минимизации ДНФ (рис. 4). Алгоритм использует двухуровневое представление термов минимизируемой функции, основанное на выделении у термов префиксов длины k и последующей группировке по ним. Таким образом, исходное множество термов T разбивается на несколько блоков. Количество таких блоков равно числу уникальных префиксов длины k в множестве T. Процесс минимизации осуществляется посредством итеративного выполнения следующих этапов: выбор блока; генерация множества всех простых импликант 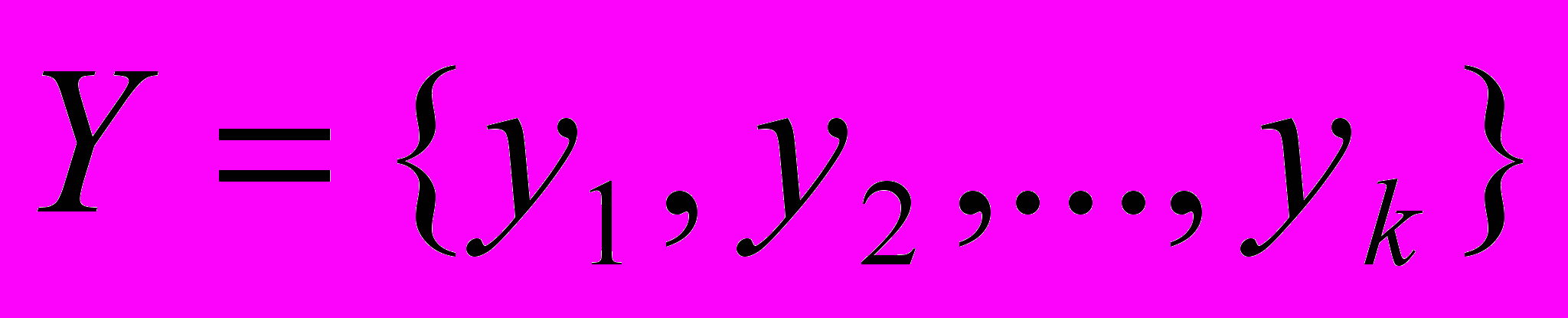, покрывающих термы из данного блока; решение задачи о покрытии, в матрице которой столбцам соответствуют простые импликанты из Y, а строкам – термы, содержащиеся хотя бы в одном элементе Y. Данная процедура продолжается до тех пор, пока не останется ни одного блока, содержащего не покрытые термы. Результатом минимизации является объединение решений всех сгенерированных задач о покрытии. Генерация простых импликант выполняется за счет склеивания термов. Для решения задачи о покрытии использовался метод ветвей и границ. Реализация быстрого поиска термов основана на использовании хеширования. Данный алгоритм минимизации ориентирован на применение к задаче сжатия таблиц маршрутизации и наиболее эффективен для функций с большим количеством конъюнкций в исходном ДНФ представлении.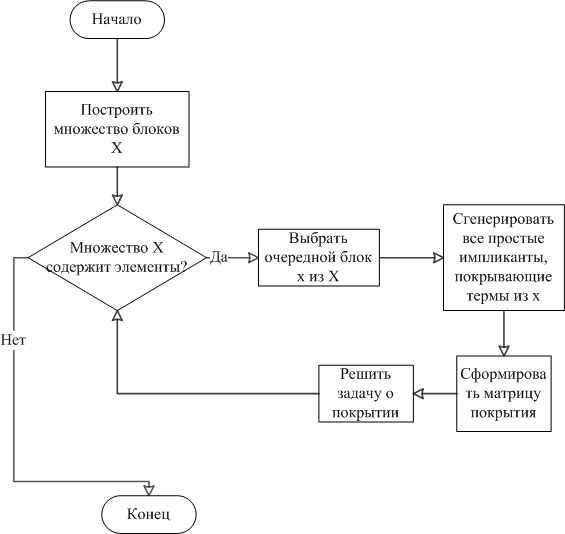



Рисунок 4. Схема приближенного алгоритма минимизации ДЕФ

В третьей главе рассматриваются вопросы программной реализации разработанных алгоритмов, а также полученные экспериментальные оценки их качества.

Первый раздел третьей главы посвящен логическому моделированию программной системы уменьшения таблиц маршрутизации. Построение модели позволяет выявить основные требования, желаемую структуру и поведение системы, не вдаваясь, при этом, в детали реализации. В качестве средства графического моделирования был выбран язык UML¹⁴, являющийся в настоящее время стандартом де-факто в области средств визуального проектирования. В рамках данной диссертации были использованы следующие диаграммы UML, отражающие основные аспекты проектируемой системы: диаграмма вариантов использования (Use Case Diagram), диаграмма классов (Class Diagram) и диаграмма последовательности) действий (Sequences Diagram).

Приведено описание разработанного программного комплекса, его основные характеристики. Программная реализация была выполнена на языке C++ и скомпилирована с помощью gcc версии 3.

Проведено сравнение предлагаемых методов минимизации булевых функций в классе ДНФ с двумя известными минимизаторами – Espresso и Rondo. Эксперименты проводились на компьютере с процессором Intel Pentium 2.6 Ггц, и оперативной памятью 1 Гб. В качестве входных данных использовались псевдослучайно сгенерированные примеры и набор MCNC Benchmarks.

На рисунках 5 и 6 приведена зависимость времени работы алгоритмов от количества простых импликант функции и от количества термов в исходном представлении функции, полученная для псевдослучайно сгенерированных входных данных. На задачах большой размерности (с количеством простых импликант больше 50000 и с количеством термов больше 800) наилучшие результаты показывает алгоритм MINDNF. Суммарное время его работы в 1,23 раз меньше, чем у Rondo, и в 2,24 раз – чем у Espresso, для функций с числом простых импликант большим 50000 и с количеством термов большим 800 такое отношение составляет – 1,32 и 3,18, соответственно.



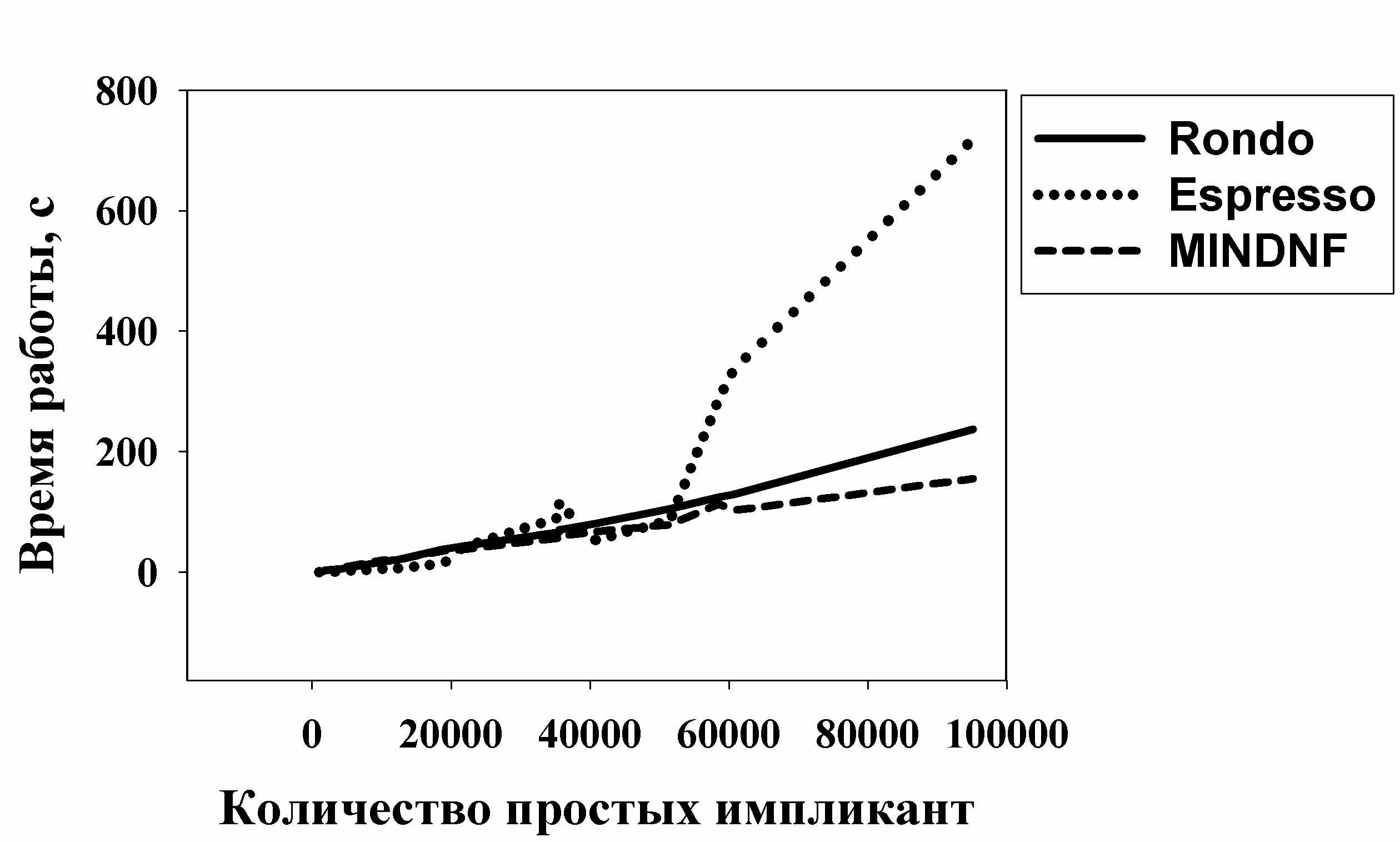
Рис 5. Зависимость времени работы от количества простых импликант



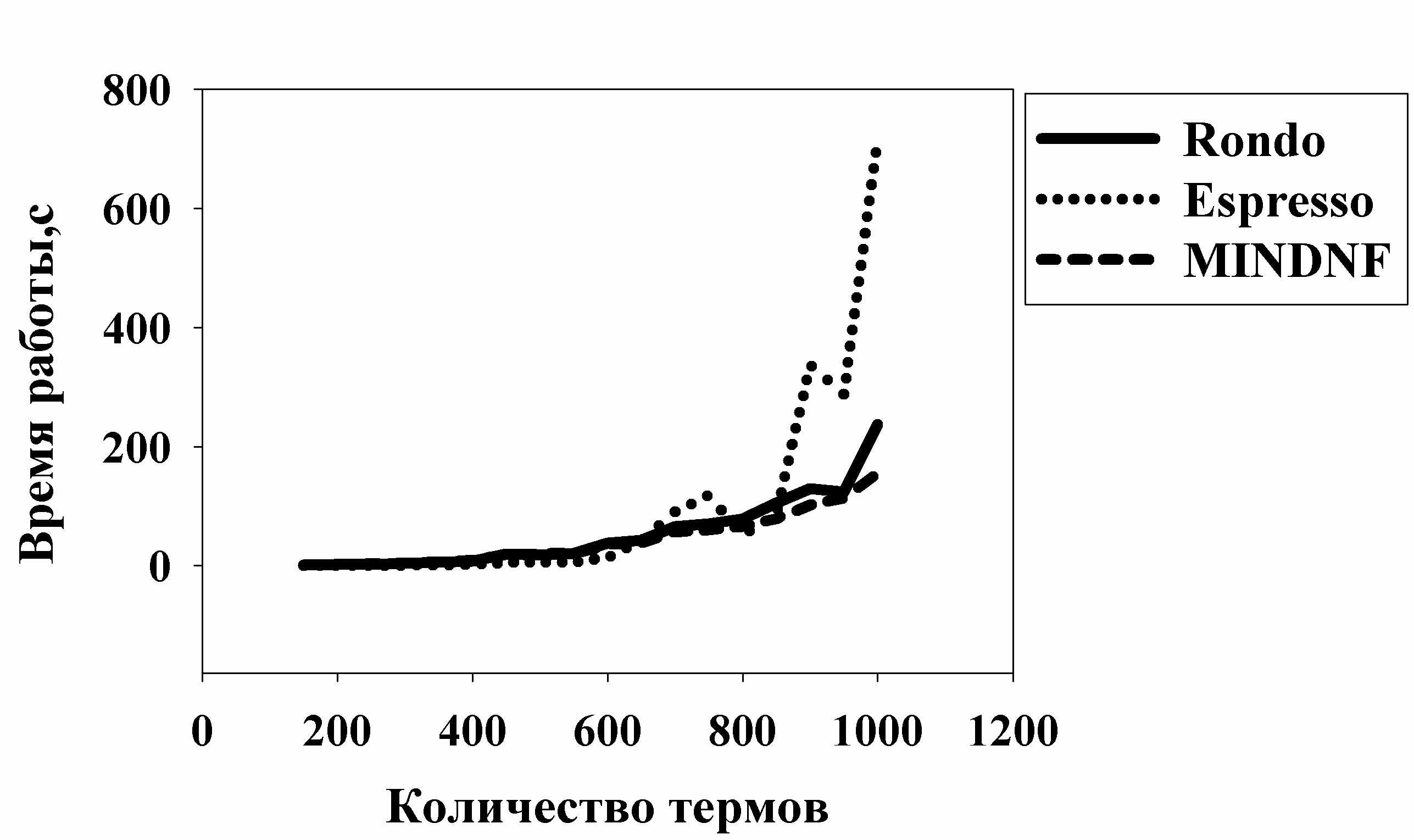
Рис 6. Зависимость времени работы от количества термов

Результаты экспериментов для задач из набора MCNC Benchmarks приведены в таблице 3. При этом для систем булевых функций использовалось представление в виде характеристической булевой функции. Были исследованы две версии предлагаемого алгоритма MINDNF, отличающиеся процедурой вычисления верхних границ – в таблице им соответствуют столбцы TCP1 (метод последовательного увеличения верхней границы) и TCP2 (получение верхней границы на основе локального поиска ). При этом было установлено ограничение на время работы – 1 час. С помощью espresso за данное время не удалось найти решение ни для одной из задач. Программа Rondo не нашла решения для 4 задач, отмеченных *. Оба варианта MINDNF нашли решения для всех приведенных задач, при этом суммарное время, затраченное алгоритмом, использующим метод последовательного увеличения верхней границы в 1.7 раз меньше, чем у традиционного подхода.

Исследование предлагаемого метода оптимизации размера таблиц маршрутизации проводилось на оборудовании и данных, предоставленных провайдером «АйПи Телеком» (г.Ульяновск), а также в качестве тестовых данных были использованы таблицы маршрутизации из нескольких крупных точек обмена интернет-трафиком – PAIX и Mae-West.

Приведены результаты сравнения времени работы предлагаемых методов MINDNF (точный), MINDNF_A(приближенный) и классического метода espresso-exact, который использовался в большинстве работ по сокращению таблиц маршрутизации. Суммарное время минимизации при использовании MINDNF_A в 3.35 раз меньше, по сравнению с MINDNF, и в 71.2 - по сравнению с espresso-exact. Стоимость решений, получаемых с помощью MINDNF_A на 2-3% больше стоимости оптимальных решений. Данные результаты показывают, что предлагаемые методы можно использовать для оптимизации таблиц маршрутизации в режиме реального времени, в том числе и для обработки изменений в таблицах маршрутизации, которые могут происходить каждые 30-60 секунд.

Таблица 3. Сравнение алгоритмов минимизации ДНФ на наборе MCNC Benchmarks

Название	I	O	Количество простых импликант	Rondo		MINDNF
				TCC	TCP	TCC	TCP1	TCP2
ex5*	8	63	2532	6.3	T	9.3	76.55	90.94
ibm	48	17	1047948792	0.53	0	0.72	0	0
jbp	36	57	2496809	3	0.08	2.17	0.08	0.06
mainpla	27	54	87692	83.9	0	176.41	0	0
max1024*	10	6	1278	0.7	T	0.84	216.41	400.2
misg	56	23	6499491840	0.27	0	0.34	0	0
misj	35	14	139103	0.145	0	0.17	0	0
pdc	16	40	28231	4.15	2.1	4.14	2.06	2.58
prom2*	9	21	2635	14.5	T	17.72	10.58	54
shift	19	16	165133	1.54	0	0.53	0	0
signet	39	8	78735	6.48	0	6.41	0	0
soar*	83	94	330477287437440	30.8	T	15.2	49.5	58.73
ti	47	72	836287	3.2	0.4	3.83	0.34	0.33
ts10	22	16	524281	0.5	0	0.58	0	0
x7dn	66	15	566698632	19.2	2.3	8.55	4.72	4.63
xparc	41	73	15039	5.3	0.01	4.2	0.11	0.09

I – число входных переменных

O - число выходных переменных

TCC - время построения упрощенной матрицы (сек)

TCP - время поиска минимального покрытия (сек)

На основании проведенного компьютерного моделирования были построены оценки влияния применения разработанного метода на скорость поиска записей в таблицах маршрутизации, а также на энергопотребление маршрутизатора.

Как указывалось в постановке задачи диссертации, одной из проблем, которые решаются в рамках задачи уменьшения размера таблиц маршрутизации является уменьшение времени поиска записей в таблице маршрутизации. Данная операция напрямую зависит от среднего времени доступа к памяти, определяющегося как

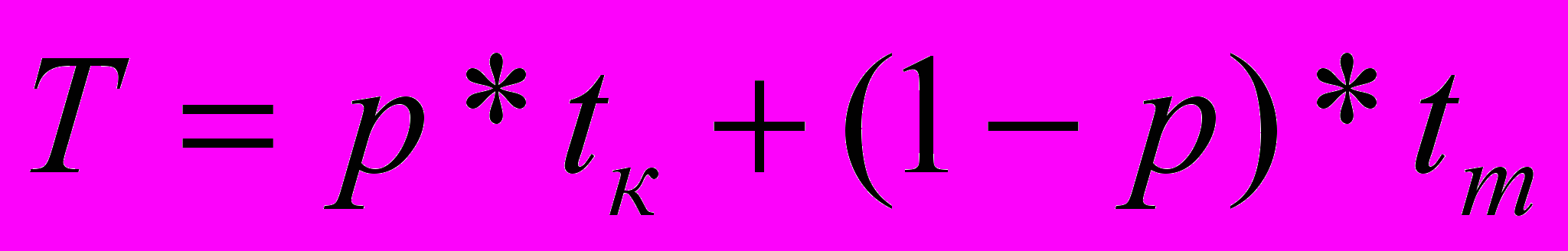, (3)

где p – вероятность успешного обращения к кешу,

t – время доступа к памяти кеша,

t – время доступа к памяти основной таблицы маршрутизации,

Проведенные экспериментальные исследования показали, что коэффициент уменьшения таблиц маршрутизации в среднем составляет 1.8. Это приводит к тому, что увеличивается число успешных обращений к кешу, т.е. в формуле (3) возрастает значение p, что приводит к уменьшению времени поиска записи в таблице маршрутизации на 3-5% . Еще одним важным практическим результатом является снижение энергопотребления маршрутизатора, за счет уменьшения на 40-45% энергопотребления модулей памяти, которое линейно зависит от количества хранимых записей.

В заключении приведены основные выводы по диссертации, сформулированы полученные научные и практические результаты, состоящие в следующем:

1. Разработка эффективных схем хранения и поиска записей в таблицах маршрутизации является важнейшим этапом построения быстродействующих сетей. Уменьшение размера таблиц маршрутизации позволяет уменьшить энергопотребление модулей памяти и увеличить скорость обработки входящих пакетов.
   
2. По результатам сравнительного анализа работ, связанных с уменьшением размера таблиц маршрутизации, были выявлены основные недостатки известных подходов, а также выбрана математическая модель таблиц маршрутизации, основанная на использовании аппарата булевых функций.
   
3. Разработаны быстродействующие алгоритмы минимизации булевых функций в классе дизъюнктивных нормальных форм, показана возможность их применения для уменьшения размера таблиц маршрутизации большой размерности в режиме реального времени. Предложенный метод может быть реализован с помощью использования в качестве аппаратной базы тернарной ассоциативной памяти.
   
4. Разработанные алгоритмы реализованы в программном комплексе, предназначенном для уменьшения размера таблиц маршрутизации в IP-сетях. Проведено компьютерное моделирование предложенных алгоритмов, на основании которого показано, что применение на практике разработанного подхода позволяет уменьшить размер таблиц маршрутизации в среднем в 1.8 раз, приводит к снижению энергопотребления модулей памяти на 40-45%, а также к увеличению количества успешных обращений к кэшу, что дает в итоге уменьшение среднего времени поиска записей таблицы маршрутизации на 3-5%.
   

СПИСОК ПУБЛИКАЦИЙ ПО ТЕМЕ ДИССЕРТАЦИИ


В изданиях из списка ВАК:

1. Смагин А.А., Шиготаров А.В. Метод оптимизации таблиц маршрутизации // Инфокоммуникационные технологии, Самара, 2009. –т. 7, № 3. – с. 14-17.
   
2. Смагин А.А., Шиготаров А.В. Применение методов минимизации булевых функций в классе дизъюнктивных нормальных форм для оптимизации цифровых устройств // Известия Самарского научного центра РАН. Самара. Изд-во Самарского научного центра РАН, 2009. – т. 11, № 3(2). – с. 343-349.
   

В других изданиях:

3. Шиготаров А.В., Кукин Е.С. Об одном алгоритме минимизации дизъюнктивных нормальных форм // Автоматизация процессов управления – Ульяновск. ФНПЦ ОАО «НПО МАРС», 2008 №4(14) – с. 12-16.
   
4. Шиготаров А.В. Алгоритмы минимизации ДНФ // Ученые записки УлГУ. Серия Математика и информационные технологии / под ред. Смагина А.А. Выпуск 1. – Ульяновск, 2007. – с. 43-46.
   
5. Шиготаров А.В. Анализ и классификация методов сжатия таблиц маршрутизации // Техника и Технология.–Москва. Изд-во Спутник-Плюс, 2009. – № 5. – с. 31-33.
   
6. Шиготаров А.В. Неявные алгоритмы минимизации булевых функций в классе дизъюнктивных нормальных форм // Техника и Технология.–Москва. Изд-во Спутник-Плюс, 2009. – № 5. – с. 34-36.
   
7. Шиготаров А. В. О некоторых методах сокращения перебора в задаче минимизации булевых функций в классе дизъюнктивных нормальных форм // Материалы Шестой Всероссийской научно-практической конференции (с участием стран СНГ) «Современные проблемы создания и эксплуатации радиотехнических систем». – Ульяновск, 2009. – с. 91-93.