Geum.ru

Календарно-тематическое планирование Алгебра 7 класс

Вид материалаУрок

Содержание


Глава 1. Математический язык. Математическая модель.
Простейшие комбинаторные задачи
Подобный материал:

Календарно-тематическое планирование

Алгебра 7 класс


При 5 уроках в неделю сентябрь-октябрь и 3 уроках ноябрь-май

(120 уроков в год)

Учебник: Алгебра 7 Автор: А.Г. Мордкович

Задачник: Алгебра 7 Авторы: А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина, Е.Е. Тульчинская




№

урока


Тема урока

Кол-

во

уроков
Дата

проведения.
Причина и дата пропуска и дата ликвидации
Тип урока,

Форма контроля
Требования общеобразовательного минимума

знаниz , умения

Использование ИКТ




1 триместр.


















1
Повторение
1
02.09












2
Входная контрольная работа
1
03.09















Глава 1. Математический язык. Математическая модель.
15
















3
Числовые и алгебраические выражения.
4
06.09






Знать:

-понятие числового выражения;

-понятие алгебраического выражения, переменная, значения числового выражения, значения выражения с переменными;

-допустимые значения переменных;

-термины «математический язык», «математическая модель»;

-понятие о трех этапах математического моделирования.

Уметь:

- выполнять арифметические операции с обыкновенными и десятичными дробями, с положительными и отрицательными числами;

-находить числовые значения арифметических и алгебраических выражений;

-решать линейные уравнения;

-составлять математические модели реальных ситуаций (простейшие случаи);

-описывать реальные ситуации, соответствующие заданной математической моделью;

-реализовывать три этапа математического моделирования в простейших ситуациях.



4
Числовые и алгебраические выражения.



07.09









5
Числовые и алгебраические выражения.



08.09









6
Числовые и алгебраические выражения.



09.09









7
Что такое математический язык.
2
10.09









8
Что такое математический язык.



13.09









9
Что такое математическая модель
3
14.09









10
Что такое математическая модель



15.09









11
Что такое математическая модель



16.09









12
Линейное уравнение с одной переменной
3
17.09









13
Линейное уравнение с одной переменной



20.09









14
Линейное уравнение с одной переменной



21.09









8.
Координатная прямая
2
22.09









9.
Координатная прямая



23.09









10.
Контрольная работа №1.
1
24.09












Глава 2. Линейная функция.
14









Знать:

-понятия координатной прямой, координатной плоскости, координат точек на прямой и плоскости;

-понятие линейного уравнения с двумя переменными и его решения;

-понятия линейной функции и ее углового коэффициента, прямой пропорциональности;

-описание словами алгоритмов построении графиков прямой пропорциональности, линейной функции, линейного уравнения с двумя переменными;

-характеристики взаимного расположения на координатной плоскости графиков двух линейных функций, заданных аналитически.

Уметь:

-находить координаты точки в координатной плоскости, строить точки по ее координатам;

-строить графики уравнений х=а, у=b, у=kx, y=kx+m,ax+by+c=0;

-преобразовывать линейное уравнение с двумя переменными к виду линейной функции;

-находить точки пересечения графиков двух линейных уравнений, двух линейных функций;

-находить наибольшее и наименьшее значение линейной функции на заданном числовом промежутке.



11
Координатная плоскость.
2
27.09









12
Координатная плоскость.



28.09









13
Линейное уравнение с двумя переменными его график.
3
29.09









14
Линейное уравнение с двумя переменными его график.



30.09









15
Линейное уравнение с двумя переменными его график.



01.10









16
Линейная функция и её график.
3
04.10









17
Линейная функция и её график.



05.10









18
Линейная функция и её график.



06.10









19
Прямая пропорциональность.
2
07.10









20
Прямая пропорциональность.



08.10









21
Взаимное расположение графиков линейных функций.
3
11.10









22
Взаимное расположение графиков линейных функций.



12.10









23
Взаимное расположение графиков линейных функций.



13.10









24
Контрольная работа №2.
1
14.10












Глава 3. Системы двух линейных уравнений с двумя неизвестными.
14









Знать:

- понятия системы двух линейных уравнений с двумя переменными и ее решения;

-описание словами графического метода решения системы, метода подстановки, метода алгебраического сложения.

Уметь:

- определять, является ли заданная пара чисел решением заданной системы уравнений или нет;

-решать системы двух линейных уравнений с двумя переменными графическим методом, методом подстановки, методом алгебраического сложения;

-решать задачи, сводящиеся к системам указанного вида.



25
Основные понятия
2
15.10









26
Основные понятия



18.10









27
Метод подстановки
4
19.10









28
Метод подстановки



20.10









29
Метод подстановки



21.10









30
Метод подстановки



22.10









31
Метод алгебраического сложения.
3
25.10









32
Метод алгебраического сложения.



26.10









33
Метод алгебраического сложения.



27.10









34
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.
4
28.10









35
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.



29.10









36
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.



08.11









37
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.



10.11









38
Контрольная работа №3.
1
12.11












Глава 4. Степень с натуральным показателем и её свойства.
8









Знать:

-понятия степени, основания степени, показателя степени;

-определение a 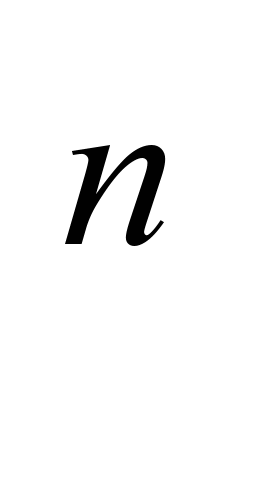в случае, когда n=1, и в случае, когда n –натуральное число, отличное от1;

-свойства степеней.

Уметь:

-вычислять a 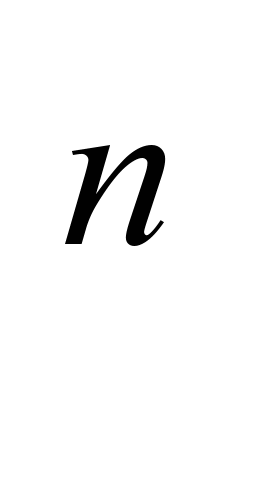для любых значений а и любых целых неотрицательных значений n;

-пользоваться таблицей основных степеней;

-использовать свойства степени для вычисления значений арифметических и алгебраических выражений, для упрощения алгебраических выражений.



39
Что такое степень с натуральным показателем.
1
15.11









40
Таблица основных степеней.
1
17.11









41
Свойства степени с натуральным показателем
2
19.11









42
Свойства степени с натуральным показателем



22.11









43
Умножение и деление степеней
2
24.11









44
Умножение и деление степеней



26.11









45
Степень с нулевым показателем
1
29.11












2 триместр.















46
Контрольная работа №4.
1
01.12












Глава 5. Одночлены. Арифметические операции над одночленами.
10









Знать:

-понятия одночлена, стандартного вида одночлена, коэффициента одночлена;

-понятия подобных одночленов;

-термины «алгоритм», «корректные», и «некорректные» задания»

-описание словами правила арифметических операций над одночленами.

Уметь:

- приводить одночлен к стандартному виду;

-складывать и вычитать подобные одночлены, умножать одночлены, возводить одночлены в натуральную степень;

-представлять заданный одночлен в виде суммы одночленов, в виде степени одночлена;

-делить одночлен на одночлен.



46
Понятие одночлена.
1
03.12









47
Стандартный вид одночлена.
1
06.12









48
Сложение и вычитание одночленов.
2
08.12









49
Сложение и вычитание одночленов.



10.12









50
Умножение одночленов.
2
13.12









51
Умножение одночленов.



15.12









52
Возведение одночлена в натуральную степень
1
17.12









53
Деление одночлена на одночлен.
2
20.12









54
Деление одночлена на одночлен.



22.12









55
Контрольная работа №5.
1
24.12












Глава 6. Многочлены. Арифметические операции над многочленами.
19









Знать:

- понятия многочлена, стандартного вида многочлена;

-уметь описывать словами правила выполнения арифметических операций над многочленами (сложение, вычитание, умножение многочлена на одночлен, умножение многочлена на многочлен);

-формулы сокращенного умножения и их словесное описание.

Уметь:

-приводить многочлен к стандартному виду;

-складывать и вычитать многочлены, приводить подобные члены, взаимно уничтожать члены многочлена;

-умножать многочлен на одночлен и на многочлен;

-применять формулы сокращенного умножения;

-делить многочлен на одночлен;

-решать уравнения, сводящиеся после выполнения арифметических операций над входящими в их состав многочленами, к уравнению вида ax=b;

-решать соответствующие текстовые задачи.



56
Основные понятия
1
27.12









57
Сложение и вычитание многочленов.
3
29.12









58
Сложение и вычитание многочленов.



10.01









59
Сложение и вычитание многочленов.



12.01









60
Умножение многочлена на одночлен.
2
14.01









61
Умножение многочлена на одночлен.



17.01









62
Умножение многочлена на многочлен.
3
19.01









63
Умножение многочлена на многочлен.



21.01









64
Умножение многочлена на многочлен.



24.01









65
Формулы сокращенного умножения.
6
26.01






Презент.

66
Формулы сокращенного умножения.



28.01









67
Формулы сокращенного умножения.



31.01









68
Формулы сокращенного умножения.



02.02









69
Формулы сокращенного умножения.



04.02









70
Формулы сокращенного умножения.



07.02






Презент.

71
Деление многочлена на одночлен.
3
09.02









72
Деление многочлена на одночлен.



11.02









73
Деление многочлена на одночлен.



14.02









74
Контрольная работа №6.
1
16.02












Глава 7. Разложение многочленов на множители.
21









Знать:

-понятия разложения многочлена на множители, тождества, тождественно равных выражений, тождественного преобразования выражения;

-описание словами сути метода вынесения общего множителя за скобки, метода группировки;

-формулы разложения на множители, связанные с формулами сокращенного умножения.

Уметь:

-использовать для разложения многочлена на множители метод вынесения общего множителя за скобки, метод группировки, формулы сокращенного умножения, метод выделения полного квадрата;

-использовать разложение на множители для решения уравнений, для рационализации вычислений, для сокращения алгебраических дробей.



75
Что такое разложение многочленов на множители и зачем оно нужно.
1
18.02









76
Вынесение общего множителя за скобки.
2
21.02









77
Вынесение общего множителя за скобки.



25.02









78
Способ группировки
3
28.02












3 триместр.















79
Способ группировки



02.03









80
Способ группировки



04.03









81
Разложение на множители с помощью формул сокращенного умножения
6
07.03









82
Разложение на множители с помощью формул сокращенного умножения



09.03









83
Разложение на множители с помощью формул сокращенного умножения



11.03









84
Разложение на множители с помощью формул сокращенного умножения



14.03









85
Разложение на множители с помощью формул сокращенного умножения



16.03






Презент.

86
Разложение на множители с помощью комбинации различных приемов
3
18.03









87
Разложение на множители с помощью комбинации различных приемов



21.03









88
Разложение на множители с помощью комбинации различных приемов



23.03









89
Сокращение алгебраических дробей.
3
04.04









90
Сокращение алгебраических дробей.



06.04









91
Сокращение алгебраических дробей.



08.04









92
Тождества.
2
11.04









93
Тождества.



13.04









94
Контрольная работа №7.
1
15.04












Глава 8. Функция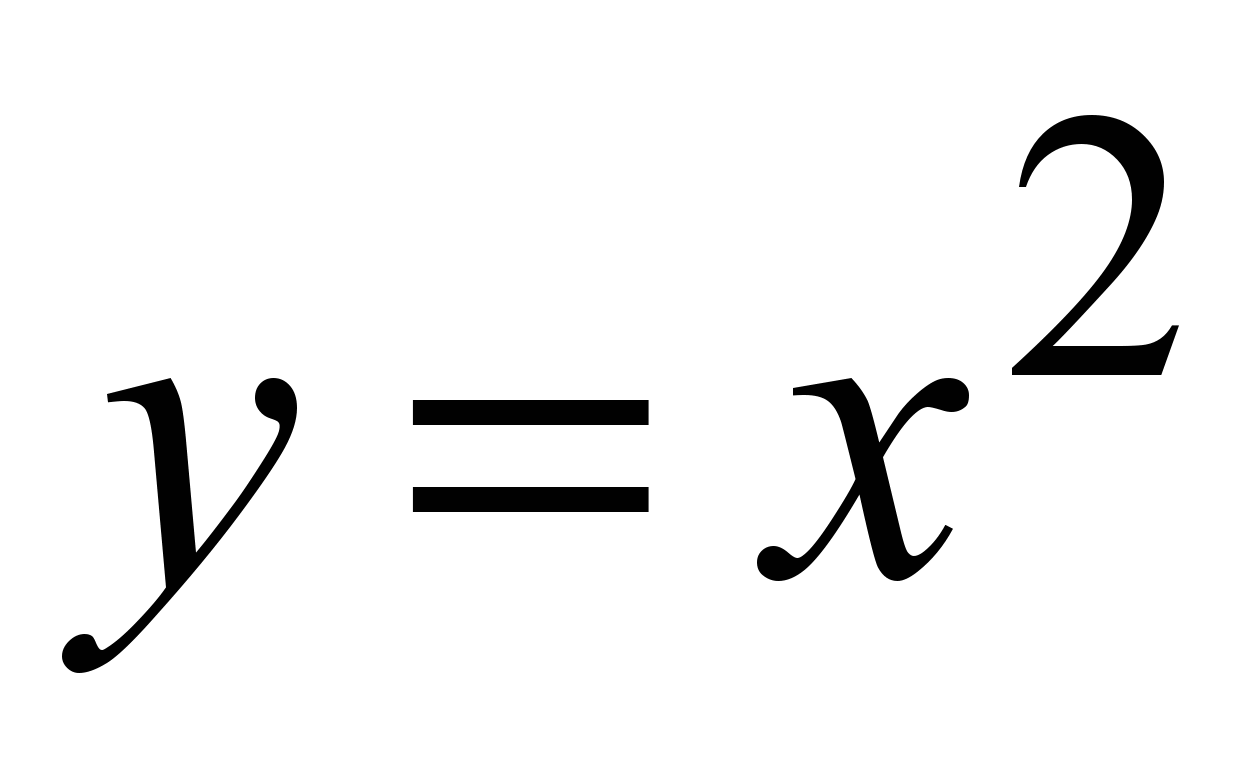

9









Знать:

-график функции y=x;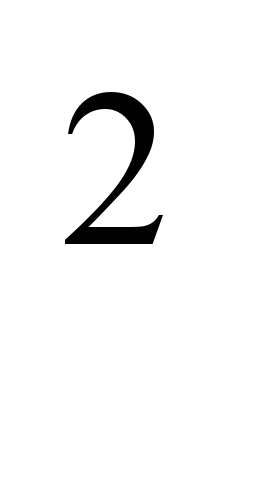

-описание словами процесса графического ре6шения уравнений и процесс построения графика кусочной функции;

-смысл записи y=f(x).

Уметь:

-вычислять конкретные значения и построение графика функции y=x;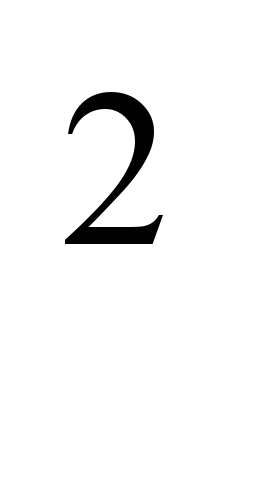

-строить графики функций, заданных различными формулами на различных промежутках;

-графически решать уравнения видаf(x)=g(x), где y=f(x) и у= g(x)-известные функции;

-находить наибольшие и наименьшие значения функции y=x 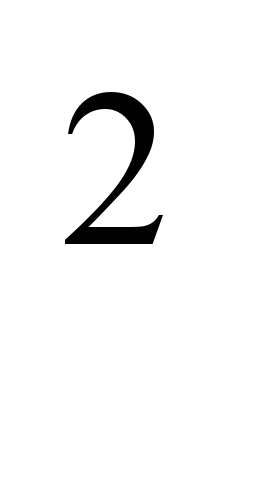на заданном промежутке;

-читать графики;

-решать примеры на функциональную символику.



95
Функция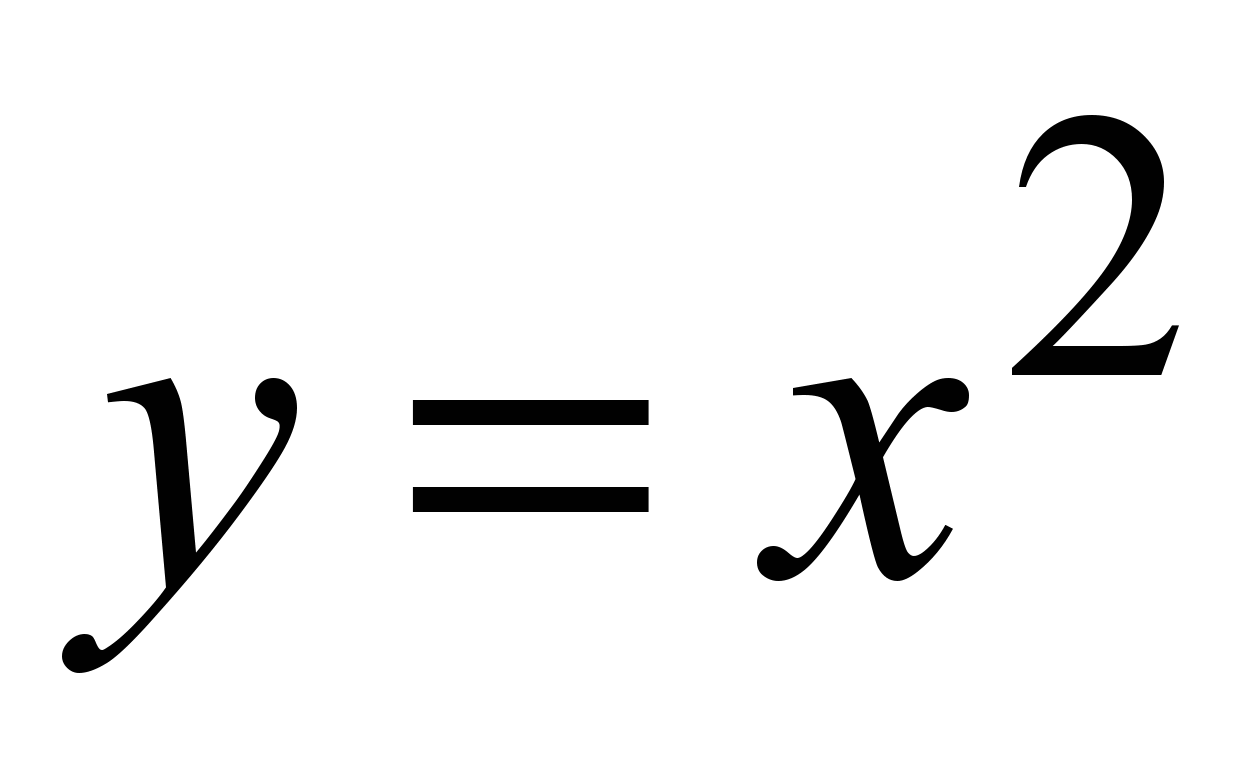

1
18.04









96
График функции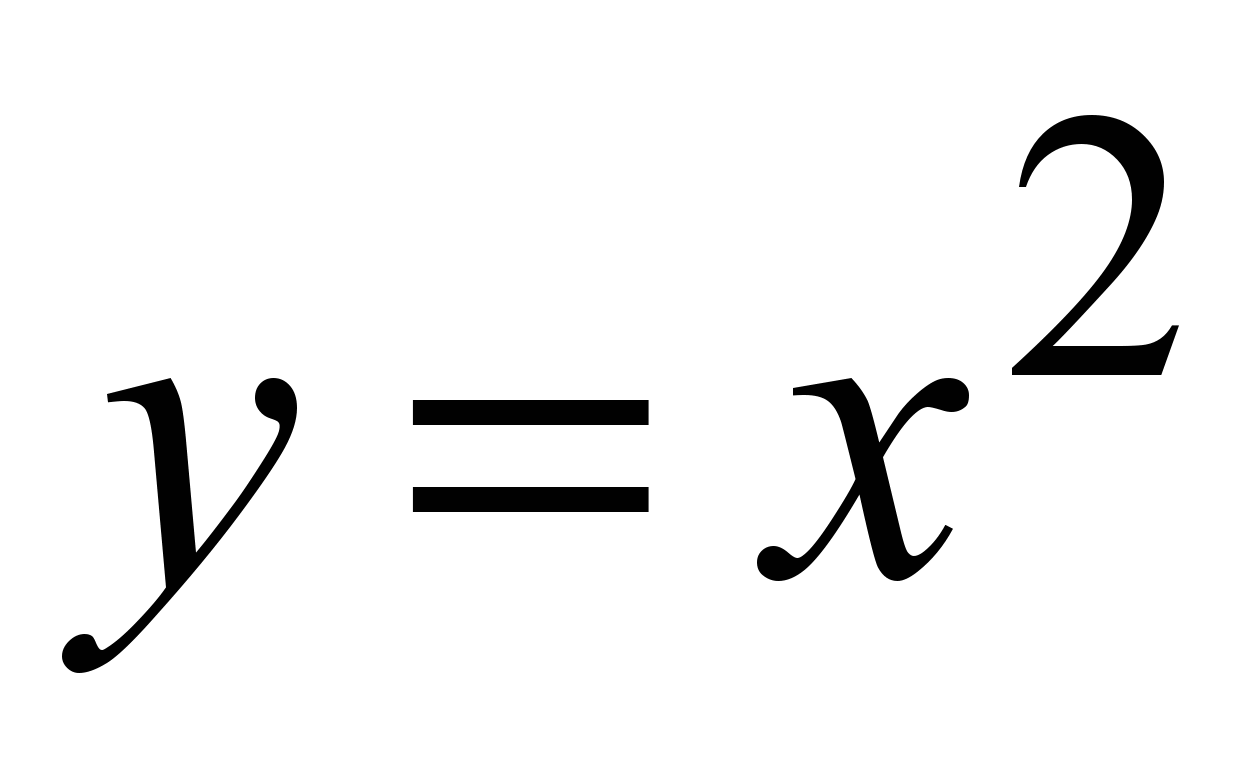

2
20.04









97
График функции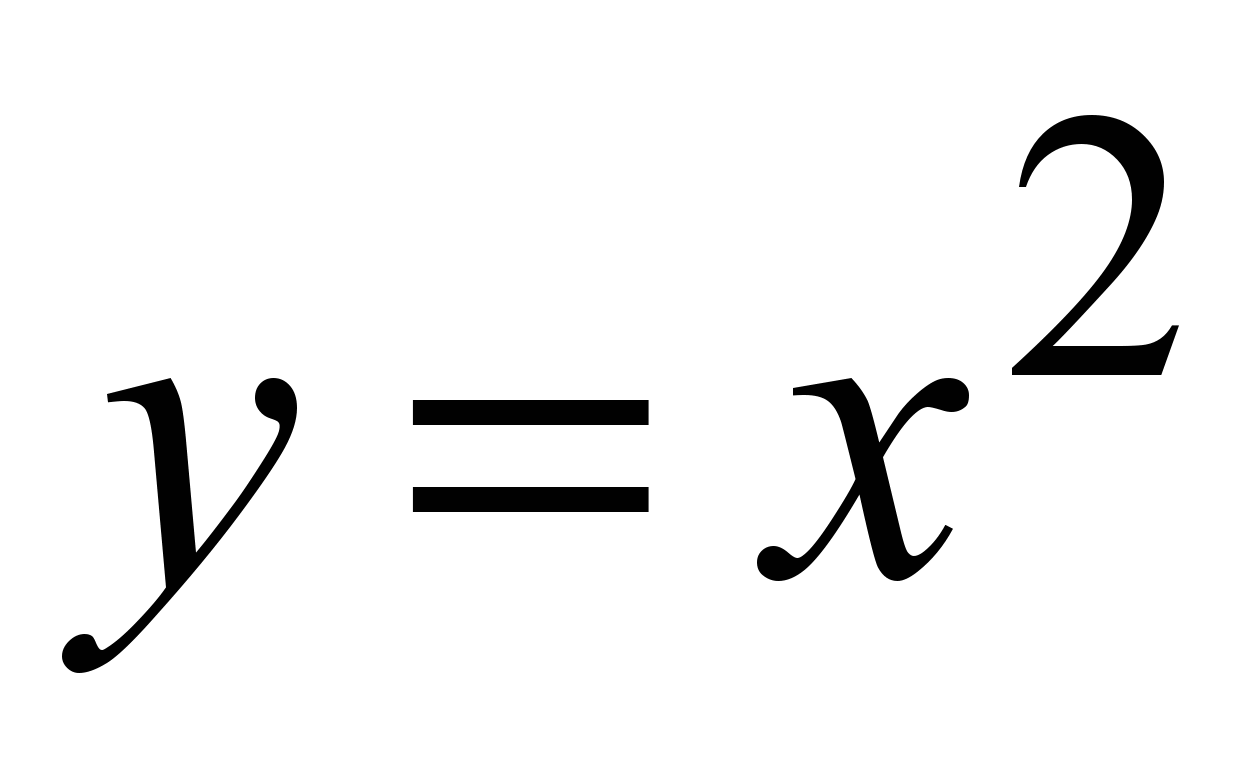




22.04









98
Графическое решение уравнений.
2
25.04









99
Графическое решение уравнений.



27.04









100
Что означает запись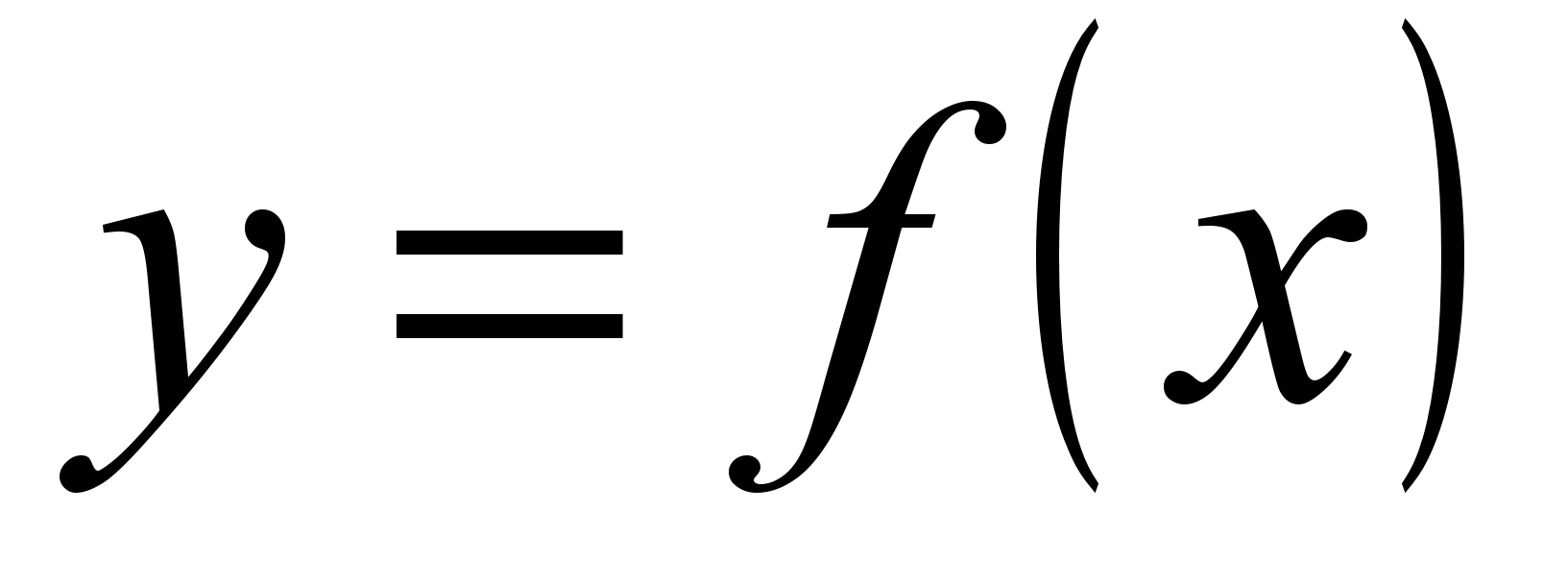

3
29.04









101
Что означает запись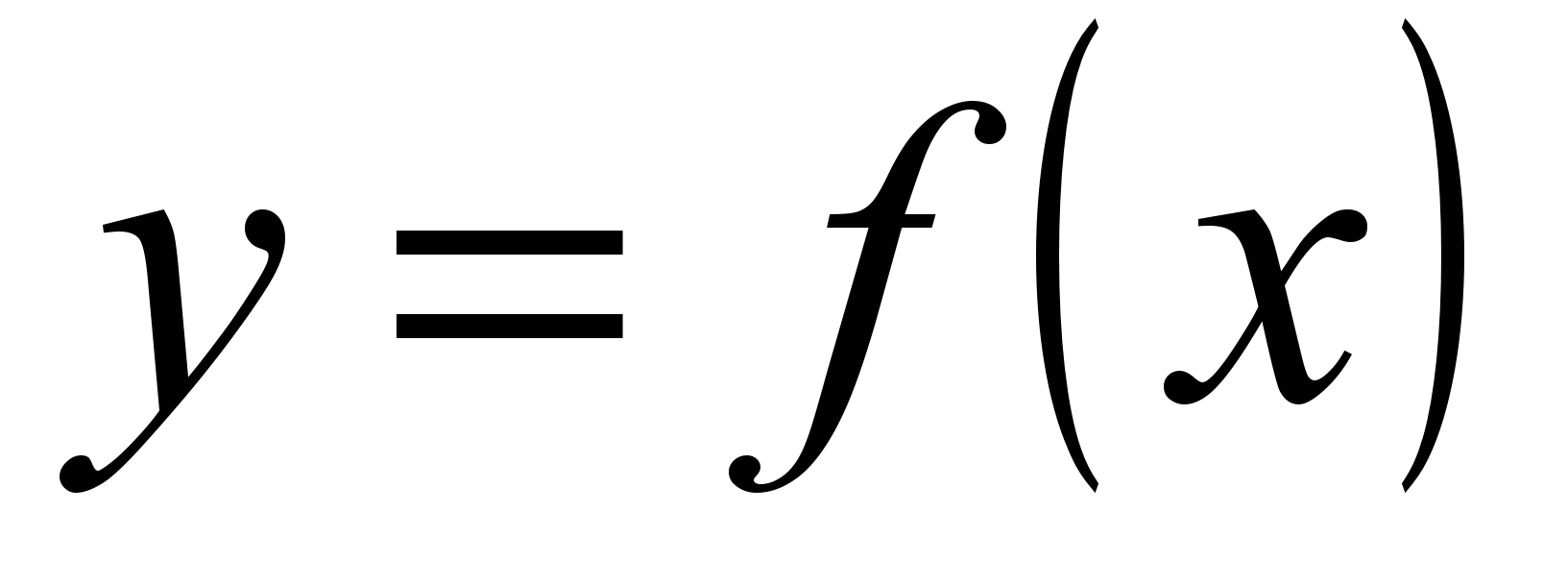




04.05









102
Что означает запись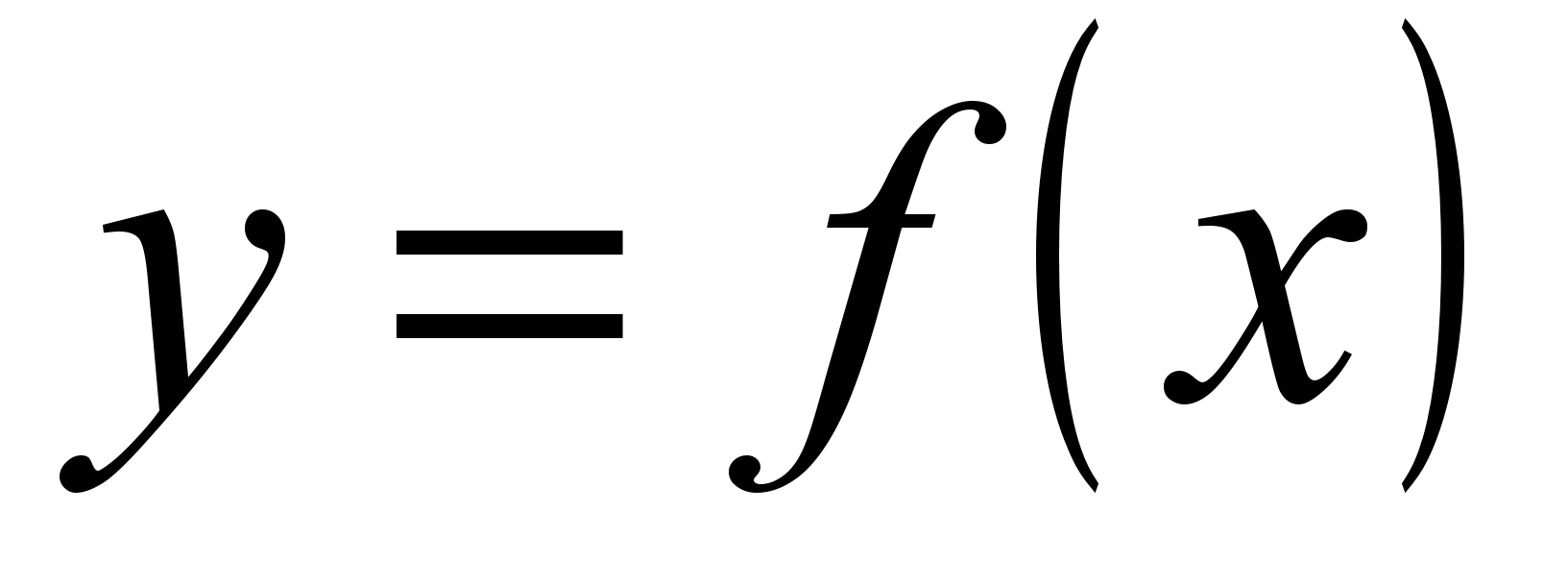




06.05









103
Контрольная работа №8.
1
11.05












Простейшие комбинаторные задачи
3









Знать:

-понятие комбинаторной задачи;

-правило умножения и дерево вариантов, метод перестановки.

Уметь:

-решать простейшие комбинаторные задачи с помощью правила умножения, дерева возможных вариантов, методом перестановки.



104
Простейшие комбинаторные задачи



13.05









105
Правило умножения и дерево вариантов.



16.05









106
Перестановки



18.05

































Повторение
14
20.05-31.05












107
Свойства степени с натуральным показателем


















108
Свойства степени с натуральным показателем


















109
Арифметические операции над многочленами


















110
Арифметические операции над многочленами


















111
Решение уравнений


















112
Решение уравнений


















113
Линейная функция.


















114
Линейная функция.


















115
Квадратичная функция.


















116
Квадратичная функция.


















117
Итоговая контрольная работа



25.05












118
Работа над ошибками


















119
Обобщающее повторение курса



















120
Итоговый урок