Удк 621. 311. 016 Определение границы динамической надежности ээс с использованием искусственных нейронных сетей

Вид материала

Содержание

Инверсия нейронной сети прямого распространения.
Определение точки на границе динамической надежности.
Втэц-2, г1

Подобный материал:

УДК 621.311.016

ОПРЕДЕЛЕНИЕ ГРАНИЦЫ ДИНАМИЧЕСКОЙ НАДЕЖНОСТИ ЭЭС

С ИСПОЛЬЗОВАНИЕМ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ

Г.П. Шумилова^¹, Н.Э. Готман, Т.Б. Старцева

Определение границы динамической надежности необходимо для превентивного управления энергосистемой [1]. Такая информация поможет оператору вывести ЭЭС в более безопасный режим работы, если система находится в устойчивом состоянии, либо перевести ЭЭС из неустойчивого в устойчивое состояние.

Оценивание границы связано с большим объемом вычислений и усложняется еще и тем, что граница постоянно меняется. Проблема требует решения комплекса задач, начиная с определения классификационных признаков надежного и ненадежного состояния и кончая оценкой результатов [2].

Для сложных больших ЭЭС вычисление границы надежности аналитическими методами трудновыполнимо. Граница может быть определена в приближенной форме, идентифицируя принадлежащие ей точки и проводя интерполяцию между ними. Известны разные подходы к определению точек на границе. Reed и Marks [3] предложили эволюционный алгоритм, который позволяет распределить точки равномерно по всей границе. Kassabalidis и др. [4] предлагают алгоритм оптимизации кучи частиц. В этом алгоритме исследовано влияние наложения различных ограничений на распределение точек на границе. Процедура оптимизации кучи частиц позволяет быстро определить эти ограничения и идентифицировать границу (или часть границы). Авторы [5] предложили подход, основанный на алгоритме приближенной инверсии искусственной нейронной сети (ИНС). Этот алгоритм ищет расположение самых близких к рабочему режиму точек на границе, которые удовлетворяют ограничениям по потокораспределению.

В данной работе для оценивания границы выбран метод инверсии нейронной сети с поиском единственного элемента [6], используя стандартную оптимизацию по методу обратного распространения ошибки. Этот метод позволяет определить ближайшую к текущему режиму точку на границе надежности и затем определить удаленность этого режима от границы. Поскольку для определения границы надежности выбрана инверсия ИНС, то целесообразно дать краткую информацию об этом методе.

Инверсия нейронной сети прямого распространения.

Инверсия нейронной сети (рис. 1) – процесс нахождения входного вектора x для получения желаемого выхода y при установленном наборе синаптических весов w.

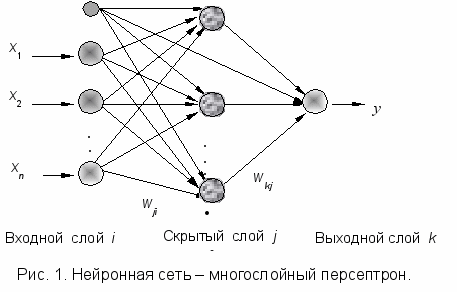
Имеется много методов для выполнения инверсии ИНС. В работе [6] дан обзор существующих методологий инверсии, которая используется в качестве инструмента для решения различных проблем.

Работа обученной нейронной сети может быть описана выражением

y_k = f_k (x,w), (1)

где y_k – k-ый выход нейронной сети, соответствующий входному вектору х, w – вектор весовых коэффициентов и f_k(×) – функция преобразования входного вектора при прохождения его через сеть от входа до k-го выхода. Если рассматривают задачу с единственным скалярным выходом (как на рис. 1), то y_k в уравнении (1) может быть заменено на y и

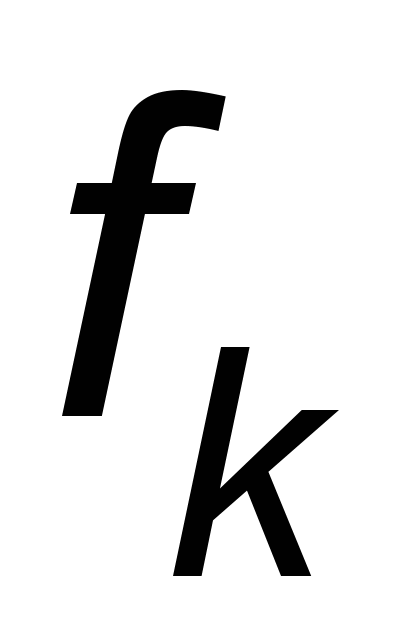(×) на f(×).

Применение метода инверсии нейронной сети состоит из двух этапов:

1) обучение ИНС для получения весовых коэффициентов w_ji , w_kj ;

2) непосредственно инверсия ИНС.

На первом этапе нейронную сеть обучают, устанавливая вход и выход и пересчитывая веса до тех пор, пока приемлемый результат не будет достигнут. Для второго этапа веса нейронной сети принимаются фиксированными, и теперь функция f(×) будет зависимостью только от входного вектора x. В общем, как проиллюстрировано на рис. 2 для двух входов x₁ и x₂ и одного выхода y = f(x), т.е. когда размерность входа больше, чем размерность выхода, многочисленные различные входы могут генерировать тот же самый выход. Каждый контур графика на рис. 2 соответствует f(x) = c для различных постоянных c.

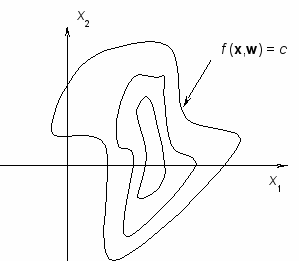
Рис. 2. Инверсия нейронной сети с множеством решений.

Инверсия для данного c состоит в нахождении одного или более элементов входного множества L на контуре (или множестве непересекающихся контуров), где

L = {x : f(x) = c} .

Для единичной выборки задачу инверсии можно сформулировать следующим образом: необходимо найти входное множество L или его подмножество, которое дает наименьшую погрешность E для указанного c, т.е. (по методу наименьших квадратов)

.

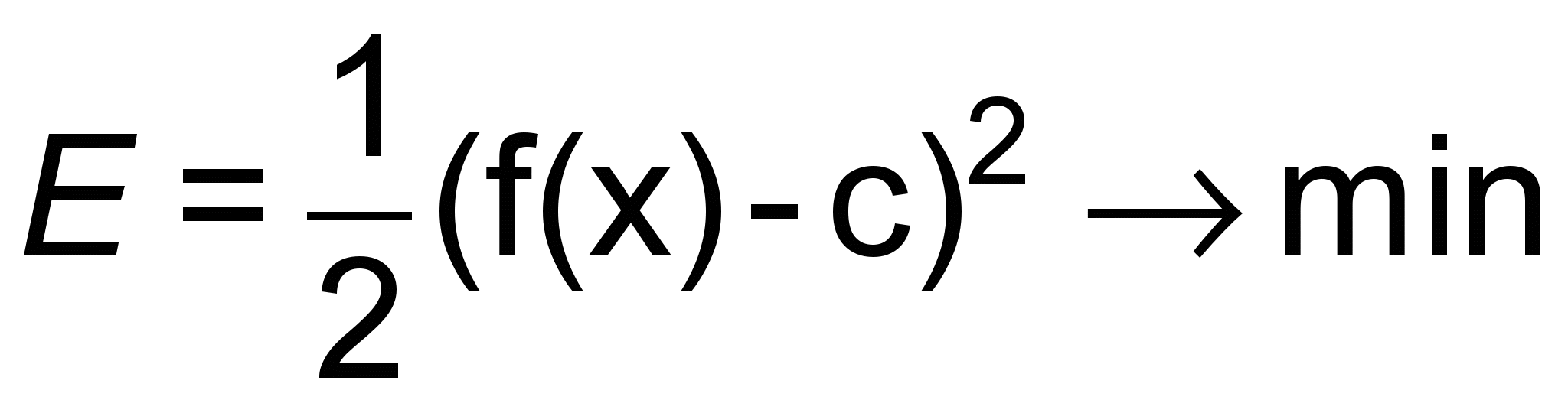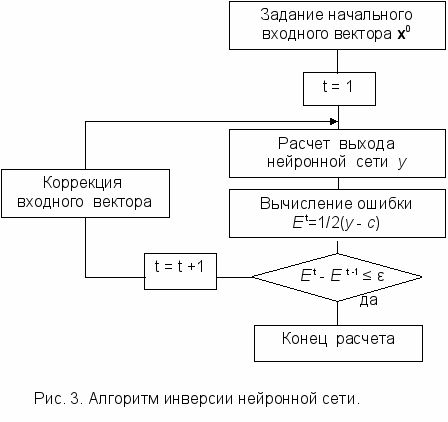
Алгоритм второго этапа инверсии представлен на рис. 3.

Определение точки на границе динамической надежности.

Для оценивания границы динамической надежности, как уже было сказано выше, выбран метод инверсии сети с поиском единственного элемента через градиентный подход. Поиск начинается с входного вектора x⁰. Если

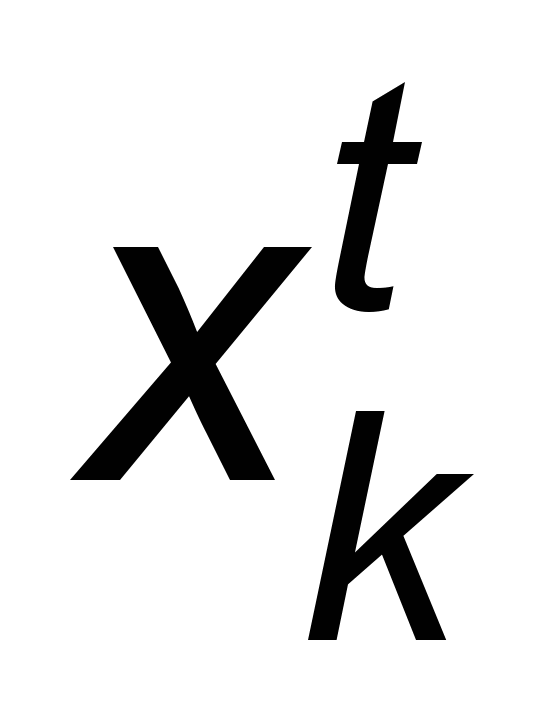– k-ая компонента вектора x^t, то градиентный спуск предполагает рекуррентное соотношение:

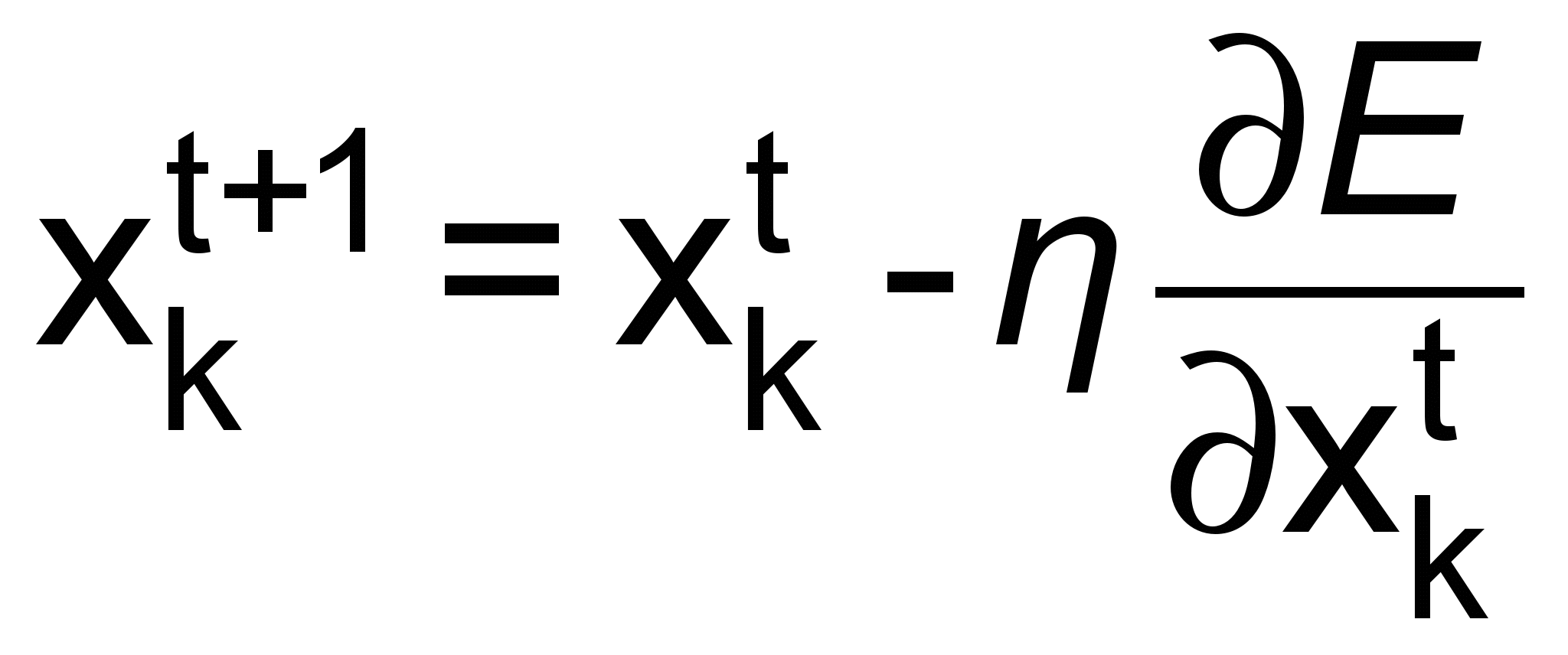, (2)

где h – размер шага и t – индекс итерации.

Обозначим

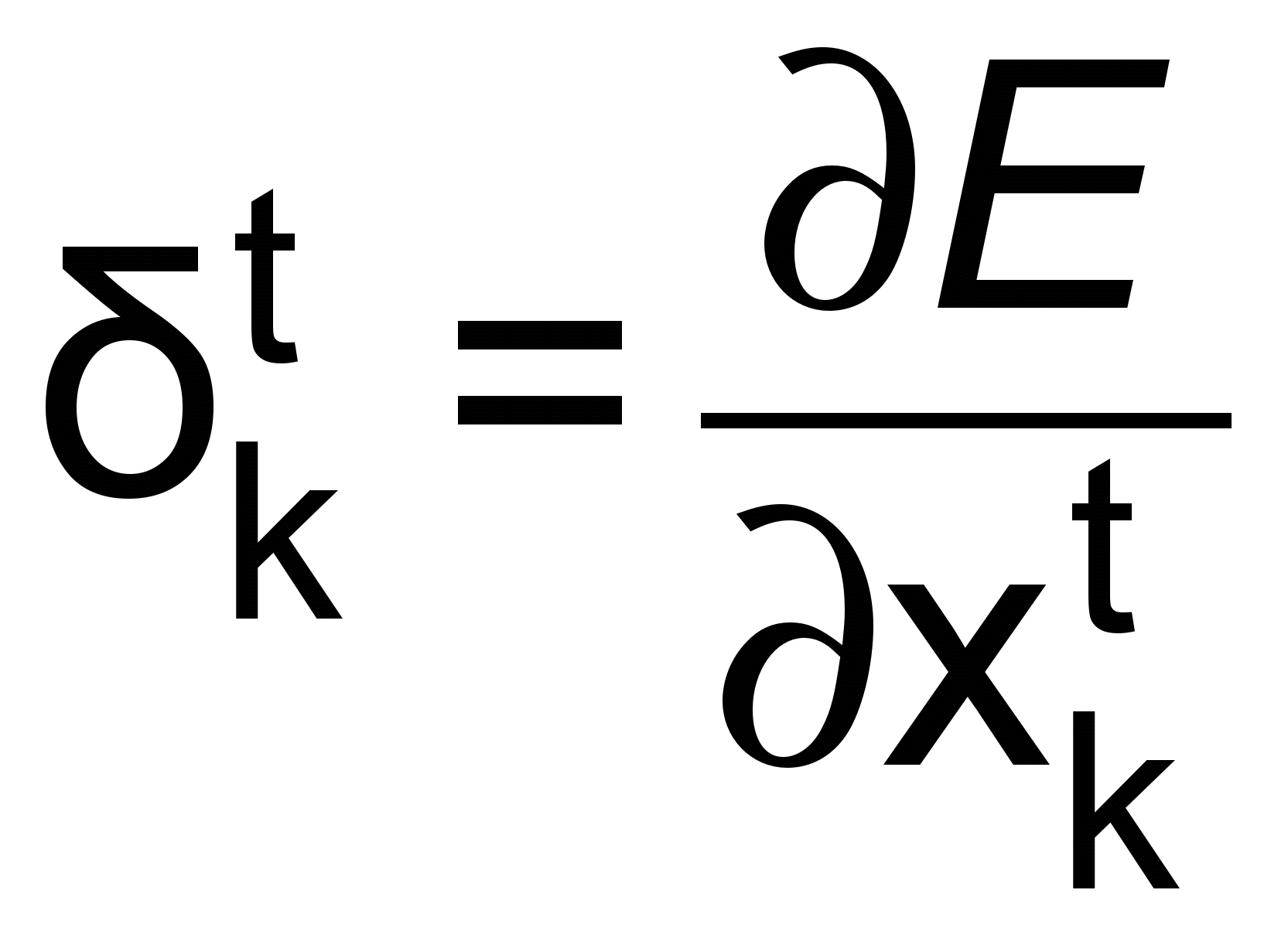. Тогда для входного и скрытых слоев, согласно [6]:

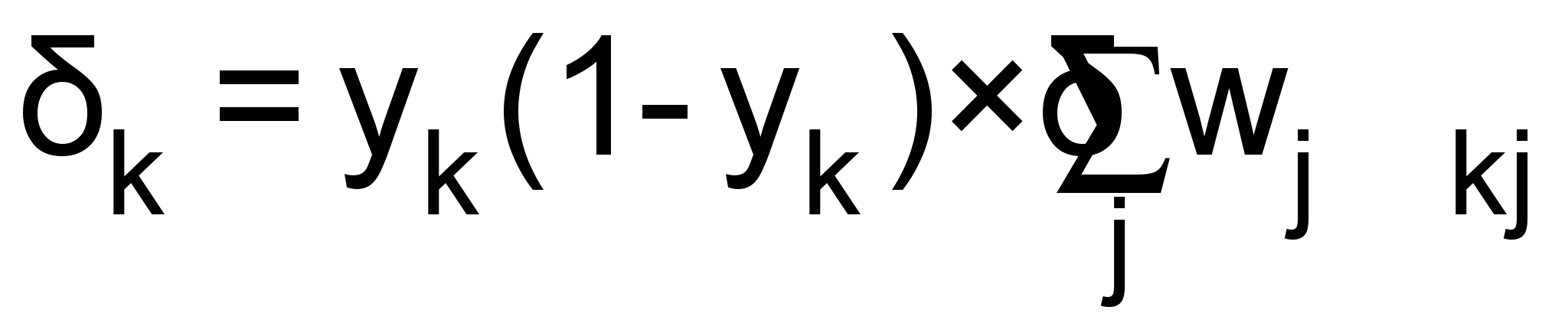, (3)

где y_k – k-ая компонента выхода нейронов в рассматриваемом слое; w_kj – весовые коэффициенты между нейронами рассматриваемого и последующего слоев.

Для выходного слоя:

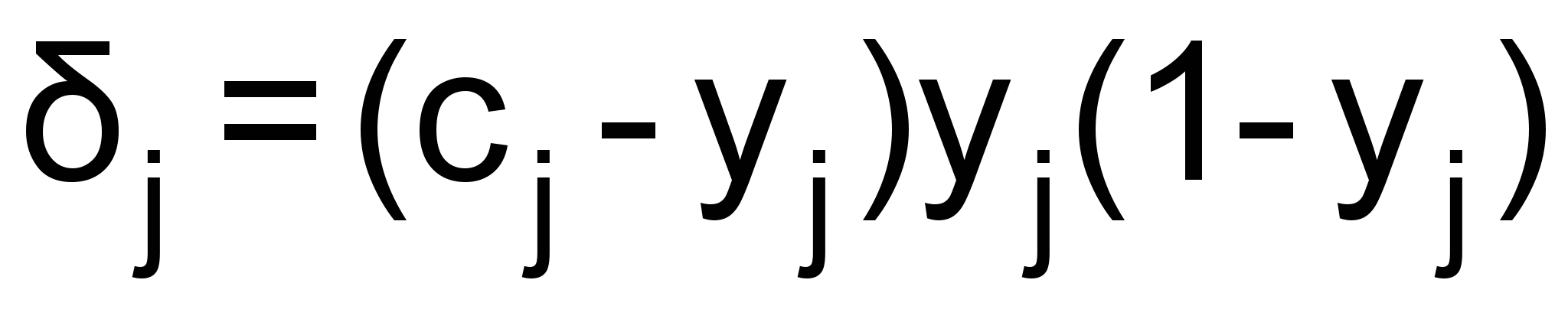. (4)

Выходы нейронов каждого слоя вычисляются по формулам:

, ,

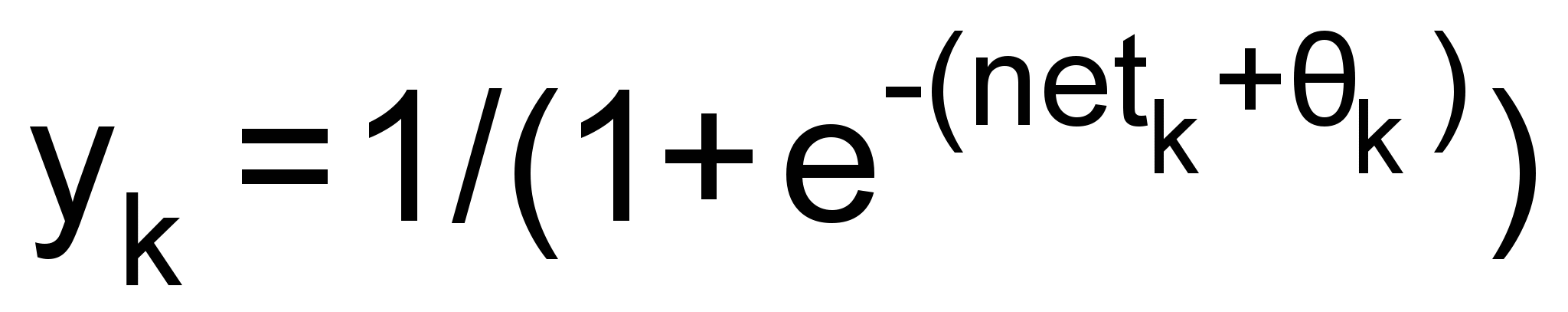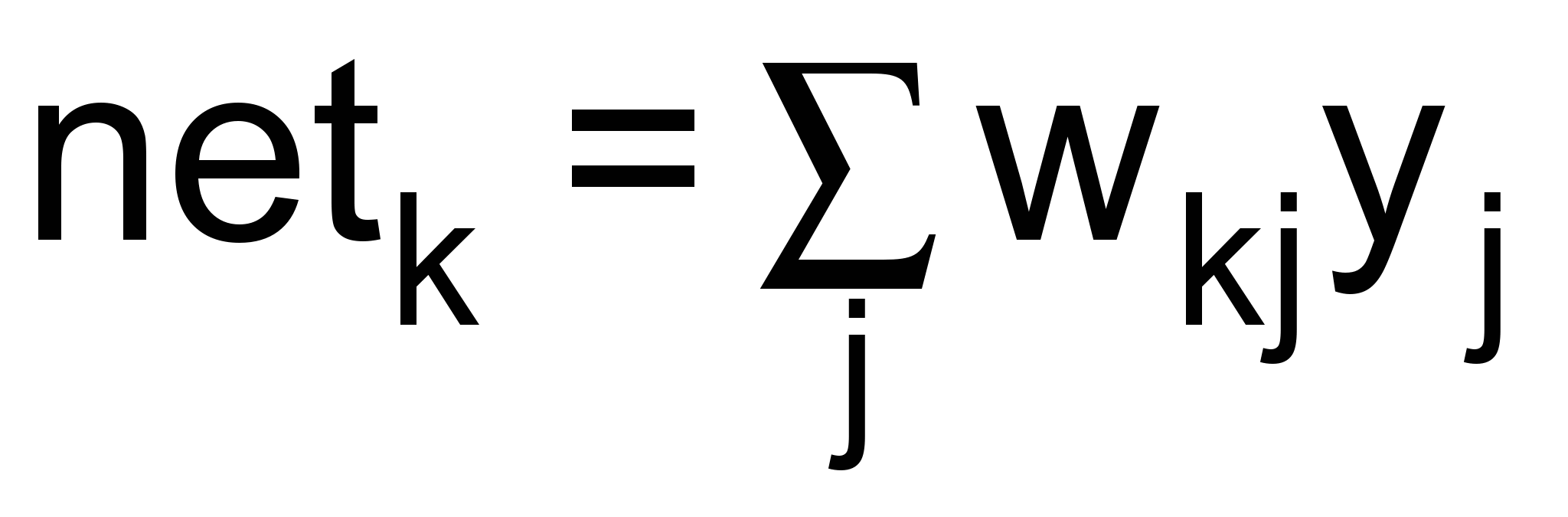где

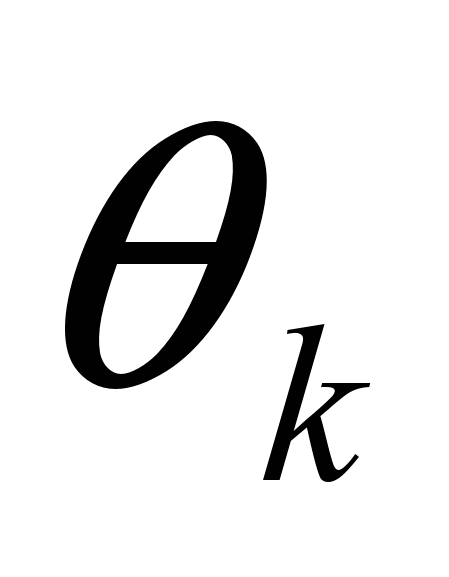– смещение, y_j – выходы предыдущего слоя.

Заметим, что производные

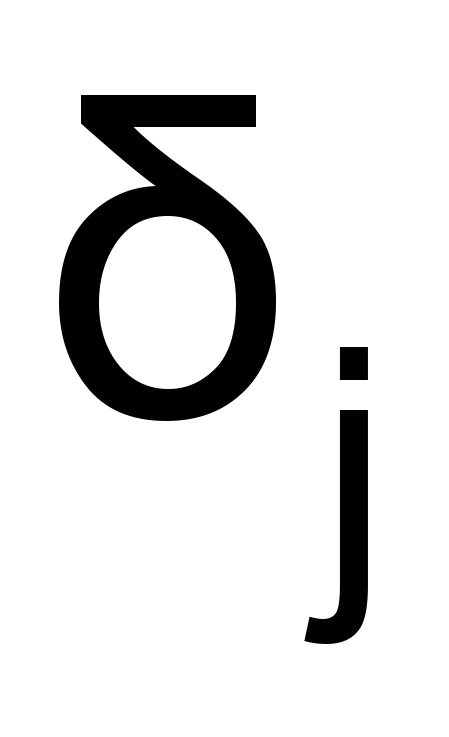нейронов в (3 и 4) должны быть вычислены в обратном порядке – от выхода к входу, подобно стандартному алгоритму обратного распространения ошибки.

В формуле (2) размер шага h может быть как постоянным, так и переменным. Однако постоянный шаг плохо учитывает особенности минимизируемой функции Е, поэтому в реальной работе мало пригоден, что и было подтверждено при определении границы. Более удачным в реализации показал себя алгоритм с переменным шагом (деление шага пополам при увеличении ошибки).

Поиск ближайшей к рассматриваемому режиму точки на границе динамической надежности можно записать в виде следующего алгоритма (рис. 4):

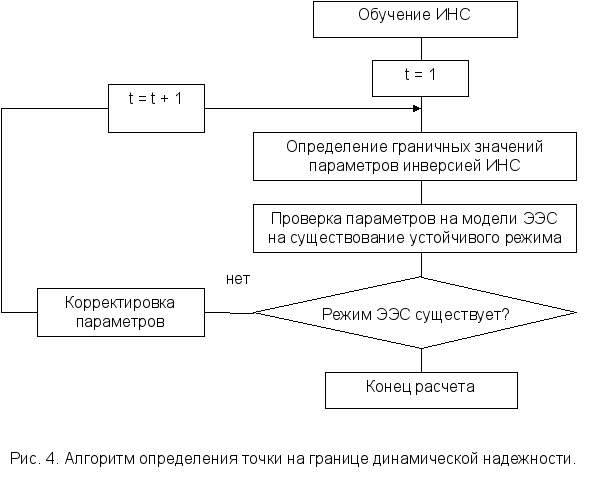
Графическая интерпретация поиска решения в двухмерном пространстве представлена на рис. 5. Начальная точка поиска соответствует текущему рабочему состоянию.

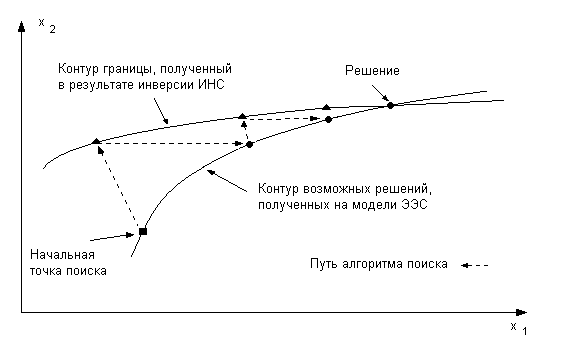
Рис. 5. Определение точки на границе надежности.

Работа алгоритма была рассмотрена на одном из динамически неустойчивых режимов ЭЭС (на примере Коми энергосистемы) [2], параметры которого, выбранные по методу дивергенции [2], приведены табл. 1.

Обучение ИНС проведено на 80 образцах (сорок устойчивых и сорок неустойчивых). Для получения образцов рассматривались следующие аварийные ситуации:

а) отключение генератора одной из станций, как правило, имеющего наибольшую загрузку:

– на Воркутинской ТЭЦ-2 – 5-ый генератор,

– на Печорской ГРЭС – 5-ый блок,

– на Сосногорской ТЭЦ – 8-ой генератор,

– на ТЭЦ СЛПК – 6-ой генератор;

б) трехфазные короткие замыкания с неуспешным АПВ на линиях:

– Микунь 110 – ВЛ170,

– Усинск 220 – Возей 220,

– ВТЭЦ2-110 – Городская 110.

Все короткие замыкания происходят в начале каждой линии.

Всего получено 160 образцов (80 устойчивого и 80 неустойчивого) состояний энергосистемы варьированием значений активной и реактивной мощностей генераторов всех станций и значений активной и реактивной мощностей нагрузок. Половина образцов, как уже было сказано, использована для обучения, вторая половина – для классификации режимов. Устойчивые и неустойчивые состояния определялись по величине углов d роторов генераторов.

Таблица 1. Параметры рассматриваемого неустойчивого режима ЭЭС

Генерирующие и нагрузочные узлы	Параметры
Генерирующие и нагрузочные узлы	Р_г, МВт	Q_г, МВар	Р_н, МВт	Q_н, МВар
ВТЭЦ-2, Г1	34,0	5,4	-	-
ВТЭЦ-2, Г5	11,7	-	-	-
ПГРЭС, блок 2	128,6	14,1	-	-
ПГРЭС, блок 3	133,6	14,2	-	-
ПГРЭС, блок 5	138,0	-	-	-
ТЭЦ СЛПК, Г1	43,0	36,6	-	-
ТЭЦ СЛПК, Г2	37,0	42,6	-	-
ТЭЦ СЛПК, Г6	52,0	20,0	-	-
ВТЭЦ2-110	-	-	38,3	-
Усинск-35	-	-	-	13,05
Возей-35	-	-	-	13,78
Сосногорская ТЭЦ	-	-	-	26,11
Генерация по ЭЭС	1043,2	450,8	-	-
Нагрузка по ЭЭС	-	-	1001,6	-

В результате работы по алгоритму, представленному на рис. 4, получены значения параметров режима на границе динамической надежности (столбец 7 табл. 2), т.е. найдена ближайшая к текущему режиму точка на границе. Расчет проводится до тех пор, пока результаты инверсии не совпадут с результатами расчета на модели ЭЭС. При этом полученный режим должен быть динамически надежным, т.е. устойчивым для всех рассматриваемых аварийных ситуаций. В данном примере завершение работы алгоритма произошло на 3-ей итерации. Во второй строке табл. 3 можно проследить, как менялся ранг надежности при приближении к границе.

Таблица 2. Результаты расчетов параметров режима по алгоритму нахождения точки на границе

Начальные параметры	Итерация 1		Итерация 2		Итерация 3
Начальные параметры	Инверсия	Коррекция	Инверсия	Коррекция	Инверсия	Граничные параметры
1	2	3	4	5	6	7
34,0	33,98	34,0	34,0	34,0	34,0	34,0
5,4	5,4	5,4	5,4	5,4	5,4	5,4
11,7	11,7	11,7	11,7	11,7	11,7	11,7
128,6	128,8	128,8	128,79	128,8	128,8	128,8
14,1	14,2	14,1	14,09	14,1	14,1	14,1
133,6	133,09	133,1	133,12	133,1	133,09	133,1
14,2	14,29	14,2	14,2	14,1	14,1	14,1
138,0	138,98	139,0	138,96	138,9	138,9	138,9
43,0	43,08	43,1	43,10	43,1	43,1	43,1
36,6	36,49	36,1	36,10	36,1	36,098	36,1
37,0	36,66	36,7	36,71	36,7	36,69	36,7
42,6	42,95	42,5	42,48	42,5	42,51	42,5
52,0	50,65	50,6	50,66	50,7	50,67	50,7
20,0	20,27	20,6	20,59	20,5	20,5	20,5
38,3	38,33	38,33	38,33	38,33	38,33	38,33
13,05	12,98	13,05	13,05	13,05	13,05	13,05
13,78	13,74	13,78	13,78	13,78	13,78	13,78
26,11	26,15	26,13	26,13	26,13	26,13	26,13
1043,2	1043,2	1042,6	1042,6	1042,6	1042,6	1042,6
450,8	448,56	448,2	448,3	448,1	448,05	448,1
1001,6	1001,75	1001,6	1001,59	1001,6	1001,6	1001,6

Оценка расстояния до границы динамической надежности.

При оценке надежности ЭЭС важно знать расстояние текущей рабочей точки до границы надежности. Авторы [7] описывают один из методов определения расстояния до границы, основанный на оценке индекса надежности. Этим методом можно воспользоваться, если заранее известна вся граница. В рассматриваемом случае, когда определяется одна ближайшая к текущему режиму точка на границе в режиме реального времени, такой принцип определения расстояния не подходит.

Самой распространенной мерой для определения расстояния между двумя точками является Евклидова мера [8]:

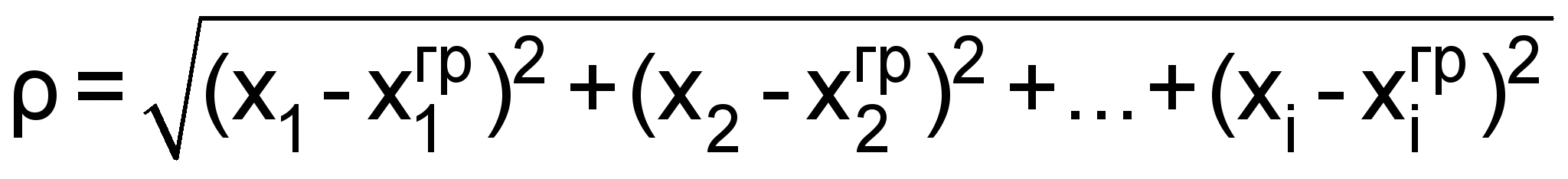, (5)

где х_i – текущее значение i-го параметра;

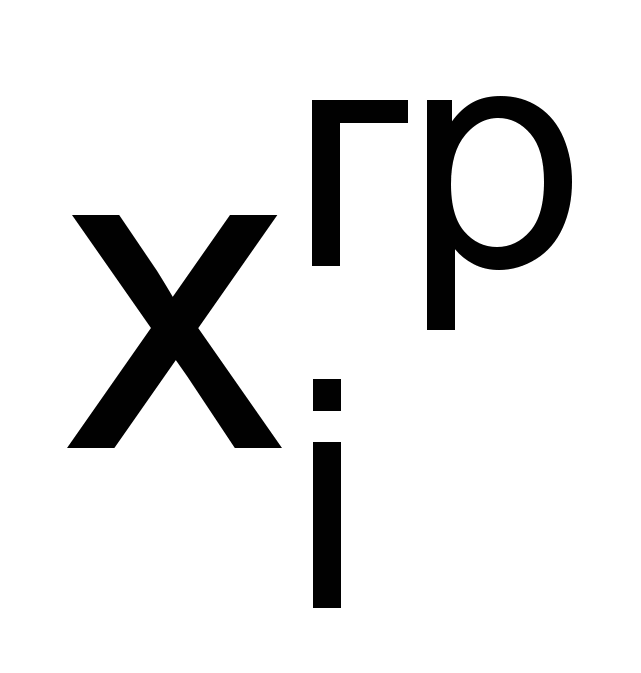- граничное значение i-го параметра.

В чистом виде такая формула не может быть использована, поскольку параметры х_i имеют разную размерность (МВт и МВар). В этом случае целесообразно рассматривать нормированные величины, которые определяются как отношение отклонения к среднему квадратическому отклонению, т.е.

.

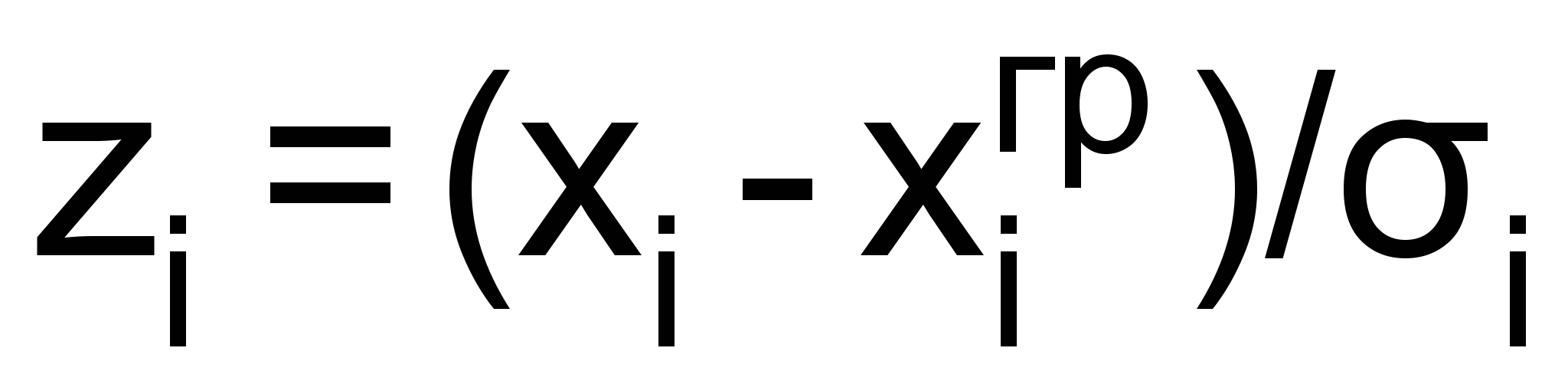Тогда формула (5) примет вид:

.

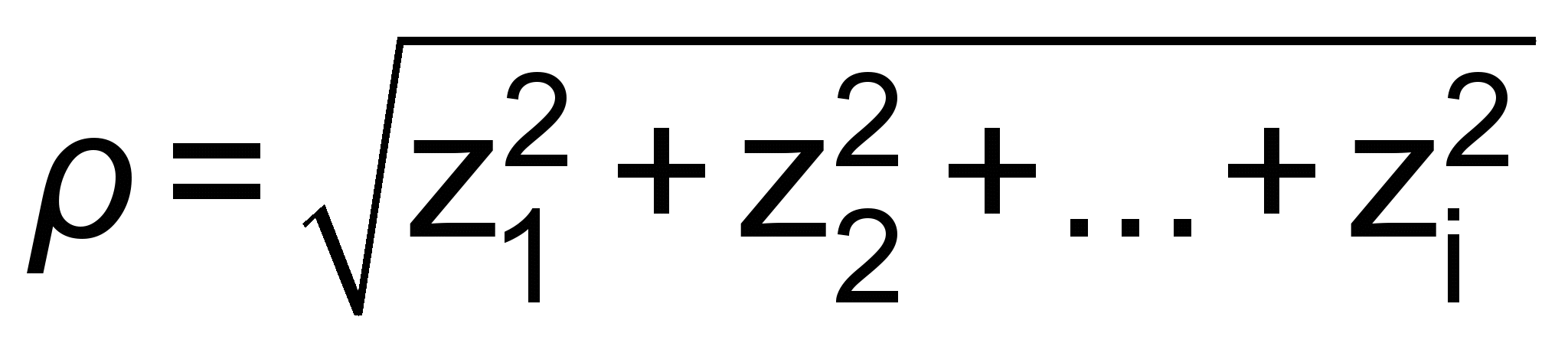Среднее квадратическое отклонение вычисляется по формуле:

,

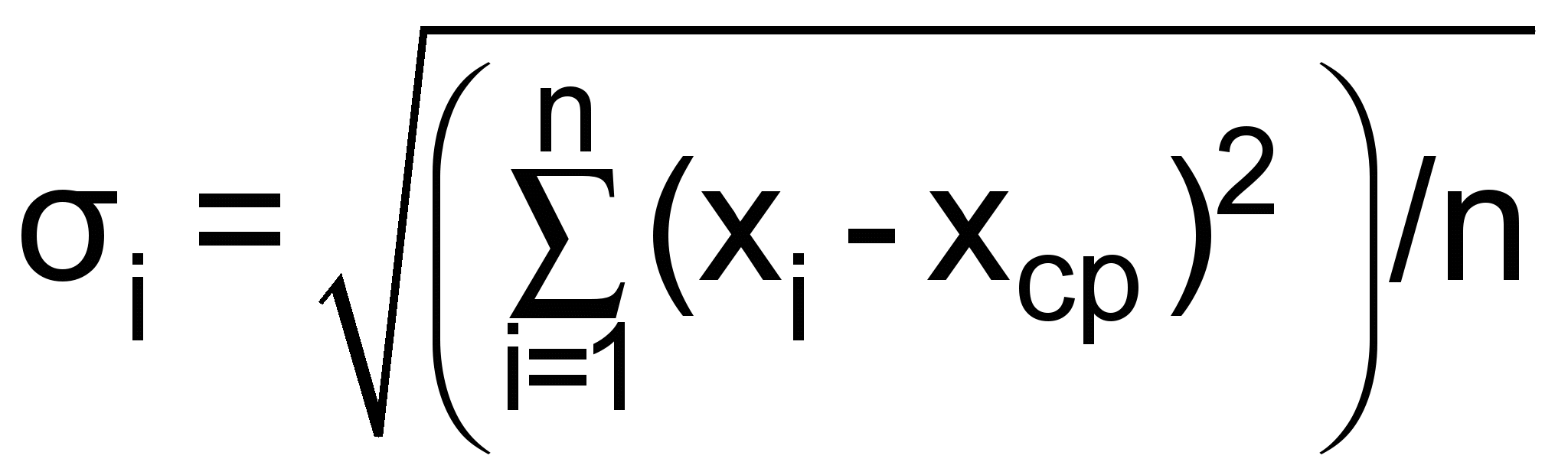где

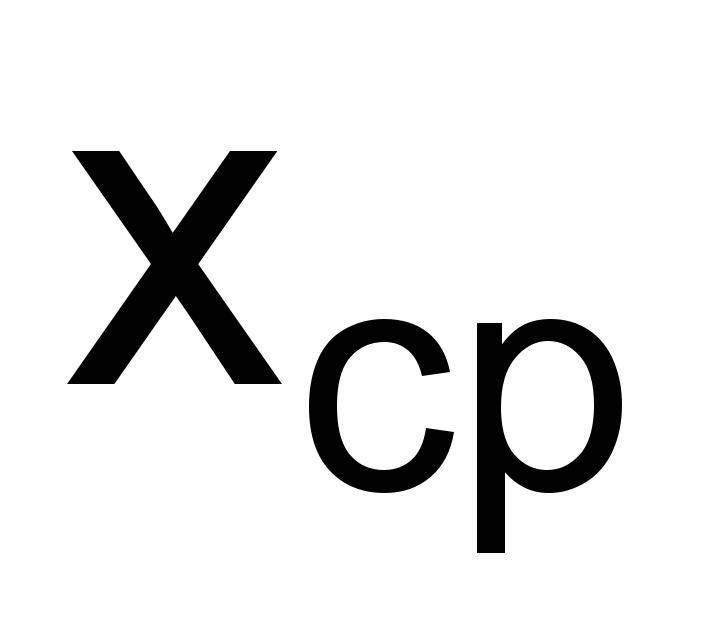- среднее арифметическое значений параметров по всем образцам, n – количество образцов.

Результаты расчета расстояния до границы по приведенным выше формулам для рассматриваемого примера приведены в третьей строке табл. 3. Расстояние от начальной точки поиска до полученной ближайшей точки на границе (точка решения на рис. 5) равно 0,301.

Таблица 3. Изменение ранга надежности и расстояния при приближении к границе

Номер итерации	1	2	3
Ранг надежности режима после коррекции	0,274	0,511	0,494
Расстояние до границы надежности ρ	0,251	0,011	0,006

Для того, чтобы определить насколько далек текущий режим с таким расстоянием до границы, проведены расчеты

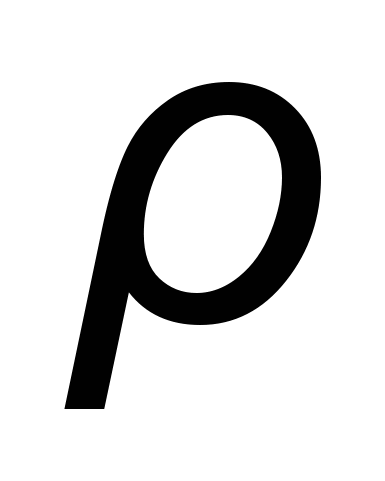для всех 80 режимов работы ЭЭС. В результате расчетов получено, что изменение расстояния до границы находится в пределах от 0 (на границе) до 3,671 при устойчивом режиме работы ЭЭС и до 5,118 - при неустойчивом режиме. Результаты расчета приведены в табл. 4.

Таблица 4. Индекс надежности и расстояние до границы динамической надежности при устойчивом и неустойчивом режимах работы ЭЭС

№ режима	Индекс надеж-ности	ρ усл.ед	№ режима	Индекс надеж-ности	ρ усл.ед	№ режима	Индекс надеж-ности	ρ усл.ед	№ режима	Индекс надеж-ности	ρ усл.ед
Устойчивый режим						Неустойчивый режим
1	0,840	1,789	21	0,902	2,006	41	0,174	0,921	61	0,274	0,334
2	0,962	1,993	22	0,864	0,915	42	0,125	0,645	62	0,424	0,109
3	0,963	3,103	23	0,716	1,674	43	0,104	0,792	63	0,175	0,837
4	0,951	1,848	24	0,769	1,834	44	0,255	0,932	64	0,183	0,429
5	0,937	1,738	25	0,709	1,967	45	0,371	0,532	65	0,082	1,364
6	0,932	1,729	26	0,741	1,765	46	0,245	0,418	66	0,385	0,496
7	0,888	1,803	27	0,786	1,987	47	0,483	0,493	67	0,129	0,654
8	0,809	1,911	28	0,952	2,532	48	0,308	0,383	68	0,128	0,572
9	0,773	1,679	29	0,795	2,178	49	0,419	0,465	69	0,049	1,494
10	0,782	1,743	30	0,965	2,874	50	0,000	2,070	70	0,000	5,118
11	0,827	2,005	31	0,825	2,673	51	0,007	3,420	71	0,012	3,045
12	0,937	2,126	32	0,887	3,051	52	0,027	1,138	72	0,013	3,041
13	0,717	1,913	33	0,732	3,009	53	0,145	0,717	73	0,000	5,006
14	0,516	0,023	34	0,789	2,346	54	0,045	1,046	74	0,000	2,583
15	0,606	0,088	35	0,826	1,954	55	0,419	0,153	75	0,000	3,231
16	0,864	1,977	36	0,683	0,879	56	0,156	0,604	76	0,000	4,155
17	0,779	1,845	37	0,714	0,896	57	0,389	0,244	77	0,390	0,289
18	0,742	1,997	38	0,859	0,678	58	0,153	0,751	78	0,282	0,567
19	0,736	1,315	39	0,905	1,475	59	0,268	0,271	79	0,004	3,634
20	0,820	1,105	40	0,987	3,671	60	0,015	3,985	80	0,320	0,696

П р и м е ч а н и е. Выделены максимальные значения расстояния до границы для устойчивого и неустойчивого режимов работы ЭЭС.

Заключение

Предложенный подход к оцениванию динамической надежности ЭЭС представляет интерес для превентивного управления энергосистемой в реальном времени, важность которого увеличивается при уменьшении эксплуатационной надежности. Использование только аналитических методов не позволяет своевременно выполнять профилактические или корректирующие действия.

Для определения границы динамической надежности разработан алгоритм, основанный на инверсии ИНС с поиском единственного элемента, с помощью которого находится самая ближайшая к текущему режиму точка на границе, а затем определяется ее расстояние до границы, позволяющее судить о надежности текущего режима. В случае необходимости, оператор производит соответствующие управляющие воздействия, уводя систему в более безопасный режим.

Данная разработка не претендует на законченность и идеальное качество. Необходимо провести еще много исследований по принципам и методам оценивания динамической надежности, по анализу динамического перехода в послеаварийное состояние. Несовершенство модели ЭЭС также накладывает некоторый отпечаток на результаты работы.

Литература

1. La Scala M., Trovato M., Antonelly C. On-line dynamic preventive control and algorithm for transient security dispatch // IEEE Trans. Power Systems. – 1998. – Vol. 13, No. 2. – P. 601–610.

2. Шумилова Г. П., Готман Н.Э., Старцева Т.Б. Выбор входных параметров нейронной сети для решения задачи оценивания границ динамической надежности электроэнергетической системы // Методические вопросы исследования надежности больших систем энергетики: Сб. науч. Тр. Вып. 58. Математические модели и методы исследования надежности либерализованных систем энергетики Отв. Ред. Н.И. Воропай, М.Ш. Мисриханов. – М.–Н.Новгород: Изд-во Волго-Вятской академии государственной службы, 2008. – С. 150–157.

3. Reed R.D., Marks II R.J. An evolutionary algorithm for function inversion and boundary marking // Proceedings of the IEEE International Conference on Evolutionary Computation. – November 26-30, 1995. – Р. 794-797.

4. Kassabalidis I.N., El-Sharkawi M.A., Marks II R.J. and others. Dynamic security border identification using enhanced particle swarm optimization // IEEE Trans. оn Power Systems. – 2002. – Vol. 17, No. 3. – P. 723-729.

5. Jensen C.A., Reed R.D., El-Sharkawi M.A., Marks II R.J. Location of operating points on the dynamic security border using constrained neural network inversion // Proc. Int. Conf. Intelligent Systems Applications to Power Systems, (ISAP 97), Seoul, Korea, July 1997.

6. Jensen C.A., Reed R.D., Marks II R.J. et al. Inversion of feedforward neural networks: algorithms and applications // Proceedings of the IEEE, Vol.87, No.9, September 1999, pp. 1536-1549.

7. Kassabalidis I.N., El-Sharkawi M.A., Marks II R.J. Border identification for power security assessment using neural network inversion: an overview // 2002 Congress on Evolutionary Computation, 2002 IEEE World Congress on Computational Intelligence, May 12-17, 2002, Honolulu, pp. 1075-1079.

8. Гусак А.А., Гусак Г.М., Бричикова Е.А. Справочник по высшей математике. – 7-ое изд. – Мн.: ТетраСистемс, 2006. – 640 с.

1 Институт социально-экономических и энергетических проблем Севера, Сыктывкар, Россия, shumilova@energy.komisc.ru

Blog

Удк 621. 311. 016 Определение границы динамической надежности ээс с использованием искусственных нейронных сетей

Содержание