Основы алгебры высказываний. Логические операции
| Вид материала | Урок |
- Сумцова Ольга Владимировна Логические основы построения компьютера Темы игры: Основные, 54.64kb.
- Вопросы по курсу: Математическая логика и теория алгоритмов (2 курс), 30.21kb.
- Лекция Логические основы компьютеров , 369.25kb.
- Контрольная работа. Основы логики. 1 вар. 1) Приведите по два примера сложных истинных, 20.33kb.
- Функции алгебры логики, 47.25kb.
- Календарно-тематический план учебная дисциплина: «Математика», 34.71kb.
- Курсовая работа по информатике на тему: «применение алгебры высказываний в информатике», 221.48kb.
- Законы алгебры логики, 44.21kb.
- Время, требуемое для выполнения проекта 7 недель, 14 часов, 8.75kb.
- Программа курса лекций по математике для учащихся 10-11 «Е» класса гимназии №1 Лектор, 84.04kb.
Урок №1 1
Основы алгебры высказываний. Логические операции (урок 1 по теме)
(урок комбинированный, включающий контроль знаний, введение нового материала, закрепление)
Цели урока:
- сформировать у учащихся представление об алгебре высказываний;
- рассмотреть основные логические операции и сформировать первичные навыки их применения;
- рассмотреть связь логических операций и теории множеств (в качестве дополнительного материала);
- проверить основные знания, умения и навыки по теме: Формы человеческого мышления;
- тренировка учащихся в написании тестов;
- развитие внимательности, памяти, логического мышления;
- развитие навыков научной речи
- воспитание навыков самоорганизации, самоконтроля.
Этапы урока
- Организационный момент. Постановка цели урока. 2 мин.
- Проверка домашнего задания. 5 мин.
- Контроль знаний (проведение теста). 7 мин.
- Введение нового материала. 21 мин.
- Первичное закрепление. 7 мин.
- Подведение итогов урока. 1 мин.
- Постановка домашнего задания. 2 мин.
Ход урока
Проверяем домашнее задание.
Далее осуществляем контроль знаний по теме Формы человеческого мышления. Проводится он в виде теста, созданного в программе PowerPoint. Учащиеся самостоятельно запускают тест, ответы записывают на листок, который предварительно раздаётся учителем. Тест предлагается в 3 вариантах. Время работы 5-7 минут. Вместе с учителем проверяются результаты. Самостоятельно выставляют оценки.
Образец для 1 варианта.
| Вариант 1. | ||
| 1. В формальной логике понятием называется | ||
| А) форма мышления, которая имеет две основные логические характеристики: содержание и логическую форму. | Б) форма мышления, в которой отражаются отличительные существенные признаки предметов или явлений. | В) форма мышления, которая что-либо утверждает или отрицает о предметах, их свойствах или отношениях между ними. |
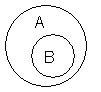 | ||
| А) А- Река; В- Океан. | Б) А- Школьники; В- Спортсмены. | В) А- Молочный продукт; В- Сметана. |
| 3. Определите логическую форму высказывания Чайка и дельфин не являются животными. | ||
| А) Некоторые S есть Р. | Б) Некоторые S не есть Р. | В) Все S не есть Р. |
| 4. Выберите неправильную логическую форму умозаключения: | ||
| А) Все S есть Р1.  А есть Р1. А есть Р1.А есть S. | Б) Все S есть Р1.  А есть S. А есть S.А есть Р1. | В) Все есть Р1.  Все Р1 есть Р2. Все Р1 есть Р2.Все S есть Р2. |
Если у человека повышена температура, то он болен. Этот человек болен. Следовательно, у него должна быть повышенная температура. Является ли она правильной? (Да/Нет). | ||
| А) Все S есть Р. А есть S.  А есть Р. А есть Р. | Б) Если S есть Р1, то S есть Р2. А есть Р1.  А есть Р2. А есть Р2. | В) Если S есть Р1, то S есть Р2. А есть Р2.  А есть Р1. А есть Р1. |
Листок для ответов может выглядеть следующим образом:
| Вариант 1 | |||||
| Фамилия | | Класс | | ||
| | 1 | 2 | 3 | 4 | 5 |
| А | | | | | |
| Б | | | | | |
| В | | | | | |
Далее вводим новый материал.
§2. Алгебра логики. Логические операции
Алгебра логики (алгебра высказываний)- раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Таким образом, объектами изучения алгебры логика являются высказывания.
Под высказыванием (суждением) будем понимать повествовательное предложение, относительно которого можно сказать, истинно оно или ложно.
Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
Если высказывание А истинное, будем писать «А=1», иначе высказывание ложное и будем писать «А=0».
Рассмотрим примеры:
- А= {Солнце светит для всех} = 1- истинное высказывание.
- В={Все ученики любят информатику} = 0 – ложное высказывание.
- D ={А ты любишь информатику? } – не высказывание.
- Е= {Посмотри в окно }– не высказывание.
- C= {x*x<0}= 0 – ложное высказывание, так как для всех х данное неравенство будет неотрицательным.
- K= {2*х-5>0} – не высказывание, так как для одних значений х это выражение будет верным, а для других нет.
В алгебре логики над высказываниями можно производить различные операции (подобно тому, как в алгебре чисел определены операции сложения, умножения, деления, возведения в степень над числами). При помощи логических операций над простыми высказываниями получаются составные или сложные высказывания. На естественном языке составные высказывания образуются с помощью союзов.
Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна.
Рассмотрим основные логические операции.
Логическое отрицание (инверсия)
Логическое отрицание образуется из высказывания с помощью добавления частицы «не» или использования оборота речи «неверно, что…».
Обозначения: ¬А; Ā.
Пример.
А= { Аристотель основоположник логики.}
Ā= {Неверно, что Аристотель основоположник логики.}
| Таблица истинности | Инверсия высказывания истинна, когда высказывание ложно, и ложна, когда высказывание истинно. | |
| А | Ā | |
| 0 | 1 | |
| 1 | 0 | |
Мнемоническое правило: слово «инверсия» означает, что белое меняется на чёрное, добро на зло, красивое на безобразное, истина на ложь, ложь на истину, ноль на один, один на ноль.
Примечания:
- Логики при образовании инверсии предпочитают иметь дело с оборотом речи «неверно, что», поскольку тем самым подчёркивают отрицание всего высказывания.
-
Логическое умножение (конъюнкция)
Логическое умножение (конъюнкция) образуется соединением двух высказываний в одно с помощью союза «и».
Обозначения: А·В; АВ; А&В.
Пример.
А= {3+4=8}.
В= {2+2=4}.
А&В={3+4=8 и 2+2=4}
| Таблица истинности | Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно. | ||||||||||||||
|
Обращаем внимание на то, что в таблице истинности значения входящих высказываний пишутся по возрастанию.
Мнемоническое правило: конъюнкция – это логическое умножение, и мы не сомневаемся, что вы заметили, что равенства 0·0=0; 0·1=0; 1·0=0; 1·1=1, верные для обычного умножения, верны и для операции конъюнкции.
Логическое сложение (дизъюнкция)
Логическое сложение (дизъюнкция) образуется соединением двух высказываний в одно с помощью союза «или».
В русском языке союз «или» используется в двояком смысле.
Например, в предложении Обычно в 8 вечера я смотрю телевизор или пью чай союз «или» взят в неисключающем (объединительном) смысле, так как вы можете только смотреть телевизор или только пить чай, но вы можете также пить чай и смотреть телевизор одновременно, потому что мама у вас нестрогая. Такая операция называется нестрогой дизъюнкцией. (Если бы мама была строгая, то она разрешила бы или только смотреть телевизор, или только пить чай, но не совмещать приём пищи с просмотром телепередач.)
В высказывании Данное существительное во множественном или единственном числе союз «или» используется в исключающем (разделительном) смысле. Такая операция называется строгой дизъюнкцией.
Определите самостоятельно вид дизъюнкции:
| Высказывание | Вид дизъюнкции |
| Петя сидит на западной или восточной трибуне стадиона. | Строгая |
| Студент едет в электричке или читает книгу. | Нестрогая |
| Ты выйдешь замуж или за Петю, или за Сашу. | Строгая |
| Ты женишься на Вале или на Свете | Строгая |
| Завтра дождь будет или не будет. | Строгая |
| Давайте бороться за чистоту. Чистота достигается так: или не сорить, или часто убирать. | Нестрогая |
| Учителя бывают или строгие , или не наши. | Нестрогая |
Далее будем рассматривать только нестрогую дизъюнкцию.
Обозначение: А
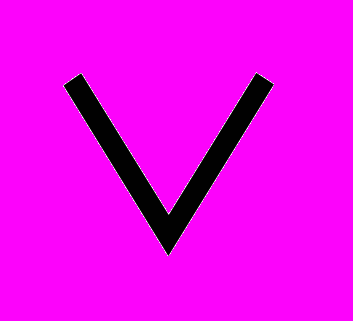 В.
В.| Таблица истинности | Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно высказывание истинно. | ||||||||||||||
|
Мнемоническое правило: дизъюнкция – это логическое сложение и легко заметить, что равенства 0+0=0; 0+1=1; 1+0=1; верные для обычного сложения, верны и для операции дизъюнкции, но 1
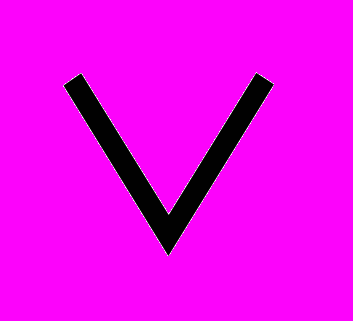 1=1.
1=1.Логическое следование (импликация)
Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если….., то…..».
Обозначения: А→В, А
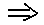 В.
В.Пример. А={2·2=4} и В={3·3=10}.
А
 В={Если 2·2=4, то 3·3=10 }
В={Если 2·2=4, то 3·3=10 }| Таблица истинности | Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное. | ||||||||||||||
|
Логическое равенство (эквивалентность)
Эквивалентность образуется соединением двух высказываний в одно при помощи оборота речи «….тогда и только тогда, когда…».
Обозначение эквивалентности: А=В; А
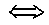 В; А~В.
В; А~В.Пример:
А={Угол прямой}; В={Угол равен 900}
А
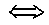 В={Угол называется прямым тогда и только тогда, когда он равен 900}
В={Угол называется прямым тогда и только тогда, когда он равен 900}| Таблица истинности | Эквивалентность двух высказываний истинна тогда и только тогда, когда оба высказывания истинны или оба ложны. | ||||||||||||||
|
Приоритет операций:
- инверсия;
- конъюнкция;
- дизъюнкция;
- импликация и эквивалентность.
Для закрепления материала выполняются следующие задания:
| 1. Ниже приведена таблица, левая колонка которой содержит основные логические союзы (связки), с помощью которых в естественном языке строятся сложные высказывания. Заполните правую колонку таблицы соответствующими названиями логических операций. | |
| В естественном языке | В логике |
| …….и……. | *конъюнкция |
| ……или…… | *дизъюнкция |
| …..Неверно, что….. | *инверсия |
| …..в том и только в том случае…. | эквивалентность |
| ……но….. | конъюнкция |
| …..а….. | конъюнкция |
| Если…., то….. | *импликация |
| ……однако…. | конъюнкция |
| ….тогда и только тогда, когда…. | эквивалентность |
| Либо….либо… | *строгая дизъюнкция |
| ….необходимо и достаточно…. | *эквивалентность |
| Из ………следует…. | *импликация |
| ……влечёт…. | импликация |
| ……равносильно…. | эквивалентность |
| *- выполняется дома. | |
| 2. Сформулируйте отрицания следующих высказываний: А) { Неверно, что город Нью-Йорк является столицей США}; Б) {Коля решил все 6 заданий контрольный работы}; В) {Неверно, что число 3 не является делителем числа 198}. | |
А) ((1 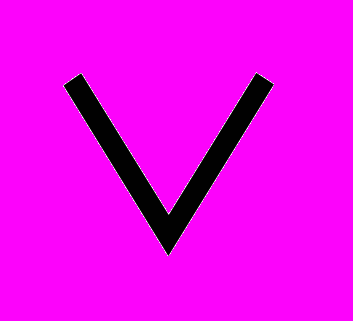 0) 0)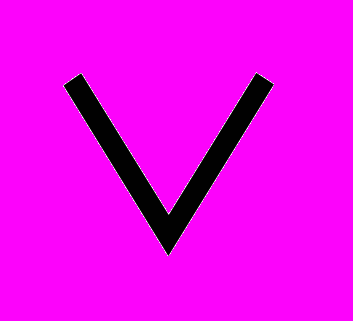 1) 1)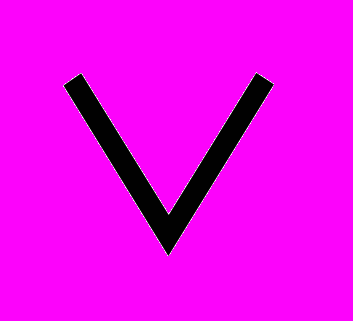 1; Б) ((1 1; Б) ((1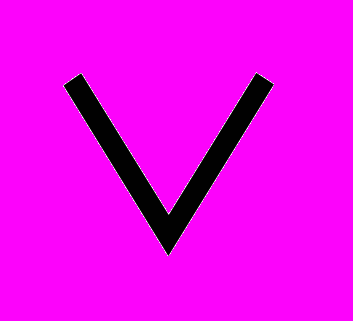 0)& (1&1))& (0 0)& (1&1))& (0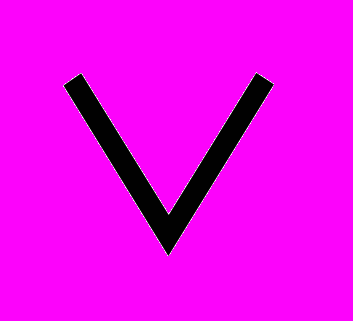 1); В) ((0&0) 1); В) ((0&0)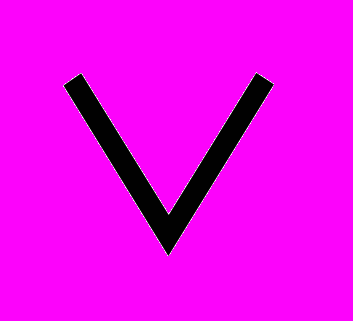 0)& (1 0)& (1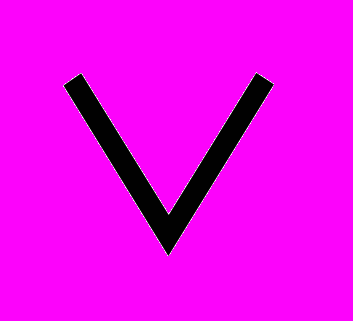 1). 1). | |
Очевидно, что А=1, В=0. В чём заключаются следующие высказывания: А) 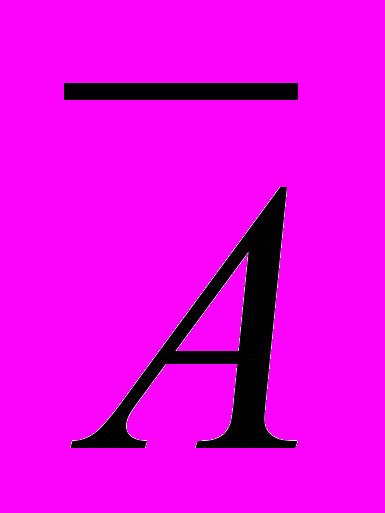 ; Б) А&В; В) А ; Б) А&В; В) А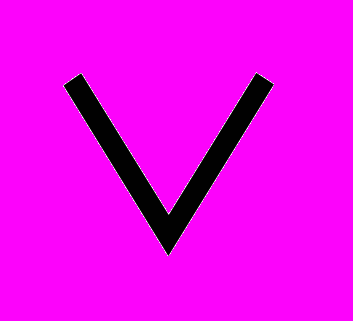 В; Г) А В; Г) А 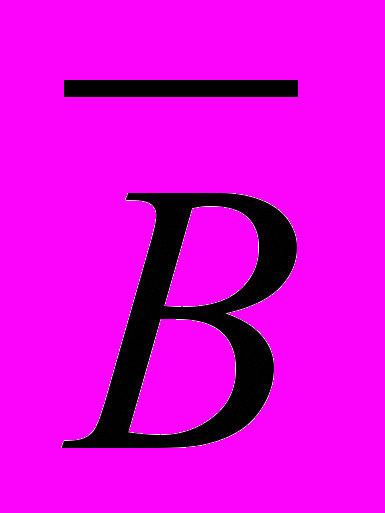 ; Д) ; Д) 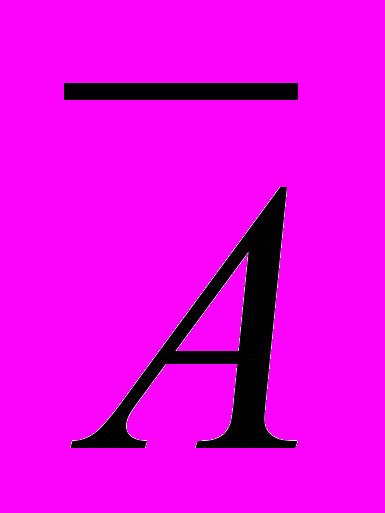 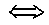 В. В.Какие из этих высказываний истинны? | |
Подведение итогов урока
- Мы рассмотрели основные логические операции:
- инверсию (логическое отрицание);
- конъюнкцию (логическое сложение);
- дизъюнкцию (логическое умножение);
- импликацию (логическое следование) и эквивалентность (логическое равенство).
- Именно в таком порядке реализуется приоритет логических операций.
Постановка домашнего задания
- Прочитать §3.2. [1].
- Выучить конспект урока (логические операции: название, обозначение, таблицу истинности, правило).
- Выполнить до конца задание 1 из классной работы.
- Выполнить упражнения с карточки в тетради. Листочек с классной работой вклеить в тетрадь, карточку принести.
Все пункты заданий на карточке учитель должен прокомментировать.
Карточка для домашней работы:
А={2·2=4}, В={4·4=15}. Составьте следующие сложные высказывания. Какие из них истинны? А) 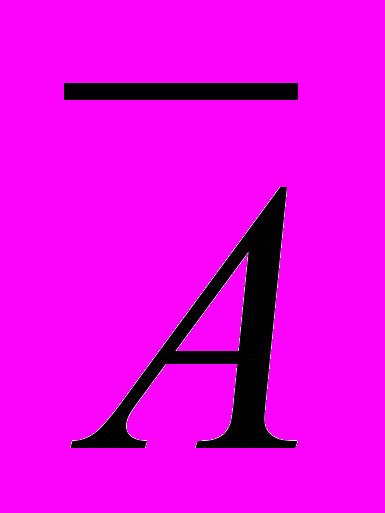 ; Б) А& В; В) А ; Б) А& В; В) А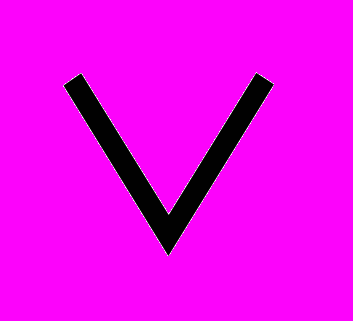 В; Г) В; Г) 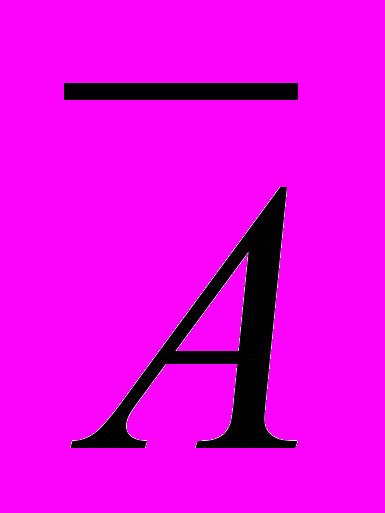  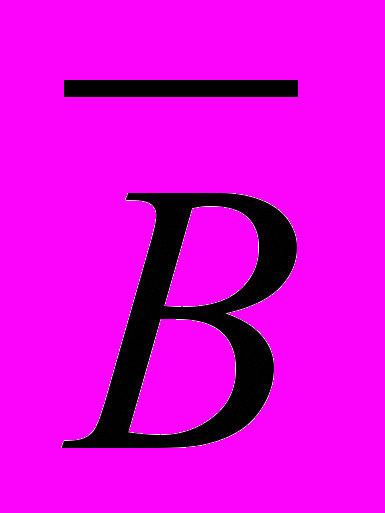 ; Д) А ; Д) А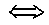 В. В. |
А) (1  1) 1) (1 (1 0); Б) (0 & 1)& 1; В) ((1& 0) 0); Б) (0 & 1)& 1; В) ((1& 0) (0&1)) (0&1))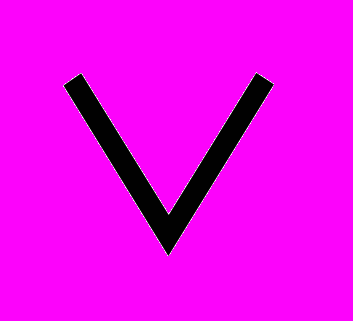 1; Г) ((1&1) 1; Г) ((1&1)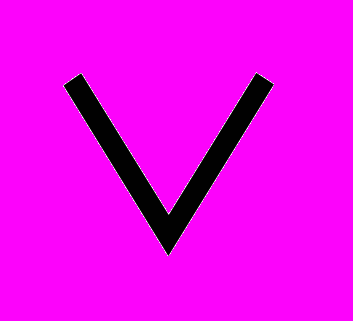 0)·& (0 0)·& (0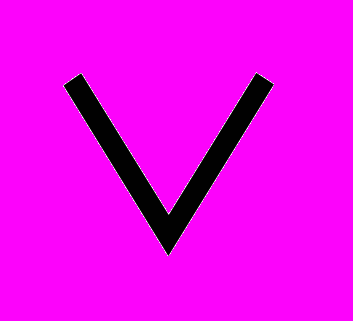 1). 1). |
| *3. Даны простые высказывания: А={Принтер- устройство ввода информации}, В={Процессор- устройство обработки информации}, С= {Монитор- устройство хранения информации}, D={Клавиатура- устройство ввода информации}. Определите истинность составных высказываний: А) (А&В)&(С 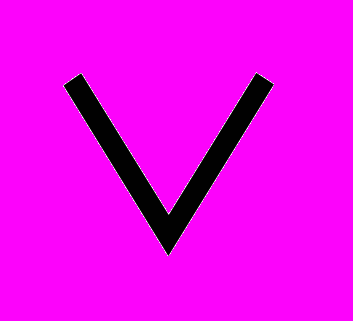 D); Б) (А& В) D); Б) (А& В) (В& С); В) (А (В& С); В) (А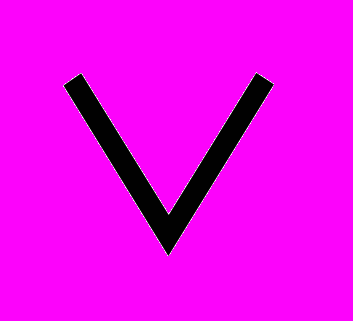 В) В)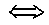 (С& D); Г) (С& D); Г) 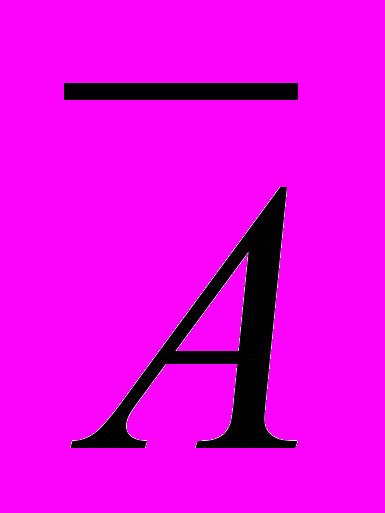 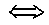 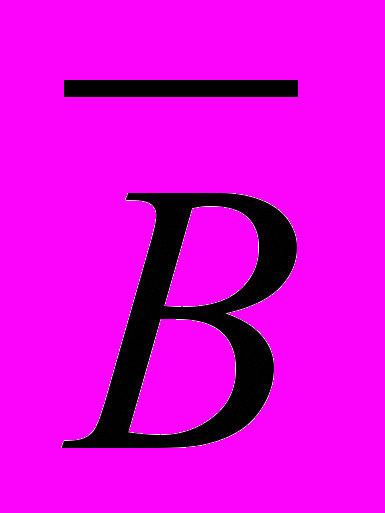 . . |
| Дополнительное задание. Дано составное высказывание не (неА и В), где А и В – простые высказывания. В каком случае данное высказывание будет ложным? |
*Задание на «5».
1 (по книге В. Лысковой и Е. Ракитиной «Логика в информатике)
