Міністерство охорони навколишнього природного середовища україни український науково-дослідний інститут екологічних проблем (Укрндіеп)
| Вид материала | Документы |
СодержаниеЕ – енергія хвиль на 1 м акваторії; u |
- Міністерство охорони навколишнього природного середовища україни український науково-дослідний, 845.13kb.
- Міністерство охорони навколишнього природного середовища україни державне управління, 2953.07kb.
- Міністерство охорони навколишнього природного середовища України Державне управління, 6929.63kb.
- Міністерство охорони навколищнього природного середовища україни державне управління, 6100.26kb.
- Міністерство екології та природних ресурсів україни державне управління охорони навколишнього, 6497kb.
- Україна міністерство охорони навколишнього природного середовища україни, 156.84kb.
- Міністерство охорони навколишнього природного середовища України, 1698.24kb.
- Форма оголошення про проведення відкритих торгів, 20.04kb.
- Форма оголошення про проведення відкритих торгів, 18.34kb.
- Охорони навколишнього природного середовища україни Державне управління охорони навколишнього, 3996.75kb.
3. РОЗРОБКА НАУКОВОГО ОБҐРУНТУВАННЯ ТА РЕКОМЕНДАЦІЙ ЩОДО УКРІПЛЕННЯ БЕРЕГІВ ПОВЕРХНЕВИХ ВОДНИХ ОБ'ЄКТІВ І УЗБЕРЕЖЖЯ МОРІВ ШЛЯХОМ СПОРУДЖЕННЯ ШТУЧНИХ РИФІВ ЯК БІОПОЗИТИВНИХ БЕРЕГОРЕГУЛЮВАЛЬНИХ СИСТЕМ
3.1 Розробка наукового обґрунтування щодо укріплення берегів поверхневих водних об’єктів і узбережжя морів шляхом спорудження штучних рифів як біопозитивних берегорегулювальних систем
Головний фактор розвитку берегів і рухома сила більшості берегових процесів, що відбуваються у морях, великих водоймищах і озерах – це хвилі, дрейфові і компенсаційні плини, виконані вітром і діючі одночасно з хвилями. У залежності від місцевих умов хвилі або роблять руйнування (абразія) корінних порід берегової зони, або нарощують його, акумулюючи уздовж берега наноси, або підтримують стабільний контур і профіль берега.
Активним фактором розвитку берегової зони є різні групи організмів, що утворюються на дні. У Чорному морі такими організмами є свердлильники, до яких з молюсків відноситься Petricola lithophoda, Pholas sp. – на кам'янистому дні і Barnea candida – на глинистому дні, а з губок – Cliona. У деяких випадках ці організми можуть впливати на береги і дно. Такі водорості як цитозира (Cistoseira Barbata) утворюють у берегів «подушку», що гасить удар хвилі. Живий черепашник на дні (наприклад, устричні банки) захищає ґрунт від розмиву. Це може відноситься і до суцільного покриву мертвого черепашнику.
Математичну модель розвитку берегової екосистеми можна представити у виді рівнянь, що враховують баланс уламкового матеріалу [20], а також продукцію уламкового ненаносоутворюючого матеріалу в береговій зоні та динаміку біомаси:
, (3.1)
, (3.2)де W – обсяг пляжі- і наносоутворюючого матеріалу (починаючи з піщаних фракцій) на одиницю довжини берегової лінії (0<W<Wmin), м3; Wmin – граничний мінімальний обсяг уламкового матеріалу на пляжі, при якому абразія припиняється, м3; В – біомаса донного біоценозу на одиницю ширини абразивної обмілини (шельфу) (0<B
Коефіцієнт стиранності k лінійно залежить від біомаси донного біоценоза В:
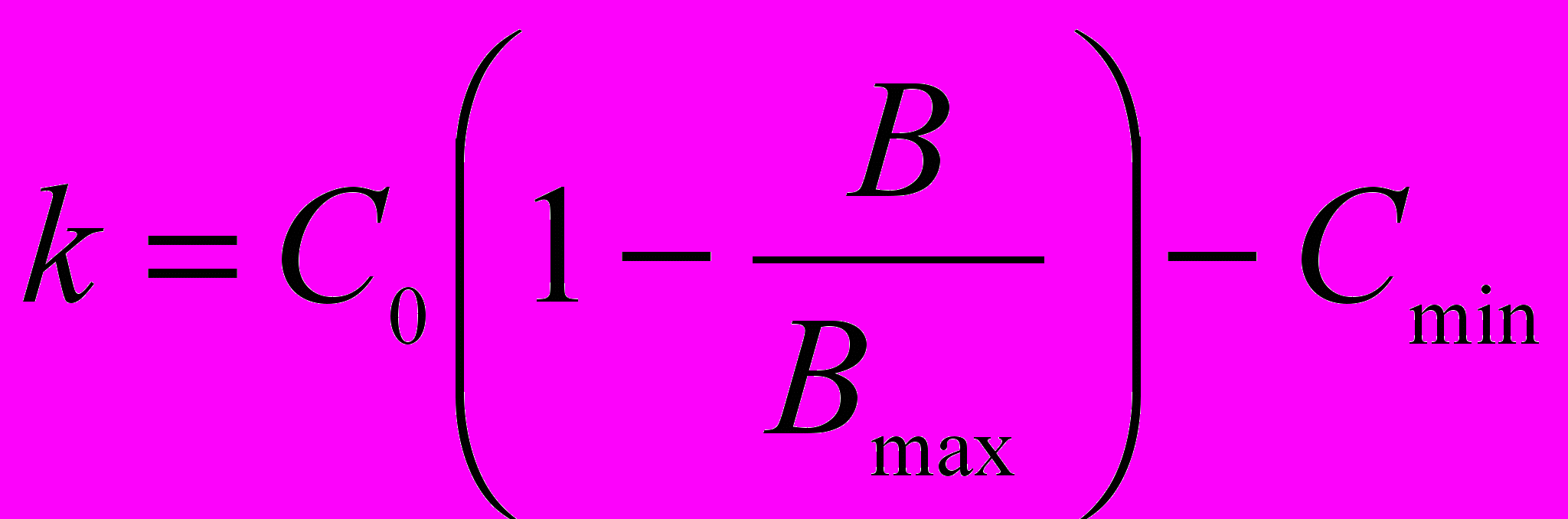(3.3)Рівняння (3.3) отримано з урахуванням наступних положень:
- приріст біомаси донного біоценозу зменшується при збільшенні обсягу уламкового наносоутворюючого матеріалу (він сприяє гнобленню і деградації донного біоценозу);
- саморегульований ріст біомаси донного біоценозу описується відомим логистическим рівнянням.
Система диференціальних рівнянь (3.1, 3.2) вирішується при наступних початкових умовах:
W(t0)=W0 (3.4)
В(t0)=В0 (3.5)
Якщо W>0, то це відповідає стійкому стану берегової лінії, W<0 свідчить про перевагу процесів абразії.
3.1.1. Наукове обґрунтування щодо укріплення берегів поверхневих водних об’єктів і узбережжя морів шляхом спорудження штучних рифів у вигляді рядів затоплених хвилеломів типу „Швейцарський сир”
Ідеї затоплених хвилеломів у СРСР були висунуті Е.Е. Кітраном в 1928 р. [21]. У 1933 р. з його ініціативи в берегів Одеси були побудовані штучні підвідні хвилеломи довжиною 250 м на відстані 90 м від урезу води, гребінь хвилелому знаходився на 1,5 м нижче рівня води. Після шторму між берегом і хвилеломом відбулося відкладення наносів [22]. Конструкція затопленого хвилелому, застосовувана для зміцнення берегів Чорного моря, представлена на рис. 3.1, 3.2.
Рис. 3.1. Схема затопленого хвилелому
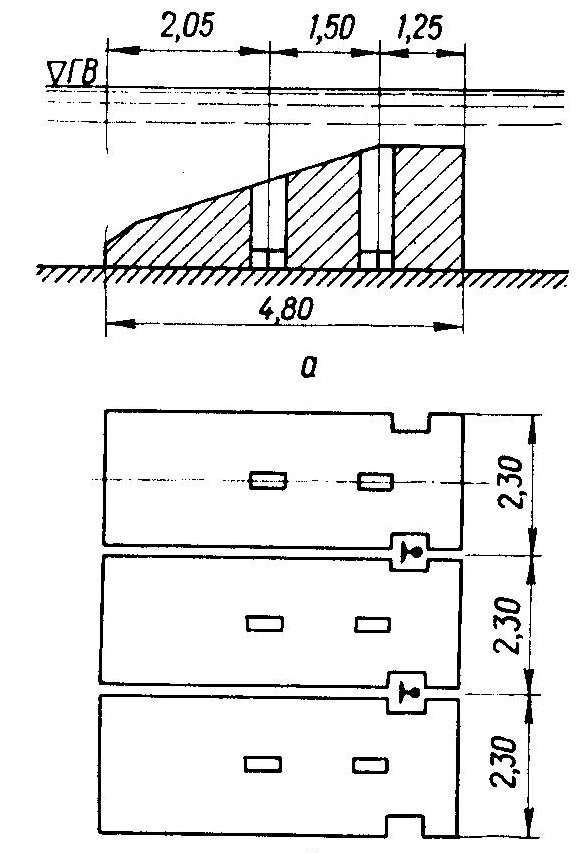
Рис. 3.2. Конструкція берегового хвилелому з бетонних масивів: а) розріз по осі; б) план
Хвилелом складався з бетонних масивів вагою 30 т. Висота масивів варіювалася в межах 1,5 – 1,9 м, ширина – 4,5 – 5,1 м, довжина – 2,0 – 2,7 м. Зовнішня грань хвилелому похила, з коефіцієнтом укосу 3,0 (m=ctg, де – кут між укосом та обрієм).
У бокових вертикальних гранях масивів передбачені пази, що утворюються при установці масивів шахти між кожною парою масивів. Через ці шахти в підставу заглиблюються на 1,5 м залізничні рейки. Потім шахти заповнюються бетоном. Це забезпечує гарне з'єднання масиву з підставою і перекриває шви між масивами, через які може відбуватися витік наносів, що відклалися між берегом і хвилеломом. Хвилеломи розташовувалися на глибинах 1,7 – 2,5 м. Гребінь хвилелому розташовувався на 0,2 – 0,6 м нижче середні рівні води. Відстань хвилелому від берега складала 20 – 40 м. Висота хвилі за хвилеломом зменшалась приблизно в 2 рази.
Перші лабораторні дослідження затоплених хвилеломів були проведені А. Стуккі та Д. Боннаром у 1937 р. у Швейцарії [23]. У СРСР лабораторні дослідження підводних хвилеломів почалися проводитися з 1940 р. [22]. З цього ж року подібні дослідження стали проводитися й у США Управлінням берегової ерозії [24].
Великий інтерес представляли експериментальні дослідження підводних хвилеломів, виконані І. Морісом [25], А.І. Лизловим [26, 27], В.С. Гамаженко [28], В.Н. Сідорчуком , В.З. Аверіним [29].
Теоретичні дослідження підводних хвилеломів і коефіцієнтів гасіння хвилі були виконані Джеффером [30], Х. Ламбом [31], Ж. Джонсоном, А. Фуксом та І. Морісом [32].
При зустрічі з підводним хвилеломом енергія вихідних хвиль частково передається залишковим хвилям між берегом і хвилеломом, частково відбиває від хвилелому. Довжина хвилі зменшується в хвилелому, а за ним відновлюється до вихідної величини. Схема затопленого хвилелому представлена на рис. 3.3.
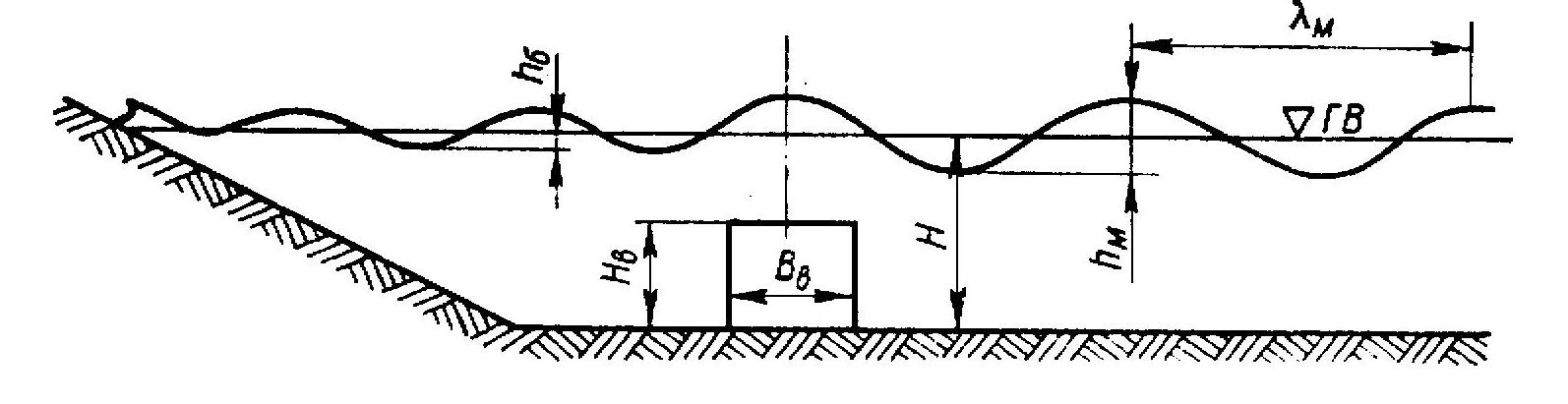
Рис. 3.3. Схема затопленого хвилелому на горизонтальному дні.
Для опису процесів ослаблення (гасіння) хвилі за хвилеломом були використані наступні роботи [22, 31, 32].
Рівняння балансу енергії вітрових хвиль має вигляд [22]:
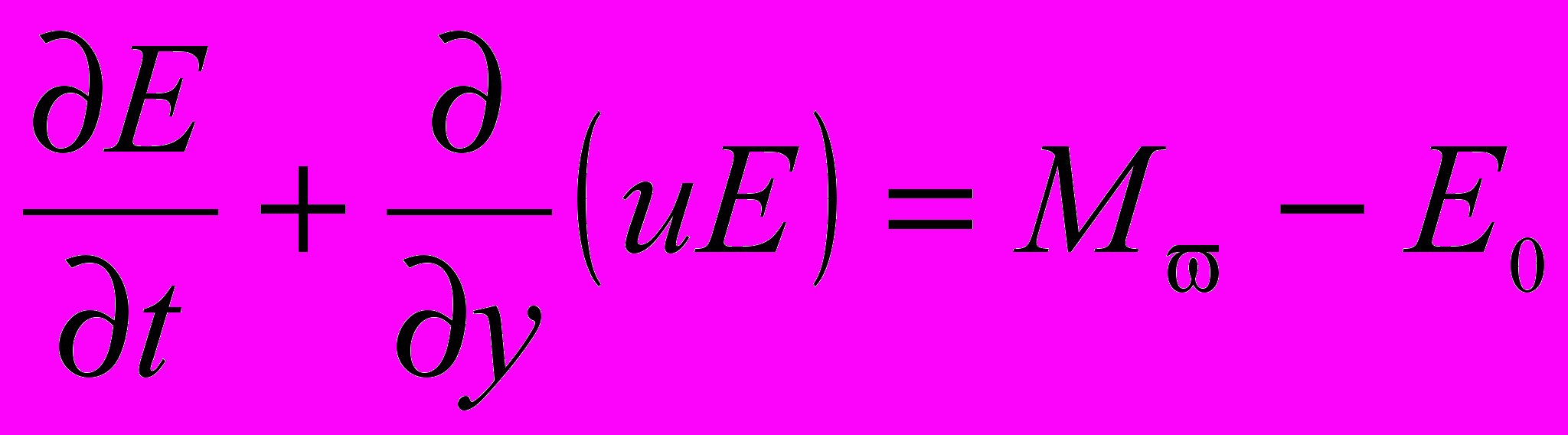(3.6)де Е – енергія хвиль на 1 м2 акваторії; u – швидкість переносу енергії; М – енергія, одержувана хвилею від вітру; Е0 – втрачена енергія хвилі,; y – напрямок руху хвилі; t – час.
Відповідно до досліджень Х. Ламба та И. Моріса [31, 32], повна енергія вихідної хвилі дорівнює
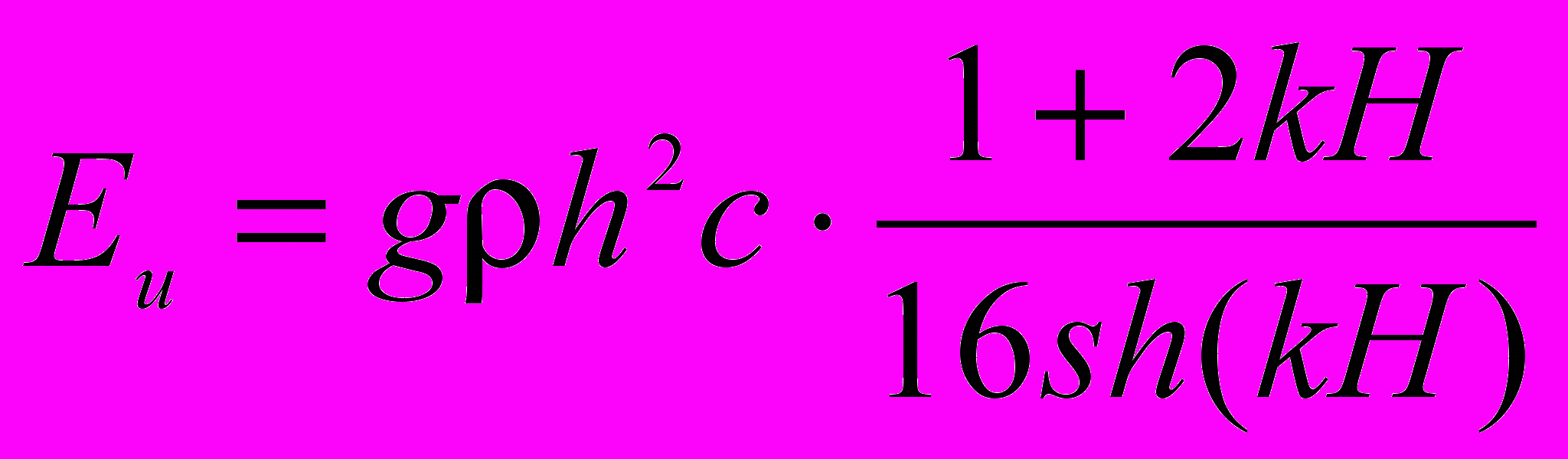, (3.7)де – щільність; с – швидкість розповсюдження хвилі на дрібній воді; k=2/ – хвильове число; – довжина хвилі.
Енергія, відбита хвилеломом, визначається за формулою [22]
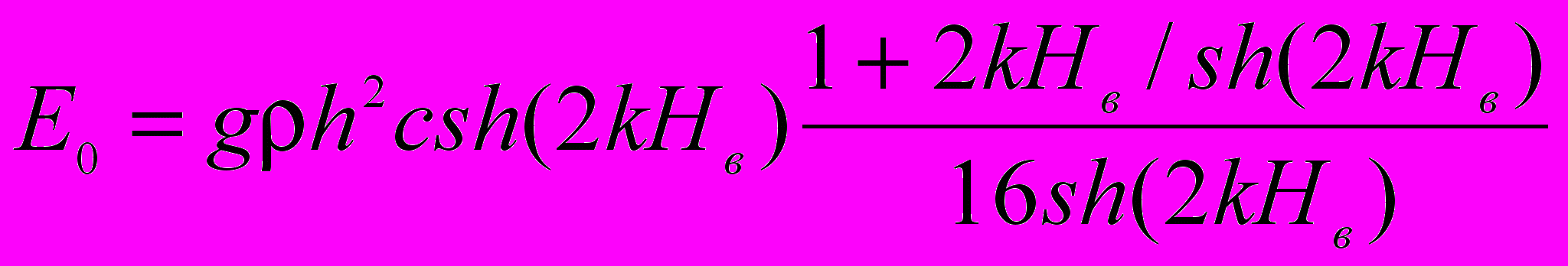, (3.8)де g – прискорення вільного падіння.
Енергія, що переходить за хвилелом, знаходиться шляхом вирахування (3.8) з (3.7):
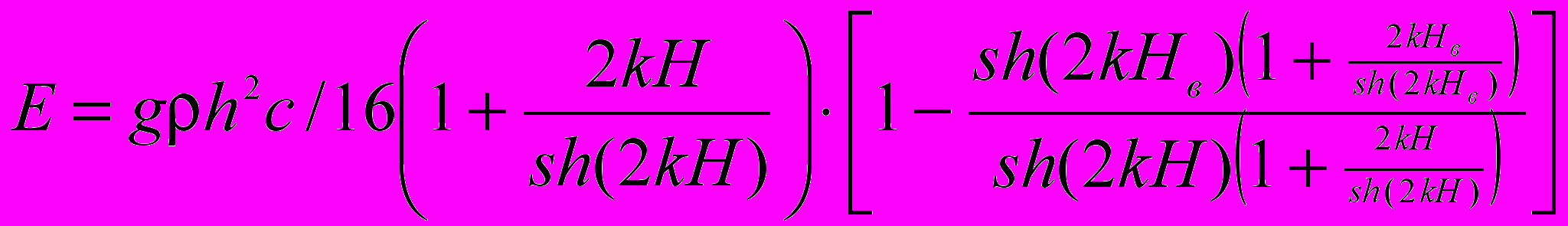(3.9)При постійному періоді хвилі її дліна та швидкість визначаються по формулах:
, (3.10)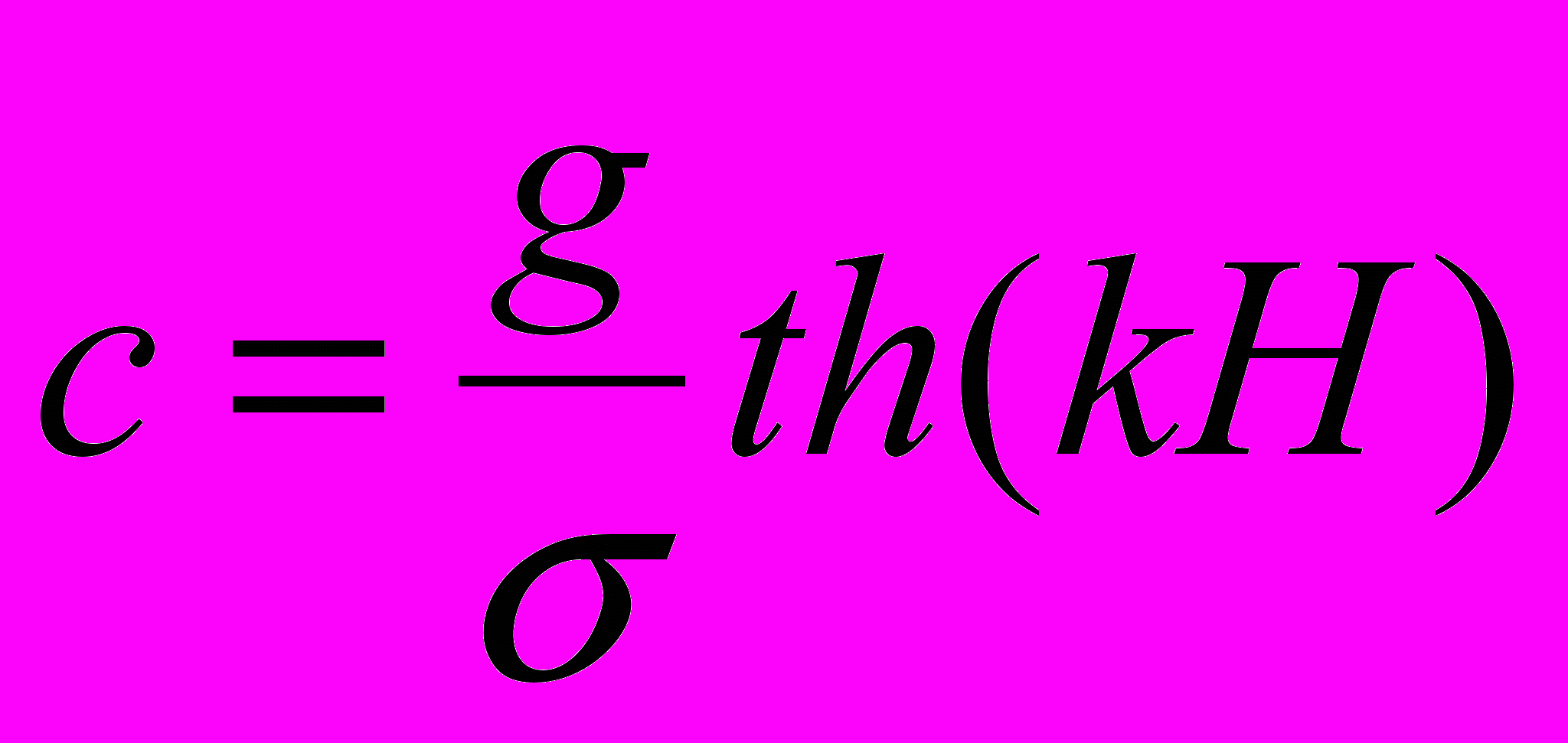
, (3.11)де =2/.
Основною характеристикою хвилелому є коефіцієнт гасіння хвилі, Кг [14]:
, (3.12)де hб – висота хвилі між берегом і хвилеломом; hм – висота хвилі з морської сторони хвилелому.
Тобто Кг показує, во скільки разів зменшується висота хвилі між берегом і хвилеломом стосовно висоти хвилі мористій хвилелому.
Якщо висота хвилі виміряється на глибині Н між хвилеломом і берегом, то Кг дорівнює [22]
, (3.13)де
, (3.14)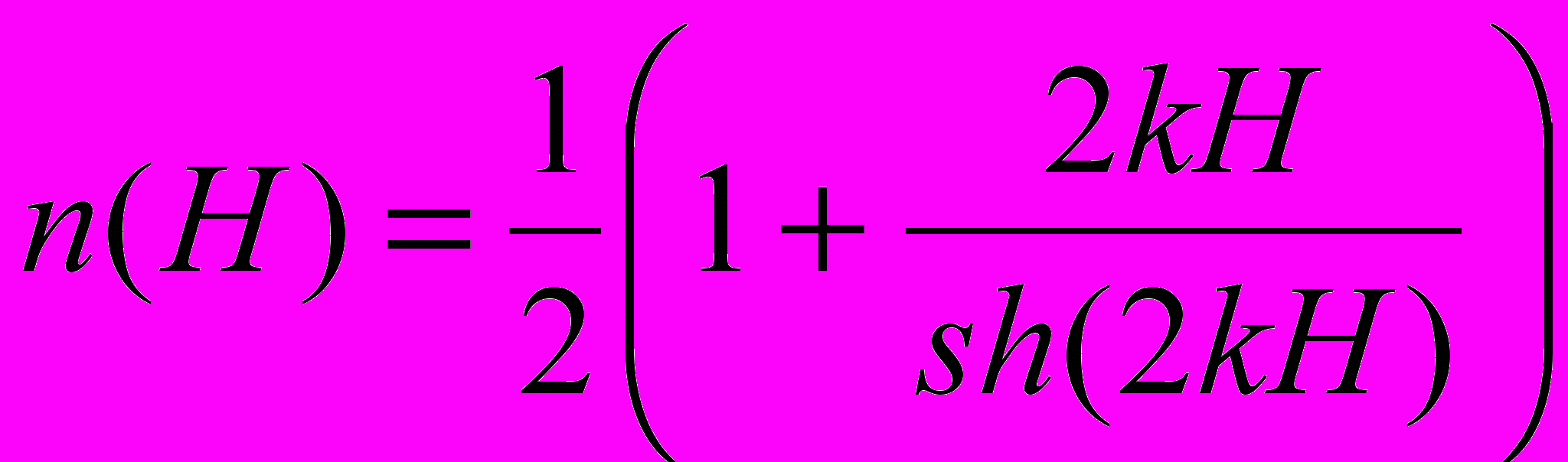
. (3.15)Якщо хвиля виміряється на хвилеломі, то коефіцієнт гасіння хвилі (Кг)а дорівнює
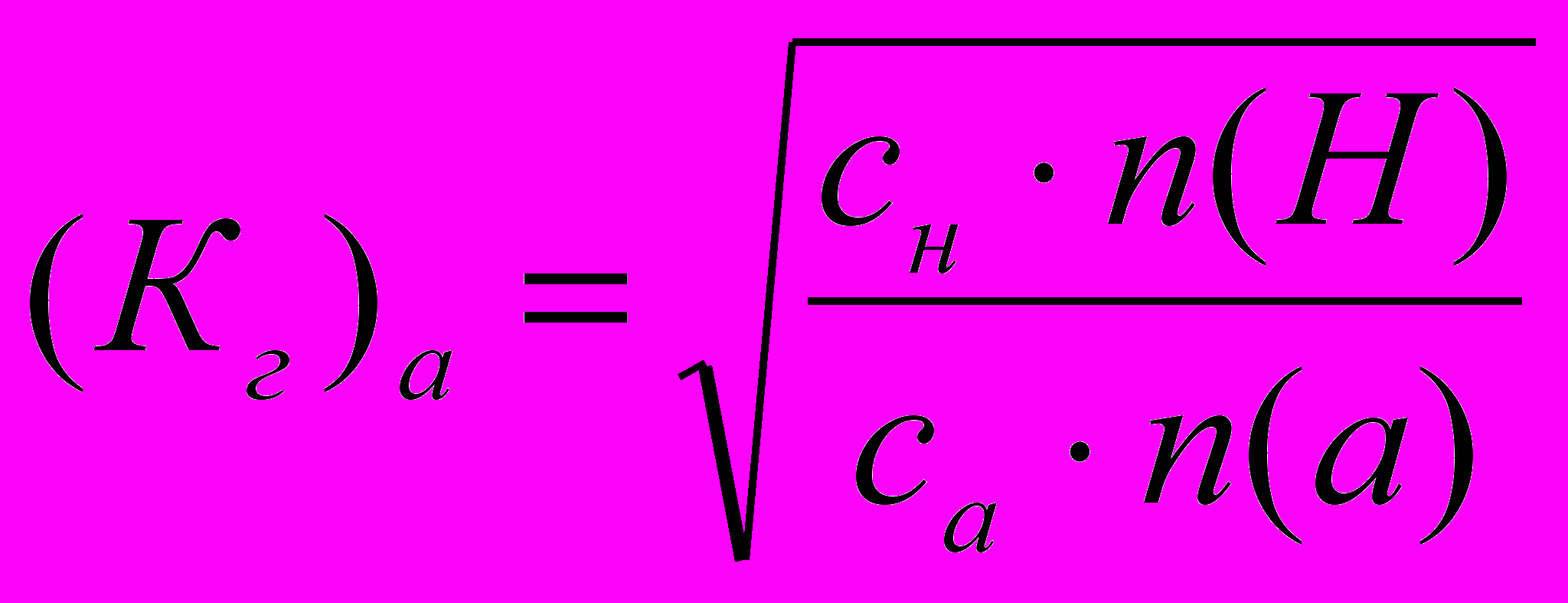, (3.16)де а=Н-Нв, са = g/6th(Ka),
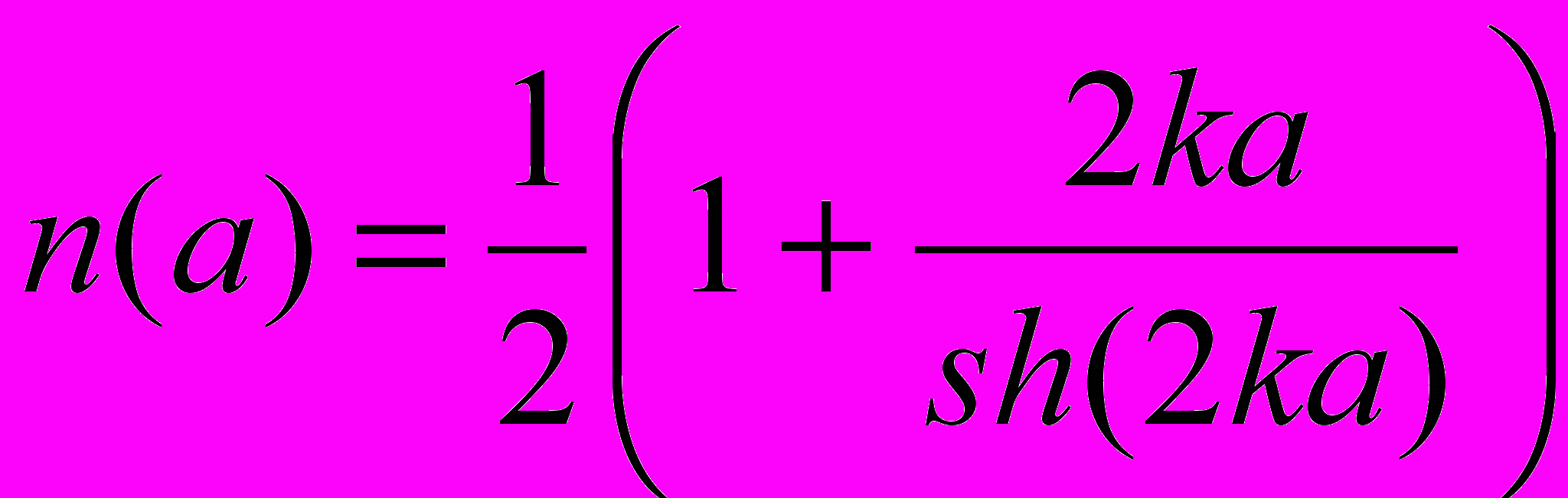, (3.18)Для дрібної води (kН<<1) коефіцієнт гасіння хвилі на березі (Кг)н і на хвилеломі відповідно рівні:
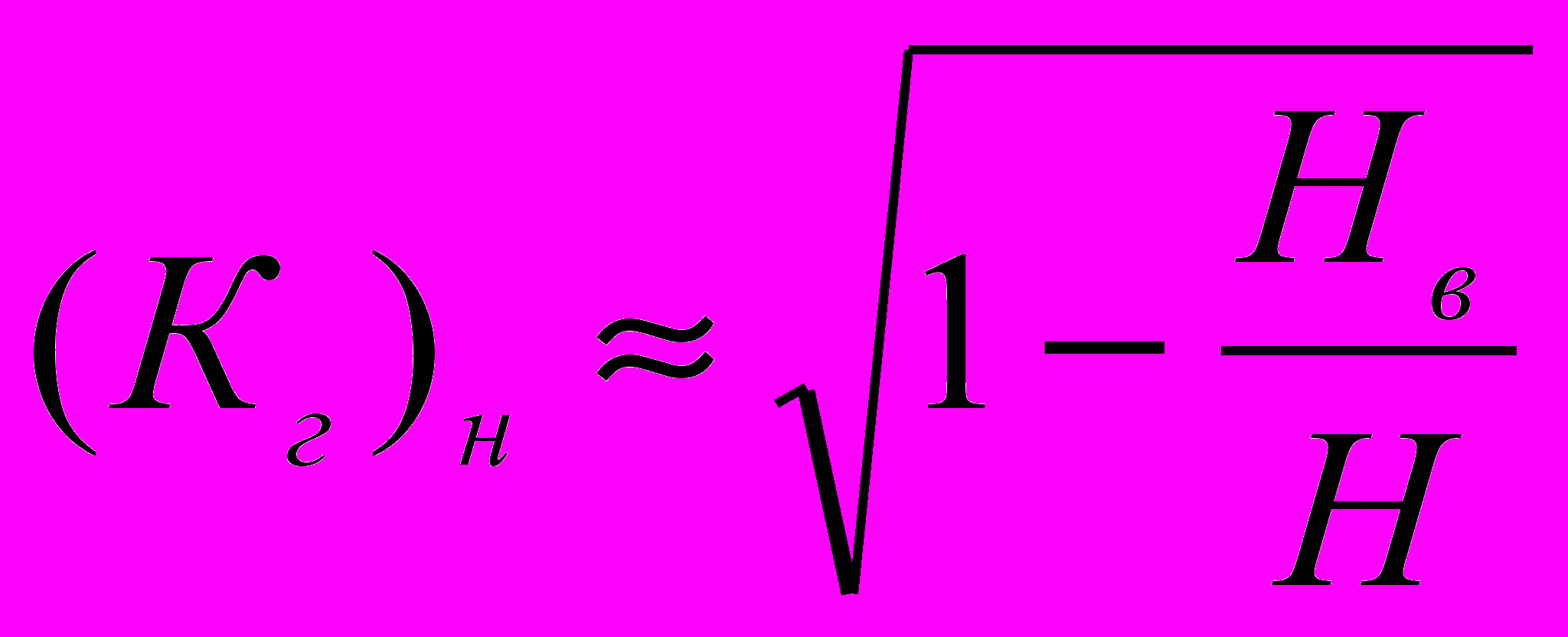, (3.19)
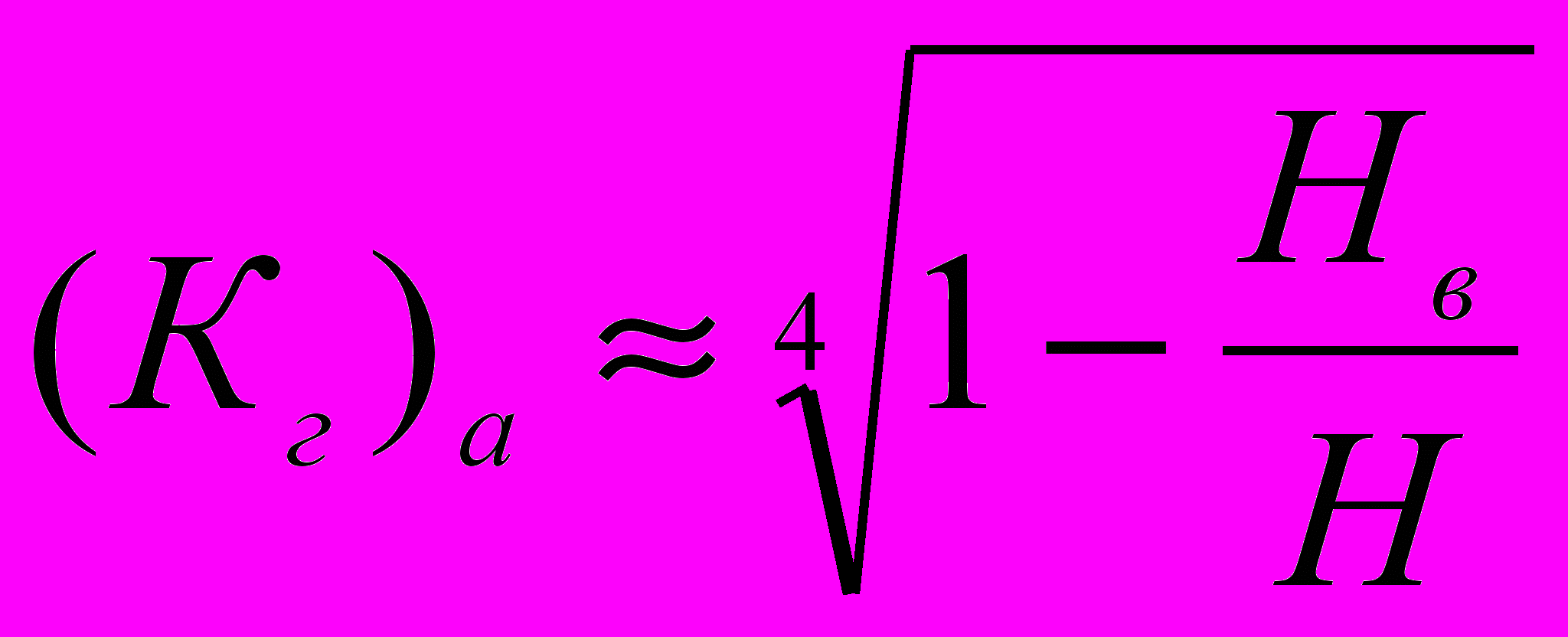, (3.20)Для глибокої води (kН>>1):
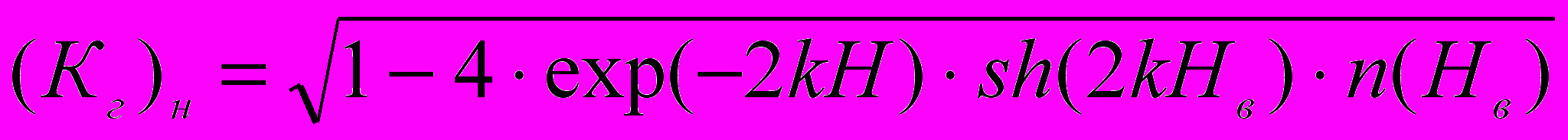,Експериментальні дослідження свідчать, що при збільшенні ширини гребеня хвилелому хвилезгаслий ефект збільшується [26] (табл. 3.1).
Таблиця 3.1. Гасіння висоти хвилі в залежності від ширини гребеня хвилелому.
| Ширина гребеня, м | Гасіння висоти хвилі, % при заглибленні гребеня | |
| до відмітки 1,0 м | до відмітки 0,0 м | |
| 5,6 | 50 | 62 |
| 3,2 | 31 | 50 |
| 0,8 | 25 | 25 |
Для більш повного гасіння енергії хвилі, а також при змінному обрії рівня води у водному об'єкті доцільно за першим рядом хвилеломів установлювати другий, третій і т.д. ряд.
Хвилелом рекомендується проектувати так, щоб хвиля розбивалася між берегом і хвилеломом, що забезпечує краще гасіння енергії хвилі. У цьому випадку штучний риф розташовують на глибині
d = 1,6·h (3.21)
Мінімальні і максимальні глибини над хвилеломом для забезпечення розбивання хвилі за хвилеломом (штучним рифом) складають:
Нг min = 0,5·h, (3.22)
Нг мах = 1,1·h. (3.23)
При цих глибинах коефіцієнти гасіння відповідно складають:
Кг1 = 0,35, (3.24)
Кг2 = 0,60. (3.25)
Нижче наводиться приклад розрахунку штучного рифа у виді затоплених масивів з прохідними отворами («Швейцарський сир»). Нехай потрібно захистити піщаний пляж від хвиль висотою 2,6 м (максимальні висоти для району Євпаторії). Хвилелом рекомендується установити на глибині
d = 1,6·h = 1,6·2,6 м = 4,16 м.
Глибину води над гребенем першого хвилелому приймаємо рівною
Нг1 = 0,5·h = 0,5·2,6 м = 1,3 м.
Розрахункова висота хвилі за першим хвилелому дорівнює
Нг2 = 0,35·h = 0,35·2,6 м = 0,91 м.
Для гасіння цієї хвилі використовуємо другий ряд хвилеломів, що розраховується аналогічно
Нг2 = 0,5·Н2 = 0,5·0,91 м = 0,46 м.
Другий хвилелом розташуємо на глибині
d = 1,6·Н2 = 1,6·0,91 м = 1,47 м.
Висоту хвилі за другим хвилеломом розраховуємо по формулі
Н3= 0,3·Н2 = 0,3·0,91 м = 0,32.
Дану висоту хвилі можна вважати безпечною для піщаного пляжу.
3.1.2. Наукове обґрунтування щодо укріплення берегів поверхневих водних об’єктів і узбережжя морів шляхом спорудження штучних рифів у вигляді ряду затоплених „шарів” (штучні рифи “Reef Ball”)
В сучасний час широке розповсюдження одержали конструкції штучних рифів за назвою «Reef Ball». Як структурний елемент рифа використовується усічена вгорі півсфера (див. рис. 2.1, 2.5).
Для затоплених рифів має місце Нв/Н<1, для надводних – Нв/Н>1. Параметр F=Нв-H характеризує заглиблення верхівки штучного рифа. Кут характеризує ухил штучного рифа до дна з боку моря, кут характеризує ухил штучного рифа до дна з боку берега.
Характер руйнування хвилі біля берегу характеризується числом Ірибаррена [33] і визначається як
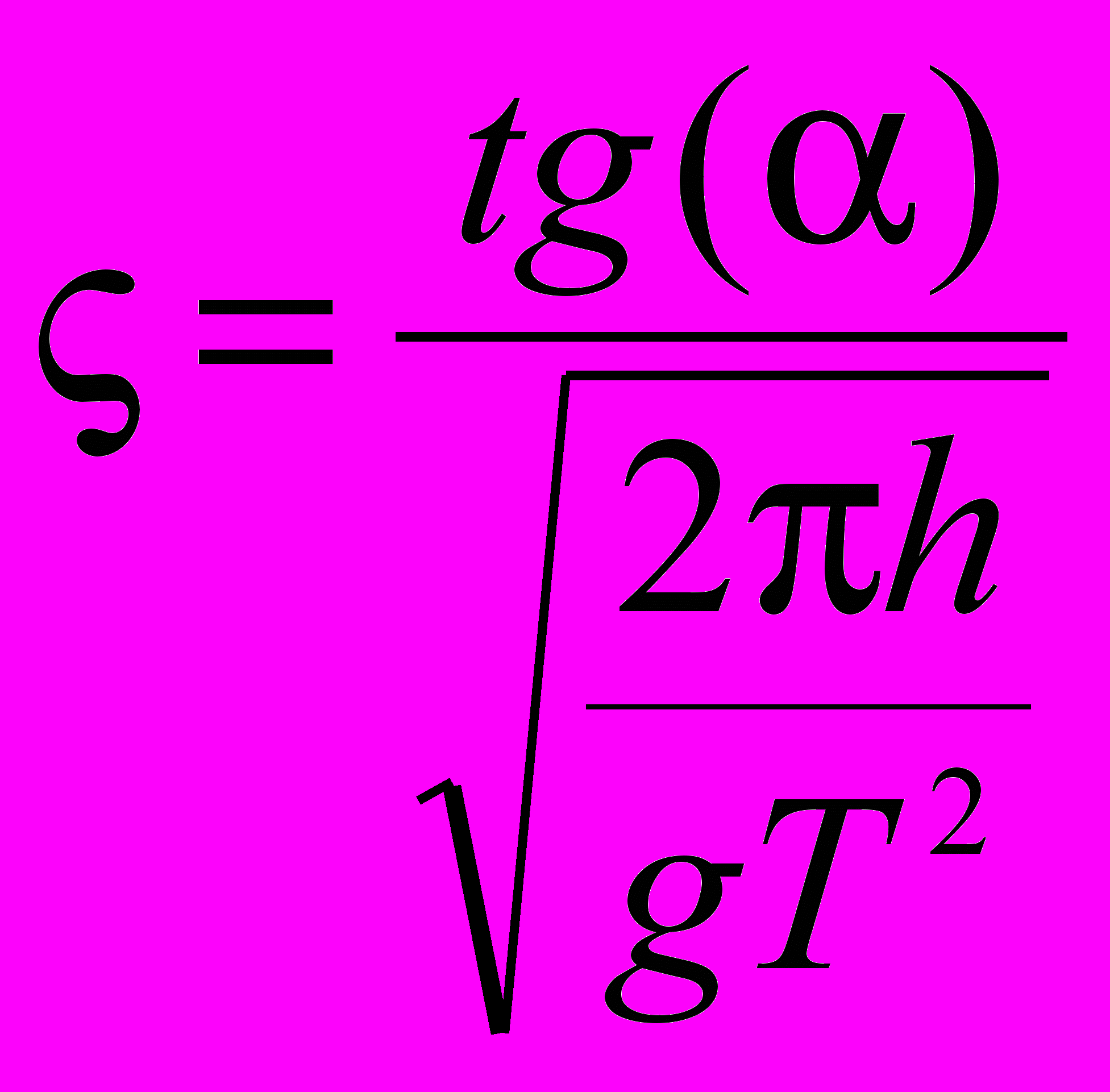, (3.26)де Т – період хвилі.
У залежності від величини ( виділяють наступні режими руйнування хвилі:
<0,5 – «розсипання» хвилі («spilling»);
=0,53 – «перекидання» хвилі («plunging»);
=33,5 – «руйнування» хвилі («collapsing»);
>3,5 – «бурхливе руйнування» хвилі («surging»).
У табл. 3.2 – 3.3 представлені характерні розміри елемента штучного рифа та типи обвалення хвилі [33].
Таблиця 3.2. Хвильові властивості передньої грані штучного рифу
| Висота хвилі, м | 1,94 | 2,51 | 2,91 | 3,18 | 3,37 | 3,51 | 3,61 |
| Хвильовий період, з | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 |
| Висота переднього схилу, м | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Ширина, м | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| Кут , радий | 2,86 | 2,86 | 2,86 | 2,86 | 2,86 | 2,86 | 2,86 |
| Параметр | 0,135 | 0,158 | 0,183 | 0,210 | 0,238 | 0,267 | 0,296 |
| Тип руйнування хвилі | розсипання (spilling) | розсипання (spilling) | розсипання (spilling) | розсипання (spilling) | розсипання (spilling) | розсипання (spilling) | розсипання (spilling) |
Таблиця 3.3. Хвильові властивості штучного рифу
| Висота хвилі, м | 1,59 | 2,03 | 2,34 | 2,54 | 2,69 | 2,79 | 2,87 |
| Хвильовий період, з | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 |
| Висота переднього схилу, м | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Ширина, м | 2 | 2 | 2 | 2 | 2 | 2 | 1 |
| Кут , радий | 26,57 | 26,57 | 26,57 | 26,57 | 26,57 | 26,57 | 26,57 |
| Параметр | 1,490 | 1,754 | 2,045 | 2,352 | 2,669 | 2,994 | 3,323 |
| Тип руйнування хвилі | руйнування (plunging) | руйнування (plunging) | руйнування (plunging) | руйнування (plunging) | руйнування (plunging) | руйнування (plunging) | бурхливе руйнування (соllарsіng) |
Відповідно до досліджень [34, 35], руйнування хвилі при підході до берега відбувається на глибині Н коли h/Н=0,78.
Важливим параметром штучного рифу є відношення
. (3.27)Коли F/H<1, то хвилі легко проходять над верхівкою структурного елемента (штучного рифу) [33]. У противному випадку, коли структурна висота більше рівня спокійної води, то хвильова енергія хвилі цілком поглинається структурним елементом. У роботі [28] приводиться емпірична формула коефіцієнта гасіння хвилі при F/H>1:
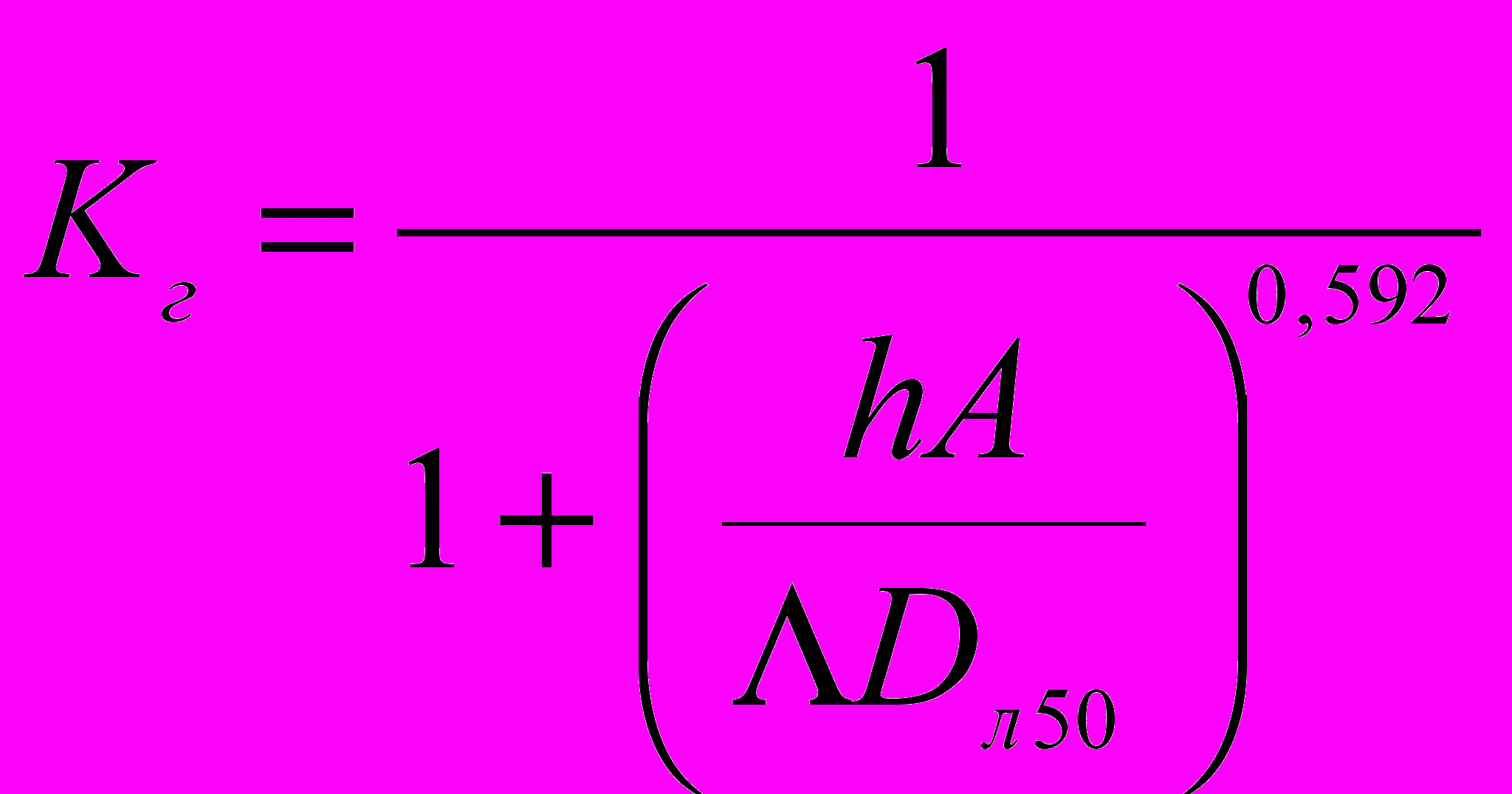. (3.28)де А – площа поперечний перетину хвилелому (штучного рифа), Dл50 – характерний середній розмір елементу штучного рифу, визначаємий за формулою
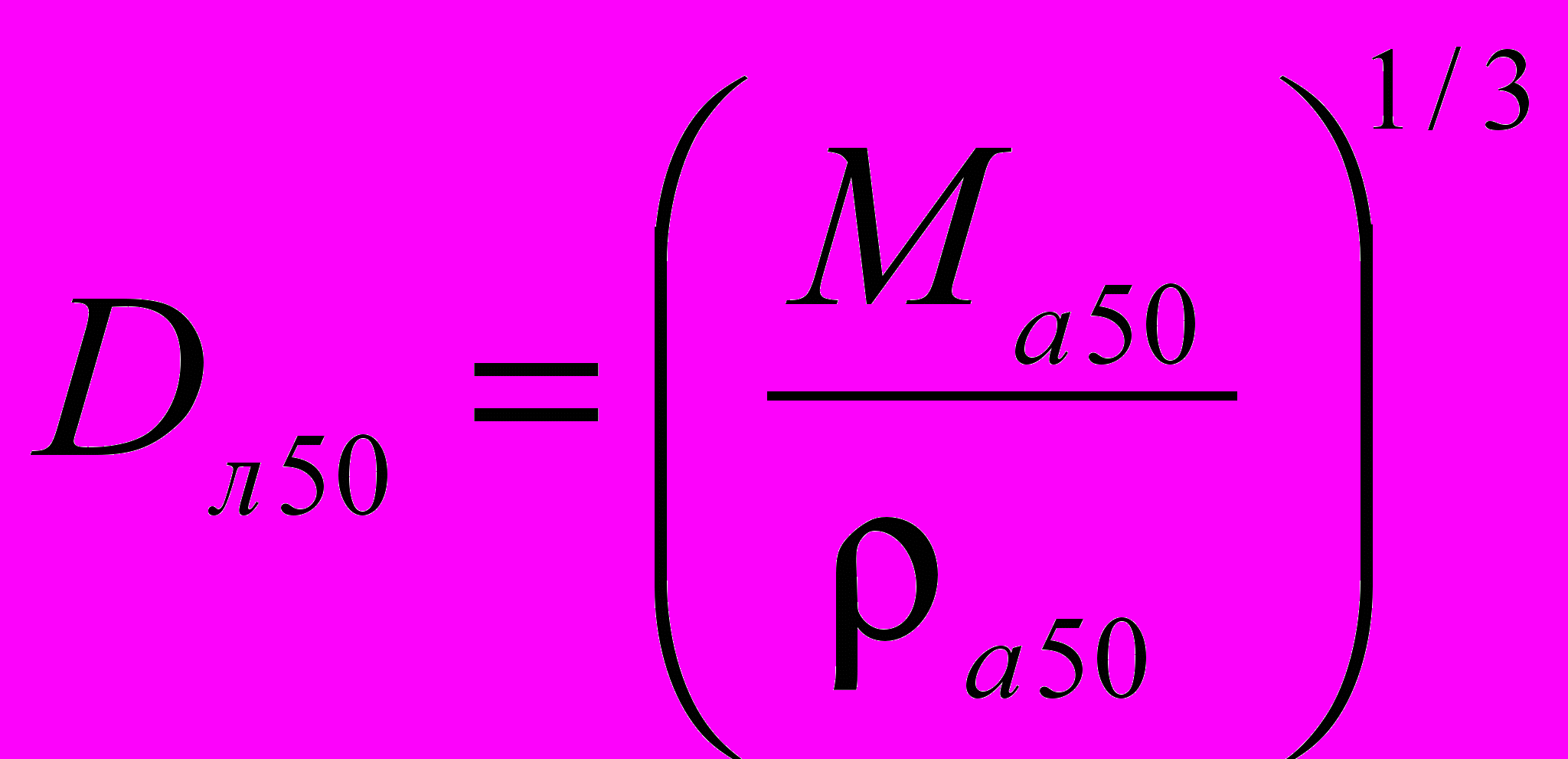. (3.29)де
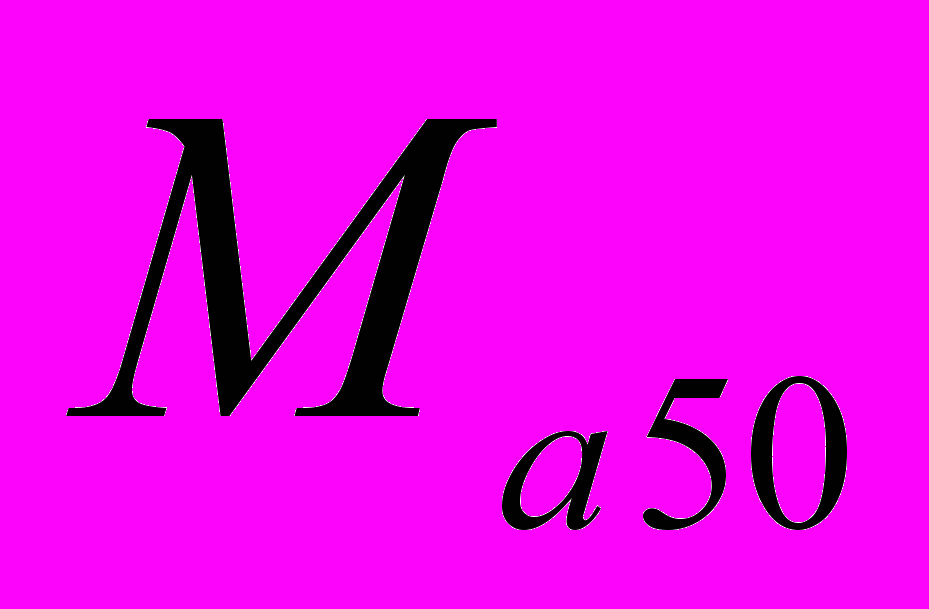– середня маса елемента штучного рифу, 
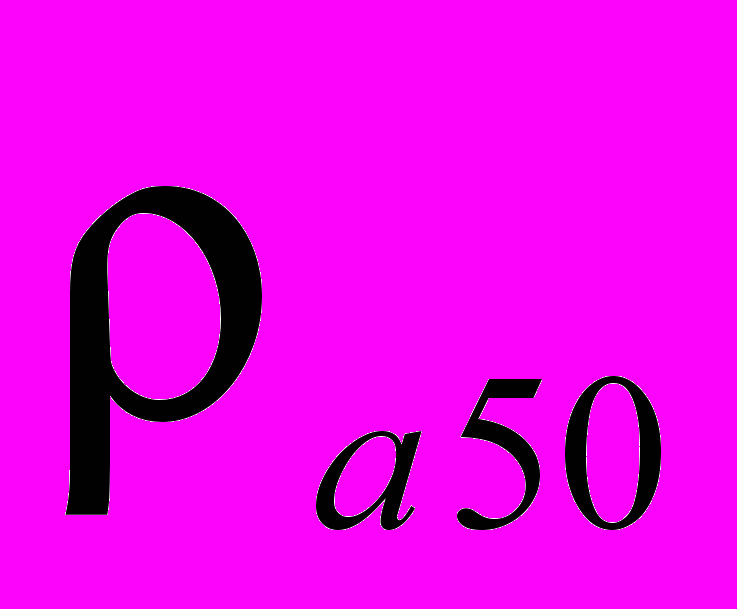– щільність матеріалу штучного рифа.Для випадку, коли F/Н<1, формула для розрахунку хвильового ослаблення штучного рифа має вигляд:
.(3.30)У роботі [37] С. Сібруком отримане вираження для коефіцієнта гасіння хвилі підводного штучного рифу, виконаного з щебеню:
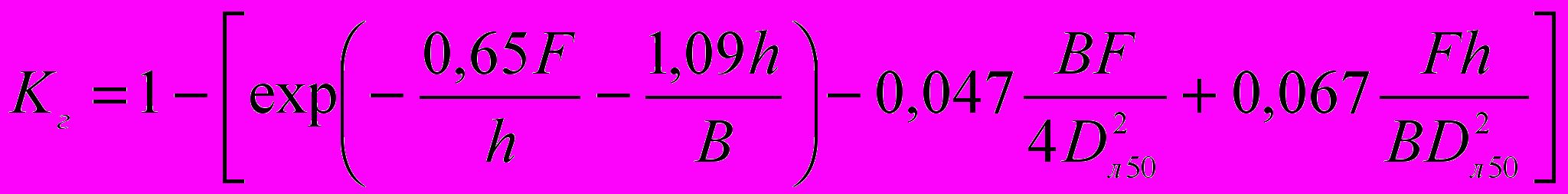.(3.31)Формула (3.31) була отримана при модельних дослідженнях у лотку, де в якості одиниці структурного елемента штучного рифу використовувався щебінь. Разом з тим, при розрахунку хвильового ослаблення формула (3.21) має переваги перед формулою (3.30), тому що враховує більшу кількість геометричних характеристик елемента штучного рифу.
Характерні розміри «Reef Ball» для створення штучних рифів приведені в табл. 3.4 [33].
Таблиця 3.4. Характерні розміри штучного рифа «Reef Ball»
| Тип конструкції | Базова ширина (діаметр), м | Висота рифа, м | Маса рифа, т |
| Goliath-Ball-E | 1,83 | 1,83 | 4,44 |
| Goliath-Ball-D | 1,83 | 1,37 | 2,81 |
| Goliath-Ball-C | 1,83 | 1,37 | 2,27 |
| Goliath-Ball-B | 1,83 | 1,37 | 1,68 |
| Bay Ball – Solid | 1,22 | 0,92 | 1,09 |
Результати розрахунків хвильового ослаблення з використанням формули Сібрука представлені в табл. 3.5 [33].
Таблиця 3.5. Розрахункові значення хвильового ослаблення
| Умови (відхилення від нормалі) | Висота хвилі h, м | Період хвилі T, с | F, м | 4 ряди | 5 рядів | 6 рядів |
| перпендикулярно | 1,22 | 8,0 | -0,305 | 0,27 | 0,25 | 0,24 |
| східніше на 10о | 1,83 | 9,0 | -1,403 | 0,53 | 0,51 | 0,49 |
| східніше на 20о | 1,83 | 9,0 | -1,46 | 0,54 | 0,52 | 0,50 |
| південніше на 10о | 1,22 | 8,0 | -1,47 | 0,67 | 0,66 | 0,65 |
| південніше на 20о | 1,22 | 8,0 | -2,04 | 0,72 | 0,71 | 0,70 |
Під умовою «перпендикулярно» мався на увазі перпендикулярний підхід хвилі до штучного рифа. Для напрямку хвилі, відмінного від перпендикулярного, коефіцієнт хвильового ослаблення змінюється від 0,24 до 0,70.
Нижче наведено приклад розрахунку штучного рифа «Reef Ball” для захисту піщаного пляжу від хвиль висотою 2,6 м і довжиною 31,5 м. Як елементи штучного рифа вибираємо конструкцію «Goliath-Ball-F» (див. табл. 3.4).
Перший ряд рифів розташовуємо на глибині d=2,5 м. Висота одного елемента штучного рифу прийнята Н=1,53 м, ширина В=1,50 м, маса – 4,44 т. При обраному параметрі F=-0,97 м (висота води над верхівкою штучного рифа 0,97 м) і кількісті рядів n=6 коефіцієнт ослаблення хвилі Кг, розрахований за формулою (3.31), складе Кг1=0,43. При цьому висота хвилі за першою лінією складе h1=1,12 м. Після першої лінії штучних рифів розташовується друга лінія на глибині h=1,9 м. При обраному параметрі F=-0,37 м (висота води над верхівкою штучного рифа 0,97 м) та кількість рядів n=6, коефіцієнт ослаблення хвилі Кг, розрахований по (3.31), складе Кг2=0,29. При цьому висота хвилі за другою лінією складе h2=0,33 м, що можна вважати безпечним для піщаного пляжу.