Уроки с измененными способами организации
| Вид материала | Урок |
- Уроки с измененными способами организации, 139.22kb.
- Уроки изучения нового учебного материала (1-й тип), 16.67kb.
- Саморегулируемые организации в сфере кадастровой деятельности, 97.49kb.
- Методическая разработка урока семинара по литературе на тему: «Образ Родины в поэзии, 97.22kb.
- М. А. Карпушкин Уроки Мастерства Конспект, 9487.82kb.
- Ценности отечественной культуры, 255.07kb.
- Уроки вдохновения Система К. С. Станиславского в действии, 5884.36kb.
- Бібліотечні уроки для учнів початкових класів екскурсія «Перші кроки до бібліотеки», 102.2kb.
- Уроки жизни». (анализ рассказа В. Распутина «Уроки французского»), 48.01kb.
- Урок литературы в 7 классе. Тема «Уроки достоинства и человечности в рассказе В. Распутина, 26.64kb.
Муниципальное общеобразовательное учреждение
средняя образовательная школа № 60 г. Липецка
Нестандартные формы и
методы работы на уроке
Выполнила: Учитель математики
Добромыслова Маргарита Анатольевна
Г. Липецк, 2008 г
Содержание
| | Введение……………………………………………………………… | 3 |
| 1. | Понятие необычного в педагогической и методической литературе……………………………………………………………. | 4 |
| 1.1. | Необычный урок по Карлу Роджерсу……………………………… | 4 |
| 1.2. | Что такое современный урок?............................................................. | 5 |
| 2. | Организация нестандартных форм и методов преподавания математики…………………………………………………………… | 6 |
| 2.1. | Виды нестандартных уроков……………………………………….. | 6 |
| 2.1.1 | Уроки с измененными способами организации. …………………. | 8 |
| 2.1.2. | Уроки, опирающиеся на фантазию. ……………………………….. | 9 |
| 2.1.3. | Уроки с игровой состязательной основой. ……………………….. | 10 |
| 2.1.4. | Уроки изобретательства, или защиты ученических проектов. ….. | 13 |
| 2.1.5. | Уроки, предусматривающие трансформацию стандартных способов организации. ……………………………………………… | 13 |
| 2.2. | Сравнительная характеристика традиционного, развивающего и личностно ориентированного обучения на уроках математики….. | 17 |
| 2.3. | Из опыта работы…………………………………………………...… | 19 |
| | Заключение …………………………………………………………. | 21 |
| | Литература…………………………………………………………… | 22 |
| | Приложение 1……………………………………………………….. | 23 |
| | Приложение 2………………………………………………………... | 25 |
Введение.
Смысл обычного в русском языке многозначен: обыденное, общепринятое, обыкновенное, заурядное, рядовое, ординарное. В этих синонимах есть позитивные значения: обычный – это нормальный. Поэтому можно сказать, что обычный урок – это хорошо, как проверенный временем залог нормального познания жизни.
Именно на уроке идет подготовка сознания: либо к обычному существованию на уровне выживания, либо к необычной активной деятельности по преобразованию себя и продвижению к благополучию – как своему, так и всего общества. Все это - обычные уроки нашей повседневной жизни.
Действительно, цель обучения изменилась и, как известно, она состоит не только в накоплении суммы знаний, умений и навыков, а в подготовке школьника как субъекта своей образовательной деятельности. Но задачи урока остаются неизменными многое десятилетия: это все то же воспитание и развитие личности, основным средством решения которых продолжает оставаться познавательная активность.
Во всех нормативных актах об образовании законодательно определено, что ученик – это не только субъект образовательный, но и социальной и общественной жизни, ее самоорганизации и самореализации.
Готовить на уроке субъекта, творчески активную личность можно. Однако, для этого необходимо изменить отношение учителя к смыслу его учебной деятельности и, соответственно, к ученикам. Проще всего сделать это не сразу, последовательно переходя к конкретным формам не совсем обычной деятельности обучения.
С другой стороны, есть традиции, отказ от которых чреват серьезными последствиями. Исследователи выделяют такие особенности российской педагогики конца XIX начала XX вв, которые составляют гордость наших национальных традиций: приоритет духовно-нравственного образования над рациональным, построения школы вокруг семьи и семейных традиций и т.д. Других, обычных, традиционных ценностей было намного больше: доминирование пассивно-репродуктивного восприятия воспитанниками знаний над творческой познавательной деятельностью; ставка на «усреднение» движение к общей цели, на фронтальные формы и методы образования в противовес индивидуализированным и групповым технологиям. Опираясь на обычные ценности, традиционная дидактика предписывает обучать, используя прямые методы передачи знаний. Основные средства – монологические объяснения при помощи рассказов, бесед, лекций. Их смысл – требование воспроизвести сказанное учителем в форме монологического ответа, привести пример на применение полученного знания, использовать информацию для решения учебных задач, выполнения заданий. Не совсем обычным становится введение так называемых «увлекательных добавок»: проблемного обучения, поисковых, исследовательских, эвристических методов обучения. Эти методы можно использовать и как фрагменты в ткани урока и как урок, полностью посвященный реализации одного из методов.
1. Понятие необычного в педагогической и методической литературе.
1.1. Необычный урок по Карлу Роджерсу
К необычному на уроке выдающиеся педагоги относились по- разному. В античной и средневековой педагогике необычное, т.е. выходящие за рамки установленных канонов преподавания, было фактически недопустимым, а учителя, нарушавшие это требование, жестоко наказывались. Были и редкие исключения, только подтверждавшие незыблемость правила: диалогистика Сократа, уроки на природе в «Доме радости» Витторино да Фельтре. Правило же, озвученное Платоном, сводилось к тому, что образование должно образовывать правильные понятия, отсекать все, что мешает осуществлению идеи нравственности и, в первую очередь, ограничить природную чувственность человека.
Первые, как бы «узаконенные» элементы необычного вносит в урок «Великая дидактика» Я.А. Каменского. Прежде всего – это принцип наглядности. введение этого принципа в строгую канву урока произвело революцию в педагогическом сознании и поколебало уверенность в неизменности классических правил.
Одним из первых ученых, обратившихся к переносу традиционных основ обычного обучения, направленного к чувственной сфере и разработавшим основы смыслового (необычного) обучения, был К. Роджерс (1902-1987, США). Он выделил два типа обучения: информационное, обеспечивающее простое знание фактов, и значимое учение, которое дает обучающимся знания, необходимые им для самоизменения и саморазвития. Благодаря такому разделению обозначилась новая сторона обучения - деятельность учения, т.е. особым образом организованная работа ученика. Она представляет собой привычный процесс обучения с непривычной стороны: как организацию взаимодействия между учителем и учениками.
Рассмотрим основные позиции значимого (личностно ориентированного) учения по Роджерсу.
а) Встреча с проблемами
Учение, значимое для учащихся, имеет место обычно в ситуациях, воспринимаемых как проблемные. Поэтому следует разрешить учащемуся на любом уровне соприкасаться с важными проблемами его жизни, спорными вопросами.
б) Конгруэнтность учителя
Конгруэнтность предполагает, что учитель должен быть именно таким, каким он есть на самом деле, открытым в отношениях с учениками. Он живой человек, а не безличное воплощение требований программы.
с) Принятие и понимание
Учитель принимает учащегося таким, каков он есть и способен понять его чувства, способен положительно относиться к нему и эмпатически понимать его чувства страха сопутствующего восприятию нового материала.
- Что такое современный урок?
Говоря словами И. М. Верзилина «Урок - это солнце, вокруг которого, как планеты вращаются все другие формы учебных занятий».
Главное требование к уроку - это достижение цели, усвоение изучаемого материала. Недопустимо ограничивать урок сообщением нового материала и контролем. При таком подходе основная тяжесть работы падает на домашнее задание. Превращение урока в пассивное время препровождение (сиди, слушай) приводят к колоссальной трате времени. Главная задача учителя - активизировать уроки, добиться включения учащихся в работу на всех этапах урока, заставить ученика трудиться, трудом добывать знания, все 45 минут работы. Урок может проходить стихийно по шаблону: - опрос - объяснение - задание на дом. При такой схеме урок может быть удачным или не удачным.
В школе важны все виды учебной работы, но объяснение нового материала занимает особое место. Что может быть проще: прочитал учебник, пересказал его - и объяснение состоялось. При таком подходе процент запоминания равен - 30 - 40%. Сам рассказ и само слушание можно резко активизировать.
Как этого добиться?
Главным, определяющим видом объяснения является - проблемное изложение. В чем суть? В умении включить мыслительный аппарат ребенка в процесс познания, ученик получает от учителя не готовые знания, а добывает их собственными усилиями. При этом учителем выдвигается проблема (вопрос, идея, положение), которую нужно доказать решить и объяснить. Выдвигаются гипотезы, далее идет обоснование предположений, приводятся примеры, проводятся опыты, эксперименты, привлекаются ранее изученные теоремы.
Как учитель математики, я часто использую проблемные ситуации, проблемные задачи при изучении новой темы.
Например: классу дается серия задач, которые дети решают с опорой на уже имеющиеся у них знания, но вдруг встречается задача, при решении которой не хватает знаний. Что же делать?
Вот тут включается познавательная деятельность учащихся, которая сопряжена с догадкой, удивлением, озадачиванием, напряженным размышлением, поиском аргументов и доказательств. Здесь мы видим и мотив, без которого не возможно подлинное развитие интеллекта. Еще К.Д. Ушинский говорил, что «..учение взятое принуждением не будет способствовать развитию мыслительных способностей». Эмоциональное восприятие материала и сознательное его усвоение в ходе собственной деятельности и есть процесс превращения знаний в убеждение.
Я считаю, что сегодня невозможно активизировать учебный процесс без опоры на принцип мотивации учения.
Если цель учителя - заставить ученика выучить стихотворение, формулу, теорему и т.д., то ученик, выполняя требование учителя выучит даже если ему это не интересно. Но может ли ученик самостоятельно «открыть» закон, правило, если он не увлечен, не переживает процесс поиска. Нет, не может, потому что мыслительный процесс всегда внутренне мотивирован.
Чем же отличаются проблемные уроки от непроблемных?
Главное - в структуре урока!
Дидактическим показателем проблемного урока является его «синтетичность», т.е. повторение пройденного материала сливается с введением нового материала, происходит как бы незаметное вхождение учащихся в новую тему.
Как показала практика передовых учителей необязательно тратить время на каждом уроке на проверку домашнего задания. Когда 3-4 ученика отвечают, а остальные слушают невразумительные ответы своих товарищей. Опроса может и не быть, а вместо него может быть решение типовых задач, похожих на домашнее задание, либо фронтальная самостоятельная работа, что бы освежить в памяти знания.
Без объяснения нет обучения. Однако теперь уже стало банальным, что если учитель весь учебный материал объясняет, «разжевывает» и в рот кладет. При этом ни о какой познавательной активности учащихся и речи быть не может.
Это не значит, что учитель ничего не должен объяснять, что ученики все должны сами открывать. Ведь сложные понятия, непосильные для самостоятельного усвоения надо конечно объяснять учащимся.
Закрепление изученного материала - третий элемент урока. Как правило это выполнение многочисленных упражнений, решение ключевых задач. Без таких видов работ не может быть проблемного обучения, т.к. на этом этапе урока развиваются обще учебные умения и навыки, развивается память.
Не обязательно, что бы все уроки были проблемными. Они могут чередоваться с не проблемными в зависимости от содержания излагаемой темы. Главное, что бы на уроках учитель мог правильно определить цель, научно насытить урок, связать обучение с жизнью, активизировать мыслительную деятельность учащихся разными методами, использовать индивидуальный подход к ученику, применять на уроках ТОО, дидактические материалы и наглядность, развивать познавательные интересы и способности, соблюдать требования возрастной и педагогической психологии.
2. Организация нестандартных форм и методов преподавания математики.
2.1. Виды нестандартных уроков.
Сегодня не совсем обычных методов обучения и целых уроков – огромное количество, но далеко не все они соответствуют общепринятым представлениям о нестандартности в образовании, о необычности урока, т.к. учитель, как правило, опирается на свою интуицию, а не на какие – либо научные основания. Это приводит к существенным недостаткам, снижающим педагогическую эффективность учебного процесса:
- стихийность и бессистемность использования (исключения составляют лишь уроки лекционно-семинарской системы, пришедшие из практики высшей школы);
- отсутствие прогноза положительных изменений – роста качества знаний и умений;
- преобладание репродуктивных технологий обучения: обращается внимание преимущественно на форму организации учебного процесса, а не на его содержание;
- перегрузка уроков учебным материалом, особенно это относится к интегрированным урокам, учебным конференциям. Отсутствуют этапы обобщения, преобладает работа с фактическим материалом, не имеющим особого образовательного материала.
Непривычные формы используются немотивированно, как уроки – одиночки, без заметной связи с ранее проведенными уроками. Преобладают итоговые формы: зачеты, семинары, решение кроссвордов. На сегодняшнее время разработана классификация нестандартных уроков.
1. Уроки, отражающие современные общественные тенденции: урок, построенный на инициативе учащихся, урок – общественный смотр знаний, урок – диспут, урок с применением компьютеров.
2. Уроки с использованием игровых ситуаций: урок – ролевая игра, урок – соревнование, урок – КВН, урок – путешествие, урок – аукцион, урок с использованием дидактической игры, урок – «домино», проверочный кроссворд, урок в форме игры «Лото», урок типа «следствие ведут знатоки», урок – деловая игра, урок – «Что? Где? Когда?», урок – эстафета, дуэль, викторина, урок – тест.
3. Уроки творчества: урок изобретательства, урок – осмотр самодеятельной выставки.
4. Традиционные уроки с новыми аспектами: урок – лекция, урок – семинар, урок решения задач, урок – конференция, урок – консультация, урок – зачет, парный опрос, экспресс – опрос, защита оценки, урок – зачет, урок – семинар, урок – общественный смотр знаний. итоговое собеседование. ученическая конференция.
5. Уроки с измененными способами организации: лекция - парадокс, защита знаний. защита идей, урок вдвоем, урок – встреча.
6. Уроки опирающиеся на фантазию: урок – сказка, урок «удивительное рядом», урок фантастического проекта, урок – рассказ об ученых, урок – портрет, урок – сюрприз.
Исследователи так представляют творческие принципы нестандартных уроков.
1. Отказ от шаблона в организации урока, от рутины и формализма в проведении.
2. Максимальное вовлечение учащихся класса в активную деятельность на уроке.
3. Не развлекательность, а занимательность и увлечение как основа эмоционального типа урока.
4. Поддержка альтернативности мнений.
5. Развитие функции общения на уроке, как условия обеспечения взаимопонимания, ощущение эмоционального удовлетворения.
6. «Скрытая» дифференциация учащихся по ученым возможностям, интересам, способностям.
7. Использование оценки в качестве формирующего, а не только результирующего инструмента.
Познакомимся более подробно с не совсем обычными методами обучения и уроками, которые будем рассматривать в соответствии с приведенной выше классификацией, что позволит выбрать любому учителю все новые и новые основания для учебной деятельности.
2.1.1. Уроки с измененными способами организации.
Урок – лекция.
Основные условия организации:
1. Если учебный материал является сложным для самостоятельного изучения.
2. В случае использования укрупненной дидактической единицы.
3. Урок обобщения и систематизации знаний как по одной теме, так и по нескольким, или как заключительные для всего курса.
4. Введение в тему.
5. Уроки, на которых рассматриваются новые методы решения задач.
6. Применение знаний для решения практических задач.
Методика проведения урока – лекции.
При лекционном ведения урока необходимы приемы и формы, позволяющие сделать учащихся активными участниками, поэтому следует предпочитать проблемное изложение материала.
Способы создания проблемной ситуации:
- постановка перед учащимися теоретической проблемы.
- создание проблемы путем изложения теории возникновения какого-нибудь понятия.
- постановка проблемы путем анализа и обобщения освоенных ранее знаний и умений.
- возникновение проблемы в результате исключения путей и способов решения задач.
Варианты организации работы на уроке.
Для каждого учащегося могут быть подготовлены таблицы с канвой изложения материала, с пропусками, которые заполняются в процессе слушания лекции. Такие таблицы готовят в случае систематизации знаний и классификации понятий.
При изучении определенного материала активными методами познания становятся аналогии, сравнения, обобщения.
Учащимся на кануне урока в качестве одного из видов домашнего задания предлагается разделить страницу на две части. В левой части выписать необходимые определения, теоремы, которые будут использоваться на уроке; а правая часть заполняется на уроке под руководством учителя.
В проблемно-развивающем обучении предлагается следующая типология лекции.
1. Проблемная лекция. В ней моделируются противоречия реальной жизни через их представленность в теоретических концепциях. Цель – приобретение знаний учащихся как бы самостоятельно.
2. Лекция – визуализация. Основное содержание лекции представлено в рисунках, графиках, схемах.
3. Лекция вдвоем. Представляет собой работу 2-х учителей (учителя и ученика), читающего лекции по одной и той же теме.
4. Лекция – провокация (или лекция с запланированными ошибками). Формирует умение учащихся оперативно анализировать, ориентироваться в информации и оценивать ее. Так называемый метод живой ситуации.
5. Лекция – диалог. Содержание подается через серию вопросов, на которые ученик должен ответить непосредственно в ходе лекции.
6. Лекция с применением игровых методов (методы мозговой атаки, методы конкретных ситуаций). Школьники сами формируют проблему и сами пытаются ее решить.
Урок – лекция «Парадокс»
Цель – повторение материала, развитие внимания и критического мышления.
1. Учитель читает лекцию, в содержании которой включает ошибочные сведения, противоречивые утверждения, неточности.
2. Учащиеся обсуждают лекцию, выполняют задания – составляют план и находят в материале ответы на поставленные учителем вопросы.
3. Учащиеся фиксируют ошибки, «допущенные» учителем.
4. Делают записи в тетради в виде таблицы
-
план лекции
ошибки
ответы на вопросы
5. Записи проверяет учитель или ученик – лаборант.
6. Обсуждение ошибки и выяснение того, почему утверждение неверно.
Такие лекции практикуются в старших классах. Их продолжительность 23 – 30 минут.
2.1.2. Уроки, опирающиеся на фантазию.
Уроки творчества
Цель – повторение и обобщение по теме на основе развития креативных навыков.
Организация урока.
1. Класс делится на 5 групп.
2. Создается жюри.
3. Каждой группе вручается задание:
- первая и вторая группа составляет кроссворд, зашифровав, строго научно или шутливо, термины по данной теме;
- третья и четвертая группы готовят аукцион игры, в котором ведущий задает играющим по два вопроса;
- пятая группа пишет план-сценарий учебного кинофильма по теме урока (на 3 мин).
4. Время работы группы – 10 мин.
5. Смотр творческих групп, баллы фиксируются и суммируются, объявляются лучшие группы.
Подобные уроки позволяют развить учащимся, творчески применять знания, воспитывать взаимоответственность. Рекомендуются в средних и старших классах.
Урок – творческий отчет
Цель: практическое применение знаний по теме или разделу.
1. Тема и дата урока объявляется заранее (один два месяца).
2. Объявляются варианты творческих заданий по теме: например, разработать проект, произвести лабораторные исследования, написать реферат, взять интервью у специалиста.
3. Работать можно индивидуально или группой, полностью самостоятельно или пользуясь консультациями учителя.
Требования к ответу: дать обоснование выбора вопроса и формы работы, изложить суть и объяснить полученные результаты, показать их практическое применение.
Подобные уроки позволяют формировать исследовательские навыки учащихся.
2.1.3. Уроки с игровой состязательной основой.
«Значительная часть игр ребенка рассчитана на то, чтобы осветить и возбуждать в уме процессы воспроизведения, чтобы неугасимо поддерживать искры мысли».
И.А. Сикорский.
«Надо прогнать с уроков бога сна Морфея и чаще приглашать бога смеха Момуса»
Ш.А. Амонашвили.
К игровым формам урока относят ролевые, имитационные, деловые игры.
Игровые формы отличаются тем, что процесс обучения максимально приближен к практической деятельности. Решения во многих принимают коллективно, что развивает мышление учащихся, коммуникативные способности. В процессе игры возникает определенный эмоциональный настрой, активизирующий учебный процесс.
Учебная игра применяется для развития умений использовать полученные знания на практике. Большинство учителей, методистов игру называют дидактической. Анализ психолого-педагогической литературы по этому вопросу, наблюдение за игровыми действиями. Позволяет выделить следующие виды игр.
- Игры – упражнения.
Они занимают 10-15 минут и направлены на совершенствование познавательных способностей учащихся, являются хорошим стимулом для развития познавательных упражнений, осмысления и закрепления учебного материала, применение его в новых ситуациях. Это – разнообразные викторины, кроссворды, ребусы, чайнворды, шарады, головоломки, объяснения пословиц и поговорок, загадки.
-Игры – путешествия
-Сложно (ролевая) игра
-Игра – соревнование. Существенная особенность – наличие соревновательной борьбы и сотрудничества.
Требования к проведению дидактических игр.
- игра - форма деятельности учащихся, в которой осознается окружающий мир, открывающая простор для личной активности и творчества.
- Игра должна быть построена на интересе;
- Обязателен элемент соревновательности
Игра – активнейшая форма человеческой деятельности. Редко встретишь ребенка, не участвующего в определенный момент в какой-либо игре. Такая система учебных игр позволяет обучаться с интересом. Эта модель обучения, по сравнению с традиционной, более перспективна.
Уроки по игровой методике существенно повышают интерес к предмету, позволяет лучше запоминать формулировки, определения, «раскрепощают» ученика, его мышление.
Урок – «Домино».
Почти все ученики ленятся запоминать формулы. Запомнить же их необходимо.
Одной формуле может быть поставлено в соответствие до 10 верных формулировок или наоборот: одной формуле соответствует несколько формул 10-120 минут.
Урок – проверочный кроссворд.
Как проверить усвоение понятий, формулировок, определений у всех учеников так, чтобы и школьникам было интересно и время было затрачено немного?
Для этого может быть использован особый кроссворд. Ученики получают карточку, размером 2.5х3.5 см, вырезанную из листа в «клеточку» и имеющую 5-7 строк. Они пронумерованы по горизонтали, как в обычном кроссворде, а внизу написаны вопросы. Если работа сделана верно, то в последней колонке читается «проверено» (для учителя) слово.
Урок в форме игры «ЛОТО».
Ученикам даются карточки с заданиями, дифференцированные по сложности работы; карточки имеют порядковые номера. Предлагается на листках подготовить ответы в течении 10 или 15 минут на эти задания. Затем начинается игра в лото: в произвольном порядке из конверта учитель достает небольшие картонные квадратики с номерами и объявляет громко «вынутый» номер; ученик имеющий карточку – задание с таким номером дает ответ. Если ответ полный и верный, то «номерок» отдается его «хозяину» и тот прикрепляет его скрепкой к своей карточке.
Урок – соревнование
Цель – закрепление умений решать задачи по теме.
- Формирование команд.
- Определение жюри.
- Разминка (решение командами качественных задач).
- Конкурс капитанов (решение экспериментальных задач).
- Конкурс команд на время решить задачи.
- Подведение итогов.
Урок – турнир
Цель – повторение пройденного.
Соревнуются два параллельных класса. Время проведения 2 часа.
Ученики каждого класса объединяются в группы консультантов, эрудитов, аналитиков.
Задачи групп:
- «консультанты» - занимаются с отстающими
- «эрудиты» - готовят сообщения.
- «аналитики» - решают усложненные задачи, подготовленные учителем.
Пред уроком столы ставят рядами так, чтобы классы сидели напротив друг друга.
Ход урока.
- Объявление темы и цели.
- представители жюри (представители от класса, учителя, родителей).
- Фронтальный опрос. Ученики класса отвечают по очереди. Жюри оценивают ответы.
- В это время «аналитики» решаю на досках задачи, затем обсуждение решений классом.
- Проверка знаний формул по теме в виде мини диктанта.
- Заслушивание подготовленных «эрудитами» сообщений.
- Решение творческих задач и индивидуальная работа по карточкам. Класс при этом делится на две группы.
- Подведение итогов.
«Клуб знатоков».
Форма игровая, доставляющая ученикам радость. На шестерки делится весь класс, игровые столы расставляются по кругу, а в центре – главный стол. На нем – конверты с вопросами и волчок. Команда, начинающая за главным столом первой, определяется по желанию или по жребию, но она уступит место другой, если та даст ответ раньше, до истечения минуты.
Команды занимают места, запускается волчок, конверт вскрывается, вопрос можно читать, или процитировать с помощью проектора на экран. Переворачиваем песочные часы (за ними следит «хранитель времени»).
Капитан поднимает руку – есть ответ! Учителю сообщает ответ шепотом или пишет на листочке. Получают баллы те столы, которые дали правильный ответ.
Если одна из «боковых» команд три раза ответила правильно, то она занимает место главной – в центре, если главная команда тоже озвучила версию, идее постоянная смена лидера.
Чтобы игра вызвала интерес, вопросы должны носить развивающий, творческий характер, называться в необычной, занимательной форме.
2.1.4. Уроки изобретательства, или защиты ученических проектов.
Команды класса получают одно общее задание: разработать фантастический проект, основанный на известных из пройденной темы знаний.
Ученики начинают готовить схемы, чертежи, делают расчеты для защиты проекта. Один из учащихся команды на уроке будет защищать этот проект, другие слушают, находят слабые стороны, задают команде вопросы. Особенность данных уроков в том, что они развивают фантазию, приучают коллективно работать, критически мыслить, оценивать факты, не принимая все на веру, учат применять знания в новых ситуациях.
Урок «Охота за пятерками».
Цель: закрепление умения решать разнообразные типы задач.
После того, как учащимся показан алгоритм, решаются типовых задач по теме, начинается отработка этих знаний.
- Классу предлагается для самостоятельного решения серия похожих задач: на доске написаны их номера.
- Каждый начинает работу в своей тетради, тот, кто без учителя решил задание, молча выходит к доске и пишет решения, учитель молча подает знак и автор получает «5» или «4»; если на «3», то оценка не выставляется.
В течении урока накапливается несколько оценок, в конце ставится итоговая.
Урок – игра «Крестики – нолики».
Игра может быть проведена как итоговый урок по теме.
На доске вывешивается таблица 3 х 3. В каждой из 9-ти ячеек записано название конкурса. Хорошо дать конкурсам оригинальные, можно шутливые названия, которые заранее красочно оформляются.
Обычно команда «Крестики» первой выбирает любой из девяти предложенных конкурсов. В дальнейшем право хода принадлежит победителю. В каждом конкурсе участвуют обе команды.
2.1.5. Уроки, предусматривающие трансформацию стандартных способов
организации.
Урок – общественный смотр знаний.
Цель – выявить качество и прочность знаний по основным разделам изученного материала и учение использования их на практике.
- На первом занятии по теме школьники получают задания и вопросы.
- Редколлегия класса выпускает стенную газету по теме урока.
- Класс делится на две команды, выбирается капитан. Команды получают задания (подготовить приветствия, эмблемы, составить кроссворды для соперников, подготовить вопросы к турниру знатоков.
- Определение жюри, приглашение гостей.
Ход урока.
- Письменно-практическая работа по карточкам. Время работы – 10 минут.
- Сдача работ на проверку членам жюри.
- Миниэкзамен: школьники по очереди берут билеты, готовятся 5 минут и отвечают (6 человек отвечают письменно). Часть учеников опрашиваются устно у доски.
- Жюри подводят итого первой части смотра.
- Турнир знатоков:
- приветствие команд.
- конкурс эрудитов (ответы на вопросы)
- конкурс кроссвордов
- подведение итогов, поощрение победителей.
Урок – семинар.
Наиболее полно использовать и развивать интеллектуальные особенности старшеклассников позволяет семинарские занятия. Их цель состоят в том, чтобы делать теоретические обобщения изучение материала, выделить основные положения, показать связь внутри темы и между темами, с жизнью, с практикой, с учетом возрастных особенностей учащихся провести систематизацию знаний.
Семинары – важная форма выработки у школьников самостоятельности, активности, умения работать с литературой, творчески мыслить и действовать.
Семинары отличаются от уроков.
- Большей степенью самостоятельности при подготовке к семинару, большой активностью учащихся, владением навыков работы с литературой.
- Изменением организации этапов обучения, например, домашнее задание носит опережающий характер, а его проверка совпадает с изучением нового материала.
- Изменение функций, выполняемых учителем, а учащимся, учащиеся выполняют информационную функцию, а учитель – регулирующую и организационную.
Основные функции семинара: систематизация знаний, улучшение знаний, закрепление умений и навыков, контроль за знаниями, развитие умений и навыков как коллективной, так и индивидуальной исследовательской и поисковой работы; развитие коммуникативности учащихся.
Классификация семинаров:
- семинар – развернутое собеседование
- семинар – обсуждение докладов и рефератов
- семинар – диспут
- семинар – с преобладанием самостоятельной работы учащихся
Он начинается со вступительного слова учителя, который знакомит класс с темой, учебными задачами, стереотипами их решения и с дополнительными сведениями. Далее учащимся или их группам предлагается на выбор несколько различных по уровню сложности заданий. Работа длится около двадцати минут, в ходе ее школьники могут обращаться за помощью к учителю. Завершается семинар коллективным обсуждением результатов деятельности групп и выполнением упражнений.
В течении месяца в одном классе может проводится не более 2-х семинаров. В дни семинарских занятий не рекомендуется проводить письменные и устные контрольные работы, зачеты, обобщающие уроки по другим дисциплинам.
Урок-семинар в игровой форме.
Практика все же показывает, что проведение урока-семинара сразу «по взрослому» варианту, приведет к его неприятию учениками, особенно в старших классах. Причина такова: ученики не обладают нужным объемом информации, опытом культурного общения, чтобы можно было свободно обсуждать изучаемую проблему. Но семинар в игровой форме они принимают. Пожалуй, лучшей его формой является игра «Что? Где? Когда?».
Урок – консультация.
Цель – оказание помощи учащимся в овладении знаний и совершенствование практических навыков.
Урок – консультация может проводиться один раз в неделю.
- План урока представлен в виде таблицы.
Время урока
(по минутам)
Деятельность
учителя
Деятельность
ученика
- В каждой графе отражено, какой отрезок времени урока и чем конкретно занимается группа.
- Во второй и третьих графах записывается вид, тема и содержание работы. Задания могут предлагаться учащимся дифференцированно.
- Каждая группа выполняет предложенные задания. Отстаивает теоретический материал, совершенствует практические навыки, проводит эксперименты, работает с дополнительной литературой.
Итоговое собеседование.
В практике некоторых учителей используются итоговые (зачетные) собеседования, в процессе которых учитель отвечает на вопросы, позволяющие уточнить и обобщить приобретенные знания, выявить уровень усвоения ведущих понятий и идей темы.
В этом плане собеседование напоминает то, что в высшей школе называется коллоквиум. Однако, контролирующая функция собеседования не является главной. Основное значение такого занятия – систематизировать и обобщить материал крупной темы или целого раздела. Уточнить знания по основным вопросам, закрепить их.
Как правило, на собеседовании целесообразно ставить крупные вопросы, требующие развернутого изложения. Разумнее раздробить содержание на большое количество вопросов, которые ставятся в логической последовательности и требуют кратких вопросов.
В этом случае в беседу вовлекаются практически все учащиеся.
Собеседование является одной из эффективных форм, позволяющих подвести итоги изученной темы.
При проведении собеседования в 8-9 классах по сравнению с 10 – 11 классами требуется более заметная помощь учителя в корректировке ответов учащихся.
Тематическая предметная неделя нетрадиционных уроков.
В современной школе особое значение приобретают формы учебно-воспитательной работы предметной направленности, когда материал, изучаемый на уроках находит свое логическое завершение во внеурочной деятельности, то есть формы работы, соединяющие в себе обучение и воспитание в единый процесс: уроки творчества, мозговая атака, университет старшеклассников, встречи с увлечением, дидактически сказки, путешествие в предмет, аукцион знаний, дидактический театр, путешествие в страну неразгаданных тайн, предметный ринг, интеллектуальные марафоны, КВН по предмету, общественный смотр знаний, творческие мастерские, мастерские подарков.
Тематические предметные недели включают различные формы работы: коллективную, групповую, индивидуальную. Рассмотрим методику ее проведения.
- Подготовительный этап.
- Подготовка плана проведение тематической недели.
- Подготовка и проведение внеклассного мероприятия в каждом классе.
- Выпуск стенгазет.
- Конкурс рефератов.
- Торжественное открытие тематической недели
- Ознакомление с планом мероприятий.
- «Круглый стол» на тему «Математика и современность».
- Книжная выставка. Конкурс знатоков математических кроссвордов.
Тематика устных журналов: В мире математики. Наука - человеку. Математика в жизни.
Тематика конкурса сочинений и творческих работ: Как моя жизнь связана с математикой? Путешествие в предмет. История моей семьи.
Турниры: рыцарей знатоков математики; математический аукцион.
Клуб интересных встреч: математики древности, математика и поэзия.
Тематический праздник «И зачем нам эта математика нужна?»
При проведении тематических праздников могут быть использованы стихи, песни, подготовленные учащимися по мини группам; кроссворды, ребусы, театрализованные факты из жизни ученых, противоборство положительных и отрицательных героев.
Во время тематической недели возможно проведение следующих типов уроков: уроки – исследования, уроки – конференции, уроки – бенефисы, уроки – открытых мыслей, уроки – «посвящение в математику».
2.2. Сравнительная характеристика традиционного, развивающего и личностно ориентированного обучения на уроках математики.
В последнее время любое изменение содержания, технологии организации образования связывают с необходимостью осуществления личностно ориентированного обучения. Рассмотрим его характеристики в сравнении с традиционной и развивающей системой обучения.
Рассмотрим этап актуализации знаний.
При традиционном обучении этап актуализации знаний часто превращается в опрос учащихся. Актуализации подвергаются формулировки определений, теорем.
Например, перед изучением смежных углов
1 вариант: повторяется определение угла, называются углы, изображенные на рисунке.
2 вариант: учащимся предлагается начертить две дополнительные полупрямые, дать название углу, узнать величину этого угла, сформулировать аксиому измерения углов.
Как видим, основное внимание при традиционном обучении уделяется математической информации. При развивающем обучении ключевым понятием является познавательная деятельность учащихся. Ключевым понятием личностно ориентированного обучения является субъективный опыт учащихся. Так при изучении смежных углов возможны вопросы: 1) что уже знаем об углах, 2) что учились делать с углами. При этом учитель старается предоставить учащимся проявить инициативу. Например, на доске изображен рисунок.
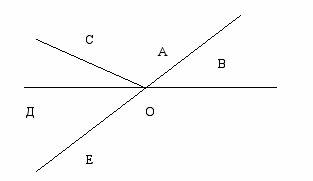
Какие геометрические вопросы вы могли бы задать, глядя на этот рисунок?
Рассмотрим этап изучения нового материала при личностно ориентированном обучении.
Пример введения определения смежных углов на основе практической работы учащихся.
- Наше знакомство с углами продолжается. Мы уже познакомились с определением угла, измерением и построением углов. Но об углах можно узнать много нового для нас.
- Выполним в тетрадях работу, в результате которой построим новые для нас углы.
- Проведите прямую а. Отметьте на ней точки А, О, В так, что бы точка О принадлежала отрезку АВ. Проведите полупрямую ОК. Появились углы, перечислите их.
- Рассмотрим угол АОК и ВОК. Назовите их вершину и стороны. Какими особенностями они обладают?
- Такие углы назвали смежными. Как вы думаете, почему? («смежные комнаты», «межа»). Далее учащиеся пытаются дать определение смежных углов.
- Итак, подведем итог. Мы узнали определение смежных углов, теперь повторим способ их построения.
- Можно ли иначе построить смежные углы?
- Далее решается вопрос об измерении смежных углов.
В том фрагменте урока нет ни групповой работы, ни дифференцированного или проблемного обучения, ни самостоятельной работы, а обучение является все равно личностно ориентированным, т.к. оно строилось на основе субъективного опыта учащихся.
Сравнительная таблица
характеристик традиционного, развивающего и личностно
ориентированного обучения.
| Характеристика | Система обучения | ||
| Традиционное обучение | Развивающее обучение | Личностно ориентированное обучение | |
| Позиции учащихся | Объект обучения | Субъект обучения | Субъект обучения и собственного развития |
| Ключевое понятие | Предметная информация | Познавательная деятельность | Субъективный опыт |
| Основной образовательный источник | Учитель | Учебный предмет | Учебный предмет и процесс его освоения |
| Основная задача учителя | Передача предметной информации | Активизация познавательной деятельности | Организация деятельности учащихся над содержанием учебного предмета с целью обогащения их субъективного опыта |
| Результат, который может быть обеспечен | Личность, которая умеет работать с информацией | Личность, которая умеет познавать | Личность, которая умеет «познавать, делать, жить вместе» |
2.3. Из опыта работы
Я, как учитель математики, применяю нестандартные методы и формы работы на своих уроках. Цель математического образования – сформулировать у учеников навыки действий с числами, умение решать задачи, сравнивать, обобщать, развивать логическое мышление, и уметь применять эти знания на практике. На уроках, начиная с пятого класса, я учу детей устно считать, т.к. считаю, что умение устно считать в уме развивает память, быстроту решения задачи. Устный счет провожу в виде игры «Эстафета», либо с использованием наглядных карточек, специальных схем. Кстати таких схем предостаточно и в самом учебнике математики 5,6 классов. Также использую соревнование трех команд. Задания: выбери верный ответ, кто быстрее и правильнее выполнит из команд.
Особое внимание уделяю на уроках 5-го и 6-х классов – оценке полученного результата. Ведь решив задание, в ответе получаем ответ, который действительности не соответствует. Например: скорость 5 м/с, высота здания 10 км. Все время обращаю внимание детей на величины при решении задач. Ученики порой не знают в чем измеряется вес, длина, площадь, начинают путать эти величины.
А ведь навыки определения величины, которые они начинают получать уже с начальной школы на уроках математики, помогут усваивать ученикам такие предметы как физику, химию, географию. Особое внимание уделяю задачам практического содержания. Например: вычислить, сколько плитки потребуется, чтобы облицевать ванную комнату с заданными размерами (задачу решить двумя способами) и т.д.
В курсе 6-го класса выделяю задачи на проценты, на повышение и понижение цены товара. Таких задач много в тетрадях с печатными основами, в дидактических материалах.
На последних уроках темы, когда учащиеся получили основные знания по изучаемой теме, знают все необходимые правила, я разбиваю класс на группы «сильных», «средних», слабых». Выбираю для них серию заданий, с учетом их умственных способностей; даю возможность детям самостоятельно домыслить, применить полученные знания.
На этих уроках я выступаю в роли консультанта. Ребятам эти уроки очень нравятся, ведь они учатся на них друг у друга, учатся общаться, объяснять, пояснять, сами и сообща находят ответ к задаче. И еще в своей работе использую прием, разработанный в 60-е годы Липецкими учителями – комментированное решение задач. Его суть состоит в том, что весь класс выполняет одно и тоже упражнение в одном и том же темпе. Это достигается таким образом: учащиеся, сидя за партой, поочередно вслух комментируют, обосновывают упражнение.
В целях привития через игру интереса к предмету, активизации мыслительной деятельности, закрепление и обобщения первоначальных сведений о десятичных дробях в 5-ом классе, я проводила урок в форме полета на планету Юпитер.
Задания во время «полета» предлагались не только на закрепление правил сложения и вычитания десятичных дробей, но и поискового характера. Например определите, сколько минут мы будем находится на планете (определить закономерность изменения чисел).
В конце путешествия проводилась письменная разноуровневая работа по вариантам. Задания: последовательно соединяя отрезки, расположите дроби в порядке возрастания. В результате проделанной работы – получают фигуры – собачки – 1и 3 варианты, а 2 и 4 самолеты.
На уроках геометрии знакомлю учащихся с таким правилом: для решения задач следует рассматривать не все элементы чертежа, а только те, куда искомые и данные задачи входят наиболее полно. В процессе нахождения решения целесообразно стремится к тому, чтобы постепенно «стягивать» данные и искомые задачи применительно к одним и тем же элементам чертежа.
Заключение
Итак, мы рассмотрели нестандартные методы и формы работы на различных этапах урока. Опыт моей работы и моих коллег показал, что использование нестандартных форм обучения дает наибольший эффект в тех классах, где преобладают ученики с неустойчивым вниманием, пониженным интересом к предмету, для которых математика кажется скучной и сухой наукой.
Использование необычных форм работы повышает интерес к математике вносит разнообразие в учебную работу, снимает утомление, при это ученики испытываю познавательную радость и удовольствие от своих успехов. Что еще важно в условиях постиндустриального общества, что ученики во время нестандартных уроков учатся быстро и самостоятельно принимать решения.
Также можно сказать, что необходимость использования нестандартных форм обучения связано с осуществлением личностно ориентированного обучения. Возникает вопрос: как, нам учителям относиться к накопленному научно - педагогическому потенциалу, касающемуся традиционного обучения и надо ли нам отказываться в дальнейшей работе?
Сравнение результатов, которые могут быть обеспечены различными системами обучения, приводит к следующему выводу: все то ценное, что касается обучения учащихся работе с информацией, с активизацией их познавательной деятельности, должно быть взято на вооружение, при осуществлении нестандартных методов и форм работы на уроке.
Литература.
- Букатов В.М. Этапы урока: режиссура школьной повседневности в невыдуманных рассказах, неожиданных советах и нескучных рекомендациях (Вячеслав Букатов, Мария Ганькина) – М.: Чистые пруды, 2006.-32с. (Библиотека «Первого сентября». Вып.2).
- Кульневич С.В., Лакоценина Т.П. Не совсем обычный урок: Практическое пособие. – Воронеж, 2006. – 175с.
- Кульневич С.В., Лакоценина Т.П. Совсем необычный урок: Практическое пособие. – Воронеж, 2006. – 159с.
- Малова И.Е., Руденкова Н.М. Как «увидеть» на уроке математики личностно ориентированное обучение?/ Малова И.Е., Руденкова Н.М.// Математика в школе. 2007. -№4.- с.6-11.
- Николаева Л.Е., Лесных Л.И. Использование нетрадиционных форм занятий. Специалист. 1992., №2, с. 5-6.
- Чередов И.М. Формы учебной работы в средней школе: Кн. Для учителя. – М.: Просвещение, 1988. – 160с.
- Якиманская И.С. Технология личностно ориентированного образования. –М.: сентябрь, 200. (Библиотека журнала «Директор школы». Выпуск 37, 2000 г.) – 145с.
- Яновицкая Е.В., Адамский М.М. Большая дидактика и 1000 мелочей в разноуровневом обучении. – СПб.: Агенство образовательного сотрудничества, 2005. -96с.
